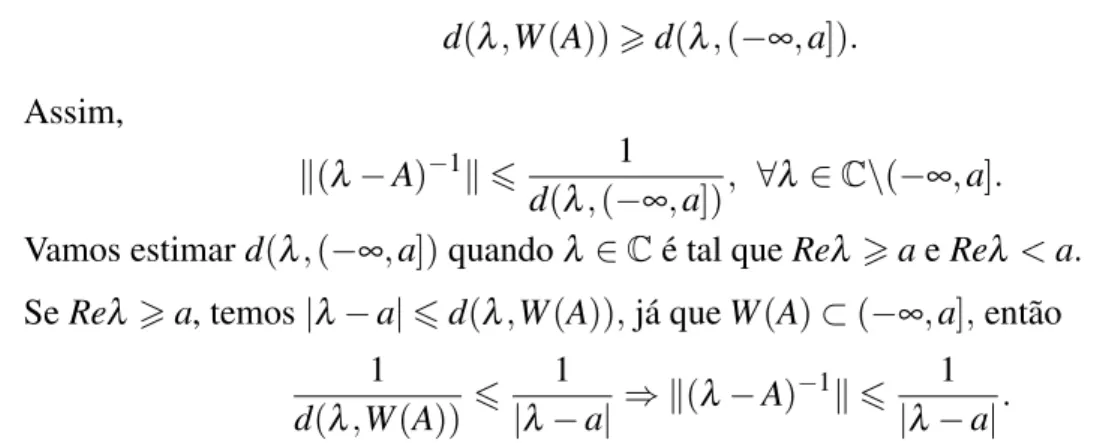Existência de variedade invariante e atrator para a equação ut = uxx + f(u).

(1)

CENTRO DE CI ÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE P ÓS-GRADUAÇ ÃO EM MATEM ÁTICA

Existˆencia de Variedade Invariante e Atrator para

a equac¸˜ao

u

_t

=

u

_xx

+

f

(

u

)

RICARDO DES ´ATELES

(2)

(3)

CENTRO DE CI ÊNCIAS EXATAS E DE TECNOLOGIA PROGRAMA DE P ÓS-GRADUAÇ ÃO EM MATEM ÁTICA

Existˆencia de Variedade Invariante e Atrator para

a equac¸˜ao

u

_t

=

u

_xx

+

f

(

u

)

RICARDO DES ´A TELES

Orientadora: Profa. Dra. Vera L´ucia Carbone

Dissertação apresentada ao Programa de Pós-Graduação em Matemática da UFSCar, como parte dos requisitos para a obtenção do t´ıtulo de “Mestre em Matemática” .

(4)

Ficha catalográfica elaborada pelo DePT da Biblioteca Comunitária da UFSCar

T269ev

Teles, Ricardo de Sá.

Existência de variedade invariante e atrator para a

equação ut = uxx + f (u) / Ricardo de Sá Teles. -- São Carlos :

UFSCar, 2007. 81 f.

Dissertação (Mestrado) -- Universidade Federal de São Carlos, 2007.

1. Análise matemática. 2. Variedade invariante. 3. Atrator global. 4. Semigrupos. I. Título.

(5)

~

-Prata. Dra.~VeraLúciã Carbone

DM

-

UFSCar

II:'-J,~

'71~il0vlt

1-/(

Prata. Dra. Cláudia Buttarello Gentile

DM - UFSCar

(6)

(7)

A Deus pela presenc¸a constante em minha vida. `

A profa. Dra. Vera Lúcia Carbone, pela orientação competente, pelo comprometimento e paciência demonstrados ao longo de todo o trabalho. A todos os professores e funcionários do DM-UFSCar, que direta ou indiretamente participaram da minha formação profissional.

Aos amigos da pós-graduação.

Aos amigos Toninho Gomes e S´ılvia Grandi pela amizade sincera desde a época da graduação. Ao grande amigo Wesley Góis.

Aos meus pais (Sr. Nivaldo e Dona Cidalia) e irm˜aos (Nilza, Neusa e Renato) pelo apoio incondicional e pela fam´ılia que formamos.

(8)

(9)

Neste trabalho, estudamos a equac¸˜ao diferencial

ut=uxx+f(u), 06x61, t >0

com condições de fronteira de Dirichlet homogênea e f _∈C1(R_,R₎ _{globalmente lipschitz e} limitada, satisfazendo as seguintes condições:

(i)lim sup_|_u_|→_∞f(u)u−160 (ii)f(0) =0.

(10)

(11)

In this work we study the differential equation

ut=uxx+f(u), 06x61, t >0

with homogeneous Dirichlet boundary conditions and f _∈C1(R_,R₎_{lipschitz and bounded} glob-ally and satisfying the following conditions:

(i)lim sup_|_u_|→_∞f(u)u−160 (ii)f(0) =0.

(12)

(13)

Introduc¸˜ao 1

1 Preliminares 3

1.1 Teoria Geral de An´alise Funcional . . . 3

1.2 Os espac¸os de Hilbert . . . 11

1.3 Espac¸os de Sobolev . . . 14

2 Teoria Geral de Semigrupos 19 2.1 Propriedades dos Semigrupos . . . 19

2.2 Teoremas de Hille-Yosida e Lumer Phillips . . . 27

2.3 Condições sob as quais um operador gera um semigrupo fortemente cont´ınuo . 38 2.4 Existência de Solução . . . 42

3 Existência de Variedade Invariante e Atrator para a equaçãout=uxx+f(u) 45 3.1 Teorema da Variedade Invariante . . . 46

3.2 Um sistema de equac¸˜oes paraut=uxx+f(u) . . . 63

3.3 Atratores para semigrupo de operadores . . . 69

3.3.1 Existência de solução e atrator . . . 75

(14)

(15)

Este trabalho versa sobre o problema de valor inicial e de fronteira



 

 

ut =uxx+f(u), 06x61, t >0 u(0,t) =u(1,t) =0

u(x,0) =φ(x)

(1)

onde f _∈C1(R_,R_),φ _∈_H1

0([0,1])satisfaz as seguintes condic¸˜oes:

(H1): fé globalmente Lipschitz, com constante de lipschitzLf e globalmente limitada, com constante de limitaçãoNf;

(H2): lim sup_|_u_|→_∞f(u)u−160; (H3): f(0) =0.

Atualmente tem sido estudado o comportamento das soluções da fam´ılia de equações parabólicas



  

  

uε_t ₋div(p_ε(x)∇uε) +λuε= f(uε) emΩ p_ε(x)∂u

ε

∂~n =g(u

ε₎ _em_Γ

uε(0) =uε₀,

quandoε _→0,λ >0, f,g_∈C2(R_),Γ₌∂Ω_{onde a difusibilidade}_p_ε₍_x₎_{´e assumida grande em} um subconjuntoΩ0⊂Ω⊂Rn, mais precisamente

p_ε(x)_→

½

p0(x), uniformemente sobreΩ1,(p0∈C1(Ω¯1,(0,∞)));

∞, uniformemente sobre subconjuntos compactos deΩ0.

quando ε _→0. Os autores em [9] mostram que esse problema possui uma fam´ılia de atra-toresA_ε_,ε _∈_[0,ε₀_{], que ´e semicont´ınua superiormente e em [10] a semicontinuidade inferior ´e}

provada.

Nosso objetivo nesse trabalho é mostrar a existência de dois conjuntos importantes para a equação (1): variedade invariante: S _{e atrator:} A_{, onde}A _⊂S_.

Sendo o operadorAu=₋uxx comD(A) =H1₀(0,1)∩H2(0,1), através de suas autofunções decompomos o espaçoX =L2(0,1)e considerando as restrições do operadorAaos subespaços

(16)

2 Introduc¸˜ao

que decompõem X podemos escrever (1) como um sistema de equações fracamente acoplado para o qual provamos a existência de uma variedade invariante S.

Com as hip´oteses(H1)₋(H3)obtemos um C0-semigrupo sobre H10(0,1)para (1) e

prova-mos a existˆencia de atrator.

Este trabalho est´a organizado da seguinte forma:

Cap´ıtulo 1: apresentamos resultados da teoria geral de An´alise Funcional que ser˜ao utiliza-dos no decorrer do trabalho.

Cap´ıtulo 2: reunimos resultados de semigrupos, caracterizamos os operadores que geram semigrupos anal´ıticos e estudamos existência e regularidade de soluções .

(17)

Preliminares

Neste cap´ıtulo apresentamos resultados da teoria geral de An´alise Funcional que ser˜ao utiliza-dos no decorrer do trabalho.

1.1 Teoria Geral de An´alise Funcional

SejaV um espac¸o vetorial. Denotamos o dual topol´ogico deV porV′,onde

V′=_{f :V _→K;f ´e forma linear e cont´ınua_},

sendoKo corpoR_ouC_{. Em}_V′_{definimos a norma dual}

kf_k_V′ = sup

kxkV61

|f(x)_|.

Definição 1.1. Uma aplicação p :V _→ R _{é uma semi-norma se satisfaz as seguintes}

pro-priedades

p(αx) =_|α_|p(x), _∀α _∈C_, _x_∈_V

p(x+y)6p(x) +p(y), _∀x,y_∈V.

Definição 1.2. Uma função p:V _→R_{é sublinear se}

p(x+y)6p(x) +p(y)

p(αx) =αp(x), _∀α >0.

O próximo lema é um dos Teoremas de Hahn-Banach, cuja demonstração pode ser encon-trada em [1], Teorema I.1, p.1.

(18)

4 1.1 Teoria Geral de An´alise Funcional

Lema 1.3. (Forma anal´ıtica real do Teorema de Hahn-Banach) Seja V um espac¸o vetorial real

e p:V _→R_{uma aplicação sublinear. Se g}₀_:_V₀_→R_{é uma forma linear definida no subespaço}

vetorial V0⊂V tal que g0(y)6p(y),para todo y∈V0, ent˜ao existe uma forma linear g:V →R

tal que

(i) g(y) =g0(y), ∀y∈V0

(ii) g(y)6p(y), _∀y_∈V.

♦

Proposição 1.4. Seja V um espaço vetorial normado e V0⊂V subespaço. Se g é um funcional

linear e cont´ınuo em V0de norma

kg_k_V₀′= sup

x∈V0

kxk61

|g(x)_|,

ent˜ao existe um funcional linear cont´ınuo f em V que estende g e tal que_kf_k_V′ =kgk_V₀′.

Demonstrac¸˜ao: Tomemos

p:V _→R

x_7→p(x) =_kg_k_V₀′kxk

Parax,y_∈V eα _∈C_{, temos}

p(αx) =_kg_k_V₀′kαxk=|α|kgk_V₀′kxk=|α|p(x),

p(x+y) =_kg_k_V₀′kx+yk6kgk_V₀′(kxk+kyk) = p(x) +p(y),

isto é, pé uma seminorma. Além disso,

|g(x)_|6_kg_k_V₀′kxk=p(x).

Segue do Lema 1.3 que existe f :V _→R_{, tal que}

f(x) =g(x), _∀x_∈V0

(19)

Como

|f(x)_|6p(x) =_kg_k_V₀′kxk ⇒ kfkV′6kgk_V₀′

e

kg_k= sup

x∈V0

kxk61

|g(x)_|6 sup

x∈V0

kxk61

|f(x)_|6 sup

x∈V

kxk61

|f(x)_|=_kf_kV,

obtemos

kf_kV′=kgk_V₀′.

Proposição 1.5. Seja V um espaço vetorial normado. Então para todo x0∈V existe um

fun-cional linear cont´ınuo f tal que_kf_kV′=kx0ke f(x0) =kx0k2.

Demonstração: Seja o subespaçoV0=x0R. Consideremos

g:V07→R

tx07→g(tx0) =tkx0k2.

g é um funcional linear cont´ınuo. Então pela Proposição 1.4 existe um funcional linear e cont´ınuo f emV que estendege tal que_kf_k_V′ =kgk_V₀′.

Como

|g(tx0)|=|tkx0k2|=|t|kx0k2=kx0k|t|kx0k ⇒ kgkV0′=kx0k.

Portanto_kf_kV′ =kx0k.

Como f(x) =g(x)para todox_∈V0=x0R, em particular parax=x0, temos

f(x0) =g(x0) =kx0k2.

Definição 1.6. Seja X espaço topológico, f :X _→R_{é dita semicont´ınua inferiormente em X se}

f−1((₋∞,a]) =_{x_∈X : f(x)6a_} ´e fechado em X para cada a_∈R_.

(20)

f−1([a,+∞)) =_{x_∈X : f(x)>a_} ´e fechado em X, para cada a_∈R_.

Definição 1.7. Um espaço topológico X é um espaço de Baire se dada uma coleção enumerável

{An}∞n=1de conjuntos fechados de X tal que cada um deles tem interior vazio em X, ent˜ao

∞

[

n=1

An

tamb´em tem interior vazio em X.

A demonstração do próximo resultado pode ser encontrada em [1], Lema II.1, p.15.

Lema 1.8. (Teorema de Baire) Todo espaço métrico completo é de Baire.

♦

O Teorema de Baire pode ser enunciado da seguinte forma:

SejamX ₆= /0 um espaço métrico completo,_{Xn}n>1fechados tais queX =S∞n=1Xn. Então existen0tal que

◦

Xn06= /0. ♦

Teorema 1.9. (Osgood) Seja X espaço de Baire e _{f_α_}_α_∈A uma fam´ılia de funções semi-cont´ınua inferiormente com a propriedade que para cada x _∈ X existe Mx tal que sup

α∈A

f_α(x) 6 Mx. Ent˜ao existe um aberto O 6= /0 e uma constante M satisfazendo

sup

α∈A x∈O

f_α(x)6M.

Demonstrac¸˜ao: Para cadan>1, seja

Un={x∈X,fα(x)6n,∀α ∈A}=

\

α∈A

{x_∈X,f_α(x)6n_}.

Ent˜aoUn ´e fechado, poisUn=

\

α∈A

f_α−1((₋∞,n])onde f_α ´e semicont´ınua inferiormente.

Al´em disso, X =

∞

[

n=1

Un. De fato, sex∈X ent˜ao existe Mx tal que sup

α∈A

f_α(x)6Mx, logo

f_α(x)6Mxpara todoα ∈A; portantox∈Unparan>Mx. Consequentementex∈

∞

[

n=1

Un.

Assim,X =

∞

[

n=1

UnondeX ´e espac¸o de Baire, existen0>1 tal que

(21)

Seja O =U◦n0⊂Un0 e M = n0 ent˜ao O ´e aberto e fα(x) 6n0 = M, para todox∈ O e

para todoα_∈A. Portanto

sup

x∈O α∈A

f_α(x)6M.

SejamX eY espac¸os de Banach sobre um corpoK.Identificamos

L₍_X_,_Y_{) =}_{_T _:_X _→_Y_;_T_{é uma aplicação linear e cont´ınua}_}_.

ParaT _∈L₍_X_,_Y₎_definimos

kT_kL₍_X_,_Y₎=sup

x∈X x6=0

kT x_kY

kx_kX

= sup

kxkX61

kT x_kY = inf

x_∈X{L,kT xkY 6LkxkX}.

Em particular, seX =Y escrevemosL₍_X₎_{ao inv´es de}L₍_X_,_X_).

Usaremos a seguinte notac¸˜ao<x∗,x>=x∗(x),parax∗_∈X′ex_∈X.

Corolário 1.10. (Princ´ıpio da Limitação Uniforme) Sejam (X,_{k · k}) espaço de Banach, (Y,_|·|)um espaço normado e_{T_α_}_α_∈Auma fam´ılia de elementos deL(X,Y)tal que para todo x_∈X,existe Mxsatisfazendosup

α∈A|

T_α(x)_|6Mx. Ent˜ao existe M tal quesup

α∈Ak

T_α_k6M.

Demonstração: Seja f_α(x) =_|T_α(x)_|, f é cont´ınua poisT_α é cont´ınua. Além disso, como X é um espaço de Banach segue do Lema 1.8 que X é espaço de Baire e, para cadax_∈X, existeMx tal que

sup

α∈A

f_α(x) =sup

α∈A|

T_α(x)_|6Mx.

Segue do Teorema 1.9 que existem aberto O₆= /0 e portanto B(x0,r)⊂O⊂X, x0 ∈X e

constanteM1tal que

sup

α∈A x∈B(x0,r)

|T_α(x)_|6M1.

Notemos que paraz_∈X,_kz_k61 se, e somente se,(x0+r1z)∈B(x0,r1), r1<r.

Portanto, para todoα _∈A, temos

kT_α_k= sup kzk61|

T_α(z)_|= sup kzk61|

T_α(x0+r1z−x0 r1

)_|6 sup kzk61

1 r1|

T_α(x0+r1z)|+

1 r1|

T_α(x0)|

6 1

r1

(22)

Logo,_kT_α_k6M, ondeM= _r1

1(M1+Mx0),para todoα ∈A.

Conseq¨uentemente, sup

α∈Ak

T_α_k6M.

SejamX espac¸o de Banach,X′o dual deX com a norma

kf_k= sup

x∈X

kxk61

|< f,x>_|

eX′′ o bidual deX, isto ´e, o dual deX′com a norma

kξkX′′= sup

f∈X′

kfk61

|<ξ,f >_|.

Consideremos uma injeção canônicaJ:X _→X′′ definida, para cadax_∈X, por: J(x):X′_→R

f _7→< f,x> .

J assim definida uma isometria linear, pois,

kJ(x)_kX′′= sup kfkX′61

|<J(x),f >_|= sup kfkX′61

|< f,x>_|=_kx_kX,

a linearidade ´e imediata.

Definição 1.11. Dizemos que X é reflexivo se J(X) =X′′, isto é, J é sobrejetor.

EmX′temos duas topologias, a saber:

(i) (X′,_{k · k})topologia forte dada pela norma

kf_k= sup

x∈X

kxk61

|< f,x>_|.

(ii) (X′,σ(X′,X′′))topologia fraca que ´e a menos fina que deixa todosξ _∈X′′ cont´ınuos. Vamos definir em X′ uma outra topologia que ser´a menos fina (menos abertos) do que a topologia fraca.

Para cadax_∈X, considere

ϕx:X′7→R

f _7→ϕx(f) =< f,x> .

(23)

Definição 1.12. A topologia fraca* é a menor topologia em X′ que deixa cont´ınua todas as

aplicac¸˜oes_{ϕx}x_∈X.Vamos denotar esta topologia porσ(X′,X).

Se dimX <∞ou X ´e reflexivo ´e poss´ıvel mostrar queσ(X′,X) =σ(X′,X′′).E claro que´

σ(X′,X)_⊂σ(X′,X′′)_⊂σ(X′,_{k · k}).

A topologia fraca* tem as seguintes propriedades:

(i) A topologia σ(X′,X) é de Hausdorff, ou seja, quaisquer dois elementos distintos desse espaço podem ser separador por vizinhanças disjuntas.

(ii) Uma base de vizinhanc¸as de f0∈X′na topologiaσ(X′,X)´e dada por

V =_{f _∈X′,_|< f₋f0,xi>|<ε, ∀i∈I},

ondeI ´e finito,xi∈X eε>0.

A convergˆencia fn→ f emσ(X′,X)ser´a indicada por fn⇀∗ f.

O próximo teorema é a razão da existência da topologia fraca*, cuja demonstração pode ser encontrada em [1], Teorema III.15, p.42.

Teorema 1.13. (Teorema de Banach - Alaoglu - Bourbaki) Seja X espac¸o de Banach, ent˜ao a

bola fechada

B_X′={f ∈X′:kfk61}

´e compacta na topologia fraca*.

♦

Vejamos agora os operadores adjuntos.

SejaA:D₍_A₎_⊂_X _→_Y _{linear. Queremos encontrar}_A∗_:D₍_A∗₎_⊂_Y′_→_X′_{tal que}

<v,Au>=<A∗v,u>, _∀v_∈D₍_A∗₎_e_u_∈D₍_A_).

Dadov_∈Y′, consideremos a aplicac¸˜ao g:D₍_A₎_→R

(24)

Claramenteg ´e linear. Segfor cont´ınua, existec>0 tal que_kg(u)_k6c_ku_k, _∀u_∈D₍_A_).

Pela Proposição 1.4,gpode ser estendida a uma aplicação linear f :X _→R_{tal que}_|_f₍_u₎_|6

c_ku_k, _∀u_∈X.

SeD₍_A₎_{for denso então existe única} _f_{. Seja} _f _{tal extensão então podemos definir}_A∗_v₌ _f_.

Com isso,

D₍_A∗_{) =}_{_v_∈_Y′_:_u_∈D₍_A₎_7→_<_v_,_Au_> _{´e cont´ınua}_}

eA∗v= f ´e tal que

<g,u>=<v,Au>=<A∗v,u>=< f,u>,

ondeu_∈D₍_A₎_e_v_∈D₍_A∗_).

O operadorA∗:D₍_A∗₎_⊂_Y′_→_X′_{´e chamado adjunto de}_A_.

Definição 1.14. Dizemos que S:D₍_S₎_⊂_X _→_{X é simétrico se} D₍_S_{) =}_{X e S}_⊂_S∗_,_{ou seja,}

<x∗,Sx>=<Sx∗,x>,_∀x_∈D₍_S₎_{(isto ´e,} D₍_S₎_⊂D₍_S∗₎_{e S}₌_S∗_emD₍_S_))._{Dizemos que S ´e}

auto-adjunto se S=S∗.

Proposição 1.15. Seja A:D₍_A₎_⊂_X_→_{Y . Se}D₍_A_{) =}_{X então A}∗ _{é fechado.}

Demonstrac¸˜ao: Temos queA∗:D₍_A∗₎_⊂_Y′_→_X′_eG₍_A∗₎_⊂_Y′_×_X′_.

Sejavn∈D(A∗)tal quevn→vemY′eA∗vn→ f emX′.Queremos mostrar quev∈D(A∗) eA∗v= f.

Comovn∈D(A∗), temos

<vn,Au>=<A∗vn,u>, u_∈D₍_A_).

Logo,

<v,Au>= lim

n→∞<vn,Au>=nlim→∞<A

∗_v_n,_u_>=< _f_,_u_>, _∀_u_∈_D₍_A_).

Sendo f cont´ınua, a aplicaçãou_7→<v,Au>é cont´ınua e portantov_∈D₍_A∗_).

Como<v,Au>=<A∗v,u>, segue que f =A∗v.

PortantoG₍_A∗₎_{é fechado e conseqüentemente}_A∗ _{é fechado.}

(25)

Teorema 1.16. (Gráfico Fechado) Sejam X e Y espaços de Banach. Se T :X_→Y é um operador linear. Se o gráfico de T ,G₍_T₎_{, é fechado em X}_×_{Y então T é cont´ınuo.}

♦

Proposição 1.17. Seja Y _⊂X um subespaço vetorial tal que Y ₆=X . Então existe f _∈X′, f ₆=0 tal que f(x) =0, _∀x_∈Y .

♦

1.2 Os espac¸os de Hilbert

Definição 1.18. Um espaço de Hilbert é um espaço vetorial H dotado de produto escalar_h·,_·i e que é completo relativamente a norma_ku_k_H=p

hu,u_i.

Exemplo 1.19. O espac¸o L2(Ω)dotado do produto interno

hu,v_i=

Z

Ωu(x)v(x)dx

´e um espac¸o de Hilbert.

Observação 1. Os espaços de Hilbert gozam de uma propriedade importante todos são

refle-xivos.

Definição 1.20. Seja H espaço de Hilbert. Uma base Hilbertiana ou conjunto ortonormal

completo é uma seqüência_{en}de elementos de H tais que

(i) _kenk=1, ∀n; <em,en>=0, ∀m,n,m6=n.

(ii) O espac¸o vetorial gerado pelos_{en}´e denso em H.

Observação 2. Em [1] encontramos a demonstração do seguinte fato: se _{en} é uma base Hilbertiana para H então todo u_∈H se escreve da forma

u=

∞

∑

n=1

<u,en>en com kuk2=

∞

∑

n=1

|<u,en>|2.

(26)

12 1.2 Os espac¸os de Hilbert

Teorema 1.21. Sejam H espaço de Hilbert separável, isto é, existe D_⊂X enumerável e denso, e T:D₍_T₎_⊂_H_→_{H um operador compacto e auto-adjunto. Então H admite uma base}

Hilber-tiana formada por autovetores de T .

O próximo resultado diz sob quais condições um operador é auto-adjunto.

Proposição 1.22. Sejam H espaço de Hilbert, A:D₍_A₎_⊂_H_→_{H densamente definido, simétrico}

e sobrejetor ent˜ao A ´e auto-adjunto.

Demonstração: Como A :D₍_A₎_⊂ _H _→ _H _{é simétrico temos} D₍_A₎_⊂ D₍_A∗₎ _{e para} _x_∈ D₍_A_), _Ax₌_A∗_x_.

Para concluirmos queA=A∗basta mostrarmos queD₍_A∗₎_⊂D₍_A_).

Sejay_∈D₍_A∗₎_e_z₌_A∗_y_{. Como}_R₍_A_{) =}_H_existe_u_∈D₍_A₎_{tal que}_z₌_Au_.

Para todox_∈D₍_A₎_{temos que}

<Ax,y>=<x,A∗y>=<x,z>=<x,Au>=<x,A∗u>=<Ax,u> .

Ent˜ao

<Ax,y₋u>=0, _∀x_∈D₍_A_).

Como D₍_A_{) =}_H_{, segue da Proposic¸˜ao 1.17 que} _y₋_u₌ ₀_⇒_y ₌_u_∈ D₍_A_). _Portanto, D₍_A∗₎_⊂D₍_A_).

Conseq¨uentemente,A=A∗, ou seja,A ´e auto-adjunto.

Demonstraremos agora o importante Teorema de Lax-Milgram, que é utilizado, em geral, para garantir existência de solução fraca.

Definição 1.23. Sejam H um espaço de Hilbert e a:H_×H _→R_{uma forma bilinear:}

(i) a ´e cont´ınua se existe constante c>0tal que

|a(u,v)_|6c_ku_kkv_k, _∀u,v_∈H.

(ii) a ´e coerciva se existe constanteα >0tal que

(27)

A demonstrac¸˜ao do Teorema de Stampacchia pode ser encontrado em [1], Teorema V.6, p.83.

Teorema 1.24. (Stampacchia) Sejam a:H_×H _→R_{uma forma bilinear cont´ınua e coerciva e}

K_⊂H convexo fechado e n˜ao vazio. Dadoϕ_∈H′, existe um ´unico u_∈K tal que:

a(u,v₋u)>ϕ₍v₋u), _∀v_∈K. (1.1)

Além disso, se a é simétrica então u se caracteriza por







u_∈K

1

2a(u,u)−ϕ(u) =min_v_∈_K

½

1

2a(v,v)−ϕ(v)

¾

♦

Corol´ario 1.25. (Lax-Milgram) Sejam H um espac¸o de Hilbert e a(u,v) uma forma

bilinear, cont´ınua e coerciva. Ent˜ao para todoϕ_∈H′existe um ´unico u_∈H tal que

a(u,v) =ϕ(v), _∀v_∈H.

Além disso, se a é simétrica, u se caracteriza por







u_∈H

1

2a(u,u)−ϕ(u) =min_v_∈_H

½

1

2a(v,v)−ϕ(v)

¾

Demonstrac¸˜ao: Pelo Teorema 1.24,_∃!u_∈H tal que

a(u,v₋u)>ϕ₍v₋u), _∀v_∈H.

Como para todov_∈H,v+u_∈H, segue que

a(u,v+u₋u)>ϕ(v+u₋u)_⇒a(u,v)>ϕ(v), _∀v_∈H.

Parat_∈R_e_v_∈_H_temos_tv_∈_H _e

ϕ(tv)₋a(u,tv)60_⇒t[ϕ(v)₋a(u,v)]60 _∀v_∈H, _∀t _∈R

(28)

14 1.3 Espac¸os de Sobolev

1.3 Espac¸os de Sobolev

ConsideremosΩ_⊂R_{um aberto dotado da medida de Lebegue}_dx_.

Definição 1.26. Cc(Ω)é o espaço das funções cont´ınuas com suporte compacto, ou seja,

Cc(Ω) =_{f :Ω_→R_: _{f é cont´ınua e f}₍_x_{) =}_0,_∀_x_∈Ω_\_K_,_{onde K}_⊂Ω_{é compacto}_}_. Definição 1.27. Seja p_∈R_,₁6p<∞. Definimos o seguinte espaço vetorial normado

Lp(Ω) =

½

f :Ω_→R_: _{f ´e mensur´avel e}

Z

Ω|f(x)|

p

dx<∞

¾

com a norma dada por:

kf_k_Lp =

µZ

Ω|f(x)|

p dx

¶1/p

.

Definic¸˜ao 1.28. Se p=∞define-se

L∞(Ω) ={f :Ω_→R_: _{f ´e mensur´avel e}_∃_{constante c tal que}_|_f₍_x₎_|6c, q.t.p1em Ω_}. Em L∞(Ω)consideramos a norma:

kf_k_L∞ =inf{c:|f(x)|6c, q.t.p emΩ}. Observação 3. Se f _∈L∞, então_|f(x)_|6_kf_k_L∞, q.t.p emΩ.

Observação 4. E poss´ıvel mostrar que L´ p, 1< p<∞ é separável, reflexivo e o dual de Lp é Lp′, isto é,(Lp)′=Lp′.

A desigualdade a seguir é de extrema utilidade em muitas demonstrações.

Teorema 1.29. (Desigualdade de H¨older) Seja f _∈Lpe g_∈Lqcom16p,q6∞e 1_p+1_q =1. Ent˜ao f g_∈L1e

Z

|f g_|6_kf_kLpkgk_Lq.

♦

A demonstração da Desigualdade de Hölder para p=1 ou p =∞ é imediata. Quando 1<p<∞utilizamos a desigualdade de Young:

ab6 1

pa p₊ 1

p′b p′

paraa>0,b>0.Para mais detalhes veja em [1], Teorema IV.6, p.56.

(29)

Definição 1.30. Sejam I= (a,b) e p _∈R _com ₁ 6 p 6∞. Definimos o espaço de Sobolev W1,p(I)como sendo

W1,p(I) =

½

u_∈Lp(I):_∃g_∈Lp(I)tal que

Z

I

uϕ′=₋

Z

I

gϕ, _∀ϕ_∈C_c1(I)

¾

.

Definic¸˜ao 1.31. H1(I) =W1,2(I).

Observação 5. As funçõesϕsão chamadas de funções testes.

Seja u_∈Lp(I)diremos que g_∈Lp(I)´e a derivada generalizada de u se

Z

I

uϕ′=₋

Z

I

gϕ, _∀ϕ_∈C1_c(I)

Notac¸˜ao: u′=g.

Colocamos ent˜ao

W1,p(I) =©

u_∈Lp(I); u′_∈Lp(I)ª

,

onde u′ ´e a derivada generalizada de u.

Exemplo 1.32. Seja I= (₋1,1). A func¸˜ao

u(x) = 1

2(|x|+x) =

½

0, ₋1<x<0 x, 06x<1 pertence a W1,p(I), para todo16 p6∞e

u′(x) =H(x) =

½

0, ₋1<x<0 1, 0<x<1 pois, para todaϕ_∈C_c1(I)temos:

Z 1

−1

u(x)ϕ′(x)dx=

Z 1

0

xϕ′(x)dx=₋

Z 1

0 ϕ(

x)dx=₋

Z 1

−1

H(x)ϕ(x)dx.

H é chamada função de Heaviside. Notemos que H_6∈W1,p(I).

Observação 6. O espaço W1,pestá dotado da seguinte norma

ku_k_W1,p=kuk_Lp+

° °u′

° °

Lp

ou equivalentemente,

ku_k_W1,p = (kuk

p Lp+

° °u′

° °

(30)

16 1.3 Espac¸os de Sobolev

Observação 7. O espaço H1=W1,2está dotado do seguinte produto escalar

hu,v_i_H1=hu,vi_L2+

u′,v′®_L2

e a norma associada ´e

ku_k_H1 = (kuk2_L2+kuk2_L2)1/2.

Definição 1.33. Dado um inteiro m> 2 e um real 16 p 6∞, definimos por recorrência o espaço

Wm,p(I) =©

u_∈Wm−1,p(I); u′_∈Wm−1,p(I)ª

.

Coloque

Hm=Wm,2(I).

Em particular H2(I) =©

u_∈H1; u′_∈H1ª.

Definic¸˜ao 1.34. Dado16p<∞denotamos por W₀1,p(I)o fecho de C_c1(I)em W1,p(I)e ainda

H₀1(I) =W₀1,2(I).

Teorema 1.35. (Derivada do Produto) Sejam u,v_∈W1,p(I)com16 p6∞, ent˜ao:

uv_∈W1,p(I) e (uv)′=u′v+uv′.

Portanto, temos também a regra de integração por partes

Z x

y

u′v=u(x)v(x)₋u(y)v(y)₋

Z x

y

uv′,_∀x,y_∈I¯.

Teorema 1.36. (Desigualdade de Poincar´e) Seja I limitado e16p<∞. Ent˜ao existe constante c, dependendo de_|I_|, tal que

ku_k_W1,p 6cku′kLp.

∀u_∈W₀1,p(I). Em outras palavras,_ku_k_W1,p eku′kLp s˜ao equivalentes em W1,p

0 (I).

Demonstrac¸˜ao: SejaI= (a,b). Consideremosu_∈W₀1,p(I). Comou_∈C1

c(I)⊂W1,p(I)segue do Teorema 1.29 segue que

|u(x)_|=_|u(x)₋u(a)_|=

¯ ¯ ¯ ¯

Z x

a

u′(t)dt

¯ ¯ ¯ ¯

6

Z x

a |

u′(t)_|dt 6

Z b

a |

(31)

Temos

ku_kLp=

µZ b

a |

u(x)_|pdx

¶1_p

6

µZ b

a k

u′_k_Lpp(b−a) p p′

¶1_p

=_ku′_kLp(b−a)

1

p′₍_b₋_a₎

1

p ₌_k_u′_k

Lp(b−a).

Como_ku_k_W1,p =kukLp+ku′k_Lp 6(b−a)ku′k_Lp+ku′k_Lp, sec=1+ (b−a)ent˜ao

ku_k_W1,p 6cku′kLp.

A demonstrac¸˜ao do teorema a seguir pode ser encontrada em [1], Teorema IX.16, p.169.

Teorema 1.37. (Rellich-Kondrachov) SejaΩlimitado de classe C1(Ω_∈Rn_).

(i) Se p<n ent˜ao W1,p(Ω)_⊂Lq(Ω), _∀q_∈[1,p∗), onde _p1_∗ = 1_p₋1_n;

(ii) Se p=n ent˜ao W1,p(Ω)_⊂Lq(Ω), _∀q_∈[1,∞);

(iii) Se p>n ent˜ao W1,p(Ω)_⊂C(Ω);

com injec¸˜oes compactas.

(32)

(33)

Teoria Geral de Semigrupos

O objetivo principal deste cap´ıtulo é encontrar condições sob as quais um operador gera um semigrupo fortemente cont´ınuo. As referências para este assunto são [2] e [11].

2.1 Propriedades dos Semigrupos

Definição 2.1. Um semigrupo de operadores lineares em X é uma fam´ılia _{T(t) :t >0_{} ⊂}

L₍_X₎_{tal que}

(i) T(0) =IX,

(ii) T(t+s) =T(t)T(s), _∀s,t >_0.

Se adicionalmente,

(iii) _kT(t)₋IXkL₍_X₎→0quando t →0+ ent˜ao dizemos que o semigrupo ´e uniformemente

cont´ınuo.

(iv) _kT(t)x₋x_kX →0quando t →0+,∀x∈X , ent˜ao o semigrupo ´e fortemente cont´ınuo ou um C0-semigrupo.

Se os operadores estão definidos para t,s_∈R _{e as condições}₍_i₎_e ₍_ii₎_{se verificam então}

{T(t):t_∈R_} _{´e um grupo. Al´em disso, se} _k_T₍_t₎_x₋_x_k_X _→₀_{quando t}_→₀_{, para todo x}_∈_X

ent˜ao esse grupo ´e dito um C0-grupo.

Definic¸˜ao 2.2. Seja∆=_{z:φ1<argz<φ2,φ1<0<φ2}e, para z∈∆, seja T(z)um operador

linear limitado. A fam´ılia_{T(z):z_∈∆_} ´e um semigrupo anal´ıtico sobre∆se

(34)

20 2.1 Propriedades dos Semigrupos

(i) z_7→T(z)´e anal´ıtica em∆.

(ii) T(0) =I elim

z→0T(z)x=x para cada x∈X .

(iii) T(z1+z2) =T(z1)T(z2), ∀z1,z2∈∆.

Observação 8. Todo semigrupo uniformemente cont´ınuo é fortemente cont´ınuo.

Definição 2.3. Se _{T(t),t >0_{} ⊂}L₍_X₎ _{é um semigrupo fortemente cont´ınuo, seu gerador}

infinitesimal ´e o operador definido por A:D₍_A₎_⊂_X _→_X

Ax= lim t→0+

T(t)x₋x

t , ondeD(A) =

½

x_∈X, lim t→0+

T(t)x₋x t existe

¾

.

Exemplo 2.4. T(t) =eAt=∑∞_n₌₀A_nn_!tn,t>0para algum A_∈L₍_X₎_{´e um semigrupo fortemente}

cont´ınuo, cujo gerador infinitesimal ´e A,D₍_A_{) =}_{X , pois para x}_∈_{X , temos:}

lim t→0+

T(t)x₋x

t =t→lim0+

1 t(e

At

x₋x) = lim t→0+

1 t

·µ ∞

∑

n=0

Antn n!

¶

x₋x

¸

= lim t→0+

1 t · x+ µ ∞

∑

n=1

Antn n!

¶

x₋x

¸

= lim t→0+

1 t

· ∞

∑

n=1

Antn n!

¸

x

= lim t→0+

µ ∞

∑

n=1

Antn−1 n!

¶

x= lim t→0+

µ

Ax+

µ ∞

∑

n=2

Antn−1 n!

¶

x

¶

=Ax+ lim t→0+

µ ∞

∑

n=2

Antn−1 n!

¶

x=Ax,

a última igualdade é obtida usando o fato que a série converge uniformemente.

Portanto, A ´e o gerador infinitesimal de T(t).

Os semigrupos uniformemente cont´ınuos s˜ao da forma eAt para algumA_∈L₍_X_{), ´e o que}

afirma o seguinte resultado:

Teorema 2.5. S˜ao equivalentes:

(i) _{T(t):t>0_{} ⊂}L₍_X₎_{´e um semigrupo uniformemente cont´ınuo sobre X .}

(ii) Seu gerador infinitesimal est´a definido em todo X .

(35)

Demonstrac¸˜ao: (iii)_⇒(ii)SeT(t) =eAtpara algumA_∈L₍_X_{), mostramos no Exemplo 2.4}

que o gerador infinitesimal ´eAe portanto est´a definido em todoX.

(ii)_⇒(i)SejaAo gerador infinitesimal de_{T(t):t>0_}, ondeAest´a definido sobre todo X. Ent˜ao dadox_∈X, temos que

Ax= lim t_→0+

T(t)x₋x t .

Assim,

lim t→0+

° ° ° °

T(t)x₋x t

° ° ° °

=_kAx_k.

Dadoε>0, existeδ >0 tal que

−ε+_kAx_k<

° ° ° °

T(t)x₋x t

° ° ° °

<_kAx_k+ε

parat_∈[0,δ]. Ou seja,

½° ° ° °

T(t)x−x t ° ° ° ° ¾

06t6δ

´e limitado para cadax_∈X. Segue do Corol´ario 1.10 que

½° ° ° °

T(t)−I t ° ° ° ° ¾

06t6δ

´e limitado. Sejak>0 tal que

° ° ° °

T(t)−I t

° ° ° °

6kpara 06t6δ. Ent˜ao

kT(t)₋I_k6tk_→0,comt_→0+.

Portanto,T(t)_→I, com t_→0+ e assimT(t) ´e uniformemente cont´ınuo sobreX.

(i)_⇒(iii)Assumimos inicialmente que T(t) =eAt e encontramos a express˜ao pra definir A_∈L₍_X₎

A= (T(t)₋I)

µZ t

0

T(s)ds

¶−1

e ent˜ao provamos queA_∈L₍_X₎_{e que}_T₍_t_{) =}_eAt_,_t >0.

Os semigrupos fortemente cont´ınuos possuem uma limitação exponencial que é dada no teorema a seguir.

Teorema 2.6. Suponha que_{T(t),t>0_{} ⊂}L₍_X₎_{´e um semigrupo fortemente cont´ınuo. Ent˜ao}

existem M>1eβ _∈R_{tais que}

kT(t)_kL(X)6Meβt, ∀t>0.

(36)

Demonstrac¸˜ao: Inicialmente observamos que sup t∈[0,η]k

T(t)_kL(X)<∞para algumη>0 pois,

caso contrário, existiria uma sequência_{tn}∞_n₌₁→0+ tal quekT(tn)kL(X)→∞. ComoT(t) é

fortemente cont´ınuo lim t_n_→0+

T(tn)x=x, para cadax_∈X, logo_{T(tn)x_}n>1 ´e limitada para cada

x_∈X. Segue do Corol´ario 1.10 que _{kT(tn)_kL(X)}n>1 ´e limitada, contrariando o fato que

kT(tn)_kL(X)→∞.

Assim, sup t∈[0,η]k

T(t)_k<∞,para algumη>0 e com isso podemos afirmar que sup t∈[0,T]k

T(t)_k<

∞para qualquerT >0,pois dadoT >0,t_∈[0,T],tpode ser escrito da format=mη+λ com m_∈N∗_,λ _∈_(0,η₎_e

kT(t)_k=_kT(mη+λ)_k=_kT(mη)T(λ)_k=_kT(η)mT(λ)_k6_kT(η)_km_kT(λ)_k<∞.

Sejal>0 arbitr´ario tal que ˜

M=sup_{kT(t)_kL(X),06t6l}<∞

e sejaβ > 1_llog_{kT(l)_kL(X)}, isto ´e,kT(l)kL(X)6eβl. Ent˜ao,

kT(nl+t)_k=_kT(nl)T(t)_k=_kT(l)nT(t)_k

6_kT(l)_kn_kT(t)_k6Me˜ βnl

6Me˜ βnleβt+|β|l6Me˜ |β|leβ(nl+t). Logo

kT(nl+t)_k6Meβ(nl+t), 06t6l,n_∈N _e _M₌_Me˜ |β|l_.

Assim dadot>0, podemos escrevert=nl+t0, para algumn>0 e 06t06le portanto

kT(t)_k6Meβt, _∀t>0.

Dado um operadorA:D₍_A₎_⊂_X _→_X_{, denotaremos por}ρ₍_A_{), o conjunto resolvente de}_A

onde

ρ(A) =_{λ_∈C_:λ_I₋_A_{é injetora,} _Im(λ_I₋_A_{)é densa,} ₍λ_I₋_A₎−1_{: Im(}λ_I₋_A₎_→ _{é cont´ınua}_}_. O espectro deA, denotado porσ(A) é definido por

(37)

Observac¸˜ao 9. O operador A comuta com o operador resolvente(λI₋A)−1_.

De fato, sejau= (λ₋A)−1v, ou seja,(λ₋A)u=v. ComoAcomuta com(A₋λ)temos que

(λ₋A)−1Av= (λ₋A)−1A(λ₋A)u= (λ₋A)−1(λ₋A)Au=Au.

Por outro lado,

A(λ₋A)−1v=A(λ₋A)−1(λ₋A)u=Au.

Portanto,A(λ₋A)−1v= (λ₋A)−1Av,ou seja,Acomuta com(λ₋A)−1.

Vejamos agora alguns fatos importantes sobre semigrupos fortemente cont´ınuos.

Teorema 2.7. Suponha que_{T(t),t>0_{} ⊂}L₍_X₎_{´e um semigrupo fortemente cont´ınuo.}

(i) Para qualquer x_∈X , t_7→T(t)x ´e cont´ınua para t>_0.

(ii) t_{7→ k}T(t)_kL(X) ´e semicont´ınua inferiormente e portanto mensur´avel.

(iii) Seja A o gerador infinitesimal de T(t), então A é densamente definido e fechado. Para x_∈D₍_A₎_{, t}_7→_T₍_t₎_{x é continuamente diferenciável e}

d

dtT(t)x=AT(t)x=T(t)Ax, t>0.

(iv) Para Reλ >β, ondeβ ´e obtido no Teorema 2.6,λ est´a no conjunto resolvente de A e

(λ₋A)−1x=

Z ∞

0

e−λtT(t)xdt,_∀x_∈X.

Demonstrac¸˜ao:

(i)Vamos calcular os limites laterais. Sejamt>0 ex_∈X.

kT(t+h)x₋T(t)x_kX =kT(t)T(h)x−T(t)xkX =kT(t)(T(h)−I)xkX 6kT(t)kkT(h)x−xk

(38)

Analogamente, temos:

kT(t)x₋T(t₋h)x_kX =kT(t−h+h)x−T(t−h)xkX =kT(t−h)T(h)x−T(t−h)xkX =_kT(t₋h)(T(h)x₋x)_kX 6kT(t−h)kL(X)kT(h)x−xkX

6Meβ(t−h)_kT(h)x₋x_{k →}0, h_→0+. Portanto, para todox_∈X,t_7→T(t)x´e cont´ınua parat>0.

(ii)Devemos provar que, dado b_∈R_, _A₌_{_t >0 :_kT(t)_kL(X) >b} ´e aberto em[0,+∞).

Sejat0∈A. ComokT(t0)kL₍X)>bent˜ao existex∈X comkxk=1 tal quekT(t0)xk>b. De

(i)a aplicaçãot_7→T(t)xé cont´ınua, segue que existe uma vizinhançaV det0tal que set ∈V

então_kT(t)x_k>b. Portanto_kT(t)_kL(X)>bparat ∈V e isso conclui a demonstração.

(iii)Vamos mostrar queA´e densamente definido. Sejamx_∈X,ε >0 dado ex_ε= 1

ε

Z ε

0

T(t)xdt.Ent˜ao:

x_ε₋x=1

ε

Z ε

0

T(t)xdt₋1

ε

Z ε

0

xdt= 1

ε

Z ε

0 (

T(t)x₋x)dt.

Como _{T(t):t >0_} ´e fortemente cont´ınuo, T(t)x_→x quandot _→0+, logo dado δ >0 existeε_δ >0 tal que_kT(t)x₋x_k<δ para 06t6ε_δ. Assim,

kx_ε_δ₋x_k6 1 ε_δ

Z ε_δ

0 k

T(t)x₋x_kdt<δ 1

ε_δ

Z ε_δ

0

dt=δ.

Portantox_ε_→xquandoε_→0+. Verifiquemos quex_ε _∈D₍_A_).

Parah>0, temos que

T(h)x_ε₋x_ε

h =

(T(h)₋I)

εh

µZ ε

0

T(t)xdt

¶

= 1

εh

Z ε

0 (

T(h)₋I)T(t)xdt

= 1

εh

Z ε

0 (

T(h)T(t)x₋T(t)x)dt= 1

εh

µZ ε

0

T(h+t)xdt₋

Z ε

0

T(t)xdt

¶

= 1

εh

µZ h+ε

h

T(t)xdt₋

Z ε

0

T(t)xdt

¶

= 1

εh

µZ ε+h

0

T(t)xdt₋

Z h

0

T(t)xdt₋

Z ε

0

T(t)xdt

¶

= 1

εh

µZ ε+h

0

T(t)xdt₋

Z ε

0

T(t)xdt

¶

−_ε1_h

µZ h

0

T(t)xdt₋

Z 0

0

T(t)xdt

¶

.

Logo,

lim h→0+

T(h)x_ε₋x_ε

h =

1

(39)

Portantox_ε _∈D₍_A₎_{e assim}D₍_A_{) =}_X_.

A´e fechado. De fato, seja_{xn} ⊂D(A)comxn→x∈X eAxn→y, quandon→∞. A seguinte igualdade ser´a mostrada adiante,

T(t)xn−xn=

Z t

0

T(s)Axnds. (2.1)

ComoT(s)Axn→T(s)yuniformemente sobre intervalos limitados, obtemos: lim

n→+∞T(t)xn−xn=n→lim+∞

Z t

0

T(s)Axnds=

Z t

0

lim

n→+∞T(s)Axnds=

Z t

0

T(s)yds.

Isto ´e,

T(t)x₋x

t =

1 t

Z t

0

T(s)yds.

Fac¸amost_→0+ na ´ultima igualdade acima lim

t→0+

T(t)x₋x

t =tlim→0+

1 t

µZ 0+t

0

T(s)yds₋

Z 0

0

T(s)yds

¶

=T(0)y=y.

Como o limite existe,x_∈D₍_A₎_e_Ax₌_y_{. Portanto}_A_{´e fechado.}

Sex_∈D₍_A₎_ent˜ao

µ

d+ dt

¶

T(t)x= lim h_→0+

1

h(T(t+h)x−T(t)x) =hlim_→0+

1

h(T(h)T(t)x−T(t)x) = lim

h_→0+

1

hT(t)((T(h)−I)x) =hlim_→0+T(t)

µ

T(h)₋I h

¶

x

=T(t) lim h→0+

T(h)x₋x

h =T(t)Ax.

Como lim h→0+

T(h)T(t)x₋T(t)x

h existe,T(t)x∈D(A)eAT(t)x=T(t)Ax. Por(i)a aplicação t _7→T(t)Ax é cont´ınua, isto é,t _7→

µ

d+ dt

¶

T(t)x é cont´ınua, e portantot _7→T(t)x é continua-mente diferenciável e

µ

d+ dt

¶

T(t)x= _dtdT(t)x.

Logo,

d

dtT(t)x=T(t)Ax=AT(t)x.

2.1 ´e obtido integrando essa igualdade

Z t

0

d

dsT(s)xds=

Z t

0

T(s)Axds_⇒T(t)x₋x=

Z t

0

T(s)Axds.

(iv)Sejamλ _∈C_{tal que}_Reλ _>β ₍β _{do Teorema 2.6). Defina}_R₍λ₎_:_X _→_X _por

R(λ)x=

Z ∞

0