Modelo semiclássico para emissão espontânea

I

<}zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

_----,

t

-I I -~ í

~NIVERSIDADE DE SÃO PAULO

Instituto de Física e Química de São Carlos

Departamento de Física e Ciência dos MateriaisIHGFEDCBA

lI u m

m O D E lO I E m I E I _ I I I E O

P A R A

A E m llllo

E I P o n T ln E A I I

ROGÉRIO C. T. DA COSTA

(Tese apresentada ao Instituto de Física e Química de São Carlos, USP, para a obtenção do título de Livre-Docente).

SÃO CARLOS

UM ~lODELO SEMICLÁSSICO PARA A

EMISSÃO

ESPONTÂNEA

por

Rogério C.T.da Costa

Tese apresentada ao Instituto

de Física e Química de São

/

Carlos, USP,

para a obtenção

do Título de

Livre-Docente.

Departamento de Física e Ciência

dos Materiais-São Carlos

ÍNDICE

CAPITULO I

Introdução: Um ~odelo Semi-elãssico para a

Emissão Espontinea

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA1

CAP!TULO 11

As Equaç6es do Meio Material ...••...

13

II.A

A Aproximação de

Dipolo EI~trico •...

13

II.B

A Equação de Schrtldinger para Átomos de Dois

IHGFEDCBA

N í v e i s l S

CAPITULO 111

O Problema da Emissão para o Decaimento

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA6m=±1. •••••. 22

I I

I.A

I I L B I I L C

CAPITULO IV

A Solução das Equaç6es Auto-Consistentes

22

Discussão das So

Luç

ôes : ,Acoplamento Fraco

30

Discussão das Soluções: Acoplamento Forte

36

O Problema da Emissão para o Decaimento

6m=0 •••••••.

42

CAPITULO V

o

Problema da Emissão com um Nivel Degenerado

50

V.A

Obtenção das Equaç6es Auto-consistentes

50

V.B

Solução das Equaç6es para Acoplamento Fraco

66

AP~NDICE I

O Tratamento de Dicke para a Emissão Coletiva de

Áto-m o s d e D o i s N í v e i s 8 2

AP~NDICE 11

Radiação Emitida por um Plano de Dipolos Girantes ....94

A EMISSÃO ESPONTÂNEA

INTRODUÇÃOzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

A emiss~o de padiaç~o eletPomagn~tiaa pela matipia exci tada i, em ppin~{pio, um probLema bastante aompZezo. Entre as

ra-zões que concorrem para este fim podemos cital": a) O fato da maté-riaponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAconfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAte r muitos átomos; b )zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAO fato de m esm o os átomos mais simples

(hidY'ogênio, por exemplo) p o eeuirem muitos nlve-is de energia e, fi

naZmente; cJ O fato da Teoria Quântica dos Campos, utiZizadano tY'a tamento destes problemas, dar origem a equações matemáticas de so-lução muito diflcil.

O primeiro tratamento que se pode fa,zer"e que vem sendo efetivamente utilizado, ainda que com várias modificações, desde o

começo da Mecânica Quântica (Weisskopf e Wignep, (Z 9 S 0 ) (l)J, _con

-siste em resolver perturbativamente um átomo de dois nlveis. A ju~ tifiaativa para este cáLculo baseia-se na p08sib~Zidade de reduzip o n~mero de transições a considerar (regras de seLeção, etc.) e espeaiaZmente, na idiia de que a emissão de radiação por um só á -tomo é um proaesso essencialmente lento, Levando muitos aicLos das osciLações atômiaas para ser compLetado. Para o aaso da emissão ao

2zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

so interesse, merece ser descrito com um pouco mais de detalhe'+!,

Dicke considerou um sistema-de

N

átomos iguais,

disti~-Juí.veis, com dois nponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAioeie separados pela energiafedcbaZYXWVUTSRQPONMLKJIHGFEDCBAE . Devido à com=

p leta analogia existente com um sistema de N partIo u l.a e d e spin Z /2 ,

podemos intro du zzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAir au toes tado s comuns, ,10 , da energia não D e

r-~ v,m '

turbada Ho (análogo da componente

Lz

na direção do eixo de

2

zação) e de um novo operador

R

(correspondente ao quadrado

_2zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA+ L2 + L2 do momentum angular) de modo que

x y a

.) L '"'

=

H I/J

₌

mE _I/J

o v,m

v,m

l l . 1 )

e R2 I/J

₌

v (v+l)l/!

,

v,m

v,m

IV

N

onde v

=

,

2 2

chamado número

- l , v ,

de cooperação, e que representa o análogo

quânti-co das diferenças de fase entre os dipolos radiantes da teoria

clássica, desempenha, como veremos logo a seguir, um papel

rele-vante no processo de emissão. De fato, suponhamos que os nossos ~

tomos interagem apenas através de um campo eletromagnético

quan-uma

constante de movimento, de modo que v mantem-se constante

duran-(+)0 cilculo de alguns dos resultados de Dicke pode ser visto no

Apêndice

I deste trabalho. Acreditamos,

entretanto, que a dis

cussão apresentada nesta Introdução seja suficiente para

uma

•

te a emissão,

enquanto

que o valor

de m diminui.

Usando

a Teori~

das Perturbações

em primeira

ordem,

Di~ke

mostrou

que a taxa

emissão

num

estado

v,m

fedcbaZYXWVUTSRQPONMLKJIHGFEDCBAi

dada

por

I

=

10zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA(v+m) (v-m+ 1) (I. 2)

onde

I , que

não depende

de vem,

ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

i

a

taxa de emissão

correspon-o

dente

a um sistema

com um único

átomo

(v=I/2,m=±Z/~.

Este

resuLt~

')

do pode

ser escrito

numa

soma

de duas

parcelas,

a primeira,

I

(v--o ')

_m

w),

contendo

os

termos

quadráticos

nos

números

quânticos,

e

~

segunda,

I

t

v+m ),

os

termos

l

ineas-e

e , Para

sistemas

oom muitas

pap-o

ti~ulas

podemos

desprezar,

supondo

vFm,

a contribuição

do segundo

termo

na emissão

produzida

pelos

estados

com v-N

("super-radian

-:es

N

).

Esta

aproximação

i

chamada,

algumas

vezes,

de

"semi-clás

-~ ~ (3).,

sica",

pois

e poss~vel

mostrar

que e&a

está

r~lacionada

com

o

fato

de se

tratar

os operadores

do campo,

na representação

de

Heisenberg,como

simples

funç5es

do tempo.

Seguindo

este

caminho

e supondo

para

m uma

variaçãoqua-se contInua

(análoga

ao caso

de grandes

momentos

angulares)

Dicke

o~eve,

para

a taxa de emissão,

uma dependência

temporal

da

forma

a=I v/E.

t

importante

notar

que além

do decréscimo

o :w

tipo

exponencial

para

t++~,

existe

um curioso

arescimento

expone~

c

i

a

7.,

para

t+-~;

fato

este

devido

ao abandono

do termo

linear I

(0+ o

+m).

Realmente,

consideremos,

para

exemplificar,

a situação

onde

4zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

va le entao a introduzir um fa~so "eq uponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAi lLb rio instável" nos eefedcbaZYXWVUTSRQPONMLKJIHGFEDCBAtac ce

com V em .•zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAo qual será inicialmente quebrado pela emissão

~ espanta -aea (termo linear) até que a emissão induzida .•que pode ser trata

da classicamente, predomine e possa tomar sozinha conta de todc processo. (Note-se que no estado fundamental do sistema temos v =

=

-mzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

=

N/2, o que anula simultaneamente os dois termos presente2 em I.2)).É fácil ver, destes resultados, que a validade da apro-ximação semiclássica requer essencialmente uma dupla limitação so

bre a vida m~dia do nosso sistema. De fato, por um lado ela deve ser muito menor do que a vida média de um átomo isotado, uma vez que a energia de excitação é proporciona1 a N enquanto a taxa de emissão cresce com N2( v-N»lJ. Por ~utro lado, entretanto, e i.- Q

tem de ser muito maior do que o pe riodo lhJo= h/E de uma oeoi ia=

ção atômica, de modo a justificar o uso da Teoria das Perturba -~

Desde os resultados de Dicke o problema da interação e-letromagnética dos sistemas at6micos tem sido discutido por

mui-tos autores (4-l0) . Os tratamentos mais recentes, sobre os quais não pretendemos nos "alongar, consistem em, partindo de um

siste-ma de átomos de dois n{veis, que interagem com um campo de cavid~

-ae quantizado, obter as equaçoes de movimento para os operadores da matéria e do campo na representação de Heisenberg. Como estas

equações não podem ser resolvidas exatamente, utiliza-se um trat~ me n to não-pe rtur ba tivo que coneie te numa in tegl'ação ap rox-ima da das equações do campo (lineares) e na substituição dos resultados nas

~ais comumente emppegadas est~o a chamada appoximaç~o de onda

gi-pante (onde se desppeza as intepações fopa de fase com a solução não pepturbada ) e novamente a hipótese de que a emiss~o da padia

ção é um processo pelativamente lento. As equações obtidas também fopnecem um pesultado semiclássico, onde os operadores são trata-dos como numeros e os autovalopes considepados no limite de gran-des números quânticos.

Todos estes fatos sugerem a idéia dezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAse investigar azyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA ••.c.

possibilidade de uma solução puramente clássica, isto é, um cáZc~

Zo

onde o campo eletromagnético seja tratado classicamente desdefedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

J começo, através das equações deponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAtãaxue lõ , Tal idéia, aliás, nao

-é de maneira nenhuma nova, pois um tratamento baseado no eZetromafl.. netismo clássico vem senáo abundantemente utilizado, junto com o~

tras hipóteses (envoltópia lentamente variável, etc.), no estudo

d-a propagaçao- de pu~sos1 ~um~nososl' em me~os: nao- 1·~~neares (11) . Nos-sa intenção, poptanto, consiste simplesmente em aplicar o mesmo

ti

pc de tpatamento na soZuç~o de um problema mais simples; simplici-dade esta que nos permitirá, como veremos mais adiante, obter uma

solução exata (respeitadas naturalmente as limitações impostas p~

Zo modelo escolhido).

Antes de começar qualquer cálculo espec{fico vale a pena fazep um julgamento a-priopi dos prós e contra envolvidos no uso de

um modelo deste tipo. É claro que do lado desfavorável da balança irão ceptamente pesar dois tipos de apgumento:

(

6zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

ácomoponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

é

simplesmente

o campo

fedcbaZYXWVUTSRQPONMLKJIHGFEDCBAp

ro du z

i

do pelos

out1'osátomos.

2) Alá,., zo

uso

e

xc lue

i

vo da

i

n

t

e

raç áo e

le

t rom aç né ti

ea

(inerente

a

todos ::1'a

tamentos

deste

tipo)

ter>emos difiouldades

ao defini1'

as

"fon

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAz c s "

das

equações

de Maxwell,

sendo

neoessá1'ia

alguma

hipótese

de

na::u

reza

dr>ástioa pal'a relaoionar>

gr>andezas mao1'osc~picas

e

locais.

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Co

mo

o estado

totalmente

exoitado

tem

momento

de dipolo

nu~o

(Sirnc-tpia

de

Car>gaJ já

é

pr>evislvel

J

desde

agor>a. o aparecimento

de fe

n3meno

de

"equillbr>io

instável".

Quanto

aos

ar>gumentos

favol'áveis,

é

claro

que

eles

poder>ão

ser

apr>esentados

de

um modo

oonvincente

após

a obtenção/

doa

r>esultados.

Entr>etanto,

é sempr>e posslvel

alinhar>, como

uma

forma

de motivação,

as vantagens

que

se esper>a obter

caso

os

culos

sejam

bem

sucedidos:

AJ

Sendo

o modelo

olássico

muito

mais

eimples,

existe

semp1'e a possibilidade

de descob1'i1' um a1'1'anjo geomét1'ico

onde

ele

possa

ser> r>esolvido

exatamente.

Embor>a a vantagem

de se

conhecer

uma

situação

onde

todas

as dificuldades

estão

concent1'adas

nas

0i

~3teses,

e não

no método

de

solução,

seja

muitas

vezes

ilusória

J

é

dificil

fioar>mos

indifel'entes

ao apelo

estético

que

inegaveZme~

ts- »

o s eu

en:

os

ch ama do e

"modelos

solúveis".

B)

De posse

de

uma

solução

fechada

será

igualmente

Jt

[{oil

resistir>

à

tentação

de l'ealiáar algumas

incursões

no

tel'r>e~

no das

altas

densidadesJ

onde

a hipótese

da emissão

lenta

nao

-

e

~

c~rtamente

aplioável.

Embor>a n~o

haja,

na BotuÇ~O

do "OS~o

mode

~

~o, r>estr>ições a-pl'ior>i sobr>e a intensidadé

do campo

elétrico~

~ L

",::tações de outr>o tipoJ

conforme

ver>emos mais

adiantej

impedir>àc

C) A relativa simplicidad~ das 8olu~~e8 poder~ serzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

a-proveitada na investigaç~o da emissao por sistemas de ~tomos c~~

mais de dois n{veis.

Esperamos que tenha ficado claro, das observações ac~

~a, 1ue os nossos esforços devem estar orientados na obtençao de

umaponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAeo luç áo exata que com p en ee, de alguma forma, as co nc ee eoe efedcbaZYXWVUTSRQPONMLKJIHGFEDCBAfei

tas na estrutu~a do modelo escolhido. Sendo assim, é natural que

voltemos a nossa a tençao parao arranjo geométrico mais simples po~

s{vel~ que i o caso da emissao unidimensional de radiaçao por um

pLano material infinito. Para esta escolha concorre a necessidade

de evitar situações onde a emissao origi~ada em um ponto é

influ-en ci a da pelo comportamento passado de outros pontos do próprio sis

t.ema~o que certamente dar~ origem a complexidad8-8 matem~ticas

in-~esej~veis. Sao assim eliminados todos os emiS&Or68 volumétricos

(tY'idimensionais)~ por causa da existência de propagação interna

-equaç o ee de derivadas parciais) ou mesmo sistemas como uma casca

esf~rica~ por causa do aparecimento de equações diferenciais com

retal'damento.

Comecemos entao considerando as equaçoes de Maxwell

Para um meio materiaZ descarregado~ nao magnético~ descl'ito ape

nas peZa poZarizaçao macroscópica

P,

temos:

aD

-+

rotH

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA1

rotÊ

1

aB

-+ -+

=

_•

=

divD=O.

divB=O

(I . ~)

c

at

c

at

-r -r -r -+ -r

com

B

₌

H e D=E+41TP (I. 4)

8

-+ -+ -+zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

rut rotE

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA=

grad(divE)-óE

=

1

a

at

-+

(rotB)

=

c

=

-+ -+

(E+41TP)

(1. 5)zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Supondo que toda mat~ria est~ concentrada uniformemente

no plano

i=o

(Fig.1) dando origen a dois pulsos planos que se

pro-pagam no v~cuo, nas direç5es

ti,

teremos:

-+

E(z,t)

=

E (z,t)x+E

_x

(z,t)y

y (I .6)ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

do n de

-+

divE==ü.

( L"7)

DefedcbaZYXWVUTSRQPONMLKJIHGFEDCBA(l . .5 )~ (:.e ; e (Z. 7) obtemos:

'l-+ ')-+

a

2

p

ó"E 1 ó •...E 4n

( 1 .8 )

-

_-

--

=

dZ 2 c2 d t2 c2

a

t2

Sendo a densidade do plano dada por

o

(xy

z )

=

aÔ (

z )

( J .9)

~ ~

?nde cr e o numero de atomos por unidade de area, podemos escrever:

-+

2-+ êl E(z,t)

at2

=

4nfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAaô (z) -+

P (t) . ( I . 1 1)

2 C

Fara do plano material o campo eLitrico i descrito pelas soluçics

~ivres deU.Z ) (Veja Fig.])

Ed(z, t)zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA=

-+d

Er(z+ct) + ER(z-ct),

-+d

z>O,

(1.:2)

..•.

e

..•.

e

_-+e

zcO • E (z,t) = Er(z-ct) + ER(z+ct) ,

nde~ d~e~I e R rep1"esentam~ respectivamente abreviaç~es de ,r ...•l.;.' ._.~•

r eit a!", "ceq ue rda !", "incidente" e "refletido", Estas soluções

»em , n atu r a lmen t:e , satisfazer as condições de contorno para Q_-'om

~cnente ta:ngencial do campa elitrico:

-+

= E(t) II . 1:;i

"7

te E(tJ i o vaZar do campo el~trico sobre o plano materiaZ.

t.cq r emo e agora ( [ . '0 desde Z= -E a t.e z= + €, tomando o limite do Y',

2uZtado auando € -+ O . Obtemos então:

z=0

= ,:'14)

lO

o que, comzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAo auxIlio de(I.Z2J transforma-se em:

(1.15)ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

In t.eq r an do (I. l.S)em l'el.aç ao ao tempo e levando em con ta o fa to de

-+

que o estado fundamental (onde naturalmente dp(tJ/dt=O) deve ser

compatIvel com a ausência de campos extel'nos, obtemos:

=

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA411"0zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

d~(t)

c

dt

(I.16)

Este l'esultado pode sel' escl'ito numa fOl'ma mais conveniente com c

auxilio das condições de confedcbaZYXWVUTSRQPONMLKJIHGFEDCBAto rn o (I.l3J •. De fato, usando as re la

-çoes

-+d

-+d

-+

-ERCü,t) = _{ErCü,t)-ECt)}

e (I.17)

-+e

-+e

-+

-ERCü,t) = _{ErCü,t)-ECt) ,}

podemos e li.mi.n a» os campos r ef let ido e que aparecem em ( I . ,:8), ob t.e r.

do

21TO

C

-+

dp(t)

dt

(J.18)

A equação (I.l8)nos pel'mite obter o campo elitl'ico irtJ em função

. ~d -+e

nhe cponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAida ,zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAW

r+E I'

Como estamos 'interessados numa situação de emis

-são e tx p on tânea vamos admi ti » que não exie tem campos inciden tes ~'o -+d -+e_

Iocando

Er+Er::O:

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

-+

E(t)

=

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA2no

-+ dp(t)

dt

(J.19)

c

Eata relação constitui~ na verdade, a equação b~sica Q O

nosso trabalho. O que vamos fazer daqui para frente

é

utilizar

J

me

todos bastante bem conhecidos para descobrir uma maneira de reZa-cionar as derivadas de p(tJ (a partir da equação de Schr8dinger )

-+

com o campo elétrico E(t). O b tier emo e assim um si etema d e equações

ordinarias para as variaveis que definem simultaneamente o estado ia matéria e do campo em 3=0.

..•.

.

(O valor de E nos ·demat.s pontos do eepaço é ob tido eimp l.esmen te das condições ( T . Lô)); Note-se que co=

-+- -- ~ "fi

mo E aparece exp lici tado na Equaç ao (I.Z9) e sempre po e eive L e lsmi=

n~-lo das equações que descrevem o comportamento do meio material. Nosso sistema, portanto, sera sempre redutlvel

a

equações de pri-meira ordem que envolvem apenas v~riaveis atõmicas. Bastara dar então a função de onda inicial do problema para resolvi-lo compl~

tamente. Devemos lembrar mais uma vez o papel de.sempenhado pet-::' geometria plana na obtenção da expressão (I.l9). Seria muito mais t.n

teressante se o nosso sistema possuisse um comprimento caracte -r{stico (como no caso da superflcie esférica, ou mesmo dois pIa

-nos paralelos); mas este e o preço que vamos pagar para reduzir o

problema a um sistema diferencial ordinario, com mais possibilid~ des portanto de obter uma solução exata.

Z2

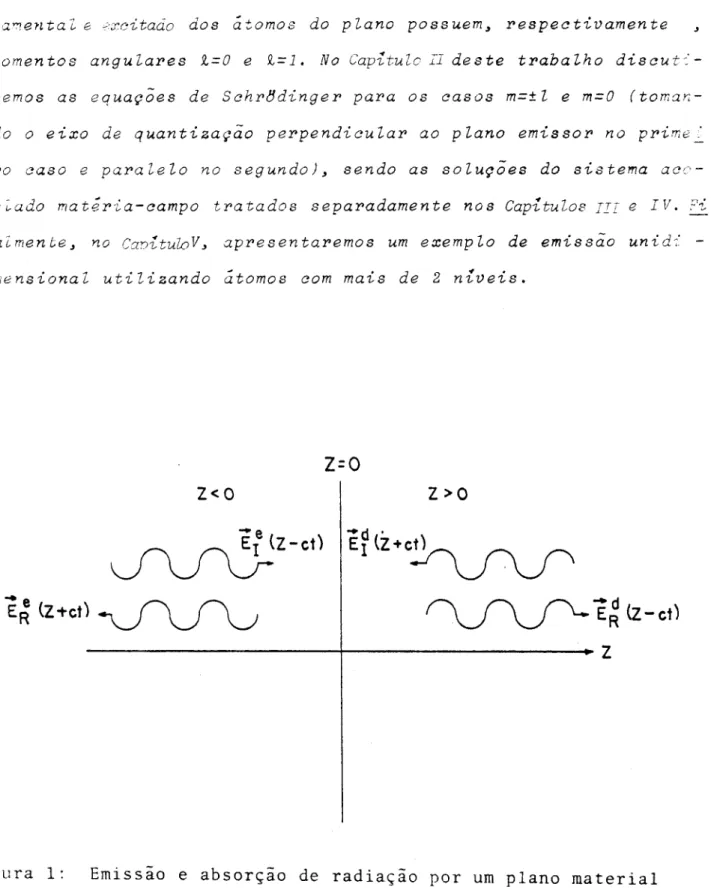
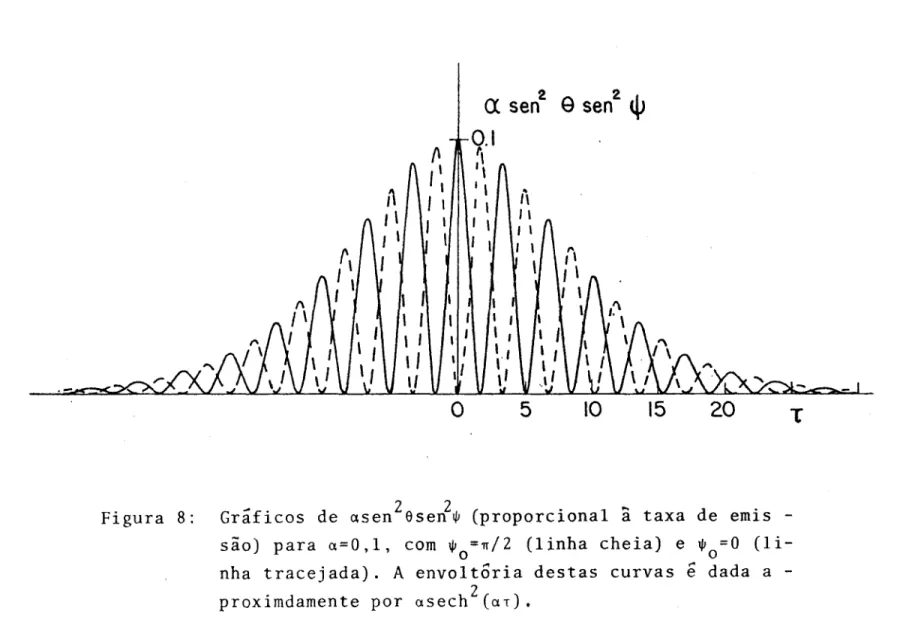
ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

dam en tazyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAZ- 8 «xc itado aosfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAá tom os do plano poss uem .. r e s p e c tivam en te m om entos angulares 1.= 0 e Q ,= 1. N o C apitulo Ti deste trabalho d i e cu t :»

rem os as equaç~e8 de Schr8dinger para os casos m = ±l e m = O (tom

an-do o eixo de quantização perpendicular ao plano em issor no prim ei

ro caso e paralelo no segundo), sendo as soluç~es do sistem a

aco-p ia do m ater i a+ cam p o tratados separadam ente nos C apitulas TlI e IV . ~r;'i

nai m en te , no C anituloV .• apresentarem os um exem plo de em issão un i di m ensional utilizando átom os com m ais de 2 niveis.

z=o

IHGFEDCBA

Z < O Z > O

- ezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

~Z-ct) " dEl(Z+C~.

'\f\J"-

Ê~

(z-ct)

---~---.Z

Figura

1:

_Emissio

_{e absorçio}

_{de radiaçio}

_{por um plano material}

IT-A

A aproximação

de dipolo elétricozyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Consideremos a Hamiltoniana de um ~tomo de N el~tro~s

soo a aç~o de um campo de radiaç~o exterior descrito pe~o pote~-zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA -+ -+

~ial vetor A(r,t):

H

=

(11.1)

ofedcbaZYXWVUTSRQPONMLKJIHGFEDCBAY LponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAde e e m sao,

-

respectivamente, a carga e a massa do el~tron> ~ ..

=

" J

z: -fJ í

V

j' -;;l'~2' ... ~lV se referem aos diferentes el.etsronedo átomo, e o pote" cial V contém todas as interações Coulombianas. Para o caso do nosso interesse

o ~omprimento de onda da radiação emitida numa transição eletrônica é muito maior do que o tamanho de um átomo, de modo que podemos considerar, em todo :1 0

- - -+ -+ -+

:ume atomico, o potencial vetor como independente da posiçao:A (r,t)~A(t).

equaç~o de Schr8dinger toma então a forl'lU

.

/j

1

2m

N

E

j=1 2 (p. J

2e

7 -+

e2

7

2

-+ -+ -+

-- A(t).p.

+

-z

A(t) )~(xl,x2"" ~,t)

+

c J c

(I1.2)

(*)

-A s

Seçoes 11,111 e IV correspondem

a uma descrição ampliada e com

- 30nveniente introduzi~ agora a transformaç~o unitaria:zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

li =zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAe xp {ie

7\ (

t ) .zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

te

~ L:

i=l

-+ x . }

1 (11.:';

i~bstituindo (II.3) no primei~o membro de (II.2) obtemos as r~_J-;,ões seguintes:

2e

7"-+

(A.p.)UW

J e

e

2

( 2 '

p.u1J!=IHGFEDCBA

u . p~1jJ)

J J

e

V<p= Vu1j!.

--JC~

o primeiro membro de (I1.2) fica reduzido apenas a

1fedcbaZYXWVUTSRQPONMLKJIHGFEDCBA L

U(pf1j!)

+

VU1j!.

j

2m

n 'r outro lado, no segundo membro temos:

in

a

(U1j!) =

iÉ

U

31jJ

3t at

eponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA(dA e dt

-+

I

Xi)

UI(! .

i=l

(11.4)

(II.5)

(Il.6)

(HO+HI(t)1j.I

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA=zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

it

:jt

onde

2

N _p.

Ho

=

I ~ + V

j =1

_2m

(II.ln)

e

onde

N

~ -+., 4 1 . ~

E=-[/c

aA/at

e c campo eletr&co e p

=

L

i=l

-+ ~

eX

i e o operaac.'

~~polo el~trico, o que justifica o nome dado a esta aproximaç;.

I I. B A Equação de Schr õ ding er para Átomos de Dois Níveis

Devido ao fato do nosso plano ser muito fino

(infini+o-~ente fino na formu=ação matemática), vamos supor que o campo ( :

; o mesmo em toda sua espessura, isto i , que todos o s a~te

",,:::8 do plano "vêem", no mesmo instante, o mesmo valor de

t.

A .C

\u:-~~~ de onda ~ , para todos os átomos (identificados peZo {ndici

<)~ e a t-i sf 'a z en t ao a:

=

il1

.L 'I' • ~t

(II.l1)

:~bstituindo

~= ~

I/!k ' vemos que cada função de onda individua

lezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

01.12)

-

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA Desta fopma~ desacoplamos a equaçao de Schp8dingep papa todoo

S~B-tema substituindo aponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAinteraça o entr e os átomcs pela inte raç a o com -+

~ampo elitpico classico extepno E(t). Natupalmente o sistema sezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA1"a

-~ovamente Nreacoplado"~ como ver>emos mais adiante~ atpav~s da E

-auação (I. 19)~ que representa a dependincia do campo el~tricozyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

~a-cposc5pico) com a polarização da mat~pia. Pop opa~ entpetanto. v~ mos nos !imitap ao estudo da equação (11.l2) aplicada aos atomos

1e dois n{veis. Considepemos então um atomo aom n{veis de energt~ ~.~/2hw e o r r ee p on den te e , r e cpe oti.oamen te , às funções de onda

nor-o

ma~i3adas ~. e ~ dos estados excitado e fundamental. Qualquer es

t a

t2do do atamo sepá então descrito pela função de onda

(I1.13)

SubJtituindo este resultado em (II.l2)~ obtemos:

da

dt

2

(11.14

db

dt

2

*

b - i/t(~a,HI(t).b) a ,

~nde utilizamos a ortogonaZidade de .a e 'b 83 su~ondo a origem Jp

coordenadas no centpo do átomo (potencial esfepiaamenre 8im~tr~~o)~

a(tJ e b(t) ~ ppefeplvel utilizarzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAtris funç5es reais do tempo~ na l5)

forma

1jJt

_oxw

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

*

*

V

_x

=

<o

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA>

₌

₌

ab +a b

x

t

*

*

v

_y =

<o

>

₌

_w

0yW

=

i (ba -b a)

(11.15)

y

W

t

9

_z

W

*

*

V

_z

₌

<o

_z

> =

₌

bb -aa

ondeponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA0x~oy e "« são as matrizes de 8pin de Pau li (~ ;J~ (~-~) e

(~ ~lJ. Em termos de V~~vy e V_z as equaç~e8 fII.l4) podem ser

es-oritas oompactamente como(*)

d~ -+-+

•• wl\v

(11.16)

dt

2

R

_(~a,H1~b)

W

x

=

-11

e

(11.17)

2

1m (~a .H1~b)

w

y

=

_ti

-

•

( *)

Uma vez que as partes reais e imaginárias de a e

_b

_fornecem

_qu~

tr0 números reais,

é

impossível obter w(t) partindo apenas

dos

valores de vx,vy e vz'

S

sempre possível, entretanto. dados vx'

v

_y

e

V

_{z determinar, através de (I1.l5) , [a],}

[b ]

e a diferença

de fase entre a e b, faltando apenas um fator de fase irrelevan

te em w(t).

l8zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

A Equaç~o de Schr8dinger fica ent~o transformada numa equaç~o de torque clássica, onde a veLocidade anguLarfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAé uma funç~o do campo

- d - -+ -+d-+d'

eletrico.zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAO fato o modulo de v ser constante (v. vi t~O) expr~me

agora a conservaç~o da probabilidade, uma vez que, por (II.l5J , 2 2 2 I 12 12 2

v +v +vzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA=( a +Ib ) . No futuro,

x

y

z

de onda ~(t) estão normaLizadasponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAà

suporemos sempre que as funções unidade, de modo que v2~L.

Precisamos agora obter o valor do elemento de matriz ~~e aparece nos segundos membros de (II. L7). Como o estado fundamcn

-taZ

é

um estado s (potencial centraL), ~~ deve então ter momentum angular t=Z, do contrário a Hamiltoniana de interação seria ider.-ticamente nula (consequência óbvia do acopLamento dipolar introd~ zido em (II.l7,)).Existem então duas eeeo l-hae p oeeiueie para a pr~ jeç~o do momentum angular de ~b:m=±7, ou m=O, para as quais, usan-do funções de onda do tipo hidrogênio(*)

<Pa

=

RlO(r)

(*)Naturalmente

os elementos de matriz

(11.17)

dependem dos

fato-res de fase contidos em <Pa e </lb'As expfato-ressões

(11.18) acima

t=l,m=+l.

(11.18)

, +

..1.

R

Z1

(r)senefedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

f i

-ict

e . ,

l.=l.m=-l,

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Obtemos:

Px

=

_{±pox' py=po}

y'

Pz = O

m=±l,

Px

=

O

Py =0

•

Pz =

ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA-l"Zpo _x'

m=O

, (IJ.19)

(lI. 20)

- GO 3

onde

p=-4

n

e/312

!

R2ZRlOr

dr~

~ o pssuZtado

de uma

integral

de

s~

o

perposiç~o

que contem

as partes

radiaic

de

ta

e

t

_b

.

De

(II.I?),

(II.lB),

(II.l9)

e

(II.20)

vemos

ent~o

que:

W_x

=

₊

~

E_x' w

1'1 y

=

-~E

~ y

m=±l

(11.21)

w

X

=

O •

m=O

(11.22)

-As equaçoes

de movimento

para

e

v

podem

ser agora

obtidas

2

de

(II.l6}:

avx

=

at

-w

. 20zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

2nzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

=zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA.::...t:. (v.E +v E )

11

'x y y x (11.23)

a

v

a

v

x ~ -w v

--Y

=w

v - ~

I2E

7

v

,

at o y' a t o x

11

-

z

ãv

z=~I2Ev

1': z Y

3t n

(11.24

J _zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Q que falta agora e junta~, conforme o caso~ as expressoesfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAr "T T ., ,-.., \ .••••• .J. • • ~.)

ou (II.24J com a Equaçao (I. Z9) de modo Q obter um sistemaeim

neo para c campo eZitrico e a~ variaveis que descrevem c mei ~~

terial. A maneira mais simplei de fazer istc~ e que sera a

adota-da no p r e e ent:e tr ab a lho , envolve infelizmente duas hip ote e e e

.f:A.!Z-dame n tais de v ev-ificaçao mui t-<:l dif-íaiZ:

o

campo el.e t r-ieo. que apar'eae em (I. Z9)

J

e o mesmo ..c'c;

(II.23) e (11.24), isto

i~

acampo que atua num particular' ~tom0

i

o ~esmc que comparece nas equaç~e8 de MaxweZI.

9 )

w,

o

dipala eZétrico médio

p(tJ

de (I'19) ac

jaZor midio do operador dipolo elétrico para um ~nico ~tomo.

quer dizer que todos os atamos t5m, no mesmo instante, a mesma _

De (II.l9) e tLl; 2 0 ) obtemos entao

15

(t)

=

P (±

v xX

+

v

y

y )

m=±l ( _{I I -2 :~;}

l

.

'+

_{- /Z-pv ;;}

m=O

Uma ~Ztima ob8ervaç~o: Como o aampo .L~~riaofedcbaZYXWVUTSRQPONMLKJIHGFEDCBAi sempre paralelo ao plano emissor o eixo

z

devezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

ser

perpendiaular a este plano para m=

±l e estar nele aontido para m=O. Assim sendo~ o estado exaitado/ com M=O (numa direçio paralela ao plano) passa a

ser

uma combina

CAPrTULO

III

o

PROBLE~~ DA EMISSÃO PARA O

DE

CA I'1ENTO

fedcbaZYXWVUTSRQPONMLKJIHGFEDCBAlim = ±zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA1

IIl.A

A

Soluçio

das Equações

Autoconsistentes

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Vamos estudar separadamente o caso onde as transiç~e2 ~

~6micas s~o do tipo ~m=±l. Conforme acabamos de ver, devemos usa~

para esta situaç~o, as equações (11.23) e (I. t9), comzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAo dipolc~{

dio obtido de (11.25) . Jbtemos entao um sistema de cinco e q u aponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAç o e e

-cara as ~~nco inc6gnitas o ,J ,v,E e E :

x li Z x Y

dV

.?E dV +2n

x _{= - J.) v - E v} - - L

=

_{w v}

---

_{E v}

o v y .,

.

o

x

₁₁

x z

3

t

11 '-

_ar

=

lE

Cv E :;v E )

11

x v y x

~

dv

..,

dv

E_x

=

+ x E

₌

~ -1

dt

y c

dt

c

dV..,

=

(111.11

(111 .2)

~ae 0 3 duplos stna~s se referem, respectivamente, aoe ~o~s vaZ

re2 de 60. Antes de disuutir a soluç~o das equações (111.7,2)

";..;v.Jenienteoo n eid e r av du a e das suas p ro p rie da d e e q e r ai e : Q P i,!'" ~ i'

1"'1 ; a

ja

conhecida conservaç5o da probabilidade (expressa pela

, . 2 2 2 l ) d

~onstante ae mov~mentc V +v +v = , e a segun a, que vamos Ver

1-x !f Z

J:.ra, é '1 conservaç~o da energia. Para i eto muZt1:pl'icamos:1s :J7A;,:,L

-equaçoes (IIT. l) respectivamente por ± E

x e Ey e

dv dv

{±EzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

--l

+ E x}.

x dt

Y dt

(II1.3)ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

C ub ezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

ti tu indo

em

(TII.

3) oe

Da

l o r e e

de

dv /

dt e

dv

/dt dados

em

(III.

x

Y

2) vem

v

E

-

v

E

=

x Y

+

Y x

(I11.4)

Substituindo

agOI'a o 19 membI'o de

(III.4)

n~ ~Ztim~

das

equaç~es!

(III.L)

obtemos

finalmente

d

dt

fedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

(1 .

hw

ov ) =

2

o

Z

C

2'11"

-+2

E

•

(I11.5)

qualqueI' que

seja

o

vaLoI' de

6m.

t

fáail

veI' de

(II. 15) que

l/2tíw o»

é o

va l.o

r mé di

o, pOI' unidade

de áI'ea~ da

en erqi a não

pe_I'

o .8

.,. L O

t

urb aâa

8

0

(Ho=l/2n

w

o

o

z

na

vep re een

t aç

ào em que

4Jb=(

O )

e

CPa=(

L}} ,

de modo

que

(III.5)

nos

dá simplesmente

uma expressão

para

a taxa

de emissão

do sistema

(o fato

da de!'ivada ser sempre

negativa

e,

uma

aonsequência

de não

haver

ondas

inaidentes

em

(I.l9)).

Jáo

se-gundo

membI'o de

(III.5)

nos

dia que

toda

energia

dos

átomos

é

con

ve!'tida em radia~ão

(aonsequência

aliás

do modelo

esaolhido)~

poie

a taxa de emissão

é

duas

vezes

(soma das duas

direções

opostas)

o ( * )

m5dulo

de vetor

de Poynting

na vizinhança

imediata

do plano

(*)Nesta emissão bilateral

o vetor

B

é

descontínuo

sobre o plano

material,

segundo a bem conhecida expressão(16)

ZA(~-Be)

=

4'IT/c

K,

onde

i

é

a densidade superficial de corrente. Para o

De posse destes resu[tados podemos começar agora

soZverzyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAo sistemafedcbaZYXWVUTSRQPONMLKJIHGFEDCBAa l I . l,2), Para tanto ~ conveniente introduz • variáveis comp[exaszyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAe v-=vponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA+ ±1-V.

x y (para~ r e ep e c t i u

a tr:« . ..zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

6~=~ !.Obtemos ent~

d

dt

±

v = ±iu: y"++ O

~

+ d

:!:

V • lIll. -.

c

dt

Substituindo (III,?) em (111,6) ficamos com

J

dt

± i +.n: z

w

o ( 1 I 1 , "

')

»n de a= 4rrp~(J/1íc~é Ama constante adi me n eio na l , Como a cons"i'

. b b '1'd ' - d + - 2, d -.

aa pro a 1-~~'aae 3 'ada por v v + v =t, po emos reduz"tr

z

ro de variáveis introduzindo coordenadas esféricas no espaçc

+ +irf

v

=

sen6e-

,

r 1 I

l..i

nosso caso

ê

fácil mostrar

que,

para

os dois

v a

lo

r e s de

i\11I.

7. C - - ~ - ~}

a

..,.

')

t\.

= -

Zi\{Z,fd.:-(-ZJ\c)

= --

(crptt)

4rr

at

011.10)zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Vamos interromper o cálculo por um instante para anali

sar o significado fisico de

a

e ~ : De (III.lO) vemos que cosa

mede o valor m~dio de H em unidades de l/2~w ; 6=0 corresponde~ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

o o

do ao estado excitado e 6=w ao estado fundamental.

Já o vaZor de ~ pode ter duas interpretaç5es: Por um ~a do temos de (III.9J e (II.25) que

v

tgcp=zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA.J.. v

x

tgx.

donde

t

está relacionado com o angulo X que a polarizaçao faz com o eixo dos x. Por outro lado~ usando ag~ra (II.l5J e escrevendo

a=\a\ eita ~ b=lbl eilPb, obtemos

*

*

vv=i(ba-ba)

tg+=

-L -

*

*

-

=

ab +a b

ou seja~ • também dá a diferença de fase ent1"e a e b. A função de

onda (II.l.õ ) pode ser escrita em termos de

a

e 4> através de

I'

bj > cose /

2.

I

ai =

sen

a/2.

~

a-epb

=

4>; (I I 1.11)

donde

011.12)

26zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

+zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

Voltemos

agora

fedcbaZYXWVUTSRQPONMLKJIHGFEDCBAà

Eq , (III.

zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA8):

Substituindo

v- eponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

V PO I'

Z

(III.9)

e

(III.lO)

chegamos,

para

os

2

valores

de ~m, a

cose

de :

dt

aw sen8cos8

o

')

2

l+a.•..

cos

e

(lI1.13)

sene

d<l>

=

dt

W

sene

o

2

.,

1+0.

cos~e

(l1I.14)

A solução

8=n/23

<l>=w t+<l>

é

matematicamente

espúria,

pois

o o

7 ~ •

tt:'

/

.

± i

(w t+<l> )

gem

a um campo

e~etr~co

E

= -

2npow

o

c ~e

o

o)

que

nao

-

sa-tis faz

(II I .

5).

Já P a

r

a a sol uçã

o

een

e

=

o

tem

o

eJ

a Lém d

o

ee ta do fu!l:.

damental

8=n,

o

estado

excitado

e=o.

Repete-se

então

aqui

a

ques-tao do falso

equiltbrio

instável(de/dt~O)

já discutida

na Introdu

ção

deste

trabalho.

De fato,

no estado

excitado

temos

(II.25)),

de modo

que

a polarização

clássica,

por

si só,

é

inea

-paz

de produzir

um campo

elétrico

que

d; inicio

ao processo

de d~

caimento.

Cancelando

então

cose

e sene

nos

dois

membros

de

(III.

Z3) e

(III.l4)

ficamos

finalmente

com

de

=

a.

dT

sene

_(111.15)

1

(lII.1b)

2

2

1+a cos

e

-onde

fizemos

T=W

t. Temos

agora

duas

equaçoes

diferenciais

qUf ~0

o

da interaçao e8t~ concentrada. Comecemos por (1II. l5): como ela

nao depende explicitamente de T sua 80luç~0 geral sera do tipo

8(1--T ), on~e T ~ uma constante arbitr~ria,zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAo que ~ uma consequ~n -ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

o o

cia naturaZ da invariancia do processo de emiss~o por translaç5es

temporais. Um valor particular para TO deveria ser obtido, emp~~ clpio, dando o instante de tempo onde a emissao começa. Isto,

na-turaZmente, ~ imposslvel de se fazer se a emissão começar no e8t~ do de m~xima excitação, o qual, pelas razões j~ discutidas, só alcançado para t~-oo. O que vamos fazer então ~ considerar e=TI/2p~ ra t=O, pois estes estados possuem tris propriedades,

independen-tes de a , qU€ 08 tornam adequados para ~ste tipo de escolha:

a) sao os estados com metade da energia de excitação, assim sendo, com esta condiçao inicial, metade da energia disponi veZ

é

emitida para t<O e a outra metade para t>O.

b) s~o os estados onde a taxa de emiss~o é m~xima (Ve-ja (111.5) e (111.25)).

c) são os estados em re2ação aos quais a taxa de

emis-sao é sim~trica (mesmos valores para 8 e TI-e; veja-se novamente (111.5) e (111.15)).

Resolvido este ponto, a integração de (111.l5) faz-se imediata~en

te. O resultado é

t=wot =(a+l/a)~n(tge/2)+acose.zyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

(111.17)

Substituindo (II1.17) em (111.26) obteremos uma solução geral ~o

tipo $=$(t)+$ ($ =constante arbitr~ria), o.que é naturalmente u-fedcbaZYXWVUTSRQPONMLKJIHGFEDCBA

uma consequincia da invariancia do problema por rotaç3es em torn~

do eixo perpendicular ao plano emissor. Como $=$a-$b concluimos

quezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAas emiss3es originadas de estados iniciais que s6 se

diferen-ciam pelo valor de ~ estão relacionadas por meio de uma rotaçaozyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAn·

gida. Isto pode ser paradoxal~ ~ primeira vista~ quando ~ons~ae

-ramos o estado de m~xima excitação (a=OJ onde $ não ~ definido.ponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAA

resposta para isto é que nossa teoria não se aplica para este

es-tado (que não decairia)~ mas quezyxwvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAse dele nos aproximarmos

(fazen-do ,al+O em (II. 13)) fixando de cada vez, diferentes valoresfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAd e ~~-~b~ a radiação emitida no futuro vai sempre Nlembrar-seN deB~u

diferença de fase inicial3 produzindo rotaç3es correspondente2 ~t

campo emitido. Naturaímente este efeito ~ muito sensivel ao Va l'

da constante a . Se a«l temos d$/dt»d8/dt, de modo que o atp,

elétrico executa muitas voltas praticamente sem mudar de m6du~o

diluindo o efeito da fase ini cia l , Se a= l , entretanto, :1 in tei-:

-ção é tão forte que pequenas diferenças no estado inicia! pode~

pro~uzir, no decorrer de um tempo longo~ modificaç3es radicais na

distribuição angular da radiação emitida (isto podera ser vieta ~L

vamente acompanhando a discussão que faremos sobre o comportamen-to de 8(t; e 1J(t)). P ic :J .~ de qualquer forma, claro que po a em o e ,

~o!her um valor arbitr~rio para ~(O) que todas as demais soZuçZec

serão desta obtidas por uma rotação rigida. Ponhamos então ~(O

=

o c tem o e de (11. Z5" Z,6J:

de

=

asen6, d~

(III.18)