ÁLGEBRA NA EDUCAÇÃO BÁSICA:
AS MÚLTIPLAS SINALIZAÇÕES DO QUE SE ESPERA
QUE DEVEM SABER OS ALUNOS
MESTRADO EM EDUCAÇÃO MATEMÁTICA
PUC - SP
São Paulo
ÁLGEBRA NA EDUCAÇÃO BÁSICA:
AS MÚLTIPLAS SINALIZAÇÕES DO QUE SE ESPERA
QUE DEVEM SABER OS ALUNOS
Dissertação apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para a obtenção do título de MESTRE EM EDUCAÇÃO MATEMÁTICA, sob orientação da Prof.a Dr.a Célia Maria Carolino Pires.
PUC - SP
São Paulo
________________________________________
________________________________________
Aos meus queridos pais, por tudo que me proporcionaram na vida.
À Vilma, pelo companheirismo e compreensão, sempre contínuos.
À professora Dr.a Célia Maria Carolino Pires, minha orientadora, que, com sabedoria e conhecimento, direcionou este trabalho.
À professora Dr.a Adair Mendes Nacaratto e à professora Dr.a Sônia Pitta Coelho, pelas valiosas sugestões.
“… Se um dia, já homem feito e respeitado, sentires que a terra cede a teus pés,
que tuas belas obras se desmoronam, que não há ninguém à tua volta para te estender a mão, esquece tua maturidade, passa pela tua mocidade, volta à tua infância e balbucia,
entre lágrimas e esperanças, as últimas palavras que sempre te restaram na alma:
Meu Pai, Minha Mãe”.
O presente trabalho procura investigar algumas das sinalizações do que se espera que devem saber os alunos sobre Álgebra, ao final do Ensino Médio, pretendendo assim contribuir para a reflexão sobre o ensino de Álgebra na Educação Básica. Analisa e compara orientações de novas propostas curriculares, questões de alguns vestibulares e do Exame Nacional do Ensino Médio - ENEM, que orientam projetos de ensino nas escolas de nível médio. Por meio de pesquisa bibliográfica e documental, busca identificar orientações constantes em documentos oficiais para o ensino da Álgebra, programas de Álgebra presentes em vestibulares como a FUVEST, VUNESP, a UNICAMP e também do ENEM. Estudamos questões dessas avaliações, nas edições de 2001 a 2003, destacando os aspectos mais valorizados.
Palavras-chave:
This work seeks to investigate some of the signs about what is expected from the students’ knowledge of Algebra by the end of their high school term. It intends to contribute for the reflection about the teaching of Algebra during the basic education in Brazil. This work analyses and compares guidelines and new curricular proposals, questions of some university admitance exams and the National Examination for High School (ENEM), which orient teaching projects in schools. Through a bibliographic and documental research, this work aims to identify permanent guidelines in official documents for the teaching of Algebra, syllabuses of Algebra present in examinations as FUVEST, VUNESP, UNICAMP and also ENEM (the abbreviations stand for Brazilian public universities). We have studied items of these examinations from 2001 to 2003, highlighting the most valuable aspects.
Key words:
APRESENTAÇÃO . . . 1
CAPÍTULO 1 . . . 3
Apresentação da Pesquisa . . . 3
1.1 Relevância do Tema . . . 3
1.2. Problema de Pesquisa . . . 6
1.3. Procedimentos Metodológicos . . . 7
CAPÍTULO 2 . . . 9
As Sinalizações para o Ensino de Álgebra em Documentos como os Parâmetros Curriculares Nacionais, Exames Vestibulares Realizados no Estado de São Paulo e Exame Nacional do Ensino Médio . . . 9
2.1 Introdução . . . 9
2.2 Sinalizações Encontradas na Literatura sobre o Tema . . . 9
2.3 Concepções da Álgebra . . . 13
2.4 Sinalizações Encontradas nos Parâmetros Curriculares Nacionais . . . 18
2.5 Sinalizações Encontradas nos Programas de Exames Vestibulares . . . 27
2.5.1 Orientações dos programas de Álgebra da FUVEST . . . 28
2.5.2 Orientações dos programas de Álgebra da VUNESP . . . 32
2.5.3 Orientações dos programas de Álgebra da UNICAMP . . . 33
2.6 Sinalizações Encontradas no Exame Nacional do Ensino Médio - ENEM 35 2.7 Considerações Sobre o Capítulo . . . 37
CAPÍTULO 3 . . . 38
Uma Análise das Questões de Álgebra de Exames Vestibulares Realizados no Estado de São Paulo . . . 38
3.1 Introdução . . . 38
3.2 Seleção de Critérios de Análise das Questões . . . 39
3.2.1.2 FUVEST 2002 . . . 48
3.2.1.3 FUVEST 2003 . . . 55
3.2.1.4 Considerações gerais sobre os exames da FUVEST - 1ª fase de 2001 a 2003 . . . 59
3.2.2 Análise das questões de Álgebra da VUNESP - Conhecimentos Gerais . . . 65
3.2.2.1 VUNESP 2001 . . . 65
3.2.2.2 VUNESP 2002 . . . 67
3.2.2.3 VUNESP 2003 . . . 70
3.2.2.4 Considerações gerais sobre os exames da VUNESP -Conhecimentos Gerais de 2001 a 2003 . . . 73
3.2.3 Análise das questões de Álgebra da UNICAMP - 1ª fase . . . 76
3.2.3.1 UNICAMP 2001 . . . 76
3.2.3.2 UNICAMP 2002 . . . 77
3.2.3.3 UNICAMP 2003 . . . 79
3.2.3.4 Considerações gerais sobre os exames da UNICAMP -1ª fase de 2001 a 2003 . . . 81
3.2.4 Análise das questões da UNICAMP - 2ª fase . . . 84
3.2.4.1 UNICAMP 2001 . . . 84
3.2.4.2 UNICAMP 2002 . . . 87
3.2.4.3 UNICAMP 2003 . . . 90
3.2.4.4 Considerações gerais sobre os exames da UNICAMP -2ª fase de 2001 a 2003 . . . 93
CAPÍTULO 4 . . . 97
Uma Análise das Questões de Álgebra do Exame Nacional do Ensino Médio -ENEM . . . 97
4.1 Introdução . . . 97
4.2 ENEM 2001 . . . 98
4.3 ENEM 2002 . . . 100
4.4 ENEM 2003 . . . 104
Conclusões e Recomendações . . . 113 5.1 Introdução . . . 113 5.2 Uma Comparação entre as Propostas para o Ensino de Álgebra na
Educação Básica e as Sinalizações do Vestibular e do ENEM: Coerências e Incoerências . . . 113 5.3 Os Conhecimentos Algébricos Priorizados pelos Exames Vestibulares e
pelo ENEM . . . 117 5.4 O Desempenho em Álgebra revelado por Alunos do Ensino Médio, com
Tabela 1 - Incidências das Questões de Álgebra . . . 38
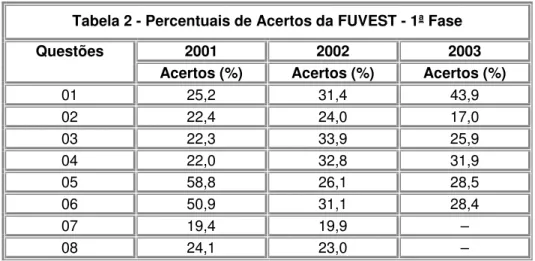
Tabela 2 - Percentuais de Acertos da FUVEST - 1ª Fase . . . 63
Tabela 3 Percentuais de Acertos das Questões da VUNESP -Conhecimentos Gerais . . . 74
Tabela 4 Percentuais de Acertos das Questões de Álgebra da UNICAMP -1ª Fase . . . 82
Tabela 5 Percentuais de Acertos das Questões de Álgebra da UNICAMP -2ª Fase . . . 95
Tabela 6 - Incidências das Questões de Álgebra do ENEM . . . 97
Tabela 7 - Interdisciplinaridade . . . 115
Tabela 8 - Contextualizações . . . 115
Tabela 9 - Habilidades Requeridas (H) . . . 116
Tabela 10 - Conteúdos do Ensino Fundamental e Ensino Médio . . . 117
Tabela 11 - Incidência de Assuntos . . . 118
Tabela 12 - Concepções de Álgebra e Diferentes Usos de Variáveis . . . 119
Tabela 13 - Indicações de Desempenho dos Alunos . . . 120
APRESENTAÇÃO
O presente trabalho insere-se na linha de pesquisa “A Matemática na Estrutura Curricular e Formação de Professores”, do Programa de Estudos Pós Graduados em Educação Matemática da PUC-SP. Pretende contribuir para a reflexão sobre o ensino e a aprendizagem da Álgebra no Ensino Médio, identificando diferentes sinalizações existentes, considerando as orientações de propostas curriculares, questões de vestibulares e o Exame Nacional do Ensino Médio - ENEM que, como sabemos, acabam influenciando os projetos de ensino nas escolas.
Por meio de pesquisa de documentos curriculares e de exames vestibulares, coletamos dados para nosso trabalho e os organizamos em cinco capítulos:
No primeiro capítulo, apresentaremos a pesquisa, destacando a relevância do tema, o problema de pesquisa e a metodologia utilizada.
No segundo capítulo, “As Sinalizações para o Ensino de Álgebra em Documentos como os Parâmetros Curriculares Nacionais, Exames Vestibulares Realizados no Estado de São Paulo e Exame Nacional do Ensino Médio”, apresentaremos as orientações constantes em documentos oficiais para o ensino de Álgebra e os programas de Álgebra presentes em vestibulares como a FUVEST, VUNESP a UNICAMP, buscando identificar os conteúdos apresentados nessas avaliações. Analisaremos também o Exame Nacional do Ensino Médio - ENEM, que introduziu formas de avaliação bastante diferenciadas em relação à dos vestibulares.
No quarto capítulo, “Uma Análise das Questões de Álgebra do Exame Nacional do Ensino Médio - ENEM”, que envolvem conteúdos de Álgebra, analisaremos questões dos exames dos anos de 2001 a 2003, buscando identificar características que consideramos relevantes.
CAPÍTULO 1
APRESENTAÇÃO DA PESQUISA
1.1 RELEVÂNCIA DO TEMA
As investigações sobre as organizações curriculares de Matemática para o Ensino Médio ainda são bastante escassas, ou seja, há pouca discussão acumulada e poucas pesquisas tematizando o ensino e a aprendizagem de Matemática nessa etapa da escolaridade.
Segundo Pires (2004), questões de diferentes naturezas permeiam as discussões sobre currículos de Matemática. Estas questões envolvem aspectos amplos como os de natureza política e educacional e, também, aspectos mais particulares como os de natureza didática e epistemológica.
Pires destaca, dentre os aspectos de natureza política e educacional, algumas indagações históricas, provocadas por autores como Bourdieu e Sacristán entre outros. Tais perguntas questionam em que medida a opção curricular adotada é um instrumento de possível exclusão para os alunos, tendo em vista que, na visão de Bourdieu, citado por Sacristán (2000) os currículos dominantes costumam pedir a todos os alunos o que só uns poucos podem cumprir. Já Sacristán (2000) pondera que o debate sobre a composição de currículos, referentes aos níveis obrigatórios da escolaridade, pode ser uma absoluta necessidade, tendo em vista que aí se está decidindo a base da formação cultural comum para todos os cidadãos, seja qual for sua origem social, independentemente de suas probabilidades de permanência no sistema educativo em níveis de educação não obrigatórios.
o questionamento mais freqüente é o que se refere à Matemática que deve ser ensinada aos jovens do Ensino Médio de hoje e com que finalidade. Outra pergunta freqüente refere-se à forma como as teorias didáticas e metodológicas devem ser incorporadas aos currículos sem que sejam distorcidas e tragam prejuízos para a aprendizagem dos alunos, como é o caso de idéias como as de contextualização e interdisciplinaridade, recentemente incorporadas ao debates.
Por outro lado, no caso do Ensino Médio, as práticas vigentes são muitas vezes orientadas pelo que cobram os exames vestibulares, mesmo que os alunos a que se destinam não tenham o ensino superior como uma possibilidade real. Constata-se que a cultura do cursinho está cada vez mais presente no sistema de ensino: materiais elaborados pelas grandes redes de cursinhos pré-vestibulares são usados em escolas particulares e começam a chegar nas escolas públicas.
A propósito de currículos para o Ensino Médio, Sacristán (2000) faz uma observação interessante. Ele avalia que não é tarefa difícil, chegar a consensos sobre currículos, para os primeiros momentos da escolaridade obrigatória e que se pode encontrar um certo acordo sobre habilidades e conhecimentos iniciais básicos. Mas o consenso sobre o currículo, segundo esse autor, complica-se à medida que o propomos para outros momentos posteriores da escolaridade, quando já se fazem mais evidentes as diferenças individuais entre os alunos, entre distintos grupos de alunos quando começam as manifestações das expectativas deles próprios ou de suas famílias em relação às carreiras a seguir.
Quadro 1 - PCN+*: Unidades Temáticas - Conteúdos
1. Noção de função; funções analíticas e não-analíticas; análise gráfica; seqüências numéricas; função exponencial ou logarítmica.
1. Trigonometria do triângulo retângulo.
2. Geometria plana: semelhança e congruência; representações de figuras. 1ª Série
3. Estatística: descrição de dados; representações gráficas. 1. Funções seno, cosseno e tangente.
1. Trigonometria do triângulo qualquer e da primeira volta.
2. Geometria espacial: poliedros; sólidos redondos; propriedades relativas à posição; inscrição e circunscrição de sólidos.
2. Métrica: áreas e volumes; estimativas. 2ª Série
3. Estatística: análise de dados. 3. Contagem.
1. Taxas de variação de grandezas.
2. Geometria analítica: representações no plano cartesiano e equações; intersecção e posições relativas de figuras.
3ª Série
3. Probabilidade.
Fonte: <http://cenp.edunet.sp.gov.br/Ens_medio/em_pcn.htm> Acesso em: 19 ago.2004. * Documentos complementares aos Parâmetros Curriculares Nacionais do Ensino Médio.
É interessante destacar ainda que a proposição de currículos de
tecnológicos dos processos produtivos” (Art. 35, incisos I a IV).
Nesse contexto, com o intuito de colaborar para o debate sobre currículos de Matemática no Ensino Médio, dedicamos nossa investigação a identificar as diferentes sinalizações sobre as expectativas de aprendizagem relativas à Álgebra, para alunos ao final da Educação Básica, apresentadas em documentos curriculares, exames vestibulares e no Exame Nacional do Ensino Médio - ENEM.
1.2. PROBLEMA DE PESQUISA
Pesquisando currículos, Exames Vestibulares e o Exame Nacional do Ensino Médio, nosso objetivo é estudar diferentes sinais existentes em nosso sistema educacional, a respeito do ensino e da aprendizagem da Álgebra.
Buscamos inicialmente conhecer pesquisas existentes sobre o ensino de Álgebra. A delimitação do problema de pesquisa e a formulação das questões de pesquisa apoiaram-se, mais especificamente, nas leituras dos textos de Usiskin (1994), e Kieran(1992).
Nossa pesquisa busca responder às seguintes questões:
•
Existe coerência entre as propostas para o ensino de Álgebra, na educação básica e as sinalizações do vestibular e do ENEM?•
Que conhecimentos algébricos os exames vestibulares e o ENEM estão priorizando e quais as possíveis conseqüências disso para o ensino de Álgebra ao longo da Educação Básica?•
Que desempenho em Álgebra é revelado por alunos do Ensino Médio, com base nos percentuais de acertos das questões dos exames analisados, fornecidos pelas instituições realizadoras desses exames?Pires, denominado “Inovações curriculares nos Ensinos Fundamental e Médio e formação de professores para essa etapa da escolaridade”. Esse projeto tem na organização curricular dos Ensinos Fundamental e Médio seu eixo temático. Inclui análises sobre a trajetória da Matemática na organização curricular brasileira para estas etapas da escolaridade e as atuais propostas de ensino de Matemática para os Ensinos Fundamental e Médio. Focaliza o processo de desenvolvimento curricular, as variáveis que intervêm em sua formulação, as mudanças que ocorrem nos currículos. Discute como as diretrizes veiculadas por documentos oficiais são traduzidas nos livros didáticos e investiga o “currículo como práxis”, identificando como são incorporadas na prática dos professores em sala de aula, as orientações dos currículos oficiais. Investiga a relação entre processos de formação de professores e os processos de mudança, inovação e desenvolvimento curricular.
1.3 PROCEDIMENTOS METODOLÓGICOS
Em nosso trabalho, utilizamos como metodologias de pesquisa, a pesquisa bibliográfica e a pesquisa documental.
Para Pádua (2002), a pesquisa bibliográfica tem a finalidade de colocar o pesquisador em contato com o que já se produziu e registrou a respeito de seu tema de pesquisa. Já a pesquisa documental é aquela realizada a partir de documentos considerados cientificamente autênticos e permite comparar ou descrever fatos estabelecendo suas características ou tendências. Pádua (2002) afirma que o pesquisador pode usar fontes documentais primárias ou secundárias. Considera como fontes primárias os documentos originais, livros escritos pelo autor e como fontes secundárias documentos com dados estatísticos, textos escritos sobre o pensamento de um autor, documentos de referência de associações profissionais, resoluções ministeriais, prontuários, dede que o pesquisador tenha certeza da autenticidade desses documentos e cite em sua pesquisa a fonte de coleta de dados.
consultando a literatura sobre o tema e também realizando a leitura dos PCNEM. Na seqüência, desenvolvemos a pesquisa de documentos referentes a exames vestibulares realizados no estado de São Paulo, a saber, FUVEST, VUNESP, UNICAMP. Para complementar nosso estudo sobre as sinalizações dadas por avaliações, além dos exames vestibulares, incluímos o Exame Nacional do Ensino Médio - ENEM, organizado pelo INEP. Optamos por analisar as questões de Álgebra dessas provas, nos últimos três anos (2001, 2002 e 2003), com o intuito de identificar possíveis tendências. Outra decisão foi a de analisar as questões que se destinam a todos os vestibulandos, independentemente da carreira pleiteada, pois consideramos que tais questões, de certo modo, revelam o que se considera essencial que um egresso do Ensino Médio deve saber sobre Álgebra; assim, analisamos as questões da 1ª fase da FUVEST, de conhecimentos gerais da VUNESP e as questões da 1ª e da 2ª fase da UNICAMP. Os critérios de análise das questões serão apresentados no Capítulo 3.
CAPÍTULO 2
AS SINALIZAÇÕES PARA O ENSINO DE ÁLGEBRA EM
DOCUMENTOS COMO OS PARÂMETROS CURRICULARES
NACIONAIS, EXAMES VESTIBULARES REALIZADOS NO ESTADO
DE SÃO PAULO E EXAME NACIONAL DO ENSINO MÉDIO
2.1 INTRODUÇÃO
Nos últimos anos, as discussões sobre o ensino de Álgebra e sobre expectativas a respeito dos conhecimentos dos alunos ao final da Educação Básica vêm sendo discutidas e há sinalizações diferentes a esse respeito. Para compreendê-las melhor, neste capítulo, analisaremos as orientações constantes em documentos oficiais para o ensino de Álgebra e os programas de Álgebra de alguns vestibulares como FUVEST, UNESP e UNICAMP. Analisaremos também o Exame Nacional do Ensino Médio - ENEM, que tem trazido indicações que se pretendem diferenciadas das dos vestibulares para os professores de Ensino Médio.
2.2 SINALIZAÇÕES ENCONTRADAS NA LITERATURA SOBRE O TEMA
conteúdos, sobre o ensino e as aplicações da Álgebra. Ele identifica como origens dessas forças, as tecnologias da informação e as forças sociais.
Para esse autor, o advento das tecnologias da informação, outras áreas como as das ciências sociais e biológicas tornaram-se altamente dependentes dos processos matemáticos. Nessas áreas, os conceitos e processos algébricos, como manipulação de variáveis e avaliação de tendências, são de importância fundamental. Outra implicação das tecnologias da informação nos currículos de Álgebra refere-se ao fato de que os algoritmos terão seu papel diminuído e ao mesmo tempo realçado — diminuído em termos de memorização para obter respostas e, realçado, no que se refere a aprender a planejar e criar algoritmos para execução pelas pessoas e pelo computador. As ferramentas tecnológicas certamente suscitam reflexões interessantes: se a tecnologia de computação oferece sua abordagem interativa para aproximar as raízes de uma função com graus de precisão cada vez maiores e num tempo extremamente pequeno, para que ensinar a fatoração de polinômios, simplificação de expressões racionais, fórmulas como a de Bháskara?
House (1994) alerta para o fato de que, desde o Ensino Fundamental, alunos que planejam um fluxograma ou que programam um algoritmo, que coletam dados para a organização de uma tabela, que acham o valor de uma expressão variável ou que formulam perguntas do tipo “e se”…? com a planilha eletrônica, estarão lançando fundamentos importantes para o estudo da Álgebra. Concordamos com ele, e acrescentamos que tais fundamentos provavelmente serão muito mais eficazes do que os que hoje são construídos em aulas expositivas, baseadas em um numeroso conjunto de regras. Além disso, a velocidade de cálculo e exatidão das calculadoras permitirão que dediquemos mais tempo a processos heurísticos, como construção de tabelas, em busca de modelos.
Em termos de Brasil, Fiorentini, Miguel e Miorim (1992) destacam que houve durante todo o período anterior ao Movimento da Matemática Moderna, em nosso país, um equilíbrio enciclopédico no ensino dos ramos fundamentais da Matemática. Entretanto, apesar desse equilíbrio, não seria contraditório afirmar que o pêndulo, nesse período, oscilou levemente para a Geometria. Eles apontam duas razões fundamentais para sustentar essa afirmação:
A primeira apóia-se no fato de que o equilíbrio enciclopédico só existia no plano legal; na prática escolar, o ensino da Álgebra era menos favorecido, uma vez que os professores, até o início deste século, pouco a conheciam.
A segunda razão baseia-se no pensamento pedagógico racionalista, dominante nessa época no Brasil, segundo o qual o ensino de Geometria desempenhava um papel mais nobre do que o da Álgebra e da Aritmética. Por razões históricas e ideológicas, esse fato gerou um dualismo metodológico, fazendo com que a Álgebra e a Geometria fossem encaradas como dois campos distintos e independentes.
Ao tentar superar esse dualismo através da unificação dos diferentes campos da Matemática, com base na concepção epistemológica do formalismo estrutural, o Movimento da Matemática Moderna acabou rompendo o equilíbrio enciclopédico, tanto no plano legal quanto no da prática escolar. Esse rompimento contribuiu para que o ensino da Geometria sofresse um processo de descaracterização, levando-o ao quase abandono na sala de aula. Podemos dizer, portanto, que nesse momento histórico, o pêndulo deslocou-se para o campo da Álgebra.
Os autores destacam que esse repensar implica alguns desafios. Um deles: a realização de estudos que procurem explicitar a especificidade da Álgebra e o papel por ela desempenhado na história do pensamento humano, particularmente na história do pensamento científico e matemático. Um outro estudo consiste na discussão dos principais argumentos e justificativas que pedagogos e pesquisadores em educação Matemática, de âmbito mundial, têm apresentado com relação ao ensino da Álgebra.
Em relação ao primeiro desafio, Fiorentini, Miguel e Miorim (1992) destacam que as concepções mais freqüentes de Álgebra, que aparecem nas diferentes leituras do desenvolvimento histórico a esse respeito, nos levam à seguinte questão: como elas se interagem com as concepções dominantes da Educação Algébrica que surgiram ao longo da história da Educação Matemática Elementar?
Uma primeira concepção de Educação Algébrica, durante o século XIX até a primeira metade do século XX, tanto no Brasil como em outros países, é a que chamamos de lingüístico-pragmática. Ela vincula o papel pedagógico da Álgebra como instrumento de resolução de problemas às concepções lingüístico-semântico-sintática dessa disciplina. Nessa concepção, acredita-se que a aquisição de técnicas algébricas, ainda que mecânicas, é suficiente para o aluno resolver problemas, mesmo que artificiais, e fabricados com o propósito de se utilizar técnicas aprendidas.
Contrapondo-se a essa concepção, aparece uma outra de cunho lingüístico, denominada fundamentalista-estrutural. De acordo com essa nova concepção baseada na concepção lingüístico-postulacional da Álgebra, a Álgebra é tida como fundamentadora dos vários campos da matemática escolar. Nessa concepção, acredita-se que a introdução de propriedades estruturais das operações capacitaria o estudante a identificar e a aplicar essas estruturas nos diferentes contextos em que estivessem subjacentes.
dessa disciplina. Essa nova concepção tenta efetuar uma síntese entre as duas anteriores, só que não mais de forma lógico-estrutural de justificação das passagens presentes no transformismo algébrico característico da segunda concepção. Nessa concepção, a nova forma de justificar, na maioria dos casos, baseia-se em recursos analógicos geométricos e, portanto, visuais. Nesse sentido, essa concepção acredita que uma “álgebra geométrica” seria didaticamente superior a qualquer forma de abordagem estritamente lógico-simbólica. Nessa concepção, outro recurso analógico bastante comum é a “justificação” de certas passagens do transformismo algébrico através da utilização de leis do equilíbrio físico, recorrendo para isso, a materiais concretos como balanças, gangorras, etc., nos quais o “concreto” tem um significado diferente do “concreto” ao qual fazem apelo os recursos estritamente geométrico-visuais.
Todas essas concepções de Educação Algébrica tomam como ponto de partida a existência de uma Álgebra simbólica já constituída. Assim, segundo Fiorentini, Miguel e Miorim, em todos esses casos, o ensino-aprendizagem da Álgebra reduz-se ao “transformismo algébrico”.
2.3 CONCEPÇÕES DA ÁLGEBRA
1. A Álgebra como aritmética generalizada
Nesta concepção, as variáveis são pensadas como generalizadoras de modelos. Por exemplo, generaliza-se: 3 + 5 ⋅ 7 = 5 ⋅ 7 + 3 como a + b = b + a
Dentro dessa concepção de Álgebra, as introduções-chave para o aluno são traduzir e generalizar. São técnicas importantes, não só para a Álgebra mas também para a aritmética.
Historicamente, a invenção da notação algébrica em 1564, por François Viète, teve efeitos imediatos. Em cinqüenta anos a geometria analítica foi inventada e trazida a uma forma avançada. Em cem anos surgiu o cálculo. Essa trajetória evidência o poder da Álgebra como aritmética generalizada.
2. A Álgebra como um estudo de procedimentos para resolver certos tipos de problemas
Consideremos o seguinte problema:
Adicionando 5 ao dobro de um certo número, a soma é 17. Traduzindo-o para a linguagem da Álgebra: 2x + 5 = 17
Dentro da concepção 1, da Álgebra como generalizadora de modelos, não temos incógnitas. Assim, sob essa concepção, o problema apresentado terminou, pois já encontramos o modelo geral.
No entanto, dentro da concepção da Álgebra com um estudo de procedimentos, estamos apenas começando.
3. A Álgebra como estudo de relações entre grandezas
Consideremos, por exemplo, a fórmula A = bh que fornece a área de um retângulo de lados b e h. Nela estamos expressando uma relação entre as três grandezas. Não estamos lidando com uma incógnita, pois não estamos resolvendo nada. Fórmulas como essa transmitem uma sensação diferente de generalizações como
=
n 1 n
1 , embora se possa pensar numa fórmula como
um tipo especial de generalização.
Considerando que a concepção de Álgebra como o estudo das relações pode começar com fórmulas, a distinção crucial entre esta concepção e a anterior é que, neste caso, as variáveis variam. Que há uma diferença fundamental entre estas concepções fica evidente pela resposta que os alunos geralmente dão à seguinte pergunta:
O que ocorre com o valor de x
1 quando x se torna cada vez maior?
Isso parece simples, mas é suficiente para confundir os alunos. Neste caso, x não é incógnita, e só pedimos para que o aluno traduza isso.
Dentro dessa concepção, uma variável é um argumento (isto é, representa os valores de domínio de uma função) ou um parâmetro (isto é, representa um número do qual dependem outros números).
4. A Álgebra como estudo das estruturas
Nos cursos superiores, o estudo da Álgebra envolve estruturas como grupos, anéis, domínios de integridade, corpos e espaços vetoriais. Isso parece ter pouca semelhança com a Álgebra do Ensino Médio. Contudo, reconhecemos a Álgebra como o estudo das estruturas pelas propriedades que atribuímos às operações com números reais e polinômios. Consideremos o seguinte problema: Fatorar: 3x2 + 4ax – 13a2
discutidas anteriormente. Não se trata de nenhuma função ou relação; a variável não é um argumento. Não há equação alguma a ser resolvida, de modo que a variável não atua como incógnita. Também não há nenhum modelo matemático a ser generalizado.
No quadro 2, estão sintetizadas as diferentes concepções de Álgebra e os diferentes usos de variáveis.
Quadro 2 - Concepções de Álgebra e Diferentes Usos de Variáveis
Concepção de Álgebra Uso das Variáveis
Aritmética generalizada Generalizadoras de modelos (traduzir, generalizar) Meio de resolver certos problemas Incógnitas, constantes
(resolver, simplificar) Estudo de relações Argumentos, parâmetros
(relacionar, gráficos) Estrutura Sinais arbitrários no papel
(manipular, justificar)
Um trabalho de destaque nas pesquisas sobre o ensino de Álgebra é o de Kieran (1992). Ela utiliza os termos “processual” e “estrutural” da seguinte forma:
O termo processual refere-se a operações aritméticas realizadas sobre números para produzir números. Por exemplo, se tomamos a expressão algébrica 3x + y e substituirmos x e y por 4 e 5 respectivamente, o resultado é 17. Um outro exemplo envolve a resolução de 2x + 5 = 11 substituindo vários valores para x até que o correto seja encontrado. Em ambos esses exemplos aparentemente algébricos, os objetos que são trabalhados não são as expressões algébricas, mas suas instanciações numéricas. Além disso, as operações que são realizadas nesses números são computacionais — elas produzem um resultado numérico. Assim, esses dois exemplos ilustram uma perspectiva processual em Álgebra.
ser simplificada para resultar 11x + y ou dividida por z para resultar z
y x 11 + .
Equações como 5x + 5 = 2x + 4 podem ser resolvidas subtraindo 2x de ambos os lados para se obter 5x – 2x + 5 = 2x – 2x + 4, que pode subseqüentemente ser simplificada para 3x + 5 = 4. Nesses dois exemplos, os objetos que são trabalhados são as expressões algébricas, não alguma instanciação numérica. As operações que são realizadas não são computacionais. Além disso, os resultados são ainda expressões algébricas.
Para Kieran, a maioria dos livros didáticos de Álgebra apresenta uma fachada de abordagens processuais em sua introdução a objetos algébricos fornecendo alguns poucos exercícios envolvendo substituição em expressões algébricas e várias técnicas aritméticas para resolver equações algébricas — técnicas que permitem aos estudantes, em um sentido, evitar o simbolismo algébrico. Contudo, essa simulação desaparece rapidamente quando expressões devem ser simplificadas e equações resolvidas por métodos formais. Os objetivos implícitos da Álgebra escolar são estruturais. As exigências cognitivas envolvidas no trabalhar com expressões algébricas como objetos com operações que são distintas das operações da Aritmética são claramente reminiscentes das lutas intelectuais que ocorreram durante o desenvolvimento histórico da Álgebra, quando interpretações processuais abriram caminho para as estruturais.
Kieran sugere que três fatores são potenciais contribuintes para as dificuldades que o estudante tem em aprender Álgebra: aprendizagem, ensino e conteúdo.
requer um período prolongado de prática antes que as concepções processuais possam ser transformadas em estruturais.
O Ensino: conforme Kieran, o volume de pesquisa que tem sido realizada com os professores de Álgebra é mínimo. Resultados desses poucos estudos sugerem que suas concepções são estruturais e que essa é a abordagem que eles favorecem em seu ensino. Apesar da natureza do ensino da Álgebra, os estudantes raramente parecem capazes de desenvolver concepções estruturais maduras.
O Conteúdo: Kieran relata que, se os estudantes sentem dificuldade com a Álgebra que é ensinada por seus professores e os professores ensinam a Álgebra que é apresentada nos livros didáticos. Então, o maior fator contribuindo para a dificuldade em Álgebra poderia ser atribuído, por falta de outra razão, ao conteúdo da Álgebra como disposta na maioria dos livros didáticos. Atualmente, o conteúdo da maioria dos livros didáticos não incorpora uma perspectiva processual-estrutural sobre a aprendizagem do estudante de Matemática, nem parece refletir como a Álgebra evoluiu historicamente.
2.4 SINALIZAÇÕES ENCONTRADAS NOS PARÂMETROS CURRICULARES NACIONAIS
Ao definir objetivos para o quarto ciclo do Ensino Fundamental (freqüentado majoritariamente por jovens de 13 e 14 anos), os PCNEF incluem o desenvolvimento do pensamento algébrico por meio da exploração de situações de aprendizagem que levem o aluno a:
• produzir e interpretar diferentes escritas algébricas — expressões, igualdades e desigualdades —, identificando as equações, inequações e sistemas;
• resolver situações-problema por meio de equações e inequações do primeiro grau, compreendendo os procedimentos envolvidos;
• observar regularidades e estabelecer leis matemáticas que expressem a relação de dependência entre variáveis;
• resolver situações-problema que envolvam a variação de grandezas direta ou inversamente proporcionais, utilizando estratégias não-convencionais e convencionais, como as regras de três;
• representar em um sistema de coordenadas cartesianas a variação de grandezas, analisando e caracterizando o comportamento dessa variação em diretamente proporcional, inversamente proporcional ou não-proporcional.
O documento ressalta que ao se proporem situações-problema bastante diversificadas, o aluno poderá reconhecer diferentes funções da Álgebra.
Os conceitos e procedimentos sugeridos pelos PCNEF, para o quarto ciclo, relativos à Álgebra (Números e Operações), são:
• Constatação que existem situações-problema, em particular algumas vinculadas à Geometria e medidas, cujas soluções não são dadas por números racionais (caso do π, da 2, 3 etc.).
• Análise, interpretação, formulação e resolução de situações-problema, compreendendo diferentes significados das operações, envolvendo números naturais, inteiros, racionais e irracionais aproximados por racionais.
• Resolução de situações-problema de contagem, que envolvem o princípio multiplicativo, por meio de estratégias variadas, como a construção de diagramas, tabelas e esquemas sem a aplicação de fórmulas.
• Construção de procedimentos para calcular o número de diagonais de um polígono pela observação de regularidades existentes entre o número de lados e o de diagonais.
• Identificação da natureza da variação de duas grandezas diretamente proporcionais, inversamente proporcionais ou não-proporcionais (afim ou quadrática), expressando a relação existente por meio de uma sentença algébrica e representando-a no plano cartesiano.
• Resolução de problemas que envolvem grandezas diretamente proporcionais ou inversamente proporcionais por meio de estratégias variadas, incluindo a regra de três.
• Resolução de situações-problema que envolvem juros simples e alguns casos de juros compostos, construindo estratégias variadas, particularmente as que fazem uso de calculadora.
• Tradução de situações-problema por equações ou inequações do primeiro grau, utilizando as propriedades da igualdade ou desigualdade, na construção de procedimentos para resolvê-las, discutindo o significado das raízes encontradas em confronto com a situação proposta.
• Construção de procedimentos para calcular o valor numérico e efetuar operações com expressões algébricas, utilizando as propriedades conhecidas.
• Obtenção de expressões equivalentes a uma expressão algébrica por meio de fatorações e simplificações.
• Resolução de situações-problema que podem ser resolvidas por uma equação do segundo grau cujas raízes sejam obtidas pela fatoração, discutindo o significado dessas raízes em confronto com a situação proposta.
Já os Parâmetros Curriculares para o Ensino Médio – PCNEM destacam que, em nossa sociedade, o conhecimento matemático em uma grande diversidade de situações, como apoio a outras áreas do conhecimento, é um instrumento para lidar com situações da vida cotidiana ou, ainda, uma forma de desenvolver habilidades de pensamento.
Defendem que aprender Matemática de uma forma contextualizada, integrada e relacionada a outros conhecimentos traz, em si, o desenvolvimento de competências e habilidades que são essencialmente formadoras, à medida que instrumentalizam e estruturam o pensamento do aluno, capacitando-o para compreender e interpretar situações, para se apropriar de linguagens específicas, argumentar, analisar e avaliar, tirar conclusões próprias, tomar decisões, generalizar e para muitas outras ações necessárias à sua formação.
Nos PCNEM, a área de Ciências da Natureza, Matemática e suas Tecnologias elegeu três grandes competências como metas a serem perseguidas durante essa etapa da escolaridade básica e complementar do Ensino Fundamental para todos os brasileiros:
• Representação e comunicação, que envolvem a leitura, a interpretação e a produção de textos nas diversas linguagens e formas textuais características dessa área do conhecimento;
procedimentos peculiares do fazer e pensar das ciências;
• Contextualização das ciências no âmbito sócio-cultural, na forma de análise crítica das idéias e dos recursos da área e das questões do mundo que podem ser respondidas ou transformadas por meio do pensar e do conhecimento científico.
Escolhidas essas competências, que os PCNEM indicam como temas estruturadores do ensino de Matemática, a proposta dos PCNEM é que cada escola e grupo de professores proponham um trabalho pedagógico que permita o desenvolvimento das competências almejadas.
Relativamente à seleção de conteúdos, um critério básico e geral é que os conteúdos ou temas escolhidos devem permitir ao aluno desenvolver as competências descritas no item anterior, avançando a partir do ponto em que se encontra.
Para isso, sugerem então que os temas selecionados devem ter relevância científica e cultural. Isso significa que, além das justificativas relativas às aplicações e à linguagem, sua importância está em seu potencial explicativo, o que permite ao aluno conhecer o mundo e desenvolver sentidos estéticos e éticos em relação a fatos e questões desse mundo.
Observam ainda que os temas devem, ainda, permitir uma articulação lógica entre diferentes idéias e conceitos para garantir maior significação para a aprendizagem, possibilitar ao aluno o estabelecimento de relações de forma consciente para caminhar em direção às competências da área, e até mesmo tornar mais eficaz a utilização do tempo disponível.
Os PCNEM estabelecem que um conjunto de temas que possibilitem o desenvolvimento das competências almejadas com relevância científica e cultural e com uma articulação lógica das idéias e conteúdos matemáticos, pode ser sistematizado nos três seguintes eixos ou temas estruturadores, desenvolvidos de forma concomitante nas três séries do Ensino Médio:
3. Análise de dados.
Cada tema estruturador é um campo de interesse com organização própria em termos de linguagens, conceitos, procedimentos e, especialmente, objetos de estudo. Apesar da unidade característica de cada tema estruturador, para organizar o planejamento do ensino, cada um deles foi dividido em unidades temáticas que, por sua vez, são parcelas autônomas de conhecimentos específicos que podem ser organizadas dentro do projeto pedagógico de cada professor ou escola, em função das características de seus alunos e dos tempos e espaços para sua realização.
Passamos a sintetizar algumas das orientações apresentadas pelos PCNEM relativamente ao tema “Álgebra: números e funções”, em função de foco de nossa pesquisa.
Segundo o documento PCN+, o primeiro tema ou eixo estruturador, Álgebra, na vivência cotidiana se apresenta com enorme importância enquanto linguagem, como na variedade de gráficos presentes diariamente nos noticiários e jornais, e também enquanto instrumento de cálculos de natureza financeira e prática, em geral.
No Ensino Médio, esse tema trata de números e variáveis em conjuntos infinitos e quase sempre contínuos, para serem completos. Os objetos de estudo são os campos numéricos dos números reais e, eventualmente, os números complexos e as funções e equações de variáveis ou incógnitas reais. Para o desenvolvimento desse eixo são propostas duas unidades temáticas: variação de grandezas e trigonometria.
Outro ponto ressaltado é o de que o estudo das funções permite ao aluno adquirir a linguagem algébrica como a linguagem das ciências, necessária para expressar a relação entre grandezas e modelar situações-problemas, construindo modelos descritivos de fenômenos e permitindo várias conexões dentro e fora da própria Matemática. Assim, a ênfase do estudo das diferentes funções deve estar no conceito de funções e em suas propriedades em relação às operações, na interpretação de seus gráficos e nas aplicações dessas funções.
Um destaque interessante é o de que, tradicionalmente, o ensino de funções estabelece como pré-requisito o estudo dos números reais e de conjuntos e suas operações, para depois definir relações e, a partir daí, identificar as funções como particulares relações. Todo esse percurso é, então, abandonado assim que a definição de função é estabelecida, pois para a análise dos diferentes tipos de funções todo o estudo relativo a conjuntos e relações é desnecessário. Assim, o ensino pode ser iniciado diretamente pela noção de função para descrever situações de dependência entre duas grandezas, o que permite o estudo a partir de situações contextualizadas, descritas algébrica e graficamente. Toda a linguagem excessivamente formal que cerca esse tema deve ser relativizada e em parte deixada de lado, juntamente com os estudos sobre funções injetoras, sobrejetoras, compostas e modulares.
resolução de equações logarítmicas e exponenciais e o estudo das propriedades de características e mantissas podem ter sua ênfase diminuída e até mesmo suprimidas.
Nos PCN+, a respeito das seqüências, há uma orientação no sentido de que é preciso garantir uma abordagem conectada à idéia de função, na qual as relações com diferentes funções possam ser analisadas. Assim, por exemplo, o estudo da progressão geométrica infinita com razão positiva e menor que 1 oferece talvez a única oportunidade de o aluno estender o conceito de soma para um número infinito de parcelas, ampliando sua compreensão sobre a adição e tendo a oportunidade de se defrontar com as idéias de convergência e de infinito. O documento destaca que essas idéias foram e são essenciais para o desenvolvimento da ciência, especialmente porque permitem explorar regularidades.
Propõe também que o ensino deste assunto deve se ater à lei de formação dessas seqüências e a mostrar aos alunos quais propriedades decorrem delas. Associar às seqüências seus gráficos e relacionar os conceitos de seqüências crescente ou decrescente aos correspondentes gráficos permite ao aluno compreender melhor as idéias envolvidas, ao mesmo tempo que dá a ele a possibilidade de acompanhar o comportamento de uma seqüência sem precisar decorar informações.
épocas, como é o caso do período das navegações ou, atualmente, na agrimensura, o que permite aos alunos perceberem o conhecimento matemático como forma de
resolver problemas que os homens se propuseram e continuam se propondo.
O documento do MEC ressalta que, ao explorar Álgebra no Ensino Médio, é possível alargar e aprofundar o conhecimento dos alunos sobre números e operações, mas não isoladamente dos outros conceitos, isto é, pode-se tratar os números decimais e fracionários, mas mantendo de perto a relação estreita com problemas que envolvem medições, cálculos aproximados, porcentagens, assim como os números irracionais devem se ligar ao trabalho com geometria e medidas. É ainda importante para o aluno, nessa etapa de sua formação, o desenvolvimento da capacidade de estimativa da ordem de grandeza de resultados de cálculo ou medições e da capacidade de tratar com valores numéricos exatos ou aproximados de acordo com a situação e o instrumental disponível.
Os Parâmetros destacam ainda que, tradicionalmente, a Matemática do Ensino Médio trata da ampliação dos conjuntos numéricos, introduzindo os números complexos. Como esse tema isolado da resolução de equações perde seu sentido para os que não continuarão seus estudos na área, ele pode ser tratado na parte flexível do currículo das escolas.
2.5 SINALIZAÇÕES ENCONTRADAS NOS PROGRAMAS DE EXAMES VESTIBULARES
Conforme já destacamos anteriormente, os exames vestibulares também são sinalizadores da seleção de conteúdos, e mesmo de sua abordagem, no trabalho de muitos professores de escolas de nível médio. Para caracterizar o que os exames vestibulares estão sinalizando a respeito dos conhecimentos algébricos esperados de um aluno ao final da Educação Básica, analisaremos os programas de alguns vestibulares do Estado de São Paulo: a FUVEST, a VUNESP e a UNICAMP.
Recuperando a trajetória histórica dos vestibulares, verificamos que até a primeira metade da década de 60, eles eram realizados isoladamente, ou seja, um vestibular para cada escola. O primeiro passo de unificação foi dado pelas escolas de Medicina, em seguida pelas escolas de Humanas e, por fim, por três escolas de Engenharia.
A Escola Politécnica da Universidade de São Paulo, a Escola de Engenharia Mauá e a Faculdade de Engenharia Industrial organizavam vestibulares isoladamente. Em 1968, essas instituições decidiram unificar seus vestibulares em benefício de seus candidatos. Foi criado o MAPOFEI: MA (Mauá), PO (Politécnica) e FEI (Faculdade de Engenharia Industrial), cujo primeiro vestibular ocorreu em 1969.
O vestibular do MAPOFEI era constituído por provas dissertativas, sendo uma prova para cada matéria e cada prova era composta por dez questões. O último vestibular do MAPOFEI foi realizado em 1975. É interessante destacar que, na década de 60, o Centro de Seleção de Candidatos às Escolas de Medicina -CESCEM e o Centro de Seleção de Candidatos às Escolas de Economia e Administração - CESCEA elaboravam, respectivamente, vestibulares para as áreas de Biológicas e Humanas. No entanto, seus conteúdos eram os mesmos dos programas do vestibular do MAPOFEI.
exame de seleção unificando os vestibulares de todas as suas instituições. Para isso foi criada uma organização autônoma denominada Fundação para o Vestibular -FUVEST. Assim, a partir de 1976, todos os candidatos à USP passaram a participar desse vestibular unificado, dividido em duas partes. A primeira parte era constituída por questões de múltipla escolha (testes) e, a segunda parte, por questões discursivas.
Esse exame recebeu o apoio da UNICAMP, da Escola Paulista de Medicina e da Santa Casa de Misericórdia de São Paulo. Mais tarde, a UNICAMP se separou da FUVEST e, posteriormente, o mesmo ocorreu com a Escola Paulista de Medicina.
Já a Fundação para o Vestibular da Universidade Paulista - VUNESP foi criada em 26 de outubro de 1979 pelo Conselho Universitário da UNESP.
2.5.1 Orientações dos Programas de Álgebra da FUVEST
Os documentos que apresentam Programas da FUVEST, na edição de 2003, destacam que os conhecimentos matemáticos são aplicados na interpretação de fenômenos, em diferentes áreas da ciência, nas atividades tecnológicas e cotidianas. O cidadão necessita da capacidade de leitura e interpretação de informações por gráficos ou outras formas de linguagem matemática, de percepção da coerência ou não de uma argumentação, bem como da competência para formular suas próprias idéias de forma consistente, para uma inserção crítica e autônoma na sociedade contemporânea.
problemas da Matemática, das outras áreas do conhecimento e da realidade. a FUVEST declara que a avaliação da capacidade de raciocínio, sem dar ênfase à memorização de fórmulas, prioriza a mecanização de técnicas ou a cálculos
excessivos, desvinculados de contexto significativo ou de aplicações relevantes,
dentro ou fora da Matemática.
Na 1ª fase do vestibular, o objetivo é avaliar o candidato quanto ao domínio e
utilização da linguagem e quanto à compreensão de conceitos e procedimentos da
Matemática Elementar, bem como quanto à capacidade de aplicá-los na resolução
de problemas.
Na 2ª fase, além destes aspectos, a FUVEST propõe-se também a avaliar o
candidato quanto ao domínio de conceitos, ferramentas e procedimentos
matemáticos necessários para o aprofundamento de estudos em áreas de ciências
exatas, bem como quanto à capacidade de utilizá-los em situações-problema mais
abstratas.
As provas de Matemática do concurso vestibular da FUVEST visam o
conhecimento de problemas nodais que impulsionaram a necessidade de ampliação
dos campos numéricos e o domínio dos conceitos básicos que deles surgiram,
proporcionando ao indivíduo uma inserção mais completa na cultura universal
desenvolvida por homens e mulheres ao longo da História. E divide o programa em
dois itens, que passamos a apresentar:
A. Conceitos e relações numéricas básicas e aplicações
A FUVEST ressalta que o cidadão freqüentemente necessita lidar com dívidas
ou crediários, interpretar descontos, entender reajustes salariais, escolher aplicações
financeiras, etc. Daí a importância da Matemática Financeira com suas aplicações
práticas. E completa: sistemas lineares e matrizes são instrumentos da linguagem
matemática na modelação de situações-problema, além de representarem técnicas
de grande utilidade para outros domínios da Matemática de nível superior.
a) Números inteiros: compreensão dos algoritmos das quatro operações fundamentais no sistema decimal de numeração, divisibilidade e a decomposição em fatores primos.
b) Insuficiência dos números inteiros para a comparação de grandezas e para
medir partes de um todo: razões e proporções; os números racionais; operações e a relação de ordem entre números racionais; representação decimal dos números racionais e sua relação com PG.
c) Insuficiência dos números racionais para medir segmentos a partir de uma
unidade fixada; o conceito de número irracional e a representação decimal dos números reais.
d) Insuficiência dos números reais para a resolução de equações algébricas de 2°
e 3° graus; o conceito de número complexo e suas representações — geométrica, algébrica e trigonométrica; interpretação algébrica e geométrica das operações e das raízes de números complexos — raízes da unidade.
e) Matemática financeira como instrumento para a resolução de problemas: os
conceitos de porcentagem, juro simples e juro composto e sua relação com PA e
PG, respectivamente.
f) Sistemas lineares e matrizes como organização e sistematização de informações; discussão e resolução de sistemas lineares (de até 4 equações e até 4 incógnitas) por escalonamento ou por substituição de variáveis.
B. Funções
O documento da Fundação para o Vestibular destaca que, na história mais recente da Matemática, as funções têm um papel de grande destaque por serem instrumentos eficazes na modelagem de problemas reais ou imaginados e por fornecerem formas eficientes de estudá-los. Assim, por exemplo, é importante entender que fenômenos periódicos são descritos principalmente com funções
trigonométricas; que certas situações de crescimento ou decrescimento rápido podem ser representadas por funções exponenciais; que distâncias podem ser
expressas utilizando a função módulo e que a função logaritmo surgiu para permitir simplificações no cálculo de produtos ou potências dos números com muitos dígitos
Enfatiza o documento que a linguagem gráfica, sob várias apresentações, por sua comunicação direta e global, ganha cada vez mais destaque na era da comunicação. Tomam, assim, relevância especial não só a capacidade de leitura e interpretação de gráficos funcionais, conferindo significado às variações das grandezas envolvidas, mas também a competência de saber analisá-los para estimar resultados e fazer previsões. Por outro lado, no que tange à intervenção entre diferentes áreas da própria matemática, os gráficos funcionais são ferramentas importantes para tornar mais significativas as resoluções de equações e inequações algébricas.
Os tópicos referentes a este idem são:
a) A noção de função como instrumento para lidar com variação de grandezas. Os conceitos de domínio e imagem. Caracterizações e representações gráficas e algébricas das seguintes funções: funções módulo, polinomiais de 1° e 2° graus, raiz quadrada, f(x) = xn, f(x) = 1/x, f(x) = 1/x2, funções exponenciais e logarítmicas (cálculo de valores aproximados em casos de expoentes irracionais) e as funções seno, cosseno e tangente (definições geométricas no ciclo trigonométrico e valores nos arcos notáveis) e suas transladadas. Aplicações. b) Reconhecimento e interpretação de gráficos de funções: domínio, imagem,
2.5.2 Orientações dos Programas de Álgebra da VUNESP
Segundo os documentos divulgados pela VUNESP, na edição de 2003, as provas de Matemática de seus concursos vestibulares visam identificar nos candidatos um conhecimento integrado, construído ao longo dos Ensinos Fundamental e Médio, bem como sua criatividade, raciocínio lógico, capacidade de
generalização, enfim, autonomia intelectual. Portanto, as questões de Matemática, segundo essa Fundação, deverão ser elaboradas de modo a evitar a memorização e cálculos excessivos, privilegiando o raciocínio.
Os tópicos de conteúdos Indicados são os seguintes:
A. Conjuntos numéricos
a) Números naturais e números inteiros: indução finita, divisibilidade, máximo divisor comum e mínimo múltiplo comum, decomposição em fatores primos.
b) Números racionais e noção elementar de números reais: operações e propriedades, ordem, valor absoluto, desigualdades.
c) Números complexos: representação e operações nas formas algébrica e trigonométrica, raízes da unidade.
d) Seqüências: noção de seqüência, progressões aritmética e geométrica, noção
de limite de uma seqüência, soma da série geométrica, representação decimal de um número real.
e) Grandezas direta e inversamente proporcionais. f) Porcentagem; juros simples e compostos.
B. Polinômios
C. Equações algébricas
a) Equações algébricas: definição, conceito de raiz, multiplicidade de raízes, enunciado do Teorema Fundamental da Álgebra.
b) Relações entre coeficientes e raízes. Pesquisa de raízes múltiplas. Raízes: racionais, reais e complexas.
D. Funções
a) Gráficos de funções injetoras, sobrejetoras e bijetoras; função composta; função
inversa.
b) Função linear e função quadrática.
c) Função exponencial e função logarítmica. Teoria dos logaritmos; uso de
logaritmos em cálculos.
d) Equações e inequações exponenciais e logarítmicas.
e) Funções trigonométricas: periodicidade, gráficos.
2.5.3 Orientações dos Programas de Álgebra da UNICAMP
O programa de Matemática dos concursos vestibulares da UNICAMP, em sua versão de 2003, indica que a prova de Matemática procura identificar nos candidatos um conhecimento crítico e integrado da Matemática do Ensino Fundamental e do Ensino Médio.
Propõe que, em geral, as questões não devem exigir a repetição de demonstrações de teoremas clássicos, mas o conhecimento das definições e a
compreensão dos principais teoremas é de fundamental importância para um bom desempenho do candidato.
O documento ressalta que, a leitura atenta dos enunciados das questões, a elaboração cuidadosa dos cálculos e de respostas claras, são procedimentos
relacionados ao seu cotidiano bem como interpretar dados expressos em tabelas e gráficos.
Os tópicos de conteúdos indicados são:
A. Conjuntos numéricos
a) Números naturais e inteiros: operações fundamentais.
b) Divisibilidade, números primos, fatoração (teorema fundamental da aritmética), número de divisores, m.d.c. e m.m.c.
c) Números reais (racionais e irracionais): operações, módulo, desigualdades, representação decimal.
d) Seqüências numéricas: Progressões Aritméticas e Geométricas. e) Porcentagens e juros.
f) Números Complexos: operações, módulo, representação trigonométrica, raízes complexas de números complexos (em particular, de um número real).
B. Funções e gráficos
a) A função afim: y = ax + b e seu gráfico. b) As funções y=kx2, k
x
y
=
e y = x e seus gráficos.c) Os gráficos de y = f (x + a), y = –f (x) e f (–x) a partir do gráfico de y = f (x). d) Função composta, função inversa, função par e função ímpar.
e) A função quadrática: y = ax2 + bx + c e seu gráfico (raízes, concavidade, ponto
máximo ou de mínimo, estudo do sinal).
C. Polinômios com coeficientes reais a) Operações com polinômios;
b) Raízes reais e complexas. Divisão por x – a; c) Relações de Girard;
D. Logaritmos e exponenciais
a) A função logaritmo natural y = lnx e sua inversa, a função exponencial y = ex b) A função exponencial y = ax sendo a > 0 e a ≠1.
c) Propriedades dessas funções e estudo de seus gráficos. d) Equações e inequações logarítmicas e exponenciais.
2.6 SINALIZAÇÕES ENCONTRADAS NO EXAME NACIONAL DO ENSINO MÉDIO - ENEM
O Exame Nacional do Ensino Médio - ENEM - foi instituído pela portaria N°0438, de 28 de maio de 1998, do Ministério da Educação e Desporto e tem sido realizado anualmente desde então, sob a responsabilidade do INEP - Instituto
Nacional de Pesquisas Educacionais. Para a criação desse exame, a portaria
N°0438 aponta os seguintes objetivos:
a. conferir ao cidadão parâmetro para auto-avaliação, com vistas à continuidade de
sua formação e sua inserção no mercado de trabalho;
b. criar sua referência nacional para os egressos de qualquer das modalidades de
Ensino Médio;
c. fornecer subsídios às diferentes modalidades de acesso à educação superior;
d. constituir-se em modalidade de acesso a cursos profissionalizantes de Ensino
Médio.
O exame do ENEM é constituído de uma redação e de 63 questões objetivas,
envolvendo assuntos de Português, Matemática, Biologia, História, Geografia, Física
e Química, abordados ao longo de Ensino Médio.
Os resultados obtidos pelos alunos podem ser aproveitados para o ingresso
em várias faculdades do país. O MEC sugere ainda que os relatórios do ENEM
também possam orientar empresas na contratação de funcionários.
demonstradas em 21 habilidades decorrentes de 5 competências fundamentais. Os documentos apresentados pelo ENEM destacam que competências são as modalidades estruturais da inteligência, ou melhor, ações e operações que utilizamos para estabelecer relações com e entre objetos, situações, fenômenos e pessoas que desejamos conhecer. As habilidades decorrem das competências adquiridas e referem-se ao plano imediato do “saber fazer”. Por meio das ações e operações, as habilidades aperfeiçoam-se e articulam-se, possibilitando nova reorganização das competências (INEP, ENEM: documento básico, 1999, p. 7).
As competências avaliadas são:
1. Dominar a norma culta da Língua Portuguesa e fazer uso das linguagens matemática, artística e científica.
2. Construir e aplicar conceitos das várias áreas do conhecimento para a compreensão de fenômenos naturais, de processos histórico-geográficos, da produção tecnológica e das manifestações artísticas.
3. Selecionar, organizar, relacionar, interpretar dados e informações representados de diferentes formas, para tomar decisões e enfrentar situações-problema.
4. Relacionar informações, representadas em diferentes formas, e conhecimentos disponíveis em situações concretas, para construir argumentação consistente.
5. Recorrer aos conhecimentos desenvolvidos na escola para elaboração de propostas de intervenção solidária na realidade, respeitando os valores humanos e considerando a diversidade sociocultural.
É intenção do ENEM não priorizar a avaliação dos conteúdos pré-conhecidos como se observa no texto a seguir:
processamento de informações, as experiências que os contextos socioculturais nos quais o indivíduo se encontra. (INEP, ENEM: Relatório pedagógico 2002, p. 15)
2.7 CONSIDERAÇÕES SOBRE O CAPÍTULO
Muito embora tenhamos analisado a programação de álgebra de edições
mais recentes apresentadas por FUVEST, UNICAMP e VUNESP, nossa prática como professor de curso de preparação ao vestibular, ao longo de muitos anos, mostra que as alterações nesses programas são muito pequenas, de tal forma que nos limitamos a pesquisar uma de suas edições. Em 1976, na época da criação da FUVEST, foram eliminados assuntos que antes eram avaliados como transformações de equações polinomiais, equações recíprocas, limites e derivadas. Essas eliminações também podem ser observadas nos outros vestibulares, com
algumas exceções, como é o caso do vestibular para o Instituto Tecnológico de Aeronáutica — o ITA. Mesmo assim, alguns livros didáticos para o Ensino Médio inclui em seus conteúdos os assuntos Limites e Derivadas, visto que esses tópicos ainda são ensinados em algumas escolas de Ensino Médio.
CAPÍTULO 3
UMA ANÁLISE DAS QUESTÕES DE ÁLGEBRA DE EXAMES
VESTIBULARES REALIZADOS NO ESTADO DE SÃO PAULO
3.1 INTRODUÇÃO
Neste capítulo analisaremos as questões dos vestibulares da FUVEST (1ª fase), VUNESP (conhecimentos gerais) e UNICAMP (1ª fase), nas versões de 2001 a 2003. Analisaremos também as questões da UNICAMP (2ª fase), nas versões de 2001 a 2003.
O objetivo dessa análise é verificar, por meio das questões desses vestibulares, os conteúdos e habilidades que essas instituições estão requisitando dos alunos e compará-las com as orientações dos PCN. Uma primeira constatação é a de que as questões de Álgebra têm participação importante nos exames vestibulares. A tabela 1 mostra a porcentagem de incidência das questões de Álgebra nas provas de Matemática dos anos de 2001, 2002 e 2003 da FUVEST, VUNESP e UNICAMP. Pode-se observar que a presença das questões de Álgebra é considerável, tendo aumentado de ano para ano no período analisado.
Tabela 1 - Incidências das Questões de Álgebra 2001
(%) 2002(%) 2003(%)
FUVEST - 1ª fase 40 40 50
VUNESP - Conhecimentos Gerais 25 33 50
UNICAMP- 1ª fase 25 25 50
3.2 SELEÇÃO DE CRITÉRIOS DE ANÁLISE DAS QUESTÕES
Para analisar as questões dos vestibulares, elegemos alguns critérios, que explicitamos a seguir:
1. Em primeiro lugar, identificaremos os conteúdos algébricos envolvidos na
questão e a sua localização curricular, no Ensino Fundamental ou Médio.
2. Em segundo lugar, procuraremos caracterizar as habilidades exigidas, ou seja:
H1 - Reconhecer e utilizar a linguagem algébrica nas ciências, necessária para
expressar a relação entre grandezas e modelar situações-problema, construindo
modelos descritivos de fenômenos e fazendo conexões dentro e fora da
Matemática.
H2 - Compreender o conceito de função, associando-o a exemplos da vida
cotidiana.
H3 - Associar diferentes funções a seus gráficos correspondentes.
H4 - Ler e interpretar diferentes linguagens e representações envolvendo
variações de grandezas.
H5 - identificar regularidades em expressões matemáticas e estabelecer
relações entre variáveis.
H6 - Utilizar e interpretar modelos para resolução de situações-problema que
envolvam medições, em especial o cálculo de distâncias inacessíveis, e para
construir modelos que correspondem a fenômenos periódicos.
H7 - Compreender o conhecimento científico e tecnológico como resultado de
uma construção humana em um processo histórico e social, reconhecendo o uso
de relações trigonométricas em diferentes épocas e contextos sociais.
3. Em terceiro lugar, buscaremos identificar o nível de conhecimento mobilizado na
resolução da questão, ou seja: técnico, mobilizável e disponível. Essa
classificação foi formulada pela educadora matemática francesa, Aline Robert,
que em seu artigo “Ferramentas de análise de conteúdos a ensinar” (1998)
técnico, mobilizável e disponível.
Robert considera que o aluno põe em funcionamento um conhecimento de nível técnico quando resolve uma questão simples que corresponde a uma aplicação imediata de um teorema, de uma propriedade, de uma definição ou de uma fórmula. Em geral, há indicação do método a utilizar.
No nível de funcionamento mobilizável, os conhecimentos que serão utilizados são bem identificados, mas necessitam de alguma adaptação ou de alguma reflexão antes de serem colocados em funcionamento.
O nível de funcionamento disponível corresponde a resolver uma questão proposta sem nenhuma indicação ou sugestão fornecida pelo professor. É preciso achar nos conhecimentos anteriores o que favorece a resolução da questão.
É interessante destacar que Aline Robert sugere que nenhum desses três níveis
seja negligenciado no ensino da Matemática.
4. Em quarto lugar, analisaremos se a questão foi formulada de modo a associar os conteúdos a um dado contexto. Segundo os PCNEM, a contextualização tem
como característica fundamental o fato de que todo conhecimento envolve uma relação entre sujeito e objeto, ou seja, quando trabalha o conhecimento de modo contextualizado, a escola está retirando o aluno da sua condição de espectador passivo.
Ainda segundo esse documento, a contextualização possibilita ao aluno uma aprendizagem significativa do conteúdo ensinado, estabelecendo entre ele (o aluno) e o objeto do conhecimento uma relação de reciprocidade. Por essa
razão, a contextualização busca resgatar áreas, âmbitos ou dimensões presentes na vida pessoal, social e cultural do aluno e mobiliza competências cognitivas já adquiridas.
experiência escolar para a compreensão da experiência pessoal em níveis mais
sistemáticos e abstratos e o aproveitamento da experiência pessoal para facilitar o processo de concretização dos conhecimentos abstratos que a escola trabalha. Isso significa que a ponte entre teoria e prática, recomendada pela LDBEN (Lei de Diretrizes e Bases da Educação Nacional - 1996), deve ser de mão dupla.
5. Em quinto lugar, analisaremos se a questão foi formulada de modo a evocar conhecimentos de outras disciplinas, para resolver o problema ou para compreender um determinado fenômeno. Aline Robert propõe que chamemos
também de interdisciplinaridade, a qualquer integração, articulação ou conexão
entre grandes eixos temáticos de Matemática como Funções, Geometria, Probabilidade, Trigonometria, etc. Com mais forte razão, consideraremos interdisciplinaridade a aplicação de conceitos matemáticos na solução de problemas de outros temas curriculares como Física, Química, Biologia, etc.
Consideraremos uma questão como de caráter interdisciplinar quando apresentar articulação, entre diferentes áreas de conhecimento, entre disciplinas de uma mesma área ou entre temas integrantes de uma área (Álgebra, Geometria, Análise de dados etc.).
6. Para cada questão, apresentaremos o índice de acertos apurado pela instituição realizadora do exame analisado.
Ainda, para cada questão, procuraremos reconhecer a dimensão da Álgebra envolvida, concepções formuladas por Usiskin (1994).
3.2.1 Análise das Questões de Álgebra da FUVEST - 1ª Fase
3.2.1.1 FUVEST 2001
1. A elipse
4 9 2 y x 2
2+ = e a reta y=2x+1, do plano cartesiano, se interceptam nos
pontos A e B. Pode-se, pois, afirmar que o ponto médio do segmento AB é:
a) − − 3 1 , 3 2 d) − 3 1 , 3 1 b) − 3 7 , 3 2 e) − 2 1 , 4 1 c) − 3 5 , 3 1 Comentário
Trata-se de um item do Ensino Médio sobre Geometria Analítica em que os conteúdos algébricos envolvidos são um sistema não linear de duas equações a duas incógnitas e ponto médio de um segmento no sistema cartesiano. O item exige
H5 (habilidade de identificar regularidades em expressões matemáticas e estabelecer relações entre variáveis). O funcionamento do conhecimento é o de
nível mobilizável; a questão apresenta um contexto matemático e é de caráter interdisciplinar (articulação entre eixos temáticos da Matemática). A dimensão da
Álgebra envolvida nesse item é a de Equação (as letras são vistas como incógnitas). O percentual de acerto foi 25,2%.
2. Sendo P = (a,b) um ponto qualquer da circunferência com centro na origem e
raio 1, que satisfaça b > 0 e a • b, pode-se afirmar que
−
− b 1
a b a
b
log 2 3 2 44
vale:
a) 0 d) log b
b) 1 e) 2 log b