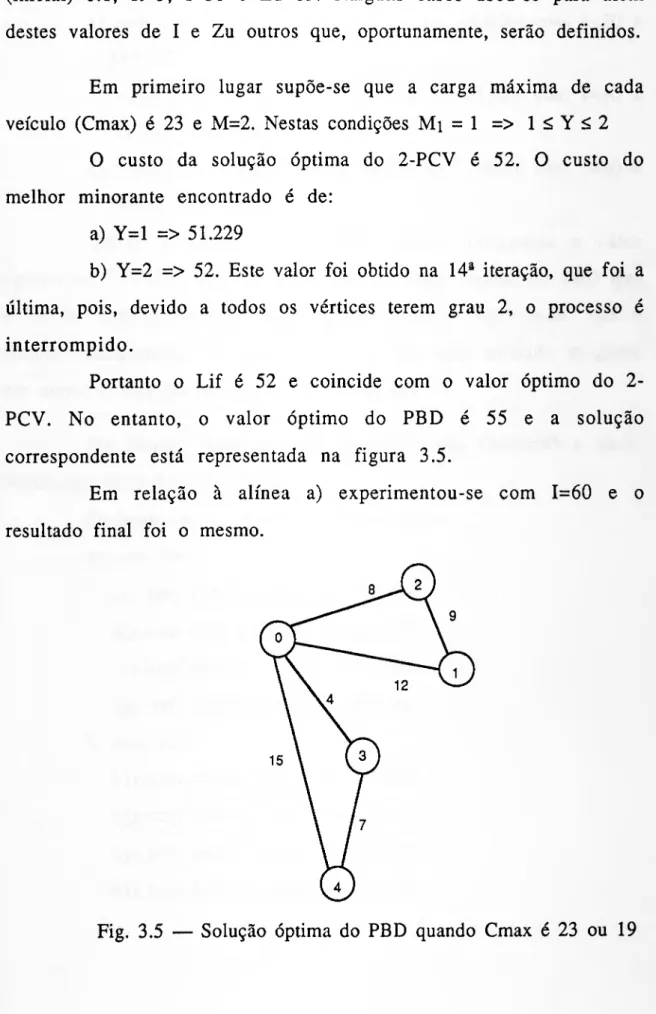
"i-AJ ajQ/Is A(:Ln\ Ç-\ZJ fvc.
APLICAÇÃO DA INTELIGÊNCIA ARTIFICIAL À RESOLUÇÃO DO PROBLEMA DA DISTRIBUIÇÃO
JOSÉ CARLOS SOARES BRANDÃO
UNIVERSIDADE TÉCNICA DE LISBOA r o. <5 66-6' 3 HDMs. Z. 8Z3 SVPLIC&ÇÃO (Dtt I9&LLig'Ê9{pm
MSlflCI&L Â RESOLUÇÃO (DO
(DROELmíJl (DA (DISTXKBílIÇÂO
Dissertação apresentada como requisito parcial para obtenção do grau de Mestre em Métodos Matemáticos Aplicados Economia e Gestão de Empresas
JOSÉ CARLOS SOARES BRANDÃO
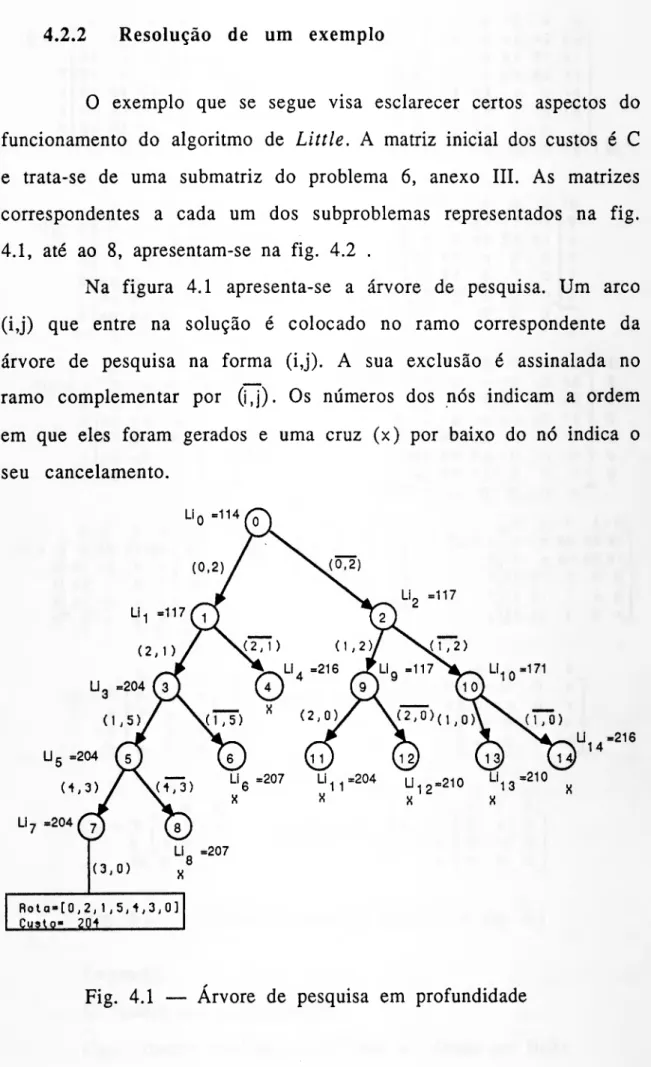
v C O I ^
Expresso um agradecimento muito especial ao orientador desta tese Prof. Doutor Helder Coelho, pelas valiosas sugestões e críticas feitas a esta dissertação e pelo incentivo dado no decurso da sua realização.
Agradeço também ao Centro de Informática do Laboratório Nacional de Engenharia Civil (LNEC) por ter permitido a utilização do computador VAX 8700, sem o qual não teria sido possível processar os exemplos apresentados nesta dissertação.
Finalmente, um agradecimento para todos os colegas e amigos que, de uma forma ou de outra, contribuiram para melhorar a qualidade deste trabalho.
A resolução do problema básico da distribuição consiste em definir um conjunto de rotas e em minimizar o custo total de as percorrer. Cada rota é constituída pelo depósito ou armazém e um conjunto de clientes, cada um dos quais tem uma procura e uma localização geográfica definidas, e é percorrida por um veículo, com uma determinada capacidade, o qual parte do depósito visita uma e uma só vez cada cliente e regressa novamente ao depósito. Cada cliente pertence a uma e uma só rota e o depósito é o mesmo para todos os veículos.
Este problema surge na prática inúmeras vezes, como por exemplo, quando uma empresa armazenista deseja distribuir os produtos pelos seus clientes, na recolha das moedas das cabinas telefónicas, na recolha do correio dos marcos, numa empresa produtora que pretende colocar os seus produtos em diferentes armazéns geograficamente afastados.
Nesta dissertação abordam-se e comparam-se duas formas de resolução do problema básico da distribuição: a exacta, que recorre à técnica da ramificação em árvore e a aproximada que usa o método heurístico de Jameson e Mole.
A resolução exacta pelo método da ramificação em árvore implica a determinação de um minorante e de um majorante para cada subproblema gerado pela ramificação e, ainda, a resolução exacta do problema do caixeiro viajante (PCV) a fim de definir o percurso óptimo de cada veículo.
Aquele minorante é determinado através da introdução de alguns melhoramentos num minorante para o problema do caixeiro
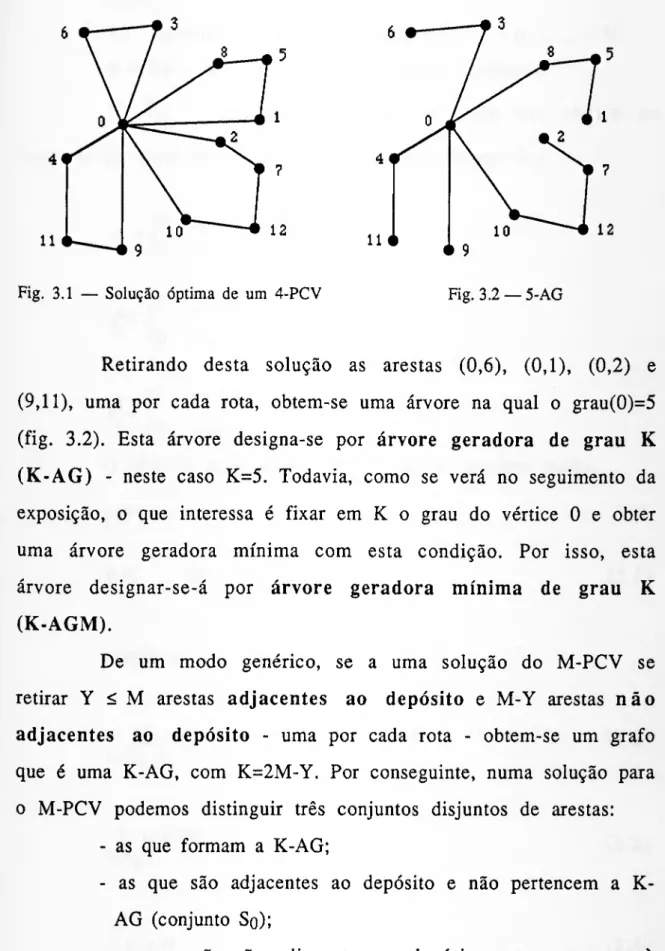
três parcelas: o custo de uma árvore geradora mínima de grau K no depósito, o custo de Y arestas adjacentes ao depósito e o custo de M- Y arestas não adjacentes ao depósito, sendo M o número total de veículos. Mas, para que o valor de um minorante seja o mais alto possível, o problema formado pelo conjunto destas três parcelas é maximizado (dual Lagrangeano) pelo método de optimização subgradiente.
O majorante é determinado pelo método de Jameson e Mole ou por outro método concebido pelo autor deste documento que se designa por exploração sistemática.
A resolução exacta do PCV é feita através do algoritmo de Little, cuja eficiência é aumentada pela introdução de um majorante
inicial que se obtém pela 2-optimização da rota.
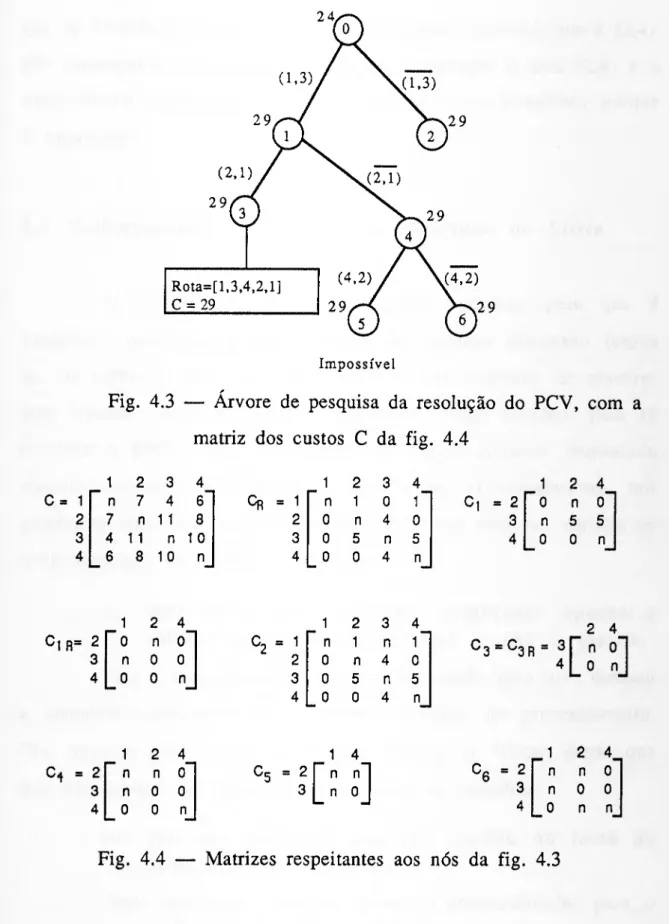
O trabalho de experimentação computacional foi realizado através do recurso a uma linguagem de programação de muito alto nível, Prolog, dialecto CProlog. Os resultados da execução de diversos exemplos mostraram que a versão da linguagem Prolog (interpretador), que se encontrava disponível no ISEG e LNEC, é pouco eficiente computacionalmente quando comparada com as linguagens imperativas em certos tipos de problemas, mas espera- -se que esta desvantagem possa ser ultrapassada, através da utilização de computadores funcionando em paralelo, de uma versão de Prolog compilada e de estruturas de representação do conhecimento mais eficientes, nomeadamente, árvores 2-3. Em contrapartida, as suas vantagens são já uma realidade, como seja, a eficiência do desenvolvimento de protótipos e a facilidade de compreensão, manutenção, modificação e expansão.
The resolution of the basic distribution problem consists of defining a set of routes such that the total cost of travei them be minimum. Each route is composed of the depot or store and a set of clients, each of which has defined a demand and a geographic localization, and it is covered by a vehicle, with a certain capacity, which departs from the depot visits once and only once each client and returns to the depot. Each client belongs to one and only one route and the depot is the same for every vehicles.
This problem appears many times in practice, by example, when a wholesaler enterprise wishes distribute the products by is clients, in gathering of coins of the telephone boxes, in the collection of the mail from the boxes, in an industrial company that pretends
to put its products in differents warehouses geographically distant.
In this dissertation are studied and compared two forms of resolution of the basic distribution problem: the exact, which uses the technique of branch and bound and the approximate resolution which uses the heuristic method of Jameson and Mole
The exact resolution by the tree search algorithm implies the determination of a lower bound and an upper bound for each subproblem created by the ramification and, yet, an exact resolution of the travelling salesman problem (TSP) in order to define an optimal trip for each vehicle.
That lower bound is determined through the introduction of some improvements in a lower bound for the multiple travelling salesman problem (M-TSP). Its value is the result of adding three parts: the cost of a shortest spanning K-degree tree with centre in
depot, the cost of Y edges adjacents to depot and the cost of M-Y edges not adjacents to it, beeing M the total number of vehicles. But in order the value of a lower bound becomes so high as possible, the problem composed by the set of this three parts is maximized (Lagrangean dual) by the subgradient optimization method.
The upper bound is determined by Jameson and Mole's method or for other method conceived by the author of this document which is designated for svstematic exploration.
An exact resolution of TSP is made through LittWs algorithm, which efficiency is improved by the introdution of an mitial upper bound which is get by 2-optimization of the route.
The experimental of computation was realized through the use of the programming language of very high levei, Prolog, on dialect CProlog, The results of execution of various examples shew ^at this version of Prolog language (interpreter), wich was
available at ISEG and LNEC, is computationally inefficient when
compared with the imperative languages in certain type of problems, but is expected that this disadvantage can be overtaken, through the utilization of parallel computers, of one version of Prolog compiled and more efficient of knowledge representation structures, namely, 2-3 trees. In counterpart, its advantages are a reality, like prototype development efficiency, and the facility of understanding, debugging, maintenance, modification and expansion.
ÍNDICE
1 INTRODUÇÃO 1 1.1 Introdução 1 1.2 Definição de objectivos 11 1.3 Organização 12 2 RESOLUÇÃO EXACTA DO PROBLEMA DA DISTRIBUIÇÃO .... 15 2.1 Definição informal do problema 16 2.2 Tipos 18 2.3 Aplicações 2 2 2.4 Definições e notação 2 3 2.5 Formulação matemática do PBD 2 5 2.6 Complexidade computacional 2 7 2.7 Método de ramificação e limitação {"branch
and bound") 2 9 2.7.1 Definições 29 2.7.2 Fases do método 3 2 2.8 Exposição da resolução exacta do PBD pelo método de
pesquisa directa em árvore 3 7 2.9 Exemplo 4 1 2.9.1 Versão 1 4 1 2.9.2 Significado das variáveis dos nodos 4 2 2.9.3 Cancelamento de um nó 4 4 2.9.4 Formação de um nó 4 7 2.9.5 Versão 2 5 1 3 DETERMINAÇÃO DOS MINORANTES 5 4 3.1 Fundamentação matemática 5 5 3.2 Determinação da árvore geradora mínima (AGM) .... 62 3.2.1 Definições 6 3 3.2.2 Algoritmo de Prim 6 4 3.2.2.1 Introdução 6 4 3.2.2.2 Algoritmo 6 6 3.2.2.3 Implementação computacional 6 7 3.3 Determinação da árvore geradora mínima de grau
3.6 Optimização subgradiente para a determinação do dual Lagrangeano 7 9 3.6.1 Resultados dos testes 8 5 3.6.2 Exemplo da determinação de um minorante
através da optimização subgradiente 91 4 PROBLEMA DO CAIXEIRO VIAJANTE 9 5 4.1 Introdução 9 6 4.2 Exposição do método de Little 9 7 4.2.1 Ramificação e escolha do nodo 9 8 4.2.2 Resolução de um exemplo 9 9 4.3 Algoritmo de Little 104 4.4 Implementação computacional 107 4.5 Melhoramentos a introduzir no algoritmo de Little ... 112 4.6 Influência do majorante inicial no algoritmo de Little. 114 4.7 Resolução aproximada do PCV 116 5 RESOLUÇÃO APROXIMADA DO PBD 121 5.1 Critérios de expansão das rotas 122 5.2 Classificação dos métodos quanto à forma de
construção das rotas 124 5.3 Método de Jameson e Mole 125 5.3.1 Dedução das fórmulas para o algoritmo 126 5.3.2 Algoritmo 131 5.3.3 Teste ao programa 132 5.3.3.1 Apresentação e análise dos resultados ... 134 6 IMPLEMENTAÇÃO COMPUTACIONAL 140 6.1 Introdução 140 6.2 Inicialização e apresentação dos resultados 143 6.3 Informação a reter em cada nodo e tratamento da
solução obtida com HJMPBD 144 6.4 Método de exploração sistemática 148 6.5 Geração de combinações de clientes admissíveis 15 2 6.5.1 Determinação dos dados 153 6.5.2 Minimização das combinações geradas 154 6.5.3 Algoritmo 157
6.6.1 Exemplos e conclusões 164 7 RESULTADOS DA RESOLUÇÃO DO PBD 167 7.1 Introdução 167 7.2 Apresentação dos resultados 169 7.3 Análise dos resultados 170 7.4 Conclusões 172 8 CONCLUSÕES E PROPOSTAS DE MELHORAMENTOS 175 8.1 Propostas de melhoramento 177
Anexo I - Tabelas com os resultados da execução de problemas cujos dados se encontram no anexo III. Os problemas foram processados em CProlog, num computador VAX 8700 182 Anexo II - Programas escritos em CProlog, designados por
REPBDM, MPB DM, PCVPBDM, HJMPBDM, HMOJM e OP2SYM 187 Programa REPBDM 189 Programa MPB DM 201 Programa PCVPBDM 208 Programa HPBDM 214 Programa HMOJM 217 Programa OP2SYM 224 Ficheiro de dados 226 Anexo III - Dados dos problemas utilizados como exemplos. .. . 227
1
INTRODUÇÃO
1.1 Introdução
Recentemente, têm surgido cada vez maior número de artigos nos quais se procura aprofundar a relação da Inteligência Artificial (IA) com a Investigação Operacional (IO), a fim de se tentar resolver mais eficazmente uma enorme variedade de problemas. Na verdade, quase todos os problemas típicos da Investigação Operacional poderão beneficiar, aquando da sua aplicação à vida real, da colaboração com a Inteligência Artificial, e inversamente. A justificação para este facto é elementar, pois, como
e óbvio, os problemas reais não pertencem a nenhuma destas
ciências, mas a sua resolução pode aproveitar a sinergia da aplicação conjunta das duas, consoante se tentará provar no texto que se segue.
Antes de mais vai-se procurar definir cada uma destas ciências, muito embora, em muitos aspectos elas se confundam, o que, segundo Simon [39] é benéfico e deve, inclusivamente, ser incentivado.
Segundo Simon [39], a IO é aplicação de técnicas de optimização à resolução de problemas complexos que podem ser
O objecto de estudo da IA não é tão pacífico como o da IO, por isso, vão ser dadas duas definições que enquadram bem o conteúdo do presente trabalho.
Ainda segundo Simon, a IA é a aplicação de métodos de pesquisa heurística à solução de problemas que desafiam a optimização matemática, contém componentes não quantificáveis, envolvem vastas bases de conhecimento (incluindo conhecimento expresso numa língua natural), incorporam a descoberta e o projecto de alternativas para escolha e admitem metas e restrições vagamente especificadas.
Por sua vez, Scown (1985), citado por Coelho [14], define a IA como o conjunto de técnicas de resolução de problemas em computador que têm sido desenvolvidas para imitar o pensamento humano ou os processos de tomada de decisão, ou ainda para produzir os mesmos resultados que aqueles processos.
Ainda no mesmo artigo atrás citado, Simon exprime com ênfase a opinião de que a IA e a IO deverão dar as mãos para atacarem os problemas reais, nomeadamente os que se levantam no domínio da Ciência da Administração. Este autor exemplifica com os problemas de escalonamento nos seguintes termos: "while OR has been able to provide a theoretical analysis of scheduling problems for very simple situations - automatic scheduling of large job shops with many machines and processes has been beyond the scope of exact optimization methods. A scheduling system in such a situation, must be built upon a data base that contains a detailed description of machines, scheduling routes, and jobs. That kind of description can be achieved with the help of the data-base
diz mesmo que em vez de se diferenciar a IO e a IA se deve confundi-las, misturá-las e sintetizá-las o mais possível.
Mesmo na tradição corrente, a fronteira entre a IA e a IO nem sempre é nítida o que é comprovado pelo facto de existirem muitas técnicas e problemas que são tratados, quer em livros de IA, quer de IO. Por exemplo, em livros de IA de Bratko [5], Kowalski [26], Nilsson [34] e Pearl [35], são tratados os métodos de pesquisa em árvore, os quais são expostos neste trabalho no capítulo 2, bem como os métodos heurísticos ou de procura heurística para a resolução de problemas. Ora, ambas estas questões são comuns à IO. Quanto a problemas concretos que tradicionalmente são tratados pela IO e que são também estudados em livros de IA pode citar-se, a título de exemplo, o problema da sequenciação de tarefas nas
máquinas, a determinação do caminho de menor custo entre dois
vértices de um grafo e a determinação da árvore geradora mínima de um grafo.
Phelps [36], num artigo recente (1986) indica para cada uma das áreas tradicionais da IA, propostas da aplicação da IO e da Estatística. Em seguida dá-se alguns exemplos das suas propostas.
Quanto á área da criação de visão nas máquinas, Phelps tnostra em que questões se podem aplicar técnicas de IO como, por exemplo, a programação dinâmica e a linear. Na área da linguagem cie sugere a aplicação da programação dinâmica no reconhecimento das palavras faladas, mas não sugere nenhuma técnica de IO para a interpretação do discurso. Na área de engenharia do conhecimento Phelps aponta como possíveis aplicações da IO a teoria dos jogos, na análise de diferentes respostas (por peritos distintos) a situações
hipotéticas, e o escalonamento multidimensional, na descoberta das verdadeiras razões que motivaram determinadas decisões.
A presente tese de Mestrado surge precisamente nesta linha de pensamento, isto é, na procura de uma solução para o problema da distribuição recorrendo à IA e à IO.
O problema da distribuição consiste em definir as rotas que devem ser percorridas por um conjunto de veículos (cada um dos quais tem uma determinada capacidade) a fim de satisfazer as necessidades (por exemplo, entrega e/ou recolha de mercadorias) de um conjunto de clientes, com uma localização geográfica conhecida. As rotas são definidas de modo a que sejam atingidos determinados objectivos, em que, o mais frequente é a minimização do custo total das rotas. Cada cliente é visitado por um e um só veículo, que parte do armazém ou depósito e a ele regressa no final.
A importância prática do problema da distribuição dispensa grandes comentários, visto que é do conhecimento geral o facto de haver actualmente uma enorme movimentação de pessoas e coisas e de o custo de transporte relativamente ao custo total de qualquer bem ou serviço ser muito significativo. Além disso, a tendência actual é no sentido do crescimento do peso relativo do custo de transporte.
A definição dada anteriormente sobre o problema da distribuição corresponde, sensivelmente, ao que no capítulo 2 se designará por problema básico da distribuição (PBD). Quando se define o problema deste modo pode-se afirmar que ele pretence ao domínio da IO, mas, mesmo assim, ainda é um problema complexo cuja resolução exacta ou aproximada poderá beneficiar da aplicação das técnicas e ferramentas da IA. Acrescente-se, todavia, que os problemas de distribuição da vida real são normalmente mais
poderão verificar na prática, cita-se as seguintes: existência de vários depósitos de mercadorias, possibilidade de ultrapassar ligeiramente a capacidade nominal dos veículos, o mesmo cliente necessita de diferentes tipos de mercadorias que não podem ser misturadas, um cliente não é servido num determinado período mas sim no seguinte, a frota de veículos pode ser aumentada, a visita aos clientes tem de se verificar num determinado período do dia, um cliente é rejeitado porque é demasiado dispendioso servi-lo, o horário normal de um condutor é ultrapassado mediante o pagamento de horas extradordinárias.
A restrição de os clientes só poderem ser visitados em determinados períodos do dia pode ser abordada como um problema de escalonamento ("scheduling problem"). O facto de existirem diferentes mercadorias que não podem ser misturadas pode ser abordado como um problema de carregamento ("loading problem"). Por conseguinte, a resolução de um problema concreto de distribuição pode necessitar da resolução simultânea do problema básico e de diversos outros problemas típicos da IO. Portanto, aonde a IA poderá desempenhar um papel importante é no estabelecimento de um sistema informático que permita estabelecer uma ligação eficaz entre os diversos subproblemas e, simultaneamente, estabelecendo a ligação com o utilizador. Este, principalmente se for especializado, poderá inserir no dito sistema — no início e durante a resolução — nova informação de natureza qualitativa e/ou quantitativa, que possivelmente contribuirá para facilitar a resolução e/ou melhorar a qualidade das soluções. Esta informação será fornecida pelo utilizador, quer com base nos seus conhecimentos à priori, quer com base nos resultados intermédios
eficazes na resolução daqueles subproblemas.
Note-se que naquela interacção com o utilizador já se está a incluir a possibilidade de gerar diversas alternativas motivadas pela variação de certos parâmetros — como seja, a supressão de determinado cliente, a ultrapassagem, em segurança, da capacidade nominal do veículo, o pagamento de horas extraordinárias ao condutor, etc. — por conseguinte, aproveitando a sensibilidade do utilizador.
Na presente tese dada a vastidão do problema que aborda, não se pretende criar um sistema informático final pronto a ser usado na prática, o qual se poderia designar por sistema de apoio à decisão (SAD), para usar a terminologia corrente. Apenas se pretende criar uma estrutura básica que, futuramente, possa ser ampliada e melhorada, mediante um número reduzido de alterações evoluindo para um sistema completo. Isto só é possível, por se usar como linguagem de programação o Prolog que tem como uma das principais vantagens, a facilidade de compreensão dos programas e modificação posterior, e simultaneamente, é excelente para fazer a interacção com o utilizador e para criar e processar bases de conhecimento.
O Prolog é de todas as linguagens de programação existentes actualmente aquela que mais se aproxima da linguagem natural. Mais propriamente, é uma linguagem de muito alto nível que se fundamenta na lógica matemática e daí a origem do seu nome ("Programming in Logic"). Por conseguinte, o paradigma da programação em Prolog é programa = lógica + controlo, enquanto que o paradigma da programação em linguagens imperativas, como
dados, veja-se por exemplo, Coelho et al [15].
Um programa em Prolog é constituído por um conjunto de procedimentos e estes são compostos por cláusulas. Uma cláusula pode ser um facto uma regra ou uma pergunta. Numa regra deve-se considerar a cabeça e o corpo, sendo a cabeça formada por uma meta e o corpo por uma ou mais metas. Um facto é representado através de uma estrutura, e uma meta através de uma estrutura ou uma expressão aritmética. Uma estrutura, tal como uma expressão aritmética, exprime uma relação entre objectos, os quais, por sua vez, podem ser simples objectos — átomos, números ou variáveis — ou também estruturas. Geralmente, uma estrutura — objecto com várias componentes — é representada através de um functor com os argumentos entre parêntesis curvos, embora a representação possa ser outra, mediante a utilização de operadores. Estes argumentos podem ser simples objectos ou também estruturas. Pode-se dizer que todas as estruturas são árvores. Uma das estruturas mais utilizada para representar grupos de objectos é a lista, que é uma árvore binária. Mas trata-se de uma árvore totalmente desequilibrada (degenerada), isto é, na qual um dos ramos que parte de cada nó tem muitos mais elementos que o outro. Por isso, as operações com listas de N elementos têm uma complexidade que é O(N). Todavia, é possível usarem-se outros tipos de árvores cuja complexidade computacional é O(logN), sendo N o número de elementos da árvore. De entre estas árvores cite-se: árvores 2-3 e árvores-AVL.
Embora nos programas desta tese se tenham usado listas foram envidados todos os esforços para maximizar a eficiência computacional. Por exemplo, para a ordenação de listas foi usado
matriz dos custos associados às arestas destes é representada por uma lista de N listas cada uma com N-l elementos (cf. capítulo 3 e programas, anexo II). Portanto, para encontrar um elemento nessa lista é necessário, no pior caso, procurar N+N-l elementos. Ora, se a representação fosse feita como uma lista com N(N-l)/2 elementos (a matriz é simétrica) seria necessário, no pior caso, procurar este número. Obviamente, que mesmo com aquela representação por listas de listas ainda seria possível aumentar a rapidez, aproveitando o facto da matriz ser simétrica.
Relativamente à equação referida anteriormente as cláusulas correspondem à primeira parcela, isto é, a lógica — relações lógicas entre os fenómenos, enquanto que o controlo é feito através da ordenação das metas e das cláusulas e do corte (!). O corte é uma espécie de "pseudo-meta" que é inserida entre as outras metas do corpo ou também no início ou no fim deste. A ordem das metas e cláusulas não afecta o significado do programa, apenas pode alterar a sua eficiência computacional. Quanto ao corte ele pode ser de dois tipos: o corte verde ("green cut") que apenas poderá ter implicações na eficiência computacional e o corte vermelho ("red cut") — este vem sempre assinalado nos programas que se encontram no anexo II — que, além disso, modifica o significado do programa.
Em todas as publicações de que o autor tem conhecimento é afirmado que o corte aumenta a eficiência computacional porque reduz o retrocesso ("backtracking") e, por conseguinte, quando ele actua, isso traduz-se numa diminuição do tempo de processamento e do consumo de memória central. Todavia, conforme se verá no
central (o tempo de processamento mantem-se), sem que isso esteja relacionado com a redução efectiva do retrocesso.
Embora o Prolog tenha sido amplamente utilizado por muitos especialistas da IA em problemas de optimização em redes — veja-se, por exemplo, Lee [28] — não existe, que o autor conheça, nenhum estudo comparativo da sua eficiência computacional com a de outras linguagens, nomeadamente as imperativas. Aliás, não existem sequer dados relativamente à eficiência do Prolog apenas. Além disso, que o autor saiba, é a primeira vez que o Prolog é aplicado na resolução do problema da distribuição. Por isso, um dos contributos que se pretende dar com esta dissertação é ajudar a preencher essa lacuna. Naturalmente, que se tem consciência que, se o estilo de programação for diferente, se as soluções encontradas para estruturar e desenvolver o programa forem outras e se o computador for de outro tipo, também a eficiência virá diferente da apresentada neste trabalho. Por isso mesmo, se apontam propostas de melhoramento no capítulo 8.
A escolha do Prolog deveu-se, para além das razões já expostas, a que esta linguagem está especialmente vocacionada para pesquisa em árvore, sendo este um método particularmente indicado para a resolução exacta do problema da distribuição.
Resumidamente, a ideia central deste trabalho é desenvolver um projecto amplo e com vastas aplicações práticas. Contudo, como esse projecto seria demasiado extenso, procurar-se-á criar apenas alicerces sólidos que possam suportar futuros desenvolvimentos. Dizendo de outro modo, o sistema desenvolvido na presente tese, permite obter soluções finais exactas ou aproximadas, para o problema básico da distribuição (PBD).
Ou seja, soluções para os casos mais "simples" do problema da distribuição, visto que não se tomam em consideração muitas das restrições que poderão aparecer na prática. Por outro lado, só permite obter a solução exacta em exemplos de dimensão reduzida. Portanto, o presente sistema deverá evoluir orientado pelos seguintes vectores:
— melhorar a interacção com o utilizador;
— permitir a resolução de casos com maior variedade de restrições;
— aumentar a eficiência computacional, quer em memória gasta, quer em tempo de execução, de modo a permitir a resolução exacta, em tempo útil, de problemas de maior dimensão.
Os dois primeiros aspectos são relativamente mais fáceis de implementar que o último. Quanto a este dão-se, no final do presente documento, algumas sugestões que poderão ajudar parcialmente a aumentar a eficiência computacional. Todavia, as principais melhorias, no caso da resolução exacta, só poderão advir de novas descobertas nesta área da Investigação Operacional — por exemplo, descoberta de algoritmos mais eficientes, melhoria dos minorantes e majorantes, descoberta de novas formas de redução.
Todos os programas utilizados nesta dissertação foram executados pelo autor. O programa em Basic foi executado no âmbito de um outro trabalho ([4]) e os exemplos também. Estes foram resolvidos num computador VAX 11/780, após a compilação do programa. Por sua vez, os programas em Prolog foram codificados em CProlog (versão de Edimburgo) e em BIM_Prolog 2.3 VAX/VMS. Contudo, os exemplos cujos resultados se apresentam nesta
computador VAX 8700, instalado no LNEC, sendo esta versão não compilada. Esta opção pelo CProlog foi motivada pelo facto do BIM_Prolog 2.3 VAX/VMS, apesar de ser compilado, estar instalado apenas num computador VAX-3600 cuja memória central se mostrou insuficiente para para o processamento dos exemplos desejados.
Todos os programas executados em Prolog no âmbito desta tese usam estruturas de representação do conhecimento semelhantes, tendo-se recorrido, fundamentalmente, às listas.
1.2 Definição de objectivos
O conteúdo da secção anterior justifica plenamente que se defina como principais objectivos a atingir no trabalho que agora se apresenta, os seguintes:
1 - aplicar uma ferramenta que é por excelência o suporte básico da Inteligência Artificial - a programação em lógica (Prolog), a um problema da Investigação Operacional - o problema da distribuição;
2 - tirar conclusões sobre as vantagens e desvantagens da aplicação do Prolog sobre outras linguagens de programação, tomando como base, quer a experiência do autor, na resolução computacional de diversos exemplos, quer os dados recolhidos na literatura;
3 - indicar quais os principais aperfeiçoamentos que o Prolog e/ou o equipamento computacional de processamento deverão sofrer para que as desvantagens sejam ultrapassadas, como corolário do objectivo anterior.
Para a resolução exacta do problema da distribuição é necessário encarar também diversos outros problemas de optimização combinatória. A cada um destes problemas é dedicado um capítulo no qual se tratam todos os aspectos importantes que lhe dizem respeito: apresentação, implementação computacional, resultados da resolução de um número significativo de exemplos, análise dos resultados, e conclusões. No início de cada capítulo é feito um resumo de todos os assuntos tratados nesse capítulo.
O capítulo 2 é dedicado à apresentação do problema da distribuição - enunciado, aplicação, uma formulação exacta e exposição detalhada do método que foi seguido neste trabalho para a sua resolução exacta.
O capítulo 3 ocupa-se da descrição do método para a determinação de minorantes para o problema da distribuição, baseando-se em minorantes para o problema do caixeiro viajante múltiplo (M-PCV), mas melhorados através da introdução de restrições adicionais. A metodologia seguida é a proposta por Christofides et al. [12].
No capítulo 4 trata-se da questão da resolução exacta do problema do caixeiro viajante (PCV). A solução obtem-se através da ramificação em árvore ("branch and bound"), fazendo-se reduções sucessivas na matriz dos custos, segundo o método proposto por Little et al. [31]. No entanto, elaborou-se uma modificação original com vista a reduzir o espaço de procura, aumentando-se desta forma a eficiência computacional.
resolução do problema da distribuição, que conduz a obtenção de soluções aproximadas, geralmente de boa qualidade. O método utilizado é o proposto por Jameson e Mole [25], embora não seja integralmente seguido, como depois se verá.
Por sua vez, o capítulo 6 é preenchido com a implementação computacional. O que se descreve neste capítulo é a forma como foram resolvidas algumas das questões mais intrincadas, mas relativamente apenas ao caso da resolução exacta, apontando-se também outras soluções que poderiam ter sido adoptadas.
O capítulo 7 é dedicado à apresentação e análise dos resultados da resolução de diversos exemplos. Estes exemplos foram recolhidos na literatura da especialidade.
No capítulo 8 são apresentadas as conclusões e feitas as propostas de desenvolvimento futuro.
No anexo I encontram-se as tabelas com os resultados dos exemplos resolvidos.
No anexo II encontram-se todos os programas escritos em CProlog que serviram para correr todos os exemplos referidos ao longo da tese. Em primeiro lugar aparece o programa que permite fazer a resolução exacta do PBD, que é constituido por 4 módulos: REPBDM, MPBDM, PCVPBDM e HJMPBDM. Em seguida apresenta-se o programa que permite fazer a resolução aproximada do PBD e que é designada por HMOJM, Por último, apresenta-se o programa que permite fazer a 2-optimização de uma rota segundo o algoritmo proposto por Syslo et al. [41] — designado por OP2SYM — e um exemplo de um ficheiro de dados. Os programas que são utilizados no capítulo 3 para a determinação dos minorantes e no capítulo 4
se a que eles se encontram implícitos, respectivamente, em MPBDM, PCVPBDM e HMOJM e, por conseguinte, a sua apresentação não iria acrescentar nada de específico. Portanto, os módulos MPBDM e PCVPBDM permitem determinar, respectivamente o minorante de um problema e o percurso óptimo numa rota, mas para trabalharem independentemente é necessário acrescentar-lhes algumas cláusulas genéricas que se encontram no módulo principal REPBDM. O mesmo se passa relativamente ao programa para se fazer a 2-optimização que faz parte de HMOJM (e também de HJMPBDM) e nele se encontra devidamente discriminado.
RESOLUÇÃO EXACTA DO PROBLEMA DA DISTRIBUIÇÃO
Este capítulo é, como o seu título indica, o dedicado à resolução exacta do problema da distribuição. Por isso, são expostos aspectos básicos do método de resolução utilizado, mas, como alguns desses aspectos são por si sós muito amplos, são explicados separadamente nos capítulos subsequentes. Os diferentes assuntos são tratados na sequência seguinte: definição genérica do problema de distribuição e suas designações mais correntes na literatura; classificação dos diversos problemas práticos em dois grupos, um dos quais — o problema básico — é estudado neste trabalho; aplicações; formulação matemática do problema básico, aonde se incluem também certas definições e notação que servirá para todo o documento; complexidade computacional do PBD; resolução pelo método da ramificação e limitação, aonde se expõem os conceitos fundamentais sobre este método, os quais serão aplicados na secção seguinte na qual se explica como se resolve o caso concreto do PBD; e, para terminar, dá-se um exemplo da resolução do PBD a fim de clarificar alguns aspectos mais obscuros da secção anterior.
O problema da distribuição consiste na determinação dos percursos que uma frota de veículos (cada um dos quais com uma dada capacidade) deverá efectuar para satisfazer a procura de um conjunto de clientes, com uma localização geográfica conhecida, de modo a que o custo total dos percursos seja mínimo. Cada cliente é visitado uma e uma só vez por um único veículo que parte do depósito ou armazém e regressa novamente ao local de partida.
Por exemplo:
0-0
DEPÓSITO
rota 2
Fig. 2.1 — Exemplo de uma solução para um problema da distribuição
Legenda:
1, 2, ... , 10 - clientes
ideias, que o objectivo a atingir é minimizar o custo total dos percursos, na realidade pode haver outros objectivos que serão enumerados na seccão seguinte.
Há dois problemas de optimização combinatória que se assemelham com o problema da distribuição, os quais são enunciados de seguida.
Problema do caixeiro viajante (PCV) — determinar o trajecto que um caixeiro viajante deve efectuar, para que percorra a menor distância possível, partindo de uma qualquer cidade visite todas as restantes uma e uma só vez e regresse novamente à cidade de partida. A localização geográfica das diferentes cidades supõe-se conhecida.
Problema do caixeiro viajante múltiplo (M-PCV) — determinar o trajecto de M caixeiros viajante que partem da mesma cidade, visitam uma ou mais cidades e regressam novamente à cidade de partida, de modo a que a distância total a percorrer pelos M caixeiros seja mínima. Cada cidade é visitada uma e uma só vez por um único caixeiro e todas as cidades têm uma localização geográfica conhecida.
Antes de mais deve-se notar que o PCV é um caso particular do M-PCV em que M=l. Por sua vez, o M-PCV é um caso particular do problema básico de distribuição (é definido com rigor na secção seguinte) em que os M caixeiros correspondem a M veículos com capacidade infinita e a cidade de partida corresponde ao depósito ou armazém e as restantes correspondem aos clientes.
O problema da distribuição tem sido abordado na literatura sob as mais diversas designações:
- problema do loteamento de veículos {"vehicle routing problem" (VRP) - Christofides [8,11,12], Savelsbergh [38], etc.):
- problema do escalonamento de veículos {"vehicle scheduling problem" - Clarke & Wright, 1964\ Gaskell [20]; Christofides et al. [10], etc.);
- problema do despachamento de camiões ("truck dispatching problem" - Dantzig & Ramser, 1959', Christofides & Eilon
[9], etc.);
- problema das entregas {"delivery problem" - Balinski e Quandt [2]; Hays, 1967, etc.).
Contudo, a designação mais comum na literatura inglesa do problema da distribuição é VRP.
2.2 Tipos
Na prática poder-se-ão verificar uma enorme variedade de situações, quer quanto aos objectivos a atingir, quer quanto às restrições associadas aos clientes, quer quanto às características dos veículos, quer quanto às características da carga. Por conseguinte, não é fácil arranjar uma classificação que enquadre todos estes aspectos e que, simultaneamente, seja aceite por todos. Contudo, uma sistematização tem o maior interesse para facilitar o estudo e a modelização das situações práticas.
A divisão aqui adoptada é a proposta por Christofides [8,11,12]: problema básico e problema alargado. Embora sendo uma divisão muito elementar é perfeitamente adequada para os objectivos em vista. Note-se, todavia, que mesmo aquele autor, relativamente ao problema básico, dá uma definição que é
apresentar em seguida as diferenças entre os dois tipos de problemas através dos seus enunciados formais.
No problema básico da distribuição (PBD) considera- -se o seguinte:
- existe um conjunto de N clientes: {1, 2, ... , N) e um depósito ou armazém {0};
- cada cliente i necessita de uma determinada quantidade qi de um certo produto;
- o custo de descarga de qj no cliente i é uj;
- existe um conjunto de M veículos V = {vk: k=l, 2, ... , M), estacionados no depósito, os quais têm todos a mesma capacidade máxima Q;
- o custo de caminho de menor custo de i, a j é cjj e o tempo de percurso correspondente é ty;
- cada rota não pode ter um custo superior a um determinado valor T;
- supõe-se que o número M de veículos é suficiente para que haja uma solução admissível;
- todos os clientes deverão ser satisfeitos;
- o objectivo é minimizar o custo total das rotas, respeitando as restrições existentes.
Note-se que aqui como, aliás, em toda esta dissertação o termo custo é empregue em sentido genérico, podendo significar tempo, distância, etc. Na prática, poderá existir uma matriz de custos propriamente ditos e uma matriz de tempos. A matriz dos tempos é indispensável, nos casos em que se impõe um tempo
máximo de viagem para cada veículo, bem como nos casos em que há períodos próprios para servir os clientes.
Por sua vez, o problema alargado, tem como suporte o problema básico, mas são-lhe introduzidas algumas alterações e/ou adicionadas novas condições, de modo a adaptá-lo mais rigorosamente às situações práticas.
a) Quanto aos clientes
Um cliente i poderá ter as seguintes necessidades ou características:
- um conjunto L\ de diferentes tipos de produtos a serem entregues por um veículo, a cada um dos quais está associada uma determinada quantidade qn, 1=1,2, ... , Lí;
- um conjunto de intervalos de tempo Pi, durante os quais as entregas podem ser feitas. Estes intervalos de tempo estão dispersos ao longo do dia e são definidos pelo momento inicial e final - Xip e T^p, com p=l, 2, ... , Pj, Fora destes intervalos não é possível fazer entregas. Esta restrição é muito frequente e costuma a ser designada na literatura por janelas temporais ("time windows"). Os problemas de distribuição em que ela aparece já foram estudados por muitos autores, tais como, Savelsbergh [38], Christofides, etc. ;
— apenas uma parte dos veículos disponíveis o poderão visitar, VicV. Isto pode dever-se, por exemplo, a que as estradas de acesso ao cliente não permitem a passagem de veículos superiores a uma determinada carga;
— pode tratar-se não só de entregas mas também de recolhas. As quais poderão ser feitas num único percurso da rota ou, pelo contrário, deverá fazer-se primeiro todas as entregas da rota e, só em seguida, é que o veículo irá repetir o percurso para proceder às recolhas.
b) Quanto aos veículos
O veículo Vk tem as seguintes características:
— um conjunto de compartimentos Hk para transportar os produtos. A cada compartimento (k, h), h=l,2, ... , Hk está associada a capacidade Qkh;
— um conjunto Gk de períodos de trabalho, sendo cada período definido pelo momento inicial e final, respectivamente, Tkg
e Tkg, g = 1, ... , Gk- Fora destes períodos, devidos normalmente ao
horário de trabalho dos condutores, o veículo está parado;
— um tempo 0k necessário para carregar o veículo no depósito;
— pode percorrer mais do que uma rota desde que não seja ultrapassado o tempo máximo de percurso Tk, previamente estabelecido;
— existem múltiplos depósitos das mercadorias interdependentes — cada veículo pode partir de um depósito visitar um grupo de clientes e terminar o percurso noutro depósito, aonde carrega para servir novo grupo de clientes;
— cada veículo tem um custo fixo associado Ck
c) Quanto aos objectivos
O i — maximizar a soma das prioridades dos clientes que podem ser servidos por uma frota de veículos;
O2 — minimizar os custos fixos dos veículos usados nos percursos;
O 3 — minimizar o custo total variável das rotas.
Em cada problema particular pode-se fixar que se pretende atingir um ou mais destes objectivos, por ordem de prioridade. Todavia, o objectivo Oi deve estar sempre presente, pois, de contrário, o valor óptimo para os outros seria O, o que corresponderia a nenhum veículo e a nenhum cliente ser satisfeito.
2.3 Aplicações
As diversas aplicações referidas a seguir enquadram-se na definição do problema feita anteriormente, desde que se substitua os termos clientes, mercadorias e veículos por outras entidades de função equivalente:
a) - entrega e ou recolha de mercadorias a clientes; b) - recolha do correio dos marcos;
c) - transporte de crianças pelos autocarros escolares;
d) - visitas de um médico ou de um conjunto de médicos de um posto clínico, à casa dos doentes;
e) - inspecções de manutenção preventiva; f) - percurso do caixeiro viajante.
Visto que as aplicações práticas do problema da distribuição são muitas e variadas e que os custos associados — combustível, veículos, mão-de-obra, etc. — também são elevados, há todo o interesse em determinar boas soluções.
O PB D pode ser representado por intermédio de um grafo G = (V,A), sendo V o conjunto dos vértices e A o dos arcos ou arestas. V={0, 1, 2, ... , N}, em que 0 representa o depósito e 1, 2, ... , N os clientes. Os vértices também poderão ser designados por nodos ou nós.
A={0} xNuIuNx {0}, em que {0} x N contém os arcos que vão do depósito para os clientes e N x {0}, os que vão dos clientes para depósito. Por sua vez, IcNxN é o conjunto dos arcos que ligam os clientes entre si.
A cada arco (i, j)e A corresponde um custo Cij. Cada cliente ieV\{0} tem uma procura qj. Portanto,
Cij - é o custo do caminho de menor custo entre o vertice ie V e o vertice je V. Ou seja,
C = [cij] i = 0, 1, 2, ... , N é matriz dos custos j = 0, 1,2, ... ,N
A matriz C diz-se;
— simétrica se Vi, je V Cij=Cji, por isso, ao problema chama-se simétrico. Se a matriz não é simétrica o problema diz-se assimétrico;
— completa se Vi^jeV, cij existe e é finito;
— que satisfaz a desigualdade triangular se Cik^Cij+Cjk, Vi, j, k, e V.
Ao longo desta dissertação supõe-se que a matriz dos custos é simétrica, completa e que satisfaz a desigualdade
Na prática, quando se está a programar, para impedir a ligação entre determinados vértices, costuma-se representar o custo correspondente por um valor arbitrariamente alto. Todavia, ao longo desta dissertação, bem como na programação, em vez disso usar-se-á um n, uma vez que a linguagem de programação o permite facilmente, e tem a vantagem de ser sempre válido independentemente dos valores assumidos pelos custos.
Se a matriz C é simétrica, cada elemento de A costuma designar-se por aresta e G é um grafo não orientado. Caso contrário, os elementos de A designam-se por arcos e G é um grafo orientado.
Num grafo não orientado chama-se grau de um vértice — representa-se por grau(v) — o número de arestas que nele incide.
Uma rede é um grafo orientado ou não orientado no qual se faz corresponder a cada arco um número real, designando-se este por peso ou custo.
Cadeia de comprimento k em G=(V, A), é uma sequência de arestas:
em que a, tem um vértice em comum com a. , e outro
4 'r 1 r-1
com a. 1 ^ r ^ k-1. r+1
Caminho entre i e k é uma cadeia cujos extremos são os vértices i e k.
Grafo conexo é aquele no qual para qualquer par de vértices existe uma cadeia que os une. Se um grafo G não é conexo é sempre possível fazer a sua partição em subgrafos conexos.
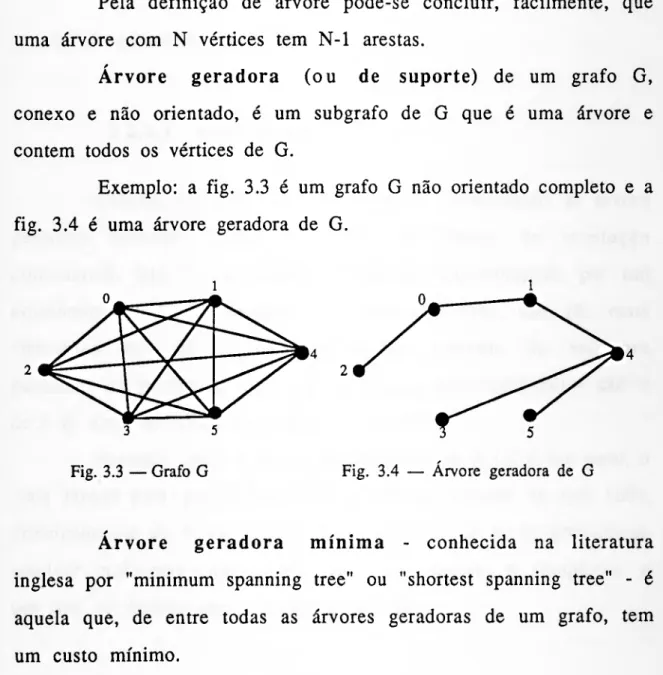
Um subgrafo de G=(V,A) é um grafo Gs=(Vs,As), em que
Vs ç V, As ç A. Portanto, o conjunto As é formado pelas arestas
de G que ligam os vértices de Vs, ou seja:
As = {(i, j) eA: i, j e Vs}
Outras definições:
— rota é um conjunto formado pelo depósito e um ou mais clientes. A rota inicia-se e acaba-se sempre no depósito; — rota óptima é a sequência dos seus elementos a que
corresponde um custo mínimo;
— circuito óptimo é um conjunto de rotas óptimas às quais corresponde a solução óptima do PBD.
2.5 Formulação matemática do PBD
Existem inúmeras formulações matemáticas para o problema básico, cada uma das quais aponta para um determinado método de resolução. A formulação que aqui se adopta é a que põe em evidência a relação entre o PBD e o M-PCV, de modo a usar este para obter minorantes para o PBD, a qual foi sugerida por Christofides et al. [12]. Portanto, como o M-PCV é um caso particular de PBD conforme se viu na secção 2.1, mas com menos restrições, a solução óptima do primeiro é menor ou igual que a do segundo. Por isso, é óbvio, que se um valor é menor ou igual (minorante) que o óptimo do M-PCV então também é minorante do PBD. Portanto, uma vez que a forma de determinar o minorante do M-PCV está
Seja,
|l, seo veiculo k visita o cliente j imediatamente apos ter visitadoo cliente i, yijk:
0, caso contrario (c.c.).
N N M F.O.: Z* = Min X Êc.. Xy...
• IJ , / ijk 1=0 j=o J k=1 1 (2.1) sujeito a: N N z kI1yiik = 1' i=o k=1 j = 1.2 N (2.2) N N D yj k - Iypik=0. k = 1,2,...,M, p = 0,...,N i=o p j=0 (2.3) N I i=1 ^ N ^ ^i.^yijk ^ j=o y , k= 1,2 M (2.4) N N N I Ic.. y... + I . , I| 7 'Jk . , 1=0 j=1 1=1 í N uiZyiik v j=o y <T. k = 1,2 M (2.5) |yojk=1 - k=1-2 M (2.6) M Yj-Yj + N Syijk < N - 1 , 1,2,....N k = 1 (2.7) yjjke{0,1}. V, i, j, k (2.8)
Y j arbitrário
A função objectivo (2.1) estabelece a minimização do custo total de percurso dos M veículos.
As restrições (2.2) garantem que cada cliente é visitado por um, e um só, veículo.
As restrições (2.3) estabelecem que se um veículo visitar um cliente também deverá deixá-lo.
As expressões (2.4) e (2.5) são, respectivamente, as restrições de capacidade e de custo. Em todos os exemplos resolvidos neste trabalho as restrições (2.5) não são consideradas, excepto no caso da resolução aproximada de alguns exemplos (cap. 5).
As restrições (2.6) garantem que cada veículo deverá ser usado exactamente uma vez.
As desigualdades (2.7) devidas a Miller, Tucker e Zemlin, eliminam a possibilidade de formação de subciclos no PCV (portanto, em cada rota).
Finalmente, as condições (2.8) são as de integralidade,
Repare-se que se forem retiradas as restrições (2.4) e (2.5), as restantes restrições constituem a formulação de um M-PCV.
2.6 Complexidade computacional
Segundo a teoria da complexidade computacional de Garey et al. [19] existem duas classes de problemas: os de fácil resolução, para os quais existem algoritmos de optimização cujos tempos de processamento são limitados por uma função polinomial da
dimensão do problema, que, normalmente, se designa por O (f(N)), e os NP-completos, para os quais existe uma forte evidência de que qualquer algoritmo de optimização tem, no pior caso, um tempo de processamento que cresce exponencialmente com a dimensão do problema,
O PBD, tanto quanto se sabe, pertence à classe dos NP- completos tal como o PCV e o M-PCV. No entanto, na prática, o PBD mostra ser de muito mais difícil resolução que o PCV ou o M-PCV e daí o facto de, relativamente a estes, se terem já resolvido problemas com uma dimensão muito grande, quando comparada com o que existe para o PBD.
Assim, Gavish et al. [22], (1986) resolveram problemas M- PCV simétricos, não euclidianos de 500 nós e 10 caixeiros em 619 s, ou 500 nós e 8 caixeiros em 1092 s num computador IBM 3081D. Do mesmo modo, Padberg (1986) citado por Matos [32] resolveu um PCV com 532 cidades, em algumas horas. Todavia, em relação ao PBD, a dimensão máxima conhecida aproximadamente na mesma altura (1985) era de 53 clientes e 8 veículos ([8]). Embora neste caso o problema seja um pouco mais genérico que o PBD, pois, existem restrições temporais para servir os clientes, mas não muito apertadas.
Todavia, há um caso particular, estudado por Christofides e Thornton (1982), citado em [8], em que o PBD pode ser resolvido exactamente, com relativa facilidade, devido ao facto de poder ser formulado como um problema de emparelhamento generalizado. Isto verifica-se quando os veículos têm todos a mesma capacidade Q, e a soma da procura de três quaisquer clientes é superior a Q. O que é equivalente a dizer que qn+qn-l+qn-2 > Q» Vn>2. Por este facto cada rota tem um máximo de dois clientes.
bound")
O método de ramificação e limitação é um dos mais eficazes para resolver problemas de optimização combinatória e é o que se usa neste trabalho para a resolução exacta do PBD. Por isso, nesta secção definem-se conceitos gerais sobre ele bem como o seu funcionamento, os quais serão aplicados na secção 2.8 ao caso concreto de PBD.
2.7.1 Definições
A tradução literal de "branch and bound" é ramo e fronteira (limite). No entanto, apesar de ser esta a designação mais corrente na literatura inglesa há outras de funções equivalentes: "tree search", "branching"", etc. Por isso, neste trabalho se preferiu utilizar a designação de ramificação e limitação ou ramificação em árvore, por parecerem ser as mais sugestivas, embora a primeira dê uma noção mais correcta do conteúdo do método.
A ideia básica deste método consiste em dividir o problema inicial em subproblemas de mais fácil resolução devido à sua menor dimensão e, em alguns casos, com estrutura mais simples. Em seguida, repete-se o processo em relação a cada um dos subproblemas e assim sucessivamente, até que cada um dos subproblemas fique resolvido.
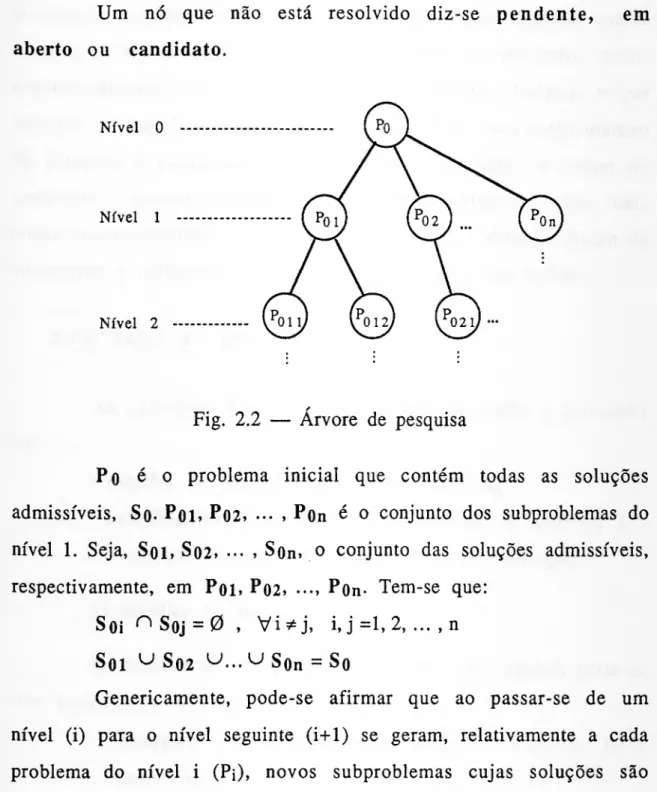
A representação gráfica deste processo de resolução assemelha-se a uma árvore, como pode ver-se na fig. 2.2, e daí a
origem do seu nome. A cada subproblema corresponde um conjunto de soluções e a sua representação designa-se por nó ou nodo1. Por
isso, para simplificar, costuma-se referir o nó quando se pretende significar o problema que lhe está associado.
Um nó n diz-se antecessor (ou predecessor) de um nó ni se n pertencer a um nível superior a ni e se existe um caminho na árvore de pesquisa que liga n com ni. Por sua vez, ni designa-se por sucessor. Por exemplo, na fig. 2.2 Pqi é antecessor Pqh e Pq é antecessor de todos os outros. Mais especificamente, Pqi é o antecessor imediato de Pon e, inversamente, este sucessor imediato daquele.
A pesquisa inicia-se sempre pelo nível 0 a que também se chama raiz da árvore, e termina quando todos os nós tiverem sido resolvidos.
Um nó fica resolvido quando se efectuar uma das duas acções seguintes:
a) cancelamento
Para se efectuar o cancelamento de um nó basta provar um dos dois aspectos seguintes:
- que ele é impossível;
- que o valor da sua solução óptima é pior ou igual que a melhor solução conhecida.
b) determinação da sua solução óptima
Como se viu na secção 2.4 esta designação também se aplica aos vértices de um grafo. Por isso, para evitar confusões reservar-se-á este termo para o presente contexto e os vértices serão simplesmente designados por este nome ou por aquilo que eles representam — os clientes e o depósito.
Um nó que não está resolvido diz-se pendente, em aberto ou candidato. Nível 0 Nível 1 Nível 2 ✓
Fig. 2.2 — Arvore de pesquisa
Po é o problema inicial que contém todas as soluções admissíveis, So- Pol. P02, ••• » Pon é o conjunto dos subproblemas do nível 1. Seja, Sqi, S02. ••• > Son. o conjunto das soluções admissíveis, respectivamente, em Poi, P02. •••» POn- Tem-se que:
SoinSoj = 0, Vi^j, i, j =1, 2, ... , n
Sol u S02 ^...^Son =So
Genericamente, pode-se afirmar que ao passar-se de um nível (i) para o nível seguinte (i+1) se geram, relativamente a cada problema do nível i (Pi), novos subproblemas cujas soluções são
✓
uma partição do conjunto das soluções de Pi (Sj). E precisamente este facto que garante que todas as soluções vão ser enumeradas, explicita ou implicitamente, e que não se repete a exploração de soluções idênticas.
Este método é muito usado em problemas de optimização combinatória, para os quais não são conhecidos algoritmos de resolução em tempo polinomial. Contudo, no pior caso, terão de ser
Po
02
enumeradas explicitamente todas as soluções o que significa que o número de nós e, consequentemente, o tempo de resolução, cresce exponencialmente com N (a dimensão do problema). Todavia, o que acontece na maior parte dos casos práticos, é que um vasto número de soluções é enumerado implicitamente e, portanto, o tempo de resolução é substancialmente reduzido. Esta redução é tanto mais eficaz quanto melhores - mais próximos do valor óptimo - forem os minorantes e majorantes ("bounds") determinados nos nodos.
2.7.2 Fases do método
As principais fases do método de ramificação e limitação são:
• escolha do nó (problema) para ramificar
• ramificação ("branching", "partitioning" ou "splitting") • avaliação do valor da função objectivo (limitação)
a) Escolha do nó
Na escolha do nó, para ser ramificado em seguida, pode-se usar basicamente três estratégias distintas:
- pesquisa em profundidade primeiro {"depth first search")',
- pesquisa em largura primeiro ("breath first search"); - pesquisa do melhor primeiro {"best first search").
Quando se opta pela pesquisa em profundidade o primeiro nó a ser explorado é o último que foi gerado. A pesquisa prossegue para níveis cada vez mais baixos até que um nó seja resolvido. Logo que isto suceda há um retrocesso ("bactraking") para o nível
imediatamente superior reiniciando-se a procura no último nodo gerado e pendente.
Veja-se, por exemplo, a fig. 2.3, na qual o número do nó indica a ordem pela qual ele foi gerado. Neste exemplo embora o nível 4 seja o mais baixo há nós cujos sucessores não atingiram esse nível precisamente porque foram resolvidos antes. Além disso, a partição não gera sempre o mesmo número de subproblemas, o que é devido à estrutura própria do problema e ao tipo de ramificação escolhida. Nível 0 Nível 1 Nível 2 Nível 3 Nível 4 14 12
Fig. 2.3 — Pesquisa em profundidade
Repare-se que dentro deste tipo ainda existem variantes. Por exemplo, o nó 7 poderia ter sido gerado logo a seguir ao 1, isto é, poderiam ser gerados em primeiro lugar todos os subproblemas de um nó e depois é que se passava ao nível seguinte. Esta variante usa-se, sobretudo, na ramificação bivalente. Todavia, a variante apresentada no exemplo, tem sobre esta última a vantagem de exigir menos memória computacional.
Esta estratégia tem sobre as outras, como principal vantagem, a de ser a que gasta menos memória computacional, devido a ser aquela que, em qualquer fase do processo necessita de armazenar menos nós candidatos à ramificação. Uma outra vantagem resulta de ser aquela em que, em princípio, se obtém mais cedo uma solução admissível. Esta pode ser muito útil no caso em que a pesquisa não é levada até ao final por falta de tempo ou memória computacional.
A pesquisa em largura, exemplificada na fig. 2.4, consiste em explorar primeiro todos os nós de um dado nível, pesquisando- se, em seguida, os nós do nível imediatamente abaixo e assim sucessivamente. Da utilização desta estratégia resulta um elevado consumo de memória computacional. Em contrapartida a primeira solução admissível encontrada tem um valor que, provavelmente, está próximo do óptimo.
©
© ©
Fig. 2.4 — Procura em largura
A pesquisa do melhor primeiro consiste em explorar em primeiro lugar aquele nó que aparenta conter a solução
correspondente ao valor óptimo da função objectivo. Para isso, em relação a cada nó candidato, é feita uma estimativa do valor da solução que lhe corresponde, através de uma dada heurística. É precisamente da fiabilidade desta heurística que depende a eficácia da pesquisa. Por exemplo, na resolução do PBD pode-se usar como estimativa o minorante do nó, pelo que, neste caso o primeiro nó a ser ramificado é aquele que tiver menor minorante.
Presumivelmente esta é a estratégia a que corresponde a exploração de menor número total de nós e, consequentemente, a maior rapidez computacional, desde que a heurística usada seja de boa qualidade. Todavia, o número médio de nós pendentes é superior à pesquisa em profundidade e, portanto, exige mais memória computacional. Além disso, também não se obtém tão prematuramente como naquela estratégia, uma solução admissível.
Na resolução exacta do PBD bem como do PCV usou-se a estratégia da pesquisa em profundidade devido, principalmente, à escassez de memória computacional.
b) Ramificação
Quanto à ramificação a partir de um nó escolhido, a decisão a tomar é a seguinte: quantos e quais os subproblemas que deverão ser gerados?
A resposta a esta questão implica a escolha da variável (ou variáveis) na qual se vai apoiar a ramificação e a definição do critério de ramificação.
No caso de se optar pela ramificação bivalente (ou binária), isto é, que de cada nó partem sempre dois ramos, basta escolher a
variável para ramificar. Esta será uma daquelas que ainda não foi fixada nos nós antecessores deste.
Na resolução exacta do PBD, tal como foi feita neste trabalho, o número de ramos gerados de cada nó é desconhecido à partida, pois, isso vai depender do número total de combinações de clientes admissíveis. Unicamente se sabe que o conjunto de subproblemas sucessores imediatos constitui uma partição do problema antecessor imediato, visto que o processo de os gerar garante isso.
c) Avaliação
A avaliação de um nó consiste em determinar um minorante ou um majorante para o valor das soluções correspondentes a esse nó.
A qualidade dos minorantes e dos majorantes é o factor que mais influencia a eficiência computacional dos algoritmos de pesquisa em árvore.
Suponha-se que o problema é de minimização e que pertence à classe NP-completo, como é o caso dos problemas estudados neste trabalho - PBD e PCV. Nestas condições supõe-se que o minorante e o majorante de cada nó podem ser determinados em tempo polinominal, pois, caso contrário, seria vantajoso, em princípio, determinar-se logo a solução óptima. Veja-se qual a utilidade do minorante e do majorante:
- se o minorante é igual ou superior ao valor da melhor solução conhecida para o problema, então o nó pode imediatamente ser cancelado. Supõe-se que só se quer conhecer uma solução óptima mesmo que existam mais, pois, de contrário, o cancelamento só se poderia verificar nos casos em que o minorante fosse superior.
- se o minorante é inferior então nada se pode concluir e o nó continua pendente.
- se o majorante é inferior ou igual ao valor da melhor solução conhecida então esta solução pode ser rejeitada e substituída pela que deu origem ao majorante. No caso em que aqueles valores são iguais, poderá significar que existe mais do que uma solução óptima e, portanto, a melhor solução conhecida até ao momento só se mantém se pretendermos descobir todas as soluções óptimas. O nó que deu origem ao minorante mantem-se pendente.
- se o majorante é superior ao valor de melhor solução conhecida, nada se pode concluir.
*
E óbvio, que na comparação anterior do minorante (majorante) de um nó com a melhor solução conhecida para o problema se supõe o seguinte: este problema é o problema inicial, que contém todas as soluções, e que antes de efectuar a comparação se somou ao minorante (majorante) o custo das soluções parciais correspondentes aos nós antecessores deste. Esta questão ficará perfeitamente clara na secção 2.9.
2.8 Exposição da resolução exacta do PBD pelo método de pesquisa directa em árvore
Para resolver o PBD pelo método da procura em árvore existem diversas variantes. Estas variantes dizem respeito, quer à escolha dos nodos, quer ao tipo de ramificação, quer aos algoritmos usados para a determinação de minorantes e majorantes.
Uma das variantes de pesquisa consiste em ramificar em torno de um arco (i,j) ([12]), Portanto, em cada nodo da árvore de
pesquisa é escolhido um arco (i,j), para ampliar a rota já parcialmente construída (0, k, ... , i). Um ramo corresponde, precisa- mente, a incorporar o arco (i,j) na rota em construção, enquanto que o outro corresponde à sua proibição. Os minorantes são determinados com base numa relaxação apoiada numa formulação do PBD em termos de programação dinâmica.
A estratégia de pesquisa directa em árvore usada neste trabalho é proposta por Christofides et al. [12] e descreve-se em seguida.
O método de resolução usado exige que se conheça à partida o número de veículos. Para que o problema tenha uma solução admissível é necessário, mas não suficiente, que se verifique a seguinte desigualdade:
/" N A
Iq, /Q (2.9) Vi=1
Em que, M é o número de veículos, Q a capacidade máxima de cada veículo e qj a procura do cliente i.
Cada nodo da árvore de pesquisa corresponde a uma rota admissível que, como se disse na secção 2,4, é constituída por um ou mais clientes e o depósito. Mas, também corresponde a um subproblema cuja solução terá de ser determinada.
A procura é feita em profundidade e, portanto, o último nó gerado é o primeiro a ser explorado. No caso de um nó não ter nenhum sucessor admissível inicia-se o retrocesso.
O número de sucessores imediatos de um nó é dado, aproximadamente, pela fórmula (2,10),
Nmax ... s x. (Npa)
p=Nmin
(2.10)
Na = número de clientes admissíveis relativamente ao nó, Nmin = número mínimo de clientes que uma rota (nó
sucessor) deve conter para ser admissível,
Nmax = número máximo de clientes que uma rota admissível pode conter.
A criação de um nodo ns sucessor imediato do nodo n
consiste em gerar uma combinação de clientes admissíveis distinta de todas as combinações já geradas e sucessoras de n. O processo seguido para o fazer é explicado no capítulo 6.
Naturalmente, que quanto menor for o número de rotas distintas (nodos) gerados nos níveis superiores mais fácil é, em princípio, a resolução do problema. Uma vez que a única restrição que está a ser considerada, no que diz respeito à constituição das rotas, é a capacidade máxima do veículo, selecciona-se em cada nível o cliente de maior procura para iniciar a rota, de entre os clientes livres. Deste modo garante-se a criação do menor número possível de nodos nos níveis superiores.
Os clientes livres para a criação de um nodo são todos aqueles que não pertencem aos nodos antecessores.
Os nodos do penúltimo nível têm um, e um só, sucessor porque os clientes livres correspondem exactamente a uma rota. Quando muito poderá acontecer que a rota não seja admissível, conforme será explicado na secção 2.9.4 .
Conforme se viu na secção 2.7.2 é necessário fazer a avaliação de cada nó através da determinação de um minorante e
de um majorante para o valor das soluções correspondentes a esse nó.
Logo na raiz de árvore pode-se determinar um majorante e um minorante, se eles coincidirem então o majorante é o valor óptimo do problema e a solução correspondente a solução óptima do problema, visto que, como se verá no capítulo 5, o majorante é determinado através de uma solução admissível para o problema. Contudo, na prática isso é quase impossível de acontecer, desde que o número de veículos seja superior a 2 e se use, para determinar o minorante, o algoritmo usado neste trabalho. Por isso, pode-se evitar o cálculo do minorante para não haver perdas de tempo, mas o majorante é conveniente que seja calculado, pois, poderá contribuir para o cancelamento permaturo de muitos nodos. A discrepância entre os majorantes e os minorantes, como se verá no capítulo 7, deve-se mais e com mais frequência à má qualidade dos minorantes do que dos majorantes. Ou seja, geralmente, o hiato do majorante relativamente ao óptimo é menor que o do minorante. Na verdade, pelo menos em problemas de pequena dimensão, é frequente o valor do majorante coincidir com o valor óptimo.
Para além do majorante do problema inicial, correspondente a uma solução admissível, que é determinado na primeira fase de execução do programa, é possível introduzir um majorante artificial na fase de introdução dos dados. Este majorante é uma estimativa do valor óptimo que, no caso de ser inferior a este, irá originar um problema impossível mesmo que, na realidade, ele tenha solução. Se isto acontecer deve-se repetir a resolução do problema com um majorante artificial superior ou sem este, a fim de se verificar se efectivamente o problema tem solução.
A forma de determinar os minorantes e majorantes é apresentada com detalhe nos capítulos 3 e 5, respectivamente.
2.9 Exemplo
Este exemplo destina-se a clarificar o funcionamento do método de pesquisa directa em árvore usado neste trabalho para a resolução exacta do PBD. As eventuais dúvidas que tenham subsistido da explicação precedente, sobre o mecanismo concreto da resolução, serão dissipadas através deste exemplo.
Os dados completos para este exemplo encontram-se no anexo III, aonde é designado por problema 11. Alguns dos dados são:
- clientes: [1, 2, ... , 10];
- procura ordenada por ordem crescente e na forma cliente/procura: [1/1, 7/3, 2/5, 3/6, 8/9, 10/10, 4/12, 5/13, 6/13, 9/21];
- veículos: 4 de igual capacidade, Q = 24
2.9.1 Versão 1
Esta versão (que corresponde à figura 2.5) consiste em usar para a determinação dos majorantes o método de Jameson e Mole (cf. cap. 5) , iniciando-se cada rota com o cliente de maior procura de entre os não roteados. Os restantes parâmetros para os majorantes e os minorantes, cujo significado se pode ver, respectivamente, nos capítulos 5 e 3 foram fixados assim:
a) para os majorantes • u = 0.75 ; v = 1.75
• a 2-optimização é feita desde o início da rota e no final da mesma determina-se a rota óptima.
b) para os minorantes
• Y = V, sendo V o número de veículos livres em cada nodo. Na raiz da árvore V=4;
• 1=18, A=0.1, It=5.
2.9.2 Significado das variáveis dos nodos
A árvore resultante da resolução do problema é apresentada na fig. 2.5. O número de níveis ou estágios, em qualquer PBD que tenha uma solução admissível, é igual ao número de veículos.
Relativamente a cada nó tem-se:
- o número dentro do círculo, na parte superior, indica a ordem em que o nó foi gerado;
- os números dentro de parêntesis recto (lista) representam os clientes que formam a rota. O número escrito com tinta mais carregada é o de maior carga. Os clientes deverão ser visitados pela ordem em que aparecem na lista de forma a que o custo do percurso seja mínimo. Para além dos clientes da lista ainda há o depósito, que é aonde a rota começa e termina;
- Cr = custo da rota óptima. Determina-se através da resolução do PCV formado pelos clientes da rota mais o depósito;
^ "i ò Cs sO -O sO <N <N II <S II II õ u 3 J 3 S « - ii " U O U J %* «... U O U J X -H ^ CO Os ^ 00 r- . — <N í ^ "ii 7 u> « .«. O O U -3 f-» Os 00 17 cs ii 1? O U O J X o 3 3 cn vo ^ oo rt 2 ^ ^ II II U U O J «J Ê 3 o u. Cu O cd -* CO \Q 0 <s ^ 17 ^ 1717 Õ o í 2 a ed 'S Ph CA S ed 00 *3 cr CA O Cu <u -a II <s u ii ^ O U U J o t sO vS sO =23 ss II Cru o «• n li1 » ii »« «i .— U O U J 3 17 11 li Ou ô 2 -s^a - a u o u in (N ob E u u u "O $ ll 11 u u 3 á
- Ca = custo acumulado. Este custo é a soma do custo do nó (rota) com todos os seus antecessores. Por exemplo, o nó 7 tem como antecessores o 2, o 1 e o 0. A soma dos seus custos é 64+65.6+22,1 = 151.7;
- Li = limite inferior do subproblema resultante da criação de um nó. Por exemplo, após a criação do nó 8 o subproblema resultante é formado pelos clientes [1, 2, 3, 4, 5, 10], pelo depósito e existem 2 veículos livres. Os clientes nas condições anteriores serão designados nesta dissertação por livres ou não roteados:
- Cm = custo da melhor solução conhecida até ao momento. No caso de se usar um majorante artificial inicial este irá ocupar o lugar de Cm até que apareça uma solução com um majorante melhor. Nesta resolução não se usou majorante artificial e por isso, o primeiro valor de Cm só foi conhecido após a criação de 4 nós correspondentes a uma solução admissível.
2.9.3 Cancelamento de um nó
As condições para que um nó possa ser cancelado já foram indicadas na secção 2.7, só que aqui são-no de uma forma mais concreta e aplicadas a este exemplo. Para que um nó possa ser cancelado basta que se verifique uma das condições seguintes:
1. o (sub)problema associado é impossível; 2. Ca ^ Cm;
3. Ca + Li ^ Cm.