Modelo HJM multifatorial integrado com distribuições empíricas condicionais: o caso brasileiro

(1)

ESCOLA DE ECONOMIA DE S ˜

AO PAULO

LUIZ HENRIQUE MORAES DA SILVA

MODELO HJM MULTIFATORIAL INTEGRADO COM

DISTRIBUIC

¸ ˜

OES EMP´IRICAS CONDICIONAIS: O CASO

BRASILEIRO

S ˜

AO PAULO

2018

(2)

MODELO HJM MULTIFATORIAL INTEGRADO COM

DISTRIBUIC

¸ ˜

OES EMP´IRICAS CONDICIONAIS: O CASO

BRASILEIRO

Disserta¸c˜ao apresentada ao Programa de Mestrado Profissional da Escola de

Economia de São Paulo da Funda¸cão Getúlio Vargas, como requisito para a obten¸cão do t´ıtulo de Mestre em Economia.

´

Area de concentra¸c˜ao: Finan¸cas Quantitativas

Orientador: Afonso de Campos Pinto

S ˜

AO PAULO

2018

(3)

Silva, Luiz Henrique Moraes da.

Modelo HJM multifatorial integrado com distribuições empíricas : o caso brasileiro / Luiz Henrique Moraes da Silva. - 2018.

53 f.

Orientador: Afonso de Campos Pinto

Dissertação (MPFE) - Escola de Economia de São Paulo. 1. Taxas de juros. 2. Mercado financeiro - Brasil. 3. Análise de componentes principais. 4. Monte Carlo, Método de. 5. Instituições financeiras – Brasil - Regulamentação. I. Pinto, Afonso de Campos. II. Dissertação (MPFE) - Escola de Economia de São Paulo. III. Título.

CDU 336.781.5(81)

Ficha catalográfica elaborada por: Isabele Oliveira dos Santos Garcia CRB SP-010191/O Biblioteca Karl A. Boedecker da Fundação Getulio Vargas - SP

(4)

MODELO HJM MULTIFATORIAL INTEGRADO COM

DISTRIBUIC

¸ ˜

OES EMP´IRICAS CONDICIONAIS: O CASO

BRASILEIRO

Disserta¸c˜ao apresentada ao Programa de Mestrado Profissional da Escola de

Economia de São Paulo da Funda¸cão Getúlio Vargas, como requisito para a obten¸cão do t´ıtulo de Mestre em Economia.

´

Area de concentra¸c˜ao: Finan¸cas Quantitativas

Data da aprova¸c˜ao: 31/07/2018

Banca examinadora:

Prof. Dr. Afonso de Campos Pinto (Orientador)

FGV - EESP

Prof. Dr. Roberto Barbosa Cintra FGV - EESP

Prof. Dr. Marcos Eugˆenio da Silva FEA - USP

(5)

Em primeiro lugar, agrade¸co a minha fam´ılia, sobretudo minha mãe Vânia e meu irmão Victor, por sempre me apoiarem.

Agrade¸co ao meu orientador, Prof. Dr. Afonso de Campos Pinto, pela sua ´otima orienta¸c˜ao ao longo deste trabalho, e principalmente por sugerir o tema do mesmo.

Agrade¸co a Yuka, por todo o carinho e paciˆencia durante todos esses meses.

Também agrade¸co ao Roberto Cintra e ao Maur´ıcio Iriê pelas ideias e discussões esti-mulantes.

(6)

O presente estudo propõe um modelo de simula¸cão que combina o modelo multifatorial de Heath, Jarrow e Morton e distribui¸cões de probabilidade emp´ıricas condicionais para simular curvas de juros e ativos do mercado financeiro. Em seguida, utilizamos o modelo proposto para simular a evolu¸cão do Dólar, da estrutura a termo das taxas de juros do Brasil obtida a partir dos contratos de DI futuro e da curva de Cupom Cambial de Dólar Sujo de maneira integrada, sendo os resultados das simula¸cões utilizados para realizar o apre¸camento de ativos. Também aplicamos os resultados obtidos em um problema de otimiza¸cão de portfólios, que busca maximizar o lucro de um participante sujeito às restri¸cões regulatórias impostas pelas resolu¸cões de Basiléia III, empregando novamente o conceito de distribui¸cões emp´ıricas condicionais.

Palavras-chave: HJM. Análise de Componentes Principais. Distribui¸cões emp´ıricas condicionais. Monte Carlo. Gestão de ativos e passivos. Basiléia III.

(7)

This work proposes a simulation model that combines the multifactor Heath, Jarrow and Morton model with empirical conditional probability distributions to simulate interest rate curves and securities from the financial market. The work then utilizes the proposed model to simulate the USD/BRL exchange rate, the interest rate term structure obtained from the DI Future contracts and the Cupom Cambial de D´olar Sujo interest rate curve in an integrated way, using the obtained results to price securities. In addition, we apply the results obtained in a portoflio optimation problem, which seeks to maximize the profit of a market partcipant subject to the regulatory constraints imposed by the Basel III resolutions, utilizing once again the concept of empirical conditional distributions.

Keywords: HJM. Principal Component Analysis. Empirical conditional distributions. Monte Carlo. Asset and liability management. Basel III

(8)

1 Estrutura da ´arvore binomial. . . 26 2 Densidade de probabilidade do d´olar, ano de 2015. A figura apresenta a

probabilidade de um certo retorno em t + 1 dado um retorno em t . . . 40 3 Histogramas contendo os resultados das simula¸c˜oes dos pre¸cos de mercado

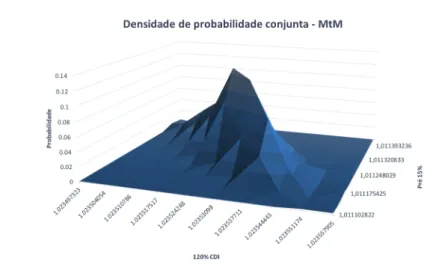
dos ativos, 21 DU. . . 44 4 Densidade de probabilidade conjunta do MtM dos ativos 21 dias ´uteis ap´os

a data de referência. . . 45 5 Lucro esperado como fun¸cão do peso ativo 120% CDI. Os parâmetros

uti-lizados foram kf loat = 0, 025, kP re = 0, 01, klev = 0, 015 e ⇢ = 1, 0122.

. . . 48 6 Peso no ativo 120% CDI como fun¸c˜ao do seu requerimento de capital, para

diferentes requerimentos de alavancagem. Os parˆametros utilizados foram kf loat = 0, 025, kP re = 0, 01, e ⇢ = 1, 0122. Em azul, klev = 0, 02; em

(9)

1 Exemplo: retornos e frequˆencias da curva de Cupom Cambial Sujo . . . 24

2 Estados e probabilidades . . . 26

3 PCA, 2015 . . . 38

4 Market price of risk (MPR) . . . 39

5 USD/BRL (utilizando 2015), RMSE com 500 simula¸c˜oes . . . 40

6 Propriedades das distribui¸c˜oes dos retornos dos fatores do cupom cambial (utilizando 2015) simulados (S) e reais (R) . . . 41

7 Valores de mercado simulados e realizados, para uma simula¸cão de 21 dias ´ uteis. O cálculo do pre¸co foi realizado utilizando as curvas médias. . . 42

8 Valores de mercado simulados e realizados, para uma simula¸cão de 42 dias ´ uteis. O cálculo do pre¸co foi realizado utilizando as curvas médias. . . 43

9 Densidade de probabilidade conjunta . . . 45

10 Probabilidades de estados . . . 46

11 Valores esperados . . . 46

12 Resultados do modelo. As duas primeiras colunas referem-se ao requeri-mento de capital necess´ario para cada R$ investido no ativo, enquanto que a terceira refere-se ao requerimento de capital de alavancagem. . . 46

(10)

Lista de Figuras Lista de Tabelas

1 Introdu¸c˜ao 11

2 Revis˜ao Bibliogr´afica 13

3 Fundamentos te´oricos 17

3.1 Movimento Browniano geom´etrico . . . 17

3.2 O modelo HJM e a parametriza¸c˜ao de Musiela . . . 17

3.3 Distribui¸c˜oes emp´ıricas . . . 20

3.4 Modelo de simula¸c˜ao integrado . . . 22

3.5 Aplica¸c˜ao em problemas de tomadas de decis˜ao . . . 25

3.6 Tipos de ativos considerados . . . 29

4 Metodologia 32 4.1 Dados . . . 32

4.2 Componentes Principais . . . 33

4.3 Resumo do procedimento . . . 35

4.4 Valida¸c˜ao das simula¸c˜oes . . . 36

5 Resultados 38 5.1 An´alise do PCA . . . 38

5.2 Market price of risk . . . 38

5.3 Resultados do backtest . . . 39

5.3.1 D´olar . . . 39

5.3.2 Cupom cambial sujo . . . 40

5.4 Evolu¸c˜ao de pre¸cos . . . 41

5.5 Arvores e tomada de decis˜ao . . . 43´

6 Conclus˜oes 48

(11)

1 Introdu¸c˜

ao

A partir da implanta¸cão do Plano Real, a economia do Brasil experimentou um per´ıodo de relativa estabilidade após anos tumultuados por pol´ıticas econômicas equivocadas e per´ıodos de hiperinfla¸cão. Desde então, a economia brasileira tornou-se alvo de investido-res globais que se voltavam para o nosso mercado, significativo entre os pa´ıses emergentes, tanto para investir diretamente na economia brasileira quanto para fazer hedge de posicões em outras economias emergentes, sobretudo no mercado de taxa de juros.

A consequência natural desta evolu¸cão foi o crescimento em profundidade e liquidez do mercado brasileiro, e consequentemente um aumento da demanda e necessidade de diferentes instrumentos financeiros, principalmente derivativos. Dentre eles, podemos citar o futuro de DI. Portanto, dada a importância do mercado brasileiro no grupo de pa´ıses emergentes, as elevadas taxas de juros e a necessidade de modelos capazes de auxiliar praticantes deste mercado, propor ferramentas capazes de auxiliar praticantes do mercado é um ponto central deste trabalho.

Nos últimos anos, muitos estudos foram conduzidos de modo a entender as principais causas das crises financeiras recentes, em particular a de 2008. Dentre as causas, a alavan-cagem excessiva possui um lugar de destaque. De fato, na crise mais recente muitos bancos apresentavam alavancagem excessiva apesar de possu´ırem bons indicadores baseados uni-camente em risco. Isto motivou o Comitê de Basiléia a introduzir um novo requerimento de capital, desta vez baseado apenas em alavancagem, na resolu¸cão de Basiléia III. Na prática, este requerimento impõe mais uma restri¸cão na escolha das aloca¸cões do portfólio de uma institui¸cão financeira, tornando este problema mais complexo.

No momento em que este trabalho é escrito, as novas resolu¸cões de Basiléia estão sendo implementadas no Brasil através de novas exigências do Banco Central. Este aspecto re-gulatório, somado ao cenário atual de incertezas (a maioria oriunda da atual crise pol´ıtica e necessidade de reformas estruturais da economia), refor¸ca a necessidade de institui¸cões financeiras e participantes do mercado de realizar uma gestão sólida de seus portfólios em meio a um mercado cada vez mais sofisticado e competitivo.

Em termos objetivos, um dado participante do mercado estaria então sujeito a dois desafios. O primeiro, envolve o apre¸camento de ativos; o segundo, restri¸cões quanto à forma¸cão e manuten¸cão de um portfólio composto por estes mesmos ativos. Tendo isto em mente, nosso objetivo neste trabalho é propor um modelo de simula¸cão integrado,

(12)

combinando o modelo HJM multifatorial proposto por Heath, Jarrow e Morton (1992) com a utiliza¸cão de distribui¸cões emp´ıricas condicionais, capaz de simular diversas estruturas a termo de taxas de juros e ativos simultaneamente e utilizar o resultado para realizar o apre¸camento de instrumentos financeiros. Finalmente, vamos apresentar uma forma de empregar estes resultados em problemas de otimiza¸cão no contexto da gestão de ativos e passivos de um portfólio sujeito às restri¸cões de requerimento de capital enunciadas em Basiléia III.

Este trabalho está dividido em seis cap´ıtulos. No cap´ıtulo dois apresentamos a revisão bibliográfica, de modo a contextualizar o trabalho em rela¸cão a estudos anteriores. No cap´ıtulo três apresentamos o arcabou¸co teórico utilizado, que contempla o modelo HJM, a parametriza¸cão de Musiela, distribui¸cões emp´ıricas e um modelo de aloca¸cão sujeito às restri¸cões de Basiléia III. No cap´ıtulo quatro apresentamos a metodologia para imple-menta¸cão do modelo, detalhando as práticas utilizadas. No cap´ıtulo cinco, apresentamos os resultados do modelo de simula¸cão integrado e uma aplica¸cão do mesmo. Finalmente, no cap´ıtulo seis encerramos com a conclusão do trabalho e poss´ıveis extensões do mesmo.

(13)

2 Revis˜

ao Bibliogr´

afica

A modelagem e o estudo da dinâmica das taxas de juros são problemas antigos na área de finan¸cas. Diversos modelos foram utilizados ao longo de décadas, tais como Vasicek (1977), Hull e White (1990), Cox et al (1985) e Black e Karasinski (1991), cujo foco consistia essencialmente na modelagem das taxas spot1_{. Heath, Jarrow e Morton}

(1992) modelam a dinˆamica de todas as taxas forward2 _{instantˆaneas de uma dada curva.}

Pouco tempo depois, Brace e Musiela (1994) propõem uma reparametriza¸cão do modelo, utilizando a taxa forward com prazo até o vencimento ao invés da data de maturidade. Finalmente, Chiarella e Kwon (2001) mostram que os modelos anteriores aqui citados eram na verdade casos particulares do proposto por Heath, Jarrow e Morton, popularmente conhecido como HJM.

Litterman e Scheinkman (1991) realizam um estudo, com uma abordagem emp´ırica, a fim de determinar os fatores comuns que explicam retornos passados de US Treasuries. A conclusão é a de que a maior por¸cão (ao menos 96%) da variância dos retornos pode ser explicada em termos de três fatores da yield curve: n´ıvel, inclina¸cão e curvatura.

Scherer e Avellaneda (2002) utilizam a Análise de Componentes Principais (PCA, do inglês Principal Component Analysis) para estudar os t´ıtulos de d´ıvida de Argentina, Brasil, México e Venezuela, os pa´ıses devedores com maior importância da America La-tina. Nesse trabalho, observou-se que alguns componentes são altamente significativos (explicam mais de 90% da variância), sendo suas contribui¸cões dependentes do tempo, o que sugere uma conexão com movimentos particulares do mercado.

Pixiolini (2014) aplica a Análise de Componentes Principais ao mercado brasileiro em per´ıodos de crise. A viabilidade do método é observada no fato de que a utiliza¸cão dos três principais fatores leva a uma explica¸cão total da variância dos dados originais superior a 95%, sendo esta ainda maior quando os vértices da curva escolhidos são os mais negociados.

Reno e Uboldi (2002) descrevem a implementa¸cão de um modelo para a representa¸cão da estrutura a termo da taxa de juros desenvolvido utilizando o modelo HJM. Em seu trabalho, eles indicam que o modelo é capaz de representar as principais caracter´ısticas da estrutura a termo, ao mesmo tempo em que exclui as oportunidades de arbitragem por

1_{Taxa spot: indica a taxa de juros que est´}_{a sendo praticada entre a data atual e uma certa data futura.} 2_{Taxa forward: indica a taxa de juros que dever´}_{a vigorar entre uma data futura e um certo vencimento.}

(14)

constru¸cão. O modelo HJM é, assim, atraente por suas propriedades teóricas e por sua flexibilidade embora sua calibra¸cão normalmente não seja trivial, mas através de PCA pode ser feita de maneira mais rápida e simples, facilitando a sua utiliza¸cão. Os autores utilizam uma forma funcional para a volatilidade cujos parâmetros são calibrados através de PCA sobre yield curves de taxas de juros de Euro.

Barbedo, Vicente e Lion (2010) implementam o framework HJM utilizando a Análise de Componentes Principais com um a três fatores para precificar op¸cões de ´ındice DI (IDI). O estudo mostra que o modelo de apenas um fator apresenta menor erro e menor desvio padrão comparado com os pre¸cos observados no mercado, o modelo de dois fatores aumenta o erro de precifica¸cão, enquanto o de três fatores aumenta para os dados obtidos em mercado de balcão e diminui para os dados de op¸cões negociadas em bolsa. A sugestão dos autores em relacão a este comportamento é de que o mercado simplifica a estrutura de volatilidade de taxa de juros a apenas um fator, ou que o mercado de op¸cões de IDI pode não ser apropriado para quantificar a qualidade de um modelo HJM. Finalmente, os autores mostram que existe uma rela¸cão direta entre o vencimento da op¸cão e o erro de precifica¸cão e uma rela¸cão negativa entre o moneyness da op¸cão e o erro gerado na precifica¸cão.

Nojima (2014) implementa o modelo HJM em sua forma discreta e multifatorial, uti-lizando a parametriza¸cão proposta por Brace e Musiela (1994), a abordagem numérica proposta por Glasserman e Kou (2003) e Análise de Componentes Principais para ca-libra¸cão dos parâmetros do modelo. Os dados utilizados foram as cota¸cões diárias de futuros de DIs da BM&F Bovespa entre 2003 e 2012, e os ativos precificados foram op¸cões de compra sobre IDI, op¸cões de venda sobre futuro de DI e o futuro de DI propriamente dito, sendo os resultados bastante significativos. Os erros foram pequenos em rela¸cão ao pre¸co de fechamento, sobretudo para op¸cões de compra sobre IDI e contratos futuros de DI.

Suzuki (2015) utiliza uma abordagem similar a de Nojima (2014), mas introduz um termo de jump como forma de considerar o efeito das reuniões realizadas pelo Comitê de Pol´ıticas Monetárias (Copom). O autor utiliza simula¸cões de Monte Carlo para descrever a evolu¸cão da Estrutura a Termo das Taxas de Juros, ETTJ, e compará-la com os dados observados no mercado, bem como para precificar op¸cões de derivativos de taxas de juros. Lueska (2016) segue a linha proposta por Suzuki (2015) ao incluir processos de jump,

(15)

porém garantido condi¸cões de não arbitragem. Em seu estudo, o autor utiliza uma nova abordagem ao modelar os processos geradores de jumps definindo saltos de n´ıvel, in-clina¸cão e curvatura, combinando processos de Poisson com o modelo HJM usual. A calibra¸cão do modelo é realizada através de dados históricos e as simula¸cões geradas por Monte Carlo, sendo utilizadas para precificar op¸cões de IDI, realizar forecasts da ETTJ e em estratégias de trading de DI futuro.

Outro problema central na área de finan¸cas aborda a modelagem e simula¸cão de taxas de câmbio. Em seu famoso trabalho, Meese e Rogo↵ (1983) comparam diversos métodos de proje¸cão com um simples random walk. A conclusão é que não é fácil superá-lo, em um resultado que ficou conhecido como “MR puzzle”.

Evans e Lyons (2002) apresentam um modelo que incorpora um elemento de microes-trutura financeira: o fluxo de ordens. Esta nova abordagem aumenta significativamente o poder explicativo de regress˜oes baseadas unicamente em fatores macroeconˆomicos, em todos os casos analisados em seu trabalho.

No aspecto de regula¸cão bancária, em particular relacionada a melhores práticas e preven¸cão de cenários de crise, o Comitê de Basiléia (BCBS (2009), BCBS (Jan 2014), BCBS (Dez 2014)) tem produzido diversos estudos com o objetivo de orientar bancos centrais. Em especial, podemos citar o conjunto de medidas conhecido por Basiléia III. Dentre suas principais medidas, podemos mencionar o requerimento de capital associado à introdu¸cão de uma Razão de Alavancagem.

Dell’Aricia, Laeven e Marquez (2014) propõem um modelo quantitativo para bancos e analisam o efeito que redu¸cões nas taxas de juros reais têm na alavancagem dos bancos. Os autores concluem que quando bancos podem ajustar suas estruturas de capital a redu¸cão das taxas leva a um aumento da alavancagem e risco para certos tipos de fun¸cões de demanda; quando a estrutura de capital é fixa, o efeito depende do grau de alavancagem. Grill, Lang e Smith (2017) estendem o modelo de Dell’Aricia, Laeven e Marquez (2014) para analisar o trade o↵ entre uma capacidade de absor¸cão de perdas e tomada de risco maior por parte dos bancos devido à razão de alavancagem introduzida em Basiléia III. Dentre as conclusões dos autores, este tipo de requerimento pode incentivar bancos a aumentar os riscos tomados, mas este problema é superado pelos benef´ıcios de possuir um maior capital reservado, levando a bancos mais estáveis.

(16)

multi-fatorial em conjunto com técnicas envolvendo distribui¸cões de probababilidade emp´ıricas, de modo a simular, de maneira simultânea e consistente, diversas curvas de juros e ati-vos presentes no mercado brasileiro. Estes resultados serão utilizados em duas aplica¸cões práticas. Na primeira, precificaremos instrumentos e construiremos a distribui¸cão de pro-babilidade dos pre¸cos dos mesmos após um certo horizonte de tempo. Na segunda, mos-traremos como os resultados obtidos podem ser empregados em um problema de aloca¸cão de ativos, de modo a otimizar o lucro de um banco sujeito a requerimentos de capital aos moldes de Basiléia III.

(17)

3 Fundamentos te´

oricos

A seguir, apresentaremos os diferentes aspectos teóricos que serão utilizados. Iniciare-mos a exposi¸cão passando pelo movimento Browniano geométrico, pelo modelo HJM, e em seguida pelo conceito de distribui¸cões emp´ıricas. Após isso, mostraremos como integrar estes diferentes pontos em um modelo de simula¸cão, o objetivo central deste trabalho. Concluiremos abordando uma poss´ıvel aplica¸cão do modelo proposto em um problema concreto.

3.1 Movimento Browniano geom´

etrico

Considere um processo estoc´astico S da forma dS

S = µdt + dB, (1)

em que µ e são constantes e B é um movimento Browniano. Note que µ corresponde ao drift do processo, enquanto que ( dB)2 ₌ 2_{dt é a sua varia¸cão no mesmo intervalo de}

tempo. ´

E importante mencionar que caso nosso objetivo seja simular os pre¸cos de ativos no “mundo real”, não podemos trabalhar com a medida neutra ao riscoQ, mas com a medida de risco realP (a principal utilizacão da primeira é para precificar derivativos). Portanto, seria necessário estimarmos µ; esta, no entanto, não é necessariamente uma tarefa simples (Back, 2009).

A hipótese do movimento Browniano geométrico pode ser relaxada em uma simula¸cão de Monte Carlo. A utiliza¸cão de um outro tipo de distribui¸cão paramétrica que tente incorporar aspectos particulares do ativo em questão, como uma t-Student por exemplo, ou até mesma uma distribui¸cão emp´ırica para os retornos constru´ıda a partir de dados históricos, também pode ser realizada.

3.2 O modelo HJM e a parametriza¸c˜

ao de Musiela

Antes do in´ıcio da década de 90, os modelos que descreviam a evolu¸cão de taxas de juros tinham seu foco na taxa spot. Em seu famoso trabalho, Heath, Jarrow e Morton (1992) propuseram um modelo que descreve as dinâmicas das taxas forwards da curva

(18)

inteira. Este modelo, conhecido como HJM, ser´a utilizado de acordo com a parametriza¸c˜ao proposta por Brace e Musiela (1994).

Seja f (t, T ) a taxa forward instantˆanea de T vista em t, t T . Vamos denotar o pre¸co de um zero-coupon bond 3 _{em t de P (t, T ). Desse modo,}

f (t, T ) = @

@TlogP (t, T ), (2)

P (t, T ) = eRtTf (t,s)ds, 0 t  T, (3)

com a dinˆamica do diferencial df da taxa dada por:

df (t, T ) = µ(t, T )dt +

n

X

i=1

idWi, (4)

em que µ(t, T ) corresponde ao drift, n ´e o n´umero de fatores do modelo e Wi, 1 i  n,

são movimentos Brownianos independentes, sob a medida realP. É importante ressaltar que tanto o µ quanto Wi são fun¸cões de f. Na medida neutra ao risco Q, o drift passa a

ser uma fun¸c˜ao da volatilidade, de modo que a dinˆamica de df nesta medida se torna

df (t, T ) = n X i=1 i(t, T ) Z T t i(t, s)ds ! dt + n X i=1 i(t, T )d ˜Wi(t), (5)

estando d ˜Wi(t) na medida neutra ao risco. Sob a parametriza¸c˜ao de Musiela, definimos

r(t, ⌧ ) = f (t, t + ⌧ ), (6)

sendo r(t, ⌧ ), portanto, a taxa forward vista em t para um vencimento t + ⌧ . Ap´os a mudan¸ca de vari´avel, dr(t, t + ⌧ ) = ✓ @r(t, ⌧ ) @⌧ + µ(t, ⌧ ) ◆ dt + n X i=1 i(t, ⌧ )d ˜Wi(t), (7) µ(t, ⌧ ) = n X i=1 i(t, ⌧ ) Z ⌧ 0 i(t, s)ds. (8)

O modelo, conforme apresentado acima, encontra-se em sua forma cont´ınua. Para poder utilizá-lo em simula¸cões é necessário discretizá-lo, sendo o processo amplamente

(19)

descrito em Nojima (2014), Suzuki (2015) e Lueska (2016). O modelo HJM em sua forma discreta sob a parametriza¸c˜ao de Musiela ´e dado por:

r(ti, ⌧j) = r(ti 1, ⌧j) + ✓ r(ti 1, ⌧j+1) r(ti 1, ⌧j) ⌧j+1 ⌧j + a(ti 1, ⌧j) ◆ (ti ti 1) + N X n=1 n(ti 1, ⌧j) p ti ti 1Win, (9) 2(⌧j+1 ⌧j)a(ti 1, ⌧j) = N X n=1 j X m=0 n(ti 1, ⌧m) !2 N X n=1 j 1 X m=0 n(ti 1, ⌧j)(⌧m+1 ⌧m) !2 , (10)

para um modelo com N fatores. ´

E importante ressaltar que o modelo HJM, conforme apresentado acima, encontra-se na medida neutra ao risco (d ˜Wi). Nas nossas simula¸c˜oes, no entanto, vamos precisar

colocar o modelo na medida de probabilidade real. Precisamos, portanto, entender como fazer a transi¸cão entre estas medidas. Esta conversão é realizada utilizando-se o market price of risk.

A existência do market price of risk é demonstrada em Heath, Jarrow e Morton (1992), mas não é muito explorado uma vez que os autores estão preocupados em formular seu mo-delo na medida neutra ao risco. Yasuoka (2015) abordada esta questão em mais detalhe. Matematicamente, ele aparece como um termo extra no drift,

µ(t, ⌧ ) = n X i=1 i(t, ⌧ ) Z ⌧ 0 i(t, s) + ids, (11)

o qual denotamos por i.

´

E poss´ıvel discretizar a expressão que contêm o market price of risk, sendo o proce-dimento exibido em detalhe em Yasuoka (2015). No nosso contexto, é poss´ıvel estimá-lo como4_: l⇡ 1 ⇢l m X i=1 Ehist  ri t e l i, (12)

4_{A aproxima¸c˜}_{ao vale quando o termo do drift neutro ao risco ´e muito menor que a m´edia hist´}_orica

(20)

onde ⇢l ´e o autovalor correspondente ao fator l, el o autovetor5 do fator l, eEhist[ ri/ t]

a média histórica das varia¸cões da taxa forward no prazo ti e m é o número de vértices

considerados.

3.3 Distribui¸c˜

oes emp´ıricas

Um dos maiores desafios presentes em simula¸cões de Monte Carlo é representar de maneira consistente o fato de que os ativos não são inteiramente independentes entre si. De uma maneira geral, a abordagem usual apresenta algumas limita¸cões; dentre elas, o fato de que utilizamos dados passados na esperan¸ca de que eles possuam certo poder de previsibilidade em rela¸cão ao futuro e a hipótese de movimento Browniano geométrico e correla¸cões.

Em rela¸cão à primeira, não há muito o que ser feito; o fato de possu´ırmos uma quan-tidade finita de dados que só pode ser aumentada por observa¸cão direta afeta a área de finan¸cas em sua totalidade. A segunda limita¸cão, no entanto, pode ser tratada.

Ao invés de assumir uma distribui¸cão normal, uma possibilidade é construir a dis-tribui¸cão emp´ırica a partir dos dados históricos. Assim, não só atacamos a questão da hipótese gaussiana mas também utilizamos nosso conjunto de dados ao máximo. No pre-sente trabalho, como temos o objetivo de simular o comportamento de diversos ativos e estruturas a termo de maneira simultânea, iremos construir distribui¸cões emp´ıricas condi-cionais. Falando objetivamente, dada uma varia¸cão no pre¸co de um ativo (ou conjunto de ativos) A, iremos construir a distribui¸cão de probabilidades do ativo B. Isto introduz um aspecto “model free” à abordagem; em princ´ıpio, aspectos particulares do comportamento do ativo já devem estar naturalmente incorporados, dispensando a utiliza¸cão de métodos anal´ıticos mais complexos (e consequentemente uma maior imposi¸cão de hipóteses).

A abordagem emp´ırica, no entanto, possui algumas limita¸cões. Por constru¸cão, todo o conjunto dos poss´ıveis resultados de simula¸cão está limitado aos dados históricos. Em outras palavras: não é poss´ıvel simular um cenário totalmente novo, independente da história passada do ativo. Este problema pode ser significativamente amplificado caso o conjunto de dados seja limitado. No caso brasileiro, felizmente, as curvas e ativos a

5_{Os autovalores e autovetores aqui mencionados s˜}_{ao obtidos a partir da diagonaliza¸c˜}_{ao da matriz de}

covariância das taxas forward. Estes conceitos, relacionados ao uso da Análise de Componentes Principais, são detalhados mais adiante.

(21)

serem modelados apresentam um hist´orico que inclui diversas crises financeiras, e portanto espera-se que este problema seja minimizado.

´

E importante ressaltar um ponto que ficou impl´ıcito no parágrafo anterior: só é poss´ıvel utilizar a distribui¸cão emp´ırica condicional dos retornos do ativo B para simulá-lo se for-mos capazes de simular o comportamento do ativo A em primeiro lugar, ativo ao qual B está condicionado. Como consequência, na nossa abordagem, algums ativos deverão ser simulados primeiro para em seguida simular os outros mediante a constru¸cão de distri-bui¸cões emp´ıricas condicionais. Isto naturalmente introduzirá uma hierarquia no nosso modelo. No momento, não vamos explorar este ponto em profundidade; isto será feito um pouco mais adiante.

Para ilustrar o procedimento de constru¸cão das distribui¸cões, suponha que possu´ımos a série temporal dos retornos de dois ativos, A e B, e queremos obter a distribui¸cão emp´ırica dos retornos de B condicionada a A. Com efeito, seja rA o retorno observado em

um instante t. Definimos um intervalo I,

I(t)_{⌘ [r}A(t) , rA(t) + ]2 R, (13)

onde possui um valor arbitr´ario, independente de t. Vamos denotar por ⌦ o conjunto dos pares ordenados constru´ıdos a partir dos retornos dos ativos observados em um mesmo instante de tempo, ⌦ ={(r(0)A , r (0) B ), (r (1) A , r (1) B ), ..., (r (i) A , r (i) B), ...}, i 2 [0, T ] ⇢ R. (14)

A partir de ⌦, definimos o conjunto ! como sendo um conjunto de pares ordenados,

! ={(r(i)A, r (i)

B)2 ⌦ | r (i)

A 2 I}. (15)

Ou seja, coletamos todos os pares ordenados em que o retorno do ativo A se encontra dentro do intervalo I definido acima. Uma vez possuindo esta amostra, podemos coletar os retornos do ativo B e construir uma distribui¸c˜ao emp´ırica,

! _{! F}B|A(x), (16)

sendo esta distribui¸cão (acumulada) condicionada, portanto, ao retorno observado do ativo A. Uma vez obtida a distribui¸cão, podemos empregar o método da amostragem

(22)

inversa, sorteando n´umeros de uma distribui¸c˜ao uniforme no intervalo [0, 1] e obtendo um retorno simulado rB,

[0, 1]_{! x ) F}_B_|A1(x) = rB. (17)

Por simplicidade, como o conjunto de dados é discreto e como temos que lidar com o fato de que vamos construir distribui¸cões condicionais inúmeras vezes durante a simula¸cão, elas serão constru´ıdas através de histogramas (isto é, definindo-se um “bin size”) e inter-pola¸cão linear. Apesar de existirem métodos mais sofisticados para realizar a interinter-pola¸cão, caso o conjunto de dados possua um tamanho razoável, a abordagem aqui apresentada não é ruim, além de apresentar uma boa performance em termos de processamento.6

3.4 Modelo de simula¸c˜

ao integrado

Neste ponto, já estamos prontos para detalhar o procedimento através do qual as diferentes técnicas apresentadas podem ser integradas, especificamente o modelo HJM e o uso de distribui¸cões condicionais para simular um número arbitrário de ativos do mercado. Considere o seguinte universo de ativos: a curva Pré, a cota¸cão do dólar (USD/BRL) e a curva de Cupom Cambial Sujo. Sabemos que estes três ativos estão relacionados de maneira direta e não trivial, o que dificulta qualquer tentativa direta de modelagem. Dessa forma, a atitude mais sensata é tentar reduzir o número de hipóteses e procurar alguma abordagem “model free” que de alguma maneira capture estas dependências.

Conforme mencionado na introdu¸cão e revisão bibliográfica, é bastante razoável aplicar o modelo HJM para modelar a curva Pré, uma vez que isto já foi feito em trabalhos ante-riores com elevado grau de sucesso (Nojima (2014), Suzuki (2015), Lueska (2016)). Outra hipótese razoável é tratar a cota¸cão do dólar como uma simula¸cão independente, dada sua semelhan¸ca ao movimento Browniano geométrico. Isto pode ser realizado através do uso de distribui¸cões emp´ıricas: utilizando retornos passados, constru´ımos a distri-bui¸cão dos mesmos e simulamos o comportamento do dólar de modo não-paramétrico. Resta, portanto um ativo do nosso universo a ser incorporado na simula¸cão: a curva

6_{E importante ressaltar que a abordagem acima pode ser aplicada para outros invariantes de mercado.}_´

Para a¸c˜oes, o log-retorno desempenha esse papel; para renda-fixa, um invariante sugerido seria a raz˜ao entre PU’s (ver Meucci (2005)), sendo esta equivalente a mudan¸ca no valor da yield to maturity (YTM) do papel.

(23)

de Cupom Cambial Sujo. A solu¸cão proposta neste trabalho consiste em utilizar distri-bui¸cões emp´ıricas condicionais para resolver este problema. Vamos construir distridistri-bui¸cões emp´ıricas dos log-retornos dos fatores da curva de Cupom Cambial Sujo, condicionadas à curva Pré e ao dólar. Nos parágrafos seguintes, vamos explicar este procedimento em detalhe.

No nosso modelo, vamos assumir que o CDI e o d´olar s˜ao os principais agentes do universo de ativos, sendo todas as outras curvas e ativos condicionados aos mesmos7_{. Na}

hierarquia do nosso modelo de simula¸cão, estes ativos serão os “drivers” fundamentais de todo o processo. Sendo assim, na primeira etapa do nosso processo de simula¸cão, a curva Pré será simulada através do modelo HJM e a cota¸cão do dólar será simulada através de uma simula¸cão de Monte Carlo utilizando uma distribui¸cão emp´ırica.

No caso do dólar, os retornos serão simulados utilizando-se uma distribui¸cão emp´ırica na qual a distribui¸cão dos retornos a ser utilizada na simula¸cão de um certo dia é con-dicionada ao retorno do dia anterior. Ou seja, dado o retorno em t, iremos construir a distribui¸cão em t + 1 e obter o retorno simulado a partir da mesma; tal processo será repe-tido dia a dia para todo o horizonte de tempo da simula¸cão. Esta abordagem possui uma vantagem sutil: caso existam desvios da hipótese do movimento Browniano geométrico no comportamento do dólar na forma de algum tipo de “memória” de retornos passados (ou seja, se a distribui¸cão de retornos não for i.i.d.) os mesmos serão em algum grau (ao menos hipoteticamente) capturados por esta abordagem.

Uma vez sendo capazes de simular o dólar e a curva Pré, partimos para a curva de Cupom Cambial Sujo. A primeira etapa consiste em escolher quais vértices da curva serão simulados. Note que a escolha dos vértices na implementa¸cão do HJM induz natu-ralmente um certo conjunto de vértices a serem modelados na curva de Cupom Cambial, mas é necessário tomar alguns cuidados. Suponha, por exemplo, que tenhamos utilizado os vértices de 21, 42, 63 e 126 dias úteis na curva Pré, e estes foram simulados pelo mo-delo HJM; vamos escolher, portanto, quatro vértices na Curva de Cupom Cambial: os vértices de 30, 60, 90 e 180 dias corridos. É importante ressaltar que as conven¸cões de contagem de dias e interpola¸cão das duas curvas são diferentes: a curva Pré utiliza dias ´

uteis e interpola¸c˜ao exponencial, enquanto que a curva de Cupom utiliza dias corridos e

7_{Seria poss´ıvel incluir o Bovespa nesta lista. N˜}_{ao o faremos exclusivamente pelo fato de que n˜}_ao

realizaremos simula¸c˜oes envolvendo a¸c˜oes. Fosse este o caso, o ´ındice IBOV certamente pertenceria a esta categoria de agente principal do mercado

(24)

interpola¸cão linear. Nosso principal motivo para escolher estes vértices é poder preservar a propor¸cão: 21 30 = 42 60 = 63 90 = 126 180 = 0, 7. (18)

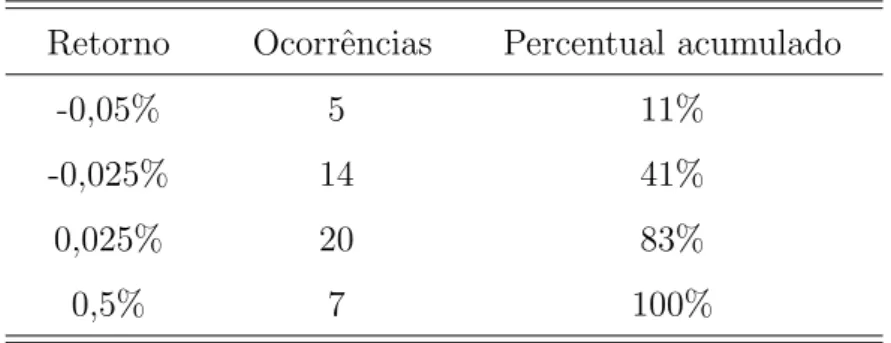
Uma vez escolhidos os prazos dos vértices, passamos para a etapa seguinte: a cons-tru¸cão das distribui¸cões emp´ıricas necessárias para simular a curva de Cupom Cambial. Considere o seguinte exemplo: tomemos o dólar, o vértice de 30 dias corridos da curva de Cupom Cambial e o vértice de 21 dias úteis da curva Pré. Utilizamos então o modelo HJM e Monte Carlo para simular a Pré e o dólar, um dia adiante, calculamos o log-retorno do fator do vértice de 21 dias úteis (DU) e o log-retorno do dólar e obtemos, digamos, 1% e 2% respectivamente. Na etapa seguinte, observamos os dados históricos e notamos que nas ocasiões em que o log-retorno do fator spot do vértice 21 da curva Pré foi 1% e o log-retorno do dólar foi 2%, os log-retornos dos fatores spot históricos da curva de Cupom Cambial foram os indicados na Tabela 1.

Tabela 1: Exemplo: retornos e frequˆencias da curva de Cupom Cambial Sujo

Retorno Ocorrˆencias Percentual acumulado

-0,05% 5 11%

-0,025% 14 41%

0,025% 20 83%

0,5% 7 100%

Dessa forma, somos capazes de construir um histograma e obter a distribui¸cão emp´ırica condicional do vértice de 30 dias corridos da curva de Cupom. Finalmente, utilizando uma distribui¸cão uniforme, sorteamos um número entre 0 e 1; digamos que o resultado seja 0,75. Utilizando interpola¸cão linear, encontramos o retorno r correspondente:

r = 0, 00025 + 0, 00025 ( 0, 00025)

0, 83 0, 41 ⇤ (0, 75 0, 41)⇡ 0, 00015 = 0, 015%. (19) Dessa forma, simulamos a curva de Cupom Cambial Sujo seguindo o mesmo procedimento para os demais v´ertices.

´

E importante ressaltar o aspecto modular do modelo de simula¸c˜ao. Poder´ıamos simular um ativo X condicionado, digamos, ao v´ertide de 60 dias corridos do Cupom Cambial e

(25)

a taxa over do CDI, um ativo Y condicionado a X e a USD/BRL, e assim por diante. O procedimento é facilmente replicável; os únicos detalhes a serem observados são a ordem em que as simula¸cões devem ser realizadas e o custo computacional do procedimento como um todo.

3.5 Aplica¸c˜

ao em problemas de tomadas de decis˜

ao

Um dos problemas centrais enfrentados por institui¸cões financeiras, empresas e mesmo indiv´ıduos, refere-se à gestão de ativos e passivos. Em termos simples, dado um conjunto de ativos e passivos, suas expectativas de retornos esperados, bem como poss´ıveis eventos de perda, o problema se resume a definir a melhor estratégia de aloca¸cão e tomadas de decisão dadas as informa¸cões dispon´ıveis.

Estratégias de hedge podem ser empregadas neste tipo de análise. Por exemplo, supo-nha que uma determinada institui¸cão precisa realizar pagamentos, e estes estão atrelados a uma determinada taxa pré-fixada. Caso exista um risco desta taxa se tornar desvantajosa em rela¸cão à taxa de mercado, pode-se empregar um swap DI x Pré como instrumento de hedge. O inverso também é válido: se a institui¸cão realiza pagamentos em uma taxa flu-tuante e existe um risco de existir um desequil´ıbrio no fluxo de caixa devido às flutua¸cões da taxa de mercado, um swap pode novamente ser utilizado.

Diversas crises financeiras atingiram a economia global recentemente, notavelmente a crise de 2008. Naturalmente, diversos estudos foram realizados com o objetivo de entender as causas destas crises, bem como maneiras de evitá-las (ou ao menos minimizar seus impactos). Neste aspecto, o comitê de Basiléia possui um papel fundamental em realizar estudos, propor e disseminar boas práticas de gestão entre bancos e institui¸cões financeiras. Em particular, as novas resolu¸cões de Basiléia III (BCBS (2009), BCBS (Jan 2014), BCBS (Dez 2014)), dentre outras medidas, introduzem uma medida da Razão de Alavacagem (a qual vamos nos referir por RA daqui em diante) não baseada na abordagem usual de capital de risco, tendo como objetivo evitar a alavancagem excessiva de bancos, um fator considerado fundamental nas crises recentes.

Para utilizar nosso modelo de simula¸cão simultânea em uma aplica¸cão prática, vamos propor uma varia¸cão do modelo definido em Grill, Lang e Smith (2017). Nosso foco será partir do modelo proposto pelos autores e realizar algumas altera¸cões de modo a adequá-lo ao contexto desta disserta¸cão. De um modo geral, iremos utilizar a estrutura de árvore

(26)

de probabilidades definida por Grill, Lang e Smith (2017), bem como os fundamentos da descri¸cão matemática do comportamento de um banco sujeito a restri¸cões.

Seja A um certo ativo eleg´ıvel para ser escolhido como um investimento de uma dada instituic˜ao financeira. Sejam s1 e s2 dois estados poss´ıves da natureza, que podem ocorrer

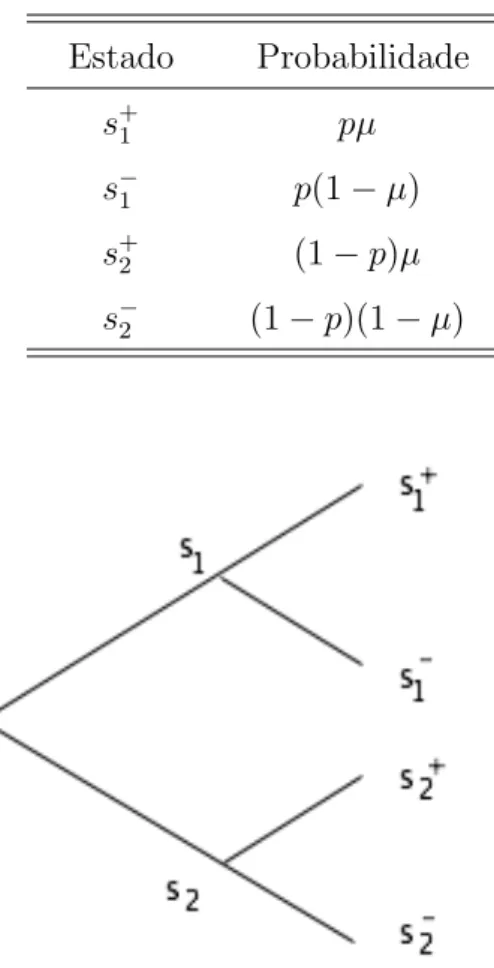
com possibilidades p e 1 p, e que podem novamente se ramificar em um instante de tempo subsequente em dois estados, sendo µ e 1 µ as suas probabilidades. Em um diagrama de ´arvore, ter´ıamos quatro estados finais poss´ıveis, que ocorrem com as seguintes probabilidades:

Tabela 2: Estados e probabilidades

Estado Probabilidade

s+₁ pµ

s1 p(1 µ)

s+₂ (1 p)µ

s2 (1 p)(1 µ)

Figura 1: Estrutura da ´arvore binomial.

Uma vez que somos capazes de simular as trajetórias das curvas que determinam o pre¸co de A, somos capazes de estimar as probabilidades dos estados finais em questão, já que podemos construir a distribui¸cão de pre¸cos poss´ıveis de A no instante final, que comtempla os quatro poss´ıveis estados da natureza. Tal procedimento também é aplicável a um portfólio de ativos no qual o pre¸co de cada um de seus componentes é calculado com base nas curvas simuladas, uma vez que seremos então capazes de extrair a distribui¸cão

(27)

conjunta dos pre¸cos. Suponha que a densidade de probabilidade do pre¸co do ativo em t é descrita por f (x), x _{2 R, constru´ıda a partir do método de Monte Carlo aplicado} ao pre¸co do ativo. Como estamos interessados em quatro estados finais, considere uma parti¸cão da reta em quatro subconjuntos disjuntos, de modo que:

4

[

i=1

Si =R. (20)

Desta forma, podemos calcular o valor esperado de A em cada um dos estados finais,

Esi_{[A] =}

Z

Si

A f (x)dx. (21)

Claramente a parti¸cão não é única, sendo esta decidida por aquele que construir a árvore. Note que o argumento acima pode ser imediatamente extendido para um número ar-bitrário de ativos mediante o uso da densidade de probabilidade conjunta dos mesmos.

Para simplificar a nota¸cão (e torná-la mais próxima da utilizada em Grill, Lang e Smith(2017)), vamos introduzir algumas constantes multiplicativas. Seja E[A] o valor esperado do ativo A no instante final, independente do estado, e si um dado estado final

da ´arvore de probabilidades. Assim, podemos escrever:

Esi_{[A] = (1}

i)E[A], 2 R. (22)

Outro aspecto importante ´e o requerimento de capital. Vamos atribuir ao ativo A um requerimento de capital (baseado em risco) kA. Tamb´em definiremos um requerimento

klev, n˜ao baseado em risco mas em alavancagem, de modo que o requerimento de capital,

ou seja, a quantidade de dinheiro que a institui¸c˜ao deve manter guardada para se proteger de eventuais perdas, seja dada por:

k max klev, X i !ikAi ! , (23) X i !i = 1, (24)

onde o conjunto {Ai} representa o portf´olio de ativos da empresa e !i o valor financeiro

alocado em cada um deles, cujo total estamos normalizando para 1. Naturalmente, como o objetivo de qualquer investidor racional ´e maximizar o lucro, o capital k reservado dever´a sempre ser o m´ınimo poss´ıvel, de modo que:

(28)

k = max klev, X i !ikAi ! . (25)

Seguindo Allen e Gale (2000), introduzimos uma fun¸c˜ao de custo convexa para se investir no ativo arriscado, c(!i), de modo que c0(!i) < 0, c00(!i) 0 para todo i. Assim,

investir em um ativo deste tipo se torna cada vez mais caro. O propósito desta fun¸cão é restringir o tamanho dos portfólios individuais. Seguimos a parametriza¸cão de Grill, Lang e Smith (2017), fazendo

c(!i) =

c

2(1 !i)

2_, ₍₂₆₎

e c deve ser tal que o custo c de se investir no ativo arriscado seja maior que o aumento no retorno esperado ao substituir o ativo seguro pelo arriscado.

Além de institui¸cões financeiras (vamos chamá-las apenas de bancos daqui em diante), existem outros componentes de uma certa economia. Vamos considerar dois componentes extras: depositantes e acionistas. Os depositantes aplicam dinheiro no banco e esperam recebê-lo mais tarde, corrigido por alguma taxa. Vamos supor que existe seguro para os depósitos (algo como um Fundo Garantidor de Crédito), de modo que os depositantes aceitam um retorno rf igual a taxa livre de risco em seus investimentos, que totalizam um

capital d. Os acionistas, por outro lado, assumem o risco de falˆencia, e portanto desejam um retorno ⇢ > rf. O capital arrecadado a partir dos mesmos ser´a utilizado para cobrir

os custos de requerimento de capital, totalizando k. Deste modo assumindo que o capital ´e 1 (normalizando), em t = 0, temos:

d + k = 1. (27)

Podemos escrever a expressão do lucro do portfólio ⇧ ao final da árvore, lembrando que p e µ são probilidades:

⇧ = [µp(1 1) + µ(1 p)(1 2) + (1 µ)p(1 2) + (1 µ)(1 p)(1 4)] X i !iE[Ai] (1 + rf)d. (28)

Finalmente, vamos denotar por 1 ✓ a fra¸c˜ao do lucro que deve ser destinada aos acionistas, de modo a satisfazer a exigˆencia dos mesmos:

(29)

(1 ✓)⇧ ⇢k. (29) Assumindo que o pagamento aos acionistas será o m´ınimo necessário, nosso problema de otimiza¸cão se resume a: max _{✓⇧ X i=1 c(!i)}, (30) sujeito a (1 ✓)⇧ ⇢k, (31) d + k = 1, (32) k = max klev, X i !ikAi ! . (33)

Conforme mencionado no in´ıcio deste item, este problema será resolvido utilizando a abordagem de simula¸cão simultânea, a qual será utilizada para calcular os pre¸cos nos estados finais, bem como as probabilidades destes estados ocorrerem; o procedimento será mostrado em detalhe mais adiante. A seguir, vamos apresentar quais ativos serão utilizados para compor o portfólio de ativos do banco.

3.6 Tipos de ativos considerados

Para implementar o modelo de árvore binomial proposto, vamos utilizar alguns papéis de renda fixa de modo a construir um portfólio que, ainda que simples, contenha os tipos de indexadores comumente encontrados e utilizados no mercado.

Considere inicialmente opera¸cões atreladas a taxas pré-fixadas, bem como a certos percentuais do CDI. A marca¸cão a mercado, M tMt, destes papéis é dada por:

M tMt= n X i=1 " SDti 1(f index ti 1!tif f ixo ti 1!ti 1) + Ati fdesc t!ti # , (34) com SDti = SDti 1 Ati, (35)

(30)

onde

n é o número de fluxos; t é a data de cálculo; v é a data de vencimento;

ti ´e a data do i-´esimo pagamento;

SDt ´e o saldo devedor em t (em t = 0 ele corresponde ao valor nominal);

At´e a amortiza¸c˜ao em t;

f_tf ixo₀_!t_i ´e o fator pr´e-fixado entre t0 e ti;

findx

ti 1!ti ´e o fator de indexa¸c˜ao entre ti 1 e ti;

fdesc

t!ti ´e o fator de desconto entre t e ti.

Os fatores da expressão acima são calculados utilizando-se a conven¸cão exponencial, com 252 dias úteis por ano. Também é utilizada a conven¸cão usual do mercado de “carecar o indexador” (ou seja, a indexa¸cão come¸ca a partir do in´ıcio do fluxo).

Dando prosseguimento aos ativos tratados na simula¸cão, notamos que opera¸cões em moeda estrangeira também são realizadas com grande frequência. Portanto, também consideraremos papéis de renda fixa ligados ao dólar. Neste caso, a marca¸cão a mercado, M tMt, é dada por:

M tMt = P c " _n X i=1 f_tf ixo₀_!t_i_{⇥ P T AX}ti d fdesc t!ti ! +P T AXv d fdesc t!v # , (36) P T AXti d P T AXt = f pre t!ti d f_t!tcupom_i _{d 1}, (37) com

t ´e a data de referˆencia;

ti ´e a data do i-´esimo fluxo, ti > t, i = 1...n;

(31)

d ´e o per´ıodo de defasagem; P ´e o principal;

c ´e a taxa de cˆambio inicial;

f_tf ixo₀_!t_i ´e o fator do i-´esimo pagamento;

P T AXté a cota¸cão média da moeda em t 1;

fdesc

t1!t2 ´e o fator de desconto entre t1 e t2;

f_tpre₁_!t₂ ´e o fator pr´e entre t1 e t2.

O vencimento de ambos os papéis ocorrerá no mesmo dia, 126 dias úteis (ou 180 dias corridos) a partir da data de referência.

Neste ponto, conclu´ımos a apresenta¸cão do modelo e de uma aplica¸cão prática do mesmo. Nas se¸cões a seguir, vamos abordar os aspectos práticos da sua implementa¸cão, desde dados até a análise de seus resultados.

(32)

4 Metodologia

Neste cap´ıtulo, descreveremos em detalhe os passos necessários para implementar o modelo HJM, construir as distribui¸cões emp´ıricas e realizar as simula¸cões das curvas e dos pre¸co de ativos, além de implementar o modelo de aloca¸cão descrito anteriormente em conjunto com os resultados das simula¸cões.

4.1 Dados

Dentre os objetivos deste trabalho, temos a aplica¸cão do modelo HJM às taxas de juros nominais do Brasil. Para obter as taxas correspondentes foi utilizado o mercado de DI futuro, um dos mercados mais l´ıquidos negociados na B3, cujo ativo subjacente é a taxa do certificado do depósito interbancário, o CDI.

Os dados utilizados correspondem aos fechamentos históricos dos vencimentos de DI futuro negociados no per´ıodo de janeiro de 2015 a dezembro de 2016, além dos dados do CDI diário fornecidos diariamente pela CETIP (estes são usados para o vértice de um dia ´

util; os demais vértices da curva são obtidos a partir dos futuros de DI). Foi necessário utilizar um critério de interpola¸cão para obter as taxas em vértices fixos, e para tanto adotamos a interpola¸cão exponencial. Considere os instantes de tempo t1 e t2, nos quais

conhecemos as taxas spot. A taxa spot entre zero e t, t1 < t < t2 ´e:

taxat = (1 + taxat1) t1/252  (1 + taxat2) t2/252 (1 + taxat1)t1/252 (t t1)/(t2 t1)!252/t 1. (38)

Uma vez obtidas as taxas spot nos v´ertices desejados (1, 21, 42, 63, 126 e 252 dias ´

uteis), a etapa seguinte ´e obter as taxas cont´ınuas forward. Realizando a convers˜ao:

erc(t/252) _{= (1 + r)}t/252_{) r}

c = ln(1 + r), (39)

onde rc ´e uma taxa cont´ınua e r a taxa di´aria usual. Finalmente, para calcular a taxa

forward r1,2 entre as datas t1 e t2 faremos:

er1t1_er1,2(t2 t1) _{= e}r2t2 _{) r}

1,2 =

r2t2 r1t1

t2 t1

. (40)

Após esta última etapa, já é poss´ıvel realizar a decomposi¸cão da curva em componentes principais e empregar o modelo HJM.

(33)

A próxima curva que abordaremos é a curva de Cupom Cambial Sujo, a qual é utilizada para projetar o PTAX. Para construir a curva (estamos utilizando o mesmo horizonte de tempo do DI), utilizamos as taxas referenciais do swap DI x dólar dispon´ıveis no site da B3. A conven¸cão utilizada foi a interpola¸cão linear, base de 360 dias corridos, e os vértices escolhidos foram os de 30, 60, 90, 180 e 360 dias corridos. Novamente, considere os instantes de tempo t1 e t2, nos quais conhecemos as taxas spot, taxat1 e

taxat2, respectivamente . A taxa spot, taxat entre zero e t, t1 < t < t2, de acordo com a

interpola¸c˜ao linear, ´e:

taxat=  (t2 t) t2 t1) taxat1 + (t t1) t2 t1) taxat2 (41)

Note que o modelo HJM simula taxas forward cont´ınuas. Na etapa de simula¸cão seguinte, a etapa das distribui¸cões emp´ıricas condicionais, não utilizaremos taxas e sim fatores spot. Portanto, após realizar a simula¸cão HJM temos que converter o resultado de volta em taxas spot utilizando as expressões mostradas acima e então calcular fatores da curva. Seja r a taxa spot da curva Pré com prazo em t. O fator da curva é dado por:

f ator = (1 + r)252t . (42)

No caso do fator spot da curva de Cupom Cambial Sujo, temos:

f ator = ✓ 1 + r⇥ t 360 ◆ . (43)

onde r ´e a taxa spot, tamb´em com prazo em t.

Por último, também utilizamos a cota¸cão diária do dólar no mesmo horizonte de tempo.

4.2 Componentes Principais

Neste trabalho, utilizamos PCA para obter as componentes da estrutura de volatili-dade das taxas forward com maior poder explicativo em rela¸cão à variância total da curva DI. A idéia essencial que fundamenta o PCA é de que um sistema com alta dimensiona-lidade pode ser aproximado com boa precisão por um sistema composto por um número menor de dimensões, utilizando-se para isso as correla¸cões entre as variáveis originais do sistema.

(34)

Existem muitas maneiras de se determinar o conjunto dos componentes principais de uma certa amostra de dados. Um deles, utilizado em Nojima (2014), Suzuki (2015) e Lueska (2016) consiste em realizar uma decomposi¸cão em autovalores e autovetores da matriz de covariância emp´ırica das taxas forward, preferencialmente após centralizar e escalar os dados (subtrair a média e dividir pela variância). A abordagem que utilizare-mos baseia-se na decomposi¸cão SVD, Singular Value Decomposition (ver Gentle, 1998), aplicada diretamente sobre os dados, ou seja, as taxas, conforme exibido em McLean e Redfern (2014).

Seja M uma matriz de ordem m⇥ n, com entradas reais (a decomposi¸cão também se aplica a matrizes complexas). Após a decomposi¸cão SVD,

M = U ⌃VT, (44)

onde U é uma matriz ortonormal m⇥ m, ⌃ é uma matriz diagonal m ⇥ n (que contém os valores singulares) e V uma matriz ortonormal n_{⇥ n. Para obter os componentes} principais, a primeira etapa consiste em construir uma matriz com as observa¸cões, onde as colunas correspondem aos prazos, e as linhas são as observa¸cões das taxas forward cont´ınuas. A segunda etapa consiste em subtrair a média, de modo que as colunas tenham média zero (também é poss´ıvel dividir pela variância, mas não é fundamental no nosso caso).

Uma vez que os dados estão preparados, realizamos a decomposi¸cão SVD. As colunas de V são os componentes principais na forma normalizada, e os autovalores estão presentes na diagonal de ⌃. A razão para descrevermos este método de cálculo do PCA em particular reside no fato de que utilzaremos a biblioteca Stats da linguagem R. Em particular, utilizaremos o comando prcomp, que utiliza o método da decomposi¸cão SVD.

Finalmente, a variância total é dada pela soma dos autovalores calculados. Portanto, a propor¸cão da variância total explicada pela i-ésima componente principal é dada por:

c = _P_Ni

j=1 j

, (45)

(35)

4.3 Resumo do procedimento

Neste ponto, podemos descrever, passo a passo, as etapas do processo desde o trata-mento dos dados at´e as simula¸c˜oes.

1. Obter os dados hist´oricos do futuro de DI.

2. Realizar a interpola¸cão exponencial e obter as taxas spot da curva Pré nos vértices desejados.

3. Com as taxas, construir os fatores hist´oricos spot da curva. Eles ser˜ao utilizados mais tarde.

4. Converter as taxas spot para taxas forward cont´ınuas e aplicar o modelo HJM. 5. Converter o resultado da simula¸c˜ao HJM para taxas spot.

6. Obter os fatores spot simulados da curva Pré. Guardar o resultado. 7. Obter os dados históricos das taxas referenciais de swaps DI x dólar.

8. Realizar a interpola¸cão linear e obter as taxas spot históricas da curva de Cupom Cambial nos vértices desejados.

9. Obter os fatores hist´oricos spot da curva de Cupom Cambial Sujo. Eles ser˜ao utili-zados mais tarde.

10. Obter os retornos hist´oricos do d´olar.

11. Construir as distribui¸c˜oes emp´ıricas condicionais do d´olar spot.

12. Realizar a simula¸c˜ao de Monte Carlo do d´olar, e guardar os resultados.

13. Uma vez que possu´ımos os resultados da simula¸cão HJM da curva Pré e do dólar prontos, simulamos o Cupom Cambial, utilizando os dados históricos (fatores e re-tornos mencionados nas estapas anteriores) para construir as distribui¸cões emp´ıricas condicionais necessárias, como descrito no Item 3.4.

A partir deste ponto, todas as etapas do procedimento est˜ao esclarecidas. Podemos agora prosseguir e validar o modelo proposto.

(36)

4.4 Valida¸c˜

ao das simula¸c˜

oes

Um fato bastante conhecido na área de finan¸cas é a dificuldade em prever cota¸cões de moedas. Conforme mencionado em Back (2009), obter o drift de um ativo é uma tarefa bastante complicada, especialmente quando o mesmo apresenta uma volatilidade consi-derável (este argumento está mais ligado aos aspectos práticos de estima¸cão e simula¸cão, uma vez que o dólar é provavelmente o ativo que mais se assemelha ao comportamento errático esparado de um movimento Browniano geométrico). Em seu famoso trabalho, Messe e Rogof (1983) mostraram que modelos complexos eram superados em sua ca-pacidade de previsão por um simples random walk, resultado que ficou conhecido como “MR puzzle”. Desde então, diversas estudos que tinham como objetivo entender melhor a dinâmica das taxas de câmbio foram realizados. Podemos citar, por exemplo, Evans e Lyons (2002), e alguns estudos aplicados diretamente ao mercado brasileiro, entre eles o de Mar¸cal e Junior (2016). No entanto, o modelo simples de random walk permanece um adversário formidável e dif´ıcil de ser superado, principalmente para horizontes de tempo mais longos. Tendo isto em mente, o random walk, com e sem drift, aparecem como escolhas naturais de benchmarks.

Utilizaremos a abordagem das distribui¸cões emp´ıricas para simular os retornos do dólar. As distribui¸cões serão constru´ıdas condicionando-se a distribui¸cão dos retornos em t + 1 ao retorno observado em t. Explicitamente, seja rt o retorno mais recente observado,

de modo que queremos simular o retorno em t + 1. Vamos denotar por {r} a série de retornos históricos do dólar. Definimos:

= max{r} min{r}

10 , (46)

A próxima etapa consiste em buscar na série histórica todos os retornos que pertencem ao intervalo rt± /2, e então coletar todos os retornos que ocorreram no dia seguinte a

estas observa¸cões. Por exemplo, suponha que nossa observa¸cão mais recente, em t = 100, é r100 = 0, 005, com /2 = 0, 001. Observando a série histórica, notamos que em t = 10

temos um retorno r10= 0, 0055, dentro do intervalo desejado. Assim, coletamos o retorno

do dia seguinte, r11 e damos prosseguimento `a busca na s´erie. Ao final do processo,

possu´ımos um conjunto de retornos e podemos construir uma distribui¸cão emp´ırica dos retornos subsequentes poss´ıveis, condicionados a uma observa¸cão presente no intervalo 0, 005±0, 001. Somos então capazes de sortear um retorno empregando o método descrito

(37)

anteriormente. Uma vez realizado o sorteio, o processo se repete. No entanto, apenas retornos históricos são utilizados na constru¸cão de distribui¸cões emp´ıricas; os retornos simulados não são contabilizados na constru¸cão da distribui¸cão, servindo apenas para definir o intervalo r_{± /2.}

Nosso critério para avaliar a qualidade da simula¸cão será realizar um backtest8_{: vamos}

utilizar os dados de 2015 para simular o dólar durante diferentes horizontes de tempo e comparar com as cota¸cões que efetivamente ocorreram em 2016. A métrica utilizada para determinar a qualidade da simula¸cão será o erro quadrático médio,

Erro =E[(x xobs)2], (47)

ondex representa a vari´avel simulada e xobs a observada. Os benchmarks de compara¸c˜ao

serão dois random walks, um com drift igual a média histórica dos retornos e volatilidade calculada a partir do desvio padrão usual dos retornos em 2015, e o outro com drift nulo e a mesma variância.

Conforme mencionado no Item 3.4, os vértices da curva de Cupom Cambial Sujo serão condicionados aos vértices da curva Pré e ao dólar. Para construir a distribui¸cão emp´ırica, utilizaremos o log-retorno (a dificuldade de usar o YTM está nas taxas obtidas do cupom cambial, especialmente para vértices mais curtos). Nosso critério de compara¸cão serão as propriedades estat´ısticas (média, variância etc) dos dados simulados em rela¸cão aos observados, para diferentes horizontes de tempo de simula¸cão.

8_{Backtest ´e o processo de confrontar um modelo de simula¸c˜}_{ao ou an´}_{alise com dados hist´}_{oricos, de modo}

a avaliar sua qualidade. Por exemplo: podemos simular a cota¸cão do dólar utilizando algum modelo em janeiro de 2016 e então comparar os resultados da simula¸cão com o que realmente aconteceu.

(38)

5 Resultados

O modelo proposto nesse trabalho foi aplicado ao mercado brasileiro, utilizando dados históricos de modo a calibrar o modelo de simula¸cão com dados da curva Pré, curva de Cupom Cambial Sujo e dólar.

Neste cap´ıtulo estão apresentados os resultados das simula¸cões e sua utiliza¸cão para gerar distribui¸cões de pre¸cos de ativos. Também apresentamos a aplica¸cão do modelo no problema de tomada de decisão abordado nos itens anteriores.

5.1 An´

alise do PCA

Uma vez obtidas as taxas spot interpoladas a partir dos futuros de DI, calculamos então as taxas forward entre os vértices desejados (no nosso caso, 1, 21, 42, 63, 126 e 252 dias úteis). Os resultados, então colocados em uma planilha de Excel, são importados no programa RStudio, e utilizamos a biblioteca Stats e o comando prcomp para realizar a decomposi¸cão em componentes principais.

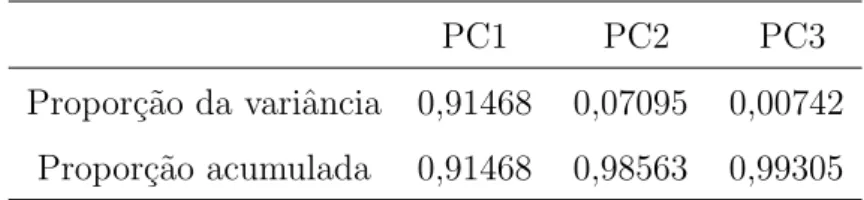
A an´alise realizada utilizando-se a curva constru´ıda a partir dos futuros de DI para 2015 est´a apresentada na Tabela 3.

Tabela 3: PCA, 2015

PC1 PC2 PC3

Propor¸cão da variância 0,91468 0,07095 0,00742 Propor¸cão acumulada 0,91468 0,98563 0,99305

De acordo com a tabela, apenas três componentes são suficientes para explicar a maior parte da variância, sendo isto condizente com o esperado. Como diversos outros trabalhos já realizaram extensas análises a respeito das propriedas da curva (entre eles Nojima (2014), Suzuki (2015) e Lueska (2016)) e nosso foco é a integra¸cão dos modelos de simula¸cão, não iremos fazer uma análise histórica extensa neste trabalho.

5.2 Market price of risk

Ao estimar o market price of risk utilizando os dados hist´oricos de 2015, encontramos valores que, quando multiplicados pela volatilidade, tornam-se pequenos frente aos outros

(39)

termos que acompanham o t na parametriza¸c˜ao de Musiela. Sejam 1, 2 e 3 os market

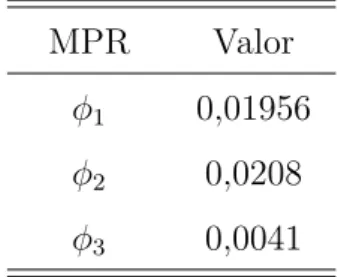
price of risk calculados para cada um dos fatores segundo a expressão do Item 3.2, com t igual a um dia, e os autovalores e autovetores obtidos pelo PCA. Os resultados para os mesmos estão presentes na Tabela 4. Note que estes valores são pequenos quando comparados aos outros termos que compõem o drift e acompanham o t do HJM na parametriza¸cão de Musiela e portanto não foram considerados9

Tabela 4: Market price of risk (MPR)

MPR Valor

1 0,01956

2 0,0208

3 0,0041

5.3 Resultados do backtest

Aqui vamos analisar com um pouco mais de detalhe o dólar e o Cupom Cambial, por estarmos utilizando uma abordagem diferente e condicionada à curva Pré.

5.3.1 D´olar

O backtest utiliza como dados históricos o ano de 2015, simulando (até) os 126 pri-meiros dias de 2016. Além disso, também apresentamos uma imagem da densidade de probabilidade do dólar no ano de 2015, onde condicionamos o retorno em t + 1 ao retorno ocorrido em t. No caso dos benchmarks, o drift é calculado utilizando a média dos retornos nos dados históricos, enquanto que a volatilidade é o desvio padrão calculado utilizando os mesmos dados, e utilizamos a expressão do movimento Browniano geométrico.

Existem alguns pontos importantes a serem comentados. O primeiro refere-se ao fato de que a densidade de probabilidade do dólar apresenta uma certa assimetria. Seria razoável esperar, caso os retornos diários fossem realmente independentes e igualmente distribu´ıdos, que na escala de tempo considerada (1 ano) isto ficasse aparente. No entanto,

9_{Pela estimativa, a contribui¸c˜}_{ao n˜}_{ao seria de grande importˆ}_{ancia e o ganho obtido por se realizar uma}

(40)

Tabela 5: USD/BRL (utilizando 2015), RMSE com 500 simula¸c˜oes

Dias RMSE Distribui¸c˜ao emp´ırica RMSE Random walk com drift RMSE Random walk sem drift 21 0,00024536 0,000305809 0,000261761 42 0,00024854 0,000305683 0,000260576 63 0,00031069 0,000304542 0,000321775 126 0,00028351 0,000268777 0,000292902

Figura 2: Densidade de probabilidade do d´olar, ano de 2015. A figura apresenta a probabilidade de um certo retorno em t + 1 dado um retorno em t

observamos caudas e notamos que retornos muito negativos (positivos) tendem a ser seguidos de retornos muito positivos (negativos).

O segundo ponto refere-se à tabela onde apresentamos os resultados para o RMSE. Estes são comparáveis ao random walk sem drift e superam o random walk com drift nas escalas de tempo consideradas, o que consideramos um bom resultado, dado o estudo realizado por Meese e Rogo↵ (1983) e o “MR puzzle”.

5.3.2 Cupom cambial sujo

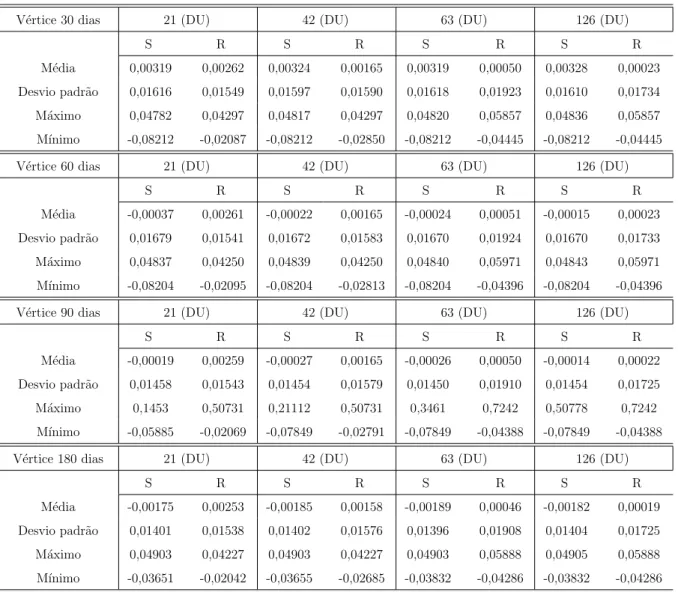
Para o cupom cambial sujo, realizamos 1000 simula¸cões para cada vértice, utilizando os dados históricos do ano de 2015. Foram simulados (até) 126 dias, e comparamos as propriedades da distribui¸cão dos resultados com os resultados efetivamente observados. Notamos que conforme o horizonte de tempo de simula¸cão aumenta, nosso forecast de-teriora. A Tabela 6 compara os resultados das simula¸cões para diferentes vértices, em diferentes horizontes de tempo. De uma maneira geral, os resultados das simula¸cões pa-recem deteriorar a partir de um horizonte de tempo simulado de 42 dias úteis. A curva

(41)

de Cupom Cambial Sujo acaba sendo sens´ıvel não apenas à informa¸cão contida nos seus dados históricos dispon´ıveis, mas também depende da qualidade das simula¸cões dos outros ativos aos quais ela está condicionada.

Tabela 6: Propriedades das distribui¸c˜oes dos retornos dos fatores do cupom cambial (utilizando 2015) simulados (S) e reais (R)

V´ertice 30 dias 21 (DU) 42 (DU) 63 (DU) 126 (DU)

S R S R S R S R

M´edia 0,00319 0,00262 0,00324 0,00165 0,00319 0,00050 0,00328 0,00023

Desvio padr˜ao 0,01616 0,01549 0,01597 0,01590 0,01618 0,01923 0,01610 0,01734

M´aximo 0,04782 0,04297 0,04817 0,04297 0,04820 0,05857 0,04836 0,05857

M´ınimo -0,08212 -0,02087 -0,08212 -0,02850 -0,08212 -0,04445 -0,08212 -0,04445

S R S R S R S R

M´edia -0,00037 0,00261 -0,00022 0,00165 -0,00024 0,00051 -0,00015 0,00023

Desvio padr˜ao 0,01679 0,01541 0,01672 0,01583 0,01670 0,01924 0,01670 0,01733

M´aximo 0,04837 0,04250 0,04839 0,04250 0,04840 0,05971 0,04843 0,05971

M´ınimo -0,08204 -0,02095 -0,08204 -0,02813 -0,08204 -0,04396 -0,08204 -0,04396

S R S R S R S R

M´edia -0,00019 0,00259 -0,00027 0,00165 -0,00026 0,00050 -0,00014 0,00022

Desvio padr˜ao 0,01458 0,01543 0,01454 0,01579 0,01450 0,01910 0,01454 0,01725

M´aximo 0,1453 0,50731 0,21112 0,50731 0,3461 0,7242 0,50778 0,7242

M´ınimo -0,05885 -0,02069 -0,07849 -0,02791 -0,07849 -0,04388 -0,07849 -0,04388

S R S R S R S R Média -0,00175 0,00253 -0,00185 0,00158 -0,00189 0,00046 -0,00182 0,00019 Desvio padrão 0,01401 0,01538 0,01402 0,01576 0,01396 0,01908 0,01404 0,01725 Máximo 0,04903 0,04227 0,04903 0,04227 0,04903 0,05888 0,04905 0,05888 M´ınimo -0,03651 -0,02042 -0,03655 -0,02685 -0,03832 -0,04286 -0,03832 -0,04286

5.4 Evolu¸c˜

ao de pre¸cos

Neste ponto, vale a pena recordar que nosso objetivo é ser capaz de simular diversas curvas e ativos simultaneamente de maneira consistente. Desse modo, não empregaremos instrumentos financeiros altamente sofisticados; nosso foco estará concentrado em um portfólio de renda fixa, composto por instrumentos comumente utilizados pelo mercado.

Vamos considerar quatro tipos de instrumentos de renda fixa. São eles: 1. Operacão pré-fixada, com taxa de 15% ao ano

(42)

2. Opera¸c˜ao indexada a percentual do CDI, com percentual de 120% ao ano

3. Opera¸c˜ao indexada a percentual do CDI, com percentual de 110% ao ano + pr´e-fixado 5% ao ano

4. Opera¸cão de renda fixa indexada ao dólar, com uma taxa pré-fixada de 5% ao ano Todos os instrumentos serão constru´ıdos com vencimento em 126 dias úteis, sendo os mesmos emitidos no primeiro dia útil de 2016, com fluxo apenas no vencimento. Em particular, para o ativo de renda fixa dólar,

M tMt= P c  P T AXv d fdesc t!v , (48)

onde v representa vencimento e d defasagem. Vamos ainda escolher a cota¸c˜ao da moeda especificada no contrato:

c = P T AXt, (49)

sendo t a data de referˆencia. Desse modo, podemos escrever:

M tMt = P  f_tpre_{!v d} fdesc t!vftcupom!v d 1 , (50) com d = 0 e P = 1.

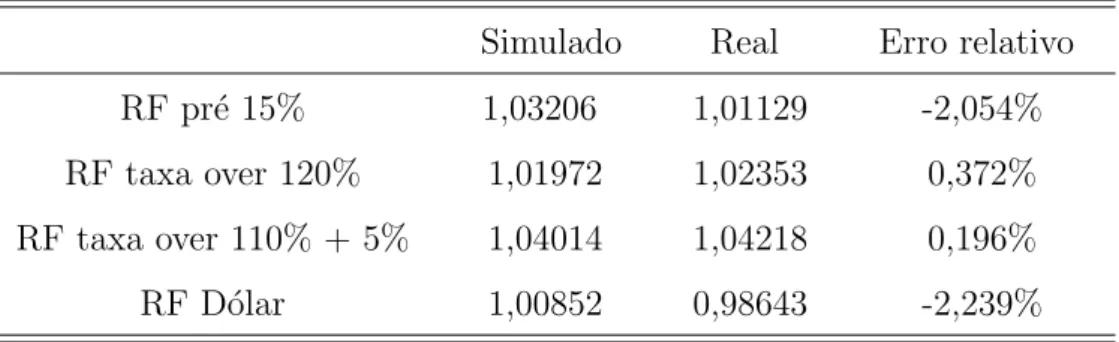
O modelo de simula¸cão foi capaz de gerar uma distribui¸cão de valores de mercado poss´ıveis para os ativos, com uma boa eficácia e consistência. Conforme pode ser obser-vado na tabela, quando utilizamos as “curvas médias” geradas pela simula¸cão apresenta-mos um bom grau de previsibilidade.

Tabela 7: Valores de mercado simulados e realizados, para uma simula¸cão de 21 dias úteis. O cálculo do pre¸co foi realizado utilizando as curvas médias.

Simulado Real Erro relativo

RF pr´e 15% 1,03206 1,01129 -2,054%

RF taxa over 120% 1,01972 1,02353 0,372%

RF taxa over 110% + 5% 1,04014 1,04218 0,196%

(43)

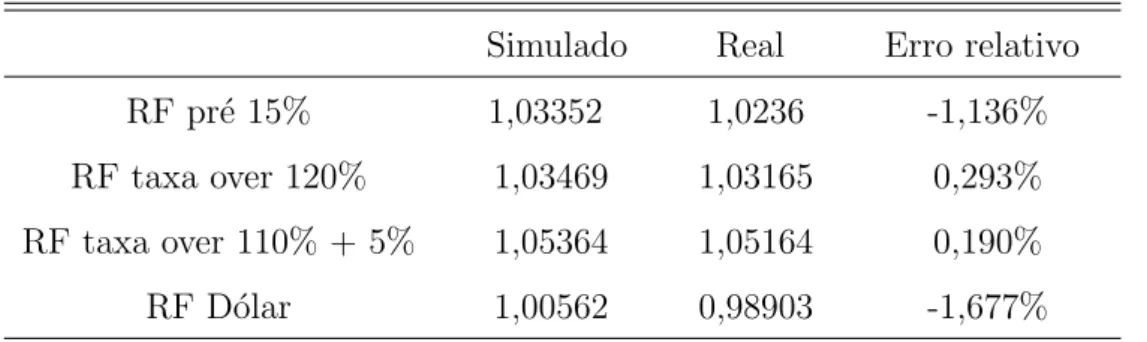
Tabela 8: Valores de mercado simulados e realizados, para uma simula¸cão de 42 dias úteis. O cálculo do pre¸co foi realizado utilizando as curvas médias.

Simulado Real Erro relativo

RF pr´e 15% 1,03352 1,0236 -1,136%

RF taxa over 120% 1,03469 1,03165 0,293%

RF taxa over 110% + 5% 1,05364 1,05164 0,190%

RF D´olar 1,00562 0,98903 -1,677%

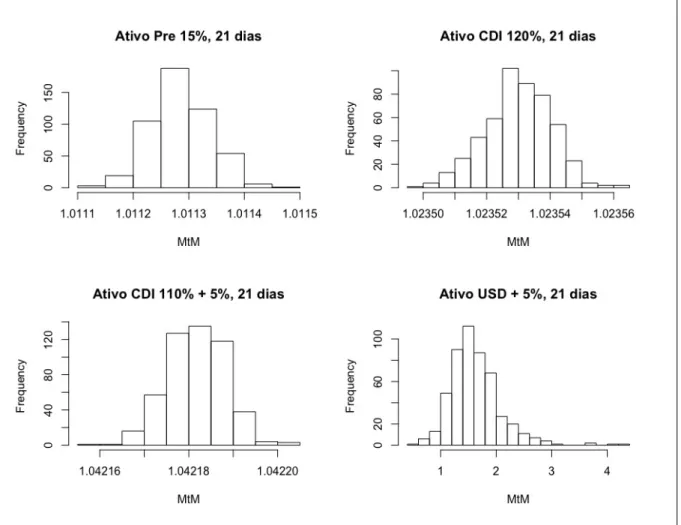
Na Figura 3, também apresentamos histogramas com os valores de mercado simulados para cada ativo. Em cada trajetória simulada, calculamos o pre¸co dos instrumentos mencionados. É poss´ıvel notar uma maior dispersão no caso do ativo renda fixa dólar, em parte devido a uma maior variabilidade dos valores simulados da cota¸cão USD/BRL.

5.5 Arvores e tomada de decis˜

´

ao

Considere um portfólio formado por dois ativos, o qual acompanharemos por um horizonte de tempo de 21 dias úteis. Os dois ativos escolhidos serão uma opera¸cão pré-fixada a 15% a.a. e uma opera¸cão indexada a 120% do CDI. Ao último será atribu´ıdo o t´ıtulo de “arriscado” por possuir um maior potencial de valoriza¸cão conforme observado nos histogramas anteriores, sendo o pré-fixado o ativo “seguro”. Tal distin¸cão se faz necessária para implementar o modelo de árvore descrito anteriormente.

Uma razão para a escolha espec´ıfica deste par deve-se à sua natureza complementar. Um deles está atrelado a uma taxa fixa, enquanto que o outro a uma taxa flutuante; varia¸cões nas condi¸cões de mercado os afetam de maneira oposta. Valoriza¸cão de um implica em desvaloriza¸cão do outro, conforme pode ser observado na sua distribui¸cão conjunta de probabilidade (Fig 4).

Aqui fica evidente a utilidade de utilizarmos o modelo HJM (na verdade simula¸cões de Monte Carlo em geral): somos capazes de gerar um número enorme de cenários poss´ıveis, e portanto uma distribui¸cão para os pre¸cos dos ativos. A partir da densidade de proba-bilidade conjunta, somos capazes de estimar as probaproba-bilidades e os valores esperados nos nós finais da árvore.

A escolha dos estados s1 e s2 não é única, sendo a parti¸cão evidenciada na Tabela 9.

(44)

Figura 3: Histogramas contendo os resultados das simula¸c˜oes dos pre¸cos de mercado dos ativos, 21 DU.