Alexander dos Santos Dutra

(1)

Universidade Federal da Bahia

Instituto de Matem´atica

Curso de Pós-graduação em Matemática Dissertação de Mestrado

M´

etodo de Pontos Interiores Aplicado a um

Problema de Seq¨

uenciamento Job-Shop

Alexander dos Santos Dutra

Salvador-Bahia

(2)

M´

etodo de Pontos Interiores Aplicado a um

Problema de Seq¨

uenciamento Job-Shop

Disserta¸cão apresentada ao colegiado do curso de Pós-Gradua¸cão em Matemática da

Universidade Federal da Bahia, como requisito parcial para obten¸c˜ao do T´ıtulo de

Mestre em Matem´atica Pura.

Banca examinadora

Prof. Dr. Isamara Carvalho Alves (Orientador).

Prof. Dr. Akebo Yamakami

(3)

Dutra, A.

“Método de Pontos Interiores Aplicado a um Problema de Seqüênciamento Job-Shop. ” / Alexander dos Santos Dutra. Salvador-Ba, 2004.

Orientador: Isamara de Carvalho Alves (Universidade Federal da Bahia).

Disserta¸cão de Mestrado apresentada ao curso de Pós-graduacão em

Matem´atica da UFBA, 99 p´aginas.

(4)

(5)

“Não há nada a temer a menos que me esque¸ca de como Deus me condu-ziu até aqui. ”

(6)

Agradecimentos

A Deus, pelos sinais e maravilhas operadas na vida de minha fam´ılia durante

este per´ıodo de estudos. O Senhor tornou realidade aquilo que todos julg´avamos

im-poss´ıvel. A Deus todo louvor por mais esta vit´oria.

A Suzy, Alexander Junio e Adrielle. Suzy, minha esposa amada, sou grato por

acreditar em mim mesmo nos momentos que nem eu pude acreditar, seu amor faz de

mim o que sou. Meus filhos, Alexander Junio e Adrielle, n˜ao foi f´acil ter papai tanto

tempo perto dos olhos e com a mente t˜ao distante, obrigado por me fazerem sorrir.

A todos os colegas de mestrado agrade¸co pelo companheirismo e amizade.

Aos grandes matem´aticos e amigos Andrade, Augusto, F´abio e Gustavo obrigado pela

contribui¸c˜ao sempre iluminada nos estudos. Jos´e Lu´ıs, obrigado pelo incentivo e

apre-senta¸c˜ao a esta linha de pesquisa que tanto me fascina. Ernesto, meu companheiro de

pesquisa saiba que tem sido ”massa”trabalhar contigo.

Aos professores que contribu´ıram para que este momento fosse poss´ıvel. Em

particular sou grato aos professores Jos´e Fernandes, Elinalva Vergasta e Marco Antˆonio

pelo incentivo e apoio para que pudesse enfrentar esta etapa de estudos.

Um agradecimento especial a professora Isamara Alves pela orienta¸c˜ao e

(7)

Resumo

O problema de seq¨uenciamento do tipo job-shop ´e um problema que desperta

o interesse de pesquisadores por sua caracter´ıstica computacional na categoria de um

problema NP - dif´ıcil . Além disto, como um problema de programa¸cão matemática, o

job-shop constitui um particular desafio por possuir um espa¸co de busca n˜ao convexo.

Tratamos neste trabalho de um problema de job-shop est´atico, determin´ıstico

e com m´aquinas especializadas, para o qual adotamos uma modelagem matem´atica

cont´ınua e não linear. É verdade que modelos de programa¸cão não linear são muitas

vezes evitados em fun¸c˜ao da dificuldade encontrada em garantir a convergˆencia para

um m´ınimo global. Contudo, essa dificuldade pode ser superada com o uso do M´etodo

de Pontos Interiores (MPI) o qual tem sido aplicado com sucesso na resolu¸c˜ao de

problemas dessa natureza. Este trabalho realiza, portanto, uma an´alise matem´atica a

fim de viabilizar o uso de MPI na resolu¸c˜ao de um problema de job-shop espec´ıfico.

Propomos o uso de MPI associado com o Lagrangeano Aumentado que foi

usado para guiar o algoritmo por um caminho decrescente para a fun¸c˜ao objetivo.

Para tal, foi preciso alterar algumas das informa¸c˜oes de segunda ordem a fim de

encon-trar dire¸c˜oes primais que garantam esse decrescimento. Mostramos que as mudan¸cas

efetuadas não alteram a convergência do problema primal, porém a convergência do

problema dual é influenciada. Em fun¸cão disso, adotamos uma varia¸cão na dire¸cão

dual ajustando-a à fun¸cão de penalidade usada e determinamos as condi¸cões favoráveis

à convergência para um ponto que minimize a fun¸cão objetivo do problema tratado.

(8)

Abstract

The job-shop-type scheduling problem is an issue that has called the attention

of researchers because of its computational characteristic in the category of an

NP-hard problem. Besides, as a mathematical programming problem, job-shop poses a particular challenge because it comprises a non-convex search environment.

We deal, here, with a specific job-shop problem for which we adopt a

con-tinuous, non-linear mathematical model. Non-linear programming models are often

avoided viz-`a-viz the difficulty we meet when we try to ensure the convergence to a

global minimum. However, this difficulty can be overcome with the use of the Interior

Point Method (IPM), which has been successfully applied when we try to solve

pro-blems of this kind . This thesis proposes, therefore, a mathematical analysis in order to

make possible the use of IPM in the resolution of a specific type of job-shop problem.

We propose the use of IPM together with a Augmented Lagrangean so as

to lead the algorithm in a decreasing way towards the objective function. For that

reason, we needed to alter a few items of second-order information so that we could find

primal directions to ensure that reduction. We shall demonstrate that the accomplished

changes did not significantly alter the convergence of the primal problem. Nevertheless,

the convergence of the dual problem is affected. On account of that, we have resorted

to a variation in the dual direction, fine-tuning it to the penalty utilized. By that

means we are able to determine the conditions that are favorable to a convergence to

a point which minimizes the objective function of the problem we are dealing with.

(9)

Sum´

ario

Lista de Figuras xii

Lista de Tabelas xiii

Introdu¸cao Geral 1

1 O Problema de Seq¨uenciamento Job-Shop 3

1.1 Problemas de F´abrica . . . 4

1.2 O Problema de Seq¨uenciamento Job-Shop . . . 5

1.2.1 Modelagem por grafos disjuntivos . . . 7

1.2.2 Representa¸c˜ao de solu¸c˜oes pelo diagrama de Gantt . . . 8

1.3 Formula¸c˜ao Matem´atica para o Job-Shop . . . 10

1.3.1 Crit´erios de otimiza¸c˜ao . . . 10

1.3.2 Modelo de programa¸cão linear com variáveis binárias . . . 11

1.3.3 Modelo de programa¸c˜ao n˜ao-linear . . . 12

1.4 M´etodos de Resolu¸c˜ao para o Job-Shop . . . 13

1.4.1 M´etodos exatos . . . 13

1.4.2 M´etodos heur´ısticos . . . 14

1.4.3 M´etodos de decomposi¸c˜ao . . . 15

Conclus˜ao . . . 16

2 M´etodo de Pontos Interiores 18 2.1 O M´etodo de Pontos Interiores: Ontem e Hoje . . . 19

2.1.1 Breve hist´orico . . . 19

2.1.2 Aplica¸c˜oes do m´etodo de pontos interiores . . . 20

2.1.3 O m´etodo de pontos interiores versus m´etodo simplex . . . 21

(10)

x

2.2 O M´etodo de Pontos Interiores para Programa¸c˜ao Linear . . . 23

2.2.1 M´etodo primal-dual . . . 25

2.2.2 O passo central . . . 26

2.2.3 M´etodos primais . . . 29

2.3 Método de Pontos Interiores Aplicado a Programa¸cão Não Linear . . . 30

2.3.1 Um m´etodo primal-dual barreira-logar´ıtmica (PDBL) . . . 31

2.3.1.1 Fun¸c˜ao de m´erito . . . 33

2.3.1.2 Aplicando o M´etodo de Newton . . . 34

2.3.1.3 Sele¸c˜ao do parˆametros β e µ . . . 36

2.3.2 Um m´etodo primal-dual (PD) . . . 39

3 Método de Pontos Interiores Aplicado ao Problema Job-Shop 44 3.1 Análise do Modelo de Seqüenciamento Job-Shop Adotado . . . 45

3.1.1 An´alise do Espa¸co de Busca . . . 46

3.1.2 An´alise da Hessiana do Lagrangeano . . . 49

3.2 M´etodo de Pontos Interiores e o Seq¨uenciamento Job-Shop . . . 53

3.2.1 Defini¸cões iniciais e fun¸cões de mérito . . . 54

3.2.2 Mudan¸ca da matriz normal N(t, s, y) . . . 56

3.2.3 Um algoritmo de pontos interiores aplicado ao seq¨uenciamento job-shop . . . 62

3.2.3.1 Ponto de partida e parˆametros iniciais . . . 63

3.2.3.2 Encontrando as dire¸c˜oes de busca . . . 66

3.2.3.3 Definindo o tamanho de passo . . . 66

3.3 An´alise de Convergˆencia . . . 69

3.3.1 Condi¸cões para a convergência global do problema de job-shop . 69 3.3.2 Prova de Convergência . . . 70

Conclus˜ao Geral 82

Referˆencias Bibliogr´aficas 85

(11)

xi

A.1 Tipos de Fun¸c˜oes . . . 91

A.2 Condi¸c˜oes de Otimalidade para Problemas com Restri¸c˜oes . . . 92

A.3 Regra de Armijo . . . 95

A.4 Fun¸c˜ao de m´erito . . . 95

B Algoritmos Sugestivos 97 B.1 Algoritmo para ajuste da matriz Normal Nβ . . . 97

(12)

Lista de Figuras

1.1 Grafo potencial-tarefa representando problema-exemplo 1 de job-shop. . 8 1.2 A representa¸c˜ao de uma sele¸c˜ao completa ac´ıclica para o problema-exemplo

de job-shop. . . 9 1.3 A representa¸c˜ao de duas solu¸c˜oes para o problema exemplo 1 no

dia-grama de Gantt . . . 9

(13)

Lista de Tabelas

1.1 Dados do problema-exemplo 1 de job-shop. . . 7

3.4 An´alise ponto inicial . . . 64

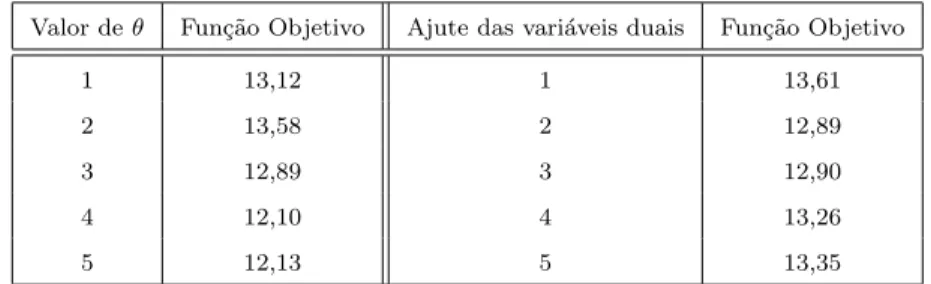
3.5 Análise dos parâmetros para defini¸cão das variáveis de excesso e variáveis duais . . . 65

(14)

Introdu¸c˜

ao Geral

O mercado atual possui uma tendˆencia a consumir uma variedade grande de

produtos, com uma vida ´util reduzida e com custo o mais baixo poss´ıvel Jain e Meeran

[29]. Atender a estas necessidades requer processos mais complexos. ´E preciso buscar

maneiras de economizar em cada detalhe com a finalidade de obter custos competitivos.

Neste contexto, o problema do seqüenciamento de tarefas é freqüente em indústrias e

empresas de um modo geral, que buscam reduzir seu custo operacional e alcan¸cando

uma maior produtividade.

Os problemas de seqüenciamento são essencialmente de otimiza¸cão restritos

que, num contexto de produ¸cão, envolvem descobrir uma seqüência para aloca¸cão de

recursos limitados com a finalidade de atender determinado objetivo. Trataremos neste

trabalho de um tipo particular de seq¨uenciamento em f´abrica conhecido por problema

dejob-shop.

Apesar da grande relevância prática de problemas de job-shop, há carac-ter´ısticas teóricas particularmente importantes a serem consideradas. A primeira, diz

respeito a sua complexidade computacional, sendo classificado como um problema

NP-dif´ıcil (Lenstra e Rinnoy Kan [35], Johnson [30]). A segunda, refere-se a seu espa¸co

de busca de solu¸c˜oes n˜ao conexo, despertando assim, o interesse como problema de

programa¸cão matemática dada a maior dificuldade na busca de solu¸cão por um

cami-nho cont´ınuo para este tipo de problema. Estas duas caracter´ısticas agregadas fazem

do problema de job-shopum particular desafio tanto do ponto de vista computacional como do ponto de vista de an´alise matem´atica.

(15)

Introdu¸c˜ao Geral 2

direta a n˜ao convexidade do problema em quest˜ao. Para tanto, tomamos um problema

de job-shop com caracter´ısticas espec´ıficas e adotaremos uma modelagem matemática cont´ınua de programa¸cão não linear conforme proposta de E. Pinson [42]. Com esta

modelagem estamos diante de um modelo matemático de programa¸cão não linear e não

convexo. Este modelo possui ainda caracter´ısticas particulares que o tornar˜ao ainda

mais desafiador. Diante desses desafios, encontramos no M´etodo de Pontos Interiores

(MPI) um aliado poderoso na busca de solu¸c˜ao para o problema dejob-shopem quest˜ao.

O MPI tem sido utilizado com sucesso na resolu¸c˜ao de problemas de

pro-grama¸cão não linear e não convexos, conforme inúmeras pesquisas encontradas dentre

os quais citamos os trabalhos de El Bakry et al [17], Granville [27] e Vanderbei e

Shanno [56]. Isto nos levou a buscar uma an´alise mais acurada das caracter´ısticas

ma-temáticas do problema de job-shop buscando garantias de convergência para solu¸cões que minimizem o tempo de seqüenciamento desejado.

Nosso trabalho est´a organizado da seguinte forma:

No primeiro cap´ıtulo apresentamos uma vis˜ao geral do problema de job-shop

descrevendo suas principais caracter´ısticas e ressaltando aquelas adotadas em nossa

análise. Também, descrevemos duas formas particulares de modelagem matemática,

além de discutir métodos usados na resolu¸cão desse problema.

O MPI ´e o objeto de nossa aten¸c˜ao no segundo cap´ıtulo. Partimos de uma

breve visão histórica e seguimos apresentando algumas dentre as inúmeras

possibilida-des de aplica¸c˜ao possibilida-deste m´etodo que tanto tem possibilida-despertado o interesse de pesquisadores.

Conclu´ımos esta exposi¸cão apresentando o método de pontos interiores aplicável a

modelos de programa¸c˜ao linear e n˜ao-linear.

Os cap´ıtulos anteriores fornecem subs´ıdios para as an´alises realizadas no

ter-ceiro cap´ıtulo onde verificamos com detalhes o modelo matem´atico adotado para o

(16)

Cap´ıtulo 1

O Problema de Seq¨

uenciamento

Job-Shop

O problema de seq¨uenciamento do tipo job-shop ´e o mais geral dos

proble-mas de seq¨uenciamento cl´assico conforme Jain e Meeran [29]. Este possui um espa¸co

de busca irregular e caracter´ısticas computacionais capazes de fornecer id´eias e

in-forma¸cões na busca de algoritmos referentes a outras aplica¸cões práticas. Além disto,

o job-shop ´e um problema combinat´orio de complexidade computacional classificado como NP-dif´ıcil (Johnson [30], Zwaneveld et al. [59], Strusevich [52]) e sendo

conside-rado um dos mais complexos membros desta classe (Yamada e Nakano [58]).

Uma indica¸c˜ao da complexidade envolvida na busca de solu¸c˜ao de um problema

de job-shop pode dado por um problema proposto em 1963 por Muth e Thompson [40] que consiste no planejamento de 10 tarefas em 10 máquinas, cuja solu¸cão ótima

foi provada somente em 1987, por Carlier e Pinson [12].

O objetivo num problema de seqüenciamento job-shop é a realiza¸cão de de-terminadas tarefas que podem ser interligadas por restri¸cões de sucessão ou restri¸cões

de localiza¸cão no tempo. Para execu¸cão destas tarefas são necessários certos recursos

(máquinas, mão de obra), os quais introduzem restri¸cões disjuntivas no problema. Os recursos disjuntivos acrescentam restri¸cões não lineares, formando um espa¸co de busca

(17)

Problemas de F´abrica 4

Apresentamos, neste cap´ıtulo, as caracter´ısticas b´asicas referente ao seq¨

uenci-amentojob-shopjá restrito às caracter´ısticas a que nos propomos estudar. Analisamos, em seguida, alguns modelos matemáticos e métodos de resolu¸cão comumente usados.

1.1 Problemas de F´

abrica

Problemas de fábrica são problemas onde se pretende seqüenciar a execu¸cão

das opera¸cões necessárias à confeçcão de determinados produtos que passam por

máqui-nas distintas ou não (Alves [3]) com o objetivo de minimizar o tempo de produ¸cão.

Neste caso, as m´aquinas constituem os recursos a serem compartilhados e os servi¸cos

(jobs) são as opera¸cões realizadas na produ¸cão de cada item.

Uma m´aquina pode realizar apenas uma opera¸c˜ao de cada vez. Desta forma,

a execu¸cão de opera¸cões nas máquinas devem ser planejadas a fim de evitar a

sobre-posi¸cão numa mesma máquina num dado instante. O seqüenciamento dos problemas

de fábrica resulta geralmente na procura de seqüências de opera¸cões sobre as máquinas.

Podemos considerar problemas de f´abrica em que as opera¸c˜oes podem ser

realizadas em qualquer máquina (fábrica com máquinas paralelas), casos onde todas as opera¸cões são realizadas numa única máquina, ou ainda, os casos em que uma

opera¸cão só pode ser realizada numa determinada máquina (fábrica com máquinas especializadas). Dentre os problemas de fábrica com máquinas especializadas podemos distinguir os seguintes casos principais:

• problema de open-shop- quando as opera¸cões elementares são independentes, ou seja, a ordem de execu¸cão das opera¸cões de um mesmo trabalho é indiferente.

• problema de flow-shop- quando as opera¸c˜oes elementares dos trabalhos s˜ao liga-das por uma mesma ordem total, ou seja, todos os produtos seguem um percurso

unidirecional.

(18)

O Problema de Seq¨uenciamento Job-Shop 5

Na pr´atica pode ser que nem todos os produtos estejam dispon´ıveis para serem

processados no instante inicial. Neste caso, os produtos possuem tempos de partida que

definem a sua data de chegada ao ch˜ao da f´abrica. Os tempos de partida dos produtos

s˜ao eventos que n˜ao podem ser previstos, portanto seus requisitos de processamento

também não podem ser conhecidos com antecedência. Neste caso o seqüenciamento de

tarefas torna-se um problema n˜ao determin´ıstico que deve ser realizado em um per´ıodo

de tempo totalmente aberto, sendo definido como um problema dinˆamico.

Podemos considerar tamb´em o caso em que, uma vez iniciado o processo de

produ¸cão, os recursos utilizados por cada atividade não podem mais ser alterados até

que todos os produtos estejam conclu´ıdos. Nesse sistema ideal, todos os recursos est˜ao

sempre dispon´ıveis no in´ıcio do per´ıodo de seq¨uenciamento, e n˜ao existe a

possibili-dade de interrup¸c˜ao do processo ora iniciado. Problemas com estas caracter´ısticas s˜ao

conhecidos como problemas estáticos, e, apesar de serem pouco prováveis em situa¸cões

reais, o seu estudo é de fundamental importância para o desenvolvimento de técnicas

eficazes para a solu¸c˜ao de problemas dinˆamicos.

1.2 O Problema de Seq¨

uenciamento Job-Shop

Neste trabalho trataremos o problema de job-shop de um ponto de vista industrial. Teremos como recurso básico a utiliza¸cão de máquinas capazes de executar

apenas uma tarefa de cada vez, sendo por este motivo, consideradas como recursos

disjuntivos. Geralmente, chama-se a confeçcão de certo produto, de trabalho (job). As opera¸cões de um mesmo trabalho são organizadas em seqüências conhecidas por gama operatória.

Podemos classificar o problema a que nos propomos lidar como um problema

de job-shopestático e determin´ıstico com máquinas especializadas, pois estaremos su-pondo que todos as informa¸cões sejam conhecidas antecipadamente (estático) e os dados perfeitamente determinados (determin´ıstico). As máquinas são consideradas especiali-zadas pois cada produto possui uma lista de opera¸cões com uma seqüência pré-definida.

(19)

estando dispon´ıveis todo o per´ıodo de atividade, mas n˜ao podendo executar mais de

uma tarefa ao mesmo tempo. Consideraremos tamb´em que n˜ao existe prioridade na

execu¸cão de determinada tarefa; assim não será poss´ıvel interromper a execu¸cão de

uma opera¸c˜ao para realiza¸c˜ao de outra.

Quanto aos produtos, consideraremos produtos independentes sem prioridades

na execu¸cão de suas opera¸cões. Cada produto deverá ser processado em dada máquina

uma única vez e eles deverão respeitar uma ordem de execu¸cão dentro da gama

ope-rat´oria. Al´em disto, consideraremos que os produtos chegam na unidade produtiva

num mesmo instante.

Estudaremos casos de unidades fabris contendom_e máquinas distintas e p pro-dutos. Cada produtoPi é constitu´ıdo depi opera¸cões elementares. Desta forma, numa fábrica serão executadas p0 =

p

X

i=1

pi opera¸c˜oes, cada uma delas sendo realizada em uma m´aquina diferente Mk.

O número total de opera¸cões que é executada em uma máquina Mk será de-notado por m_ek. A dura¸cão de execu¸cão de uma opera¸cãoOj em Mk será chamada de

tempo operatório e denotada por dj. Durante este tempo, a máquina estará ocupada e todas as outras opera¸cões nesta máquina terão que aguardar para serem processadas.

Assim, toda opera¸cão em uma máquina terá seu tempo de in´ıcio de processamento

denotado por tj que depende do instante de finaliza¸cão da opera¸cão precedente nesta máquina. O instante de término de execu¸cão de uma opera¸cão Oj será denotado por

Cj, sendo Cj =tj+dj.

Os problemas de seq¨uenciamento job-shop, que denotaremos por Πj s˜ao cons-titu´ıdos por:

• P =_{Pi|i= 1, ..., p} - o conjunto de p produtos (ou trabalhos) Pi.

• M={Mk|k= 1, ...,me}- o conjunto de me m´aquinasMk.

• O =_{Oj|j = 1, ..., p0} - o conjunto de todas as opera¸c˜oes Oj.

Para tornar mais claras as defini¸c˜oes aqui vistas, apresentaremos um exemplo

(20)

p= 4 e p0= 11 me = 3

p1=p2=p3= 3, p4= 2 me1=me2= 3, me3= 2

produto opera¸cão dura¸cão máquina

1 1 3 2

1 2 3 3

1 3 1 1

2 4 3 3

2 5 2 2

2 6 3 1

3 7 1 2

3 8 4 1

3 9 4 3

4 10 4 1

4 11 3 2

Tabela 1.1:Dados do problema-exemplo 1 de job-shop.

1.2.1 Modelagem por grafos disjuntivos

Os problemas de job-shoptambém podem ser descritos através de uma mode-lagem por grafos conforme proposto por Balas et al. [1]. Consideremos então o grafo

disjuntivo G = (V,C ∪ D), onde:

• V é um conjunto de nós que representam as opera¸cões Oj de cada produto unido a duas opera¸cões fict´ıcias , fonte (O0) e sorvedouro (Of im).

• C é o conjunto de arcos conjuntivos que representa a seqüência tecnológica das opera¸cões dentro de um mesmo produto, ou seja, a ordem em que as opera¸cões

Oj de um mesmo produto pi devem ser processadas. Cada arco é ponderado de acordo com o tempo de execu¸cão da opera¸cão que o origina (Oj).

• Dé o conjunto dos arcos disjuntivos que representam as restri¸cões de capacidade das máquinas, cada arco é ponderado com o tempo de execu¸cão de sua oper¸cão

respectiva, existem portanto pares de arcos ((Ou →Ov),(Ov →Ou)) que devem ser realizadas na mesma m´aquina Mk.

(21)

máquina, isto é, determinar a precedência entre estas opera¸cões. No modelo de grafo

disjuntivo isto ´e realizado definindo dire¸c˜oes para todos os arcos disjuntivos. Assim,

temos que uma sele¸cão é um conjunto de arcos direcionados selecionados de arcos disjuntivos. Por defini¸cão, uma sele¸cão é completase todas as disjun¸cões forem seleci-onadas e esta sele¸cão será consistente se o grafo direcionado resultante for ac´ıclico.

MAQUINA 1

1

3

4

2

O

12

O

9

O

₆

O

3

0 0

3

1

4

O

4

O

7

O

10

3

2

4

3

O

2

5

O

8

O

11

O

0

O

1

O

fin

O

MAQUINA 2 MAQUINA 3

´ ´ ´

Figura 1.1:Grafo potencial-tarefa representando problema-exemplo 1 de job-shop.

Na figura 1.1 apresentamos o grafo para o problema-exemplo 1. Nele ´e poss´ıvel

ver o conjunto de arcos conjuntivosC representados pelas flechas cont´ınuas e o conjunto de arcos disjuntivos_D representados pelas flechas pontilhadas. Cada opera¸c˜ao ´e

repre-sentada por um nó e os arcos que partem de cada nó são ponderados pelo dura¸cão da

opera¸c˜ao correspondente. Neste exemplo todos os produtos s˜ao lan¸cados no instante

0. Uma sele¸cão completa com a defini¸cão de todas as dire¸cões no arcos disjuntivos é

representada pela figura 1.2

1.2.2 Representa¸c˜

ao de solu¸c˜

oes pelo diagrama de Gantt

Uma forma ´util para visualizar uma solu¸c˜ao encontrada para um problema de

seqüenciamentojob-shopé o diagrama de Gantt. Este diagrama representa a ocupa¸cão das máquinas em fun¸cão do tempo. A constru¸cão deste diagrama é feita associando

(22)

O Problema de Seq¨uenciamento Job-Shop 9 MAQUINA 1 1 3 4 2

O

12

O

9

O

6

O

3

0 0 3 3 1 4

O

4

O

7

O

10

3

2

4

3

O

2

O

5

O

8

O

11

O

0

O

1

O

fin

MAQUINA 2 MAQUINA 3

´ ´ ´

Figura 1.2:A representa¸c˜ao de uma sele¸c˜ao completa ac´ıclica para o problema-exemplo de job-shop.

retˆangulos localizados nesta barra. Os retˆangulos possuem o comprimento proporcional

à dura¸cão da opera¸cão que representa e a posi¸cão que ocupa na barra é definida pelo

instante de in´ıcio da respectiva opera¸c˜ao. A figura 1.3 apresenta o diagrama de Gantt

para o problema-exemplo 1 de job-shop onde é poss´ıvel constatar a superioridade da segunda solu¸cão (S2) com tempo total de produ¸cão igual a 13 unidades de tempo em rela¸cão à primeira (S1) com tempo total de produ¸cão igual a 33 unidades de tempo.

tempo tempo M₁ M₂ M₃ C max C max

Solucao S₁ 0 0 33 13 M₃ M₂ M₁ P₂ P₃ P₄ P₁ P₂ P₃ P₄ P₁ : _{= 33}

1

: _{= 13} 2 Solucao S₂

´ ´

~ ~

(23)

Formula¸c˜ao Matem´atica para o Job-Shop 10

1.3 Formula¸c˜

ao Matem´

atica para o Job-Shop

As restri¸c˜oes disjuntivas introduzem um espa¸co de busca n˜ao convexo para

seqüenciamentojob-shop. A lineariza¸cão destas restri¸cões pode ser feita acrescentando-se variáveis binárias na formula¸cão do problema, obtendo-acrescentando-se um modelo inteiro-misto.

O mesmo problema tamb´em pode ser modelado de forma cont´ınua como um problema

de programa¸cão não linear. Apresentaremos a descri¸cão de uma proposta de formula¸cão

matemática de cada tipo além de critérios de otimiza¸cão que podem ser considerados.

1.3.1 Crit´

erios de otimiza¸c˜

ao

O objetivo a ser alcan¸cado num problema de seqüenciamentojob-shopaplicado ao chão de fábrica é otimizar o tempo total de produ¸cão. Há vários critérios que podem

ser utilizados na otimiza¸cão de tais problemas (Ramos [44]). Um critério de otimiza¸cão

comumente usado é a minimiza¸cão da dura¸cão total do seqüenciamento denominado

makespane denotado por Cmax, sendo:

Cmax = max 1≤j≤p{Ci}

ondeCié o momento de término de execu¸cão de um produtoPi, ou seja,Cié momento do término de execu¸cão da última opera¸cão referente a esse produto.

Uma outra forma igualmente útil de avaliar o tempo de produ¸cão total é pela

soma de todos os tempos de in´ıcio de todas as n0 opera¸cões tj. Esta forma apresenta como critério de otimiza¸cão uma fun¸cão linear definida por:

f(t) = p0

X

j=1

tj (1.1)

Existe ainda uma diversidade grande de crit´erios empregados na otimiza¸c˜ao

de um problema de job-shop. Uma descri¸cão destes critérios pode ser encontrada no trabalho de Ramos [44]. Neste trabalho estaremos utilizando como critério de

otimiza¸cão a soma dos tempos de in´ıcio das opera¸cões conforme fun¸cão (1.1) pela

(24)

1.3.2 Modelo de programa¸c˜

ao linear com vari´

aveis bin´

arias

Uma forma comumente encontrada para tratar as restri¸c˜oes disjuntivas ´e o uso

de variáveis binárias. Uma das propostas de modelagem desta natureza é a feita por

Manne e citado por Thompson, et al [55] que define uma nova vari´avel bin´aria para

cada par ordenado de opera¸cões utilizando a mesma máquina. Esta variável em 0-1 é

denotada por yuv, tal que:

yuv=

  

1, seOv precedeOu sobre Mk 0, se Ou precede Ov sobre Mk.

Este modelo também utiliza um limite superior B para dura¸cão total do seqüenciamento. Este limite pode ser, por exemplo, a soma de todos os tempos

ope-rat´orios das opera¸c˜oes do problema:

B = p0

X

j=1;

dj. (1.2)

As restri¸c˜oes do problema podem ser expressas pelas equa¸c˜oes:

h

tj+1 ≥ tj +dj, ∀j ∈ C (1.3)

h

tv ≥ tu+du−B(yuv), ∀(u, v)∈ D (1.4)

h

tu ≥ tv+dv −B(1−yuv), ∀(v, u)∈ D (1.5)

As restri¸cões (1.3) representam as restri¸cões da gama operatória. As restri¸cões

(1.4) e (1.5) representam as restri¸c˜oes disjuntivas. Neste modelo, para cada escolha de

um par de arcos disjuntivos, somente uma das restri¸c˜oes (1.4) e (1.5) ´e ativada. Assim,

quando se escolher fazer Ou antes de Ov (yuv vale 0) a restri¸cão (1.5) é então inativa já que tu ≥ tv +dv −B, e da forma em que B foi definida (como

p0

X

j=1

dj) o segundo termo desta inequa¸c˜ao ser´a sempre negativo e, como consideramos todos os tempos de

in´ıcio sendo positivos, esta restri¸cão fica inutilizada. Por outro lado, a restri¸cão (1.4) é

ativada j´a que torna-se

(25)

Neste caso o makespan pode facilmente ser obtido acrescentando-se uma nova

variável (tf im) para representar o momento de término de toda a produ¸cão e o seguinte conjunto de restri¸cões:

h

tf im ≥ tj+dj, ∀j ∈ O

Dessa forma um problema de seq¨uenciamento job-shopΠj pode ser escrito como:

M in. f(t) = tf im

S.a. tj +dj −tj+1 ≤0 ∀(j, j + 1)∈ C

tu+du−B(yuv)≤tv ∀(u, v)∈ D

tv+dv −B(1−yuv)≤tu ∀(v, u)∈ D

tj+dj ≤tf im ∀j ∈ O

tj ≥0 ∀j ∈ O

Obtemos assim um problema de programa¸c˜ao inteira-mista. A principal

difi-culdade na resolu¸cão desse modelo refere-se às variáveis inteiras (binárias). Uma forma

comum na resolu¸cão desse modelo consiste na jun¸cão de um método de

Branch-and-Bound com o m´etodo simplex.

1.3.3 Modelo de programa¸c˜

ao n˜

ao-linear

O modelo proposto por Pinson [42] agrupa em uma única equa¸cão quadrática

as duas equa¸cões disjuntivas para cada par de opera¸cão numa mesma máquinaMk. As restri¸cões deste modelo são representadas pelas equa¸cões:

tj+dj ≤ tj+1 , ∀j∈ C (1.7)

(tv−tu+dv)(tu−tv +du)≤0, ∀(u, v)∈ D (1.8) As restri¸cões (1.7) representam as restri¸cões da gama operatória. As restri¸cões

(1.8) representam as restri¸cões disjuntivas das máquinas. Essas restri¸cões disjuntivas

introduzem um espa¸co de busca cont´ınuo mas n˜ao conexo.

Acrescentando a este conjunto de restri¸c˜oes o crit´erio de otimalidade expresso

pela fun¸cão (1.1) obtemos o seguinte problema de programa¸cão não-linear para um

(26)

M´etodos de Resolu¸c˜ao para o Job-Shop 13

M in. f(t) = n0

X

j=1

tj

S.a. tj +dj −tj+1 ≤0 ∀j ∈ C (tv−tu+dv)(tu−tv+du)≤0 ∀(u, v)∈ D

tj ≥0 ∀j ∈ O

(1.9)

Modelos de programa¸cão não linear e não convexo têm sido evitados em fun¸cão

das dificuldades encontradas na busca de solu¸c˜ao por m´etodos tradicionais [57]. O

m´etodo de pontos interiores ´e uma ferramenta capaz de superar este problema conforme

apresentado na se¸c˜ao 2.3.

1.4 M´

etodos de Resolu¸c˜

ao para o Job-Shop

A solu¸cão de um problema de seqüenciamento job-shop pode ser obtida por métodos exatos, mas devido a sua complexidade (NP-dif´ıcil) em muitos casos só é

viável o uso de métodos que buscam solu¸cões aproximadas para a obten¸cão de boas

solu¸cões em tempo útil para fundamentar as decisões a tomar no dia-a-dia na indústria.

Métodos de decomposi¸cão são também aplicáveis a problemas de job-shop na medida em que reduzem a dimensão do problema a ser resolvido.

1.4.1 M´

etodos exatos

Métodos de solu¸cão exatos são aqueles que pretendem obter a solu¸cão ótima

para um problema no menor tempo poss´ıvel.

Entre os métodos de solu¸cão exata aplicáveis a problemas de otimiza¸cão

com-binatória o mais usado é o método de parti¸cão e avalia¸cão sucessivas (Branch and

Bound). Encontramos diversos trabalhos nesta dire¸c˜ao dentre os quais podemos

des-tacar os trabalhos de Carlier e Pinson ([12], [13]).

As técnicas de programa¸cão matemáticas também são métodos exatos, mas

(27)

seu uso sistemático em casos como o do seqüenciamentojob-shopdevido a sua comple-xidade (Np-Dif´ıcil). Nesta dire¸cão, temos os trabalhos de Schall et al ([51], [48], [49],

[50]) que utilizam técnicas de programa¸cão matemática de forma h´ıbrida com métodos

heur´ısticos aplicáveis ao seqüenciamento job-shop modelado de forma linear com o uso de variáveis binárias. Particularmente, usa técnicas de programa¸cão matemática

tendo o m´etodo de pontos interiores (MPI) como principal ferramenta de resolu¸c˜ao.

As heur´ısticas utilizadas de forma h´ıbrida com o (MPI) nestes trabalhos são: simulated annealing e algoritmos genéticos. Tais algoritmos são descritos brevemente na se¸cão seguinte.

1.4.2 M´

etodos heur´ısticos

Os métodos de solu¸cão aproximada (heur´ısticas) permitem obter planos opera-cionais aceitáveis em tempo útil, mas não garantem a obten¸cão de uma solu¸cão ótima.

Dentre os diversos métodos aplicáveis ao job-shop, os mais utilizados são os métodos de lista devido a sua simplicidade. Estes métodos são baseados em regras de

despacho priorit´ario ou algoritmos de lista (Blazewicz et al.[10], Blazewicz [11]) onde o

plano operacional é constru´ıdo através de uma seqüência de decisões baseadas no que

localmente parece ser ´otimo. Alguns algoritmos conhecidos s˜ao:

• SPT(Shortest Processing Time) - Seleciona a opera¸c˜ao com menor tempo de processamento.

• EDD (Earliest Due-Date) - Seleciona a opera¸cão que pertence à tarefa cuja data de entrega é a mais próxima.

• FIFO (First In First Out) - Seleciona a opera¸c˜ao na ordem crescente de chegada nas m´aquinas.

• MWKR (Most WorK Remaining) - Seleciona a opera¸c˜ao que pertence ao produto que tem o tempo de processamento restante maior.

(28)

O método heur´ıstico conhecido por Simulated Annealing faz uma analogia entre a otimiza¸cão combinatória e a evolu¸cão do equil´ıbrio térmico dos sólidos. No

caso particular do job-shop, busca-se um procedimento iterativo, onde a solu¸cão do problema desempenha o papel do estado energético do sólido. Como mencionado na

se¸cão anterior Schall et al ([50], [51]) propõem uma hibrida¸cão do simulated annealing

juntamente com m´etodo de pontos interiores para a resolu¸c˜ao de problemas de job-shop.

Um outro m´etodo heur´ıstico utilizado ´e denominado como Shifting Bottleneck

e foi desenvolvido por Adams et al [1] e consiste em um m´etodo iterativo baseado no

grafo disjuntivo. Em cada itera¸c˜ao ´e resolvido um problema relaxado de planejamento

em uma única máquina com datas de disponibilidade e de entrega, de modo a seqüenciar

as máquinas que formam o problema dejob-shop. Assim as máquinas são seqüenciadas uma de cada vez, seqüencialmente.

Al´em destes m´etodos aqui mencionados, vale ressaltar trabalhos realizados com

m´etodos de busca adaptativos como os algoritmos gen´eticos (AG) . Estes algoritmos

têm sido aplicados com sucesso a problemas combinatórios. Seu modelo é constitu´ıdo

por uma popula¸cão de indiv´ıduos que são solu¸cões potenciais. Os AG combinam o

intercâmbio de informa¸cões e a sobrevivência dos melhores indiv´ıduos, representados

por cadeias estruturadas. Dentre os diversos trabalhos nesta ´area podemos citar os

trabalhos de Goldberg [25], Yamada e Nakano [58] que s˜ao aplicados a problemas de

seq¨uenciamento job-shop.

1.4.3 M´

etodos de decomposi¸c˜

ao

O princ´ıpio geral destes métodos é o de substituir a resolu¸cão de um problema

inicial complexo pela resolu¸cão de vários subproblemas cuja resolu¸cão seja mais fácil.

A conseqüente redu¸cão da dimensão é particularmente importante quando o problema

tem uma complexidade elevada como o caso do job-shop.

Dentre os m´etodos de decomposi¸c˜ao aplicados aojob-shop temos os trabalhos de Fischer ([19], [20]) que utiliza os multiplicadores de Lagrange para formar o dual

(29)

res-Conclus˜ao 16

tri¸cões de produto (precedência), e o problema mestre fica encarregado das restri¸cões

de m´aquina obtendo os multiplicadores de Lagrange de modo a manter a factibilidade.

Num outro trabalho, Fischer [21] prop˜oe uma metodologia que realiza um procedimento

próximo da Relaxa¸cão Lagrangeana clássica.

Métodos de decomposi¸cão espacial são aplicados a problemas de job-shop de grande dimensão reagrupando máquinas em células de produ¸cão e os produtos em

fam´ıliasde forma que produtos de uma mesma fam´ılia sejam executados por máquinas de uma célula principal e, excepcionalmente, sejam executados em máquinas de outras

células. Estas opera¸cões que são executadas em outras células são conhecidas como

elementos residuais. Esta filosofia ´e conhecida como tecnologia de grupos (Kusiak [33]).

Recentemente temos a proposta de Alves [3] que utiliza a tecnologia de grupos

para particionar o problema dejob-shope, em seguida, utiliza a t´ecnica da relaxa¸c˜ao la-grangeana para resolver os subproblemas coordenados por um problema mestre. Neste

caso os subproblemas se aproximam do problema original j´a que as restri¸c˜oes a

se-rem relaxadas s˜ao apenas as referentes ao elementos residuais. Assim, a factibilidade

das solu¸c˜oes locais ´e garantida de forma mais eficiente. Com o objetivo de tornar

a convergência nesta metodologia mais rápida, Ramos [44] propõe ajustes de alguns

parˆametros no m´etodo do subgradiente quando utilizado para resolver o problema

mes-tre.

Ainda há que ressaltar o trabalho de Santana [46] que propõe a decomposi¸cão

de um problema de job-shop usando o m´etodo de Dantzig-Wolfe.

Conclus˜

ao

Neste cap´ıtulo apresentamos um importante problema de f´abrica conhecido

(30)

Conclus˜ao 17

Neste trabalho estaremos adotando um modelo cont´ınuo (_§1.3.3) devido `a boa

performance apresentada pelo método de pontos interiores na resolu¸cão de problemas de programa¸cão não linear, como é o caso. Vamos nos deter agora a uma análise deste

m´etodo e suas principais aplica¸c˜oes. A seguir, no cap´ıtulo 3, veremos que o problema

(31)

Cap´ıtulo 2

M´

etodo de Pontos Interiores

O método de pontos interiores (MPI) tem sido em programa¸cão matemática

uma das mais interessantes ´areas de pesquisa em otimiza¸c˜ao desde o desenvolvimento

do m´etodo simplex conforme Freund e Mizuno[22]. Diversas formula¸c˜oes de MPI foram

propostas inicialmente tendo em mente problemas de programa¸c˜ao linear (Karmarkar

[31], Mehrotra [38], Renegar [45], Wright [57]). Motivados pelo sucesso do MPI para

programa¸cão linear tiveram in´ıcio as investiga¸cões de poss´ıveis extensões para

proble-mas de programa¸c˜ao n˜ao linear (Akrotirianakis e Rustem [4],El Bakry, et al. [17],

Granville [27], Vanderbei e Shanno [56]).

Neste cap´ıtulo fazemos uma breve descri¸cão da relevância do método de pontos

interiores no âmbito da busca de solu¸cão de problemas de otimiza¸cão. Apresentamos

inicialmente uma breve vis˜ao hist´orica do MPI acompanhado de diversas possibilidades

de aplica¸cão às mais variadas áreas. Seguimos apresentando uma descri¸cão sucinta do

MPI aplicado a problemas de programa¸c˜ao linear. Finalmente, conclu´ımos com a

apresenta¸cão de duas versões do MPI aplicado a problemas gerais de programa¸cão não

(32)

M´etodo de Pontos Interiores 19

2.1 O M´

etodo de Pontos Interiores: Ontem e Hoje

2.1.1 Breve hist´

orico

No ano de 1984 N. Karmarkar [31] apresentou `a comunidade cient´ıfica um novo

algoritmo para resolver problemas de programa¸c˜ao linear em tempo polinomial. Uma

caracter´ıstica de tal algoritmo é o fato de chegar a uma solu¸cão ótima para o problema

caminhando através de pontos interiores da região viável ao contrário do algoritmo

simplex, que a atinge gerando uma seq¨uˆencia de pontos extremos adjacentes. O artigo

de Karmarkar [31], e trabalhos anteriores reconhecidos posteriormente, deram in´ıcio a

um novo campo chamado de m´etodo de pontos interiores.

Nos primeiros anos ap´os o artigo inicial de Karmarkar, os trabalhos em

pro-grama¸c˜ao linear usando pontos interiores centravam suas aten¸c˜oes em algoritmos que

lidavam com o problema primal, possuindo uma implementa¸c˜ao mais amena que o

método original e tendo melhores limites de complexidade. Neste per´ıodo é notável a

contribui¸c˜ao do algoritmo de Renegar [45], que usou um limite superior para a fun¸c˜ao

objetivo obtendo sucessivamente subconjuntos do conjunto fact´ıvel, cada um contendo

uma solu¸c˜ao, e usando o m´etodo de Newton para analisar o centro deste subconjunto

primal ´otimo. Uma nova era foi inaugurada com o artigo de Megiddo [37], que descreve

uma estrutura para um algoritmo primal-dual. O ponto de vista primal-dual mostrou

ser extremamente produtivo. Isto levou a novos algoritmos com interessantes propostas

teóricas, formando uma base para algoritmos melhores, e extensões para programa¸cão

convexa e complementariedade linear. Em 1989, Mehrotra [38] descreve um algoritmo

pr´atico para programa¸c˜ao linear que se tornou a base para a maioria dos softwares

existentes; seu trabalho ´e publicado em 1992.

Os trabalhos em torno do m´etodo de pontos interiores tiveram um maior

´ımpeto ap´os o reconhecimento de solu¸c˜oes de problemas NP-dif´ıcil obtidas em tempo

polinomial. Os métodos que têm sido propostos possuem vários ingredientes, incluindo

(33)

2.1.2 Aplica¸c˜

oes do m´

etodo de pontos interiores

Do ponto de vista teórico várias pesquisas têm sido conduzidas quanto a

melho-ria da eficiência computacional para programa¸cão linear (LP), programa¸cões quadrática

(QP), problemas de complementaridade lineares (LCP) e algumas classes de problemas

de programa¸c˜oes convexos. Outros trabalhos envolvendo m´etodo de pontos interiores

(MPI) est˜ao sendo desenvolvidos para programa¸c˜oes semi-definidas, os quais possuem

uma grande variedade de aplica¸cões em áreas de controle e otimiza¸cão estrutural.

Pro-grama¸cão semi-definida, também tem se mostrado ser uma área de grande impacto

(Potra e Wright [43]).

´

E poss´ıvel provar a convergˆencia super-linear de algoritmos primal-dual

assu-mindo a independência linear das restri¸cões ativas nas solu¸cões (Potra e Wright [43]).

Esta observa¸c˜ao incitou pesquisas na melhoria das propriedades de convergˆencia de

outros algoritmos, notavelmente programa¸cão quadrática. Aplica¸cões à programa¸cão

quadr´atica apresentam-se como uma ´area promissora devido a habilidade superior que

a aproxima¸c˜ao por pontos interiores possui ao explorar a estrutura deste problema.

Como exemplo tem-se, dentre outros, o trabalho de Castro [15] que prop˜oe o MPI

para resolu¸c˜ao de problemas de multifluxo de produtos (MFP) com uma formula¸c˜ao

quadrática e verifica um melhor desempenho que o mesmo método aplicado à

modela-gem linear do mesmo problema.

O MPI tem permitido obter resultados eficientes para problemas de

pro-grama¸cão não linear, o que tem levado muitos pesquisadores a se dedicarem a esta área

(Akrotirianakis e Rustem [4], El Bakry et al. [17], Granville [27], Vanderbei e Shanno

[56]). Em particular, existe um grande n´umero de trabalhos que aplicam o MPI na

resolu¸cão de problemas de fluxo de potência que é um problema de programa¸cão não

linear, n˜ao convexo e de grande porte. Dentre estes, temos os de Sousa e Costa que,

num primeiro trabalho, apresentam um problema de fluxo de potˆencia ´otima resolvido

via MPI primal-dual com barreira logar´ıtmica (Sousa e Costa [53]) e, em outro trabalho

(Sousa e Costa [54]), é proposta a determina¸cão das barras para aloca¸cões de reativos

a partir de uma análise dos multiplicadores de Lagrange associados às restri¸cões de

(34)

resolvido pelo m´etodo apresentado no artigo anterior. Castronuovo et al [16] apresenta

um método baseado na centraliza¸cão da trajetória da solu¸cão ótima onde a distância

entre a solu¸c˜ao corrente e o passo central ´e monitorada.

Problemas de programa¸c˜ao inteira tamb´em podem ser resolvidos com o aux´ılio

de MPI. Nesta linha temos uma s´erie de trabalhos de Schall et al ([51], [47], [48], [49],

[50]) que estuda a resolu¸c˜ao de problemas lineares inteiros fazendo uma hibridiza¸c˜ao de

métodos exatos (MPI) com outras heur´ısticas tais como: algoritmo genético ,simulated annealing e scatter search. Em particular, em trabalho publicado em 1999 (Schall et al [51]) é apresentada uma compara¸cão dos métodos discutidos nos artigos anteriores

bem como uma proposta de aplica¸c˜ao a problemas de seq¨uenciamento job-shop.

Outra aplica¸cão freqüente é o uso de MPI na resolu¸cão de problemas de fluxos

em redes de multi-produtos (MFP). Os fluxos em redes de multi-produtos podem ser

usados em diversos campos, como telecomunica¸c˜oes, transportes e log´ıstica. Neste

tipo de problema diversos produtos devem ser transportados de um conjunto de n´os

de produ¸c˜ao para um conjunto de n´os de consumo compartilhando a mesma rede de

transporte. Este tipo de problema normalmente tem um grande n´umero de vari´aveis.

Um trabalho interessante de Azevedo et al [5] prop˜oe a resolu¸c˜ao de uma modelagem

por grafos explorando os diferentes graus de esparsidade do problema com o uso de

MPI . Nesta mesma linha h´a outros trabalhos como o de Castro [14].

O MPI permanece uma ´area ativa e frut´ıfera de pesquisa. Sobretudo, ´e poss´ıvel

notar a grande diversidade das aplica¸cões deste método de resolu¸cão.

2.1.3 O m´

etodo de pontos interiores versus m´

etodo simplex

Diversos autores tentaram comparar implementa¸c˜oes de algoritmos de pontos

interiores com o método simplex, mas não obtiveram tempo de solu¸cão competitivo.

Com a implementa¸c˜ao do m´etodo primal apresentado por Karmarkar apresenta-se a

primeira evidˆencia computacional de que MPI pode ser comparado em velocidade com

o m´etodo simplex.

(35)

realizadas com resultado superior ao do m´etodo simplex, n˜ao necessariamente para

cada problema individual, mas para um conjunto de problemas. De forma pr´atica, para

problemas pequenos o m´etodo simplex tem rendimento satisfat´orio. O MPI justifica-se

particularmente em problemas com grande n´umero de vari´aveis e maior complexidade

computacional (Wright [57]).

Um exemplo pr´atico onde o MPI possui consider´avel superioridade sobre o

método simplex é no planejamento do tratamento de câncer por radioterapia onde são

usados modelos de programa¸c˜ao linear. Conforme Barbosa [7] neste caso o desafio

matemático consiste em programar a emissão de uma alta dosagem de radia¸cão no

tumor, e simultaneamente, minimizar a radia¸c˜ao nas regi˜oes vizinhas compostas por

tecido saudável. Na presen¸ca de múltiplas solu¸cões o MPI convergirá para aquelas

solu¸cões distanciadas dos vértices o que não ocorre com o método simplex. Para este

modelo uma solu¸cão próxima do vértice pode não ser a mais adequada do ponto de

vista m´edico pelo fato das vari´aveis de folga estarem no seu limite, significando que em

determinadas partes tecido saudável receberá uma dosagem grande de radia¸cão.

Uma vantagem adicional do MPI ´e a possibilidade de trabalhar com pontos

infact´ıveis durante o processo de otimiza¸c˜ao, facilitando a identifica¸c˜ao de modelos mal

formulados (Wright [57]).

2.1.4 M´

etodos de decomposi¸c˜

ao e m´

etodo de pontos interiores

Usar a aproxima¸cão por ponto interior nos métodos de decomposi¸cão parece

ser promissor, ainda que n˜ao estejam sendo feitos estudos comparativos rigorosos nesta

´area (Potra e Wright [43]).

Nos m´etodos de decomposi¸c˜ao para problemas lineares e convexos de grande

porte, como a decomposi¸c˜ao de Dantzig-Wolfe, m´etodo de pontos interiores tem sido

usado para descobrir uma solu¸c˜ao para o problema master, ou para obter uma solu¸c˜ao aproximada para os subproblemas gerando pontos de teste. Zhao [60] mostra que

o algoritmo de pontos interiores com a decomposi¸c˜ao Dantzing-Wolfe ´e globalmente

(36)

resultados quando o método de pontos interiores é usado como meio de resolu¸cão de

um problema master na aproxima¸c˜ao por decomposi¸c˜ao e aplica sua metodologia a um

problema de multifluxo de produtos de grande porte (5.000 arcos e 10.000 produtos).

2.2 O M´

etodo de Pontos Interiores para Programa¸c˜

ao

Linear

Apesar de boa parte dos modelos matem´aticos atuais serem n˜ao lineares,

for-mula¸c˜oes de modelos lineares s˜ao vantajosas tendo em vista a qualidade dos softwares

à disposi¸cão e a garantia da convergência para um m´ınimo global. Portanto, entender o

m´etodo de pontos interiores aplicado a problemas de programa¸c˜ao linear permite uma

boa vis˜ao geral deste m´etodo.

Consideremos um problema de programa¸c˜ao linear formulado na forma padr˜ao:

Minimizar cT_x

Sujeito a A_·x = b x ≥ 0

(2.1)

ondecexsão vetores doRn_,_b_{é um vetor do}_Rm_e_A_{é uma matriz}_m_×_n_{. Aqui} vale ressaltar que estamos considerando pontos interiores aqueles pontos que atendam

estritamente as restri¸c˜oes do problema (2.1), ou seja, pontos em que x >0.

Associado com cada problema de programa¸c˜ao linear primalexiste uma outra programa¸c˜ao linear chamada de dual. O dual para (2.1):

Maximizar bT_λ

Sujeito a At_·_λ₊_s ₌ _c

s _≥ 0

(2.2)

onde λ é um vetor deRm _e _s_{é um vetor} _Rn_{. Nós chamamos as componentes} deλ de variáveis do dual enquantos é o vetor das variáveis de folga.

(37)

Teorema 2.1. Considere o vetor x de (2.1) e (λ, s) de (2.2) , ent˜ao temos que:

bTλ ≤cTx

Em outras palavras, o valor da fun¸c˜ao objetivo do dual ´e limitado inferiormente

pelo valor da fun¸cão objetivo do primal e o valor da fun¸cão objetivo do primal é limitado

superiormente pelo valor da fun¸c˜ao objetivo dual. As duas fun¸c˜oes objetivo podem ter

o mesmo valor, de forma que

bλ∗ =cx∗

quando x∗ _{é solu¸cão de (2.1) e (}_λ∗_{, s}∗_{) é solu¸cão de (2.2).}

Teorema 2.2. Pelas condi¸c˜oes de otimalidade (kkt) sabe-se que o vetor x∗ _∈ _Rn _´e

solu¸c˜ao de (2.1) se e somente se existem vetores s∗ _∈ _Rn _e _λ∗ _∈ _Rm _{que atendem as}

seguintes condi¸c˜oes

(i) At_λ₊_s ₌ _c

(ii) Ax = b

(iii) xisi = 0 i= 1,2, ..., n, (iv) (x, s) _≥ 0

(2.3)

considerando (x, λ, s) = (x∗_{, λ}∗_{, s}∗₎_.

Os vetoresλessão geralmente chamados de multiplicadores de Lagrange para as restri¸cões Ax =b e x_≥0, respectivamente. A condi¸cão (iii) implica que para cada ´ındice i = 1,2...n uma das componentes xi ou si é nula. Esta condi¸cão é conhecida

como condi¸c˜ao de complementaridade.

Examinando as condi¸c˜oes (2.3) do ponto de vista do primal e do dual,

con-clu´ımos que:

(38)

2.2.1 M´

etodo primal-dual

Este método encontra a solu¸cão primal-dual (x∗_{, λ}∗_{, s}∗_{) aplicando uma varia¸cão}

do método de Newton nas três equa¸cões das condi¸cões de (2.3) e modificando a busca de

dire¸cões e comprimentos tais que as inequa¸cões (x, s)_≥0 sejam estritamente satisfeitas em cada itera¸cão.

Vamos reapresentar as condi¸c˜oes de otimalidade (2.3) de uma forma diferente,

considere a fun¸c˜ao F :R2n+m _→_R2n+m _{definida por:}

F(x, λ, s) =

    

At_λ₊_s₋_c

Ax₋b XSe

    = 0

(x, s)≥0

(2.4)

onde:

X =diag(x1, x2, ..., xn)

S =diag(s1, s2, ..., sn)

e= (1,1, ...,1)t

Note que F é linear nos dois primeiros termos (At_λ₊_s₋_{c, Ax}₋_b_{) e o ´}_unico termo não linear desta fun¸cão é o termo XSe.

Todos os métodos primal-dual geram em cada itera¸cão pontos (xk_{, λ}k_{, s}k_{) que} satisfazem estritamente os limites de (2.4), ou seja, xk_>_{0 e} _sk _>_{0. Esta propriedade} é a origem do termoponto-interior. Respeitando estes limites o método evita solu¸cões falsas dadas por pontos que satisfazem F(x, λ, s) = 0 mas não (x, s) _≥ 0. Solu¸cões falsas não fornecem nenhuma informa¸cão quanto à solu¸cão do primal (2.1) ou do dual

(2.2), por isto ´e prefer´ıvel exclu´ı-las completamente da regi˜ao de busca. A maior

parte dos m´etodos de ponto interior requerem que em cada itera¸c˜ao (xk_{, λ}k_{, s}k_{) seja} estritamente fact´ıvel, ou seja,(xk_{, λ}k_{, s}k₎_{∈ F}0_{, onde:}

F0 ₌_{₍_{x, λ, s}₎_|_Ax₌_{b, A}t

λ+s=c,(x, s)>0}

(39)

origem no método de Newton que forma um modelo linear para F em torno do ponto corrente e obtém a dire¸cão de busca (∆x,∆λ,∆s) para a solu¸cão do seguinte sistema de equa¸cões lineares:

J(x0, λ0, s0)

     ∆x ∆λ ∆s    

=−F(x0, λ0, s0)

sendo J o Jacobiano de F. Se o ponto corrente ´e estritamente fact´ıvel, o passo de

Newton torna-se: _

   

O At _I

A 0 0

S 0 X

          ∆x ∆λ ∆s     =      0 0 −XSe      (2.5)

Um passo completo nesta dire¸cão é usualmente não permitido, já que poderia

violar o limite de não negatividade (x, s)_≥0. Para evitar esta dificuldade, caminha-se ao longo da dire¸cão de Newton (2.5), só que a nova itera¸cão é dada por:

(x, λ, s) +α(∆x,∆λ,∆s) onde α_∈(0,1]

Infelizmente quando o ponto corrente est´a pr´oximo ao limites do espa¸co de

busca só podemos tomar pequenos passos (α <<1) sem violar a condi¸cão de (x, s)>0, por este motivo o método de Newton oferece pouco progresso na busca da solu¸cão. É

necess´ario, portanto, fazer algumas mudan¸cas no m´etodo de Newton original.

2.2.2 O passo central

O passo centralC pode ser definido como sendo o arco de pontos (xτ, λτ, sτ)∈

F0 _{parametrizado por um escalar positivo} _τ_{. Cada ponto de} _C _{satisfaz as condi¸c˜oes} abaixo:

(i) At_λ₊_s ₌ _c

(ii) Ax = b

(iii) xisi = τ i= 1,2, ..., n, (iv) (x, s) > 0

(40)

Essas condi¸cões diferem das condi¸cões KKT (2.3) unicamente pelo termoτ na terceira condi¸cão . Esta é a chave para os pontos do arco C, pois cada produto xisi tem o mesmo valor. O passo central, portanto, equilibra o algoritmo primal-dual por

prover uma rota que pode ser seguida dentro do conjunto solu¸c˜ao.

Uma outra forma de definir_C ´e usando a nota¸c˜ao de (2.4) e escrever

F(xτ, λτ, sτ) =

     0 0 τ e    

, (xτ, sτ)>0 (2.7)

A equa¸cão (2.7) se aproxima de (2.4) quando τ tende a zero. Se _C converge sempre que τ _→ 0, esta converge para a solu¸cão primal-dual da programa¸cão linear. O passo central deste modo guia a solu¸cão ao longo de uma rota que evita solu¸cões

indesejadas fixando todo produtoxisi estritamente positivo e decrescendo at´e zero com alguma taxa.

Boa parte dos algoritmos primal-dual fazem passos de Newton em torno de

pontos deC paraτ >0 ao invés de um passo de Newton puro paraF. Para descrever a inclina¸cão da dire¸cão de procura, usa-se umparâmetro central σ _∈[0,1] e umamedida de dualidade µ definidos por:

µ= 1

n

X

i=1

xisi =

xT_s

n

que mensuram um valor médio para o produtoxisi. A equa¸cão genérica para distância torna-se:     

O At _I

A 0 0

S 0 X

          ∆x ∆λ ∆s     =      0 0

−XSe+σµe

   

 (2.8)

A distˆancia (∆x,∆λ,∆s) ´e um passo de Newton para o ponto (xσµ, λσµ, sσµ)∈

C, onde todo os produtos (xisi) s˜ao iguais a σµ.

(41)

s˜ao iguais a µ. No outro extremo, o valor de σ = 0 refere-se ao passo de Newton original (2.5). Muitos algoritmos usam valores intermedi´arios de σ no intervalo (0,1) com a dupla finalidade de reduzirµ e melhorar a centralidade.

´

E poss´ıvel provar que se F0 ₆₌ _∅ _{ent˜ao (2.6) tem solu¸c˜ao (}_x

τ, λτ, sτ) para cada τ > 0. Mais ainda, as componentes x e s desta solu¸cão são únicas. Para tanto, considere H0 _{como a proje¸cão de}_F0 _{no espa¸co reduzido de vetores (}_{x, s}_{), definido por:}

H0 ₌_{₍_{x, s}₎_|₍_{x, λ, s}₎_{∈ F}0 _{para algum}_λ _{∈ ℜ}m

}

e ent˜ao identifique (xτ, sτ) como o menor valor de H0 da fun¸c˜ao barreira definida por

fτ(x, s) = 1

τx

T_s

−

j=1

X

n

log(xjsj)

as componentes x e s s˜ao definidas unicamente se a matriz A tem posto completo. A fun¸c˜ao fτ(x, s) aproxima-se do infinito sempre que (x, s) se aproxima da fronteira de

H0_{, ou seja, sempre que algum par primal-dual} _x

jsj se aproxima de zero. Acerca de

fτ tamb´em pode se afirmar (Wright [57]) que:

• fτ ´e estritamente convexa em H0

• fτ ´e limitada por H0

• Dado τ > 0, e algum n´umero K, todos os pontos (x, s) no plano do conjunto

{(x, s)_{∈ H}0_|_f_τ(_{x, s}₎_≤_K_} _satisfazem

xi ∈[Ml, Mu], si ∈[Ml, Mu], i= 1,2, ..., n sendo Ml, Mu n´umeros positivos.

temos os seguinte teorema apresentado por (Wright [57]):

Teorema 2.3. Suponha que_F0 ₆₌_∅_{, e tome um n´}_{umero positivo} _τ_{. Ent˜ao} _f

τ tem um

´

unico m´ınimo local em _H0 _{e as condi¸cões para o passo central (2.6) têm solu¸cão.}

O passo central também pode ser definido como uma seqüência de valores

m´ınimos de uma fun¸c˜ao de barreira logar´ıtmica para o dual ou para o primal. Na

(42)

2.2.3 M´

etodos primais

Algoritmos primais tamb´em tˆem sido incorporados a algoritmos para

pro-grama¸c˜ao n˜ao linear da mesma forma que algoritmos primal-dual.

Um elemento importante na maioria dos algoritmos primais ´e a aproxima¸c˜ao

com o uso da fun¸c˜ao barreira logar´ıtmica para (2.1), que ´e definida como:

min x c

T_x

−τ

i=1

X

n

logxi sujeito a Ax=b, x >0 (2.9)

onde τ > 0 é um parâmetro positivo. Note que o dom´ınio desta fun¸cão é o conjunto de pontos estritamente fact´ıveis para o problema 2.1. Para atender as

condi¸cões de otimalidade a solu¸cão xτ de (2.9) satisfaz as seguintes condi¸cões: (i) τ X−1_e₊_At_λ ₌ _c

(ii) Ax = b

(iv) (x, s) > 0

(2.10)

para λ∈Rm_{. Podemos definir o vetor} _s _por

si =

τ xi

, i= 1,2, ..., n

estas condi¸cões são transformadas nas condi¸cões do passo central (2.3).

Por-tanto, o valor m´ınimo xτ do subproblema com barreira logar´ıtmica (2.10) ´e simples-mente a componentex do vetor de passo central (xτ, λτ, sτ)∈ C.

Quando τ decresce até zero, xτ aproxima-se da solu¸cão x∗ do problema de programa¸cão linear (2.1). Solu¸cões do problema (2.9) para cada valor de τ pode ser formada, por exemplo, pelo uso do método de Newton.

Algoritmos baseados em fun¸c˜oes de barreira logar´ıtmica n˜ao se tornaram

po-pulares tanto em programa¸cão linear quanto em programa¸cão não linear, devido a

dificuldade crescente de tornar o parˆametro de barreira τ tender a zero. O interesse neste algoritmo foi reavivado em 1985 quando se notou a rela¸c˜ao entre o algoritmo de

(43)

Método de Pontos Interiores Aplicado a Programa¸cão Não Linear 30

Algoritmos de Karmarkar avaliam o progresso na dire¸cão ótima através da

média de uma fun¸cão potencial logar´ıtmica. Uma variante da fun¸cão deste algoritmo é

(n+ 1)log(cTx−Z)−

n

X

i=1

logxi

ondeZ é um limite inferior para o valor objetivo de (2.1), que pode ser obtido durante as itera¸cões pelo uso de informa¸cões do problema dual. Logo após Karmarkar,

Renegar [45] desenvolveu um algoritmo que usa o m´etodo de Newton em conjunto com

uma fun¸c˜ao logar´ıtmica, definida por:

minx−nlog(Z−cTx)− n

X

i=1

xi sujeito a Ax=b, x >0, cT_{x < Z}

(2.11)

ondeZ é um limite superior para o valor ótimoZ∗ _{do objetivo}_cT_x_{para (2.1).} De fato cada solu¸cão de (2.11) é um passo primal central. O algoritmo de Renegar

seguiu este passo usando o m´etodo de Newton para obter solu¸c˜oes aproximadas de

(2.11) numa seqüência de valores decrescentes de Z. Ele alcan¸cou um melhor limite de complexidade do que o método de Karmarkar [31], requerendo O(√nlog1/ǫ) itera¸cões para identificar o ponto primal fact´ıvel xtal que cT_x _{esteja a uma distância}_ǫ_{do valor} objetivo ótimo Z∗_{, para dado} _{ǫ >} _{0. Não se tem identificado outro método de pontos}

interiores com complexidade melhor do que o apresentado por Renegar.

Apesar do algoritmo de Karmarkar ter se tornado sinˆonimo de m´etodo de

pontos interiores a maior parte dos algoritmos pr´aticos levam em conta a estrutura

primal-dual (Wright [57]).

2.3 M´

etodo de Pontos Interiores Aplicado a

Pro-grama¸c˜

ao N˜

ao Linear

O m´etodo de pontos interiores tem sido muito utilizado tanto em programa¸c˜ao

(44)

Um m´etodo primal-dual barreira-logar´ıtmica (PDBL) 31

Granville [27], Sousa e Costa [53][54]). Nesta se¸c˜ao apresentamos uma breve descri¸c˜ao

de uma vers˜ao do m´etodo primal-dual barreira-logar´ıtmica proposto por Vanderbei

e Shanno [56] que é uma versão do método de pontos interiores bastante utilizada

em programa¸cão não linear. Em seguida veremos uma versão de método de pontos

interiores primal-dual apresentada por Akrotirianakis e Rustem [4] tamb´em ´util.

2.3.1 Um m´

etodo primal-dual barreira-logar´ıtmica (PDBL)

O m´etodo primal-dual barreira-logar´ıtmica (PDBL) aqui apresentado tem como

base o trabalho de Vanderbei e Shanno [56], que permite uma boa vis˜ao do m´etodo

tanto em casos convexos como em casos n˜ao convexos.

Suponha o problema geral de programa¸c˜ao n˜ao linear representado por:

M in. f(t)

S.a. g(t)≥0 (2.12)

Consideremost_∈Rn _{e as fun¸cões}_f₍_t_{) e}_g₍_t_{) sendo duplamente diferenciáveis.} A resolu¸cão do problema (2.12) pelo método PDBL requer que as restri¸cões de

desi-gualdade se transformem em restri¸c˜oes de idesi-gualdade, o que pode ser feito pela adi¸c˜ao

de variáveis de excesso estritamente positivas (s >0). É incorporada à fun¸cão objetivo uma fun¸cão barreira-logar´ıtmica que garante a não negatividade das variáveis de folga.

Assim o problema (2.12) pode ser reescrito assim:

M in. f(t)₋µlns

S.a. g(t)₋s= 0 (2.13)

Agora temos para µ >0, a seguinte fun¸c˜ao objetivo:

fµ(t, s, µ) =f(t)₋µlns (2.14)

A fun¸c˜ao lagrangeana correspondente ao problema (2.13) ´e:

L(t, s, y;µ) =f(t)₋µlns₋yT₍_g₍_t₎

(45)

Um m´etodo primal-dual barreira-logar´ıtmica (PDBL) 32

As condi¸cões de otimalidade de primeira ordem (KKT) para a equa¸cão (2.15) são:

∇tL(t, s, y) =∇f(t)−(A(t))Ty= 0

∇sL(t, s, y) = −µe+SY e= 0

∇yL(x, s, y) = (g(t)−s) = 0

(2.16)

onde

A(t) = ∂g(t)_∂t que ´e a matriz Jacobiana de g(t)

S ´e uma matriz diagonal contendo as vari´aveis de folga sr;

Y ´e uma matriz contendo na diagonal os elementos yr;

e= (1, ...,1);

∇tf(t) = (1, ...,1).

Observa¸cão 2.1. Note que da segunda equa¸cão de 2.16 decorre que y _≥ 0, sendo consistente com fato de y ser o vetor dos multiplicadores de Lagrange associado com as inequa¸cões relativas ao problema original (2.12).

De forma semelhante ao que foi feito para programa¸c˜ao linear podemos

rees-crever as condi¸c˜oes de KKT para equa¸c˜ao (2.16) como:

F :R2m+n _→_R2m+n _{definida por:}

F(t, y, s) =

    

∇f(t)₋(A(t))T_y

−µe+SY e

(g(t)₋s)

    = 0

(t, s)_≥0

(2.17)

O método de Newton (MN) será usado para encontrar as ra´ızes para a fun¸cão

F(t, y, s). Antes de verificar isto, buscaremos encontrar uma fun¸cão de mérito que seja compat´ıvel com dire¸cão de busca encontrada. A fun¸cão de mérito será definida com a

´

unica finalidade de guiar e medir o progresso do algoritmo. O objetivo ´e que ela seja

minimizada com a solu¸c˜ao do problema original e, dentro de circunstˆancias adequadas

ela servir´a como uma fun¸c˜ao de descida para o algoritmo, decrescendo o seu valor a