(Annals of the Brazilian Academy of Sciences) ISSN 0001-3765
www.scielo.br/aabc
On Focal stability in dimension two
MAURICIO M. PEIXOTO1 and CHARLES C. PUGH2
1Instituto de Matemática Pura e Aplicada (IMPA), Estrada Dona Castorina, 110, 22460-320 Rio de Janeiro, RJ, Brasil. 2Mathematics Department, University of Toronto, Toronto, Ontario, M5S 2E4, Canada
Manuscript received on August 3, 2006; accepted for publication on October 2, 2006; contributed byMAURICIOM. PEIXOTO*ANDCHARLESC. PUGH*
ABSTRACT
In Kupka et al. 2006 appears the Focal Stability Conjecture: the focal decomposition of the generic Riemann structure on a manifoldMis stable under perturbations of the Riemann structure. In this paper, we prove the conjecture whenMhas dimension two, and there are no conjugate points.
Key words:geodesics, focal decomposition, focal stability, genericity, Teichmuller space.
1 INTRODUCTION
Let M be a compact, smooth manifold of dimension m, and let R = Rr be the space of Cr Riemann structures on M, equipped with the natural Cr topology, 2 ≤ r ≤ ∞. Fix p ∈ M. The kth focal componentwith respect tog∈Ratpis
σk = {v∈TpM: ∃exactlykvectorsv =v1, . . . , vk ∈TpM with
|v1| = · · · = |vk| and exp(v1)= · · · =exp(vk)},
where 1≤k≤ ∞, and| |, exp refer to the Riemann structureg. The focal decompositionTpM =
kσk is said to befocally stable if a small perturbation ofg has only a distant topological effect on
σk. Precisely, we require that givenǫ >0 and given a compact set
S⊂TpM, there is a neighborhoodU ofginRand there are ballsB,B′⊂TpMsuch that for eachg′∈U,
(a) S⊂ B∩B′.
(b) There is a homeomorphismh :B → B′that sends eachσk(g)∩Bontoσk(g′)∩B′.
Thus, the focal decomposition
σk enjoys a kind of structural stability.
In Kupka et al. 2006 we investigated the concept of focal stability with an eye to proving the following
Focal Stability Conjecture: the generic Riemann structure is focally stable. (SinceRis an open subset of a complete metric space, genericity makes sense.) The main result of this paper concerns Riemann structures that have no conjugate points. It is most easily stated for the open setN ⊂ Rof Riemann structures on
T M whose Gauss curvature is everywhere negative. See Section 7 for a discussion of the more general case thatghas no conjugate points.
THEOREMA.For a compact manifold of dimension two, the generic Riemann structure g∈ N is focally stable.
A different sort of result is also given. It concens surfaces of constant negative curvature. Fix a compact smooth surface of genuss ≥2, such as the bitorus, and letHdenote the nonempty set of Riemann structures on M with curvature everywhere equal to−1. SinceH is a clsoed subset ofR, genericity in Hmakes sense. Modulo isometric deformationsHis the Teichmuller spaceτs.
THEOREMB.
(a) Fix g ∈ H. For the generic p ∈ M, the focal decomposition of TpM is stable with respect to
perturbations of p in M.
(b) Fix p ∈ M. For the generic g ∈ H, the focal decomposition of TpM is stable with respect to
perturbations of g withinH.
2 MEDIATRICES
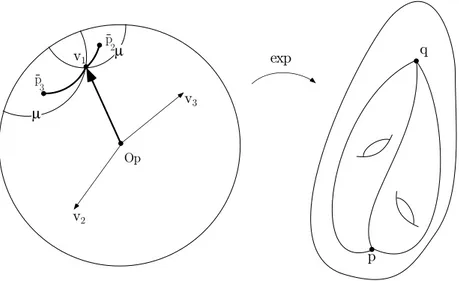
When the Riemann structure onMhas non-positive curvature, there are no conjugate points and so expp: TpM → M is the universal covering space. Letg¯ be the lift ofgtoTpM, and letd¯ be the corresponding metric onTpM. The focal decomposition ofTpM can be described in terms of equidistance loci, called
mediatricesby Bernhard and Veerman in Bernhard and Veerman 2006, as follows. A vectorv1∈σk hask “friends” – vectorsv1, . . . , vk ∈TpMof equal length and equal exponential image. (A vector is always a friend of itself.) This implies that there are exactlyk points in exp−1
p (p), one of which is the origin Opof
TpM, and from whichv1is equidistant with respect to the metricd¯. See Figure 1.
3 A MULTITRANSVERSALITY RESULT
In Kupka et al. 2006, following Mather, we considered the multi-exponential map
Ek :Vpk ×R→(M×R)k
(v1, . . . , vk,g)→(exp(v1),|v1|, . . .exp(vk),|vk|),
where Vpk is the set of k-tuples of distinct nonzero vectors in TpM, and exp, | | refer to the Riemann structureg. The diagonal of(M×R)k is
Op
µ
µ
v1 exp
p
q
p
-3
p
-2
v2
v3
Fig. 1 – Mediatricesµcorresponding to the focal decomposition. Thed¯-distance fromv1toOp,p¯2,p¯3isℓ. The vectorsv1, v2, v3have common exponential image
q, whileOp,p¯2,p¯3have exponential imagep.
Theorem 6.1 of Kupka et al. 2006 states that ifk ≥ 3 thenEk is transverse to. Here we need also the casek =2. Although the proof becomes easier if we use a negative curvature hypothesis, we give the proof in general, since we hope to use the theorem as tool whenMhas conjugate points.
Theorem 3.1. E2 :V2
p ×R→(M×R)2is transverse to.
PROOF. We give the proof in the case that M has dimension two, the main difference from the higher dimensional case being notational.
Lemma 6.3 of Kupka et al. 2006 states that, givenL >0, there is an open-dense setG(p,L) ⊂ R
such that forg ∈G(p,L), there are at most a finite number of geodesic loops γ at p having length≤ L, and that
(a) γ is not a closed geodesic. (That is, the vectors tangent toγ at its beginning and end are distinct.)
(b) γ is “single” in the sense that it meets ponly at its beginning and end, although other self-intersections are permitted.
(c) Under perturbation ofg,γ evolves continuously: it does not disappear or bifurcate.
Although some of the geodesic loopsγ may be self-conjugate in the sense that there is a transverse Jacobi field J alongγ that vanishes at both ends ofγ, a perturbation ofgeliminates this feature. No such self-conjugacy can be created by a small perturbation ofg, so we can restrict attention to Riemann structures in an open-dense subsetG∗(p,L)⊂G(p,L)that have no self-conjugate geodesic loops of length≤ L.
Let P = (v1, v2,g) ∈ Vp2×G∗(p,L) have E2-image Q = (q, ℓ,q, ℓ) ∈ . Let S be the sum
S=Image(TPE2)+TQ. We must show
To do so we choose a basis ofTQ(M×R)2as follows. The natural inclusions
M ֒→(M×R)2 M֒→(M×R)2
z →(z, ℓ,q, ℓ) z →(q, ℓ,z, ℓ)
induce isomorphisms
i1:TqM →TqM×ℓ×q×ℓ i2:TqM→q×ℓ×TqM×ℓ
into the tangent spaceTQ(M×R)2.
We refer to the geodesics t → exp(tvj) as γj, j = 1,2, and to their terminal tangent vectors as
w1=γ1′(1),w2=γ2′(1). The time parametertis always restricted to[0,1]. Choose vectorsu1,u2∈TqM, normal tow1, w2. This gives bases{u1, w1}, {u2, w2} ofTqM, which the inclusions convert to a basis
{e1, f1,h1,e2, f2,h2}ofTQ(M×R)2; namely
e1=i1(u1) f1=i1(w1) e2=i2(u2) f2=i2(w2)
whereh1,h2are tangent to the appropriate factorRin(M×R)2.
CASE1. The geodesicsγ1,γ2are unequal pointsets. We will show that E2is submersive atP, i.e., that
ImageTPE2=TQ(M×R)2.
Becauseγ1, γ2have the same length, neither contains the other, so there are “free spots” – pointsz1∈γ1\γ2
andz2 ∈γ2\γ1. (Note that even for the genericg,q may be conjugate to palong these geodesics.) See
Figure 2.
z
p
γ
(1)
Fig. 2 – Varyinggat a free spotzcontrols the endpointq =γ (1)of the geodesicγ.
Lemma 6.2 in Kupka et al. 2006 states that perturbation of g in the neighborhood of the free spots causes free and independent motion of the endpoints ofγ1, γ2. Furthermore, perturbation ofv1along itself
makesℓ1= |v1|vary linearly; and yoked to this variation ofℓ1, the endpointq1=γ1(1)varies dependently
along f1. The corresponding facts hold forv2, so we see that the image ofTPE2contains the vectors
which is a basis for TQ(M×R)2. This demonstrates that E2is submersive at P. Submersivity implies transversality.
CASE2. γ1,γ2are equal as point sets – they are merely the same geodesic loopγ atp, traversed in opposite directions. See Figure 3. This implies that there are no free spots, so perturbation of the Riemann structure is futile.
p
u
2w
2= - v
1w
1v
1b
γ
Fig. 3 – A geodesic loop.
Becauseγ is a geodesic loop, but not a closed geodesic, the terminal vectors w1, w2 are linearly independent. Since they have equal length and are perpendicular tou1, u2, the coefficients b,d in the expression
w1=au2+bw2 w2=cu1+dw1.
satisfy
|b|,|d|<1. (1)
Because the loopγ is not self-conjugate, variation of v1 perpendicular to itself produces free and independent variation of the endpointq1 =γ1(1)perpendicular tow1. The same is true forv2. Thus, the
image ofTPE2contains the vectorse1,e2.As in Case 1, variation ofv1,v2along themselves gives vectors f1+h1, f2+h2in the image ofTPE2. Altogether, then, we have four vectors
e1, f1+h1,e2, f2+h2∈TPE2.
The curves
are contained in, and henceTQcontains their tangents att =1, namely,
δ1′(1)= f1+i2(au2+bw2)= f1+ae2+b f2
δ2′(1)=i1(cu1+dw1)+ f2 = f2+ce1+d f1.
The linear combination
δ=δ′1(1)−bδ2′(1)=(1−bd)f1+ae2−bce1
of these vectors is tangent to. By (1), this gives an explicit expression for f1∈S =TPE2+TQas
f1= 1 (1−bd)
bce1−ae2+δ
.
In the same way, f2belongs toS, and so do
h1=(f1+h1)− f1 h2=(f2+h2)− f2.
Since S contains the whole basis {e1, . . . ,h2}, it equals TQ(M × R)2, which completes the proof in
Case 2.
COROLLARY3.2. For the generic g ∈R, and for all k ≥1, the multiexponential Ek
g :Vpk →(M×R)k
is transverse to the diagonal. When M has dimension two, the pre-image ofis empty for k ≥4, is a discrete set of points for k=3, and is a smooth1-manifold for k =2.
PROOF. The Abraham Transversality Theorem asserts that if a smooth map F :X ×A→Y ⊃W
is transverse toW whereAis a Banach manifold and X,Y,W are finite dimensional, then for all a in a resdual subset ofA, the map
F(a, ):X →Y ⊃W
is transverse toW. In our case,Ris an open set of a Banach space, and we know that
E2:R×V2→(M×R)2⊃
is transverse to. Thus, for the genericg∈R,E2gis transverse to.
When k = 1, transversality is trivial because the diagonal coincides with M×R, while fork ≥ 3, transversality is proved in Kupka et al. 2006, Theorem 6.1.
Now assume that M has dimension two. The codimension of in(M ×R)k is 3k −3, and the dimension ofVpk is 2k. Thus, ifk ≥ 4 then the codimension in the target exceeds the domain dimension, so transverse intersection implies empty intersection: Ek
g(Vpk)∩= ∅. Similarly, because transversality preserves codimension, the pre-image ofunder Eg3is a discrete set of points inVp3, and the pre-image of
4 FOCAL BRANCHES Fix ag∈Rand let
νk =(Ekg)
−1
()= {(v, . . . , vk)∈ Vpk :E k
g(v1, . . . , vk)∈}.
Clearlyνk is invariant under permutation of the factorsTpM inVpk. Thus, ifπj :Vpk →TpM projectsVpk onto the jthfactor,
βk =πj(νk)
is independent of j. Furthermore,β2⊃β3⊃β4⊃. . . and,
σ1=TpM\β2 σ2=β2\β3 . . . σk =βk\βk+1.
PROPOSITION4.1. When M has no conjugate points, the projectionπj :νk →TpM is a proper immersion
onto a closed subset of TpM.
PROOF. Properness means that the pre-image of a compact set is compact. Thus, from any given a sequence(v1n, . . . , vkn)inνksuch that for some fixed j,vj nconverges inTpMasn → ∞, we must extract a subsequence, convergent inνk.
Whenk =1 the assertion is trivial since the projection is the identity map. Thus we assumek ≥2. Convergence ofvj n, say tovj ∈TpM, implies that|vj n| → |vj| =ℓ. Since all the othervi nhave the same length, there is a subsequence (unrelabeled) such that(v1n, . . . , vkn) → (v1, . . . , vk). Eachvi has lengthℓ. Fixi = j. Thenvi n = vj n. Since expp(vi n) =expp(vj n), the facts thatk ≥ 2 and that exp is a local diffeomorphism from a neighborhood of the origin inTpMto a neighborhood of pinMimplies that
ℓ= 0. Also, since there are no conjugate points, exp is a local diffeomorphism atvj, which implies that
vi =vj. Thus(v1, . . . , vk)∈νk, which completes the proof of properness.
A continuous proper map into a metric space necessarily has a closed range. Henceπj(νk)is closed inTpM.
To check thatπj is an immersion, we must show that the projectionvj(t)of each nonsingular curve
(v1(t), . . . , vk(t)) inνk is nonsingular inTpM. Fix at0 ∈ (a,b) where(a,b) is the curve’s domain of definition. For at least onei,v˙i(t0) = 0. Thus, vi(t)is nonsingular at t0. Since there are no conjugate points, exp(vi(t))is also nonsingular att0. Since(v1(t), . . . , vk(t))∈ νk, exp(vj(t)) =exp(vi(t))is also nonsingular att0. Therefore,vj(t)is nonsingular att0.
5 PROOF OF THEOREM A
We assume that M is a compact surface of genus ≥ 2, that p ∈ M is fixed, and we denote by N the nonempty set of Riemann structures onT M having negative curvature. Clearly,N is an open subset ofR
and so it makes sense to speak of the genericg ∈N.
A Riemann structure with negative curvature has no conjugate points. Thus, according to Corollary 3.2 and Proposition 4.1, the focal decomposition ofTpMis quite simple for the genericg ∈N. Namely:
(b) σ3=β3is a discrete subset ofTpM.
(c) σ2=β2\β3andβ2consists of a closed set of immersed curves inTpM.
Furthermore, in any fixed compact subset ofTpM, properties (a), (b), (c) remain valid for all small pertur-bations ofg.
Consider a vectorv1 ∈ β3. It has two friendsv2, v3 ∈ β3 with equal length and equal exponential
image. Thus(v1, v2)∈ν2, and there are nonsingular curvesv1(t),v2(t)with
v1(0)=v1 v2(0)=v2 (v1(t), v2(t))∈ν2.
Likewise there are nonsingular curvesv1∗(t),v3(t)with
v∗1(0)=v1 v3(0)=v3 (v1∗(t), v3(t))∈ν2.
We claim thatv1(˙ 0)andv˙∗1(0)are linearly independent. Suppose not. Nonsingularity implies that there is ac=0 such that
˙
v1(0)=cv˙∗1(0).
At timet =0 the curve exp(v3(ct))has tangent
d dt
t=0exp(v3(ct))=Tv3expp(cv˙3(0))=c Tv3expp(v˙3(0)) =c Tv1expp(v˙∗1(0))=Tv1expp(v˙1(0))
= d dt
t=0exp(v1(t))
Similarly, d dt
t=0|
v3(ct)| = d dt
t=0| v1(t)|.
Thus, att =0
t→ Eg3(v1(t), v2(t), v3(ct))
is tangent to the diagonal⊂(M×R)3. The upshot is that the range of T(v1,v2,v3)E 3
gcontains a nonzero vector tangent to the diagonal in(M×R)3. This contradicts the fact thatE3
g :Vp3→(M×R)3is transverse to, sincehas codimension 6, which is the same as the dimension ofVp3.
Now we know thatv1(˙ 0)andv˙1∗(0)are linearly independent. This means that in addition to properties (a) - (c), above, we have
(d) Branches ofσ2meet transversally in pairs, they do so only at points ofσ3, and every point ofσ3is such
a crossing point,
where by abranchofσ2we mean the projection of an arc inν2. Since transversality is an open property,
(d) also remains valid under perturbation of the Riemannn structure.
the focal decomposition amounts to a smooth one-dimensional graph, namelyŴ = σ2∪σ3, which has
transverse crossings of multiplicity two. We adjust B so that its boundary is transverse to Ŵ. Let g′ be a small perturbation of g and letŴ′ be the corresponding graph. Since all aspects of the graph depend continuously on the Riemann structure, and all are transverse, if g′ is sufficiently close to g, then there exists a homeomorphism from Bto itself that sendsŴ∩BtoŴ′∩B.
6 PROOF OF THEOREM B
We assume that M is a compact surface of genus≥ 2 and we denote byH ⊂ R the nonempty set of Riemann structures whose curvature is identically equal to−1.
Fixg ∈ Hand p ∈ M. As described in section 2, we can lift gto a Riemann structure g¯ on TpM and view the focal decomposition in terms of mediatrices for the corresponding metricd¯. Since g has constant negative curvature,d¯is isometric to the Poincaré metricρon the unit discD, and mediatrices are
ρ-geodesics. As such, mediatrices are circular arcs meeting∂Dperpendicularly. Thus, any two mediatrices meet one another transversally, and they do so at most once.
LetPbe the lattice of pre-images of pinTpM, and denote the corresponding mediatrix set as
µ= {v∈TpM: for some p¯ ∈ P\ {0}and|v| =ρ(v,p)¯ }.
Fix a compact setS⊂TpM. At most finitely manyµ-mediatrices meetS. Choose a constant Rand let B denote the compact disc
TpM(R)= {v∈TpM: |v| ≤R}.
WhenRis large,BcontainsSin its interior and we can adjustRso that∂Bis transverse to theµ-mediatrices. Letτ be the finite set of points inB at which theµ-mediatrices intersect one another. Thus
τ =(σ3∪σ4∪ · · · ∪σℓ)∩B
for some finiteℓ. Ifv∈σk, there arek−1µ-mediatrices that pass through it. They are pairwise transverse. A small change of ppreserves all transversalities in the disc of radius R; such a perturbation of the base point can not increase the multiplicity of a vector inτ, although it may lower it. (Here is where the argument uses the fact that the curvature is constant – mediatrices in the constant curvature case are always transverse to one another.) Thus, there is an open-dense setU ⊂ M such that if p ∈ U and p′ is sufficiently near p then all multiplicities of theµ′-mediatrices inB′=Tp′M(R)are the same as those inB. (Byµ′we denote
the mediatrices between the origin ofTp′Mand the other lifts of p′inTp′M.) In other words, the graph of µ′-mediatrices in B′is homeomorphic to the graph ofµ-mediatrices inB. Taking a sequence of compact setsSn that exhaustsTpMleads to a sequence of such open dense setsUninM, and if p ∈
Un then the focal decomposition inTpM is stable with respect to perturbation of the base point p. This completes the proof of the first assertion in Theorem B.
exhaustsTpMleads to a sequence of open dense setsUninH, and ifg ∈
U
nthen the focal decomposition
ofTpMis stable with respect to perturbation ofgwithinH.
REMARK. Theorem B does not assert the multiplicity of the focal decomposition of the genericg ∈His at most three. We believe, however, that such an assertion is correct, and we can phrase our expectation as follows. IfM has genuss ≥ 2 then the Teichmuller spaceτs of hyperbolic structures on M amounts toH/DwhereDdenotes isometric deformations. It is a space smoothly parameterized by 6(s−1)real variables, and we expect that for a residual subset of these parameter values the corresponding hyperbolic structure hasσk = ∅for allk ≥ 4. From this it would follow at once that the generic g ∈ His focally stable with respect to variation ofginR, not just with respect variation ofgwithinH, as in Theorem B.
7 CONJUGATE POINTS
A Riemann structure with non-negative curvature has no conjugate points, but the setS of such Riemann structures does not form an open subset ofR. For example, a flat Riemann structure on the torus has no conjugate points although it can be perturbed so that conjugate points appear. See Kupka et al. 2006, Proposition 4.8, where a bump is glued to a cylinder. Thus, the assertion of Theorem A′, below, should be viewed with caution, for a generic subset ofSneed not be dense inS.
THEOREMA′. Focal stability (for a fixed p∈ M) holds for the generic g∈S.
PROOF. In the proof of Theorem A, we only used the assumption that expp is a local diffeomorphism, i.e., that there are no conjugate points, and the fact that the genericg ∈Rstably possess the transversality
properties (a)-(d).
The next result shows that Theorem A′has wider scope than Theorem A.
PROPOSITION7.1. The interior ofSis strictly larger thanN.
PROOF. LetMbe the bitorus, or any surface with genus≥2. Equip it with a Riemann structure of constant curvature−1. Cut out a small disc inMand replace it with a small polar cap having unit positive curvature. A smoothing collar is used to attach the cap. This gives a new Riemann structureg on M,g ∈/ N. Any
g-geodesic spends relatively little time in the polar cap or collar. Most of the time the geodesic travels through the part of the surface with curvature−1. Thus, there are no conjugate points, sogbelongs toS, and the same holds for all nearby Riemann structures.
ACKNOWLEDGMENTS
Both authors were partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).
RESUMO
Em Kupka et al. 2006, consideramos a Conjectura da Estabilidade Focal: a decomposição focal da estrutura
Riema-niana genérica em uma variedadeMé estável por perturbações dessa estrutura. No presente trabalho demonstramos
essa conjectura quandoM tem dimensão dois e não existem pontos conjugados.
Palavras-chave:geodésicas, decomposição focal, estabilidade focal, genetricidade, espaço de Teichmuller.
REFERENCES
KUPKAI, PEIXOTO MM AND PUGH C. 2006. Focal Stability of Riemann Metrics. J Reine Angew Math 593: 31–72.
BERNHARD JAND VEERMAN JJP. 2006. Minimally Separating Sets, Mediatrices and Brillouin Spaces. Topol Appl 153: 1421–1433.