Geometria Basica Aula5 Volume1

Aula 5 – Perpendicularidade e paralelismo

Objetivos

• Introduzir os conceitos de perpendicularidade e de paralelismo.

• Introduzir o quinto postulado de Euclides, ressaltando sua grande

im-portˆancia hist´orica e te´orica.

• Apresentar os primeiros resultados decorrentes do quinto postulado.

Introdu¸

c˜

ao

Discutiremos nesta aula os importantes conceitos de perpendicularidade e paralelismo entre retas.

J´a vimos, na aula 1, que duas retas s˜ao paralelas quando n˜ao se inter-sectam. A seguir, veremos o que significa dizer que duas retas s˜ao perpendi-culares.

Defini¸c˜ao 12

Duas retas s˜ao ditasperpendicularesse elas se intersectam formando ˆangulos retos.

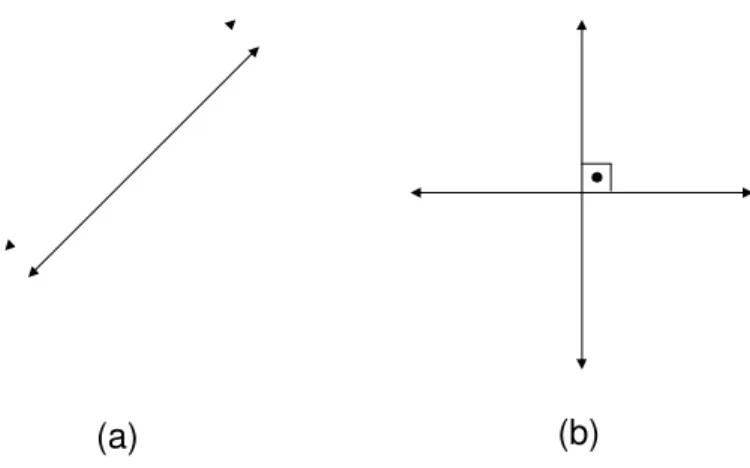
(a) (b)

Fig. 68: a) Retas paralelas. b) Retas perpendiculares.

Observe o desenho abaixo. As retas s˜ao paralelas ou n˜ao?

As retas s˜ao paralelas. Verifique com uma r´egua.

Usando os resultados das aulas anteriores, ´e poss´ıvel provar as seguintes proposi¸c˜oes:

Proposi¸c˜ao 7

Dados uma reta r e um ponto P, existe uma ´unica reta s perpendicular a r

passando por P.

s

r

P

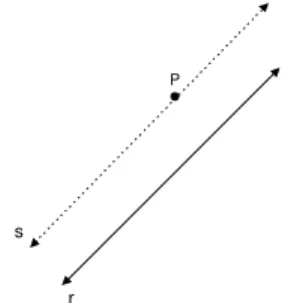
Fig. 69: Retasperpendicular arpassando porP.

Proposi¸c˜ao 8

Dados uma reta r e um ponto P fora de r, existe uma reta s paralela a r

contendoP.

s

r

P

Fig. 70: Retasparalela arcontendoP.

As provas dessas proposi¸c˜oes est˜ao no Apˆendice que aparece no final da aula, e vocˆe deve estud´a-las num segundo momento, ap´os ter dominado o uso destas proposi¸c˜oes para resolver problemas.

Observe a figura 71.

s

r

P

T Q

Fig. 71: O pontoQ´e o p´e da perpendicular.

Note que a palavra unica´ no enunciado da proposi¸c˜ao 7 n˜ao aparece no enunciado da proposi¸c˜ao 8. Na verdade, n˜ao ´e poss´ıvel provar, usando apenas os axiomas e os resultados anteriores, que s´o existe uma reta com a propriedade desejada.

Vocˆe sabia que... A unicidade da paralela (chamado de Quinto Postulado de Euclides) foi proposta por Euclides como um axioma. Por muitos anos (mais de 2.000!) v´arios matem´aticos tentaram provar, sem sucesso, que a unicidade da paralela decorria dos outros axiomas. Foi somente na primeira metade do s´eculo XIX que os matem´aticos chegaram `a conclus˜ao de que o quinto postulado n˜ao era demonstr´avel a partir dos outros quatro. Isso ocorreu com a descoberta das chamadas geometrias n˜ao-euclidianas em que o quinto postulado de Euclides ´

e substitu´ıdo por uma outra afirma¸c˜ao que lhe ´e contradit´oria. Essa

descoberta est´a associada ao nome de dois matem´aticos que a obtiveram

independentemente: J´anos Bolyai (1802-1860) e Nikolai I. Lobachevsky (1793-1856).

Apresentamos, agora, o axioma que ´e conhecido como oQuinto Postu-lado de Euclides.

Quinto Postulado de Euclides

• Por um ponto fora de uma reta passa uma ´unica reta paralela

`a reta dada.

Antes de obter algumas conseq¨uˆencias do Quinto Postulado de Euclides, definiremos o importante conceito de mediatriz de um segmento.

Defini¸c˜ao 13

A mediatrizde um segmento ´e a reta perpendicular a esse segmento em seu ponto m´edio (veja figura 72).

r A

B

Fig. 72: A retar´e mediatriz do segmentoAB.

Agora considere duas retas r e s; suponha que t ´e uma reta que corta as duas. A reta t ´e chamada transversal `as retas r e s. Considere os oito ˆangulos indicados na figura 73, numerados para facilitar a explica¸c˜ao.

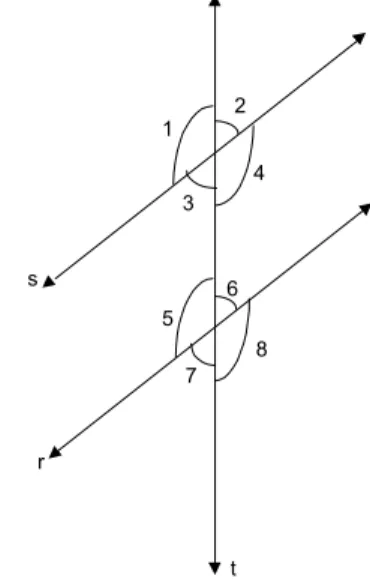
r s 1 3 2 4 5 6 7 8 t

Fig. 73: Paralelas cortadas por uma transversal.

Os ˆangulos ˆ3 e ˆ6, bem como os ˆangulos ˆ4 e ˆ5, s˜ao chamados alternos internos (pois ficam em lados alternados det, entre as retasr es), enquanto os pares ˆ1 e ˆ8 e ˆ2 e ˆ7 s˜ao ditos alternos externos. Chamam-se correspondentes os seguintes pares de ˆangulos: ˆ1 e ˆ5, ˆ2 e ˆ6, ˆ3 e ˆ7, e ˆ4 e ˆ8. Note que, se um dos pares acima for congruente, os outros tamb´em o ser˜ao.

Vocˆe sabia que...

J´anos Bolyai 1802-1860 d.C., Romˆenia.

J´anos Bolyai nasceu na Transilvˆania, naquela ´epoca parte da Hungria e do Imp´erio Austr´ıaco. Entre 1820 e 1823, ele preparou um tratado sobre um sistema completo de Geometria n˜ao-euclidiana. Antes de o trabalho ser publicado, ele descobriu que Gauss tinha antecipado muito do seu trabalho. Embora Gauss nunca tivesse publicado seu trabalho nessa ´area, isso era um ponto de honra para Bolyai. Por´em, o trabalho do Bolyai foi publicado em 1832 como apˆendice de um ensaio, por seu pai. Consulte:

http://www-groups.dcs. st-nd.ac.uk/~history/ Mathematicians/Bolyai. html

Proposi¸c˜ao 9

Se duas retas cortadas por uma transversal determinam um par de ˆangulos alternos internos congruentes, ent˜ao as retas s˜ao paralelas.

Prova:

Suponha que re ss˜ao cortadas por t, como na hip´otese da proposi¸c˜ao. Se r e s n˜ao fossem paralelas, elas teriam um ponto em comum, como na figura 74.

r s

t

Fig. 74: Proposi¸c˜ao 9.

Ter´ıamos ent˜ao um triˆangulo para o qual um ˆangulo externo seria igual a um ˆangulo interno n˜ao adjacente, o que seria contradit´orio com o teorema do ˆangulo externo. Logor es s˜ao paralelas.

Q.E.D.

Na proposi¸c˜ao seguinte utilizaremos pela primeira vez o Quinto Postu-lado de Euclides.

Proposi¸c˜ao 10

Se duas retas paralelas s˜ao cortadas por uma transversal, os ˆangulos alternos internos s˜ao congruentes.

A proposi¸c˜ao 10 ´e quivalente `

a proposi¸c˜ao 29 do livro I dosElementos_{, em que}

Euclides usou o Quinto Postulado pela primeira vez.

Prova:

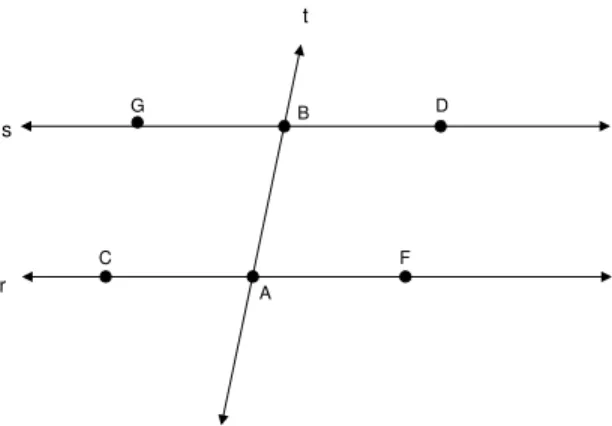
Sejam r e s duas retas paralelas cortadas por uma transversal t nos pontosAeB, respectivamente. Sejam C eF pontos der eGeDpontos de

r s t A B C D F G

Fig. 75: t´e transversal `as retas paralelasres.

Provaremos que os ˆangulos BACˆ e ABDˆ s˜ao congruentes. Para isso, vamos supor que tal fato n˜ao aconte¸ca, ou seja, queBAC > Aˆ BDˆ ouABD >ˆ BACˆ .

Vocˆe sabia que... Nikolai I. Lobachevsky (1793-1856 d.C., R´ussia) foi o primeiro a publicar um relato sobre Geometria n˜ao-euclidiana (1829). Seu trabalho atraiu pouca aten¸c˜ao quando apareceu porque foi publicado em russo e os russos que o leram fizeram severas cr´ıticas. Em 1840, ele publicou um tratado em alem˜ao, atrav´es do qual suas descobertas chegaram ao conhecimento de Gauss. Em uma carta a Schumacher, Gauss elogiou o trabalho de Lobachevsky, mas ao mesmo tempo reiterou sua prioridade nesse assunto. Lobachevsky n˜ao teve o merecido reconhecimento durante sua vida. De fato, em 1846 ele foi demitido da Universidade de Kazan, apesar dos vinte anos de not´aveis servi¸cos prestados como professor e administrador. Somente ap´os a morte de Gauss (1855), quando suas correspondˆencias foram publicadas, o mundo come¸cou a reconhecer os trabalhos de Lobachevsky sobre Geometria n˜ao-euclidiana.

Em qualquer caso, no semiplano determinado por t que cont´em C, tra¸camos a semi-reta−→AE tal que BAEˆ ≡ABDˆ , como na figura 76. O lado

esquerdo da figura 76 representa o caso BAC > Aˆ BDˆ , enquanto que o lado direito, o caso ABD > Bˆ ACˆ .

r s t A B C D F G r s t A B C D F G E E

Fig. 76: Proposi¸c˜ao 10.

As retas ←AE→ e s s˜ao cortadas por t de forma que os ˆangulos alternos internos BAEˆ e ABDˆ s˜ao congruentes. Usando a proposi¸c˜ao 9, conclu´ımos que ←AE→ ´e paralela a s, e portanto existem duas paralelas a s (←AE→ e r) passando pelo ponto A, o que contraria o Quinto Postulado de Euclides. Chegamos a essa contradi¸c˜ao porque assumimos queBACˆ n˜ao ´e congruente aABDˆ . Logo, devemos ter BACˆ ≡ABDˆ .

Q.E.D.

O teorema a seguir ´e um dos mais utilizados da Geometria euclidiana.

Lei Angular de Tales

A soma dos ˆangulos internos de qualquer triˆangulo ´e 180o_.

Prova:

Seja ABC um triˆangulo e seja s a reta que passa por A e ´e paralela `a reta ←BC→, como na figura 77.

A

B C

D E _s

Fig. 77: Retasparalela `a reta que cont´em os pontosBeC.

Sobre s marque pontos D e E. Como a reta ←AB→ ´e transversal `as retas paralelas s e ←BC→, podemos concluir, a partir da proposi¸c˜ao 10, que

ABCˆ ≡ DABˆ . Analogamente, considerando a transversal ←→

AC, podemos concluir que ACBˆ ≡EACˆ . Logo,

ABCˆ +BACˆ +ACBˆ =DABˆ +BACˆ +EACˆ = 180o

Q.E.D.

Vocˆe sabia que... Considerado o primeiro fil´osofo grego, introdutor da Geometria na Gr´ecia. Como rico negociante de azeite da cidade de Mileto, litoral da ´

Asia Menor (atual Turquia), Tales percorreu in´umeras vezes o litoral do Mediterrˆaneo, entre 600 a.C. e 550 a.C., e conheceu as obras de v´arios matem´aticos e astrˆonomos da regi˜ao, principalmente no Egito. Ao aposentar-se, dedicou-se `a Matem´atica e estabeleceu os primeiros postulados b´asicos da Geometria. ´E atribu´ıdo a ele o c´alculo da altura de uma pirˆamide a partir do comprimento de sua sombra, em determinado hor´ario do dia e dependendo da posi¸c˜ao do sol. Na Filosofia, Tales defendeu a existˆencia de uma substˆancia fundamental que d´a origem ao movimento e `a transforma¸c˜ao da vida. Para ele, o princ´ıpio de tudo

´

e a ´agua. “O morto resseca, enquanto os germes s˜ao

´

umidos, e os alimentos cheios de seiva”, ele dizia. At´e Tales, todas as explica¸c˜oes sobre o Universo eram mitol´ogicas. Consulte:

http://www-groups.dcs. st-nd.ac.uk/~history/ Mathematicians/Tales.html

Notas:

1) Como os ˆangulos internos de um triˆangulo equil´atero tˆem todos a mesma medida, segue da Lei Angular de Tales que cada um deles mede 60o_.

2) Se dois triˆangulos ABC e DEF s˜ao tais que BC ≡ EF, ˆB ≡ Eˆ e

ˆ

A≡Dˆ, ent˜ao ABC ≡DEF.

De fato, como ˆA+ ˆB+ ˆC = ˆD+ ˆE+ ˆF = 180◦_{, ent˜ao ˆA ≡D,}ˆ _Bˆ _{≡ E}ˆ

e ˆC ≡Fˆ e estamos no caso A.L.A. de congruˆencia, as vezes ´e referida

Resumo

Nesta aula vocˆe aprendeu...

• O que significa dizer que duas retas s˜ao paralelas ou perpendiculares.

• Que s´o existe uma reta passando por um ponto e perpendicular a uma

reta dada.

• Que s´o existe uma reta passando por um ponto e paralela a uma reta

dada.

• Que ˆangulos alternos internos s˜ao congruentes.

• Que a soma dos ˆangulos internos de um triˆangulo ´e 180o.

Exerc´ıcios

1. (PUC-SP, 1983) Considere a senten¸ca:

“Num plano, se duas retas s˜ao..., ent˜ao toda reta... a uma delas ´e...`a outra”

A alternativa que preenche corretamente as lacunas ´e:

(a) Paralelas, perpendicular, paralela

(b) Perpendiculares, paralela, paralela

(c) Perpendiculares, perpendicular, perpendicular

(d) Paralelas, paralela, perpendicular

(e) Perpendiculares, paralela, perpendicular

2. (UFMG, 1992) Com base nos dados da figura 78, pode-se afirmar que o maior segmento ´e:

A

B

C D

E

55

65 70

70

o

o

o

o

Fig. 78: Exerc´ıcio 2.

(a) AB (b) AE (c)EC (d) BC (e) ED

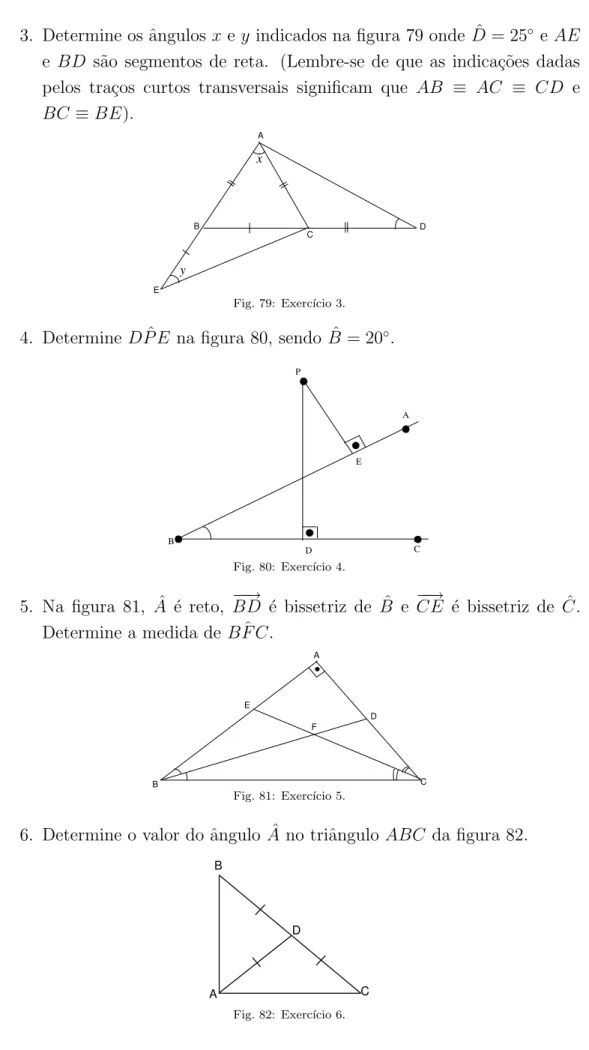
3. Determine os ˆangulosx ey indicados na figura 79 onde ˆD= 25◦ _eAE

e BD s˜ao segmentos de reta. (Lembre-se de que as indica¸c˜oes dadas pelos tra¸cos curtos transversais significam que AB ≡ AC ≡ CD e

BC ≡BE).

A

B

C D

E

x

y

Fig. 79: Exerc´ıcio 3.

4. Determine DP Eˆ na figura 80, sendo ˆB = 20◦_.

A

B

C D

E P

Fig. 80: Exerc´ıcio 4.

5. Na figura 81, ˆA ´e reto, −BD−→ ´e bissetriz de ˆB e −CE−→ ´e bissetriz de ˆC. Determine a medida de BF Cˆ .

C B

A

D E

F

Fig. 81: Exerc´ıcio 5.

6. Determine o valor do ˆangulo ˆA no triˆangulo ABC da figura 82.

C B

A

D

7. Na figura 83 , BACˆ ´e reto e D ´e o ponto m´edio de BC. Mostre que

m(AD) = m(BC)

2 .

C B

A

D

Fig. 83: Exerc´ıcio 7.

8. Determine a medida de AB na figura 84.

C B

A 60

30 10 o

o

Fig. 84: Exerc´ıcio 8.

9. Determine as medidas dos ˆangulos ˆB e ˆC na figura 85.

C B

A

6 3

Fig. 85: Exerc´ıcio 9.

10. Na figura 86, o ˆangulo BACˆ ´e reto e−M N−→´e bissetriz do ˆanguloAM Cˆ . Determine o valor de AN Mˆ .

C B

A

N

M

Fig. 86: Exerc´ıcio 10.

11. Na figura 87, BACˆ ´e reto e M ´e o ponto m´edio de BC. Determine

MANˆ .

C B

A

N M

30o 60o

Fig. 87: Exerc´ıcio 11.

12. Na figura 88, AB ≡AC. Determine o valor de ˆA.

C _B

A

D E

F

Fig. 88: Exerc´ıcio 12.

13. Considere os triˆangulos T1, T2, . . . , T12 da figura 89. Assinale os pares

de triˆangulos congruentes e indique o caso de congruˆencia.

T 3

4 70o

1

1 2 T

60o 2

35 o

3 8

T4 T3

35o

25 o

T5 3

8 35 o

3

6 4

T6 T₇

10

1

2 60o

T8 3

4 70o

T9

6

5 20o

80o

T10 3

4

T11

25o 35 o 80o 20o

5 T12

10

14. Na figura 90 tem-se m(AC) = m(P R) = 4, m(AB) = m(RS) = 3 e

m(BC) = 6.

A

B C

R

S P

3 4

6

3 4

Fig. 90: Exerc´ıcio 14.

Considere os casos:

a) ˆC ≡Pˆ, b) ˆB ≡Sˆ e c) ˆC ≡Rˆ

Em que casos podemos determinar a medida de PS?

15. Seja ABC um triˆangulo is´osceles de base BC. Prove que a mediatriz de BC passa pelo ponto A.

16. (Distˆancia de ponto a reta) Sejam r uma reta e P /∈ r. Se Q ´e o

p´e da perpendicular baixada de P `a reta r, prove que Q ´e o ponto de

r mais pr´oximo de P. A medida do segmento P Q ´e definida como a distˆancia de P ar.

17. Prove que a medida de um ˆangulo externo de um triˆangulo ´e igual `a soma das medidas dos ˆangulos internos a ele n˜ao-adjacentes.

18. (Desafio) Na figura 91, as retas r es s˜ao perpendiculares.

r s A

B

Fig. 91: Exerc´ıcio 18.

Qual ´e o caminho mais curto para ir do pontoAao pontoB tocando-se nas duas retas?

19. Seja ABC um triˆangulo e r uma reta que n˜ao corta ABC. Sejam A′_,

B′ _{e C}′ _{os reflexos de, respectivamente,A,B eC em rela¸c˜ao a r, como}

na figura 92.

r C

B

A

A'

B'

C'

Fig. 92: Exerc´ıcio 19.

Prove que o triˆanguloA′_B′_C′ _{´e congruente a ABC.}

20. (FUVEST-2001) Na figura 93, tem-se que AD ≡ AE, CD ≡ CF e

BA≡BC.

C B

A

D E

F

80o

Fig. 93: Exerc´ıcio 20.

Se o ˆangulo EDFˆ mede 80o_{, ent˜ao o ˆangulo ABC}ˆ _{mede: (a) 20}o

Apˆ

endice: Para saber mais...

Neste Apˆendice vamos apresentar uma prova das proposi¸c˜oes 7 e 8 que enunciamos nesta aula.

Proposi¸c˜ao 7

Dada uma reta r e um ponto P, existe uma ´unica reta s perpendicular a r

passando porP.

Prova:

Temos dois casos a considerar: P ∈ r e P /∈ r. O caso em que P ∈ r

pode ser demonstrado facilmente a partir dos axiomas sobre medi¸c˜ao de ˆangulos (veja a aula 2). No caso em que P /∈ r, tome pontos distintos A

e B em r e trace AP. No outro semiplano determinado por r, trace uma semi-reta −→AC de modo que BACˆ ≡PABˆ (figura 94).

A

C D

E

B P

r

Fig. 94:

Sobre −→AC marque o ponto D tal que AD ≡ AP. Seja E o ponto em

queP Dintersectar. Prove queP AE ≡DAE. Segue da´ı quePEAˆ ≡DEAˆ .

Logo, PEAˆ ´e reto e, portanto, ←P E→´e perpendicular a r.

Est´a provado, assim, que existe uma reta passando por P e perpendi-cular ar. Falta provar que n˜ao existe outra reta com essa propriedade.

Suponha que exista outra reta ←P F→ que seja perpendicular a r (figura 95).

E F

P

r

Fig. 95:

Use o teorema do ˆangulo externo para mostrar que isso ´e um absurdo.

Proposi¸c˜ao 8

Dados uma reta r e um ponto P fora de r, existe uma reta s paralela a r

contendoP.

Prova:

Sejam r uma reta eP /∈r. Seja ←→