P or ta l d a O B M E P

(1)

P

or

ta

l

d

a

O

B

M

E

P

Material Te´

orico - M´

odulo Elementos B´

asicos de Geometria Plana - Parte 1

Retas Cortadas por uma Transversal

Oitavo Ano

(2)

P

or

ta

l

d

a

O

B

M

E

P

1 Retas cortadas por uma

trans-versal

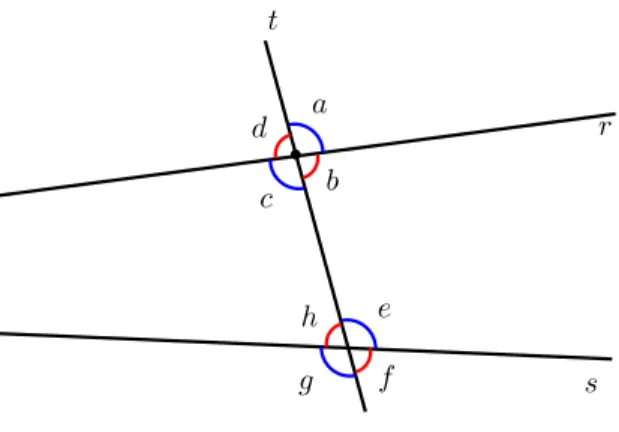
Sejam r e s duas retas situadas em um mesmo plano, ambas concorrentes com uma reta t, como mostrado na Figura??.

g h c d a

b

e

f

b

s t

r

Figura 1: retas cortadas por uma transversal.

A reta t é uma retatransversal às retas r es. A in-terse¸cão de t com r determina os ângulos a, b, c e d da figura, ao passo que a interse¸cão de t comsdetermina os ângulos e,f, g eh. Alguns pares formados por esses oito ângulos recebem denomina¸cões especiais, como veremos a seguir.

Os paresa,g ed,f são chamadosalternos externos, enquanto os pares b, h e c, e são denominados alternos internos. Os paresa, f ed,g são chamadoscolaterais externos, e os paresb, eec, hsão denominados colate-rais internos.

Destacamos, ainda, os paresa, e; b, f;c, g ed, h, cha-madosˆangulos correspondentes.

Observando mais uma vez a Figura??, note que os pares de ângulosa,cee,gsão opostos pelo vértice (OPV), logo,

c =a ee= g. Portanto, se c =e, então a=c =e=g. Da´ı, comodé o suplementar de cehé o suplementar de

g, temos

d= 180◦₋_c_{= 180}◦₋_g₌_h.

Ent˜ao, argumentando como acima, conclu´ımos que

c=e⇒b=d=f =h.

Mais geralmente, argumentando tamb´em como fize-mos acima, tefize-mos a seguinte propriedade importante dos ˆ

angulos determinados por uma transversal:

A congruência dos ângulos de qualquer um dos pares de ângulos alternos (ou correspondentes) acarreta a congruência dos ângulos que formam os demais pa-res. Se um par de ângulos colaterais (externos ou in-ternos) é formado por ângulos suplementares, então todos os pares de ângulos alternos (ou corresponden-tes) são congruentes.

A igualdade das medidas dos pares de ângulos descri-tos acima tem uma implica¸cão important´ıssima sobre a posi¸cão relativa das retasres, a qual isolamos a seguir:

Se, quando cortadas por uma reta transversal, duas retas situadas em um mesmo plano determinam um par de ângulos alternos (ou correspondentes) congru-entes, então essas retas são paralelas.

Nas nota¸c˜oes da Figura ??, como a+b = 180◦_{, temos}

a = e se, e s´o se, b+e = 180◦_{. Isto posto, podemos}

refrasear o critério acima da seguinte forma equivalente, a qual também é, por vezes, bastante útil.

No critério acima, a condi¸cão “determinam um par de ângulos alternos (ou correspondentes) congruen-tes” pode ser substitu´ıda por “determinam um par de ângulos colaterais suplementares”.

Reciprocamente, quando duas retas paralelas são corta-das por uma transversal, obtemos uma importante rela¸cão de congruência entre os pares de ângulos descritos acima, como mostra o resultado enunciado abaixo.

Se duas retas paralelas r es são cortadas por uma reta transversal t, então todos os pares de ângulos alternos (ou correspondentes) são formados por ân-gulos congruentes. Neste caso, os pares de ânân-gulos colaterais são formados por ângulos suplementares.

Vejamos algumas aplica¸c˜oes dos fatos listados acima:

Exemplo 1. Na figura a seguir, temos rk skt. Calcule, em graus, os valores dos ˆangulos xey.

Solu¸cão. Uma vez que os ângulos (alternos internos) que medem 3x−y e 45◦ _s˜_{ao formados pelas interse¸cões das}

retas paralelasrescom a transversalu, temos

3x−y= 45◦_.

Analogamente, observando agora as interse¸cões de s e t, que também são paralelas, com a retau, obtemos

5y−3x

2 = 3x−y

(3)

P

or

ta

l

d

a

O

B

M

E

P

e

f g h

a

b c d

s t

r

Figura 2: retas paralelas cortadas por uma transversal.

s t

r u

45◦

3x−y

5y−3x

2

A primeira equa¸c˜ao implicay= 3x−45◦_{. Substituindo}

esse valor dey na segunda equa¸c˜ao, obtemos:

5(3x−45◦₎₋3x

2 = 3x−(3x−45

◦₎

=⇒15x−225◦₋3x

2 = 3x−3x+ 45

◦

=⇒15x−3x

2 = 45

◦_{+ 225}◦

=⇒ 27x

2 = 270

◦

=⇒x= 20◦_.

Da´ı,

y= 3x−45◦₌_⇒_y_{= 3}_·₂₀◦₋₄₅◦₌_⇒_y_{= 15}◦_.

s

r P

t

b

b b

b

O Q

R

Figura 3: existˆencia de reta paralela a uma reta dada.

Nossa segunda aplica¸cão é muito importante, por forne-cer um método prático para tra¸carmos retas paralelas.

Nos s´eculos IV e III a.C., ao sistematizar a geometria conhecida na antiguidade cl´assica, Euclides de Alexan-dria enunciou seu famosopostulado das paralelas, que afirma que, em um plano:

Dados uma retare um pontoP, comP não perten-cente ar, existe uma única retas, paralela are que contém o pontoP.

Suponha, pois, que temos dados uma retare um ponto

P, comP /∈r. Como a paralela arpassando porP existe e é única, para constru´ı-la é suficiente construirmos uma reta passando porP que seja paralela ar.

Para tanto (veja a Figura ??), come¸camos tran¸cando por P uma reta qualquer t, concorrente com r. Em se-guida, marcamos o ponto O, de interse¸c˜ao das retas r e

t. Consideramos um ponto Q ∈ r, com Q diferente de

O, e constru´ımos o ˆangulo∠QP R, congruente a∠P OQe tal que os pontos R eQ estejam situados em semiplanos distintos, dos determinados pela retat.

A retas=←→RP ´e paralela ar, pois∠QP Re∠P OQs˜ao ˆ

angulos alternos internos congruentes.

Exemplo 2. Na figura a seguir, sabendo que rks, calcule a medida, em graus, do ˆangulo x.

Solu¸cão. Come¸camos tra¸cando pelos pontos B eC, res-pectivamente, retasteu, paralelas à retar(e, consequen-temente, paralelas também à retas– veja a figura a seguir). Em seguida, marcamos os pontosE∈r,F ∈s,G∈t e

H ∈u, tamb´em conforme mostrado na figura acima. Como

t k r e os ˆangulos ∠EAB e ∠ABG s˜ao alternos internos, temosEABb =ABGb = 70◦_{. Por outro lado,}

(4)

P

or

ta

l

d

a

O

B

M

E

P

s r b b b b A D C B 70◦ 110◦ 65◦ x s r b b A D C B 70◦ 70◦ 40◦ x b b 25◦ 40◦ u t b b G H E F b b

de onde obtemosGBCb = 40◦_.

Agora, uma vez que as retas t e u são paralelas e os ângulos ∠GBC e∠BCH são alternos internos, repetindo o argumento acima obtemos 40◦ ₌ _G_BCb ₌_B_CHb _{. Mas,}

como

65◦₌_B_CDb ₌_B_CHb ₊_H_CDb _{= 40}◦₊_H_CD,b

conclu´ımos queHCDb = 25◦_.

Agora, notando que as retasseusão paralelas e que os ângulos∠HCDe∠CDF são alternos internos, temos

x=CDFb =HCDb = 25◦_.

No exemplo anterior, observe que

EABb +BCDb = 70◦_{+ 65}◦_{= 135}◦

e

ABCb +CDFb = 110◦_{+ 25}◦_{= 135}◦_.

Repetindo o argumento utilizado, obtemos, mais geral-mente, o seguinte fato, ao qual nos referiremos como o teorema dos bicos:

Na Figura??, serks, ent˜ao

a1+a2+a3=b1+b2+b3.

s r a 1 b1 a2 a3 b2 b3

Figura 4: o teorema dos bicos.

Observe que, no exemplo ??, havia dois ângulos com vértice à esquerda e dois com vértice à direira. Por outro lado, na Figura ??, há três ângulos de cada lado. Entre-tanto, note que o argumento de tra¸car retas paralelas pelos vértices de tais ângulos nos permite concluir que a soma das medidas dos ângulos com vértices à direita é igual à soma das medidas dos ângulos com vértices à esquerda, independentemente da quantidade de tais ângulos.

O pr´oximo exemplo ilustra uma aplica¸c˜ao simples do teorema dos bicos.

Exemplo 3. Na figura abaixo, sabendo quer ess˜ao retas paralelas, calcule o valor do ˆangulox.

s r 20◦ 33◦ 30◦ 41◦ 2x

Solu¸c˜ao. Pelo teorema dos bicos, temos:

(5)

P

or

ta

l

d

a

O

B

M

E

P

Logo,

2x= 91◦₋₃₃◦_{= 58}◦₌_⇒_x_{= 29}◦_.

Dicas para o Professor

Recomendamos que sejam utilizadas duas sessões de 50min para discutir este material. Ressalte que é suficiente que apenas um par de ângulos alternos (ou corresponden-tes) seja formado por ângulos congruentes (ou, ainda. que um par de ângulos colaterais seja formado por ângulos su-plementares) para que se dê o mesmo com todos os outros pares. As referências contêm mais material relacionado aos tópicos reunidos aqui.

Sugest˜

oes de Leitura Complementar

1. A. Caminha. T´opicos de Matem´atica Elementar, Vo-lume2: Geometria Euclidiana Plana. Rio de Janeiro, SBM, 2013.