WILSON ROBERTO RODRIGUES
NÚMEROS RACIONAIS: UM ESTUDO DAS CONCEPÇÕES DE
ALUNOS APÓS O ESTUDO FORMAL
MESTRADO EM EDUCAÇÃO MATEMÁTICA
PUC/SP
SÃO PAULO
WILSON ROBERTO RODRIGUES
NÚMEROS RACIONAIS: UM ESTUDO DAS CONCEPÇÕES DE
ALUNOS APÓS O ESTUDO FORMAL
PUC/SP
SÃO PAULO
2005
Autorizo, exclusivamente para fins acadêmicos ou científicos, a reprodução total ou parcial desta dissertação por processos de fotocopiadoras ou eletrônicos.
DEDICATÓRIA
AGRADECIMENTOS
À sensação de satisfação, de entusiasmo e de dever cumprido, que necessariamente se faz presente no momento em que se conclui um trabalho como este, junta-se, com a mesma intensidade, a de gratidão para com todas as pessoas que dele fizeram parte e que possibilitaram sua concretização com orientações, amizade, compreensão e incentivo nos momentos difíceis.
À Professora Dra Tânia Maria Mendonça de Campos, pela orientação segura, pelas idéias sempre oportunas e enriquecedoras e, sobretudo, pelo privilégio de um convívio afável, propiciado pelas muitas horas de leitura e discussão do trabalho, e pela sua larga experiência de pesquisadora que me proporcionou momentos de rico aprendizado.
À Professora Dra Sandra Maria Pinto Magina, que partilha com a Profa Tânia a coordenação do Grupo de Pesquisa, pelo entusiasmo contagiante transmitido aos membros do grupo e por suas valiosas sugestões, seja individualmente, seja nas discussões dos seminários do grupo, que certamente em muito enriqueceram este trabalho.
À Professora Dra Otília Therezinha W. Paques, pela amizade e consideração que sempre me dedicou, pelas oportunidades que me proporcionou, pela motivação na busca deste mestrado e pela colaboração na leitura e julgamento do trabalho na Prova de Qualificação.
contribuíram para o enriquecimento do conteúdo deste trabalho e que me sugeriram caminhos para os trabalhos de análise que sucederam a Prova de Qualificação.
Aos colegas Alécio, Angélica, Aparecido, Conceição, Leonel, Raquel e Vera, pela oportunidade de discussões acaloradas e enriquecedoras, pelas pacientes leituras de trechos do trabalho, pelo auxílio nas análises, pela aplicação das questões a seus alunos, enfim, pelo privilégio de poder desenvolver o trabalho num autêntico grupo de pesquisa.
Aos colegas, professores da Escola Preparatória de Cadetes do Exército: Samuel, pelo apoio e trocas de experiências ao longo de todo o mestrado; Márcia e Maria da Graça, pelo auxílio na redação em inglês; e Wallace Fauth, pela meticulosa revisão do texto.
RESUMO
Este trabalho tem por objetivo identificar aspectos do conceito de fração, relativos aos significados parte-todo e quociente, que permanecem não apropriados por alunos em fase de escolarização posterior ao ensino formal desses números. Para isso, busca-se a resposta para a seguinte questão de pesquisa: “Que aspectos do conceito de fração nos significados parte-todo e quociente permanecem sem ser apropriados por alunos de oitava série do Ensino Fundamental, terceira série do Ensino Médio e Ensino Superior na área de exatas?”, a qual remete a uma segunda questão: “Que ligações existem entre essas dificuldades e as deficiências, já apontadas por outras pesquisas, da prática pedagógica,?”.
Três idéias nortearam a busca dos fundamentos teóricos: a gênese do número racional, focando-se as idéias de Caraça (1952); os princípios da psicologia cognitivista, fundamentados nas idéias de Vygotsky e Vergnaud; bem como as idéias de alguns educadores matemáticos, que propõem modelos específicos para o estudo dos números racionais, com destaque para Kieren, Behr, Nunes, Mack e Esolano e Gairín.
Foi elaborado um instrumento composto de 48 questões envolvendo o conceito de fração nos significados parte-todo e quociente, em três níveis de dificuldade, aplicado a 13 alunos de oitava série, 31 alunos do terceiro ano do Ensino Médio e 29 alunos do Ensino Superior, na área de exatas.
Os resultados obtidos foram considerados sob os pontos de vista quantitativo e qualitativo, constatando-se que, mesmo nesses níveis de escolaridade, os alunos ainda apresentam dificuldades significativas sob três pontos de vista: da compreensão do papel da unidade nos problemas envolvendo frações; das peculiaridades das situações envolvendo grandezas discretas; e de aspectos mais abstratos da construção dos números racionais, como a inclusão dos inteiros e a explicitação de soluções em termos de operações com frações.
Por fim, procurou-se associar essas dificuldades a aspectos da prática pedagógica levantados por outros pesquisadores, a fim de levantar hipóteses para suas possíveis causas.
ABSTRACT
This work is aimed at identifying the fraction concept aspects related to the part-whole and quotient meanings, which remain not learned by students during the learning period that follows the formal teaching of these numbers. For this task, we sought to answer the following research question: “Which aspects of the fraction concept in the part-whole and quotient meanings remain not learned by eighth grade students of elementary education, third grade high school students and higher education students in the exact sciences area?”. This question leads us to a second one: “What connections are there between these difficulties and the teaching practice deficiencies already mentioned in other researches?”
Three great ideas have guided the search for theoretical bases: the genesis of the rational number, focusing on the ideas of Caraça (1952), the principles of cognitivist psychology, based on Vygotsky's and Vergnaud's ideas, and the ideas of some mathematical educators who propose specific models for rational numbers, with an emphasis on Kieren, Behr, Nunes, Mack and Esolano and Gairín.
An instrument was developed containing 48 questions involving the fraction concept in the part-whole and quotient meanings, in three levels of difficulty. It was taken by 13 eighth graders, 31 high shool students and 29 higher education students in the exact sciences area.
The results obtained were considered under the quantitative and qualitative points of view, and it could be observed that, even in these learning levels, students still have considerable difficulty regarding the role of the unit in problems involving discrete situations and more abstract aspects of building rational numbers, like the insertion of integers and the clearing of solutions in terms of operations with fractions.
At last, we sought to associate these difficulties to aspects of the teaching practice listed by other researchers, in an attempt to raise hypotheses for possible causes.
ÍNDICE
INTRODUÇÃO E QUESTÃO DE PESQUISA ... 10
CAPÍTULO I - FUNDAMENTOS TEÓRICOS... 18
1.1 Caraça: A construção do Conjunto dos Números Racionais ... 19
1.2 Vygotsky: Conceitos Científicos e Cotidianos ... 22
1.3 Vergnaud: A Teoria dos Campos Conceituais ... 23
CAPÍTULO II - REVISÃO BIBLIOGRÁFICA ... 31
2.1 Kieren: Os Subconstrutos do Número Racional ... 32
2.2 Nunes e Bryant: Uma Classificação Baseada em Vergnaud ... 39
2.3 Behr: Considerações Sobre o Conceito de Número Racional ... 44
2.4 Nancy Mack: O Conhecimento Intuitivo... 46
2.5 Escolano e Gairín: Uma Crítica ao Modelo Parte-Todo ... 52
2.6 Silva: Proposta de Mudanças de Paradigma... 58
2.7 Bezerra: Construindo o Conceito por Situações Significativas ... 61
2.8 Santos: Um Diagnóstico das Concepções dos Professores... 62
CAPÍTULO III – METODOLOGIA ... 65
3.1 Fundamentos Metodológicos ... 65
3.2 Descrição do Experimento ... 66
3.2.1 Montagem do Instrumento de Pesquisa... 66
3.2.2 Universo de Estudo... 71
3.2.3 Estudos Preliminares... 72
CAPÍTULO IV - DESCRIÇÃO E ANÁLISE DO INSTRUMENTO DE
PESQUISA ... 74
CAPÍTULO V - ANÁLISE QUANTITATIVA DOS RESULTADOS ... 146
CAPÍTULO VI – UMA ANÁLISE QUALITATIVA DOS RESULTADOS ... 179
6.1 – A fração Imprópria no Significado Parte-todo e o Papel da Unidade... 180
6.2 – A Cardinalidade... 189
6.2 – Quociente e Grandezas Discretas... 194
6.4 – A Capacidade de Formalizar... 199
CAPÍTULO VII – CONCLUSÃO... 208
7.1 – Considerações Iniciais... 208
7.2 – Síntese dos Resultados Obtidos... 210
7.3 – Respondendo à Questão de Pesquisa... 217
REFERÊNCIAS BIBLIOGRÁFICAS ... 224
ANEXOS... 229
Anexo I – Fração Imprópria no Significado Parte-todo – Tabulação das Respostas... 230
INTRODUÇÃO
A aquisição do conhecimento matemático escolar, como modernamente é
concebida, pressupõe que o aluno desenvolva sua capacidade de estabelecer
relações entre conceitos correlatos, construindo uma teia de saberes
relacionados, que possibilite agregar novos conhecimentos ao seu repertório –
embasando-se em etapas anteriores – e, assim, construir um conjunto de
conceitos que, interligados uns aos outros, constituir-se-ão em seu conhecimento
matemático.
Os livros didáticos procuram estabelecer seqüências que direcionem essas
correlações, com base nos próprios critérios de verdade da Matemática e na
transposição didática1 necessária para que o conhecimento científico seja
acessível ao aluno, em cada uma das fases do estudo. É da própria natureza da
Matemática esse entrelaçamento de conceitos, e as rupturas nesse processo são
sempre traumáticas para o prosseguimento do trabalho de construir o
conhecimento matemático.
Diversos pesquisadores têm apontado, nesse processo, pontos críticos,
que são fontes de dificuldades para o ensino da matemática escolar; e alguns
1
desses pontos são particularmente sensíveis, como a introdução dos números
racionais, a partir dos naturais ou a introdução do conhecimento algébrico.
Como professor de Matemática no Ensino Médio, tenho constatado o
quanto essas deficiências dificultam o aprendizado, daí a motivação para
pesquisar as concepções de número racional dos alunos que já passaram pela
fase de estudo formal2 desses números, tentando obter um melhor conhecimento
dessas concepções, levantar pontos críticos e proporcionar subsídios para que
novos trabalhos apresentem propostas de intervenções para minimizá-los.
Assim, a pesquisa deverá ser pautada na busca de atingir o seguinte
objetivo:
Identificar aspectos do conceito de número racional cuja construção não se tem revelado eficaz no período da educação básica, quando são trabalhados em sala de aula, e que permanecem sem ser apropriados pelos alunos por longo tempo, durante o processo de escolarização.
O trabalho focará a forma fracionária do número racional positivo, ou seja,
números da forma p/q, com p e q naturais e q≠0. Estes números aqui receberão
simplesmente a denominação de fração.
Esta pesquisa faz parte de um trabalho mais amplo que se desenvolve na
PUC-SP, cuja abrangência é o ensino e a aprendizagem de frações, e procura
investigar as concepções a respeito desse objeto matemático, tanto de alunos
quanto de professores, em todas as etapas da escolarização. Esse conjunto de
2
pesquisas integra um programa de cooperação entre a Oxford University, a
Oxford Brookes University e o Centro das Ciências Exatas e Tecnologia da PUC –
SP.
No Brasil, o conceito de fração tem seu ensino iniciado, formalmente, a
partir do segundo ciclo do Ensino Fundamental, (entre 3ª e 4ª séries),
estendendo-se pelo menos até o final do terceiro ciclo (5ª e 6ª séries). Pesquisas
recentes (Kieren, 1988; Mack, 1990; Campos e Cols, 1995; e Nunes, 1997), têm
evidenciado dificuldades em relação a esse conceito, seja do ponto de vista de
seu ensino, seja de sua aprendizagem.
Alguns aspectos levantados nas pesquisas citadas merecerão especial
destaque neste trabalho, como as conclusões de Campos e Cols, citadas por
Nunes (1997), em que as pesquisadoras demonstram que, quando os alunos são
incentivados apenas a empregar procedimentos de dupla contagem para
representar uma fração, podem até resolver problemas de frações, sem, contudo
entender o significado desse novo tipo de número.
Nunes (ibid) chama a atenção para o fato de que as crianças tomam
posturas diferentes em problemas com frações, quando eles envolvem situações
cotidianas ou quando envolvem situações de avaliação escolar, sugerindo que há
uma dificuldade em relacionar os problemas contextuais aos algoritmos, que são
aprendidos para operar com as frações.
A pesquisadora ainda destaca o fato de que também pode ocorrer o
contrário: crianças que dominam os algoritmos e operam corretamente com
frações podem não ter a compreensão perfeita do que é o número racional em
todas as suas nuances. Nunes (2003) propõe uma classificação de situações em
que propor uma teoria sobre quais são os efeitos do raciocínio das crianças sobre
frações. Para a autora, os problemas envolvendo frações abrangem as idéias de
relações parte-todo, quociente, medida, operador multiplicativo e número. Esses
significados serão detalhados nos capítulos subseqüentes.
Kieren (1988), destaca que os números racionais não podem ser
considerados simplesmente como uma extensão dos naturais, e aponta algumas
de suas peculiaridades, com ênfase para a complexidade que envolve a idéia de
unidade nesse conjunto numérico. Kieren (ibid) também apresenta algumas
pesquisas que retratam o comportamento de crianças diante de situações em que
são solicitadas a manipular o referencial para representar uma grandeza através
de uma fração, identificando aí um ponto crítico na construção do conceito. O
autor também entende que a compreensão plena do número racional só será
conseguida se esses números forem estudados segundo as diversas maneiras
em que aparecem nos problemas, optando pela palavra “subconstrutos”, em vez
de significados, para definir esses tipos de situação.
Em comum com Nunes, a classificação de Kieren apresenta os
subconstrutos quociente, medida e operador, mas difere por não considerar o
significado parte-todo e por incluir o subconstruto razão.
As pesquisas comentadas acima, associadas ao fato de que os alunos
costumam apresentar dificuldades no emprego da fração mesmo após o período
de estudo formal desse conteúdo, proporcionaram a motivação para investigar até
que ponto os alunos de nível de escolaridade mais elevado dominam o conceito
de número racional em suas diversas peculiaridades, tanto em situações
A partir desses pressupostos, neste trabalho pretende-se investigar as
concepções do número racional, em sua representação fracionária e nos
significados parte-todo e quociente, por alunos que já concluíram o estudo formal
das frações. A pesquisa foi estruturada levando em conta a idéia de construção
do conceito de Vygotsky, a Teoria dos Campos Conceituais de Vergnaud e as
idéias de Kieren e Nunes a respeito dos números racionais.
A palavra “concepção”, do ponto de vista da Didática, é entendida por
Balacheff como uma quádrupla, identificada por C=(P, R, L, ∑) em que
• P é um conjunto de problemas sobre o qual C opera;
• R é um conjunto de operadores;
• L é um sistema de representação, que permite exprimir os elementos de P
e R
• ∑ é uma estrutura de controle, que assegura a não contradição de C.
Segundo esse ponto de vista, pode-se dizer que um problema p,
pertencente ao conjunto P, será considerado resolvido se existir um operador r,
do conjunto R e uma estrutura s, do conjunto ∑ tal que s(r(p)) seja verdadeira.
Para Balacheff, portanto, um operador sempre transforma um problema em
novo problema e a condição para que um problema p pertença a P é que exista
uma seqüência de transformações em R que o conduza a um problema resolvido
segundo o critério de ∑. (Balacheff, 1994, p.225).
Não será objeto do presente trabalho explicitar os componentes da
concepção, conforme proposto por Balacheff. Portanto, o termo concepção será
aqui entendido, de maneira menos formal, como o ato de criar mentalmente, de
formar idéias, especialmente abstrações, que contribuirão para a formação do
representações simbólicas assumidas por esse sujeito, tais como expressão oral
ou escrita, buscando retratar, por meio dessas expressões, o estado em que se
encontra o conceito para o sujeito.
A idéia é aplicar a sujeitos de escolaridade mais elevada as questões
propostas por Campos e Cols, Mack e Kieren, além das questões que couberem
dos trabalhos em Moutinho(2005) e Merlini(2005), juntamente com outras
elaboradas pelo pesquisador em níveis diferentes de dificuldade, que pretendem
fornecer elementos para detectar pontos críticos nas concepções e principais
dificuldades apresentadas pelos sujeitos de pesquisa.
A escolha de apenas dois significados como objeto de pesquisa deveu-se
à impossibilidade de abranger todos os significados a partir da metodologia
adotada, considerando a extensão do trabalho. A opção por parte-todo e
quociente levou em conta que esses significados estão, no entendimento deste pesquisador, mais associados às fases iniciais da construção do conceito de
número racional, sendo, portanto, mais apropriados para a identificação dos
pontos críticos desse processo.
O trabalho parte da hipótese de que o ensino formal de frações não tem
sido capaz de fornecer aos alunos elementos para que esse conceito seja
plenamente desenvolvido, mesmo em estágios avançados da escolarização. Por
isso pretende responder à seguinte questão de pesquisa:
Que aspectos do conceito de fração nos significados parte-todo
e quociente permanecem sem ser apropriados por alunos de oitava
série do Ensino Fundamental, terceira série do Ensino Médio e Ensino
Essa questão conduz, de maneira natural, a uma outra:
Que ligações existem entre essas dificuldades e as deficiências
da prática pedagógica, já apontadas por outras pesquisas?
Para tentar responder a essas questões este trabalho foi estruturado em
capítulos, cujos resumos são descritos a seguir.
Nestas palavras iniciais foram apresentadas algumas considerações sobre
os números racionais e as dificuldades relativas à aquisição desse conceito, que
nos conduziram a formular a presente questão de pesquisa.
Os capítulos 1 e 2 procuram fundamentar a pesquisa em termos teóricos,
partindo da gênese número racional, conforme proposto por Caraça (1952), das
idéias sobre a construção do conceito, segundo as visões de Vygotsky e
Vergnaud, e das considerações específicas sobre as frações de Kieren (1981,
1988 e 1993), Nunes (1997 e 2003), Behr (1983), Mack (1990 e 1995), e
Escolano e Gairín (2005) e das observações de Silva (1997), Bezerra (2002) e
Santos (2005) sobre universos próximos aos do interesse desta pesquisa.
O capítulo 3 apresenta a metodologia empregada, a seleção do público
alvo e os critérios utilizados para a elaboração do instrumento de pesquisa, sua
testagem e aplicação.
O Capítulo 4 apresenta uma descrição e uma análise do instrumento de
pesquisa, procurando detalhar os objetivos esperados com cada item, as
respostas esperadas e o grau de dificuldade.
O Capítulo 5 apresenta o resultado das tabulações das respostas
levantamento de pontos críticos que fornecerão subsídios para uma análise
qualitativa.
Os Capítulos 6 e 7 apresentam, respectivamente, a análise qualitativa do
resultado da pesquisa e as conclusões e considerações finais obtidas através
dessa análise.
Por fim, são apresentadas as referências bibliográficas. Os itens que
constituíram o instrumento de pesquisa, bem como algumas das tabelas da
CAPÍTULO I
FUNDAMENTOS TEÓRICOS
O presente capítulo procura buscar subsídios para fornecer uma base teórica ao objeto da pesquisa: a avaliação do desempenho dos alunos acerca dos números racionais em diferentes etapas da escolarização, principalmente nas mais avançadas. Três grandes idéias nortearam a busca dos fundamentos teóricos: a gênese do número racional, enquanto conceito fundamental da Matemática; os princípios da psicologia cognitivista, que procura construir modelos para compreender a construção do conceito; e as idéias de alguns educadores matemáticos, que, a partir dessas teorias, propõem modelos específicos para o estudo dos números racionais.
Com relação à origem primeira dos números racionais e sua inserção no conhecimento matemático, serão tomadas como referência as idéias de Caraça (1952), que descrevem o surgimento do campo dos números racionais a partir das necessidades humanas e de princípios gerais em que se fundamenta a construção da Matemática.
escola, se a construção do conceito for entendida como um processo dinâmico que se completa e se sofistica ao longo da vida do indivíduo.
Com relação aos aspectos peculiares à aprendizagem do número racional, diversos autores têm proposto bases teóricas para esse estudo, com destaque para Kieren(1981, 1988, 1993) e Nunes e Bryant(1997, 2003). O primeiro propõe que os números racionais sejam compreendidos segundo quatro subconstrutos, e que em seu estudo sejam considerados tanto elementos intuitivos quanto formais; e Nunes e Bryant propõem uma classificação do número racional em significados, que será tomada como base nesta pesquisa. Os tópicos seguintes pretendem detalhar cada uma dessas considerações.
1.1 - CARAÇA: A CONSTRUÇÃO DO CONJUNTO DOS NÚMEROS RACIONAIS
Um bom ponto de partida para se pensar na construção dos números racionais encontra-se em Caraça (1952). Nessa obra, o autor procura apresentar os números racionais como a resposta do homem à necessidade de comparar grandezas quando a habilidade de contar, que ele já dominava, não foi suficiente para responder à questão de quantas vezes uma grandeza era maior que a outra.
Segundo o texto citado, esse problema começou a ser resolvido a partir da idéia de se estabelecer um padrão para comparar grandezas de mesma espécie e se denominar medida da grandeza à resposta da questão “quantas vezes essa grandeza é maior que o padrão, tomado como unidade de comparação?”.
escolha da unidade, a comparação com a unidade e a expressão do resultado dessa comparação por um número.
O problema de expressar a medida de uma grandeza em relação a outra teria solução imediata, dada pelo quociente das duas medidas, sempre que fosse possível efetuar a divisão entre os números inteiros que as representavam. Um impasse viria a surgir, porém, quando essa divisão não era possível. A busca da solução para esse problema, culminou, ao fim de um longo processo, na simples negação dessa impossibilidade, e a divisão indicada, antes considerada impossível, passou a ser vista como a representação de um novo tipo de número, que expressa o resultado da divisão, agora considerado como possível, apesar de não poder ser expresso por um número inteiro.
Dois princípios básicos que orientam a evolução de toda a Matemática estão presentes na construção do conjunto dos números racionais: o princípio da extensão, segundo o qual, na construção de um novo conhecimento, este deve
manter válido e englobar o conhecimento já existente; e o princípio da economia,
segundo o qual as operações usadas para resolver problemas na situação antiga devem ser as mesmas operações usadas para resolver problemas análogos na nova situação. Assim, os casos de medição que tinham como resultado um número inteiro devem ser considerados casos particulares de medição nesse novo conjunto numérico, que será denominado conjunto dos números racionais. Isso significa que todo número inteiro deve ser também um número racional. A partir desses dois princípios, os números racionais foram definidos, com suas propriedades e operações.
trazido ao longo do tempo dificuldades à sua aprendizagem e por isso esses números têm sido objeto de inúmeros estudos.
Dos aspetos citados por Caraça(1952) na construção do número racional, um deles merecerá atenção especial nesta pesquisa: a escolha da unidade. As situações-problema que compõem o instrumento de pesquisa, baseadas nos significados parte-todo e quociente da classificação de Nunes(2003), impõem
quase sempre uma reflexão sobre o referencial a ser tomado para a apresentação das respostas e essa reflexão parece não ser enfatizada no estudo escolar dos números racionais.
Outras peculiaridades do número racional são o fato de que uma mesma quantidade pode ser representada por muitos significantes diferentes e que um mesmo número pode representar quantidades diferentes, em função da unidade tomada. Este segundo problema aparece principalmente quando se propõem situações contextuais, agregando dificuldades à compreensão do significado da relação de ordem entre os números racionais.
A idéia de estudar essas concepções em sujeitos com um nível de escolaridade mais elevado, que já ultrapassaram a fase do estudo formal das frações, é tentar buscar elementos para se verificar quais dessas peculiaridades têm resistido mais ao tempo e exigem um maior amadurecimento do sujeito para sua plena compreensão ou uma maior atenção dos educadores para elaboração de atividades de ensino que permitam que esses aspectos sejam enfatizados no estudo desses números, durante o período escolar.
conhecimentos e esquemas de que o indivíduo dispõe e pelas interações a que o sujeito está submetido.
1.2 - VYGOTSKY: CONCEITOS CIENTÍFICOS E COTIDIANOS
Do ponto de vista cognitivo, os pressupostos acima descritos têm sua origem primeira na idéia de construção do conceito proposta por Vygotsky, que faz considerações sobre a interação entre a vida escolar e as experiências cotidianas do sujeito no processo de construção do conceito.
Vygotsky divide os conceitos em dois tipos: cotidianos ou espontâneos e científicos. Os conceitos cotidianos são desenvolvidos no decorrer da atividade
prática do indivíduo e de suas interações sociais imediatas, enquanto os conceitos científicos são adquiridos por meio do ensino, como parte de um sistema organizado de conhecimentos particularmente relevantes nas sociedades letradas, em que os alunos são submetidos a processos deliberados de instrução escolar. (Oliveira, 1992 p.31)
Tanto os conceitos cotidianos como os científicos, embora estes últimos sejam transmitidos em situações formais, passam por um processo de desenvolvimento, isto é, não são aprendidos em sua forma definitiva. As
concreto, num processo em que tanto os conceitos científicos quanto os cotidianos caminham em direção a um ponto comum.
Pode-se mesmo dizer que os conceitos cotidianos têm um desenvolvimento ascendente (rumo aos científicos) e que os conceitos científicos têm um desenvolvimento descendente (em direção aos cotidianos).
A proposta de explorar o conceito de fração, que é um conceito científico na medida em que é apresentado de maneira formal nos currículos escolares, a partir de situações contextuais, procura detectar indícios da ocorrência dessa convergência e de possíveis pontos críticos, de modo a fornecer elementos para a formulação de propostas de atividades intervencionistas.
1.3 - VERGNAUD: A TEORIA DOS CAMPOS CONCEITUAIS
A idéia da construção do conceito como um processo dinâmico no desenvolvimento das estruturas cognitivas do indivíduo, que se completa ao longo do tempo, proposta por Vygotsky, ganha novos elementos com as idéias de Vergnaud, que se constituirão no referencial teórico mais significativo da presente pesquisa.
conhecimentos anteriores são mobilizados pelo sujeito para construí-lo; e 3) de que recursos dispõe esse sujeito para representá-lo.
Vergnaud parte da idéia de que o conhecimento está organizado em grandes agrupamentos informais de problemas, situações, conceitos, relações, estruturas, conteúdos e operações de pensamento, conectados uns aos outros e provavelmente entrelaçados no processo de aquisição (Vergnaud 1982), a que ele denomina campos conceituais e entende a construção do conhecimento como
um processo progressivo, contínuo e demorado de domínio desses campos. Apesar de existir uma interdependência entre os campos conceituais, sendo muitas vezes necessário lançar mão de um deles para a compreensão de um outro, Vergnaud considera importante distingui-los, sempre que eles puderem ser consistentemente descritos, constituindo-se em unidades de estudo. Eles permitem dar sentido aos problemas de aquisição e às observações feitas em relação à conceitualização. (Moreira 2004)
Dois campos conceituais destacam-se nos estudos de Vergnaud: o das estruturas aditivas, que é o conjunto de situações cujo domínio requer uma adição, uma subtração ou o conjunto de tais operações, e o das estruturas multiplicativas, em que está focada a presente pesquisa, que se compõe das situações cujo domínio requer multiplicações, divisões ou combinações dessas operações. Os conceitos de número racional, razão, fração, função linear, espaço vetorial, dentre outros, encontram-se no campo conceitual das estruturas multiplicativas.
Vergnaud entende um conceito como sendo uma terna de conjuntos, freqüentemente representada por
C=(S, I, R) em que
• S é o conjunto de situações que dão sentido ao conceito;
• I é o conjunto de invariantes que o sujeito pode mobilizar para analisar e
dominar as situações do primeiro conjunto;
• R é o conjunto dos recursos de que o sujeito dispõe para representar os
invariantes e, conseqüentemente, as situações e os procedimentos para lidar com elas, seja na forma de linguagem, de gráficos, etc (1997, p.6; 1988, p.1; 1993 p.8)
Em termos psicológicos, Vergnaud considera S a realidade, a que denomina referente, e o par (I, R) a representação, que pode ser considerada
como dois aspectos do pensamento interagindo: o significado (I), que
corresponde à representação do conceito interna ao sujeito e o significante (R),
que representa o conceito de forma mediada pela linguagem.
As considerações acima apontam para dois aspectos importantes a serem observados quando se considera o estudo do desenvolvimento de um conceito à luz da Teoria dos Campos Conceituais: 1) o de que os três elementos que
A interdependência entre os elementos da terna que constitui o conceito foi representada esquematicamente por Santos (2005) pela figura a seguir, que toma componentes do conceito de fração para exemplificar a interação entre situação, invariantes operatórios e representações:
Cada um desses elementos será objeto de uma discussão mais aprofundada nos parágrafos seguintes.
• Equivalência
• Ordenação
• Objetos,
propriedades e relações
• a/ b, com a,b
naturais e b≠≠≠≠0
• Pictórica
• Porcentagem
• Decimal
I (INVARIANTES)
(invariantes do conceito)
R (SIGNIFICANTE) (representações simbólicas) S (REFERENTE)
Problemas envolvendo o conceito de fração na linguagem escrita ou oral contemplando os significados:
• Número
• Parte-todo
• Medida
• Operador Multiplicativo
O termo situação tem, para Vergnaud, o sentido de tarefa a ser executada
pelo aluno, diferentemente do sentido que Brousseau (1998) atribui à expressão
situação didática.
O conceito de situação não tem aqui o sentido de uma situação didática, mas o de
tarefa. A idéia é que toda situação complexa pode ser analisada como uma
combinação de tarefas, cuja natureza e dificuldades específicas devem ser bem
conhecidas. A dificuldade de uma tarefa não é nem a soma nem o produto da
dificuldade das diferentes subtarefas. É claro, contudo, que o fracasso em uma
subtarefa provoca o fracasso global. (Vergnaud 1993 p.9)
Vergnaud não descarta a importância da forma dos enunciados e do número de elementos em jogo dentro de uma situação, mas entende essa importância como secundária e ressalta que a teoria dos campos conceituais privilegia os modelos que atribuem papel essencial aos conceitos matemáticos em si mesmos. (1993 p.9)
Essas idéias tiveram um papel fundamental na forma como este instrumento de pesquisa foi elaborado. Aos sujeitos sempre foram apresentadas situações contextuais, procurando dar sentido à idéia de fração, que deve ser mobilizada a partir desses contextos apresentados.
A situação, entretanto, apesar de permitir que um conceito adquira sentido, não pode ser confundida com o próprio sentido do conceito. O sentido, para Vergnaud, “é uma relação do sujeito com as situações e os significantes” (1993 p.18). O sentido está nos esquemas evocados pelo sujeito individual por uma situação ou mesmo por um significante.
eles constituem o grande legado das idéias de Piaget à Teoria dos Campos Conceituais.
A título de exemplificação, consideremos uma situação envolvendo o conceito de fração, com a seguinte proposta: um menino reparte um chocolate em 5 partes iguais, toma duas para si, dá três para seu irmão. Represente por frações esses pedaços de chocolate e indique qual das frações é maior.
Embora existam muitas maneiras de se chegar ao resultado, não deixa de haver uma organização invariante do pensamento para resolver a questão, que passa pela repartição do chocolate, valendo-se da idéia de conservação do tamanho das partes, do agrupamento dessas partes, da escolha do referencial a ser adotado, da explicitação dessas partes como uma fração e da comparação das frações, usando como suporte o fato de que a fração maior está associada ao maior pedaço de chocolate.
Uma análise mais atenta da situação descrita permite observar que o esquema recorre: a significantes (palavras, números e esquemas gráficos eventualmente utilizados pelo sujeito), a construções conceituais, (como o próprio conceito de fração), à idéia de conservação de áreas, (caso se utilize do suporte gráfico), à relação de ordem entre os números naturais. Esses conceitos e conhecimentos são geralmente implícitos e, muitas vezes, não podem ser explicitados pelo sujeito, principalmente nas fases iniciais da escolaridade, porém eles orientam o desenvolvimento da ação do sujeito, e por isso são chamados de
conhecimentos-em-ação.
construção dos esquemas durante o processo de conceitualização, mas em geral não é capaz de explicitá-los. Quando explicitados, esses conhecimentos constituem o saber científico, mas Vergnaud(1990a) insiste que “os conhecimentos explícitos são apenas a parte visível de um Iceberg, que não seria nada sem a parte invisível , constituída pelos conhecimentos-em-ação”.
A Teoria dos Campos Conceituais distingue duas grandes categorias de conhecimentos-em-ação: os conceitos em ação e os teoremas em ação. Os
primeiros são os objetos, os predicados ou as categorias de pensamento tidas como pertinentes pelo sujeito na construção dos esquemas que conduzem ao conceito, enquanto os segundos são as proposições tidas como verdadeiras sobre o real que o sujeito utiliza. Vergnaud denomina, de maneira mais genérica, os teoremas e os conceitos em ação de invariantes operatórios e atribui a eles o
papel de serem os responsáveis pela construção do significado do conceito, que é o núcleo do processo de conceitualização.
As representações, entendidas como o significante do conceito, correspondem, na teoria dos campos conceituais, ao conjunto de representações lingüísticas, gráficas ou gestuais, que podem ser usadas para representar os invariantes, as situações e os procedimentos (1997 p. 6). Embora Vergnaud atribua grande importância às representações simbólicas na construção do conceito, sobretudo na explicitação dos conhecimentos em ação, que transformam o conhecimento implícito no saber científico, ele reconhece que um objeto em geral não pode ser representado mentalmente através de símbolos. Mesmo sendo grande a importância dos símbolos no pensamento, o conhecimento não é, em essência, simbólico. O reconhecimento de invariantes operatórios, bem como a construção de objetos e predicados de nível mais alto são aspectos mais essenciais do conhecimento. (Vergnaud 1998 p.177 )
CAPÍTULO II
REVISÃO BIBLIOGRÁFICA
As considerações aqui apresentadas pretendem trazer idéias de autores
que elaboraram pesquisas específicas sobre os números racionais no âmbito do
campo de estudos da Educação Matemática. Destacam-se entre estes autores,
Kieren (1981, 1988 e 1993), que foi o primeiro a propor que os números racionais
devem ser estudados segundo subconstrutos; Nunes(1997 e 2003), que
apresenta uma classificação dos significados do número racional, adotada como
referência nesta pesquisa; Behr et al (1983), que apresentam considerações
sobre a importância do estudo dos números racionais; Mack (1990, 1993 e 1995),
que procura estabelecer relações entre o conhecimento intuitivo do aluno e a
construção formal do conhecimento e Escolano e Gairín (2005), que apresentam
modelos de introdução do conceito de número racional a partir do significado
“medida”.
Também foram destacados trabalhos de Silva (1997), Bezerra (2001) e
Santos (2005) por se reportarem universos próximos aos do interesse desta
pesquisa e enfocarem aspectos que poderão se constituir em subsídios para a
2.1 - KIEREN: OS SUBCONSTRUTOS DO NÚMERO RACIONAL
Thomas Kieren foi um dos primeiros pesquisadores a chamar a atenção da
comunidade científica para a complexidade do conceito de fração e propôs, em
artigo de 1976, que a compreensão desse conceito deve levar em conta sete
interpretações que mantêm relações entre si e que devem ser consideradas segundo as estruturas matemáticas, as estruturas cognitivas e as estruturas
instrucionais envolvidas (Martinez, 1992).
As interpretações propostas por Kieren são assim enumeradas:
• frações que podem ser somadas, subtraídas, comparadas, etc;
• frações decimais, como uma extensão do sistema decimal de numeração;
• classes de equivalência de frações;
• números da forma p/q com p e q inteiros e q≠0, isto é, razões de inteiros;
• operadores multiplicativos;
• elementos de um conjunto quociente infinito
• medidas ou pontos na reta numérica.
Em artigos posteriores, Kieren (1981, 1988 e 1993) mudou a classificação
apresentada originalmente e substituiu o termo interpretações do número racional
pelo termo subconstrutos. Kieren tomou como base o trabalho do filósofo Henry
Margenau, que denomina construtos teóricos a objetos mentais que podem ser
construídos a partir de idéias mais simples que se complementam. (Kieren, 1988
Margenau entende o processo de construção do conceito como o
estabelecimento de relações entre as percepções e compreensões de um objeto
mental (os construtos), que tem como implicações o surgimento de atos físicos ou
mentais envolvidos nessa gênese. (Kieren, 1993, p.57).
A proposta de Kieren, de substituir o termo interpretações por subconstrutos,
é comentada por Martinez (1992). Segundo esse autor (p. 36), Kieren entendeu a
noção de número racional como um construto teórico, que pode se constituir a
partir de noções mais simples, chamadas subconstrutos. Essa postura diante do
problema permite isolar com mais facilidade as noções essenciais para a
construção do conceito. Nas interpretações, conforme Kieren havia proposto
anteriormente, essas noções essenciais estavam muito interligadas e não podiam
ser isoladas e identificadas com facilidade.
Assim, para Kieren o conceito de número racional pode ser construído a
partir da consideração dos quatro seguintes subconstrutos (Kieren, 1988 p.166):
• quocientes;
• operadores;
• medidas;
• razões.
O autor não considera o subconstruto parte-todo como outros
pesquisadores, entendendo que as idéias que o constituem já estão presentes
nos subconstrutos quociente, operador e medida (Kieren, 1993, p.57).
Esse enfoque surgiu aparentemente da necessidade de isolar as noções
que são mecanismos para a construção do conceito, como as de partição e
equivalência, daquelas que são específicas do construto. Martinez (1992) ainda
interpretações, como proposto anteriormente, pois naquele caso essas idéias
aparecem muito inter-relacionadas.
A mudança proposta por Kieren também sugere um desvio de foco do
pesquisador, pois as interpretações, como apresentadas no primeiro artigo,
pareciam privilegiar as estruturas matemáticas envolvidas no conceito, enquanto
a idéia de subconstrutos parece atribuir mais ênfase às estruturas cognitivas.
Aprofundando suas considerações sobre a construção do conceito de
número racional, Kieren propõe um modelo teórico para essa construção que
procura apresentar as possíveis interconexões entre as idéias que formam o
conceito, partindo das situações presentes no conhecimento intuitivo do sujeito
até o estágio da formalização. O modelo é apresentado sob a forma de um mapa
em que se identificam quatro níveis pelos quais deve passar a construção do
conceito de numero racional (Kieren, 1993 p. 64-65):
• o nível dos conhecimentos intuitivos
• os subconstrutos,
• um terceiro nível, obtido a partir dos subconstrutos em direção a um
pensamento multiplicativo mais formal
• o conhecimento estruturado nos números racionais dentro de um conjunto
quociente.
Na busca de explicações para essa evolução do processo de construção
do conceito, Kieren (1993) considera que a partição e a obtenção da fração com
numerador unitário da forma b 1
tem, para a criança, o mesmo papel de um
axioma na construção do número racional como elemento de um conjunto
a idéia de que o número racional deve ser visto primeiro como um conhecimento
humano e só posteriormente como uma construção lógica formal.
Outro aspecto interessante do número racional é o fato de ele ter, ao
mesmo tempo, um caráter de quociente e um caráter de razão. Quando visto
como quociente ele responde à questão “quanto?” e quando visto como razão ele
estabelece uma propriedade relacional entre a parte e o todo. Essa
complementaridade fica bem expressa nas respostas de crianças de 7 a 9 anos à
situação abaixo, em que lhes foi solicitado repartir as pizzas já divididas ao meio
entre as pessoas dos grupos A e B:
Fonte: Kieren, 1993 p.54
Em resposta à pergunta “quem ganhará mais pizza, as pessoas do grupo
A ou do grupo B?”, numa pesquisa, com crianças entre 7 e 9 anos, predominaram
respostas do tipo B receberá meia pizza por pessoa, e A receberá meia pizza por
pessoa, e mais um pedaço, entendendo que a metade que sobra deva ser
dividida em 7 partes e repartida entre os membros do grupo. Esse tipo de
resposta denota uma complementaridade entre as idéias de quociente (dividir o
pedaço que sobrou em 7 partes) e razão (estabelecer a propriedade relacional
Outro fator que demonstra que os números racionais não podem ser
considerados como uma simples extensão dos números inteiros é o fato de que
nos racionais a adição e a multiplicação são operações independentes. Enquanto
nos inteiros a multiplicação conduz sempre a um número maior, nos racionais, a
multiplicação conduz ironicamente a uma sucessão de divisões, por exemplo:
multiplicar 2 1
por 3 1
significa dividir o 2 1
em 3 partes e essa operação não pode
ser reduzida a uma adição, como se fazia com os números inteiros.
Kieren também aponta o duplo papel desempenhado pelo número 1 no
campo racional como uma consideração importante a ser levada em conta na
compreensão da construção desse conceito, pois o número 1 serve tanto de
unidade divisível que forma a base de comparação quanto a base conceitual para
a formação dos inversos multiplicativos, além, é claro, de ser o elemento neutro
da multiplicação. As crianças precisam passar a ver o número 1 segundo essa
visão mais complexa. O autor ilustra esse fato com a descrição de um
experimento de Mack (1990) que será objeto de estudo mais detalhado na seção
2.4 deste trabalho. Este aspecto levantado por Kieren será objeto de especial
atenção nesta pesquisa e deverá fornecer subsídios importantes para a análise a
que este trabalho se propõe.
Uma conseqüência imediata da aplicação das idéias de Kieren é a de que
os currículos montados segundo essa orientação propiciariam uma melhor
interligação dos vários campos da Matemática. Se considerados apenas como
uma extensão dos números inteiros, ou um simples algoritmo numa relação
parte-todo estática, os números racionais permaneceriam apenas no domínio
matemático dos números. Se considerados, porém, segundo a visão dos
a criança tenha contato com outros domínios da matemática desde as séries
iniciais.
São exemplos disso o fato de que partições sucessivas podem conduzir
crianças muito jovens à idéia de grandezas infinitesimais, como no relato de um
estudante de 11 anos que respondeu que sua fração favorita era 2 1
, pois “me
fascina a possibilidade de dividir em dois e obter pedaços tão pequenos quanto
eu queira, indefinidamente”. O subconstruto medida oferece também uma ligação
importante entre a geometria, o espaço e o estudo dos números racionais.
(Kieren 1988 p.59)
O subconstruto operador proporciona uma aproximação dos números
racionais com a álgebra e com a noção de função composta, em termos não
formais. O subconstruto razão aponta na direção dos importantes conceitos de
proporção e de probabilidade.
Com relação às possibilidades de atividades significativas para as
crianças, Kieren descreve um trabalho de Streefland(1984) em que uma classe de
equivalência de frações foi construída de maneira significativa. A proposta era
imaginar que 12 crianças sentaram-se à mesa e pediram 8 pizzas que seriam
divididas igualmente. Em seguida imaginar que as crianças poderiam se dividir
em duas ou três mesas mantendo a equivalência na divisão. Depois de muito
trabalho as crianças desenvolveram sua própria notação para resolver esse
problema, através de um diagrama em forma de árvore. Uma nova questão de
como dividir 36 pizzas para 24 crianças foi resolvida facilmente pela árvore abaixo
sem que a distinção entre fração própria ou imprópria fosse significativa,
Fonte: Kieren, 1993 p.54
Kieren verificou também, por experiências, que essa consideração dos
números racionais é significativa ao notar que os sujeitos mobilizam diferentes
significados do número racional para resolver diferentes problemas: em um
problema de concentração de leite com chocolate, os estudantes mobilizam
predominantemente a idéia de razão, enquanto que num problema de repartição
de uma pizza, a idéia predominante é a de quociente.
A partir dessas idéias, o autor afirma que o estudo dos números racionais
por intermédio dos subconstrutos fornece suporte para uma análise semântica,
psicológica e pedagógica do ensino do número racional, bem como um suporte
empírico para seu estudo. Sugere também que a idéia intuitiva de partição tem
um papel importante na construção do conhecimento do número racional por
parte do sujeito e propõe, como ponto de partida para uma posterior construção
formal, a abordagem dos números racionais como um conhecimento humano, a
2.2 – NUNES E BRYANT: UMA CLASSIFICAÇÃO BASEADA EM VERGNAUD
Assim como Kieren, Nunes e Bryant(1997) também diferenciam dois
aspectos no ensino dos números racionais. Para os autores, há claramente uma
lacuna entre a compreensão das crianças em tarefas experimentais sobre divisão
e números racionais e entre as tarefas resolvidas no contexto de avaliações
educacionais.
Nunes e Bryant (ibid) afirmam que, com as frações, as aparências podem
enganar e alguns alunos podem passar pela escola sem dominar diversos
aspectos cruciais do conceito de fração, mesmo usando termos fracionais certos,
falando coerentemente sobre frações e resolvendo alguns problemas. Segundo
os autores,
... quando as crianças resolvem tarefas experimentais sobre divisão e números racionais, elas se engajam em raciocinar sobre as situações.
Em contraste, quando elas resolvem tarefas matemáticas em avaliações
educacionais, elas vêem a situação como um momento no qual elas
precisam pensar em que operações fazer com os números, como usar o
que lhes foi ensinado na escola; concentrando-se nas manipulações de
símbolos, os alunos poderiam desempenhar em um nível mais baixo do
que teriam desempenhado se tivessem se preocupado mais com a
situação-problema. Portanto, é possível que os mesmos alunos que se
engajam em tarefas de raciocínio semelhantes às descritas
anteriormente, nos quais eles podem focalizar bem a situação-problema,
desempenhem bastante diferentemente de quando eles estão
resolvendo problemas em avaliações educacionais escritas: seu
desempenho mostra uma lacuna entre o que eles entendem e o que eles
podem fazer com símbolos depois destes terem sido aprendidos de uma
Os tópicos selecionados para compor a presente pesquisa levaram em
conta essas considerações e procuraram se afastar, dentro do possível, das
situações típicas de sala de aula concentrando-se em problemas que levem o
aluno a racionar sobre situações e resolvê-las quase sempre sem a necessidade
de recorrer aos algoritmos. O trabalho tenta diagnosticar até que ponto esses
aspectos da compreensão do conceito de fração perduram no processo de
escolarização.
As propostas de Nunes e Bryant apóiam-se em várias pesquisas, das
quais serão destacadas, neste trabalho, as de Campos e Cols (1995) e
Mack(1993), sendo esta última objeto de tópico à parte.
Campos e Cols., em trabalho citado por Nunes e Bryant(1997),
demonstraram que a impressão de crianças raciocinando sobre frações poderia
ser falsa, sobretudo quando são submetidas a um método de ensino que se limita
e estimular os alunos a resolver os problemas utilizando-se de procedimentos de
dupla contagem, sem entender o significado deste novo tipo de número.
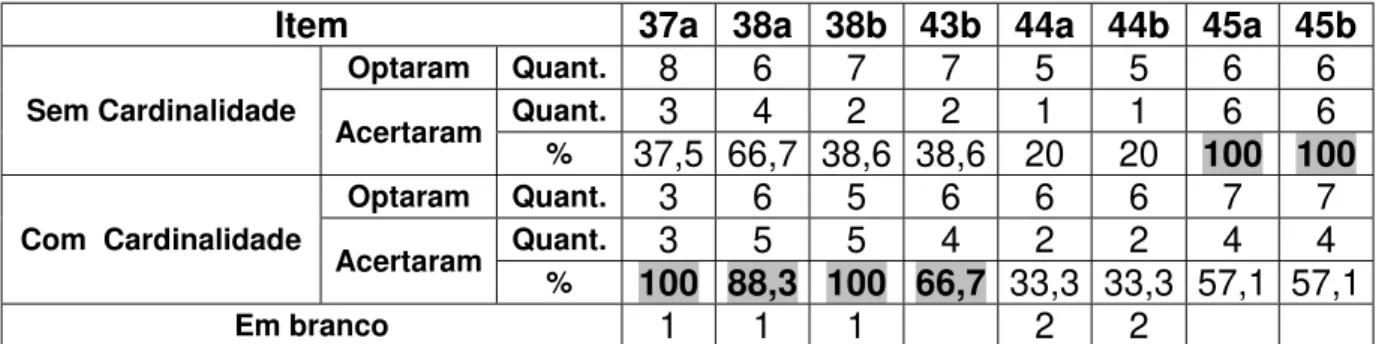
Para demonstrar sua hipótese, Campos e Cols. (1995) apresentaram os
desenhos indicados abaixo a crianças de idade aproximada de 12 anos ou mais
que haviam aprendido o procedimento de dupla contagem e pediram-lhes para
nomear as frações apresentadas em cada uma das figuras:
Item tipo 1
Item tipo 2
Este trabalho tem particular interesse nas questões do terceiro tipo, em
que o procedimento de dupla contagem simples não é suficiente, uma vez que o
todo não estava dividido explicitamente em partes iguais e o número de partes
tinha que ser descoberto pelos alunos através de uma análise das relações
parte-todo, que, no caso, implica a capacidade de perceber a conservação da área
como invariante para o estabelecimento da relação parte-todo. Na pesquisa de
Campos e Cols, foi muito significativa a queda na quantidade de acertos no item
tipo 3 em relação aos itens tipo 1 e 2.
Pretende-se, nesta pesquisa, explorar tópicos com variações do item do tipo
3, em termos de quantidades discretas ou contínuas, ou questões envolvendo
ícones ou apenas texto, tentando diagnosticar até que ponto essas observações
da pesquisadora ainda são significativas em alunos de estágios mais avançados
de escolaridade.
A hipótese de dissociação entre o desempenho dos alunos em situações
contextuais e o desempenho frente às situações de avaliação escolar foi bastante
explorada por Mack (1993), também citada por Nunes e Bryant e discutida com
mais profundidade na seção 2.4.
A análise dos resultados da pesquisa de Mack reforça as afirmações de
Nunes e Bryant e aponta para a idéia de que, embora os problemas da vida
cotidiana não pareçam causar dificuldades, muitos dos problemas apresentados
simbolicamente não são resolvidos pelos estudantes, que apresentam algoritmos
falhos e comparações inadequadas.
A verificação da persistência dessas dissociações em sujeitos de maior
contém em seu instrumento de pesquisa algumas situações semelhantes à
proposta por Mack.
A idéia das conexões entre situações contextuais e situações simbólicas,
investigada por Mack(1995), está intimamente ligada ao conceito de invariante, de
Vergnaud. A proposta de Nunes é partir da concepção mais simples de fração e
enriquecer essa definição perguntando qual é o invariante central desse conceito,
quais as situações em que ele é usado e quais os diferentes tipos de
representação.
Duas questões são significativas no caso do conceito de número racional:
“como as crianças vêm a entender essas classes de equivalência – 1/3, 2/6,
3/9... – e como essas classes podem ser ordenadas – 1/3 >1/4 >1/5....”
Com base nas idéias de Vergnaud, Nunes e Bryant (2003) propõem uma
classificação de situações em que as frações são usadas, entendendo que propor
essa classificação é o mesmo que propor uma teoria sobre quais são os efeitos
do raciocínio das crianças sobre frações. Os parágrafos a seguir pretendem
apresentar essa classificação, reiterando que, nesta pesquisa, merecerão
destaque os significados parte-todo e quociente.
A Fração como uma relação parte-todo – A idéia presente nesse significado
é a da partição de um todo em n partes iguais, em que cada parte pode ser
representada como
n
1
. Assim, assumiremos como o significado parte-todo, um
dado todo dividido em partes iguais em situações estáticas, nas quais a utilização de um procedimento de dupla contagem é suficiente para se chegar
a uma representação correta. Por exemplo, se um todo foi dividido em cinco
partes e duas foram pintadas, os alunos podem aprender a representação
pintadas, abaixo do traço escreve-se o número total de partes. Exemplo: uma
barra de chocolate foi dividida em quatro partes iguais. João comeu três
dessas partes. Que fração representa o que João comeu?
A fração como quociente, indicando uma divisão e seu resultado – Este
significado está presente em situações em que está envolvida a idéia de
divisão – por exemplo, uma pizza a ser repartida igualmente entre 5 crianças.
Nas situações de quocientes temos duas variáveis (por exemplo, número de
pizzas e número de crianças), sendo que uma corresponde ao numerador e a
outra ao denominador – no caso,1/5. A fração, nesse caso, corresponde à
divisão (1 dividido por 5) e também ao resultado da divisão (cada criança
recebe1/5). Exemplo: Três chocolates devem ser divididos para 4 crianças.
Que fração de chocolate cada criança irá receber?
A fração como uma medida – Algumas medidas envolvem fração por se
referirem a quantidades intensivas, nas quais a quantidade é medida pela
relação entre duas variáveis. Por exemplo, a probabilidade de um evento é
medida pelo quociente número de casos favoráveis dividido pelo número de
casos possíveis. Portanto, a probabilidade de um evento varia de 0 a 1, e a
maioria dos valores com os quais trabalhamos são fracionários. Exemplo:
Fizemos uma rifa na escola. Foram impressos 150 bilhetes. Minha avó
comprou 20 bilhetes. Qual a sua chance de ganhar o prêmio?
A fração como número – Frações, como os inteiros, são números que não
precisam necessariamente referir-se a quantidades específicas. Existem duas
formas de representação fracionária: ordinária e decimal. Um exemplo de
um referente específico é apresentado como a seguir: represente o número
2 1
na forma decimal.
A fração como um operador multiplicativo – Como o número inteiro, as
frações podem ser vistas como o valor escalar aplicado a uma quantidade. No
caso do inteiro, por exemplo, podemos dizer 2 balas; no caso da fração,
poderíamos dizer 3/4 de um conjunto de balas. A idéia implícita nesses
exemplos é que o número é um multiplicador da quantidade indicada.
Exemplo: Dei 3/4 das balas de um pacote de 40 balas para meus irmãos.
Quantas balas dei a eles?
2.3 – BEHR: CONSIDERAÇÕES SOBRE O CONCEITO DE NÚMERO RACIONAL
Dentre os inúmeros autores que se dedicaram ao estudo dos números
racionais nas décadas de 1980 e 1990, merecem destaque Merlyn Behr e cols
(1983), cujo trabalho abrange tanto considerações gerais sobre a importância do
estudo dos números racionais quanto considerações específicas sobre o ensino
desses números.
Os autores reconhecem que os números racionais se constituem numa das
mais importantes idéias matemáticas desenvolvidas no contexto escolar e que,
por ocorrerem em grande parte no período da transição do pensamento concreto
para o pensamento operacional formal, constituem-se também em um contexto
Entendem que a importância de se estudar o número racional no Ensino
Fundamental deve ser justificada segundo uma perspectiva prática, uma
perspectiva matemática e uma perspectiva psicológica.
Do ponto de vista prático, o estudo do conceito de número racional
aperfeiçoa a habilidade de dividir, o que permite entender e manipular melhor os
problemas do mundo real. Na perspectiva psicológica, os números racionais
proporcionam um rico campo, dentro do qual as crianças podem desenvolver e
expandir suas estruturas mentais para um desenvolvimento intelectual contínuo.
Do ponto de vista matemático, a compreensão do número racional fornece a base
sobre a qual serão construídas, mais tarde, as operações algébricas elementares.
Martinez (1992) reforça as idéias de Behr e cols. ao argumentar que reduzir
o estudo das frações aos números decimais, como uma extensão natural do
sistema decimal de numeração, provocaria uma perda de experiências
pré-algébricas importantes na formação matemática dos alunos (p. 34)
Os autores criticam a ênfase curricular nos procedimentos e algoritmos e
argumentam que, mesmo com essa ênfase, o resultados dos alunos em testes de
desempenho não costumam ser satisfatórios. Entendem que a provável causa
dessas dificuldades seja a priorização, no ensino, dos procedimentos em
detrimento de um cuidadoso desenvolvimento dos aspectos ligados à
compreensão do conceito.
Ao procederem a uma análise matemática e curricular dos conceitos de
número racional, retomam idéias de diversos autores e, a exemplo de Kieren,
identificam diferentes maneiras de interpretar o número racional, que também
denominam subconstrutos: um decimal, uma razão, um quociente indicado, um
contínuas ou discretas. Enfatizam, do mesmo modo que Kieren (1988), que a
compreensão completa do número racional requer não somente um entendimento
de cada um desses subconstrutos, mas também como eles se inter-relacionam.
Em suas considerações sobre os subconstrutos parte-todo e medida,
afirmam que as regiões geométricas, as séries de objetos e a reta numérica são
os modelos mais comumente usados para representar a fração no ambiente
escolar. Reportam-se a Piaget ao afirmar que os processos mentais usados pelas
crianças para trabalharem com quantidades contínuas é diferente daqueles
trabalhados com grandezas discretas e apontam as dificuldades apresentadas em
relação à unidade, citando que, em experiências com a reta numérica, os alunos
têm dificuldade em identificar a unidade.
2.4 - NANCY MACK: O CONHECIMENTO INTUITIVO3
O trabalho de Nancy Mack deverá fornecer importantes subsídios para a
presente pesquisa, na medida em que a autora se preocupa em analisar a
influência do conhecimento intuitivo dos alunos na construção significativa dos
procedimentos formais referentes às frações (Mack, 1990), bem como a tendência
dos alunos em fazer generalizações sobre as frações baseadas nas estruturas
simbólicas disponíveis para números inteiros e, reciprocamente, fazer
generalizações sobre números inteiros com base nas estruturas simbólicas das
frações, (Mack, 1995).
Os dois trabalhos referem-se a atividades intervencionistas aplicadas a
pequenos grupos de alunos, em atividades individualizadas, com minuciosa
descrição das respostas e procedimentos apresentados pelos sujeitos. Embora
apresentem grandes diferenças do ponto de vista metodológico em relação à
presente pesquisa, têm em comum a busca da representação simbólica da fração
a partir de situações contextuais que mobilizam, de início, conhecimentos
intuitivos. Algumas das questões tratadas pela pesquisadora são reproduzidas no
presente instrumento de pesquisa, e as observações do desempenho entre
crianças de quinta e sexta séries4 deverão ser úteis na análise de possíveis
respostas às mesmas questões por estudantes de nível de escolaridade mais
elevado, objeto da presente pesquisa.
Mack (1990) aponta dois pontos importantes a serem levados em conta na
construção do conhecimento matemático dos estudantes: a obtenção de
situações que promovam a efetiva participação dos alunos e o relacionamento
entre o seu conhecimento intuitivo e os procedimentos simbólicos.
A autora define “conhecimento intuitivo” como as respostas dadas pelo
estudante a situações extraídas da vida real. Argumenta que esse conhecimento
costuma ser pouco relacionado ao conhecimento dos símbolos matemáticos e cita
Hiebert, que propõe que esses conhecimentos devam servir de base para a
construção do conhecimento formal (Mack 1990 p. 16). Argumenta também que
os estudos recentes sobre frações estão mais focados nas falsas concepções dos
alunos sobre esse objeto matemático e partem do princípio de que os alunos não
têm nenhum conhecimento anterior ao iniciar seu estudo e não costumam
considerar esses conhecimentos intuitivos. Têm surgido evidências, porém, de
que os alunos trazem para a escola um rico histórico de conhecimentos intuitivos
não existem estudos sobre os caminhos que os estudantes podem tomar para, a
partir deles, dar significado aos símbolos e procedimentos formais referentes às
frações.
A autora observa inicialmente que, nos problemas envolvendo partições, os
alunos apresentam uma tendência a separar um todo em partes e a representar
cada uma das partes como um número inteiro, e não como uma fração do todo.
(Mack, 1990 p. 21)
Alguns resultados apresentados mostram que, em geral, os alunos são
capazes de resolver um grande número de problemas apresentados sob a forma
de situações do dia-a-dia e explicitar corretamente suas soluções, porém não
conseguem resolver os mesmos problemas quando apresentados de maneira
simbólica. Essa questão é ilustrada pelas respostas dos alunos à seguinte
proposta de atividade: “se tivermos duas pizzas de mesmo tamanho e dividirmos
a primeira em 6 partes iguais e a segunda em 8 partes iguais, qual pedaço será
maior?”. Os alunos não tiveram dificuldade em responder que o pedaço da
primeira pizza será maior, porém, quando, num outro momento, foi-lhes
perguntado “qual fração é maior, 6 1
ou 8 1
”, mais da metade dos alunos respondeu
8 1
, porque 8 é maior que 6.
Segundo a autora, o fato de que a maioria dos alunos não foi capaz de
responder simbolicamente a uma questão que haviam acabado de responder
quando proposta dentro do contexto de uma ação cotidiana, sugere que a
capacidade de comparar é inicialmente desconectada do significado que os
A questão da identificação da unidade, muito relevante para a presente
pesquisa, também foi tratada por Mack (ibid p.22), que mostrou que os alunos são
capazes de identificar corretamente a unidade a que se refere uma fração quando
trabalhando com situações contextuais, porém têm dificuldades em identificar a
unidade quando trabalham com situações simbólicas. Concluiu que os alunos
tendem, numa situação simbólica ou concreta, a tratar uma coleção de unidades
como se essa coleção fosse sempre a nova unidade. A autora ilustra esse fato
comentando os resultados obtidos da seguinte questão proposta a seus sujeitos
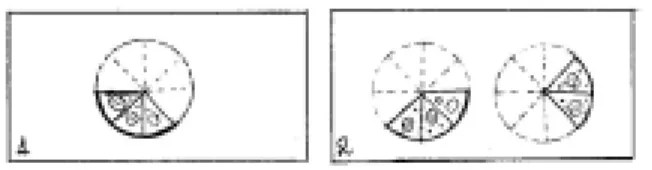
numa situação em que, mostrando a figura abaixo aos alunos pergunta: “quanto
está sombreado?”
A resposta mais comum é 5/8. Diante da afirmação “suponha que estejamos
falando de pizzas”, os alunos tendem a mudar sua resposta para 1 ¼. A autora
transcreve de um de seus protocolos a seguinte afirmação de um sujeito:
“Frações são partes de um todo... Elas são sempre menores que um todo.”
(Mack, 1990 p.22).
Essa questão também é tratada por Escolano e Gairín (2005), que
atribuem a ênfase exagerada no modelo parte-todo no início dos trabalhos
escolares com frações como uma das possíveis causas dessa falsa concepção.
Uma outra questão discutida por Mack (1990) é a influência dos
procedimentos padronizados, muitas vezes incorretos, na tentativa de resolver as
questões simbólicas, que muitas vezes se sobrepõem aos procedimentos
Mack sugere que seja pesquisada a viabilidade de se abordar o estudo das
frações inicialmente a partir da noção de partição, estendendo-se essa concepção
para outros significados antes que os alunos possam relacionar os símbolos
matemáticos ao seu conhecimento intuitivo de fração(p.30).
Segundo a autora, quando esse caminho é seguido, surge nos alunos uma
tendência a construírem algoritmos alternativos, porém corretos, para a solução
dos problemas. Esses algoritmos muitas vezes são mais trabalhosos que os
tradicionais, e os alunos tendem a substituí-los por outros mais práticos na
medida em que amadurecem em seu estudo (p. 25).
A pesquisadora também analisa a influência dos procedimentos formais já
disponíveis pelo aluno, relativos ao número inteiro, na construção dos
procedimentos simbólicos envolvendo frações. Respostas do tipo “um pedaço dos
três em que a pizza foi dividida”, em vez de “um terço da pizza”, sugerem que o
aluno está utilizando suas estruturas relativas a números inteiros para resolver
problemas de frações. A autora argumenta que esses conhecimentos anteriores
influenciam fortemente os significados a serem construídos para as
representações simbólicas da fração (p. 431). Respostas do tipo “ 8 3
significam
três tortas inteiras repartidas em 8 partes cada uma” e “ 8 1
representa uma torta
inteira dividida em 8 partes”, reforçam a afirmação dessa influência.
Uma outra demonstração da predominância da influência das estruturas do
número inteiro na construção das representações simbólicas da fração é
apontada pela autora ao descrever o fato de que, quando os alunos resolvem o
mesmo problema utilizando inicialmente seus conhecimentos intuitivos e depois