Flexion de Una Barra Delgada Empotrada en un
Extremo: Aproximaion para Peque~nas Pendientes
Tarsiio Belendez 1
, CristianNeipp 2
y Augusto Belendez 2
1
Departamentode CieniayTenologade losMateriales
UniversidadMiguelHernandezdeElhe
Avda. delFerroarril,s/n. E-03202,Elhe(Aliante), Espa~na
2
Departamento deFsia,IngenieradeSistemas yTeorade laSe~nal
UniversidaddeAliante,Apartado 99,E-03080Aliante,Espa~na
Reebidoem7dejunho,2002. Aeitoem7desetembro,2002.
EnlosursosdeFsiayMeaniaparaestudiantesuniversitariosdeCieniaseIngeniera,ydentro
del tema dediado a laelastiidad, se estudian los solidos deformables, as omo los fenomenos
de traion, ompresion, izalladura, torsion, exiony pandeo. En el aso de laexionuno de
los ejemplos que suele analizarse esel de una barra delgada empotrada en un extremo sobre la
que atuauna fuerza onentrada vertial enelextremo libre. El estudiosehaepara peque~nos
desplazamientosopeque~naspendientesdelabarra,loquepermiteintegrarfailmentelaeuaion
diferenial de la barra exionada y alular la elastia y la eha o desplazamiento vertial del
extremolibre. Sinembargo,laaproximaionparapeque~naspendientesquesehaeenlabibliografa
esinompatibleonotraonsideraionquesiempresetieneenuentayesquelalongituddelabra
neutradelabarranoambiauandolabarraexiona. Enestetrabajosepresenta,paraalproblema
delaexiondeunabarra delgadaenvoladizo,unaaproximaionparapeque~nosdesplazamientos
opeque~naspendientesdelabarra\menosaproximadadeloomun". Paraelloseintrodueomo
hipotesis laonstania dela longitudde labraneutra delabarra lo quepermiteobtener unas
euaionesmas preisasque las queapareen enlabibliografa. Losresultados obtenidossehan
omparadoonlosexatosasomoonlasmedidasexperimentalesrealizadasenellaboratorioon
unaregla deaeroempotradaenun extremo. Laseuaionesdelaelastia seobtienen siguiendo
untratamientoanalogo aldesarrolladoporFeynmanuandoestudialavigaexionadaensulibro
de Fsia, por loque el desarrollo aqu presentado puede ser seguido sin muhosproblemas por
ualquierestudiantedeFsiaoMeaniadelosprimerosursosuniversitarios.
I Introduion
Las vigas generalmente son uerpos solidos de forma
alargada y seionreta onstante, de gran interes en
ingenierayarquitetura,quenormalmente seutilizan
enposiionhorizontalysiendosulongitudgrande
om-paradaonlasdimensionesdesuseionreta. Las
vi-gaspuedenestarsometidasaargasonentradas,
ar-gas distribuidas, o a pares (momentos onentrados)
que atuen solos oen una ombinaion ualquiera,
si-endolaexionlaprinipaldeformaionquesufren[1℄.
Puededenirseunavigaomounsolidohomogeneo
eisotropoengendradoporunaseiontransversal,que
generalmente admiteunplanodesimetrayuyo
en-tro de gravedad desribe una urva o lnea,
denomi-nadadiretriz,siendoelplanoqueontienealaseion
transversal normal a diha diretriz [2℄. Cuando una
viga exiona debido ala presenia de fuerzas
exterio-res, existen algunas partes de la viga que se aortan
embargo,otraszonassealarganporefetodelmomento
etorquehaequeestensometridasatraion. Pero
hayunalneaenlavigaenlaquelasbrasnose
aor-tan ni se alargan, es deir, que no estan sometidas a
tension. Esta lnea se denomina lnea neutra o bra
neutra(Fig. 1)[2,3℄. Enlabraneutraseenuentrael
entrodegravedaddelaseiontransversal;portanto,
para onoer la loalizaion de diha bra basta on
alularelentrodegravedaddelaseiontransversal
delaviga.
/tQHD
QHXWUD
primerosursosuniversitariosdeFsiayMeaniade
las titulaionesde Ingeniera y Arquitetura einluso
en la asignatura de Meania de Bahillerato son las
estatiamentedeterminadasoisostatias[1-3℄,paralas
que se pueden obtener las reaiones en los apoyos a
partirdelaseuaionesdelaEstatia,esdeir,
imponi-endolasondiionesdequelasumadefuerzasseanula
y lasuma de momentos respetoa un punto tambien
losea. El estudiode laexionde lasvigas isostatias
puede enontrarse en algunos textos de Fsia
Gene-ral [2,4,5℄, Meania (en su parte de Estatia) [1,6℄y
Meania de Materiales [7,8℄. Asimismo, las vigas en
voladizo,esdeir,aquellasqueseenuentran
empotra-dasenunextremoy libresenelotro,han reibido
re-ientementeatenionenrevistasenlasquesepublian
trabajos relaionados onla ense~nanza de la Fsia a
niveluniversitario[9-12℄. Sinembargo,paraelanalisis
quevamosaonsiderarenestetrabajobastaontomar
omopuntodepartidaelestudiodelavigaexionada
parapeque~naspendientesquehaeFeynman[5℄,alser
bastante laro(omo no podaser de otra manera) y
suienteparaomprenderelomportamientodeestos
elementos onstrutivosuandose someten aaiones
externas.
Enelpresentetrabajosevaaanalizarlaexionde
unabarradelgadaenvoladizoenelasopartiularenel
quelosdesplazamientosdelabarrasonpeque~nos. Esto
dalugaraquelaspendientes delaurvaelastiadela
barraseanpeque~nas,loquepermitehaerunaseriede
aproximaionesque dan lugar auna euaion
diferen-iallinealdesegundoordenfailmente integrable. Sin
embargo, en este trabajo se va a omprobar omo es
posibleobtener unos resultados menos aproximadosy
mas aordes on la realidad fsia de la barra
exio-nada que los que suelen presentarse en la bibliografa
[2,5,7,8℄. En partiular, una uestion que siempre se
onsideraalestudiarlaexionde estetipode
elemen-tosesquelasdeformaionesdelabarrasonpeque~naslo
ualimpliaque, aunquelabarrasedesplaerespeto
ala horizontal,su longitud omas estritamente lade
su braneutra,permaneeonstante.
Estaesuna
u-estionmuy importante quenosueletenerse enuenta
en los libros de texto de losprimeros ursos
universi-tariospueseldesarrolloquehaen,inluidoellibrode
Feynman,notieneenuentaquelalongituddelabarra
noambiaydeheholaseuaionesquepresentanson
inompatibles on la onstania de diha longitud ya
que la oordenada horizontal del extremo libre de la
barraonsideranqueesigualalalongituddelabarra.
Sevanaobtenerdistintasaraterstiasdelabarra
delgada empotradaen un extremo: los
desplazamien-tosmaximoshorizontaly vertialdel extremolibrede
labarraenfuniondelafuerzaapliada,ylaurvaque
adoptala barraexionada y quesedenomina elastia
[2-5℄. Tanto los desplazamientos maximos omo la
elastiadependen delmaterial yde lageometrade la
barra[2,3℄.Semostraranalgunosresultadosnumerios
yseompararanonlosresultadosqueseobtienen
hai-endousodelaaproximaionparapeque~naspendientes
quesehaeenlabibliografa,onlosorrespondientes
alasoexato(sinningunaaproximaion),asomoon
losresultadosexperimentalesobtenidosenel
laborato-rioutilizandoomobarradelgadaunaregladeaero.
II Euaion diferenial de la
elastia para peque~nas
pendi-entes de la barra
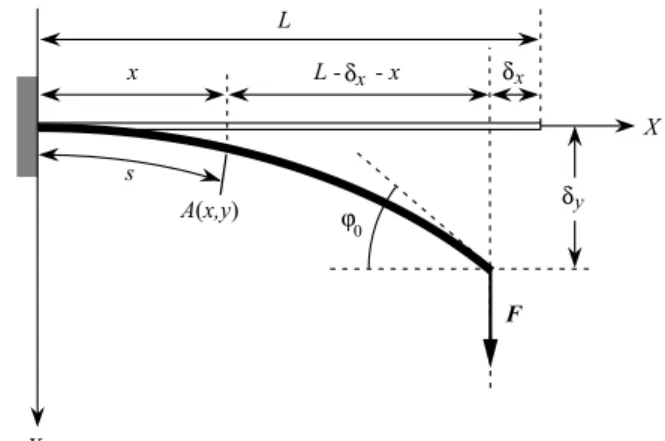
Considerese una barra delgada sometida a exion de
longitudLyseionretangularonstante debaseb y
altura h, empotradaen unextremo y sometida auna
fuerzavertialF enel extremolibre, taly omoseve
en la Fig. 2. Se supone que el material de la barra
eselastiolineal,quesu longitudesmuhomayorque
lasdimensiones laterales de lamisma, quelalongitud
de labarrano ambia(estritamente hablandola
lon-gitud de su lnea neutra [8℄) y que las deformaiones
sonpeque~nas. Bajoestashipotesispodemosutilizarla
relaiondeEuler-BernoullientreelmomentoetorM
de la fuerza apliada y el radio de urvatura de la
barradeformada[5℄:
M= EI
(1)
dondeEeselmodulodeYoungdelmaterial,I esel
mo-mentodeineriadelaseiontransversaldelabarray
eselradiodeurvatura. ElprodutoEI,quedepende
del tipo de material empleadoy de las araterstias
geometriasde la seion de la barra, reibe el
nom-bre de \modulode rigidez a la exion" de la barra o
simplemente\rigidez"[7℄.
δ\
)
/
ϕ
δ[
[
/
δ[
[
$
[\
V
;
<
Figura 2. Barra delgada empotradaen un extremo y on
una fuerza vertial onentrada enel extremolibre.
De-niiondeparametros.
El radio de urvatura de una urvade euaion
y=y(x)puedealularsemediante laeuaion[2,5℄:
1
= d
2
y=dx 2
23=2
En el aso partiular en que el desplazamiento de
los puntos de la barra exionada respeto a los de la
barra sin exionar espeque~no, esdeir, en el aso de
pendientes peque~nas, es posible despreiar el termino
(dy/dx) 2
frente ala unidad enla euaion (2), porlo
queelradiodeurvaturasepuedealularmediantela
expresion:
1
=
d 2
y
dx 2
(3)
lo que permite esribir la euaion diferenial de la
urva elastia para una barra delgada de material
elastio lineal bajo la hipotesis de peque~nos
desplaza-mientos(elastiadepeque~naspendientes)enlaforma:
d 2
y
dx 2
= M
EI
(4)
queesunaeuaiondifereniallinealdesegundoorden.
Hastaaqunohayningunadifereniaaomosetratael
problemaentodosloslibrosdelosursosuniversitarios
de Fsiay Meania[2, 5,8℄. Lamodiaion quese
vaa introduir eneste trabajoestarelaionada onel
alulodel momentoetorM yestabasada enel
he-hodequelabarraesinextensible(subraneutra),lo
queimpliaquelongituddelabarranoambiadebido
alaexion.
Figura3. Fotografadeunabarradelgadaenvoladizo.
Para obtener la euaion de la urva elastia y =
y(x) para peque~nos desplazamientos de la barra hay
que integrar la euaion diferenial (4) y para ello es
neesarioonoerelmomentoetorM. LaFig. 3
mu-estraunafotografadeunabarradelgadadelongitudL
empotradaenunextremosobrelaqueseapliauna
fu-erzavertialonentradaF enelextremolibre. Puesto
que la longitud de la barra deformada es tambien L,
elextremolibredelabarrasufretantoun
desplazami-entovertialÆ
y
omounohorizontalÆ
x
. Normalmente,
ytal y omo aparee en el libro de Feynman [5℄ y en
otrostextos[2,4, 8℄,se suponeque eldesplazamiento
horizontal Æ
x
esnulo, lo que no es ompatible on el
hehodequelalongituddelabarranoambiatrasla
deformaion. Elmomento etorM debidoalaarga
puntualFapliadaenelextremodelabarrarespetoa
laseionsituadaaunadistaniaxdelempotramiento
vienedadoporlaeuaion(Fig. 2):
M(x)=F(L Æ
x
x) (5)
y sustituyendo la euaion (5) en la euaion
diferen-ial (4) de la elastia para peque~nos desplazamientos
(peque~naspendientes),estatomalaforma:
d 2
y
dx 2
= F
EI (L Æ
x
x) (6)
dondeparalabarraenvoladizolasondiionesde
on-tornoson:
y(0)=0 (7)
dy
dx
x=0
=0 (8)
Con ayuda de las euaiones (7) y (8) es posible
integrarfailmentelaeuaion(6),obteniendose:
dy
dx =
F
2EI
2(L Æ
x )x x
2
(9)
y(x)= F
6EI
[3(L Æ
x )x
2
x 3
℄ (10)
Laeuaion(10)permitealulareldesplazamiento
vertialmaximode labarra, Æ
y
,elualsepresenta en
elextremolibredelamisma. Suvalorseobtiene,omo
sededuede laFig. 2, sustituyendox =L - Æ
x en la
euaion(10):
Æ
y =
F
3EI (L Æ
x )
3
(11)
La euaion (9) proporiona el valor de la
pendi-ente de la elastia para ada valor de la oordenada
x,mientrasquelaeuaion(10)eslaeuaion
artesi-anay=y(x) delaelastiadelabarra. Esimportante
se~nalarquelaeuaiondelaelastia(10)esvalida
siem-preyuandoeluadradodelapendiente delaelastia
sea muho menor que la unidad, pues esa ha sido la
hipotesis para obtener la euaion (4), es deir, debe
umplirselaondiion:
dy
2
Comolamaximapendientetienelugarenelextremo
libredelabarra,esdeir,paraelpuntode abisax =
L - Æ
x
,teniendoenuenta laeuaion(9)evaluadaen
esepunto,laondiiondevalidezdelaseuaionespara
peque~naspendientes es:
F 2EI 2 (L Æ x ) 4
<< 1 (13)
Parasabersien unasopratioes onoapliable
laaproximaiondepeque~naspendienteshabraque
ve-riarlaondiion(13). Sinembargo,en oasioneses
posiblequesedesonozaelvalordelmodulodeYoung
delmaterial,E, puesloquesepretendeonelestudio
experimentalquizasseasudeterminaion. Enesteaso
esfailesribirlaeuaion(13)sinqueaparezael
va-lordeEI.ParaellosedespejaEI delaeuaion(11)y
sesustituyeen laeuaion (13), obtieniendosela
on-diiondeapliabilidaddelaseuaionesparapeque~nas
pendientesenfuniondelosdesplazamientoshorizontal
y vertialdel extremo libre, Æ
x yÆ
y
, respetivamente,
losualespuedenmedirse failmenteenellaboratorio.
Delaeuaion(13)seobtiene:
9Æ 2 y 4(L Æ x ) 2
<< 1 (14)
Sin embargo, para evaluar las euaiones (9)-(11)
no solo es neesario onoer el modulo de Young, E,
elmomento deineria,I, ylafuerzaapliada,F,sino
tambienel desplazamiento horizontal,Æ
x
, delextremo
libredelabarra,yesteesunainognitadelproblema,
puesasu vez esfuniondeE,I yF:Esaqudonde se
haeusodelahipotesisdequelabarraesinextensible
y, por tanto, su longitud L no ambia (estritamente
hablando, lalongitud de su bra neutra, aunque si la
barraesdelgadasepuede deirqueambasoiniden).
Paraintroduirestanuevahipotesisbastatener en
u-entalarelaionqueexisteentre elelementodearods
ysusomponentesartesianasdx ydy:
ds= p dx 2 +dy 2 = s 1+ dy dx 2 dx (15)
porloquelalongitudLdelabarrasera:
L= Z L Æ x 0 s 1+ dy dx 2 dx (16)
dondeellmite superior deintegraiontieneenuenta
el heho de que el valor maximo de la oordenada x
de la elastia de la barra no es L, omo se india en
la bibliografa para el asode la aproximaion de
pe-que~nas pendientes, sino L - Æ
x
, omo se ve en la Fig.
2. Sustituyendolaeuaion(9) enlaeuaion(16),se
obtiene: L= Z L Æx 0 s 1+ F 2EI 2 [2(L Æ x )x x 2 ℄ 2 dx (17)
Laeuaion (17)permitealular el valordel
des-plazamiento horizontal del extremo libre de la barra
uandoseonoenlosvaloresdeL,E,I yF. Unavez
obtenidoelvalordeÆ
x
yaesposibledeterminarelresto
deparametrosquearaterizanlabarraexionada,en
partiularÆ
y
ylaeuaionartesianadelaelastia. Si
setomaÆ
x
=0enlaseuaionesanterioresseobtienen
losvaloresdey(x)yÆ
y siguientes: y(x)= F 6EI (3Lx 2 x 3 ) (18) Æ y = FL 3 3EI (19)
quesonlasqueapareenenalbibliografa[5,9-12℄.
III Resultados numerios
Para omparar los resultados que se obtienen on la
aproximaionparapeque~naspendientesqueseha
pre-sentadoeneste trabajoonlaorrespondiente
aproxi-maionque sehae en labibliografa(euaiones (18)
y (19)), as omo onel asoen el que se resuelve la
euaiondiferenial (1)sin onsiderarninguna
aproxi-maionenelradiodeurvatura[12,13℄,esonveniente
denir una serie de parametros adimensionales. Para
elloseintrodueelparametroadimensionaldefuerza:
k= FL
2
EI
(20)
lasoordenadasadimensionalesuyv:
u= x L v= y L (21)
as omo los desplazamientos adimensionales
horizon-tal y vertial del extremo libre de la barra, u
f y v
f ,
respetivamente,denidosmediantelaseuaiones:
u f = Æ x L v f = Æ y L (22)
Haiendousode laseuaiones (20)-(22),las
eua-iones(10),(11)y(17)puedenesribirseenlaforma:
v= k 6 [3(1 u f )u 2 u 3 ℄ (23) v f = k 3 (1 u f ) 3 (24) Z 1 u f 0 r 1+ k 2 4 [2(1 u f )u u 2 ℄ 2
du=1 (25)
Asimismo,laeuaion(13)devalidez dela
aproxi-maionparapeque~naspendientes seesribiraahora:
k 2 (1 u f ) 4
Laeuaion(25)permiteobteneru
f
enfuniondel
parametro adimensional k. Sin embargo, la inognita
u
f
aparee tanto en elintegrandoomo en unode los
lmites deintegraion. Paraobtener el valor de u
f se
proponeseguirunproedimiento de ensayo-errormuy
interesante e instrutivopara los estudiantes. En
pri-mer lugar sedeneuna funion g delavariable u
f de
lasiguienteforma:
g(u
f )=
Z
1 uf
0 r
1+ k
2
4
[2(1 u
f )u u
2
℄ 2
du 1
(27)
on ayuda de estafunion, la euaion(25) puede
es-ribirseomo:
g(u
f
)=0 (28)
Enestemomentosehaeusodelhehodequelos
es-tudiantes universitariossuelenestarfamiliarizadoson
software omo elMathematia, del queexiste ademas
una versionpara estudiantes. Porestarazon, la
inte-graldelaeuaion(27),paraadavalordek,puede
re-solverseutilizandoelomandodeintegraionnumeria
\NIntegrate" del programa Mathematia. La Fig. 4
muestra losresultadosobtenidos parael asok=0.5.
Como puede verse existe una soluion de la euaion
(28) que se determina mediante un proedimiento de
ensayo-errorvariandoelvalordeu
f
hastaqueg(u
f )sea
menorque10 8
,quesetomaomo0aefetos
ompu-taionales.
X
I
X
I
J
Figura4.Funiong(u
f
)parak=0.5.
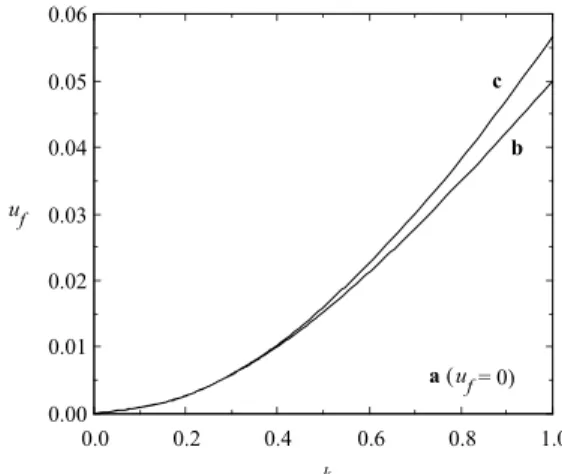
LaFig. 5muestralosresultadosobtenidosdeu
f en
funiondekomparadosonlosexatosaluladossin
haer ningunaaproximaion,resolviendolasintegrales
elptiasqueapareenenesteaso(verApendieI)[12,
13℄. Esimportantese~nalarqueenlaaproximaionque
se hae en todoslos libros universitariosque abordan
el problemadelaexion deunabarra parael asode u
f
= 0, ya que sesuponde que lafuerza F esta
apli-adasiempreen elpunto de abisa x =L. EnlaFig.
6sehanrepresentadoloserroresrelativosquese
ome-ten uandose hae uso de la aproximaionque se ha
onsideradoenestetrabajoylaquesehaeenla
bibli-ografa,respeto alosvalores exatosque seobtienen
uandonosehaeninguna aproximaion[12℄. Parala
aproximaiononsideradaenestetrabajoelerror
rela-tivo esta por debajo del 10% para k < 0:8, mientras
queonlaaproximaionqueapareeentodosloslibros
elerrorrelativoesdel100%.
N
X
I
F
E
D
X
I
Figura5. Valores delos desplazamientoshorizontales
adi-mensionalesdelextremolibredelabarra enfuniondek:
Aproximaionparapeque~naspendientesrealizada enla
bi-bliografa(a),aproximaionrealizadaenestetrabajo(b)y
valoresexatos().
N
D
(UURU
E
(UURUGH
X
I
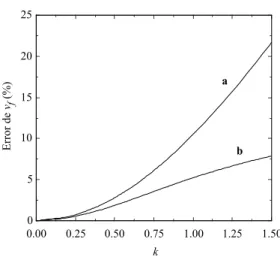
Figura6. Erroresrelativosdelosdesplazamientos
horizon-talesadimensionalesdelextremolibredelabarraenfunion
dek: Aproximaionparapeque~naspendientesrealizada en
labibliografa(a)yaproximaionrealizadaenestetrabajo
(b).
Una vez determinado el valor de u
f
para ada k
esposible alular el desplazamiento vertial
adimen-sional del extremo libre de la barra, v
f
, sin mas que
utilizarlaeuaion(23). LaFig. 7muestralos
utilizandolaeuaion(19)quesemuestraentodoslos
libros y que ahora se esribira en la forma v
f
= k/3.
Enla Fig. 8 se han representadolos erroresrelativos
orrespondondientesaambosasos. Comopuedeverse
delasFigs7y8,laaproximaionparapeque~nas
pendi-entesquesehapresentadoenestetrabajoproporiona
resultadosmasaordesonlarealidadrepresentadapor
lasoluionexataparaunrangodevaloresdekmayor,
pueselerrorrelativoestapor debajodel 10%para las
k onsideradas,mientras queonla aproximaionque
apareeenloslibrosesteerroresmuhomayor. Enla
Fig. 9 se ha representado el uadrado de la derivada
primeradelafunionvevaluadoenelextremolibrede
labarra,esdeir,enelpuntodeabisa u=1{u
f .
N
Y
I
D
F
E
Figura 7. Valores de los desplazamientos vertiales
adi-mensionales delextremolibredelabarraenfuniondek:
Aproximaionparapeque~naspendientesrealizadaenla
bi-bliografa(a),aproximaionrealizadaenestetrabajo(b)y
valoresexatos().
N
D
E
(UURUGH
Y
I
Figura8. Erroresrelativos delosdesplazamientos
vertia-lesadimensionalesdelextremolibredelabarraenfunion
dek: Aproximaionparapeque~naspendientesrealizadaen
labibliografa(a)yaproximaionrealizada enestetrabajo
N
1.50
1.25
1.00
0.75
0.50
0.25
0.00
0.0
0.2
0.4
0.6
0.8
1.0
>
′
Y
X
I
@
Figura 9. Cuadrado de laderivada primera de lafunion
v evaluadoen el extremolibre delabarra, esdeir, enel
puntodeabisau=1{u
f .
Finalmente, en laFig. 10 se han representado las
elastias que se obtienen utilizando la euaion (23)
para k =0.2, 0.4, 0.6y 0.8. Como puede verse, tanto
u
f
omov
f
sondistintos de0.
X
Y
N
N
N
N
Figura10. Elastias adimensionales paradistintosvalores
dekobtenidasonlaaproximaionparapeque~nas
pendien-tespresentadaenestetrabajo.
IV Resultados experimentales
La Fig. 11 muestra una fotografade la barra
empo-trada porunextremo ysobre laque seaplia una
fu-erzavertialonentradaenelextremolibre. Labarra
esunaregladeaerodelongitudLuyaseion
trans-versal es retangular de base b y altura h. La regla
se ha empotradoon ayuda de una doble nuez de las
queseenuentranentodosloslaboratoriosdeFsia,la
ualsehasujetadoaunavarillavertialsituadasobre
un soporte. Con ayuda de dos laminas retangulares
metaliasoloadasunaarribadelareglaylaotra
de-bajoseajustalareglaaladoblenueztalyomoseve
re-ayudade unpiede reyyunpalmer, respetivamente.
Se hantomado medidasdeb y hada5malolargo
delareglaysehaaluladolamediadeadaunadela
series demedidas. Como errorabsolutodebyhseha
tomadoelvalormasgrande delasensibilidaddel
apa-rato de medida y la desviaion media de las medidas
realizadas,siendoenambosasosmayorlasensibilidad
delosinstrumentosdemedida utilizados. Elmomento
de ineria de laseion retangular loalulamos
me-diante laeuaion[1℄:
Figura11. Fotografadelaregladeaeroempotradaenun
extremoanalizada experimentalmenteenlaque seapreia
laurvaelastiadelabarraexionada.
Figura 12. Fotografa deldetalledel empotramientode la
regladeaeroanalizadaexperimentalmente.
I = 1
12 bh
3
(29)
Conuna balanza eletronia sedetermina lamasa
delareglaytomando g=9.800.01m/s 2
sealula
su peso total y, a partir de este, el peso P para una
longituddelareglade30m. EnlaTablaIseindian
lasaraterstiasdelabarradelgadaanalizada.
TABLA I
L 0.30000.0005m
b 0.030400.00002m
h 0.000780.00001m
I (1.200.05)x10 12
m 4
P 0.5540.008N
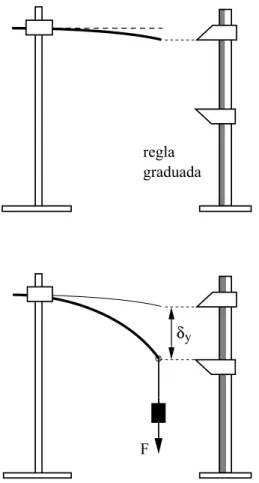
Aontinuaionsehamedidoeldesplazamiento
ver-tialmaximodelextremolibredelabarrauandose
so-meteadistintasfuerzasonentradasF tomandoomo
valordereferenialaposiiondelextremolibreuando
nose aplia ninguna fuerzaF (Fig. 13). Como seva
aanalizarlasituaionde peque~naspendientes, la
eu-aiondiferenialquehayqueonsiderareslinealloque
impliaqueeldesplazamientovertialtotaldelextremo
libredelabarraseralasumadelosdesplazamientos
de-bidosalafuerzaapliada yalpeso propio. Cuandoel
desplazamientovertialmaximodebibouniamente al
peso propio de la barra es muy peque~no (en el
labo-ratoriose hamedido experimentalmente queeste
des-plazamiento vertiales menorde 8mm)yademas las
pendientes alapliarfuerzasexternassonpeque~nas,se
puede suponer, sin ometer unerrorsigniativo,que
eldesplazamientodelextremolibre delabarra debido
asupesopropioesindependientedelafuerzaapliada.
Enla Fig. 14 se han representado los valores
experi-mentalesde losdesplazamientos vertialesÆ
y
medidos
respetoalaposiiondelextremolibreenauseniade
fuerzaapliada, en funion de la fuerzaF: Como
pu-ede verse para fuerzas apliadas peque~nas la relaion
entre Æ
y
yF eslineal,peroonformeaumenta elvalor
delafuerzaapliada,larelaionentreÆ
y
yF yanoes
lineal. Analizandola zona de omportamiento lineal,
quesepuedetomarparafuerzasapliadasentre0y1.2
N(Fig. 15),sehadeterminadoelvalordelarigidezde
labarramediante unajuste demnimosuadrados de
laeuaion(19),obteniendose:
EI =0.2380.009Nm 2
Lo que implia que el modulo de Young del aero
delque estafabriada laregla esE = 19815 GPa.
EstevaloronuerdaonelmodulodeYoungdelaero
quesepuedeenontrarenlabibliografayqueestaen
torno a 200 GPa [14℄. En la Fig. 14 se han
repre-sentado, junto on las medidas experimentales de Æ
y ,
losvaloresaluladosteoriamentehaiendousodelas
aproximaionespara peque~naspendientesdela
UHJOD
JUDGXDGD
)
δ
y
Figura13. Determinaionexperimentaldeldesplazamiento
vertialdelextremolibredelabarraexionadadebidoala
fuerzaexteriorF apliada.
δ
P
\
)1
Figura 14. Valores experimentalesde los desplazamientos
vertiales del extremo libre de la barra en funion de la
fuerza apliada F: Aproximaionpara peque~nas
pendien-tesrealizadaenlabibliografa(lnea reta)yaproximaion
)1
δ
P
\
Figura 15. Valores experimentalesde los desplazamientos
vertialesdelextremolibredelabarraenfuniondeFpara
lazonalinealdelaFig. 14yretadeajustedelaeuaion
(19).
V Conlusiones
Partiendo de la hipotesis de que el material del que
estafabriadauna barradelgadaexionada eselastio
lineal, se ha presentado la euaion diferenial de la
elastiade labarra de formaanaloga aomo sehae,
porejemplo,enellibrodeFeynman[5℄yenotroslibros
[2,4,7,8℄. Esta euaion diferenial se ha simpliado
onsiderando el aso de peque~nos desplazamientos de
ladiretrizdelabarra(pendientespeque~nas),perosin
haerunaaproximaiontanextremaaomosehaeen
lostextos universitariosdeFsia y Meania. Un
as-petoimportanteydegraninteresdidatioeslaforma
enomosehaapliadolaondiiondequelabarraes
inextensible(lalongituddesubraneutranoambia),
aspeto queno seonsideraen loslibros antes
meni-onados. Se han obtenido laseuaiones dela elastia
ylosdesplazamientosvertialyhorizontaldelextremo
libre de la barra, omparandolos on los
orrespondi-entesalasogeneraldepeque~nasyfuertespendientes,
asi omoon laaproximaionde peque~naspendientes
que aparee enla bibliografa. En esteultimo asose
suponequeeldesplazamientohorizontaldelextremo
li-brede labarra esnulo. Losresultadosteoriossehan
omparadoonlosexperimentalesobtenidosenel
labo-ratorioonunaregladeaero,omprobandoseomola
aproximaionparapeque~naspendientesonsideradaen
estetrabajoes\menosaproximada"quelaqueaparee
enlabibliografa. Porultimo,ynomenosimportante,
en eldesarrollodel trabajosehan utilizadooneptos
fsiosdegraninteresenunursodeFsiaoMeania
(esfuerzo, momentoetor, fuerzapuntual, modulode
Young, elastia, momento de ineria de una seion
plana, exion, deformaion, et.), as omo dealulo
omo elMathematiapararesolvernumeriamente
in-tegrales.
VI Apendie I: Elastia de una
barra delgada en voladizo
para el aso general
En elasogeneralen elque losdesplazamientosde la
barra delgada en voladizo songrandes, lo queimplia
fuertespendientesdelaurvaelastia,noesposible
ha-er uso de laaproximaion de la euaion (3) para el
radio de urvatura. En esta situaion, en vez de
uti-lizar laeuaion exata(2) paraelradio de urvatura
en oordenadas artesianas, es mejor resolver el
pro-blemaenfuniondelalongituddearosalolargode
laelastiadelabarraydelangulo ',queeselangulo
queformaonlahorizontallaretatangentealaurva
elastiaenunpuntodeterminadodelamisma(verFig.
2). Proediendodeestaformaseobtieneunaeuaion
diferenialnolinealdesegundoordenuyasoluionse
expresaen terminosdeintegraleselptias [12, 13℄. Se
diequeelproblemapresentanolinealidadgeometria.
Para la longitud L de la barra se obtiene la euaion
[12℄:
L= r
EI
2F Z
'0
0
d'
p
sin'
0 sin'
(A1)
Estaeuaionpermitedeterminarelangulo'
0 enel
extremolibredelabarra(Fig. 2)enfuniondela
longi-tuddelabarra,L,elmomentodeineriadesuseion
transversal, I, el modulode Youngdel material, E, y
la fuerza apliada, F: Asimismo, las oordenas (x;y)
de los puntos de la urvaelastiade la barra delgada
en voladizo pueden alularseenfuniondel angulo '
mediante laseuaiones[12℄:
x(')= r
2EI
F (
p
sin'
0 p
sin'
0
sin') (A2)
y(')= r
EI
2F Z
'
0
sin'd'
p
sin'
0 sin'
(A3)
Porultimo, losdesplazamientosvertialy
horizon-taldelextremolibredelabarrasealulantomando'
='
0
enlaseuaiones(A7)y(A8):
Æ
x
=L x('
0
) (A4)
Æ
y =y('
0
) (A5)
Lasintegraleselptiasdelaseuaiones(A1)y(A3)
pueden expresarse en terminos de funiones elptias,
sin embargo, y tal y omo seha se~nalado en una
pu-bliaion reiente [12℄ o se hae, por ejemplo, en un
problema similar a este omo es el pendulo simple
para grandesosilaiones [15℄, para losestudiantes de
losprimeros ursos universitarios esmasilustrativo y
didatiamente mas aonsejable quelas resuelvanon
ayudadealgunprogramadeordenadoromoel
Mathe-matia.
Refer^enias
[1℄ W. F. Riley y L. D. Sturges, Ingeniera Meania:
Estatia (Reverte,Barelona, 1995).
[2℄ F.Belmar,A.GarmendayJ.Llinares,CursodeFsia
Apliada: Estatia (UniversidadPoliteniade
Valen-ia,1987).
[3℄ J.L. Huertasy S.Val, Meania(2 o
de Bahillerato)
(MGraw-Hill,Madrid,1998).
[4℄ M.R.Ortega,Leionesde Fsia: Meania3 (Edita
elautor,Cordoba,1987).
[5℄ R.Feynman,R.B.Leightony M.Sands, Fsia, Vol.
II:EletromagnetismoyMateria (Addison-Wesley
Ibe-roameriana,Mexio,1987).
[6℄ A. Bedford y W. Fowler, Meania para Ingeniera:
Estatia (Addison-Wesley Iberoameriana,
Wilming-ton,1987)
[7℄ L.Ortiz-Berroal,ResisteniadeMateriales
(MGraw-Hill,Madrid,1997).
[8℄ R.C.Hibbeler,MeaniadeMateriales(PrentieHall,
Mexio,1998).
[9℄ F. R. Zypman y C. Guerra-Vela, \The marosopi
sanningfore`mirosope"',Eur.J. Phys.22,17-30
(2001).
[10℄ Th.Hop,D.SanderyJ.Kirshener,\Demonstration
ofdierentbendingprolesofaantileverausedbya
torqueorafore",Am.J.Phys.69,1113-1115 (2001).
[11℄ A.Belendez,C.NeippyT.Belendez,\Estudio
experi-mentaldeunavigaenvoladizo",Rev.Esp.Fis.15(3)
42(2001).
[12℄ T.Belendez,C.NeippyA.Belendez,\Largeandsmall
deetions of a antilever beam", Eur. J. Phys. 23,
371-379(2002).
[13℄ L. D.Landauy E. M. Lifshitz, Courseof Theoretial
Physis,Vol.7: TheoryofElastiity(PergamonPress,
Oxford,1986).
[14℄ P. A. Tipler, Fsia para la Cienia y la Tenologa,
Vol.1 (Reverte,Barelona, 1999).
[15℄ T.F.Zheng, M. Mears, D. Hall y D. Pushkin,
\Tea-hingthenonlinearpendulum",Phys.Teah.32,April,