Estudio de la Flexion de una Viga de
Material Elastio no Lineal
Tarsiio Belendez 1
, CristianNeipp 2
y Augusto Belendez 2
1
Departamento deCieniayTenologa delosMateriales
UniversidadMiguel HernandezdeElhe
Avda. delFerroarril,s/n. E-03202. Elhe(Aliante). Espa~na
2
Departamento deFsia,Ingenierade SistemasyTeora delaSe~nal
UniversidaddeAliante. Apartado 99. E-03080Aliante. Espa~na
Reebidoem31dejaneiro,2002. Aeitoem13deagosto,2002.
En los ursos de Fsia y Meania para estudiantes universitarios de Cienias e Ingeniera se
estudianlossolidosdeformables. Cuandounsolidosesometeaunesfuerzo,sufreunadeformaion
quepuedellegarinluso,uandoelesfuerzoesonsiderable,aladestruiondelsistema. Sielsolido
reupera suformaoriginaldespuesdesuprimirlasfuerzasexternas,sediequeladeformaionha
sidoelastia ysi,ademas,ladeformaionproduidaesproporionalalatensionapliadaentones
sehabladesolidoelastiolineal. Unadelasdeformaionesquepuedesufrirunsolidoeslaexion.
Cuandounabarradelgadaounavigaempotradaenunaparedsesometeaunesfuerzodeexion,
la barra sedeforma urvandose. Tambien en este aso en los primeros ursos universitarios de
lasmateriasantesse~naladas seanalizalaexiondeunavigasupondiendoqueelmaterialdelque
estafabriada eselastioy linealy aspodemosenontralo enlostextosdeFsiay Meaniade
Solidos. Sinembargo, adavezmasseutilizanmateriales uyoomportamientoesnolinealyeste
hehodeberaonsiderarse. En estetrabajo seanaliza laexiondeunaviga supondiendoqueel
materialde lamisma esnolineal. Seobtienen las euaiones delaelastia y laehasiguiendo
untratamientoanalogo aldesarrolladoporFeynmanuandoestudialavigaexionadaensulibro
de Fsia, por loque el desarrollo aqu presentadopodraser seguido sin muhosproblemas por
ualquierestudiantedeFsiadelosprimeros ursosuniversitarios.
I Introduion
Las vigas generalmente son uerpos solidos de forma
alargada y seionreta onstante, de gran interes en
ingenierayarquitetura,quenormalmente seutilizan
enposiionhorizontalysiendosulongitudgrande
om-paradaonlasdimensionesdesuseionreta. Las
vi-gaspuedenestarsometidasaargasonentradas,
ar-gasdistribuidasoapares(momentosonentrados)que
atuen solos o en una ombinaion ualquiera, siendo
laexionlaprinipal deformaionquesufren[1℄.
Puededenirseunavigaomounsolidohomogeneo
eisotropoengendradoporunaseiontransversal,que
generalmente admiteunplanodesimetrayuyo
en-trodegravedaddesribeunaurvaolnea,denominada
diretriz,siendoelplanoqueontienealaseion
trans-versalnormal adiha diretriz[2℄. Un aso partiular
devigasqueseestudianenlosprimerosursos
univer-sitariosdeFsiadelasarrerasdeIngenieray
Arqui-teturasonlasestatiamentedeterminadasoisostatias
[1,2℄, paralasque sepueden obtenerlasreaiones de
losapoyosapartirde laseuaiones delaEstatia,es
deir, imponiendo las ondiiones de que la suma de
fuerzasseanulaylasumademomentos respetoaun
punto tambien lo sea. El estudio de la exion de las
vigas isostatias puede enontrarse en algunos textos
deFsiaGeneralyMeania(ensupartedeEstatia)
[1,4℄yMeania deMateriales[5,6℄. Asimismo,las
vi-gasenvoladizohanreibidoreientementeatenionen
revistas en las que se publian trabajos relaionados
onlaense~nanzadelaFsiaaniveluniversitario[7-10℄.
Sinembargo,paraelanalisisquevamosaonsideraren
estetrabajobasta onelestudio delaviga exionada
que hae Feynman [11℄, al y suiente para
ompren-derelomportamientodeestoselementosonstrutivos
uandosesometenaaionesexternas.
Muhos problemasen Meania de Solidospueden
resolverseutilizandoelanalisislineal[6℄. Sinembargo,
estasituaionambiauandosetratadeplanteary
so-luionarproblemasnolineales. Entre lasausasdeno
linealidaden Meania deSolidosseenuentranlano
linealidad geometria, lano linealidad debida al
om-portamientodelmaterialylanolinealidaddebidaalas
so-luionanaltiasueleserompliadaoinexistentesalvo
en situaiones senillas, por lo que es neesario
reu-rrirateniasdesoluionmediantemetodosnumerios.
En los libros de Fsia General y Meania y en los
textoselementalesde Meaniade Solidosseestudian
uniamenteproblemasuyasoluionpuedeenontrarse
bajo la hipotesis del analisis lineal, mientras que los
problemas nolinealesapenas seanalizan, aun uando
hay muhas situaiones reales bastante omunes que
sonlaramente nolineales[10℄.
En el presente trabajo se plantea una forma
sen-illadeintroduiralosestudiantesdelosprimeros
ur-sos universitarios el onepto de no linealidad debida
al omportamiento del material. Para ello se analiza
la exion de una viga en voladizo en el aso
partiu-larenqueelmaterialdelqueestafabriada eselastio
no lineal, adiferenia del aso lineal que esel que se
estudia en todos los libros de texto antes se~nalados.
El desarrolloquesevaarealizaresanalogo al
presen-tado porFeynman en su libro [11℄ y material elastio
no lineal que se va a onsiderar es el onoido omo
de tipo Ludwik [12, 13℄ pues presenta laventajaque
inluyealmaterialelastiolinealomoasopartiular,
junto on un tratamiento matematio senillo. Esto
es didatiamente muy interesante pues permite a los
estudiantes derivar las euaiones que le son mas
fa-miliares orrespondientesal material elastio linealde
lasmasgeneralesdelmaterialelastionolinealdetipo
Ludwik.
Se vana obtener dos araterstiasde laviga: el
desplazamiento maximo del extremo libre de la barra
oehaenfuniondelafuerzaapliadaylaurva
de-formadaqueadoptalabarraexionadayquese
deno-mina elastia [11℄, en el aso de una viga empotrada
en un extremo, tambiendenominada viga en voladizo
omensula. Tanto laehaomo laelastiadependen
del material y de la geometra de la viga [2, 3℄. Se
estudiaranalgunas situaiones partiularesen lasque
se puede obtener la euaion de la elastia por
inte-graioninmediatadelaeuaiondiferenialque
gobier-naelomportamientodelaviga.
II Euaion momento-urvatura
para una viga de material
elastio no lineal
Consideremos una viga de seion retangular
ons-tante sometida a una serie de argas externas que la
deforman. Silabarraestaurvadasigniaqueel
ma-terialde laparte internadelaurvaestaomprimido,
mientras que el material de la parte externa esta
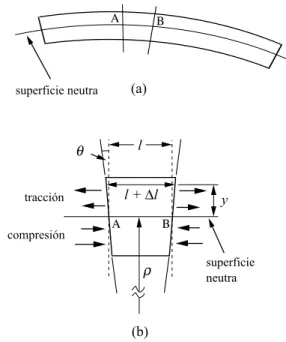
es-tirado omo se muestra en la Fig. 1(a). Existe una
superiequenoestaniomprimida niestiradayque
seonoeomosuperieneutra[2,6℄. Consideraremos
treshipotesisrelativasalaformaenqueelesfuerzo
de-formaalmaterialdelaviga[6℄. Parapeque~nasexiones
devigassimpleselejelongitudinaldelaviga,esdeir,
lalneaqueunelosentrosdegravedaddelasseiones
transversalesdelaviga,noexperimentaningunambio
delongitudyseonoeomolneaneutra. Esevidente
que lalneaneutra perteneea lasuperieneutra de
laviga. Elmomentotiendeadeformarlavigaenforma
tal queesta lnearetase vuelve una lnea urva. La
segunda hipotesis esque todas las seiones
transver-sales de la viga permaneen planas y perpendiulares
aleje longitudinal durantela deformaion. Laterera
hipotesis es que ualquier deformaion de la seion
transversaldentrodesupropioplanoseradespreiada.
Enpartiular,elejeontenidoenelplanodelaseion
tranversalyrespetoalualgiralaseionsellamaeje
neutro.
Α
Β
ρ
O
O
∆
O
\
θ
Α
Β
Figura1. (a)Vigaexionaday(b)segmentopeque~node
lavigaexionada.
Si el omportamiento del material es lineal, la ley
deBernoulli-Euler[6,11℄indiaqueelmomentoetor
esinversamenteproporionalalradiodeurvatura,sin
embargosielomportamientodelmaterialnoeslineal
estososeumple. Paraexionpura,unarebanada
del-gadadelabarrasedeformaomoseveenlaFig. 1(b).
Elmaterialpordebajodelasuperieneutratieneuna
deformaion ompresional, que veremos es
proporio-nal a ladistania a lasuperie neutra,mientras que
el material porenima esta estirado, tambien en
pro-porionaladistaniaalasuperieneutra. DelaFig.
1 (b) esfail ver que larelaionentre el estiramiento
longitudinalldeunabradelaviga,laalturay(Fig.
2) ylongituddelabraantesdeladeformaionly el
radiodeurvatura,es2=l/y=l/,dedonde:
l
= y
E
K
\
\
G6
Figura2. Seiontransversaldelaviga.
Sisuponemosqueelmaterialeselastionolinealde
tipoLudwik,larelaionentrelafuerzaporunidadde
area(elesfuerzo=dF/dS)yelalargamientopor
uni-daddelongituddeunabraualquiera(ladeformaion
"=l/l)seesribeenlaforma[12,13℄:
=E" 1=n
(2)
dondeE ynsononstantesaraterstiasque
depen-den del material. La relaion tension-deformaion no
lineal de tipo Ludwik de laeuaion(2) se ha
repre-sentado en la Fig. 3 para distintos valores de n,
in-luyendoelasoelastiolinealn=1,mientrasque en
laTablaIsepresentanlosvaloresdeEynparaalgunos
materialesdetipoLudwik[6,12℄.
σ
ε
Q!
Q
Q
Figura 3. Relaion tension-deformaion no lineal de tipo
Ludwik para distintos valores de n, inluyendo el aso
elastio linealn=1.
TABLAI-ValoresdeEynparadistintos materiales
detipoLudwik
MATERIAL E (MPa) n
AleaiondealuminioN.P.8 456 4.79
Cobreendureido 459 2.16
Fibradevidrio 300 2.00
Plastioaetal 66 3.00
Plastiopolipropileno 10 4.00
Podemosesribirlaeuaion(2)enlaforma:
dF
dS =E
l
l
1=n
(3)
Haiendo usodelaseuaiones(1) y(3)esposible
alularlafuerzaqueatuasobreunasuperiedS
si-tuadaaunadistaniaydelasuperieneutra(Fig. 2),
uyaexpresiones:
dF =E
y
1=n
dS (4)
Es evidente de la euaion (4) que n = 1
orres-pondealasoelastiolinealyentoneslaonstante E
esel modulo de Young del material, de modo en este
asolaeuaion(4) oinide onlaeuaion38.34 del
librodeFeynman[11℄.
Veamos a ontinuaion uales son las fuerzas que
danlugaratalesdeformaiones. Lasfuerzasqueatuan
sobre el peque~no segmento dibujado en la Fig. 1 (b)
estandibujadasenlamisma. Sionsideramosualquier
ortetransversal,lasfuerzasatuanatravesdeel,enun
sentidoporenimade lasuperie neutra yenelotro
pordebajo. Vienenenparesparadarlugaraloquese
onoe omo\momentoetor",M,querepresenta el
momentode lasfuerzasrespetoalalneaneutra. Es
posiblealular elmomento totalintegrandolafuerza
multipliadaporladistaniaalasupeie neutra(Fig.
2)enunadelasarasdel segmentodelaFig. 1(b):
M= Z
S
ydF (5)
dondelaintegralseextiendealaseiontransversalS
delabarra.
Haiendousodelaeuaion(4),elmomentoetor
delaeuaion(5)sepuede expresarenlaforma:
M= Z
S yE
y
1=n
dS (6)
quenalmentepuedeesribirseomo:
M= E
1=n
Z
y (n+1)=n
Laintegraldey (n+1)=n
dS esel\momentodeorden
(n +1)/n",que vamos a denominarI
n
, de laseion
transversalrespetoaunejehorizontalquepasaporsu
entrodegravedad:
I
n =
Z
S y
(n+1)=n
dS (8)
porloquelaeuaion(7)quedanalmente:
M= EI
n
1=n
(9)
Laeuaion(9)proporionalarelaionentreel
mo-mentoetorM yelradio deurvaturadelavigay
seonoeomoeuaionmomento-urvatura. La
\rigi-dez"delavigaesproporionalalprodutoEI
n .
El radio de urvatura de una urvade euaion
z=z(x)(euaionartesianadelaurvaelastiadela
viga)puedealularsemediantelaeuaion[6,11℄:
1
=
d 2
z=dx 2
[1+(dz=dx) 2
℄ 3=2
(10)
En el aso partiular en que el desplazamiento de
lospuntosdelaelastiadelavigadeformadarespeto
alos de la viga sin deformares peque~no, esdeir, en
el aso de pendientes peque~nas, es posible despreiar
el termino (dz/dx) 2
frente a launidad en laeuaion
(10),porloqueelradiodeurvaturasepuedealular
apartirdelaeuaion:
1
=
d 2
z
dx 2
(11)
Lo que permite esribir la euaion diferenial de
laurvaelastiapara unaviga dematerial elastiono
lineal de tipo Ludwik bajo la hipotesis de peque~nos
desplazamientosenlaforma:
d 2
z
dx 2
=
M
EI
n
n
(12)
que esla euaiondiferenial de la elastia de laviga
de material de tipo Ludwik en el aso de peque~nas
pendientesdelamisma.
Silaseiontransversaldelavigaesretangularde
base b yalturah(Fig. 2), entonesenlaeuaion(8)
setienedS =bdy,dedondeI
n
sepuedealularomo:
I
n =
Z
h=2
h=2 y
(n+1)=n
bdy (13)
uyaintegraionesinmediatayproporionaelvalor:
I
n =
1
2
(n+1)=n
n
2n+1
bh (2n+1)=n
(14)
que para el aso de omportamiento lineal del
mate-rial (n= 1) orrespondeal momento de ineria I de
laseionrespetoalejeperpendiularalamisma(eje
neutro)yquepasaporsuentrodegravedad:
I
1 =
1
12 bh
3
(15)
Porotraparte,esposiblealularlastensionesque
se ejeren sobre las distintas bras de laviga. De las
euaiones (1)y (9), teniendoenuenta que" =l/l
=y/,queda:
= My
1=n
I
n
(16)
III Elastia y eha para una
viga en voladizo
Paraobtenerlaeuaiondelaurvaelastiaz=z(x)es
neesarioonoerelmomentoetorM. Comoejemplo
onsideremosunavigaempotradaenunextremoylibre
en el otro, tambien onoida omo viga en voladizo o
mensula,sobrelaqueseapliaunafuerzaonentrada
FenelextremolibreyunafuerzaPuniformemente
dis-tribuidaalolargodelalongituddelaviga(quepuede
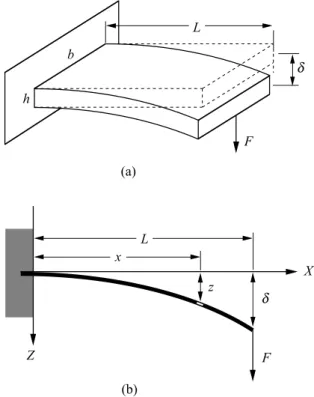
ser, por ejemplo, el peso de la propia viga). La Fig.
4muestra unaviga envoladizodelongitud L, seion
retangularonstante,pesoPuniformementerepartido
alolargodesu longitudyquesoportaunaarga
on-entrada F en elextremolibre. Elmomento etores
una funiondelaoordenadax yaqueeselmomento
on respeto al eje neutro de ualquierseion. Para
lavigaenvoladizoonsiderada,elmomentoetorM
F
debidoalaargapuntualFapliadaenelextremodela
vigarespetoalaseionsituadaaunadistaniaxdel
empotramientopuedealularsefailmentemediantela
euaion[7,11℄:
M
F
(x)=F(L x) (17)
mientrasqueelmomentoetordebidoalaarga
uni-formemente distribuida alolargode lalongitud de la
vigatiene laexpresion[2,7℄:
M
P (x)=
P
2L (L x)
2
(18)
Elmomento etortotalM(x) seralasumade los
dosanteriores,esdeir,
M(x)=F(L x)+ P
2L (L x)
2
(19)
Sustituyendoenlaeuaiondiferenialdelaelastia
(12) para peque~nos desplazamientos (peque~nas
pen-dientes),estatomalaforma:
d 2
z
dx 2
= 1
(EI
n )
n
F(L x)+ P
2L (L x)
2
n
(20)
)
K
E
/
;
)
]
/
[
=
δ
δ
Figura 4. (a) Flexion deuna viga envoladizo de seion
retangular uandoseaplia uunaargaonentrada enel
extremolibre. (b)Elastiadelavigaenvoladizo.
d 2
z
dx 2
=
F
EI
n
n
(L x) n
1+ P
2FL (L x)
n
(21)
dondepara laviga envoladizolasondiionesde
on-tornoson:
z(0)=0 (22)
dz
dx
x=0
=0 (23)
En general la euaion (20) es una euaion
dife-renia de segundoorden nolineal que deberesolverse
numeriamente. Sinembargo,esposibleonsiderar
al-gunosasospartiularesdegraninteresdidatio para
losquelaintegraionesinmediata. Veamosa
ontinu-aionalgunosdeellos.
III.1. Viga sometida a una fuerza puntual Fen
elextremolibre
EnesteasobastaonsiderarP =0enlaeuaion
(20), on lo que seobtiene la siguiente euaion
dife-renialdelaelastia:
d 2
z
dx 2
=
F
EI
n
n
(L x) n
(24)
que puede integrarse de forma inmediata teniendo en
uentalasondiionesdeontornoenelempotramiento
x=0(euaiones(22)y(23)),obteniendoselasiguiente
expresionparalaelastiadelavigaenvoladizo:
z=
1
(n+1)(n+2)
F
EI
n
n
(L x) n+2
+(n+2)L n+1
x L n+2
(25)
d
Esta expresion permite alular el desplazamiento
vertialzdeadaseiondelavigasituadaauna
dis-tania x del empotramiento. Parala viga envoladizo
laehaÆsepresentaenelextremolibreysuvalorse
obtiene sustituyendox=Lenlaeuaion(25):
Æ= L
n+2
n+2
F
EI
n
n
(26)
Esimportantese~nalarquelaeuaiondelaelastia
(25)esvalidasiempreyuandoeluadradodela
pen-diente de la elastia sea muho menor que la unidad,
pues esa ha sido lahipotesis para obtenerla euaion
(12),esdeir,debeumplirselaondiion:
dz
2
<< 1 (27)
Alahoradeanalizarunproblemapartiulares
ne-esario omprobar en primer lugar si la aproximaion
de peque~nas pendientes es apliable. Para ello basta
on derivar la euaion (25) respeto a la variable x
paraobtenerlapendientedelaelastiaenadapunto:
dz
dx =
1
n+1
F
EI
n
n
L n+1
(L x) n+1
(28)
evaluarla enel extremolibre de laviga (x =L), pues
en este punto se produe la maxima pendiente de la
elastia(tg'
0 ):
tg'
0 =
dz
dx
x=L =
L n+1
n+1
F
EI
n
n
(29)
yomprobar que su uadradoes muho menor quela
Porotraparte, para elasopartiular enel queel
materialeselastiolineal,esdeir,n=1,laseuaiones
(25)y(26)setransformanen:
z= F
EI
1
Lx 2
2 x
3
6
(30)
Æ= FL
3
3EI
1
(31)
quesonlasqueapareenenlabibliografa[11℄.
Resultainteresanteintroduirelparametro
adimen-sional denidoomo:
=L n+1
F
EI
n
n
(32)
que permite esribir las euaiones (26) y (29) en la
formamassenilla:
Æ
L =
n+2
(33)
tg'
0 =
n+1
(34)
Si laondiion devalidez dela aproximaionpara
peque~nas pendientes (euaion (20)) la suponemos
valida si el uadrado de la pendiente maxima es
me-nor,porejemplo, del10%delaunidad,loqueimplia
tg 2
'
0
<0:1;entonesdelaeuaion(34)seobtiene la
siguienteondiiondevalidez deestaaproximaion:
< n+1
p
10
(35)
Porejemplo,paraobreendureido(E=459MPa
yn =2.16)esta ondiionindia quelaaproximaion
parapeque~naspendientes esvalidapara <1:Enlas
Figs5y6sehan representado,paraobreendureido,
losvalores de'
0
y Æ/L frente alparametro
alula-dosmediantelaseuaiones(33)y(34)paralazonade
validezdelaaproximaiononsideradaenestetrabajo
(hasta =1paraestematerial).
"#
#"$
#"%
#"!
#"
#"#
#
&
#
&
#
ξ
ϕ
'
Figura 5. Valores de '0 frentea alulados mediantela
aproximaionparapeque~naspendientesparaelasodel
o-breendureido(E=459MPayn=2.16).
ξ
"#
#"$
#"%
#"!
#"
#"#
#"##
#"#&
#"#
#"&
#"#
#"&
δ
(
/
Figura 6. Valores de Æ/L frente a alulados mediante
laaproximaionparapeque~naspendientesparaelaso del
obreendureido(E=459MPayn=2.16).
III.2. Vigasometida a una fuerzadistribuida P
a lo largo de su longitud
Ahora bastaponer F =0en laeuaion(20), on
loqueseobtienelaeuaiondiferenial:
d 2
z
dx 2
=
P
2LEI
n
n
(L x) 2n
(36)
integrandoomoenelasoanterior,seobtiene la
eu-aiondelaelastia:
z=
1
(n+1)(2n+1)
P
2LEI
n
n
L 2n+2
+L 2
(L x) 2n
+2L 2n+1
(n+1)x 2L(L x) 2n
x+(L x) 2n
x 2
ysustituyendox=L enlaeuaion(37)sepuede
al-ularlaehaapartirdelaexpresion:
Æ= L
n+2
2 n+1
(n+1)
P
EI
n
n
(38)
que para n = 1orrespondenal asode
omportami-ento lineal. El valorde laehapara n= 1esel que
apareeenlabibliografaparaelasolineal[6,9℄:
Æ= PL
3
8EI
1
(39)
III.3. Vigasometida auna fuerzapuntual Fya
una fuerzadistribuidaP <<F
Si lafuerzadistribuidaP(quepuedeser,por
ejem-plo, el peso propiode laviga) esmuhomenorque la
fuerzapuntualapliadaF, podemos realizar la
si-guienteaproximaion:
1+ P
2FL
(x L)
n
1+ nP
2FL
(L x) (40)
que sustituida en la euaion (20), proporiona la
siguienteeuaiondiferenialdelaurvaelastia:
d 2
z
dx 2
=
F
EI
n
n
(L x) n
1+ nP
2FL
(x L)
(41)
uya integraion esinmediata, aunque el resultado es
algo engorroso. Por esta razon uniamente inluimos
el valor de la eha, es deir, del desplazamiento del
extremolibredelaviga:
Æ= L
n+2
[2(n+3)F+n(n+2)P℄
2(n+2)(n+3)F
F
EI
n
n
(42)
que para n = 1oinide onlaehapara el aso de
omportamiento lineal del material y no es otra osa
quelasumadelasehasdelaseuaiones(31)y(39):
Æ= L
3
24EI
1
(8F+3P) (43)
IV Conlusiones
Partiendo de la hipotesis de que el material del que
estafabriadauna vigaexionadaeselastionolineal
de tipo Ludwik, se ha obtenido la euaion
diferen-ialde laelastiade laviga deforma analogaaomo
sehaeenellibrodeFeynman. Estaeuaion
diferen-ialsehasimpliadoonsiderandoelasodepeque~nos
desplazamientos de la diretriz de la viga (pendientes
peque~nas) y se ha resuelto para el aso de una viga
empotradaenunextremosometidaadistintostiposde
argas. Sehanobtenidolaseuaionesdelaelastiayla
eha,omparandolas onlasorrespondientesalaso
de material elastio lineal. Este estudio permite
pre-sentaralosestudiantesqueelomportamientoelastio
delosmaterialesnoessiemprelinealyquelos
resulta-dosqueseobtienensondiferentesdependiendodeomo
seaeste omportamiento. Por ultimo, en eldesarrollo
sehanutilizadooneptosfsiosdegraninteresenun
urso de Meania (esfuerzo, momento etor, fuerza
puntual,fuerzadistribuida,elastia,momento de
iner-iadeunaseionplana,exion,deformaion,et.),as
omodealuloinnitesimal(derivada,integral,radio
deurvaturadeunaurva,et.).
Refer^enias
[1℄ W. F. Riley y L. D. Sturges, Ingeniera Meania:
Estatia (Reverte,Barelona, 1995).
[2℄ F.Belmar,A.GarmendayJ.Linares,CursodeFsia
Apliada: Estatia (UniversidadPoliteniade
Valen-ia,1987)
[3℄ M.R.Ortega,Leionesde Fsia: Meania3 (Edita
elautor,Cordoba,1987).
[4℄ A. Bedford y W. Fowler, Meania para Ingeniera:
Estatia (Addison-Wesley Iberoameriana,
Wilming-ton,1987)
[5℄ L.Ortiz-Berroal,ResisteniadeMateriales
(MGraw-Hill,Madrid,1997).
[6℄ R.C.Hibbeler,MeaniadeMateriales(PrentieHall,
Mexio,1998).
[7℄ A.Belendez,C.NeippyT.Belendez,\Estudio
experi-mentaldeunavigaenvoladizo",Rev.Esp.Fis.15(3)
42-45(2001).
[8℄ F. R. Zypman y C. Guerra-Vela, \The marosopi
sanningfore`mirosope"',Eur.J. Phys.22,17-30
(2001).
[9℄ Th.Hop,D.SanderyJ.Kirshener,\Demonstration
ofdierentbendingprolesofaantileverausedbya
torqueorafore",Am.J.Phys.69,1113-1115 (2001).
[10℄ T.Belendez,C.NeippyA.Belendez,\Largeandsmall
deetions of a antilever beam", Eur. J. Phys. 23,
371-379(2002).
[11℄ R.Feynman,R.B.Leightony M.Sands, Fsia, Vol.
II:EletromagnetismoyMateria (Addison-Wesley
Ibe-roameriana,Mexio,1987).
[12℄ M. Sathyamoorthy, Nonlinear Analysis of Strutures
(CRCPress, BoaRaton,1998).
[13℄ K.Lee,\Largedeetionsofantileverbeamsof
non-linearelastimaterialunderaombinedloading",Int.