TÓPICOS NA INTERSEÇÃO ENTRE A TEORIA DOS GRAFOS E ÁLGEBRA

(1)

COLÓQUIOS DE MATEMÁTICA DAS REGIÕES

REGIÃO NORTE

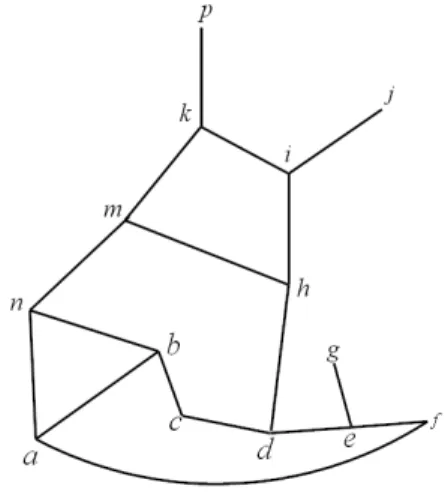
IV Colóquio de Matemática da Região Norte

ABEL AHBID AHMED DELGADO ORTIZ

THIAGO G. VELANGA MOREIRA

TÓPICOS NA INTERSEÇÃO

ENTRE A TEORIA DOS

(2)

(3)

Sociedade Brasileira de Matemática

Presidente: Hilário Alencar Vice- Presidente: Paolo Piccione Diretores:

Editor Executivo

Hilário Alencar

Assessor Editorial

Tiago Costa Rocha

Comitê Científico

Eduardo Teixeira – UFC

Giovany Malcher Figueiredo – UFPA João Xavier Cruz Neto – UFPI

José Nazareno Vieira Gomes – UFAM Sandra Augusta Santos – UNICAMP

Eliane Leal Vasquez – UNIFAP ( Coordenadora Geral) Marcel Lucas Picanço Nascimento – UNIFAP

Comitê Organizador Local (UNIFAP)

Eliane Leal Vasquez Gilberlandio Jesus Dias

Guzmán Eulálio Isla Chamilco João Socorro Pinheiro Ferreira Marcel Lucas Picanço Nascimento Naralina Viana Soares da Silva Sergio Barbosa de Miranda Simone de Almeida Delphim

Capa: Pablo Diego Regino

Distribuição e vendas

Sociedade Brasileira de Matemática

Estrada Dona Castorina, 110 Sala 109 - Jardim Botânico 22460-320 Rio de Janeiro RJ

Telefones: (21) 2529-5073

http://www.sbm.org.br / email:lojavirtual@sbm.org.br João Xavier

José Espinar Marcela de Souza Walcy Santos

Tópicos na interseção entre a Teoria dos Grafos e Álgebra

(4)

COLÓQUIOS DE MATEMÁTICA DAS REGIÕES

REGIÃO NORTE

IV Colóquio de Matemática da Região Norte

1ª EDIÇÃO

2016

MACAPÁ

ABEL AHBID AHMED DELGADO ORTIZ

THIAGO G. VELANGA MOREIRA

TÓPICOS NA INTERSEÇÃO

ENTRE A TEORIA DOS

(5)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

Sumário

1 Noções de Álgebra Abstrata 1

1.1 Relações de equivalência e partições . . . 1

1.2 Teoria dos números: pré-requisitos . . . 5

1.3 Noções elementares da teoria dos grupos . . . 6

1.3.1 Primeiras definições e exemplos . . . 6

1.3.2 Resultados básicos sobre grupos . . . 7

1.4 Subgrupos . . . 9

1.5 Noções elementares da teoria de anéis . . . 12

2 O grafo unitário de Cayley 15 2.1 Grafos: breve introdução . . . 15

2.1.1 Terminologia básica . . . 15

2.1.2 Entendendo a estrutura de um grafo . . . 17

2.1.3 Subgrafos . . . 21

2.2 Automorfismos de grafos . . . 24

2.3 Grafos de Cayley . . . 25

2.3.1 Propriedades gerais . . . 26

2.3.2 Grafos unitários de Cayley . . . 28

3 Introdução à Teoria dos Hipergrafos 33 3.1 Hipergrafos . . . 33

3.2 Representações de um hipergrafo . . . 34

3.2.1 Representação pictórica . . . 34

3.2.2 Representação matricial . . . 34

3.2.3 Representação bipartida de um hipergrafo . . . 35

3.3 Exemplos de hipergrafos . . . 37

3.3.1 Sistemas de Steiner . . . 37

3.3.2 Espaços lineares . . . 37

3.4 Ciclos em um hipergrafo . . . 38

3.5 Isomorfismo de hipergrafos . . . 39

(6)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

4 Sigrafos (ou grafos de arestas rotuladas com sinais) 43

4.1 Sigrafos . . . 43

4.2 O Teorema de Estrutura . . . 45

4.3 Sigrafos unitários de Cayley . . . 47

(7)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

Lista de Figuras

2.1 Representação de um grafo. As letras representam os vértices e as

arestas estão representadas pelas linhas entre as letras. . . 16

2.2 O grafo de Petersen. . . 16

2.3 Grafos de Petersen isomorfos. . . 19

2.4 Grafos não isomorfos. . . 20

2.5 Grafos aresta-isomorfos porém não isomorfos. . . 20

2.6 Subgrafos do grafoG. . . 22

2.7 O grafo completoK5, o grafo linha deK5e o grafo de Petersen. . 22

2.8 (a) Grafo3-partido com conjuntosV1 ={a, b, c, d},V2={h, g, k} e V3 = {m, n, e, f, i, j}; (b) grafo bipartido completo, K2,3; (c) uma estrela. . . 23

2.9 Grafo de Cayley: g=Z₆,_B ₌_{1,_2,_4,_5} . . . 26

3.1 Representação pictórica de um hipergrafo . . . 35

3.2 Representação bipartida de um hipergrafo . . . 36

3.3 O plano de Fano. . . 38

3.4 Isomorfismo de hipergrafos . . . 39

3.5 Hipergrafo Unitário de Cayley comn= 14eX={{1,3}}. . . . 41

4.1 Todos os sigrafos tendo como suporte o grafoSu. . . . 44

4.2 Sigrafo equilibrado . . . 45

4.3 Partição do conjunto de vértices no Teorema de Estrutura . . . 46

4.4 Representação Pictórica de um sihipergrafo . . . 50

(8)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

Prefácio

A ideia por traz desta proposta é introduzir tópicos de matemática que vêm sendo objeto de pesquisas na atualidade, porém, com pré-requisitos que não vão além de um conhecimento básico em demostrações matemáticas formais e de al-guma exposição a disciplinas em nível de graduação como, por exemplo, Aritmé-tica Elementar e Álgebra Abstrata [18], [10], [8] e [7]. Para este fim, a Teoria dos Grafos e sua generalização, a Teoria dos Hipergrafos, prestam-se muito bem. Por um lado, tem-se que a maioria de seus tópicos são de natureza elementar e, por outro, observamos que tais tópicos têm sido frequentemente revitalizados pelos problemas decorrentes dos avanços tecnológicos, fornecendo assim novos focos de pesquisa [14].

Da interação dessas teorias com a Álgebra Abstracta e a Teoria Elementar dos Números, nasce a possibilidade de criar novos conceitos e conectar ideias conhe-cidas a outras novas.

(9)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Capítulo 1

Noções de Álgebra Abstrata

Neste capítulo, reunimos alguns fatos básicos da Álgebra Abstrata que se farão necessários para a compreensão dos temas desenvolvidos nos capítulos seguintes. Alguns resultados encontram-se apenas enunciados, sem demonstração, deixados como exercício para o leitor. Para um estudo mais detalhado neste assunto reco-mendamos [7], [18], [8] e [10].

1.1 Relações de equivalência e partições

Definição 1.1.1. [2] Umafamília enumerávelé uma coleção enumerável de

ob-jetos iguais ou diferentes.

Definição 1.1.2. Seja Ruma relação definida num conjuntoA. Dizemos que R

é uma relação de equivalência em A quando, para quaisquer x, y, z ∈ A, as seguintes propriedades são satisfeitas:

1. xRx(Reflexiva),

2. xRy⇔yRx(Simétrica),

3. [xRyeyRz]⇒xRz(Transitiva).

Definição 1.1.3. Uma classe de equivalência do elementox ∈ Acom respeito à relação∼é o conjunto

[x] ={a∈A;a∼x}.

Definição 1.1.4. O conjunto formado por todas as classes de equivalência[x], com

x∈A, é chamadoconjunto quocientedeApela relação de equivalência∼. Para denotar tal conjunto, utilizaremos a seguinte notação:

A/∼:={[x] ;x∈A}.

Proposição 1.1.5. Seja∼uma relação de equivalência em um conjuntoAe sejam

x, y∈A. Então,

(10)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

2 CAPÍTULO 1. NOÇÕES DE ÁLGEBRA ABSTRATA

1. [x] = [y]⇔x∼y; 2. [x]6= [y]⇒[x]∩[y] =∅;

3. ∪

x∈A[x] =A.

Demonstração. 1. Suponha que [x] = [y], vamos mostrar quex ∼ y. Temos que

x∈[x] = [y]⇒x∈[y]

⇒x∼y.

Suponha quex∼y, vamos mostrar que[x] = [y]. Mostraremos que

[x]⊂[y] (1.1)

e

[y]⊂[x]. (1.2)

Sejaa∈[x], vamos mostrar quea∈[y]. Temos

a∈[x]⇒a∼x

e, temos por hipótese quex ∼y. Como∼é uma relação de equivalência, temos que

a∼y⇒a∈[y] Isso mostra (1.1). Para mostrar (1.2),

a∈[y]⇒a∼y

Comox∼y, por simetria vale quey∼x. Assim,

(a∼yey∼x)⇒a∼x

⇒a∈[x]

obtendo (1.2). Logo, obtemos a igualdade [x] = [y], provando o primeiro item.

2. Suponha que

[x]∩[y]6=∅ e sejaa∈[x]∩[y]. Então,

a∈[x]ea∈[y]

⇒[a∼xea∼y]

(11)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

1.1. RELAÇÕES DE EQUIVALÊNCIA E PARTIÇÕES 3

3. Mostraremos que

A⊂ ∪

x∈A[x]. (1.3) Sejax∈Aqualquer. Vamos mostrar quex∈ ∪

x∈A[x].

x∈A⇒x∈[x]

⇒x∈ ∪ x∈A[x], mostrando queA ⊂ ∪

x∈A[x]. Por outro lado, dadoa∈ ∪x∈A[x], então existe x0 ∈Atal que

a∈[x0] ={a∈A;a∼x0}

⇒a∈A, mostrando que

∪

x∈A[x]⊂A. (1.4) De (1.3) e (1.4), vem que ∪

x∈A[x] =Ae a proposição está provada.

Definição 1.1.6. (Partição) Umapartiçãode um conjuntoAé uma coleção de sub-conjuntos não vazios e disjuntos deAcuja união é igual aA. Mais explicitamente, dizemos que uma coleçãoP_{⊂ P}_(A)é uma partição do conjunto_Aquando forem

satisfeitas as seguintes condições:

(i) Para todosB1, B2∈P, comB16=B2, tem-se queB1∩B2=∅;

(ii) ∪

B∈PB =A.

Proposição 1.1.7. SejaAum conjunto. Dada uma partiçãoPdo conjunto_Aexiste

uma única relação de equivalência∼sobreA, tal que

A/∼=P.

Demonstração. defina sobreAa seguinte relação:

x, y∈A, x∼y⇔ ∃B ∈P;x, y∈B.

A relação é reflexiva pois, dadox∈Atemos pela condição (ii) da definição1.1.6 quex∈ ∪

B∈PB. Logo, existeB ∈

Ptal que_x_∈_B, mostrando que

x∼x,∀x∈A.

(12)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

agora a transitividade da relação. Sejam dadosx, y, z ∈ Aarbitrários. Suponha quex∼yey∼z. Então, existemB1, B2∈Ptais que

(

x, y∈B1

y, z ∈B2 =⇒y∈B1∩B2.

Segue da condição (i) da definição o1.1.6queB1 = B2. PondoB =B1 =B2,

obtemos quex, z∈B, comB ∈P. Daí, vem que_x_∼_z. Falta mostrar a igualdade

A/∼=P.

Por definição, temos que

A/∼={[x] ;x∈A}. Seja dadoC∈A/∼. Existex∈Atal que

C = [x] ={y∈A;y∼x}.

Comox ∈ A = ∪

B∈PB, existe B = Bx ∈

P tal que_x _∈ _Bx. Afirmamos que C=Bx∈P. De fato,

y∈Bx ⇒ y, x∈Bx, comBx ∈P

⇒ y∼x

⇒ y∈[x] =C.

Por outro lado,

y∈C= [x] ⇒ y∼x ⇒ ∃B′ _∈_P_;_{y, x}_∈_B′_.

Como x ∈ Bx, segue que Bx ∩B′ 6= ∅, com _{Bx, B}′ _∈ P. Então, segue da condição (i) da definição1.1.6 quey ∈ B′ ₌ _Bx_{, donde vem que}_C ₌ _Bx _∈

P_.Reciprocamente, seja _C _∈ P_.Existe _x _∈ _C, para algum _x _∈ _A (pois_C é subconjunto não vazio deA). Mostraremos queC = [x]∈A/∼.De fato,

y∈C ⇒ y, x∈C, comC ∈P

⇒ y∼x

⇒ y∈[x].

Por outro lado,

y∈[x] ⇒ y ∼x ⇒ ∃B ∈P_;_{y, x}_∈_B.

Comox ∈ C, segue quex ∈ B∩C ondeB, C ∈ P. Novamente pela condição (i) da definição1.1.6, y ∈ B = C, mostrando que C = [x] ∈ A/∼. Portanto, concluímos que

A/∼ =P.

Prova da Unicidade:Suponhamos que existem duas relações de equivalênciaR1

eR2sobreAtais que

(13)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

1.2. TEORIA DOS NÚMEROS: PRÉ-REQUISITOS 5

Mostraremos que

R1=R2.

Basta mostrar que

yR1x⇔yR2x,

para todosx, y∈A. De fato, sejam dadosx, y∈Aquaisquer e, ponha

E1={z∈A;zR1x} eE2={z∈A;zR2x}.

Então, E1 ∈ A/R1 e E2 ∈ A/R2. Segue da hipótese queE1, E2 ∈ Pe, como

x∈E1∩E2, segue queE1=E2.Assim,

yR1x ⇔ y∈E1=E2

⇔ yR2x

para todosx, y∈A. Concluímos que

R1=R2.

Podemos então enunciar agora oTeorema Fundamental das Classes de Equi-valência

Teorema 1.1.8. SejaAum conjunto não vazio.

(1) Se∼define uma relação de equivalência sobreAentão o conjunto quociente

A/∼:={[x];x∈A}

das classes de equivalência de∼forma uma partição deA.

(2) Se P é uma partição de _A então, existe uma única relação de equivalência ∼sobreAcujas classes de equivalências são exatamente os elementos da partiçãoP. Isto é,

A/∼=P.

Demonstração. É consequência imediata das proposições1.1.5e1.1.7.

1.2 Teoria dos números: pré-requisitos

Nesta seção nos limitamos a apontar alguns fatos da teoria dos números que se farão presentes nas demonstrações das propriedades dos grafos unitários de Cayley. Seguiremos o livro de Milies e Pitta Coelho [19].

Sejamaebinteiros ambos não nulos. Denotemos porD(a, b)o conjunto de todos os divisores comuns deaeb.

(14)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Definição 1.2.2. O elemento máximo do conjuntoD(a, b)é chamadomáximo di-visor comum de a e b e denota-se por mdc(a, b), ou simplesmente (a, b). Isto é,

mdc(a, b) =maxD(a, b).

Definição 1.2.3. Dizemos que dois inteirosaebsãorelativamente primosse

mdc(a, b) = 1. Exercício 1.2.4. Sejamaebinteiros. Mostre que

1. Sea|be(b, c) = 1, então(a, c) = 1;

2. (a, c) = (b, c) = 1se, e somente se,(ab, c) = 1.

Definição 1.2.5. Para cada inteiro n ≥ 1, indicaremos por φ(n) o número de inteiros positivos menores ou iguais anque são relativamente primos comn. A função assim definida chama-sefunçãoφde Euler.

Teorema 1.2.6. Sen≥2é um inteiro cuja fatoração em primos é n=pα1

1 pα22. . . pα

s

s onde p1 < p2 < . . . < ps,

então,

φ(n) =n(1− 1 p1

)(1− 1 p2

). . .(1− 1 ps

).

1.3 Noções elementares da teoria dos grupos

1.3.1 Primeiras definições e exemplos

Definição 1.3.1. Seja g um conjunto não vazio. Um grupo é um par ordenado

(g,∗), onde∗é uma operação binária definida sobreg, tais que as seguintes

pro-priedades são satisfeitas:

1. Para todosx, y, z ∈Atem-se x∗(y∗z) = (x∗y)∗z (Associativa); 2. Existee∈gtal que x∗e=e∗x, para todox∈g (Identidade deg);

3. Para todox ∈gexistex′ ∈ gtal que x∗x′ =e=x′∗x (Existência do elemento inverso).

Se o grupogverifica a propriedade comutativa:

x∗y=y∗x

para todosx, y ∈ g, entãogé chamado grupocomutativo. Um grupo possuindo um número finito de elementos é chamadofinitoe, caso contrário,infinito. Exemplo 1.3.2. SejaA um conjunto não vazio e sejaSAo conjunto de todas as

(15)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

1.3. NOÇÕES ELEMENTARES DA TEORIA DOS GRUPOS 7

1.3.2 Resultados básicos sobre grupos

Proposição 1.3.3. Seja(g,∗)um grupo, então o elemento identidade é único.

Exercício 1.3.4. Prove a proposição1.3.3.

Proposição 1.3.5. Em um grupo(g,∗):

a∗x=a∗y⇒x=y

x∗b=y∗b⇒x=y.

Isto é, vale a lei do corte. Demonstração.

a∗x=a∗y⇒a′∗(a∗x) =a′∗(a∗y).

Pela associatividade,

(a′∗a)∗x= (a′∗a)∗y.

Finalmente, pela existência do elemento identidade,

x=e∗x=e∗y=y.

Exercício 1.3.6. Demonstre a segunda propriedade da Proposição1.3.5.

Corolário 1.3.7. Em um grupo(g,∗)cada elemento tem um único inverso. Demonstração. Suponha que paraa∈g,

a∗x=eg e a∗y=eg.Então, a∗x=a∗y.

O resultado segue ao aplicar a Proposição1.3.5. Paraa∈gdenotaremos seu inverso pora−1.

Corolário 1.3.8. Paraa∈g, tem-se que(a−1)−1 =a.

Demonstração. Segue ao aplicar a Proposição1.3.5(lei do corte) à seguinte equa-ção:

a−1∗(a−1)−1 =e=a−1∗a

(16)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Proposição 1.3.10. Em um grupo(g,∗)fixe o elementoa∈ge defina a seguinte

função emg,

fa(x) =a∗x, para todox∈g.

Então,faé bijetora.

Demonstração. A injetividade resulta da contrapositiva da primeira propriedade da Proposição1.3.5. Dadoz∈g, pondox= (a−1∗z)∈g, obtemos que

fa(x) =fa(a−1∗z) =a∗(a−1∗z) = (a∗a−1)∗z=e∗z=z,

mostrando quefaé bijetora.

Exercício 1.3.11. Mostre que a conclusão da Proposição1.3.10é verdadeira tam-bém parafadefinida por

fa(x) =x∗a, para todox∈g.

Definição 1.3.12. Seja g = {g1, g2, . . . , gd} um grupo finito com g1 = eg. A

tabela do grupogé a matriz de ordemd×dcuja entradai, jé o elementogi∗gj

do grupog.

Cada linha da tabela representa os valores que a funçãofa(x) =a∗xassume. Similarmente, cada coluna representa os valores que a funçãofa(x) = x∗a as-sume. Sendofabijetora, cada elemento do grupo aparece em cada linha (coluna) uma única vez.

Exemplo 1.3.13. Determine todos os grupos de três elementos. (Adaptação de

[20]). Seja ao elemento neutro. Então a primeira linha e a primeira coluna da tabela podem ser prenchidas como aparecem nas tabelas da esquerda e do centro. Agora, notemos que b∗b é diferente de bpois, do contrário, b apareceria duas vezes nessa linha. Assimb∗b=aoub∗b=c.Da mesma maneirab∗cé diferente dece deb, logob∗c=a. Portanto,b∗b=c.

Na última linha, na interseção com a penúltima coluna da tabela do meio, vemos que só falta colocarae, na interseção da última linha com a última coluna,

b. A tabela segue agora completa.

∗ a b c

a a b c b b

c c

∗ a b c

a a b c b b c a c c

∗ a b c

a a b c b b c a c c a b

Exercício 1.3.14. Mostre queSntemn!elementos.

(17)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

1.4. SUBGRUPOS 9

Definição 1.3.16. Seja(g,∗)um grupo. Um subconjutoBdegé dito umconjunto de geradorespara o grupogse para todog∈g, existemh1, h2, . . . , hnelementos

deB tais queg=ha1

1 ∗ha22 ∗ · · · ∗hann, ondeai ∈ {1,−1}.

Definição 1.3.17. Um grupo(G,∗)é dito cíclico, seG=< h >={hi_{, i}_∈_Z_}_{, for}

someh∈G, ondehi ₌_h_∗_h_∗_{. . .}_∗_h

| {z }

i−vezes

.

1.4 Subgrupos

Definição 1.4.1. Seja(g,∗)um grupo eh⊂g. Sehfor um grupo com a operação ∗, dizemos quehésubgrupodeg.

Proposição 1.4.2. Seja(g,∗)um grupo eh⊂g, ondeh6=∅.hé um subgrupo de gse, e somente se,

1. a∗b∈h, para todosa, b∈h;

2. a−1 ∈h, para todoa∈h.

Proposição 1.4.3. Sehé um subconjunto finito não vazio de um grupoge se a∗b∈h,

para todosa, b∈hentão,hé um subgrupo deg.

Definição 1.4.4. Para qualquerN ≤ge qualquerg∈go conjunto gN ={g∗n|n∈N}

é chamado de classe lateral à esquerda deN emge, analogamente, N g={n∗g|n∈N}

é chamado de classe lateral à direita deN emg.

Definição 1.4.5. SejaHum subgrupo deg, onormalizadordeHemgé o conjunto Ng(H) ={g∈g:gHg−1 =H}.

Definição 1.4.6. Um subgrupoHdegénormalemg, segHg−1 =H, para todo

g∈g. Utilizaremos a notaçãoHEgpara indicar que H é subgrupo normal deg. Teorema 1.4.7. SeAeB são subgrupos de um grupog, o conjunto

AB:={ab;a∈A e b∈B}

(18)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Corolário 1.4.8. Se Ae B são subgrupos deg e A ≤ Ng(B), então AB é um

subgrupo deg. Em particular, seBEg, entãoAB≤g, para todoA≤g. Definição 1.4.9. (1) Uma aplicaçãoφde um grupo(g1,∗)em um grupo(g2, ⋆)é

dita um homomorfismose,

φ(a∗b) =φ(a)⋆ φ(b),

para todosa, b∈g.

(2) Dois gruposgeg∗ são ditosisomorfosse existe um homomorfismo bijetor de

gemg∗.

(3) Seφé um homomorfismo deg1emg2, onúcleo(ou kernel) deφé definido por

Ker(φ) ={x∈g1 :φ(x) =e2},

ondee2denota o elemento neutro deg2.

O seguinte conceito deação de gruposfoi principalmente explorado em [7]. Definição 1.4.10. Umaaçãode um grupo(g,∗)sobre um conjuntoAé uma apli-cação deg×AemA(denotamosg ⋆ a, para todog∈gea∈A) que satisfaz as

seguintes propriedades:

(1) g1⋆(g2⋆ a) = (g1∗g2)⋆ a, para todosg1, g2∈g,a∈A;

(2) 1⋆ a=a, para todoa∈A.

Exercício 1.4.11. Seja (g,·) um grupo qualquer e seja A = g. Mostre que a

aplicação definida porg ⋆a:=a·g−1_{para todos}_{g, a}_∈_g_{é uma ação (à esquerda)}

do grupogsobre si mesmo.

Exercício 1.4.12. Seja(g,·)um grupo qualquer e sejaA = g. Mostre que seg

não é abeliano (isto é, não comutativo) então a aplicação definida porg ⋆a:=a·g

para todosg, a∈gnãoé uma ação (à esquerda) do grupogsobre si mesmo. Exercício 1.4.13. Seja(g,∗) um grupo e sejaAum conjunto que recebe a ação

⋆deg. Para cadag ∈ gfixo se obtém uma aplicaçãoσg : A → Adefinida por

σg(a) =g ⋆ a. Mostre que

1. Para cadag∈gfixo, a aplicaçãoσgé uma permutação (isto é, uma bijeção) deA;

2. A aplicação degemSAdefinida porg7→σgé um homomorfismo (chamado arepresentação via permutações associada à ação). Reciprocamente,

(19)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

1.4. SUBGRUPOS 11

Observação 1.4.14. Alternativamente, pelo dito nos itens (2) e (3) do Exercício

1.4.13, um homomorfismo degemSAsempre pode ser definido via uma ação deg

sobreAe, reciprocamente, uma ação de um grupogsobre um conjuntoAsempre pode ser definida via um homomorfismo degemSA.

Exercício 1.4.15. SejaH um grupo agindo (com ação⋆) sobre um conjuntoA. Provar que a relação∼definida sobreApor

a∼b se, e somente se, a=h ⋆ b para algumh∈H

é uma relação de equivalência.

PeloTeorema Fundamental das Classes de Equivalência1.1.8, a relação do Exercício1.4.15nos fornece uma partição do conjuntoA. Cada elemento[a]desta partição (ou, equivalentemente, classe de equivalência deacom respeito à relação ∼) é chamada umaórbitadeasob a ação deH, a qual denotaremos porO(a).

Definição 1.4.16. Seja(g,·)um grupo agindo (com ação⋆) sobre um conjuntoA

não vazio. Diz-se que a ação⋆étransitivaseApossui uma única órbita.

Proposição 1.4.17. Seja(g,·)um grupo agindo (com ação⋆) sobre um conjuntoA

não vazio. A ação⋆é transitiva se, e somente se, dados quaisquer dois elementos

a, b∈Aexisteg∈Gtal quea=g ⋆ b.

Demonstração. Suponha que⋆é transitiva e sejam dadosa, b∈A. EntãoO(a) = O(b)e, portanto,a∈ O(b). Por definção, existeg∈gtal quea=g ⋆ b. Recipro-camente, dada uma classeO(a) ⊂ Aa hipótese nos garante queb ∼ apara todo b∈A. PortantoA=O(a), mostrando que a ação⋆é transitiva.

Definição 1.4.18. Seja(g,·)um grupo agindo (com ação⋆) sobre um conjuntoA

e fixe um elementoa∈A. Oestabilizadordeaemgé o conjunto ga={g∈g:g ⋆ a=a}.

Isto é,gaé o conjunto dos elementos degque fixama. Exercício 1.4.19. Prove quegaé um subgrupo deg.

Definição 1.4.20. Uma ação de um grupogsobre um conjuntoAé dita semirre-gularsega={e}, para todoa∈A. Ou, equivalentemente, a identidade é o único

elemento degque fixa todos os pontos deA.

Definição 1.4.21. Uma ação de um grupogsobre um conjuntoAé ditaregularse

(20)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

1.5 Noções elementares da teoria de anéis

Definição 1.5.1. Umanel(A, +,·)é um conjunto não vazio Amunido de duas operações binárias internas, denotadas por+e·, chamadas respectivamentesoma

emultiplicação, que verificam os seguintes axiomas: 1. (A,+)é um grupo abeliano;

2. A multiplicação · é associativa:a·(b·c) = (a·b)·c para todosa, b, c∈A; 3. (a) Para todox, y, z∈Atem-se x·(y+z) =x·y+y·z, (distributiva

à esquerda);

(b) Para todox, y, z∈Atem-se (y+z)·x=y·x+z·x, (distributiva

à direita);

4. Existe umelemento identidadeemA(denotado por1) tal que

a·1 = 1·a=a para todoa∈A.

5. O anel(A,+,·)é ditocomutativose a multiplicação for comutativa.

Definição 1.5.2. Um elemento x ∈Achama-se invertívelse existe um elemento

y∈Atal quex·y=y·x= 1.

É comum denotar o conjunto dos elementos invertíveis de um AnelAporA∗. O seguinte resultado será de utilidade mais adiante e deixaremos ao leitor a tarefa de sua demonstração.

Proposição 1.5.3. A∗é um grupo multiplicativo.

Exercício 1.5.4. Seja(A,+,·)um anel, então para todosa, b∈Avale 1. a·0 = 0·a= 0;

2. a·(−b) = (−a)·b=−(a·b); 3. (−a)·(−b) =a·b;

4. (−1)·a=−a; 5. (−1)·(−1) = 1.

Exercício 1.5.5. Prove a proposição1.5.3

Exemplo 1.5.6. (1) O anel dos inteiros(Z_,_+,_·)é um exemplo de anel

comuta-tivo onde1e−1são seus únicos elementos invertíveis. Assim,(Z∗_,_·₎é o

(21)

Região

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Região

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Região

1.5. NOÇÕES ELEMENTARES DA TEORIA DE ANÉIS 13

(2) Sejanum inteiro positivo fixo. Definimos

a≡b (mod n) se, e somente se, n|(a−b).

Esta relação, chamadacongruência módulon, define uma relação de

equi-valência no conjuntoZ. Pelo Teorema Fundamental das Relações de

Equi-valência1.1.8, o conjunto Zé particionado em _nclasses de equivalência.

Sobre o conjunto destas classes, denotada porZ_n={[0],[1], . . . ,[n−1]}, vamos definir uma operação de soma da seguinte maneira:

[x] + [y] = [z],

ondezé o resto da divisão dex+yporn. E também definimos uma operação de multiplicação de modo análogo:

[x]·[y] = [z],

ondezé o resto da divisão dex·yporn. Deixamos como exercício mostrar que(Z_n_,_+,_·)é um anel comutativo.

Os exercícios seguintes serão amplamente utilizados em demonstrações de vá-rios resultados ao longo do texto. Para maiores detalhes, recomendamos [18], [10] e [8].

Exercício 1.5.7. Sejam a, n ∈ Z_{, n >} ₀. Então existe _b _∈ Z com _ab _≡ ₁ (modn)se, e somente se,mdc(a, n) = 1(Isto é, os elementos[a], 0≤a < n, invertíveis no anel(Z_n_,_+,_·)são aqueles tais que_{mdc(a, n) = 1}).

Exercício 1.5.8. Sejan∈N,_n_≥₂. Seja_m _∈N. Mostre que_[m] gera o grupo (Z_n,₊₎se, e somente se,_[m] é um elemento invertível do anel₍Z_n,_+,_·).

Exercício 1.5.9. Considere o anel(Z_n,_+,_·)dos inteiros módulo_n, e seja_n₌_pα

uma potência de um primop. Então, um elementox ∈(Z_n,_+,_·)é invertível se, e

somente se,xnão é múltiplo dep.

Demonstração. Sexé múltiplo dep, digamosx = kp, então,mdc(x, n) ≥p > 1. Pelo Exercício 1.5.7, xnão é invertível em Z_n. Reciprocamente, se_x não é múltiplo depentão, a decomposicão dexem fatores primos

x=p1· · ·pm,

ondem≥1é um natural ep1 ≤ · · · ≤pmsão primos, deve ser tal quepi 6=p, para

(22)

Região Norte - Macapá - AP - UNIFAP - IV Colóquio de Matemática da Região Norte - Macapá - AP - UNIFAP - IV Colóquio de Matemática da Região

14

CAPÍTULO

1.

NOÇÕES

DE

ÁLGEBRA

ABSTRA

(23)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

Capítulo 2

O grafo unitário de Cayley

Neste capítulo iniciamos com as definições e propriedades básicas da Teoria dos Grafos com o intuito de apresentar o grafo unitário de Cayley sobre o anelZ_n dos inteiros módulo n. A terminologia e notação utilizada diferem na literatura existente e aproveitamos aqui a oportunidade para estabelecer como nossa aquela que é mais frequentemente utilizada. No decorrer deste trabalho, faremos apenas uso dos grafos simples, assim não discutiremos grafos mais gerais como aqueles que contemplam laços, arestas paralelas e orientações entre as arestas. O conteúdo deste capítulo está baseado nos seguintes livros muito conhecidos:Graph and Di-graphs[5] eGraph Theory[11].

2.1 Grafos: breve introdução

2.1.1 Terminologia básica

Definição 2.1.1. Umgrafo(simples) é um parG= (V, E)ondeV é um conjunto não vazio de objetos chamadosvérticeseE é um conjunto (possivelmente vazio)

de objetos chamadosarestas. Cada aresta (elemento deE) é um subconjunto com dois vértices deV. O conjunto de vértices deG é denotado porV(G), quando quisermos explicitar o grafo com vértices. Similarmente, o conjunto de arestas denota-seE(G).

Se a ₌ _{{u, v}} é uma aresta de um grafo _G, então_u e _v são ditos vértices

adjacentes(ou, queué adjacente av) enquanto queu ea são ditosincidentes.

Ainda mais, sea₁ea₂são arestas distintas de_Gincidentes com um vértice comum,

então a₁ e a₂ são chamadas arestas adjacentes. É conveniente daqui em diante

denotar uma aresta poruvao inves de{u, v}.

A cardinalidade do conjunto de vértices de um grafoGé chamadaordemdeG e denotada porn(G)ou, mais simplesmente, porn, quando se entende de maneira clara qual é o grafo em consideração. Analogamente, a cardinalidade do conjunto de arestas de um grafoGé chamadotamanhodeGe é denotado frequentemente porm(G)(oum, por simplicidade). Um(n_,m₎-grafotem, portanto, ordem_ne

tamanhom.

(24)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

16 CAPÍTULO 2. O GRAFO UNITÁRIO DE CAYLEY

É habitual definir, ou descrever, um grafo por meio de um diagrama no qual cada vértice é representado por um ponto e cada arestae₌_uvé representada por

um segmento de linha ou curva que une os pontos correspondentes auev. Ograude um vérticev, denotado pord(v), é o número de arestas deG inci-dentes comv. Diremos que um vértice v ∈V(G)épar(ímpar) se o número de arestas incidentes avfor par (ímpar). Um vértice de grau zero emGé chamado isoladoe um vértice de grau um,terminal. Ograu mínimodeGé o menor grau dentre todos os vértices deGe é denotado porδ(G). Ograu máximoé definido similarmente e é denotado por∆(G).

Figura 2.1: Representação de um grafo. As letras representam os vértices e as arestas estão representadas pelas linhas entre as letras.

(25)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

2.1. GRAFOS: BREVE INTRODUÇÃO 17

Exemplo 2.1.2. Designado em homenagem ao matemático Danes Julis Petersen porgrafo de Petersen, esta estrutura combinatória possui 10 vértices e 15 arestas,

como podemos observar na figura2.2. Este grafo aparece como contra-exemplo à diversas conjecturas importantes em diferentes temas da teoria dos grafos [2]. Um fato que ilustra a importancia desta configuração é o livro [13], inteiramente dedicado a ele .

Um grafo G com conjunto de vértices V(G) = {v1, . . . , vn} e conjunto de

arestasE(G) ={e₁_,e₂_{. . . ,}e_n}pode ser representado por meio de matrizes. Uma

matrizA(G) = [aij]quadrada de ordemné chamadamatriz de adjacênciadeG deGquando

aij =

(

1, sevivj ∈E(G); 0, sevivj 6∈E(G).

Assim, a matriz de adjacência de um grafoGé uma matriz simétrica com zeros na diagonal principal. Uma outra matriz é a matriz quadrada de ordemnchamada matriz de incidênciaB(G) = [bij], onde

bij =

(

1, seviee_j são incidentes_;

0, caso contrário.

2.1.2 Entendendo a estrutura de um grafo

Percurso, cadeia e caminho

Para entender a estrutura de um grafo, imaginemos primeiramente que em nosso grafo podemos tomar um percurso contínuo, primeiro caminhando através da arestae₁, depois pela arestae₂e assim por diante. Ou seja, o ponto terminal de e_ié o ponto inicial dee_i₊₁. Temos várias maneiras de realizar este percurso, por

exemplo, poderíamos repetir uma aresta ou visitar duas vezes um mesmo vértice. Definição 2.1.3. Um percurso(ou,passeio) é uma sequência alternante de

vérti-ces e arestasx1, e2, x2, e3, . . . , xk−1, ek, xkiniciando e terminando com vértices

tais que ei = xi−1xi, para cada 1 < i < k+ 1. O percurso seráfechado se

x1 =xk. Umacadeia(ou, trilha) é um percurso sem repetição de arestas e, um

caminho, é um percurso sem repetição de arestas e vértices. É comum denotar

um percurso iniciando no vérticex1e terminando no verticexkporx1−xk, ou

ainda, ignorando as arestas, comox1x2. . . xk−1xk. Para um caminho,

utilizare-mos a notaçãoPx₁,xk.

Definição 2.1.4. Um caminho em um grafoGé dito hamiltonianose passar por

todos os vértices deG.

Definição 2.1.5. Um cicloé uma sequência de vértices e arestas

x1, e2, x2, e3, . . . , xk−1, ek, xk

(26)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

1. k≥3;

2. x1x2. . . xk−1é um caminho;

3. xk=x1.

Definição 2.1.6. Umacordaem um ciclo é uma aresta que conecta dois vertices

não consecutivos.

Definição 2.1.7. Um ciclo em um grafoGé ditohamiltonianosex1x2. . . xk−1é

um caminho hamiltoniano.

Dois grafos frequentemente compartilham a mesma estrutura, diferentes so-mente na maneira em que seus vértice e arestas são rotulados ou pela maneira em que foram desenhados. Para fazer esta ideia mais precisa introduzimos o conceito de isomorfismo.

Isomorfismo de grafos

Definição 2.1.8. Um grafoG1 = (V1, E1)éisomorfoa um grafoG2 = (V2, E2)

se existe uma função

φ:V1 →V2

tais que

1. φé bijetora;

2. Para todosv, w∈V1,{v, w} ∈E1 se , e somente se,{φ(v), φ(w)} ∈E2.

Nesse caso, escrevemosG1 ∼=G2e dizemos queG1é isomorfoaG2(ou, queG1

eG2 sãoisomorfos). Uma outra alternativa é dizer que existe uma bijeçãoφde

V(G1)sobreV(G2)que preserva a adjacência; isto évw ∈E(G1)se, e somente

se,φ(v)φ(w)∈E(G2).

É fácil ver que ser "isomorfo a" é uma relação de equivalência em grafos; por-tanto, esta relação particiona a coleção de todos os grafos em classes de equiva-lência de tal maneira que dois grafos são não isomorfos se, e somente se, eles pertencem a diferentes classes de equivalência.

Comoφé bijetora,G1 e G2 têm a mesma ordem. Como vértices adjacentes

deG1são levados a vértices adjacentes emG2e vértices não adjacentes deG1são

levados a vértices não adjacentes emG2, os grafosG1eG2têm o mesmo tamanho.

Uma vez que cada vérticevemG1e seu vértice imagem devem ter o mesmo grau

em seus respectivos grafos, os graus de vértices deG1são exatamente os graus dos

vértices deG2(contando multiciplicidades). Assim, temos o seguinte teorema,

Exemplo 2.1.9. Se modificamos as linhas representando arestas da figura2.3 ob-temos a representação mais conhecida do grafo de Petersen.

(27)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

C

olóquio

de

Matemática

da

Re

gião

Figura 2.3: Grafos de Petersen isomorfos.

1. O mesmo número de vértices, ou seja, a mesma ordem; 2. O memo número de arestas, ou seja, o mesmo tamanho; 3. A mesma sequência de graus.

Apesar dessas condições serem necessárias para queG1eG2sejam isomorfos,

elas não são suficientes. A seguir, um contra-exemplo ao teorema2.1.10. Exemplo 2.1.11. SejaG1 = (V1, E1)comV1 ={a, b, c, d, e, f}e

E1 = {ab, bc, ac, cd, de, df}e, sejaG2 = (V1, E2)comV2 = {x, y, w, z, s, t}e

E2 = {xy, xw, xz, zw, zy, st}. Notemos que eles têm a mesma ordem, o mesmo

tamanho e compartilham a mesma sequência de graus: 2,2,3,3,1,1. No entanto, eles não são isomorfos como se observa na figura2.4. O grafo em2.4-(b) mostra uma aresta solta, o que não acontece em2.4-(a).

Definição 2.1.12. Um grafoG1 = (V1, E1) éaresta-isomorfoa um grafoG2 =

(V2, E2)se existe uma função

φ:E1→E2

tais que

1. φé bijetora;

2. Para todose_,f _∈_E₁tem-se quee_∩f _{6=6 ∅}se, e somente se,_φ(e₎_∩_φ(f₎_{6=6 ∅}.

Proposição 2.1.13. SeG1é isomorfo aG2então eles são também aresta-isomorfos.

Demonstração. Primeiro definimosφa : E1 → E2 assim: dada uma arestae =

{x, y} ponha-seφa(e_{) =} _{{φ(x), φ(y)}}. Sendo_φum isomorfismo,_{{φ(x), φ(y)}}

(28)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Figura 2.4: Grafos não isomorfos.

φ(x)aφ(y)e, portanto,φaé bem definida. Deixamos como exercício mostrar que φa é injetora e sobrejetora. O fato de que{x1, y1}e {x2, y2}são adjacentes em

G1se, e somente se,{φ(x1), φ(y1)}e{φ(x2), φ(y2)}são adjacentes emG2segue

da definição deφ.

Definição 2.1.14. SejamG1 = (V1, E1)e G2 = (V2, E2) grafos não vazios nos

quais existe um isomorfismoφ:V1 →V2. O isomorfismo induzido porφé aquele

aresta-isomorfismoφadefinido por

e₌_{{v, w} →}_φa(e_{) =}_{{φ(v), φ(w)}}

A figura 2.5 ilustra o fato de que em geral dois grafos podem ser aresta-isomorfos porém não aresta-isomorfos.

(29)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

2.1.3 Subgrafos

Frequentemente um grafo sob estudo está contido dentro de um grafo maior. Consideremos agora várias instâncias disto.

Definição 2.1.15. Um grafoHé umsubgrafode um grafoGseV(H)⊆V(G)e

E(H)⊆E(G), neste caso também dizemos queGé umsupergrafodeH.

Definição 2.1.16. SejamH eGgrafos. Diz-se queH é um subgrafoabrangente

deGseH ⊆GeV(H) =V(G).

Entre os mais importantes subgrafos que iremos encontrar estão ossubgrafos induzidos.

Definição 2.1.17. Se U é um subconjunto não vazio deV(G), então o subgrafo

[U]deGinduzidoporU é o grafo ondeV([U]) = U e E([U]) = { {a, b} ∈ E(G) :a∈U, b∈U}.

Definição 2.1.18. Um subgrafo H de G é chamado induzido por vértices (ou,

simplementes, induzido) seH= [U]para algum subconjuntoU deV(G).

Se v ∈ V(G) e |V(G)| ≥ 2, então G−v denota o subgrafo induzido pelo conjuntoV(G)− {v}. Em geral, seV′ ⊂ V(G), [V(G)−V′]é denotado por G−V′.

Definição 2.1.19. Se X é um subconjunto não vazio de E(G), o subgrafo [X]

induzido porXé o grafo cujos vértices deGsão incidentes com pelo menos uma aresta deXe cujo conjunto de arestas éX.

Definição 2.1.20. Um subgrafoHdeGé chamadoinduzido por arestasseH = [X]para algum subconjuntoXdeE(G).

Se e _∈ _E(G), então_G₋_eé o subgrafo com conjunto de vértices _V_(G) e

conjunto de arestasE(G)− {e_}.

Seuevsão vértices não adjacentes de um grafoG, entãoG+f, ondef ₌_uv,

denota o grafo com conjunto de vérticesV(G)e conjunto de arestasE(G)∪ {f_},

claramenteG⊆G+f.

Existem certas classes de grafos que aparecem com tanta frequência que mere-cem atenção especial e, em algums casos, notação especial. Descreveremos agora os mais proeminentes destes.

Definição 2.1.21. 1. [9] Umpolígono(ou,grafo ciclo) (Cn)é um grafo com

nvértices formado por apenas um ciclo passando por todos os vértices. 2. Um grafoGéregular de grau rsed(v) = r, para todo vérticevdeG. Tal

grafo é chamador-regular.

(a) Um grafo écompletose cada par de seus vértices são adjacentes. Um

(30)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Figura 2.6: Subgrafos do grafoG.

(b) Um grafo cúbicoé um grafo3-regular. (c) Um grafoparé um grafo regular de grau par.

3. OcomplementarGde um grafoGé o grafo cujo conjunto de vérticesV(G)

é tal que dois vértices são adjacentes emGse, e somente se, estes vértices são não adjacentes emG. Daqui em diante, seGé um(n, m)-grafo, então

Gé um(n, m)-grafo.

4. O grafolinhade um grafoG, denotado porL(G), é definido como:

V(L(G)) =E(G)

e,e_∈_E(L(G)), se, e somente se,e₌_{{a, b}, a}_∩_b₆₌_∅.

O grafo linha representa a adjacência entre as arestas do grafoG.

Figura 2.7: O grafo completoK5, o grafo linha deK5e o grafo de Petersen.

Exercício 2.1.22. Prove que o grafo completoKnpossui n(n−1)

(31)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Exemplo 2.1.23. Consideremos o grafo completoK5(veja exemplo na figura2.7

-(a)). Para obter o seu grafo linha, lembremos que uma aresta{a, b}deK5 é um

vértice em L(K5) o qual denotaremos por ab (veja exemplo na figura 2.7-(b)).

Agora, vérticesabe cdsão adjacentes se, e somente se, {a, b} ∩ {c, d} = {t}, ondet ∈ {a, b, c, d}. A figura com linhas pontilhadas é o complentar do grafo linha deK5que, como se pode ver, é o grafo de Petersen.

Um grafoGék-partido, se é possível fazer uma partição do conjuntoV(G) consistindo deksubconjuntosV1, V2, . . . , Vktal que todo elemento deE(G)une um vértice de Vi a um vértice de Vj, i 6= j (veja exemplo na figura 2.8-(a)). Note que um grafo finito simples der vértices pode ser considerado como grafo r-partido, onde os distintos conjuntosVisão osrconjuntos unitários contendo um vértice. Quando cada vértice de um grafok-partido une um vértice deVi a cada vértice deVj,i6=j, então diz-se que o grafo ék-partido completo. Neste caso te-mos uma notação especial: SeV1, V2, . . . , Vktem, respectivamente,p1,p2, . . . , pk elementos, escrevemosKp1,p2,...,pk ouK(p1, p2, . . . , pk) (veja exemplo na figura

2.8-(b)). O grafo completo den-vértices, o qual foi definido em2.1.21, é um caso particular. Quando k = 2, temos o conhecido grafo bipartido, isto é, quando V(G)pode ser particionado em dois subconjuntos disjuntosV1eV2tais que toda

aresta emE(G)une um vértice deV1 com um vértice deV2.

Umcliqueé um subconjunto deV(G)no qual cada par de vértices é adjacente. Assim, um clique é um subconjunto de vértices S ⊂ V(G) tal que o subgrafo H= [S]deGé isomorfo ao grafo completoK_|S|.

Definição 2.1.24. Seja um grafoG= (V, E).Um subconjuntoI deV, é dito um

conjunto independentedeGse cada par de seus vértices não são adjacentes.

Observação 2.1.25. [9] Alguns autores denotam o conjunto de todos os conjuntos independentes de vértices do grafo G como S(G). A noção de conjunto inde-pendente é maximal e pode ser expressa pelo parâmetroα0, chamadonúmero de

estabilidade,α0=max{|I|:I ∈S(G)}.

Figura 2.8: (a) Grafo3-partido com conjuntosV1 = {a, b, c, d},V2 ={h, g, k}e

(32)

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Norte

-Macapá

-AP

-UNIF

AP

-IV

Colóquio

de

Matemática

da

Re

gião

Proposição 2.1.26. Seja Gum grafo. A soma dos graus dos vértices é igual ao dobro do número de arestas. Isto é,

X

v∈V(G)

dG(v) = 2|E(G)|.

O seguinte teorema é utilizado mais adiante.

Teorema 2.1.27. Um grafoGé bipartido se, e somente se,Gnão possui ciclos de comprimento ímpar.

O teorema2.1.27possui a seguinte variação:

Corolário 2.1.28. Um grafoGé bipartido se, e somente se, não contém um per-curso fechado de comprimento ímpar.

2.2 Automorfismos de grafos

Seja V um conjunto não vazio. O conjunto de todas as permutações de V (confira com o Exemplo 1.3.2) também é denotado por Sym(V) ou, Sym(n), quando |V| = n. Lembremos que Sym(V) é um grupo com a composição de funções. SejaG= (V, E)um grafo simples e finito e suponha a existência de um isomorfismoφde Gem G, então φé uma permutação dos elementos deV que preserva a adjacência. Neste caso, dizemos queφé umautomorfismo do grafo G. O conjunto de todos os automorfismos deGé um subgrupo deSym(V), o qual é denotado porAut(G).