Arquimedes e Geometria Diferencial

(1)

Rui Albuquerque

Universidade de ´Evora 22 de Outubro de 2007

Aρχ´η

Este texto resulta de uma breve comunica¸cão na Escola de Verão de Ma-temática de 2007 da Sociedade Portuguesa de MaMa-temática, em que se almejou abordar os dois temas referidos no t´ıtulo.

Recordar Arquimedes e trazê-lo para a actualidade da geometria diferen-cial... Os matemáticos gregos estarão na origem, no arqué de toda a matemática moderna, mas tal não justifica dois t´ıtulos num mesmo artigo.

Mergulhar assim no mais distante do grande oceano da matemática pode le-var a um triste despertar. Porém é necessário que alguns se aventurem, para que outros conhe¸cam os perigos e as preciosidades que tal oceano esconde. Mesmo que corramos o risco de nos perguntarem o que andamos ali a fazer, onde po-derão levar tão insólitas bra¸cadas, diremos que este mar é de todos quantos o queiram perscrutar.

Três ressalvas nos parecem necessárias. Primeiro, não queremos de forma nenhuma reduzir a obra de Arquimedes a meia dúzia de enunciados. Existe uma complexa e extensa obra. Por mais aplicada que se considere a sua matemática, Arquimedes escrevia como os homens letrados da sua época e argumentava como um cientista, com proposi¸cões, lemas e teoremas. Os seus resultados são desconhecidos, a come¸car, por isso mesmo: não são triviais, carecem de uma constru¸cão e justifica¸cão teóricas.

Segundo, não pretendemos afirmar que haveria rela¸cões enigmáticas ou m´ıs-ticas entre a matemática de Arquimedes e o Cálculo Diferencial, o qual, como se sabe, apareceu algum tempo depois do fim da Idade Média. Não vamos de todo estabelecer rela¸cões. O que nos suscita é interrogar, de novo, sobre o porquê de tantos anos perdidos com a chamada Era das Trevas quando a civiliza¸cão pré-romana já havia ido tão longe, mesmo antevendo não lograr encontrar uma resposta. Se tempo houvesse, lembrar´ıamos os homens que contrariaram e

(2)

resis-Figura 1: Arquimedes de Siracusa

tiram, os que fizeram o renascimento da cultura cl´assica e com ela deram novos conhecimentos ao mundo.

Finalmente, visto o anterior, julgamos poder e dever continuar mesmo se os resultados desta breve exposi¸c˜ao fogem das nossas inten¸c˜oes, assim como ter bem avisado o leitor dos meandros do pensamento difuso que dele emergem.

Afinal, para nós, trata-se de encontrar inspira¸cão recordando o mestre da matemática do século III a.c., um dos maiores de sempre, para chegar à geome-tria diferencial, aquela que vem dando razão de ser às mais diversas áreas da matemática da actualidade.

1 Arquimedes de Siracusa, 287-212 a.c.

Em 2013 terão passado 2300 anos sobre o nascimento do grande Aρχιµηδης, génio célebre da matemática e da f´ısica.

Arquimedes nasceu e morreu em Siracusa, na Sic´ılia, filho do astrónomo F´ıdias, de uma fam´ılia respeitada pelo rei Hierão. Cedo foi estudar para Ale-xandria onde uma escola de matemática, entre outras, havia sido fundada por Euclides (c.330-265 a.c.). Em Alexandria fez numerosos amigos estudiosos com quem se correspondeu ao longo da vida, como por exemplo o matemático Era-tóstenes.

Arquimedes é autor de imensas descobertas e inventos notáveis e peripécias, cada uma mais emblemática que a outra.

Lembremos os momentos célebres em que ele diz “dêem-me um ponto de apoio e com a minha alavanca erguerei o mundo” referindo-se aos seus estudos teóricos sobre o equil´ıbrio dos corpos, o grito de ε´νρηκα saindo do banho para

(3)

Parafuso de Arquimedes, o estudo da chamada Espiral de Arquimedes ou as inven¸cões de instrumentos militares (um dos quais, muito peculiar, consistiria numa espécie de feixe solar para incendiar barcos romanos ao largo de Sira-cusa; porém, algumas experiências recentes terão levantado muito fumo sobre tal invento).

Menos conhecidas serão a cria¸cão de um método numérico para contar além da “mir´ıade” (104_{) os grãos de areia do Universo, ou o Axioma de Arquimedes,}

que afinal este atribui a Eudóxio, hoje estudado na Análise e que justifica o chamado método de “exaustão” para os matemáticos gregos (ou de ‘integra¸cão’), ie. algo aparentemente tão óbvio como ∀M > 0, ∀0 ≤ r ≤ 1

2, limnMrn= 0.

Ou, ainda, um c´alculo muito aproximado da √3.

Assim como uma elegante e simples triseçcão do ângulo com compasso e régua com apenas duas marcas, problema célebre posto por Euclides que se destinava a ser resolvido com compasso e régua não graduada — e que afinal se provou ser imposs´ıvel, cf. figura 2.

A vida de Arquimedes deverá ter sido a de um verdadeiro cientista forte-mente comprometido com a investiga¸cão, tanto pura como aplicada, e simul-tâneamente com a ajuda aos homens da sua cidade em questões e problemas práticos.

Até a sua morte nos parece quase mitológica: durante as guerras Púnicas quando as tropas do romano Marcellus, depois de muito tentarem, invadiram a ilha num ataque surpresa, ainda que soubessem do célebre cientista, um soldado ter-lhe-á cravado a espada. Com Arquimedes avisando que o deixassem concluir certos cálculos...

1.1 Um teorema sobre a par´

abola

O método de exaustão, talvez devido a Ant´ıfono e seu colega Brison de Heracleia, século V a.c., permitiu encontrar a mais famosa aproxima¸cão de pi de sempre. Durante mil anos não se encontrou melhor que

3 + 10

71 < π < 3 + 1

7, (1)

que Arquimedes conseguiu dividindo o c´ırculo em 96 partes.

O m´etodo de exaust˜ao permitiu de facto estabelecer resultados precisos. Por exemplo, cremos que o seguinte esquema, ver figura 2, era conhecido dos

(4)

P r A B C X r r

Figura 2: `A esquerda, ]CAB = 3]XAB com régua graduada com a medida do raio. À direita, Área do c´ırculo= P r

2 = πr2.

Figura 3: ´Area ∆ABT = 3

4 Area da par´abola ABT .´

matemáticos gregos mais antigos. Trata-se da justaposi¸cão de triângulos de altura r =raio, dado o per´ımetro P , deduzindo-se a área do c´ırculo.

O seguinte resultado utiliza outro método na demonstra¸cão inteiramente devido ao f´ısico-matemático, que se refere mais à frente.

Teorema 1 (Arquimedes, [2]). A ´area do maior triˆangulo inscrito num

seg-mento de uma parábola é 3/4 da área do respectivo segseg-mento de parábola. Em particular, 3 4 + 3 42 + 3 43 + · · · = 1. (2)

Sendo o eixo dos y’s o eixo de simetria de uma par´abola y = kx2_{, k > 0,}

(podemos sempre encontrar uma transforma¸cão afim do plano onde a parábola é descrita por esta equa¸cão, ou mesmo com k = 1), cf. figura 3. Repare-se que o ponto T é o ponto onde a tangente à parábola tem o declive do segmento AB. Supondo esta recta dada como y = ax + b, a, b constantes, obtivemos o valor da área do triângulo ABT como (a2+4kb)

3 2

8k2 — um exerc´ıcio simples quando armados do cálculo diferencial. Convém ainda ter presente que qualquer transforma¸cão afim preserva a razão entre duas áreas.

(5)

Arquimedes prova também que as projeçcões de A e B no eixo dos x’s são equidistantes da respectiva projeçcão de T . Lembremo-nos que Arquimedes não possui os conceitos mais elementares da ál-jbra de hoje, apenas as rela¸cões entre quantidades geométricas.

Os gregos já referiam as tangentes; Arquimedes manuseia-as com mestria para obter, por exaustão, construindo a série (2), a área da parábola através da dos triângulos inscritos. Repare-se que há um processo indutivo no problema: recortado o triângulo, surgem duas novas regiões em condi¸cões análogas e de área total 1/4 da área do segmento de parábola.

Curiosamente, o teorema parece ser pouco conhecido nos dias de hoje. O estudo das cúbicas foi outro tema que Arquimedes abra¸cou, tendo sido mais tarde continuado por Omar Khayyam (o matemático e poeta persa-árabe do século XIII, que nos legou a nota¸cão ‘chai’, ‘coisa’, que depois degenerou em

x). Recordamos que os árabes foram os guardiões de muita da cultura helénica

e, em particular, de algumas obras de Arquimedes.

1.2 O M´

etodo

Aquele que ficou conhecido como o Método de Arquimedes vem dos seus estudos da f´ısica. Foi finalmente compreendido há cerca de um século, depois de ter sido encontrado num livro de uma bilioteca de Constantinopla (hoje Istambul) pelo estudioso dinamarquês J. L. Heiberg. Este reconheceu o autor que subjazia num palimpsesto (um escrito de missas de monges bizantinos num suporte de papiro ou pele já utilizado, depois de raspado e lavado). O“palimpsesto de Arquimedes” contém muitas páginas de resultados para sempre julgados perdidos, uns que não chegaram a ser apagados e outros leg´ıveis por recursos técnicos, incluindo o texto do agora famoso “Stomachion”, um jogo inventado pelo mestre.

Vejamos uma aplica¸c˜ao do M´etodo.

Recorde-se, para o que segue, que o volume do cone em rela¸c˜ao ao cilindro com a mesma base e altura estavam j´a calculados. Com efeito, aparecem nos

Elementos de Euclides, tomando essa raz˜ao o valor de 1/3. Segundo [3],

Ar-quimedes atribui o resultado ao célebre filósofo atomista Demócrito. Sobre o volume das esferas, o caso é mais complicado.

Teorema 2 (Arquimedes). O volume da esfera de raio r ´e 4 vezes o volume do

cone com diˆametro da base 2r e altura r. (4 3πr3).

(6)

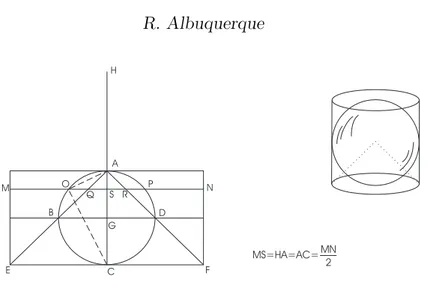
Figura 4: O M´etodo aplicado no c´alculo de volumes.

O volume da esfera é 2/3 do volume do cilindro com altura e diâmetro da base iguais ao diâmetro da esfera.

A demonstra¸cão utiliza a ideia de equil´ıbro estático de sólidos, teoria que Arquimedes desenvolvera para a f´ısica e que não considerava do mesmo rigor que as suas obras matemáticas. Eis porque se diz que o resultado terá ficado de parte. Por outro lado, também há relatos que Arquimedes terá gostado tanto do seu (grande) teorema, que pediu que esculpissem o esquema da esquerda da figura 4 no seu túmulo. Vejamos a demonstra¸cão do teorema, de acordo com o exposto em [4].

O esquema representa uma seçcão da esfera e de um cilindro e um cone com o dobro da base dos mencionados. O ponto A servirá de fulcro da balan¸ca. Passa-se uma recta (um plano paralelo ao plano da base) genérica por S. Por semelhan¸ca de triângulos, AC AO = AO AS. Logo MS · SQ = AC · AS = AO2 _{= QS}2_{+ OS}2 _{e então} HA AS = MS SQ = MS2 MS · SQ = MS2 QS2_{+ OS}2.

Estabelecidas estas rela¸c˜oes e raciocinando como com corpos em equil´ıbrio, vem, no centro de gravidade G = S para o cilindro (onde HA

AS = 2) e em H para a

esfera e para o cone,

(7)

pois que se ‘integram’ aquelas áreas circulares. Finalmente, como cilindro= 3 co-nes AEF por [Euclides, Elementos, XII] [7]; e como cone AEF = 8 cone ABD, por duplica¸cão de uma medida unidimensional, resulta daquela equa¸cão,

esfera ABCD = 4 cone ABD. Para a segunda parte, temos

cilindro pequeno = 6 cone ABD = 3

2esfera ABCD.

Note-se que o método de exaustão estava aqui interligado. Bem como que a ideia rigorosa do Método será mais complicada do que a aplica¸cão que dela aqui se faz.

Obras anteriores de Arquimedes dão-nos os enunciados do teorema acima. Mas só no Método é que ele explica como o obteve (aquele e muitos outros), defendendo ainda que o seu método mecânico lhe parecia tão bom como os demais geométricos pelos quais, ao longo da vida, por vezes em segunda ocasião havia provado os seus resultados. Cremos que um destes é o resultado sobre a parábola (teorema 1) pois são conhecidas duas demonstra¸cões.

1.3 Area da superf´ıcie esf´

´

erica

Arquimedes estudou também a área da superf´ıcia esférica, a fronteira da esfera sólida. Alguns livros de geometria diferencial atribuem-lhe o seguinte resultado (cf. [5, 12]).

Teorema 3 (Arquimedes). A projec¸c˜ao cil´ındrica φ(p) = (θ, z) de S2 _{sobre a}

superf´ıcie cilindr´ıca ´e equiareal, ie. preserva as ´areas.

Recordemos que a projeçcão cil´ındrica corresponde à projeçcão tomada na horizontal dos pontos de um paralelo na esfera sobre a respectiva circunferência no cilindro. Para vermos tal projeçcão em cartas ou mapas da esfera, utilizamos coordenadas, e então, para termos um aberto de R2_{, temos de retirar um}

semi-meridiano da esfera incluindo os p´olos (como um corte). Denotam-se as esferas de dimens˜ao n e raio r por Sn

r. Temos ent˜ao um ponto

p ∈ S2

r descrito por (θ, z), um ˆangulo θ relativo ao desvio do semi-meridiano

retirado e uma altura z correspondente ao paralelo. Calcula-se ent˜ao o elemento

de ´area:

ω = r dθ ∧ dz, (3)

(8)

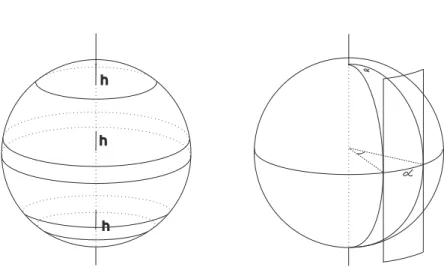
Figura 5: Dois resultados com origem no teorema de Arquimedes. Corol´ario 1. Todos os an´eis de S2

r com a mesma altura h tˆem exactamente a

mesma ´area.

Com efeito, tal área será dada pelo integral Z ω = r Z _2π 0 Z _a+h a dzdθ = 2πhr. (4) Em particular, área S2

r = 4πr2. E usando argumentos como os que vimos no

in´ıcio (fig. 2) pode-se descobrir de novo o volume da esfera. Sob a perspectiva do ângulo, temos que uma área lunar (a superf´ıcie entre dois semi-meridianos fazendo um ângulo α) é 2r2_{α. Vejam-se os dois resultados na figura 5. O último}

permite-nos provar:

Proposi¸c˜ao 1 (cf. [12]). A área de um triângulo esférico (cf. figura 6) sobre a

superf´ıcie esf´erica de raio 1 ´e α + β + γ − π.

Seja X a área que se procura. Repare-se que o triângulo dado tem um dual, ant´ıpoda, e cada um dos três ângulos admite duas correspondentes áreas iguais. Notêmo-las respectivamente por A, B, C. Pelo resultado acima, temos

X + A = 2α, X + B = 2β, X + C = 2γ.

Por outro lado, 2X + 2A + 2B + 2C = 4π, pelo que agora o valor de X se torna f´acil de encontrar.

Note-se que o triângulo considerado é geodésico, ie. as suas arestas são ‘rec-tas’ da esfera, ou seja caminhos mais curtos entre quaisquer dois dos seus pontos.

(9)

Figura 6: ´Area do triângulo esférico é α + β + γ − π.

Sabe-se que estes caminhos são dados por arcos de circunferência máximos, ie. com raio igual ao da esfera.

A projeçcão cil´ındrica conserva as áreas - não as distâncias! Não é uma

isometria. Para tal, basta ver a projec¸c˜ao de um paralelo, que aumenta. Ou a

de um meridiano, que diminui. Mas a geodesia é uma matéria que merece um estudo próprio...

Os trabalhos de Arquimedes são verdadeiramente assombrosos pela exigui-dade de instrumentos matemáticos de que ele dispunha! O seu Método ainda hoje é estudado1_{, pois não só a F´ısica que envolve é útil e verdadeira como a}

rela¸cão com a matemática está no âmago dos problemas actuais. Por isso ele é considerado um dos três maiores matemáticos de sempre2_.

Não esque¸camos todo o trabalho teórico constru´ıdo por Arquimedes ao longo de 75 anos. Ele encontra-se nas suas obras referenciadas por historiadores e cro-nistas gregos, romanos ou árabes, que o inglês Thomas L. Heath, reconhecido historiador e tradutor de Arquimedes, ordenou cronologicamente como segue:

Do Equil´ıbrio de Planos I, A Quadratura da Parábola, Do Equil´ıbrio de Planos II, Da esfera e do Cilindro I, II, Das Espirais, Dos Conóides e Esferóides, Dos Corpos Flutuantes I, II, Da Medida do C´ırculo e O Arenário. Faltando-nos

ainda descobrir onde se integram o M´etodo dos Teoremas Mecˆanicos e

Stoma-chion (obra seguramente tardia) e O livro dos Lemas (cf. [1, 6, 8, 9])3_.

1_{Fa¸ca-se uma busca em http://arxiv.org/ com archimedes no t´ıtulo.} 2_{Sendo a sua ef´ıgie aquela que aparece nas c´elebres medalhas Fields.}

3_{Outra importante referˆencia no estudo de Arquimedes parece ser com certeza E. J.}

(10)

Na dimensão 0 a medida usual é a de contagem. Na dimensão 1 temos a no¸cão de comprimento de uma curva no espa¸co como a do limite da soma do comprimento de linhas poligonais inscritas.

Mas como contamos a área de uma superf´ıcie, se nem sequer localmente a podemos planificar4_{? Que conceito afinal de volume é esse na dimensão 2 ou}

em dimens˜oes superiores?

A resposta é hoje facilmente ultrapassada por meio da teoria da ‘métrica em variedades diferenciáveis’ ou geometria riemanniana. Seja na geometria diferen-cial ou na f´ısica teórica, um tal instrumento não passa de uma idealiza¸cão.

Abstra´ımos da realidade dos objectos f´ısicos, com rigor matemático, um espa¸co vectorial tangente onde fazemos a geometria clássica e da´ı partimos para o estudo de fenómenos intr´ınsecos ou invariantes e, sob uma perspectiva nova, de propriedades globais5 _{dos espa¸cos, seus subespa¸cos e do movimento entre}

estes.

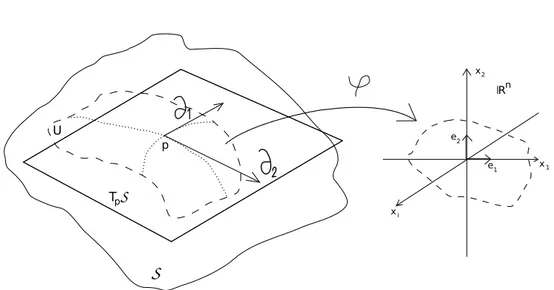
Suponhamos então que é dada uma por¸cão de superf´ıcie S ou uma variedade de dimensão n (conceito mais geral, mas a mesma ideia que em dim 2) como na figura 7. Um espa¸co tangente em cada ponto p ∈ S está bem definido, em virtude de conhecermos as cartas do espa¸co dado. Ou seja, temos um atlas de

S, que ´e um conjunto de cartas ϕ : U → Rn _{com os U subconjuntos abertos de}

S.

Agora supomos que é dada a métrica, o instrumento matemático h , i que nos permite calcular ângulos,

](u, v) = arccos hu, vi

kukkvk, e comprimentos kuk =

p

hu, ui, (5)

∀u, v ∈ TpS. A métrica é dada por uma aplica¸cão bilinear, simétrica e

definida-positiva, isto é, um produto interno com valores em R. Se esta for razoável, então tem uma varia¸cão suave com p, ou seja é de classe C∞_.

A m´etrica fica bem determinada numa carta local pelos valores h∂i, ∂ji, i, j =

1, . . . n. Recordemos que vectores ∂i, de classe C∞ por natureza, s˜ao induzidos

4_{Ter´ıamos grande problema em provar que o limite da soma de ´areas de faces poligonais}

inscritas numa qualquer superf´ıcie daria um invariante.

5_{Este conceito não tem nada a ver com a famigerada ‘globaliza¸cão’ das rela¸cões humanas}

(11)

Figura 7: Definimos espa¸co tangente TpS no ponto p sobre uma variedade S

de dimens˜ao n independente da escolha das cartas. Por outro lado, escolher uma carta ϕ significa escolher coordenadas. E adoptar o respectivo referencial tangente ∂i, i = 1, 2, ....

em T S pela própria carta ϕ. São campos vectoriais locais. Havendo necessidade, podê-mo-los denotar por ∂_iϕ.

Seja ϕ(p) = (x1, . . . , xn), ∀p ∈ U, onde cada xi é fun¸cão de p. ´E fácil

adivi-nhar que as cartas resultam em fun¸c˜oes C∞_{sobre as variedades, por constru¸c˜ao,}

e que verificar˜ao

dϕp(∂i) = ei, ou seja ∂i =

∂ϕ−1

∂xi

. (6)

Suponhamos agora que nos ´e dada outra carta qualquer ψ com dom´ınio (outro U) passando pelo dom´ınio U de ϕ. Escrevamos ψ(p) = (y1, . . . , yn).

Então temos uma ‘lei de transforma¸cão natural’ entre cartas na interseçcão dos dom´ınios ∂_iϕ = n X k=1 ∂yk ∂xi ∂_kψ (7)

e logo, por bilineariedade da m´etrica,

h∂_iϕ, ∂_jϕi = n X k,l=1 ∂yk ∂xi ∂yl ∂xj h∂_kψ, ∂ψ_l i. (8)

Note-se que esta equa¸cão nos dirá se temos uma métrica bem definida ou não: é importante que o tal aparelho para medir o espa¸co seja compat´ıvel com uma mudan¸ca de cartas, o que se verificará ou não pela equa¸cão (8).

(12)

ou seja, se G = [h∂_i , ∂_ji]i,j=1,...,n e J ´e a matriz jacobiana [_∂x_i], ent˜ao aquela

equa¸c˜ao escreve-se

Gϕ = JtGψJ (9)

com Jt _{a matriz transposta de J.}

E temos finalmente em qualquer dimens˜ao a defini¸c˜ao vol S =

Z

ϕ(U )

√

det Gϕ_dx₁_{. . . dx}_n_. ₍₁₀₎

Nota importante: esta é a ideia essencial da defini¸cão de volume, pois surge um problema de dom´ınio. Claro que aqui estamos apenas a integrar em U esque¸cendo o resto de S. Para chegar a todo o lado usar´ıamos parti¸cões da

unidade, um dispositivo algo t´ecnico que requer o seu tempo pr´oprio.

Eis essencialmente como se chega hoje ao volume sabendo apenas o integral de Riemann, o qual é bem conhecido da Análise. (A história mostrará inclusive que este é que foi feito para aquele e não o contrário, como agora parece estarmos a pretender).

Teorema 4. vol S n˜ao depende da escolha da carta.

Ressalvando a quest˜ao do dom´ınio, este resultado vem de (9), de o de-terminante de um produto de matrizes ser o produto dos dede-terminantes e de det Jt_{= det J, donde}

Z √ det Gϕ_dx 1. . . dxn= Z √ det Gψ _{det J dx} 1. . . dxn =Z √det Gψ_dy 1. . . dyn, (11)

como quer´ıamos. A ´ultima igualdade vem pela propriedade conhecida da mu-dan¸ca de vari´avel no integral de Riemann (o fundamental que falta provar).

Note-se que a ‘forma diferencial’ ΩS, de grau igual `a dimens˜ao de S,

ΩS(x) =

√

det G dx1 ∧ . . . ∧ dxn, (12)

x ∈ S, é já por si uma entidade bem definida pois é, de novo, independente da

escolha das cartas. Utiliza-se aqui a ´algebra exterior ou de Grassmann... ΩS ´e

(13)

2.1 Dois casos conhecidos

Há dois casos onde a teoria acima surge logo numa expressão conhecida. Se por exemplo γ : [a, b] → Rn _{é uma curva simples C = γ([a, b]) num}

intervalo [a, b] e a métrica no seu espa¸co tangente é aquela própria e r´ıgida do espa¸co ambiente Rn_{, então}

comprimento C = Z _b

a

kγ0_{(t)k dt.} ₍₁₃₎

A dedu¸cão é simples: uma carta de γ, de acordo com o exposto acima, é dada pela inversa ϕ = γ−1 _{e logo ∂}ϕ ₌ dγ

dt.

O segundo caso é em dimensão 2, quando temos uma por¸cão de superf´ıcie S em R3 _{dada por uma equa¸cão z = f (x}

1, x2), com (x1, x2) ∈ D ⊂ R2. Ent˜ao cada

ponto p = (x1, x2, f (x1, x2)) ∈ S fica coordenado pela carta ϕ : S → D, ϕ(p) =

(x1, x2). Os vectores coordenados tangentes s˜ao

∂1 = ³ 1, 0, ∂f ∂x1 ´ , ∂2 = ³ 0, 1, ∂f ∂x2 ´ . (14) Logo h∂1, ∂1i = 1 + (_∂x∂f₁)2, h∂1, ∂2i = _∂x∂f₁_∂x∂f₂, h∂2, ∂2i = 1 + (_∂x∂f₂)2, donde det Gϕ _{= det} " 1 + (f0 x1) 2 _f0 x1f 0 x2 f0 x1f 0 x2 1 + (f 0 x2) 2 # = 1 + (f0 x1) 2_{+ (f}0 x2) 2_. ₍₁₅₎

Assim a área de uma superf´ıcie (dimensão 2) é dada por área S = Z Z D q 1 + (f0 x1) 2_{+ (f}0 x2) 2_dx 1dx2, (16)

uma f´ormula bem conhecida.

Vejamos ainda outro exemplo. Na esfera S2

r com a m´etrica do espa¸co

eucli-diano ambiente, com as coordenadas cil´ındricas φ(p) = (θ, z), vem φ−1_{(θ, z) =}

(√1 − z2_{cos θ,}√_{1 − z}2_{sin θ, z). E logo}

∂1 = ∂φ−1 ∂θ = (− √ 1 − z2_{sin θ,}√_{1 − z}2_{cos θ, 0),} ∂2 = ∂φ−1 ∂z = µ −z cos θ √ 1 − z2, −z sin θ √ 1 − z2, 1 ¶ . (17)

Contas auxiliares mostram facilmente h∂1, ∂1i = 1 − z2, h∂1, ∂2i = 0, h∂2, ∂2i = 1

(14)

Outra propriedade intr´ınseca, ie. invariante da escolha da carta, que resulta de se ter definido uma m´etrica sobre a superf´ıcie considerada ´e a chamada curvatura

de Gauss, uma certa fun¸c˜ao escalar k : S → R que em cada ponto p nos diz

quão distante estão as mais ´ınfimas vizinhan¸cas de p de se parecerem com um dos três modelos:

k =     

−1 para o ponto de sela

0 para o plano euclidiano 1 para a esfera S2_.

(18) Estamos certos que o leitor reconhecerá aqueles três tipos de curvatura em dimensão 2, nomeadamente consultando [12].

Esta fun¸cão escalar k dependente da métrica, descoberta pelo matemático C. F. Gauss (1777-1855) e generalizada a dimensão n pelo igualmente genial B. Riemann (1826-1866), tem acrescida uma propriedade muito especial (também esta generalizável a qualquer dimensão onde entram as classes de Pontryagin). Teorema 5 (Gauss-Bonnet). Se S é compacta e orientável, R_Sk = 2πχ.

Ou seja, somada a curvatura sobre o espa¸co todo obtemos essencialmente a caracter´ıstica de Euler — regressamos a um invariante estritamente topológico! Surpresa, de uma matéria que parecia estar reservada cada vez mais e mais aos deuses da matemática.

2.3 An´

alise – ´

Algebra – Topologia

Conjugam-se em geometria diferencial vários campos da matemática. Tentare-mos uma constata¸cão deste facto ainda com o cálculo de volumes. Procurando lembrar o matemático português e nosso mestre Professor Armando Machado, introdutor no ensino português das ideias que se seguem (cf. [11]).

2.3.1 O teorema de Fubini em variedades

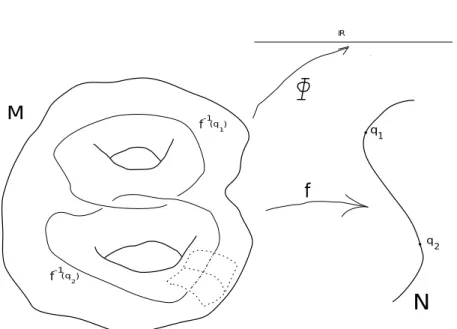
Suponhamos que nos são dadas variedades Riemannianas M e N, ie. variedades com métricas C∞_{. Suponhamos que é dada uma fun¸cão f : M → N também}

C∞_{. Um teorema devido a A. Sard (de 1942) diz-nos que os pontos cr´ıticos}6 _de

6_{Aqueles p ∈ M onde a caracter´ıstica de df}

(15)

Figura 8: Se dim M = n, dim N = n e q ∈ N é valor regular, então f−1_{(q) é}

variedade suave de dimens˜ao m − n.

f formam um conjunto de medida nula. Dito de outra forma, quase todos os

valores que f toma s˜ao regulares.

Uma consequência mais avan¸cada do teorema7 _{da fun¸cão inversa mostrará}

que os subconjuntos

f−1(q) =©x ∈ M : f (x) = qª, q ∈ N valor regular, (19) são subvariedades mergulhadas, isto é, comportam-se muito bem quando q é valor regular: existe uma carta especial (x1, . . . , xm) de M onde esses conjuntos

ser˜ao dados por equa¸c˜oes

xm−n+1 = 0, . . . , xm = 0 (20)

(cf. figura 8, a tracejado). Repare-se que M = ∪y∈Nf−1(y).

Assim, dada ainda mais uma fun¸cão escalar Φ : M → R para dar razão a este esfor¸co, temos uma nova fun¸cão definida quase por todo o N:

q ∈ N 7−→

Z

f−1_(q)

Φ(x) Ωf−1_(q)(x), (21)

7_{Se a fun¸c˜ao f tiver como derivada df}

p : TpM → Tf (p)N um isomorfismo em p, então a fun¸cão inversa f−1 _{existe numa vizinhan¸ca de p e é C}∞_.

(16)

Suponhamos f sobrejectiva. Para cada x ∈ M podemos definir o Jacobiano de f

(Jf )(x) = | dethdfx(ei), fji| = kdfx(e1) ∧ · · · ∧ dfx(en)k (22)

onde e1, . . . , en ´e uma base ortonormada (hei, eji = δij) do subespa¸co ortogonal

a ker dfx e f1, . . . , fn ´e uma base ortonormada de Tf (x)N. Prova-se facilmente

que Jf n˜ao depende da escolha de tais bases.

Note-se que dfx : TxM → TyN ´e sobrejectiva num valor regular y = f (x).

Por outro lado, se x é um ponto cr´ıtico, então (Jf )(x) = 0. O seguinte teorema remonta ao grande matemático H. Poincaré (1854-1912).

Teorema 6 (fórmula cinemática, cf. [10]). Se Φ é mensurável à Borel e tal que

x 7→ Φ(x)Jf (x) é integrável em M, então a fun¸cão (21) é integrável e

Z N µZ f−1_(y) Φ(x)Ωf−1_(y)(x) ¶ ΩN(y) = Z M Φ(x)Jf (x)ΩM(x). (23)

Este teorema exprime a forma mais geom´etrica do conhecido teorema de Fubini.

2.3.2 O grupo ortogonal

Consideremos SO(n) o grupo das isometrias de Rn _{de determinante 1:}

trans-forma¸cões lineares do espa¸co preservando a métrica euclidiana e a orienta¸cão. A sua composi¸cão, vindo de hgu, gvi = hu, vi, ∀u, v ∈ Rn_{, é a das matrizes g}

tais que gt_{g = 1 e det g = 1. Temos de facto um grupo. Claro que da primeira}

equa¸cão resulta logo det g = ±1 e nós escolhemos a parte que tem det 1. Mais, SO(n) é variedade compacta (fácil) e conexa (dif´ıcil). Eis duas pro-priedades topológicas important´ıssimas na compreensão da geometria do grupo

ortogonal.

Seja M o espa¸co vectorial de todas as matrizes a de ordem n e seja N o subespa¸co daquelas que s˜ao sim´etricas. Seja f : M → N definida por f (x) =

xt_{x. Ent˜ao f}−1_{(1) = SO(n) ∪ SO(n)}−_{. Claro que SO(n)}− _{se refere aos g tais}

que gt_{g = 1 e det g = −1.}

As direçcões em M tangentes a f−1_{(1) são aquelas sobre as quais f não varia,}

e rec´ıprocamente pois 1 ´e valor regular. Com efeito, prova-se que Tg(SO(n)) =

ker dfg. Como pela regra de Leibniz

(17)

no ponto g = 1 vem Tg(SO(n)) = ker dfg = {X ∈ M : Xt+ X = 0}, ou seja

todas as matrizes anti-simétricas. Agora torna-se muito fácil ver a dimensão de SO(n): um vector tangente é uma matriz anti-simétrica, portanto descrita pelas entradas do triângulo acima da diagonal principal e excluindo esta por ser nula. Contando, temos a fórmula

dim SO(n) = n(n − 1)

2 . (24)

Por exemplo, um ângulo dá-nos as rota¸cões de R2 _{e três parâmetros as de R}3_,

mas s˜ao precisos seis para coordenar as rota¸c˜oes de R4_...

2.3.3 A esfera como espa¸co de ´orbitas

Agora voltemos à superf´ıcie esférica de raio 1 de dimensão n − 1, denotada por

Sn−1 _{⊂ R}n_{. Fixemos uma direc¸c˜ao e}

n qualquer perpendicular a um subespa¸co

Rn−1 _{⊂ R}n_{. O grupo ortogonal actua na esfera rodando-a sobre si mesma.}

f : SO(n) → Sn−1 _{actua como g 7→ g(e}

n), uma fun¸c˜ao sobrejectiva, C∞ e

regular.

Quais são os g que fixam en? São precisamente os que só rodam Rn−1, donde

a escrita do ‘espa¸co sim´etrico’

SO(n)/SO(n − 1) = Sn−1 ₍₂₅₎

como um espa¸co de ´orbitas {SO(n − 1)g : g ∈ SO(n)}.

Com algum cuidado pode-se provar que Jf (g) = 1. Resulta então do teo-rema 6, chamemos-lhe de Fubini-Poincaré, lendo a fórmula (23), que

vol SO(n) = vol Sn−1vol SO(n − 1) = vol Sn−1vol Sn−2 · · · vol S1vol S0. (26)

A ´ultima igualdade resulta claramente por indu¸c˜ao. Como por outras vias se conhece o volume das esferas

vol Sn−1=    (2π)n2 2·4···n−2 para n par 2(2π)n−12 1·3···n−2 para n ´ımpar, (27) eg. generalizando (16) ou consultando [6], vem

vol SO(n) =      2n(n+2)4 πn24 Q(n−2)/2 i=0 (2i)! para n par 2(n+1)24 _πn2−14 Q(n−3)/2 i=0 (2i+1)! para n ´ımpar. (28)

(18)

posi¸cão da geometria diferencial, lembrando que há muitos volumes ainda por calcular de variedades muito importantes e que de ideias novas para tal está o evoluir da Ciência dependente.

Referˆ

encias

[1] Arquimedes. Geometrical solutions derived from mechanics. Tradu¸cão de o “Método” para inglês da tradu¸cão de 1909 para alemão por J. L. Heiberg; dispon´ıvel pelo Projecto Gutenberg.

[2] Arquimedes. The quadrature of the parabola.

http://www.math.ubc.ca/-cass/archimedes/parabola.html. Tradu¸c˜ao de Th. L. Heath.

[3] C. B. Boyer. A History of Mathematics. Wiley, 2nd edition, 1991. Revista por C. Merzbach.

[4] S. E. Brodie. An ancient extra-geometric proof.

http://www.cut-the-knot.-org/pythagoras/Archimedes.shtml.

[5] D. McDuff e D. Salamon. Introduction to Symplectic Topology. Oxford Mathematical Monographs. OUP, 1999.

[6] Enciclop´edias Wikip´edia e Larousse.

[7] Euclides. Elementos. http://www.mat.uc.pt/ jaimecs/euclid/elem.html. [8] I. Gratten-Guinness, editor. Companion Encyclopedia of the History and

Philosophy of the Mathematical Sciences. Taylor and Francis Books Ltd,

routledge reference edition, 1993.

[9] Th. L. Heath. The works of Archimedes. Cambridge UP, 1897.

[10] R. Howard. Classical integral geometry in riemannian homogeneous spaces.

Contemp. Math., 63:179–204, 1987.

[11] A. Machado. Geometria Diferencial - Uma Introdu¸c˜ao Fundamental. 1a

edi¸c˜ao pela Editora Cosmos, 1991, 2a _{edi¸c˜ao pelo DMFCUL.}

[12] A. Pressley. Elementary Differential Geometry. Springer Undergraduate Mathematics Series. Springer-Verlag, London, 2001.