○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
Algu ns nú m eros possu em características qu e parecem aproxim á-los m ais da m agia do qu e da Ciência. Neste artigo de estréia, Dona Fifi (ou ΦΦ, se preferirem ...) m ostra-nos a face m ais saborosa.
I
ncentivada pelo editor desta sim -pát ica r evist a, m eu con t er r â-neo e, ele próprio, u m fibonacci, anim ei-m e a escrever esse texto qu e deveria tratar de u m a tese qu e defen-do há m u ito tem po, onde argu m ento qu e o cérebro fem inino é m ais adap-tado qu e o m ascu lino para entender as su tilezas da Física Qu ântica. O edi-tor, porém , insistiu qu e eu escolhesse ou tro tem a, considerando este m u ito polêm ico. Acabou m e convencendo com o argu m ento de qu e tal assu nto não seria de interesse im ediato para m eu s ex - coleg a s, p r ofessor es de ciências do cu rso ginasial.Tu do bem . Falarei, então, de as-su nto am eno e inofensivo, m as creio qu e capaz de su stentar a atenção de m eu s leitores até o final do artigo. Tra-tarei de u m nú m ero fam oso desde os t em pos de Eu clides de Alexan dria, patriarca da geom etria qu e viveu por volta do ano 300 antes de Cristo. Este nú m ero, cham ado de Φ, foi definido por Eu clides com o resu ltado de u m a operação geom étrica m u ito sim ples.
Tom e u m segm ento de reta AB e encontre u m ponto interm ediário, C, tal qu e AC/ CB = AB/ AC.
Pois bem , essa razão é o nú m ero
Φ qu e vale:
Defin ido a ssim , o n ú m er o Φ
costu m a ser cham ado de “proporçã o á urea”, u m nú m ero de ou ro qu e su
r-ge, com o verem os, onde m enos se
es-pera, na Matem ática, na Física, na Biologia, nas artes e até nas conspi-rações esotéricas.
Vam os, para com eçar, exam inar algu m as propriedades do nú m ero Φ
e m ostrar com o obtê-lo por operações algébricas sim ples. Obser ve qu e, se considerarm os qu e o segm ento CB é igu al a 1 e qu e o segm ento AC vale x, tem os, por constru ção:
. Isto é, x2 – x – 1 = 0.
Com o toda equ ação de segu ndo grau , esta tem du as solu ções qu e são:
.
É claro qu e a solu ção positiva, x1, é ju stam ente o nú m ero Φ, a “propor-ção áu rea”. O negativo da ou tra so-lu ção será cham ado de φ. Portanto:
e
Com o já disse e vou contar logo m ais, o nú m ero Φ aparece em inú -m er as e in esper adas sit u ações, n a Ciência, nas artes e nas coisas natu -rais e sobrenatu -rais. Mas, antes, vou falar de algo qu e foi descoberto sécu -los após Eu clides por u m m atem ático cham ado Leonardo qu e, sendo m ora-dor de Pisa, a cidade on de existe a fam osa torre inclinada, era conhecido com o Leonardo de Pisa. E, com o nas-Ma ria Efigên ia Go m es de Alen ca r
(Do n a Fifi)
Hoje aposen tada, foi professora de Ciên cias em escolas de Sobral, Ceará. Den tre ou tras aven tu ras, teve o privilégio de presen ciar o fam oso eclipse qu e com provou a relatividade geral de Ein stein . Su as apostilas podem ser lidas em : w w w.seara.u fc.br
cera de fam ília de boa estirpe, ficou tam bém conhecido com o Fibonacci, qu e significa, literalm ente, “filho de boa gente”.
Pois esse Fibonacci pu blicou , em 1202, u m livro cham ado “Livro dos Ábacos” onde tratava de vários tem as m atem áticos qu e considerava com o im portantes. Um deles, provavelm en-te inventado por ele próprio, tratava do pr oblem a de calcu lar qu an t os coelhos poderiam ser produ zidos em u m ano, a partir de u m ú nico casal. Da for m a com o en u n ciado por Fi-bonacci, o problem a é m u ito artifi-cial. Su põe qu e cada casal leva u m m ês, após nascer, para ficar fértil, gera sem pre ou tro casal, a cada m ês, e nenhu m coelho m orre du rante o ano. Mas o qu e interessa é o resu ltado.
O m ês inicial (0) é u sado para qu e o prim eiro casal atinja a fertilidade. No m ês segu inte o casal está fértil e u m novo casal é gerado. Portanto, du -rante o segu ndo m ês, terem os dois casais, o original (o X na figu ra in-dica u m casal fértil) e o novo (repre-sentado por u m a cru z), ainda infértil. No terceiro m ês, o casal original gera m ais u m casal e o segu ndo casal fica fértil. Portan to, n esse terceiro m ês terem os três casais. Agora, os dois pri-m eiros casais estão férteis e cada u pri-m gera u m novo casal. Dessa form a, o nú m ero de casais no qu arto m ês será 5. E assim por diante.
O resu ltado é u m a seqü ência de nú m eros em qu e cada u m deles é obti-do pela som a obti-dos obti-dois nú m eros im e-diatam ente anteriores:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
Esta é a “seqü ência de Fibonacci”. A expressão qu e dá o nú m ero de Fibonacci de ordem n é, sim plesm ente:
F (n) = F (n - 1) + F (n - 2). Pu la n do m a is a lgu n s sécu los chegam os a Johannes Kepler, o célebre
astrônom o das três leis planetárias. Kepler notou , em 1611, qu e a divisão entre u m nú m ero de Fibonacci e seu precedente leva ao nú m ero Φ qu ando se avança para valores cada vez m aio-res n a seqü ên cia. Em t er m os m a-tem áticos, isto qu er dizer qu e F(n) / F(n - 1) tende para Φ qu ando n tende para infinito. Pegu e u m a calcu ladora e verifiqu e isso.
De m odo inverso, os núm eros de Fibonacci podem ser gerados a partir de potências de Φ segundo a expressão:
.
O interessante nessa expressão é qu e os nú m eros de Fibonacci, qu e são racionais, podem ser gerados de po-tências de Φ, qu e é irracional. Tecnica-m ente, diz-se qu e os nú Tecnica-m eros de Fi-bonacci segu em u m a “lei de potên-cia”. Nú m eros com essa propriedade não são com pletam ente aleatórios.
O núm ero Φ, por si m esm o, já tem algu m as propriedades cu riosas. Com o vim os, ele é irra cio n a l, com o seu colega m ais fam oso, o nú m ero π. Isto sign ifica qu e esses n ú m er os n ão podem ser obtidos pela divisão de dois inteiros. Só qu e o nú m ero Φ é m enos redondinho, m as m ais sofisticado e im p r ev isív el. Ele p ode su rg ir de ex pr essões m at em át icas bast an t e cu riosas. Por exem plo, con sidere a expressão abaixo:
.
Parece m u ito com plicado, m as, na verdade, é bem fácil m ostrar qu e esse nú m ero x é ju stam ente nosso Φ. Tom e o qu adrado de am bos os lados dessa expressão:
Ora, com o o nú m ero de raízes é infinito, o segu ndo term o do lado di-reito da equ ação acim a é ju stam ente x. Logo, tem os
x2 = 1 + x.
Portanto, com o vim os anterior-m ente, resu lta qu e x = Φ.
Ou tra expressão cu riosa qu e leva a Φ é essa:
.
Deixo a vocês a tarefa sim ples de m ostrar qu e esse x tam bém é nosso qu erido Φ. Mas, qu ero aproveitar essa fr ação qu e n ão acaba n u n ca par a com entar qu e o nú m ero Φ talvez seja o m ais irracional dos nú m eros irra-cionais. Pois essa fração converge tão vagarosam ente para Φ qu e parece nos m ostrar a relu tância de Φ em se asso-ciar a u m a fração, m esm o qu e a fra-ção não seja de inteiros.
O qu adrado de Φ, isto é, ΦΦ, vale 2,6180339887...
Com o vem os, o nú m ero ΦΦ é o próprio n ú m ero Φ acrescido de 1. Além disso, o inverso de Φ, isto é, 1 /
Φ é igu al a 0,6180339887..., qu e é Φ
-1 e, com o vem os, é o ou tro φ, defini-do anteriorm ente. Portanto, o nú m e-ro Φφ é igu al a 1.
Podem os constru ir u m a seqü ên-cia qu e ch am arei de “seqü ên ên-cia de Fifibonacci”, form ada pelos qu adra-dos adra-dos nú m eros de Fibonacci. Ela é: 1, 1, 4, 9, 25, 64, 169, 441, 1156, 3025, 7921,...
É claro qu e a fração entre dois nú -m eros consecu tivos dessa seqü ência co n v er g e p a r a o n ú m er o ΦΦ= 2,6180339887... Deixo para vocês a t arefa de en con t r ar u m a regr a de form ação para essa seqü ência.
A Fig. 1 m ostra u m tijo lo de Fi-bo n a cci qu e é u m paralelepípedo de
lados 1, Φ e φ. Ele tem volum e unitário e a área total de su as faces é 4Φ. Esse tijolo pode ser inscrito em u m a esfera de raio 1. Portanto, a razão entre as
áreas da esfera e do tijolo inscrito é π/
Φ, cu rioso encontro entre dois pres-tigiosos nú m eros irracionais.
Podem os, tam bém , con str u ir o tijolo de Fifibonacci, com lados 1, ΦΦ
e φφ. Esse tijolo tam bém tem volu m e u nitário m as su a área total é igu al a 8, u m sau dável retor no à raciona-lidade.
A letra Φ é a 21a letra do alfabeto
grego. 21, é claro, é u m dos nú m eros de Fibonacci. Os esotéricos adoram essas coincidências e ficam im aginan-do códigos secretos relacionaaginan-dos com esses nú m eros. Meu nom e, por sinal, tem 5 e 8 letras, dois nú m eros conse-cu tivos na seqü ência de Fibonacci, o qu e, presu m ivelm en te, m e con fere poderes m ágicos, m esm o sem ter de gritar Shaz am!
A origem de Φ, com o vim os, foi geom étrica. A proporção áu rea foi m u ito u tilizada por artistas da pós-ren ascen ça n a com posição de seu s qu adros. Um a constru ção geom étrica qu e leva a u m resu ltado interessante com eça com u m retân gu lo on de a razão entre a largu ra L e a altu ra H seja ju stam ente Φ. Esse é u m retân-gu lo áu reo. Rebaten do u m lado de altu ra H, obtem os u m qu adrado e ou tro retângu lo áu reo, este de lados L1 e H1. Pois L1/H1 = Φ, novam ente.
Se o processo for repetido no segu ndo retânsegu lo áu reo, obtem os ou tro qu adrado e ou tro retângu lo, tam -bém áu reo, sendo L2/H2 = Φ. E aí você tom a gosto e vai repetindo a brinca-deira até enjoar, obtendo retângu los áu reos cada vez m enores qu e conver-gem para u m ponto qu e cham am os de pó lo da constru ção. É fácil ver qu e
esse pólo é o encontro de t odas as dia-gonais maiores de t odos os ret ângulos áureos da const rução (Fig. 2)
Os m atem áticos adoram dar no-m es grandiosos a seu s objetos. O pró-prio nom e da proporção áu rea já é desse tipo. Pois esse pólo é cham ado, por eles, de “olho de Deu s”. Descon-tando a pretensão, vale a pena m en-cionar qu e a cu r va qu e leva ao pólo aproxim a-se de u m a espira l lo ga rít-m ica qu e René Descartes cham ava de
“espiral equ iangu lar ”, pois traçando qu alqu er reta a partir do pólo ela corta a cu r va sem pre com o m esm o ângu lo. Esse pode ser o m ote para qu e eu
com ece a com ostrar a vocês cocom o o nú -m ero Φ e a seqü ência de Fibonacci su r-gem em coisas da natu reza.
Dizem qu e as aves predadoras, co-m o águ ias, falcões e gaviões, desceco-m sobr e su as pr esas segu in do u m a espiral com o essa, com a presa n o pólo. Com o os olhos das aves são la-terais, fazendo isso, a ave m antém a presa sem pre na m esm a linha de vi-são sem qu e precise girar a cabeça, o qu e preju dicaria a aerodinâm ica do vôo.
No m u ndo vegetal o nú m ero Φ e a seqü ência de Fibonacci su rgem em m u itas situ ações. O arranjo dos ga-lhos nos troncos das ár vores e das fo-lhas nos galhos costu m a segu ir u m a
seq ü ên cia de Fibo n a cci (Fig . 3 ). Partindo de u m a folha baixa, conta-m os o nú conta-m ero de voltas econta-m torno do galho até chegar a ou tra folha exata-m en te aciexata-m a da in icial. Na figu ra, partindo da folha (1), precisam os de 3 rotações no sentido horário para chegarm os à folha (6) qu e está direta-m ente sobre a pridireta-m eira. Nessas 3 vol-tas, passam os por 5 folhas. No senti-do anti-horário, bastam 2 voltas. No-te qu e 2, 3 e 5 são nú m eros de Fi-bonacci.
Correndo o risco de ser prem atu -ram en te classificada com o cadu ca, com provei essa tendência dos vegetais em vár ios exem plares de plan t as, com o esse singelo arbu sto fotogra-fado por m eu neto Antônio no qu in-tal de nosso sítio na Meru oca. Nesse caso, precisei de 5 voltas no sentido horário para encontrar u m galho exa-tam ente sobre o m ais baixo, passando
Figu ra 2. Representação geom étrica das proporções áu reas.
Figu ra 3. A seqü ência de Fibonacci nas folhas de u m a planta.
por 8 galhos no processo (Fig. 4). Os botânicos acham qu e essa for-m a de dispor folhas e galhos tefor-m u for-m a razão prática, aproveitada pela sele-ção natu ral. Ela torna m ais eficiente a u tilização da lu z
solar e a exposição às gotas da chu va. Faz sentido, m as a seqü ência de Fibo-nacci e su a espiral característica tam
-bém aparecem em situ ações vegetais onde a explicação não é tão evidente. Um bom exem plo é o abacaxi, es-sa delicioes-sa fru ta qu e, dizem as m ás lingu as, é o sím bolo do nosso cinem a. Nessa fotografia de u m belo abacaxi (Antônio, novam ente), podem os ver as espirais form adas pelos gom os da casca (Fig. 5). Cada gom o tem a form a aproxim ada de u m hexágono e par-ticipa de três espirais qu e se cru zam .
Form ando o m enor ângu lo com o eixo do abacaxi, 8 espirais paralelas circu -lam a fru ta. Com u m ângu lo m aior, são 13 espirais paralelas e com ângu lo m aior ainda, são 21 espirais. Não pre-ciso n em lem br ar qu e 8, 13 e 21são nú m eros su cessivos na seqü ência de Fi-bonacci.
Coisa parecida, e até m ais evidente, acon tece com os girassóis, on de o nú m ero de espirais form adas pelas se-m entes da flor é bese-m grande. Infeliz-m en te, n ão en con trei girassóis eInfeliz-m nosso jardim para fotografar. Reco-m endo qu e procu reReco-m eReco-m ou tros jar-dins.
M as essa é u m a r evist a par a estu dantes e professores de Física e até agora ainda não falei de situ ações fí-sicas onde o nú m ero Φ e os nú m eros de Fibonacci aparecem . Pois, vou falar. Existem áreas da Física onde os n ú m eros de Fibon acci su rgem por constru ção proposital e dão resu lta-dos interessantes. Veja, inicialm ente, u m exem plo m u ito sim ples: du as pla-cas de vidro, com índices de refração diferentes, ju stapostas u m a sobre a ou tra (Fig. 6). Um raio de lu z qu e inci-da sobre esse conju nto pode sofrer re-flexões e desvios. Vam os con t ar o nú m ero de cam inhos possíveis de u m raio de lu z au m entando, gradu alm en-te, o nú m ero de reflexões nesses cam i-nhos.
Olhando a figu ra, podem os ver qu e o nú m ero de cam inhos segu e a seqü ência de Fibonacci. Representan-do o nú m ero de reflexões, cham aRepresentan-do
de “geração”, pela letra n, o nú m ero de cam inhos será F(n), u m nú m ero de Fibonacci. Por exem plo, a geração n = 4 leva a F(4) = 8 cam inhos.
O físico n ordest in o Eu den ilson Lins de Albu qu erqu e é u m especialista no estu do das propriedades físicas de cam adas de m ateriais em pilhadas se-gu ndo seqü ências de Fibonacci. Dos trabalhos qu e ele já pu blicou pincei u m exem plo relativam ente sim ples.
Form am -se pilhas com cam adas de dois m ateriais transparentes com índices de refração diferentes. A Fig. 7 m ost ra com o m on t ar essas pilh as segu ndo u m esqu em a tipo Fibonacci. Cada pilha é form ada colocando-se as du as pilh as an t er iores u m a sob a ou tra.
Um problem a físico interessante consiste em saber qu anta lu z conse-gu e atravessar u m a dessas pilhas. Isto é, procu ra-se saber qu al é a “trans-m itância” T da lu z através da pilha, sendo T definido com o T = I/I0, onde I0 é a intensidade da lu z incidente e I é a intensidade da lu z qu e sai do ou tro lado da pilha (Fig. 8).
As espessu ras das cam adas são feitas de m odo a serem “oticam ente equ ivalentes”. Isto significa qu e a lu z leva u m tem po igu al para atravessar qu alqu er u m dos dois tipos de cam ada ou , o qu e é o m esm o, qu e o nú m ero de ondas da lu z é igu al em cam adas de tipos diferentes. Com esse arranjo, su r g em in t er essa n t es ca so s de
Figu ra 5. O abacaxi de Fibonacci, ou m e-lh or, a seqü ên cia de Fibon acci n o aba-caxi…
Figu ra 6. Nú m ero de cam inhos possíveis, au m entando o nú m ero de reflexões, de u m raio de lu z qu e passa entre du as placas de vidro com índices de refração diferentes: a seqü ência de Fibonacci em Óptica.
Figu ra 7. Pilhas com cam adas de dois m a-teriais transparentes com índices de refra-ção diferentes segu ndo u m esqu em a tipo Fibonacci.
Figu ra 8. Medida da transm itância da lu z a t r a v és de u m a p ilh a de Fibo n a cci m ontada confor m e a Fig. 7.
Existem áreas da Física onde os números de Fibonacci
surgem por construção proposital e dão resultados
interferência entre os feixes de lu z qu e se refletem nas interfaces entre ca-m adas vizin h as. Por execa-m plo, se a esp essu r a ót ica das cam adas for exatam ente igu al a m eio com prim en-to de onda da lu z, isen-to é, d = λ / 2, os feixes refletidos nas faces su cessivas interferem destru tivam ente e se ani-qu ilam m u tu am ente. Nesse caso, por-tanto, a transm issão de lu z pelas ca-m adas é coca-m pleta,
T = 1. Se a espes-su ra das cam adas fo r ig u a l a u m q u a r t o de u m co m p r im en t o de onda da lu z, isto é, d = λ / 4, os feixes refletidos se refor-çam m u tu am ente e
a transm issão é incom pleta, T < 1. Para ou tros com prim entos de onda da lu z, T varia entre esses dois valores ex t r em os. Qu a n do o n ú m er o de cam adas cresce segu ndo as gerações de Fibon acci, a tran sm issão de lu z varia entre 0 e 1 de u m a form a qu e dep en de da or dem n a seq ü ên cia (Fig. 9).
Essa figu ra, qu e foi adaptada de u m dos t r abalh os de Eu den ilson , m ostra com o a transm issão de lu z (T) varia com o com prim ento de onda da lu z incidente para u m a pilha corres-pondente à geração S7, com 13 ca-m adas. Uca-m resu ltado interessante é qu e a forma dessas cu r vas de trans-m issão se reprodu z a cada 6 gerações de Fibonacci. Isto é, essa figu ra tam -bém está m ostrando T para u m a pilha cor respon den te à geração S13, com 233 cam adas. Basta aju star a escala dos com prim entos de onda de form a
adequ ada.
Sem pre qu e su rge u m a reprodu -ção de form as desse tipo diz-se qu e a cu r va estu dada tem “propriedade de escala”. Os físicos adoram encontrar essas “leis de escala” em seu s m odelos e experim entos. Esse com portam ento qu e acabam os de relatar talvez seja m ais u m a m anifestação da não-alea-toriedade dos nú m eros de Fibonacci, m en cion ada an t e-rior m ente.
Va m o s a g o r a falar do problem a de preencher u m plano com m osa icos de for m as arbitrárias. É u m problem a geo-m étrico cogeo-m igeo-m pli-cações na Física dos Sólidos, com o verem os. Se os m o-saicos tiverem a form a de polígonos regu lares, com lados e ângu los igu ais, topam os logo com u m a lim itação. Triângu los, qu adrados e hexágonos regu lares podem ser u sados par a cobrir u m plano, m as, pentágonos não ser vem para isso. Qu ando ten-tam os cobrir u m piso com m osaicos pen tagon ais logo con statam os qu e sobram espaços vazios. Essa obser-v a çã o leobser-v o u o s cr ist a ló g r a fo s à conclu são de qu e não poderiam existir cristais onde os átom os e m olécu las se aju stassem form ando u m a sim e-tria pentagonal, tam bém cham ada de “sim etria de ordem -5”.
Mas o plano pode ser preenchido com m osaicos n ão - regu lares. Ou , com m ais de u m tipo de m osaico, com for m as diferentes. O incrível pintor holandês Mau ritiu s Escher, qu e u m a vez m e presenteou com u m a de su as
belas gravu ras, era u m m estre nessa arte de preencher planos com figu ras de todo tipo. Sem a sofisticação dos qu adros de Escher, podem os ver qu e u m piso pode facilm ente ser coberto, sem deixar vazios, por m osaicos he-xagonais e pentagonais, em u m pa-drão sem elhante ao qu e vem os nas bolas de fu tebol.
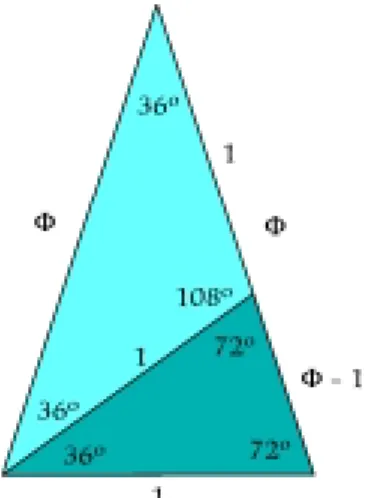
O físico inglês Roger Penrose, que foi or ien t ador do fam oso St eph en Haw king, inventou um tipo de m o-saico de duas form as com caracterís-ticas aparentem ente contraditórias: tem sim etria de ordem -5, preenche o plano e não é periódico. Os m osaicos de Penrose são form ados a partir de um triângulo isósceles de lados iguais a Φ
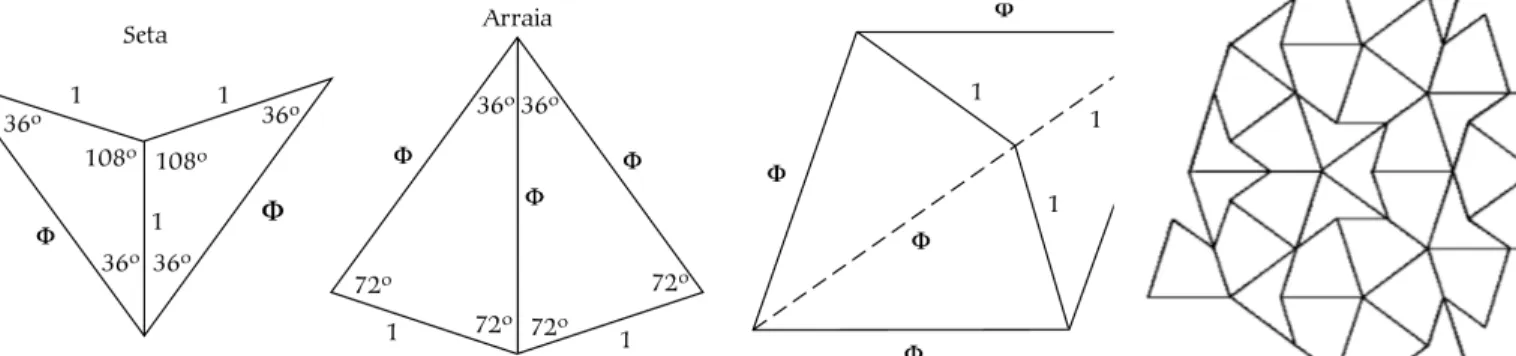
(Fig. 10). Esse triângulo converte-se em dois, m ostrados com cores diferentes na figura, dividindo-se um dos lados em um a parte que m ede 1 e outra que m ede Φ - 1. Com binando esses novos triângulos, Penrose m ontou dois tipos de m osaico, um a seta e um a arraia (que os sulistas cham am de pipa). Usando esses dois “m osaicos de Pen rose” o plano pode ser preenchido. Mais um a vez, não preciso nem dizer com o esse m osaico está repleto de proporções áureas (Fig. 11).
É su rpreendente qu e, se dividim os o nú m ero de arraias pelo nú m ero de setas em u m a dada área do m osaico de Penrose, essa fração tende para Φ
qu ando a área exam inada é cada vez m aior.
Os m osaicos de Penrose cobrem u m a su perfície plana bi-dim ensional, Figu ra 9. Variação da transm itância com o com prim ento de onda da lu z indicindo em
u m a pilha de Fibonacci com 13 cam adas.
Figu ra 10. Triângu lo isósceles de lados igu ais a Φ.
Mosaicos de Penrose: formados a partir de um triângulo isósceles de lados
iguais a F, apresentam características contraditórias:
têm simetria de ordem-5, preenchem o plano e não
m as os m atem áticos já acharam pares de for m as volu m étricas qu e preen-chem por com pleto o espaço tri-di-m ensional. São objetos qu e letri-di-m bratri-di-m cu bos com fa ces
r epu x adas, t odas idên ticas aos m o -sa ico s p la n o s de Pen rose. São ch a-m ados, por cau sa disso, de “rom boe-dros áu reos”.
O qu e n ão se esperava, porém , é qu e a sim et r ia de
ordem -5, presente nos m osaicos de Pen rose e n esses r om boedros qu e enchem o espaço, pu desse su rgir em objetos físicos reais, com o sólidos. Mas, su rgiu . Na década de 80 do sécu lo passado for am descober t os certos m ateriais qu e tinham sim etria de o r dem 5 e u m a r r a n jo n ã o -periódico. Foram cham ados de “qu a-se-cristais”, pois têm sim etria de rota-ção, com o os cristais norm ais, m as não têm sim etria de translação, isto é, não possu em u m a “célu la” qu e se repet e per iodicam en t e em algu m a direção espacial.
Penrose, qu e é u m especialista em bu racos-negros, inventou seu s m o-saicos m eio de brincadeira e não im a-ginava qu e eles chegassem a ser ú teis na descoberta e explicação dos qu ase-cristais. Mais recentem ente, Penrose passou a se dedicar à tarefa de pro-cu rar explicações para a consciência, essa propriedade espantosa qu e tem os de pensar, fazer associações e bu scar explicações até para a própria
cons-ciência, em u m processo au to-recor-rente u m tanto vertiginoso. Penrose acha qu e a consciência pode ser o re-su ltado de processos qu ânticos qu e têm lu gar no inte-rior dos microt ubos, u m em aranhado de filam entos qu e for-m afor-m o cit oesquelet o, est r u t u r a presen t e em todas as célu las dos seres vivos. Se-gu n do Pen rose, os m icrotu bos seriam o local m ais propício para abrigar os processos qu ânticos qu e resu ltariam na consciência. Não creio qu e valha a pena entrar nos de-talhes desse palpite de Roger Penrose m as cabe con tar com o ele en volve tam bém os nú m eros de Fibonacci.
A parede de u m m icrotu bo é for-m ada por colu nas de u nidades cha-m adas de t ubulins. Ao t odo, u m m icrotu bo tem 13 colu nas de tu bu -lins. A disposição dos tu bu lins form a espir ais qu e lem br am as espir ais desenhadas pelos gom os do abacaxi. Com o vem os no desenho, segu indo as espirais em torno do m icrotu bo, encontram os padrões qu e se repetem a cada 3, 5, 8 e 13 u nidades. Todos esses nú m eros, é claro, fazem parte da seqü ência de Fibonacci (Fig. 12).
Tem gente qu e já su geriu qu e o aparecim en t o dos n ú m eros de Fi-bonacci nos m icrotu bos não se dá por acaso. Do m esm o m odo qu e o arranjo de Fibonacci facilita o aproveitam ento da lu z do sol e da águ a da chu va nas folhas e nos galhos das ár vores, tam -Figu ra 11. “Mosaicos de Penrose”, qu e preenchem exatam ente u m a área plana.
Figu ra 12. Microtu bos apresentam u m a seqü ência de Fibonacci. Para Penrose, a consciência pode ser o resu ltado de pro-cessos qu ânticos qu e têm lu gar no inte-rior dessas estr u tu ras.
Referências
M. Livio, The Golden Ratio (Broadw ay Books, New York, 2002).
R. Penrose, A Ment e Nova do Rei (Editora Cam pu s, 1991).
E.L. Albu qu erqu e e M.G. Cottam , Physics Reports 3 7 6, 255 (2003).
bém poderia prom over o flu xo de in-form ações nos m icrotu bos. Haja espe-cu lação, m as, pelo m en os, é u m a especu lação excitante.
Mu ito m ais há para contar sobre esses m ar avilh osos n ú m eros m as acho m elhor parar por aqu i. Com essa introdu ção vocês já estão prontos para adqu irir a m ania de encontrar a pro-porção áu rea e os nú m eros de Fibo-nacci nas coisas do m u ndo em qu e vivem . Qu em sabe, até descobrir no-vas associações ainda desconhecidas. Ou tra vez, se o editor da revista m e perm itir e se, antes disso, o acendedor do big- bang não m e convocar para u m t êt e-à-t êt e, voltarem os a conver-sar, talvez até sobre os assu ntos polê-m icos qu e polê-m encionei.
Penrose dedicou- se à tarefa de procurar explicações para a consciência. Ele acha
que a consciência pode ser o resultado de processos quânticos que têm lugar no
interior dos microtubos, e, oh, nanotubos também