Aula 2 – Congruˆ
encia de segmentos e ˆ
angulos
Objetivos
• Introduzir um conceito fundamental em Geometria: o conceito de
con-gruˆencia.
• Estudar congruˆencia de segmentos e de ˆangulos.
Introdu¸
c˜
ao
Vamos agora estudar um conceito fundamental em Geometria: o con-ceito de congruˆencia. Intuitivamente, podemos dizer que duas figuras planas s˜ao congruentes se ´e poss´ıvel sobrepˆo-las exatamente, ou seja, sem “faltar” nem “sobrar” um ponto em nenhuma das duas, mesmo que para isso seja ne-cess´ario virar uma delas “ao avesso” (o que ocorre quando uma ´e a imagem da outra refletida num espelho). Fa¸ca uma experiˆencia desenhando a m˜ao livre a mesma figura em dois pap´eis transparentes. Procure juntar os dois e olh´a-los contra a luz. Provavelmente as figuras n˜ao ficar˜ao exatamente so-brepostas: ´e muito dif´ıcil desenhar figurascongruentes a m˜ao livre. A figura 14 mostra trˆes figuras congruentes.
Fig. 14: Figuras congruentes.
Figuras planas
Uma figura plana ´e formada por um conjunto de pontos no plano.
Congruˆ
encia de segmentos
No caso espec´ıfico de segmentos, a congruˆencia ´e relacionada ao “ta-manho”. Assim, intuitivamente, dois segmentos de reta s˜ao congruentes se tˆem o mesmo tamanho. Partindo dessa no¸c˜ao intuitiva, podemos formular os seguintes axiomas:
• Todo segmento ´e congruente a si mesmo.
• SeAB ´e congruente a CD, ent˜ao CD ´e congruente a AB.
• SeAB´e congruente aCD eCD ´e congruente aEF, ent˜aoAB
´e congruente a EF.
Congruˆencia de segmentos
O primeiro axioma sobre congruˆencia de segmentos diz que a congruˆencia de segmentos ´ereflexiva. O segundo diz que a congruˆencia de segmentos ´e
sim´etricae o terceiro diz que a congruˆencia de segmentos ´etransitiva. Uma rela¸c˜ao em Matem´atica, que satisfaz `as trˆes propriedades acima, ´e chamada derela¸c˜ao de equivalˆencia.
Para indicar que dois segmentos s˜ao congruentes, usaremos o s´ımbolo≡.
Assim, se AB e CD s˜ao dois segmentos congruentes, vamos escrever AB ≡
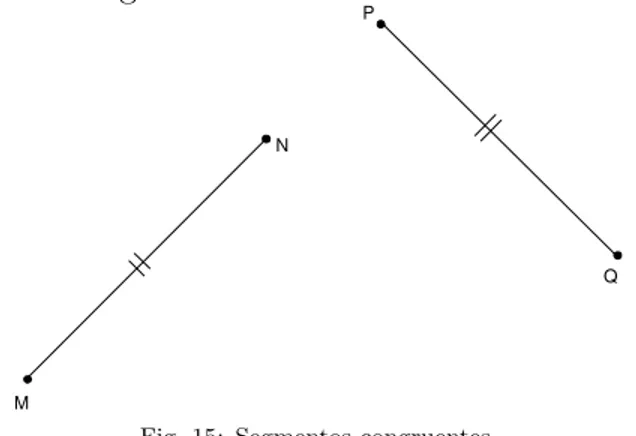
CD (lˆe-se AB´e congruente a CD). Nos desenhos, a indica¸c˜ao de segmentos congruentes ´e feita com alguns riscos curtos transversais, de modo a indicar que todos os segmentos cortados com um risco s˜ao congruentes entre si; todos aqueles cortados com dois riscos s˜ao congruentes entre si, e assim por diante, como vocˆe pode ver na figura 15.
M
N P
Q
Fig. 15: Segmentos congruentes.
O pr´oximo axioma (ilustrado na figura 16) diz que a congruˆencia de segmentos ´eaditiva:
A B
C
D E F
Fig. 16: A congruˆencia de segmentos ´e aditiva.
• Se B est´a entre A e C, E est´a entre D e F, AB ≡ DE e
BC ≡EF ent˜ao AC ≡DF. No¸c˜oes comuns
Dado um segmento de reta AB, a nossa intui¸c˜ao nos diz que existem v´arios segmentos que s˜ao congruentes a ele e que se vocˆe considerar uma reta r qualquer, e um pontoC nessa reta, v˜ao existir exatamente dois segmentos de reta congruentes a AB contidos emr e come¸cando em C (um para cada “lado” de C). O axioma a seguir formaliza essa id´eia.
Axioma de transporte de segmentos.
• Dados um segmentoAB e uma semi-reta −−→
CD, existe um ´unico pontoE ∈
−−→
CD tal que AB≡CE (veja a figura 17).
B
C E
D
A
Fig. 17: Transporte do segmentoABpara a semi-reta
→
CD.Como j´a dissemos, o que temos visto at´e agora s˜ao propriedades e ca-racter´ısticas de objetos ideais. EmDesenho Geom´etricoestuda-se como obter boas aproxima¸c˜oes dessas id´eias, usando apenas r´egua e compasso para de-senhar no papel retas, circunferˆencias, segmentos congruentes, etc. Algumas dessasconstru¸c˜oes geom´etricasser˜ao vistas na se¸c˜ao de exerc´ıcios desta aula e ao longo das pr´oximas.
Desenho geom´etrico e Geometria
Como linguagem de comunica¸c˜ao e express˜ao, a arte do desenho antecede em muito a escrita. Atrav´es de desenhos feitos nas paredes das cavernas, o homem pr´e-hist´orico registrou fatos relacionados com o seu cotidiano, deixando registros para que possamos conhecer um pouco seu modo de vida. Podemos dizer que a arte do desenho ´e algo inerente ao homem. O Desenho Geom´etrico nasceu na Geometria grega. Entre os gregos era tˆenue a diferen¸ca entre Desenho Geom´etrico e Geometria. Podemos dizer que o Desenho Geom´etrico ´e uma parte da Geometria que se prop˜oe a resolver
problemas com o aux´ılio de instrumentos.
Veja o exemplo a seguir onde dois segmentos AB e CD s˜ao somados sobre uma semi-reta −→EF. Pelo axioma de transporte de segmentos, existe um ´unico ponto G ∈
−→
EF tal que AB ≡EG. O mesmo axioma garante que
existe um ´unico pontoH na semi-reta oposta a −GE−→tal que GH ≡CD. Veja
a figura 18. O segmento EH obtido representa a soma dos segmentos AB e CD.
B E
G
A
D C
H F
Fig. 18: Soma dos segmentosABeCD.
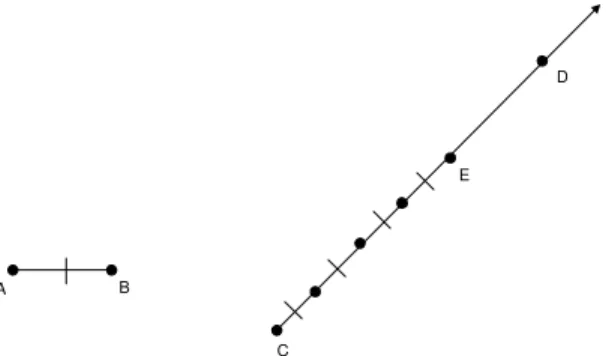
Do mesmo modo, podemos obter m´ultiplos de um segmento AB dado, somando-o repetidas vezes a ele mesmo. Veja na figura 19 um caso particular em que somamos 4 c´opias do segmento AB. Neste caso, podemos escrever
queCE = 4AB.
Quando ocorre de um segmentoCD “conter” exatamenten segmentos congruentes a AB, escrevemos simplesmente CD ≡ nAB ou AB ≡ 1
nCD. Dizemos que um segmento CD ´e m´ultiplo de AB se CD ≡ nAB para
al-gum n´umero natural n n˜ao-nulo. Nesse caso, diz-se tamb´em que AB ´e um subm´ultiplo de CD.
B
C A
E D
Fig. 19: M´ultiplo de um segmento.
Essas considera¸c˜oes nos conduzem naturalmente `a id´eia de medir seg-mentos. A id´eia de medir segmentos servir´a para fundamentarmos a no¸c˜ao de congruˆencia. Para medir segmentos adotamos um segmento AB como unidade de medida e verificamos simplesmente quantas vezes ele “cabe” em um outro segmento dado. A id´eia ´e de fato simples, mas o processo pode trazer surpresas como veremos adiante. Por exemplo, o segmento a ser me-dido pode n˜ao ser um m´ultiplo de AB. Fa¸ca um teste com os segmentos da figura 20, usando o segmento AB como unidade de medida, para medir os demais segmentos (vocˆe pode usar uma r´egua ou um palito com o mesmo comprimento de AB).
Consideramos N={0,1,2, . . .}o conjunto dos n´umeros naturais. Observe que inclu´ımos o 0 (zero) no conjunto dos n´umeros naturais. Representamos o conjunto dos n´umeros naturais, excluindo o 0 (zero), porN∗. O conjunto Z={. . . ,−2,−1,0,1,2, . . .} ´e chamado de conjunto dos n´umeros inteiros. Dizer que um n´umero ´e
inteiro positivo´e o mesmo que dizer que esse n´umero ´e
natural n˜ao-nulo. Um n´umero ´e ditoracional
se ele pode ser escrito na
forma p q
, sendopeq n´umeros inteiros eq6= 0.
B A
C D
E F
G H
Note que, na figura 20, o segmento CD ´e congruente a 2AB e o seg-mento EF ´e congruente a 3AB. Adotando AB como unidade de medida, dizemos que a medida de CD ´e 2 e que a medida de EF ´e 3. Por´em, o segmentoGH n˜ao ´e um m´ultiplo de AB. Esse segmento ´e congruente a trˆes vezes 1
2AB. Nesse caso, dizemos que a medida deGH ´e 3
2. Em geral, quando ocorre de um dado segmento ser congruente a m vezes 1
nAB, dizemos que sua medida ´e m
n.
Considere agora um segmento CD. Ainda pensando no segmento AB como unidade de medida, podem acontecer trˆes situa¸c˜oes: a medida de CD ´e um n´umero inteiro positivo, ou a medida de CD ´e um n´umero racional positivo ou CD n˜ao ´e congruente a nenhum m´ultiplo de nenhum segmento da forma n1AB, para nenhum n inteiro. Nos dois primeiros casos, dizemos que AB e CD s˜ao comensur´aveis. No ´ultimo, dizemos que AB e CD s˜ao incomensur´aveis.
A existˆencia de segmentos que n˜ao s˜ao comensur´aveis ´e atribu´ıda aos pitag´oricos. Voltaremos a falar de tais segmentos na aula 11.
Considerando essa no¸c˜ao de medida de segmento que acabamos de in-troduzir, e fixando uma unidade de medida, apresentamos os seguintes axio-mas:
• A cada segmento AB est´a associado um n´umero real positivo
que chamamos medida de AB, e escrevemos m(AB). Dois segmentos s˜ao congruentes se, e somente se, suas medidas s˜ao iguais. Do mesmo modo, se considerarmos um n´umero real posi-tivo qualquer, digamosc, ent˜ao existem segmentos com medida igual ac.
• SeB est´a entre A eC, ent˜ao m(AC) = m(AB) +m(BC).
SeAB e CD s˜ao incomensur´aveis, a medida de CD, usando AB como unidade de medida, ser´a um n´umero irracional positivo.
Usando essa no¸c˜ao de medida, definimos distˆancia entre pontos:
Defini¸c˜ao 7 (Distˆancia entre dois pontos)
A distˆancia entre dois pontos distintos X e Y ´e a medida do segmento XY.
Pit´agoras, fil´osofo e
matem´atico grego, nasceu na ilha de Samos, na costa oeste da ´Asia Menor. Foi estudioso na juventude e ent˜ao viajou cerca de 30 anos. Aos mais ou menos 50 anos de idade emigrou para a colˆonia grega de Crotona, no sul da It´alia, onde come¸cou sua vida p´ublica. Ele se estabeleceu como professor e fundou a Escola Pitag´orica, uma associa¸c˜ao semi-secreta com centenas de alunos e que disputa a honra de ser a primeira universidade do mundo. O movimento fundado por Pit´agoras chamou-sepitagorismoe tinha prop´ositos religiosos, pol´ıticos e filos´oficos. Os pitag´oricos aconselhavam obediˆencia, silˆencio, abstinˆencia de certos alimentos, simplicidade no vestir e nas posses e o h´abito da auto-an´alise.
Acreditavam na imortalidade e na transmigra¸c˜ao da alma. Pit´agoras foi o primeiro a conceber a Matem´atica como um sistema de pensamento mantido coeso por provas dedutivas. Foi mesmo o primeiro a usar a palavraMathematikepara designar a Matem´atica. Antes dele, havia apenas a palavramathemata, que designava conhecimento ou aprendizado em geral. Consulte:
http://catanduvas.g12.br/ desgeo/
Atividade 1:
(Tra¸cando segmentos congruentes) Para esta atividade vocˆe dever´a usar r´egua e compasso. O objetivo ´e construir na semi-reta −CD−→ da figura 21 um segmento de reta come¸cando no ponto C e congruente ao segmento AB dado. Ou seja, vamos marcar um ponto E em −CD−→ tal que AB≡CE.
A
C
D
B
Fig. 21: Atividade 1.
Primeiro m´etodo: Use uma r´egua graduada para medir o segmentoAB e depois marcar o pontoE de forma que m(AB) =m(CE).
Segundo m´etodo: Coloque uma das pontas do compasso no pontoAe a outra no pontoB, ao mesmo tempo. Ao fazer isso, vocˆe estar´a fixando uma abertura do compasso. Veja figura 22. Sem modificar essa abertura, coloque a ponta de metal do compasso no ponto C e fa¸ca um risco com a ponta de grafite cruzando a semi-reta −CD. Aten¸c˜ao! Se o compasso abrir ou fechar−→ um pouquinho nessa opera¸c˜ao, vocˆe deve come¸car de novo. O ponto E que fica determinado pela interse¸c˜ao da semi-reta −CD−→ com o tra¸co do compasso ´e o ponto procurado.
Congruˆ
encia de ˆ
angulos
No caso de ˆangulos, a congruˆencia ´e relacionada `a abertura de seus la-dos. Assim, intuitivamente, dois ˆangulos s˜ao congruentes se eles tˆem a mesma abertura. Partindo dessa no¸c˜ao intuitiva, formulamos o seguinte axioma:
Axioma de transporte de ˆangulos
• Dados um ˆangulo BACˆ e uma semi-reta −−→
DE, em cada semi-plano determinado pela reta ←DE→ (que ´e o prolongamento de
−−→
DE) existe uma ´unica semi-reta −DF−→ tal que BACˆ ´e congru-ente a EDFˆ . Veja a figura 23.
A
B
C
D
E F
Fig. 23: Transporte do ˆangulo ˆA.
Usaremos tamb´em o s´ımbolo ≡para indicar a congruˆencia de ˆangulos.
Assim, para denotar que BACˆ ´e congruente a EDFˆ escreveremos simples-mente BACˆ ≡EDFˆ .
Finalizamos os axiomas sobre congruˆencia de ˆangulos com os pr´oximos dois axiomas. O primeiro deles formaliza a nossa pr´atica de medir ˆangulos com ajuda de um transferidor (veja a Atividade 2 desta aula) e o ´ultimo diz que a medida de ˆangulos ´e aditiva.
• A cada ˆangulo BACˆ do plano est´a associado um n´umero real
positivo menor que 180 chamado medida do ˆangulo BACˆ , e denotado por m(BACˆ ), tal que dois ˆangulos s˜ao congruentes se, e somente se, tˆem a mesma medida. Reciprocamente, para todo n´umero real positivo c menor que 180, existe um ˆangulo cuja medida ´ec.
• Se −−→
AD ´e uma semi-reta que divide BACˆ , ent˜ao m(BACˆ ) = m(BADˆ ) +m(CADˆ ), veja figura 24.
A
B
C D
Fig. 24:m(BACˆ ) =m(BADˆ ) +m(DACˆ ).
Nota: No segundo axioma enunciado acima usamos a no¸c˜ao de semi-reta que divide um ˆangulo. Uma semi-reta divide um ˆangulo se ela tem como origem a origem do ˆangulo e est´a contida no interior do ˆangulo. Outro modo equivalente de definir este conceito seria: “uma semi-reta divide um ˆangulo se possui origem coincidente com a origem do ˆangulo, e intersecta qualquer segmento cujas extremidades perten¸cam aos lados distintos do ˆangulo”. Veja a figura 24.
Vocˆe sabia que...
A base de numera¸c˜ao hindu era decimal, exatamente como utilizamos hoje. Por´em, a base de numera¸c˜ao babilˆonica era sexagesimal. Isto significa que eles utilizavam 60 s´ımbolos (algarismos) distintos para escrever todos os n´umeros. Infelizmente o zero era representado por uma lacuna, o que tornava a leitura de alguns n´umeros confusa. Talvez essa tenha sido a dificuldade essencial, que levou esse sistema a n˜ao ser absorvido pelas civiliza¸c˜oes que sucederam a civiliza¸c˜ao babilˆonica. Para esse povo, que utilizava um sistema de numera¸c˜ao de base 60, foi muito natural dividir o c´ırculo em 360 partes (grau), e cada uma destas partes em 60 partes (minuto) e repetir o processo para essas subpartes. Assim, o “grau” ´e uma inven¸c˜ao dos babilˆonios, que entraram para a hist´oria da ciˆencia matem´atica tendo dado a ela uma contribui¸c˜ao importante que utilizamos at´e hoje.
Atividade 2:
(Tra¸cando ˆangulos congruentes) Para esta atividade vocˆe dever´a usar r´egua, compasso e transferidor. O objetivo ´e construir um ˆangulo a partir da semi-reta−BC−→ da figura 25 que seja congruente ao ˆangulo ˆA dado.
A C
B
Fig. 25: Atividade 2.
Fig. 26: Transporte de um ˆangulo usando transferidor.
O segundo passo ´e transportar o ˆangulo. Coloque o transferidor sobre a semi-reta −BC−→ de modo que seu centro fique sobre o ponto B. Fa¸ca o zero da borda cair sobre a semi-reta−BC−→e marque um ponto na posi¸c˜ao da borda correspondente `a medida que vocˆe tomou. Chame esse ponto deD. O ˆangulo CBDˆ ter´a a mesma medida de ˆA.
Segundo m´etodo: Neste m´etodo use um compasso e uma r´egua (que n˜ao precisa ter marca¸c˜ao de medida). Fixe a ponta de metal do compasso sobre o ponto A e, com qualquer abertura, trace com a outra ponta uma curva que corte as duas semi-retas que formam o ˆangulo ˆA em dois pontos, E e F. Agora mantenha a abertura do compasso e fixe-o com a ponta de metal no pontoB. Trace com a outra ponta uma curva que corte −BC−→ (em um ponto que chamaremosG) e seja grande o bastante para cortar o ˆangulo depois de transportado (vocˆe deve ter uma estimativa do tamanho que ele vai ficar). Agora marque com o compasso a distˆancia entre E e F e transporte para a curva no segundo desenho come¸cando em G, determinando um ponto H. Trace a semi-reta−BH−→. O ˆanguloGBHˆ ser´a congruente a ˆA. Confira usando um transferidor. Veja a figura 27.
A
C
B
E
F
H
G
Fig. 27: Transporte de ˆangulo usando compasso.
Unidade de Medida de ˆangulo
Por motivos hist´oricos, usa-se o grau para indicar a medida de um ˆangulo. Assim, se a medida de BADˆ ´e 50, por exemplo, dizemos que BACˆ mede 50o(cinq¨uenta graus).
Observe que...
A congruˆencia de ˆangulos tamb´em ´e uma rela¸c˜ao de equivalˆencia.
Seja BACˆ um ˆangulo e D um ponto tal queA est´a entre C e D (veja figura 28). O ˆangulo BADˆ ´e chamado ˆangulo suplementar adjacente ao ˆanguloBAC.ˆ
A
B
C D
Fig. 28:BACˆ eBADˆ s˜ao ˆangulos suplementares adjacentes.
Usando os axiomas anteriores, pode-se mostrar que a soma das medidas de dois ˆangulos suplementares adjacentes ´e 180o. Em vista disso, estendemos a no¸c˜ao de ˆangulos e de medida de ˆangulos para o caso em que seus lados s˜ao semi-retas coincidentes e para o caso em que seus lados s˜ao semi-retas opostas. No primeiro caso dizemos que o ˆangulo ´e nulo, e no segundo caso dizemos que o ˆangulo ´e raso. A medida de um ˆangulo nulo ´e zero e a medida de um ˆangulo raso ´e 180o.
Dois ˆangulos s˜ao chamados suplementares se a soma de suas medidas for 180o, e s˜ao chamados complementaresse a soma de suas medidas for 90o.
Se dois ˆangulos suplementares adjacentes s˜ao congruentes (ou seja, tˆem a mesma medida), eles s˜ao chamados retos, e indicados como o ˆanguloBACˆ na figura 29. Como a soma das medidas de dois ˆangulos suplementares adjacentes ´e 180o, tem-se que a medida de um ˆangulo reto ´e 90o.
Al´em do grau, h´a tamb´em outras unidades para medir ˆ
angulos, como o radiano e o grado. Um ˆangulo mede um grado quando corresponde a 1/400 de uma circunferˆencia. Falaremos sobre o radiano na aula 17.
A B
C D
Fig. 29:BACˆ ≡BADˆ s˜ao ˆangulos retos.
A B
C D
E
Fig. 30: BACˆ eBADˆ s˜ao ˆangulos retos,EACˆ ´e agudo eEADˆ ´e obtuso.
´
E importante enfatizar que vocˆe n˜ao deve decorar os axiomas e sim se convencer de que eles s˜ao naturais. Muitas das propriedades que est˜ao nestas duas primeiras aulas em forma de axiomas v˜ao ser usadas nas aulas seguintes sem justificativa e, muitas vezes, nem notaremos que estamos usando um desses axiomas.
ˆ
Angulo reto e ˆangulo raso
O ˆangulo reto mede 90o
e o ˆ
angulo raso mede 180o
. Mas qual ´e a raz˜ao para os valores serem justamente 90 e 180?
Para entendermos isso, retornaremos ao ano de 4000 a.C., quando eg´ıpcios e ´
arabes estavam tentando elaborar um calend´ario. Nessa ´epoca, acreditava-se que o Sol girava em torno da Terra numa ´orbita que levava 360 dias para completar uma volta. Desse modo, a cada dia o Sol percorria uma parcela dessa ´
orbita, ou seja, um arco de circunferˆencia de sua ´orbita. A esse arco fez-se
corresponder um ˆangulo cujo v´ertice era o centro da Terra e cujos lados passavam pelas extremidades de tal arco. Assim, esse ˆangulo passou a ser uma unidade de medida e foi chamado de grau ou ˆ
angulo de um grau. Pode-se concluir, ent˜ao, que para os antigos eg´ıpcios e ´
arabes o grau era a medida do arco que o Sol percorria em torno da Terra durante um dia.
Hoje, sabemos que ´e a Terra que gira em torno do Sol, mas, manteve-se a tradi¸c˜ao e convencionou-se dizer que o arco de circunferˆencia mede um grau quando corresponde a 1/360 dessa circunferˆencia. Vamos resumir a nomenclatura sobre ˆangulos e suas medidas:
ˆ
Angulos e suas medidas
• Angulo reto - Um ˆangulo cuja medida ´e 90 graus.ˆ
• Angulo agudo - Um ˆangulo cuja medida ´e menor que 90 graus.ˆ
• Angulo obtuso - Um ˆangulo cuja medida ´e maior que 90 graus.ˆ
• Angulo nulo - Um ˆangulo cuja medida ´e 0 grau.ˆ
• Angulo raso - Um ˆangulo cuja medida ´e 180 graus.ˆ
• Angulos suplementares - ˆˆ Angulos cuja soma das medidas ´e 180
graus.
• Angulos complementares - ˆˆ Angulos cuja soma das medidas ´e 90
graus.
Resumo
Nesta aula vocˆe aprendeu...
• O significado de congruˆencia em Geometria.
• Alguns axiomas de congruˆencia de segmentos e de ˆangulos.
• As no¸c˜oes de medida de ˆangulo e de medida de segmento.
Exerc´ıcios
1. Fa¸ca um desenho onde constem pontos A, B, C e D e retas r e s, satisfazendo ao mesmo tempo a todos os itens abaixo:
• r es s˜ao concorrentes,
• A∈r eB ∈r,
• C ∈s e D∈s,
• AB ≡CD,
• AB eCD n˜ao se intersectam.
2. Desenhe sobre uma reta r trˆes pontos diferentes A,B eC (n˜ao neces-sariamente nessa ordem). Diga se ´e verdadeira ou falsa cada afirma¸c˜ao abaixo, de acordo com seu desenho.
• m(AB) =m(BC),
• CB ≡AB,
• Se B est´a entreA e C, ent˜ao m(AB) = m(BC),
• m(AB) = 2m(BA).
Alguma das afirma¸c˜oes depende do desenho que vocˆe fez para ser falsa ou verdadeira? Alguma delas ´e sempre falsa (independentemente do seu desenho)? Alguma delas ´e sempre verdadeira?
3. Considere trˆes pontos A, B e C tais que B esteja entre A e C. Se m(AC) = 18cm e m(BC) = 2m(AB), determinem(AB) e m(BC).
4. Considere quatro pontosA, B, C eDtais queB esteja entreAeC eC esteja entre B e D. Sem(AD) = 30cm, m(AB) = 2m(BC) e m(BC)
= 3m(CD), determinem(AB), m(BC) em(CD).
5. Sejam AB, CD e EF segmentos tais que CD ≡ 2AB e CD ≡ 5EF.
Adotando AB como unidade de medida, determine a medida de EF.
6. Considere quatro pontosA, B, C eDdispostos nessa ordem sobre uma retar(ou seja,Best´a entreAeCeCest´a entreB eD).SeAB≡CD,