ANÁLISE DA CONVECÇÃO FORÇADA NO ESCOAMENTO
BIDIMENSIONAL LAMINAR EM DUTOS
RETANGULARES VIA GITT COM VARIÁVEIS
PRIMITIVAS.
Por
Thiago Andrade Fernandes
Dissertação de Mestrado apresentada à Universidade Federal da Paraíba
para obtenção do grau de Mestre
João Pessoa – PB Setembro, 2012.
THIAGO ANDRADE FERNANDES
ANÁLISE DA CONVECÇÃO FORÇADA NO ESCOAMENTO
BIDIMENSIONAL LAMINAR EM DUTOS
RETANGULARES VIA GITT COM VARIÁVEIS
PRIMITIVAS.
Dissertação
apresentada
à
banca
examinadora do Curso de Pós-Graduação em
Engenharia Mecânica na área de concentração
Termofluídos da Universidade Federal da
Paraíba, em cumprimento às exigências para
obtenção do Grau de Mestre.
Orientador : Prof. Dr. Carlos Antonio Cabral dos Santos
F363a Fernandes, Thiago Andrade.
Análise da convecção forçada no escoamento bidimensional laminar em dutos retangulares via GITT com variáveis primitivas. / Thiago Andrade Fernandes. - João Pessoa, 2012.
83f.
Orientador: Carlos Antonio Cabral dos Santos.
ANÁLISE DA CONVECÇÃO FORÇADA NO ESCOAMENTO
BIDIMENSIONAL LAMINAR EM DUTOS
RETANGULARES VIA GITT COM VARIÁVEIS
PRIMITIVAS.
Por
Thiago Andrade Fernandes
Dissertação aprovada em 28 de setembro de 2012
Período letivo 2012.2
Prof. Dr. CARLOS ANTONIO CABRAL DOS SANTOS
Orientador
–
UFPB
Prof. Dr. FRANCISCO ANTONIO BELO
Examinador Interno
–
UFPB
Prof. Dr. LAURIVAN DA SILVA DINIZ
Examinador Externo
–
IFPB
AGRADECIMENTOS
Primeiramente, agradeço a Deus por todas as bênçãos que derramou sobre mim, apontando sempre o caminho certo.
A minha querida mãe, por todo zelo, carinho, cuidado e amor, em todas as fases da minha vida, que me fez engrandecer.
Jamais poderia esquecer a minha fiel companheira, Priscila, por toda paciência, todo amor, carinho, por todas as conversas e incentivos, além dos estímulos para sempre continuar batalhando, além de toda a sua família.
Ao professor Cabral, não só pelos conhecimentos compartilhados, mas pelo amigo que descobri.
Aos professores Marinaldo, Paulo e Jacques, pelas ajudas, idéias e conversas.
Aos demais professores do PPGEM e funcionários, inclusive Iolanda, com sua paciência, amizade e felicidade.
Aos colegas de mestrado, Mabel, Marcos Cézar, Kleber (Shokovisk), Alysson, Felix (Jimmy), Daniel, Smeagol e Pedro.
Aos amigos de infâncias, Matheus, Raul Neto, Márcios.
Aos amigos de colégios, Paulo, Wesley, Gabriel, Luciano (rato), Vladmir, Vitor, Daniel, Pedro (Pedrinho).
Por fim, mas não menos importante, agradeço a toda a minha família, em especial minha avó, meu irmão, minhas tias Danielle e Deise, meus tios Dênis e Daniel. Aos meus primos Matheus, Kleyton.
A Capes pelo suporte financeiro.
“Um sorriso no meu rosto não significa ausência de problemas, e sim a capacidade de
ser feliz sobre eles.”
ANÁLISE DA CONVECÇÃO FORÇADA NO ESCOAMENTO
BIDIMENSIONAL LAMINAR EM DUTOS RETANGULARES VIA
GITT COM VARIÁVEIS PRIMITIVAS.
RESUMO
No presente estudo, a convecção forçada no escoamento bidimensional em desenvolvimento simultâneo laminar em dutos com geometria retangular, é analisada analiticamente através das equações de Navier-Stokes, Poisson e da Energia em sua forma primitiva. Estas equações são resolvidas pela Técnica da Transformada Integral Generalizada, que tem característica hibrida-numérica. O desenvolvimento do trabalho é composto primeiramente pela reestruturação do problema, afim de que, possa ser resolvido pelo Fortran por meio da subrotina, da biblioteca IMSL, DBVPFD. Em seguida, são obtidos os resultados considerados de interesse práticos, como o campo de velocidade, o perfil da temperatura, o comportamento da temperatura média, o numero de Nusselt e o fator de atrito, com o objetivo de proporcionar parâmetros para melhor dimensionamento de equipamentos. Esses parâmetros são avaliados tanto longitudinalmente quanto horizontalmente. Por fim, os resultados são validados através de tabelas de convergência e comparações com artigos da literatura especializada.
ANALYSIS OF FORCED CONVECTION IN TWO-DIMENSIONAL
LAMINAR FLOW IN RECTANGULAR DUCTS WITH VIA GITT
PRIMITIVE VARIABLES.
ABSTRACT
In the present study, forced convection flow in two-dimensional laminar simultaneous development pipeline with rectangular geometry, is analyzed analytically
using the Navier-Stokes, Poisson and Energy in its primitive form. These equations are
solved by the Generalized Integral Transform Technique, which is characteristic
hybrid-numeric. The development work is composed primarily by restructuring the problem, so
that, it can be solved by using the subroutine Fortran, IMSL Library, DBVPFD. Then, the
results obtained are considered of practical interest, such as the velocity field, the temperature profile, the behavior of the average temperature, the Nusselt number and the friction factor, with the goal of providing a better parameter for construction equipment. These parameters are assessed both longitudinally and horizontally. Finally, the results are validated through convergence charts in order to comparisons with literature articles.
SUMÁRIO
AGRADECIMENTOS ... iv
RESUMO ... vii
ABSTRACT ... viii
LISTA DE FIGURAS ... xi
LISTA DE TABELAS... xii
LISTA DE SÍMBOLOS ... xiii
Letras Gregas ... xv
Sobrescritos e Subscritos ...xvi
CAPÍTULO I...1
INTRODUÇÃO ...1
1.1 – MOTIVAÇÃO E OBJETIVOS ...1
1.2 – SÍNTESE DO TRABALHO ...3
CAPÍTULO II ...5
REVISÃO BIBLIOGRAFICA ...5
2.1 – DESENVOLVIMENTO DA MECÂNICA DOS FLUIDOS ...5
2.2 - TRANSFORMADA INTEGRAL ...7
CAPÍTULO III... 13
MODELAGEM DO PROBLEMA FÍSICO ... 13
3.2 – PROBLEMA HIDRODINÂMICO ... 14
3.2.1 – Parâmetros adimensionais... 16
3.2.2 – Método de Solução do Problema Hidrodinâmico pelo uso Transformada ... 19
3.2.4 – Problema auxiliar para o Campo de Velocidade ... 22
3.2.5 – Problema Auxiliar para o Campo de Pressão ... 24
3.2.6 – Pares Transformada Inversa ... 25
3.2.7 – Calculo da velocidade Média e da Pressão Média ... 25
3.2.8 – Calculo da Velocidade Transversal ... 27
3.2.9 – Fator de Atrito ... 27
3.2.10 – Transformação Integral do Problema ... 28
3.3 – PROBLEMA DA TRANSFERENCIA DE CALOR ... 31
3.3.1 – Adimensionalização do problema ... 32
3.3.2 – Método de Solução do Problema de Temperatura de Calor Pelo uso da Transformada ... 33
3.3.3– Pares Transformada Inversa ... 34
3.3.4 – Transformação Integral do Problema de Energia... 35
3.3.5 – Calculo da Temperatura Média e do Número de Nusselt ... 36
3.4 – SOLUÇÃO DO SISTEMA DIFERENCIAL ORDINÁRIO ... 37
CAPÍTULO IV ... 43
RESULTADOS E DISCURSSÕES ... 43
4.1 – ANALISE DO PROBLEMA HIDRODINAMICO ... 43
CAPÍTULO V ... 59
RESULTADOS E SUGESTÕES ... 59
LISTA DE FIGURAS
Figura 3.1 – Desenvolvimento em dutos paralelos ... 14
Figura 4.1 – Desenvolvimento da componente longitudinal da velocidade, . ... 49
Figura 4.2 – Comportamento da velocidade longitudinal média. ... 50
Figura 4.3 – Comportamento da relação f.Re ao longo da componente X. ... 51
Figura 4.4 – Perfil de velocidade na posição axial (a) X=0,208 e (b) X=0,833. ... 51
Figura 4.5 – Perfil de velocidade na posição axial (a) X=3,333 e (b) X=7,5. ... 52
Figura 4.6 – O perfil de velocidade completamente desenvolvido na posição 12,228 ... 52
Figura 4.7 – Perfil de Pressão na posição axial (a) X=0,208 e (b) X=0,833. ... 53
Figura 4.8 – Perfil de Pressão na posição axial (a) X=3,333 e (b) X=7,5. ... 53
Figura 4.9 – Perfil de pressão na posição 12,228. ... 54
Figura 4.10 – Comportamento da temperatura no centro do duto ao longo do mesmo para Reynolds 300. ... 55
Figura 4.11 – Perfil de Temperatura na posição axial (a) X=0,208 e (b) X=0,833. ... 55
Figura 4.12 – Perfil de Temperatura na posição axial (a) X=3,333 e (b) X=7,5. ... 56
Figura 4.13 – Perfil de temperatura na posição 12,228 ... 56
LISTA DE TABELAS
Tabela 4.1 – Tabela de comparação da velocidade longitudinal, no centro do duto ( ),
para Reynolds 300. ... 44
Tabela 4.2 – Tabela de convergência da velocidade longitudinal no centro do duto ... 45
Tabela 4.3 – Tabela de convergência da velocidade media. ... 46
Tabela 4.4 – Tabela de convergência da pressão longitudinal no centro do duto ( )... 46
Tabela 4.5 – Tabela de convergência da pressão média. ... 47
Tabela 4.6 – Tabela de convergência da temperatura longitudinal no centro do duto . ... 48
LISTA DE SÍMBOLOS
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
Número de Biot
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
c Fator de contração de escala
Coeficiente gerado pela transformação integral
̅ Função da autofunção da velocidade onde é integrada de y a 1 em
relação a y
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
̅ Coeficiente gerado pela transformação integral
Coeficiente gerado pela transformação integral
Coeficiente de transferência de calor por convecção
Integral de normalização
NN Ordem de truncamento global, quanto NV=NP=NT
NP Ordem de truncamento da expansão da pressão
NT Ordem de truncamento da expansão da temperatura
NU Ordem de truncamento da expansão da velocidade
Função de determinação do número de Nusselt
Peclet
Prandtl
Coeficiente gerado pela transformação integral
Pressão admencional
Filtro da pressão
Pressão inicial
Potencial da pressão do campo em desenvolvimento
̅ Pressão transformada
̅ Pressão média
Coeficiente gerado pela transformação integral
Pressão dimencional
Reynolds hidraulico
Reynolds
Temperatura adimencional
̅ Temperatura transformado
Temperatura ambiente Temperatura inicial
Velocidade longitudinal adimencional
Velocidade longitudinal completamente desenvolvido
Velocidade em desenvolvimento
̅ Velocidade longitudinal transformado
̅ Velocidade média
Velocidade longitudinal dimencional
Velocidade inicial
Velocidade transversal adimencional
Velocidade transversal dimencional
Posição longitudinal dimencional
X Posição longitudinal adimencional
Posição transversal dimencional
Y Posição transversal dimencional
k Condutividade Térmica
Letras Gregas
Autovalores da pressão
Autovalores da temperatura
Delta de kronecker
∆ Variação
Autofunção da pressão
̃ Autofunção da pressão normalizada
Autofunção da velocidade
̃ Autofunção da velocidade normalizado
Contração de escala Autofunção da temperatura
̃ Autofunção da temperatura normalizada
Viscosidade dinâmica
Autovalores da velocidade
Autovalores da temperatura
ρ Massa Específica
Tensão na parede dimensional
Sobrescritos e Subscritos
~ Referente à autofunção normalizada
– Referente à transformada
j Termo para a série
m Termo para a série
n Termo para a série
u Termo para a série
CAPÍTULO I
INTRODUÇÃO
Este capítulo tem como objetivo situar o problema físico abordado do ponto de vista de aplicações de engenharia, bem como as motivações que levaram aos estudos no presente trabalho.
1.1 – MOTIVAÇÃO E OBJETIVOS
Outros exemplos são unidades de refrigeração e ar condicionado, equipamentos eletrônicos, concepção de sistemas de refrigeração para motores elétricos, transformadores e geradores elétricos, aquecimento e refrigeração de líquidos em operações químicas, minimização de perdas de calor em construções através de melhorias das técnicas de isolamento, tratamento térmico de metais, a dispersão de poluentes atmosféricos.
A transferência de calor em geral ocorre em três formas, condução, convecção e radiação, e na maioria das situações reais, ela é consequência da combinação das mesmas.
Este trabalho tem como objetivo principal, e mais especificamente, a convecção forçada. Onde trata do escoamento quando este for provocado por meios externos, por exemplo, um ventilador ou uma bomba, ou por ventos na atmosfera (INCROPERA, 2008).
O estudo da convecção forçada tem sido objeto de interesse por parte de muitos pesquisadores, devido a sua importância pratica na engenharia. O conhecimento de determinados parâmetros possibilita o desenvolvimento, a otimização e a construção de novos equipamentos, como exemplos destes parâmetros pode-se citar o fator de atrito, velocidade média, pressão, Nusselt e a temperatura média, onde estes indicadores possibilita à análise dos equipamentos, fazendo com que evitemos efeitos indesejáveis, como a falha ou redução do desempenho térmico dos mesmos.
importantes motivos da técnica numérica ser requerida está relacionado ao fato dos computadores apresentarem capacidade de processamento cada vez maiores, assim tem-se avançado bastante na simulação de problemas em mecânica dos fluidos e transferência de calor, possibilitando assim um menor custo e minimizando o tempo despendido com o trabalho.
Os métodos puramente numéricos são muitos utilizados, porém tem-se utilizados nos últimos anos a Técnica da Transformada Integral Generalizada, conhecida pela sua sigla em inglês como G.I.T.T. (Generalized Integral Transform Technique), que é um método de manuseio analítico que apresenta soluções híbridas analíticas.
A Técnica da Transformada Integral Generalizada, apresenta algumas vantagens com relação a métodos puramente numéricos, visto que retém as mesmas características de uma solução analítica, não necessitando discretização de domínio nem geração da malha em uma geometria multidimencional, além de manter um controle automático sobre o erro relativo dos resultados, o qual é estabelecido a priori. Além disso a sua excelente performace é constatada por inúmeros trabalhos em mecânica dos fluidos (Cotta, 1993a) e transferência de calor (Santos et al., 2002; Perreira e Pérez Guerrero, 2002).
O presente trabalho tem por objetivo um estudo teórico da determinação simultânea dos perfis hidrodinâmico e de energia, na região de um canal de placas planas paralelas. A simulação numérica é baseada na solução das equações de Navier-Stokes para o escoamento e a equação da energia, considerando em um espaço bidimensional, transformando-a em termos de variáveis primitivas pelo uso da metodologia empregada na Técnica da Transformada Integral Generalizada.
O capítulo I, é introdutório, com o objetivo de situar motivações e objetivos do trabalho.
No capítulo II, é apresentado uma revisão bibliográfica, aonde é feita sínteses de vários trabalhos sobre o comportamento do escoamento dos fluido em geral e bem como é apresentado a metodologia de resolução de problema, proposta pela GITT.
No capitulo III, é apresentada todo o desenvolvimento das etapas para a obtenção e solução do problema proposto.
O capitulo IV tem toda a análise dos resultados tanto do campo hidrodinâmico quanto do campo térmico.
CAPÍTULO II
REVISÃO BIBLIOGRAFICA
No presente capítulo são apresentadas descrições da evolução da mecânica dos fluidos junto com uma revisão dos últimos trabalho utilizando a Técnica da Transformada Integral Generalizadas com ênfase em canais de placas paralelas utilizando as equações de Navier-Stokes.
2.1 – DESENVOLVIMENTO DA MECÂNICA DOS FLUIDOS
aerodinâmica e diminuir a resistência em aeronaves e para projetar motores a jato; na biomecânica, com o escoamento do sangue, dentre outras.
No final do século XVIII desenvolveu-se a mecânica dos fluidos com a criação da Escola de Engenharia Francesa liderada por Riche de Prony (1755-1839). Prony e seus associados em Paris, na Ecole Polytechnique e a Ecole Ponts et Chaussees, foram os primeiros a incluir cálculo e teoria científica no currículo de engenharia, que se tornou um modelo para o resto do mundo.
Passaram por lá Antonie Chezy (1718-1798), Louis Navier (1785-1836), Gaspard Coriolis (1792-1843), Henry Darcy (1803-1858) e muitos outros que contribuíram para a engenharia e teoria dos fluidos. Por volta do século XIX, o médico Jean Poiseuille (1799-1869) mediu com precisão o escoamento em tubos capilares de fluidos múltiplos; na Alemanha, Gitthilf Hagen (1797-1884) definiu a diferença entre escoamento laminar e turbulento em tubulações, na Inglaterra, Lord Osborne Reynolds (1842-1912) continuou esse trabalho e desenvolveu o número adimensional que leva o seu nome. De modo similar, em paralelo ao trabalho inicial de Navier, George Stokes (1819-1903) completou as equações gerais do movimento dos fluidos com atrito que levam seus nomes, ÇENGEL (2007).
As equações de Navier-Stokes tem sido largamente utilizadas no modelamento matemático para muitos fenômenos na mecânica dos fluidos. Por exemplo: escoamentos laminares ou turbulentos, que podem ser utilizados em dutos ou em placas planas com formulação em função corrente ou em variáveis primitivas. Os escoamentos podem ser estudados e analisados em função de determinadas grandezas tais como: velocidade, pressão e/ou temperatura.
de aplicações e com progresso no tratamento das equações com formulações seja com visão em camada limite ou com o uso das equações de Navier-Stokes. Devido à procura de métodos que suportem a solução destas equações, tem-se investido no estudo e na avaliação de problemas aplicados tanto na matemática quanto na engenharia.
A solução de problemas em engenharia envolvendo escoamentos de fluidos e transferência de calor, geralmente são mais complicados por se tratar de equações diferenciais parciais, que raramente possuem soluções analíticas. Sendo assim, é necessário o uso de métodos numéricos ou métodos de natureza híbrida, como os analítico-numéricos para a obtenção dos potenciais desejados. O aumento da capacidade dos computadores disponíveis tem facilitado o desenvolvimento e os testes de modelos cada vez mais sofisticados e completos para a simulação dos escoamentos.
2.2 - TRANSFORMADA INTEGRAL
Nos últimos anos, devido ao grande avanço tecnológico, têm surgido problemas cada vez mais complexos na área da engenharia, os quais necessitam de soluções mais acuradas em tempos de resolução cada vez mais reduzidos, visando o máximo aproveitamento dos recursos empregados e a rapidez na obtenção de um produto acabado. Com o surgimento de computadores de alta velocidade de processamento e de grande capacidade de armazenamento de dados, esses problemas já podem ser resolvidos e analisados. Porém a grande maioria destes problemas não apresenta solução analítica e têm que ser resolvidos por métodos numéricos ou por esquemas mistos que envolvem métodos numéricos e soluções analíticas.
e ÕZISIK (1984) apresentam uma compilação de sete classes de problemas de difusão de calor e massa que podem ser resolvidos com esta técnica. Entretanto esta técnica tem seu uso restrito a problemas lineares que podem ser transformados em sistemas não acoplados ou a problemas que envolvem problemas auxiliares não muito complicados.
Com o objetivo de reduzir a limitação imposta pela transformada integral clássica, foi desenvolvido um método híbrido. Este método consiste de uma combinação de técnicas analíticas associadas à aproximações numéricas. Este método foi denominado de Técnica da Transformada Integral Generalizada, sendo mais conhecido pelas iniciais da sua
denominação em inglês (Generalized Integral Transform Technique - GITT).
A GITT vem se tornando uma importante ferramenta na solução de problemas em convecção-difusão, com controle automático do erro global e acentuada redução nos custos computacionais, em relação aos métodos puramente numéricos. Essa metodologia está sendo utilizada com sucesso em várias classes de problemas presentes na mecânica dos
fluidos e na transferência de calor e massa. COTTA (1993) fez uma compilação dos
diversos problemas que já foram tratados com o auxílio da GITT nas últimas duas décadas.
Para ilustrar o êxito obtido por esta técnica pode-se citar alguns trabalhos desenvolvidos nos últimos anos, tais como:
LIMA (1995, 2000) usou a técnica para resolver as equações de Navier-Stokes
aplicadas ao escoamento turbulento em canais retangulares.
PEREZ GUERRERO e COTTA (1996) estudaram o problema do escoamento sobre
LEAL (1996) estudou o problema de convecção natural em cavidades retangulares, tanto para regime permanente quanto transiente.
QUARESMA (1997) resolveu o problema do escoamento permanente em uma cavidade retangular tridimensional.
GONDIM (1997), estudou a convecção forçada com difusão axial entre placas planas paralelas.
MACHADO (1998) investigou o problema de convecção natural em cavidade retangular com propriedades variáveis.
MACEDO e QUARESMA (2001) estudaram a região de entrada térmica para o escoamento de fluidos não- newtonianos em canais de placas paralelas e dutos circulares.
SANTOS et al. (2001) estudaram a intensificação da transferência de calor em dutos aletados.
QUARESMA et al (2001) estudaram o problema do desenvolvimento simultâneo dos perfis hidrodinâmico e térmico para fluidos não-newtonianos.
combustão, resfriamento de equipamentos eletrônicos, reservatórios de petróleo, entre outros.
Para a utilização da GITT alguns passos devem ser aplicados seqüencialmente:
a) Escolha de um problema auxiliar apropriado, o qual deve conter o máximo de
informações possíveis sobre o problema original, no que diz respeito à geometria e operadores nas coordenadas a serem eliminadas pela transformação integral. Quanto maior for o número de informações contidas no problema auxiliar, mais desacoplado será o sistema de equações diferenciais resultantes e menor o número de termos requeridos no truncamento do sistema;
b) Desenvolvimento de um par transformada-inversa, a partir da propriedade de
ortogonalidade das autofunções, para transformação do problema original e posterior inversão dos campos transformados obtidos. Para os problemas clássicos de Sturm-Liouville, os resultados são disponíveis na literatura para uma grande variedade de situações (MIKHAILOV & ÕZISIK, 1984);
c) Transformação integral do sistema diferencial parcial original em um sistema de
d) Resolução do sistema de equações diferenciais ordinárias, após o truncamento desse sistema infinito, encontrando-se os potenciais transformados. O truncamento deve ser feito de tal forma que se garanta que a solução do sistema esteja convergida dentro de um determinado critério pré-estabelecido. Os procedimentos numéricos utilizados para resolver o sistema normalmente envolvem o uso de sub-rotinas, como por exemplo as encontradas na biblioteca IMSL do FORTRAN (1997). Para problemas parabólicos, o sistema de equações obtido é um problema de valor inicial, enquanto que para problemas elípticos o sistema é um problema de valor de contorno. Sob certas condições pode-se usar uma solução aproximada, usando-se apenas os termos da diagonal do sistema, esta solução é chamada de solução de baixa ordem.
e) Utilização da formula de inversão para recuperar os potenciais originais, por meio dos
potenciais transformados que já foram calculados no passo anterior. Então, a solução final é analítica ou híbrida analítico-numérica, se alguma das variáveis foi resolvida numericamente.
Vem se observando que alguns passos intermediários são utilizados no intuito de melhorar a performance da técnica, dependendo da dificuldade oferecida pelo problema. Aplicação de filtros para aceleração de convergência (GONDIM, 1997; MACEDO et al,
1999), reordenamento de autovalores e potenciais (LEAL, 1996, CORRÊA et al., 1997,
MACHADO, 1998), são alguns exemplos bem sucedidos das novas tentativas de otimização na aplicação da GITT.
CAPÍTULO III
MODELAGEM DO PROBLEMA FÍSICO
Neste capítulo as equações básicas que descrevem o escoamento bidimencional, laminar, transiente de um fluido newtoniano em um canal de placas paralelas são apresentados em termos de variáveis primitivas. Também é obtido a solução pelo uso da Técnica da Transformada Integral Generalizada, ressaltando-se também as característica do algoritmo computacional.
3.1 – DEFINIÇÃO DO PROBLEMA
Figura 3.1 – Desenvolvimento em dutos paralelos
A formulação matemática do problema físico é obtida a partir das seguintes hipóteses restritivas:
- escoamento incompressível;
- impermeabilidade e não-deslizamento nas paredes do duto;
- fluido newtoniano
- dissipação viscosa desprezível;
- propriedades físicas constantes;
- Escoamento laminar, bidimensional;
- Regime permanente;
O objetivo é a determinação das características hidrodinâmicas do escoamento e análise da transferência de calor ao longo do aparato.
Para a solução do problema hidrodinâmico, o escoamento dentro do canal de placas paralelas é governada pelas equações da continuidade, Navier-Stokes, Poisson as quais são descritas a seguir:
- Equação da continuidade:
3.1
- Equação de quantidade de movimento na direção x:
[ ]
3.2
- Equação de quantidade de movimento na direção y:
[ ]
3.3
- Equação para o campo de pressão (Poisson):
Derivando a equação (3.2) com relação a x* e derivando a equação em (3.3) com relação a y*, em seguida, somando as duas e levando em consideração a equação da continuidade, obtém-se a equação de Poisson:
[ ]
Sujeitas ás seguintes condições de contorno:
- Entrada ( :
3.5 a,b
3.5c
- Centro pela simetria ( :
3.6 a,b
3.6 c
- Na saída ( :
3.7 a,b
3.7 c
- Não deslizamento e impermeabilidade na parede :
3.8 a,b
3.8 c,d
3.2.1 – Parâmetros adimensionais
3.9 a,b
3.9 c,d
3.9 e,f
Observando-se que * e ** identifica as variáveis dimensionais e o número de Reynolds é definido com base na velocidade na entrada do reator.
Portanto, as equações (3.1) a (3.8), validas agora no domínio 0 < Y < 1, X > 0 e suas condições de contorno são reescritas na seguinte forma adimensional:
- Equação da continuidade:
3.10
- Equação da quantidade de movimento na direção x:
[ ]
3.11
[ ] 3.12
- Equação para o campo de pressão (Poisson):
[ ] 3.13
Com as condições de contorno e iniciais da forma:
- Entrada ( :
3.14 a,b
3.14 c
- No centro e/ou pela simetria ( :
3.15 a,b
3.15 c
- Na saída ( :
3.16 a,b
3.16 c
3.17 a,b
3.17 c
3.2.2 – Método de Solução do Problema Hidrodinâmico pelo uso Transformada Integral
O problema hidrodinâmico é solucionado com sua formulação em variáveis primitivas, onde o perfil de velocidade é encontrado através das equações de Navier Stokes (3.11 e 3.12) e o gradiente de pressão pela equação de Poisson (3.13).
a- Filtro da velocidade
Para a apropriada aplicação da GITT e melhorar sua performance computacional é conveniente fazer uma homogeneização das condições de contorno. Isto é feito, pois
segundo Machado (1992) uma separação da velocidade, em duas fases, onde a primeira
está em desenvolvimento, função das duas dimensões, e a segunda já está desenvolvida, função apenas da espessura do canal, melhora consideravelmente a convergência das soluções das equações diferenciais transformadas, em vista disto:
3.18
Onde representa a velocidade do campo completamente desenvolvido e
A expressão que representa a parte desenvolvida é dada por:
3.19
b- Filtro para a pressão
Um filtro para pressão é necessário para fazer uma homogeneização das condições de contorno. Portanto, a solução para pressão é dada da seguinte maneira:
3.20
Onde é um filtro, obtido através da aplicação da equação de quantidade de
movimento em y=1
[
] [
] 3.21
Adimensionalizando a equação acima temos:
3.22
Onde integrando obtém-se:
3.23
3.24 3.25 3.26 | 3.27
As equações (3.11) a (3.17), devem ser escritas de forma a conter os filtros da velocidade e da pressão, junto com suas condições de contorno.
- Equação da quantidade de movimento na direção X:
[ ] [ ] 3.28
- Equação da quantidade de movimento na direção Y:
[ ] 3.29
[ ]
3.30
Com as condições de contorno e iniciais da forma:
- Entrada ( :
3.31 a,b
- No centro e/ou pela simetria ( :
3.32 a,b
- Na saída ( :
3.33 a,b
- Não deslizamento e impermeabilidade na parede :
3.34 a,b
3.2.4 – Problema auxiliar para o Campo de Velocidade
O problema auxiliar para a velocidade selecionado é da forma:
Sujeitas às seguintes condições:
| 3.36 a,b
Este problema é um problema de Sturm-Liouville, tendo solução analítica e explicita (Özisik, 1993).
Onde os autovalores, autofunções e a norma são dadas por:
3.37
3.38
∫( ) 3.39
As soluções dos problemas auxiliares, ou seja, as autofunções, apresentam a propriedade de ortogonalidade:
∫ ̃ ̃ 3.40
Onde,
{
3.41
̃
√ 3.42
3.2.5 – Problema Auxiliar para o Campo de Pressão
O problema auxiliar para a pressão selecionado é da forma:
3.43
Imposto às seguintes condições:
|
| 3.44 a,b
Este problema também tem solução analítica e explicita, onde as autofunções, os autovalores e a norma são dados por:
3.45
3.46
∫( ) 3.47
As soluções dos problemas auxiliares, como visto anteriormente, apresentam a propriedade de ortogonalidade:
∫ ̃ ̃ 3.48
̃
√ 3.49
3.2.6 – Pares Transformada Inversa
A GITT baseia-se na idéia de que uma função pode ser escrita como uma expansão em termos de autofunções. Assim, os pares transformada-inversa são definidos para cada campo como:
-Velocidade:
∑ ̃ ̅ Inversa 3.50 a
̅ ∫ ̃ Transformada 3.50 b
-Pressão:
∑ ̃ ̅ Inversa 3.51 a
̅ ∫ ̃ Transformada 3.51 b
3.2.7 – Calculo da velocidade Média e da Pressão Média - Velocidade
̅ ∫
Onde, após utilizar o filtro e substituir pela inversa, obtém-se:
̅ ∑ ̅ 3.53
Onde;
√ ∫ 3.54
-Pressão
̅ ∫
∫ 3.55
Onde, após utilizar o filtro e substituir pela inversa, obtém-se:
̅ ∑ [ ̅ ] 3.56
Onde;
√ ∫ 3.57
3.2.8 – Calculo da Velocidade Transversal
É necessário eliminar a dependência espacial da velocidade transversal para encontrar a solução do sistema de equações da velocidade. Assim sendo a equação da continuidade (3.10) será integrada de y a 1 obtendo:
∫ 3.59
Aplicando a inversa (3.50 a) na equação (3.59), tem-se:
∑ ̅ ̅ 3.60
Onde:
̅ ∫ ̃ 3.61
3.2.9 – Fator de Atrito
O fator de atrito é definido por:
3.62
∑ ̃
̅
3.63
3.2.10 – Transformação Integral do Problema
O processo de transformação integral das equações diferenciais parciais num sistema diferencial ordinário é iniciado ao multiplicar a equação pela autofunção do problema auxiliar escolhido e depois integrado de 0 a 1 na direção Y. Assim, de forma
simplificada, devemos multiplicar a equação (3.28) pelo operador ∫ ̃ , bem como
o operador ∫ ̃ na equação (3.30). Desta forma as equações citadas ficam da
forma: ∫ ̃ [ [ ] [ ]] 3.64 ∫ ̃ [ [ ]] 3.65
ortogonalidade onde for possível. A utilização da inversa assegura a transformada de uma equação diferencial parcial, inclusive onde os termos não forem transformados exatamente, resultando: ̅ {∑ [∑ ̅ ] ̅ ∑ ̅ } ̅ 3.66 ∑ ̅ ̅ ∑ 3.67 Onde: ̅ ̅ ∑ ∑ ̅ ̅ ∑ [∑ ̅ ] ̅ 3.68 ∑ ∑ ̅ ̅ ∑ [∑ ̅ ] ̅ ̅ 3.69 ∑ 3.70
Onde os coeficientes são calculados analiticamente a partir das integrais:
∫ ̃ ̃ ∫ ̃ ̅ 3.72
∫ ̃ ̃ 3.73
∫ ̃ 3.74
̅ ∫ ̃ 3.75
∫ ̃ ̃ ̅ 3.76
∫ ̃ ̃ ̅ 3.77
∫ ̃ ̅ 3.78
∫ ̃ ̃ 3.79
̅ ∫ ̃ ∫ ̃ 3.80
̅ 3.81
̅ 3.82
̅
∫ ̃ 3.83
Desta forma, o problema diferencial parcial foi transformado em uma serie de equações ordinárias não lineares, com condições de contorno em dois pontos.
3.3 – PROBLEMA DA TRANSFERENCIA DE CALOR
A equação da energia para o problema proposto é dada como:
[ ]
3.84
Onde é a difusividade térmica que mede a velocidade com a qual o calor se
difunde através do material, devido às alterações de temperatura que são impostas.
3.85
3.86
| 3.87
[ |
3.88
3.3.1 – Adimensionalização do problema
Utilizando os parâmetros adimencionais já mencionados anteriormente pela equação (3.9), juntamente com os definidos abaixo:
3.89
3.90
Adimencionalizando a equação (3.84) e aplicando o filtro da velocidade, obtem-se:
-Equação da Energia
[
] 3.91
3.92
3.93
3.94
3.95
3.3.2 – Método de Solução do Problema de Temperatura de Calor Pelo uso da Transformada Integral
-Problema auxiliar
Para Resolver a equação da energia (3.84) utiliza-se a técnica da Transformada Integral Generalizada (G.I.T.T.), onde é escolhido o seguinte problema auxiliar da direção transversal do escoamento.
Sujeito as seguintes condições:
|
| 3.96
3.97
Os autovalores são as raízes da equação:
3.98
As soluções dos problemas auxiliares, como visto anteriormente, apresentam a propriedade de ortogonalidade:
∫ ̃ ̃ 3.99
Onde, pela equação 3.41:
{
Lembrando que ̃ é a função normalizada e é dada por:
̃
√ 3.100
Com,
∫ ( ) 3.101
3.3.3– Pares Transformada Inversa
∑ ̃ ̅ Inversa 3.102 a
̅ ∫ ̃ Transformada 3.102 b
3.3.4 – Transformação Integral do Problema de Energia
Da mesma forma que foi feito para as equações da quantidade de movimento (3.28) e a equação de Poisson (3.30) será feita para a equação da energia, ou seja, aplica-se o
operador ∫ ̃ na equação (3.91), resultando:
∫ ̃ [ [ ]] 3.103
Em conseguinte usa-se a equação da inversa (3.102 a), que fará a transformação da equação diferencial parcial e aplica-se as propriedades de ortogonalidade onde couber, resultando em: ̅ {∑ [∑ ̅ ] ̅ ∑ ∑ ̅ ̅ } ̅ 3.104
∫ ̃ ̃ ̃ 3.105
[ ∫ ̃ ̃ ] 3.106
∫ ̃ ̃ ̅ 3.107
̅ ∫ ̃ 3.108
O mesmo procedimento deve ser feito com as condições de contorno, ou seja,
vamos multiplicar todas as equações (3.92) a (3.95) por ∫ ̃ e fazer uso da equação
da inversa (3.102 a).
̅ 3.109
̅ ∫ ̃ 3.110
3.3.5 – Calculo da Temperatura Média e do Número de Nusselt
Após ter solucionado o sistema, então teremos o campo de temperatura transformado e com isto será possível determinar a temperatura média e o número de Nusselt. Como segue:
∫ ̅ 3.111
-Número de Nusselt
|
3.112
3.4 – SOLUÇÃO DO SISTEMA DIFERENCIAL ORDINÁRIO
Pelo fato de não possuir solução analítica as equações ordinárias de segunda ordem (3,66),(3.67) e (3.104), será resolvida a partir de procedimentos numéricos.
A Técnica da Transformação Integral Generalizada, possui como uma de suas característica importante, a garantia de convergência das soluções, para ordem crescente do número de termos da série. O método da GITT também é conhecido pelo seu fator de precisão controlado, pois este com determinados quantidade de termos da série garante a convergência da solução. Devido esse controle estabelecido na ordem de truncamento das expansões, que pode ser automaticamente determinado durante o processo de solução, assemelhando bastante esta técnica ao de uma puramente analítica.
Como as condições de contorno para a saída do canal estão especificadas no infinito faremos uma contração de escala, ou seja, iremos fazer uma transformação de
coordenadas tal que se possa mapear o domínio semi-infinito [ [ em um domínio finito
[ . Esta mudança no comprimento do canal já foi utilizada por Pérez Guerrero (1995), que é da forma:
3.119
E sua derivada,
3.120
Onde a constante c é o fator de escala.
Para resolver numericamente os sistemas de equações resultantes foi utilizado algoritmos bem estabelecidos e testados, disponíveis no sistema de biblioteca IMSL (1997). A subrotina utilizada desta biblioteca foi a DBVPFD que resolve problemas diferenciais ordinários não lineares, com duas condições de contorno. Porém nosso problema são sistemas de equações de segunda ordem, então devemos reescrever o sistema dito como um de primeira ordem, ou seja:
̅ 3.121
̅ 3.122
̅
̅ 3.124
̅ 3.125
̅
3.126
̅ 3.127
̅ 3.128
̅
3.129
Os termos são transformados pela regra da cadeia em função da mudança de domínio, como segue:
Onde
é uma função que depende de
e do parâmetro c.
O sistema diferencial ordinário de equações (3.113), (3.114) e (3.115) tornam-se:
{∑ [∑ ] ∑ } 3.133 ∑ ̅ ∑ 3.134 {∑ [∑ ] ∑ ∑ } 3.135
Com as seguintes condições de contorno:
∫ ̃ ∫ ̃ 3.136
3.137
∫ ̃ 3.139
3.140
∫ ̃ 3.141
Agora sim é possível resolver o problema, basta calcular o jacobiano e fornecer para subrotina as condições de contorno. Lembrando que o jacobiano indica a direção da melhor convergência do sistema e representa as derivadas do mesmo com relação a cada um dos componentes do vetor solução x.
CAPÍTULO IV
RESULTADOS E DISCURSSÕES
O código computacional foi construído em linguagem Fortran 90 e executado em uma plataforma de trabalho Intel Core i5 primeira geração do Laboratório de Energia Solar do DEM/UFPB.
As principais etapas numéricas envolvidas são:
- Cálculo dos coeficientes integrais, equações (3.71) à (3.79) e (3.105) à (3.108)
- As soluções dos sistemas de equações diferenciais ordinários, equações (3.66), (3.67),
(3.104), foram obtidos dentro de uma precisão relativa pré-estabelecida de 10-4 na solução
do mesmo, utilizando a subrotina de cálculo DBVPFD da biblioteca IMSL.
- Uso da formula da inversa, equações (3.50), (3.51) e (3.102), para resgatar os potenciais originais.
Visando solucionar o problema de transferência de Energia associado ao problema hidrodinâmico é determinado e analisado o comportamento dos campos de velocidade e pressão para o sistema de equações em formulação em termos de variáveis primitivas.
Foi construído o código computacional onde sempre o problema é resolvido para
Reynolds igual a 300, Prandtl igual a 0.7 e um domínio finito [ pelas transformações
do domínio (3.119). Também é importante destacar que todos os cálculos foram feitos com as mesmas quantidades de autofunções, ou seja, NU igual a NP, que é igual a NT, que iremos tratar elas por NN. O fator de contração, vale 0,55 (zero vírgula cinquenta e cinco).
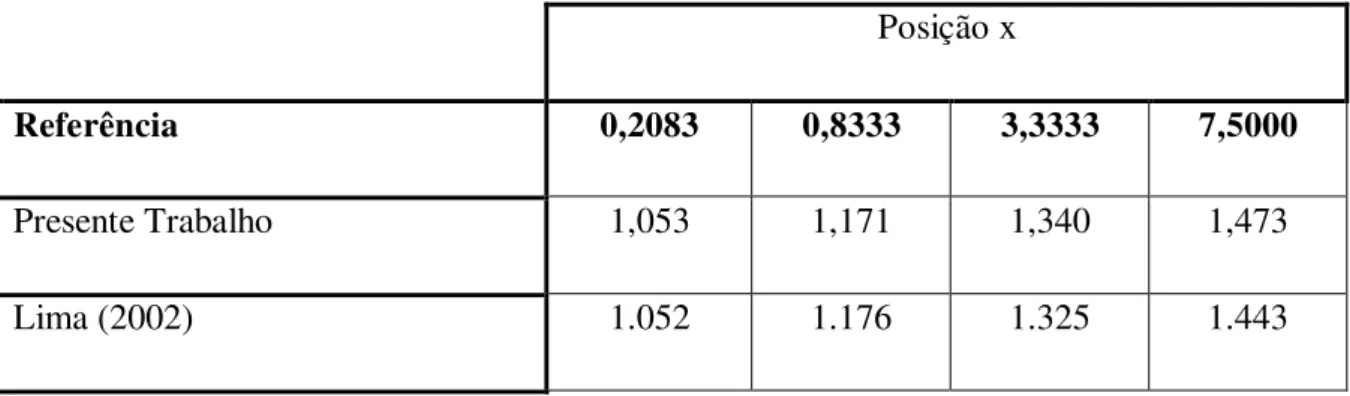
Na tabela 4.1 são mostrados resultados de diversas obras com resultados para Reynolds 300, onde vale lembrar que o mesmo trata-se do Reynolds hidráulico.
Constata-se que os resultados do presente trabalho estão de acordo com a literatura e condiz com os resultados de tanto de Lima (2002) que trabalha com variáveis primitivas, quanto para Pérez Guerrero (1995),que trabalha com condições de entrada irrotacional e para os de Wang e Longwell (1994) e Mac Donald et al. (1972), estes que utilizam os métodos de diferenças finitas e elementos finitos. Os dados comparados são referentes a Reynolds igual a 300, onde são considerados 60 termos na expansão da série.
Tabela 4.1 – Tabela de comparação da velocidade longitudinal, no centro do duto
( ), para Reynolds 300.
Posição x
Referência 0,2083 0,8333 3,3333 7,5000
Presente Trabalho 1,053 1,171 1,340 1,473
Peréz Guerrero (1995) 1,052 1,170 1,337 1,444
Wang e Longwell (1994) 1,058 1,188 1,357 1,451
Mac Donald et al, (1972) 1,050 1,170 1,340 1,440
As tabelas 4.2 à 4.7 mostram a convergência da velocidade, da velocidade média, da pressão, pressão média, da temperatura e da temperatura media. Com o objetivo de comprovar a estabilidade numérica do problema proposto, para números crescente de termos.
Tabela 4.2 – Tabela de convergência da velocidade longitudinal no centro do duto
( ).
Posição x
NN 0,2 0,208 0,4 0,6 0,8 0,833 3,333 7,5 12,228
5 1,057 1,057 1,067 1,084 1,104 1,108 1,298 1,468 1,497
10 1,035 1,036 1,071 1,102 1,129 1,134 1,317 1,471 1,497
15 1,043 1,044 1,080 1,113 1,141 1,147 1,325 1,472 1,497
20 1,044 1,045 1,084 1,118 1,147 1,153 1,329 1,472 1,497
30 1,047 1,049 1,089 1,125 1,155 1,161 1,334 1,473 1,497
40 1,049 1,050 1,092 1,129 1,160 1,165 1,337 1,473 1,497
50 1,050 1,052 1,094 1,131 1,163 1,168 1,339 1,473 1,497
60 1,051 1,053 1,096 1,133 1,165 1,171 1,340 1,473 1,498
Tabela 4.3 – Tabela de convergência da velocidade media.
Posição x
NN 0,2 0,208 0,4 0,6 0,8 0,833 3,333 7,5 12,228
5 0,9657 0,9659 0,9708 0,9747 0,9778 0,9784 0,9904 0,9982 0,9997
10 0,9909 0,9912 0,9977 1,0014 1,0034 1,0036 0,9995 0,9993 0,9998
15 1,0014 1,0017 1,0086 1,0120 1,0134 1,0136 1,0030 0,9998 0,9999
20 1,0072 1,0076 1,0146 1,0178 1,0190 1,0191 1,0049 1,0000 0,9999
30 1,0138 1,0142 1,0215 1,0245 1,0253 1,0252 1,0071 1,0003 0,9999
40 1,0176 1,0180 1,0254 1,0282 1,0288 1,0288 1,0083 1,0004 0,9999
50 1,0201 1,0205 1,0279 1,0307 1,0312 1,0311 1,0091 1,0005 0,9999
60
1,0219 1,0223 1,0298 1,0325 1,0329 1,0327 1,0097 1,0006 1,0000 70
1,0233 1,0237 1,0312 1,0339 1,0342 1,0340 1,0101 1,0006 1,0000
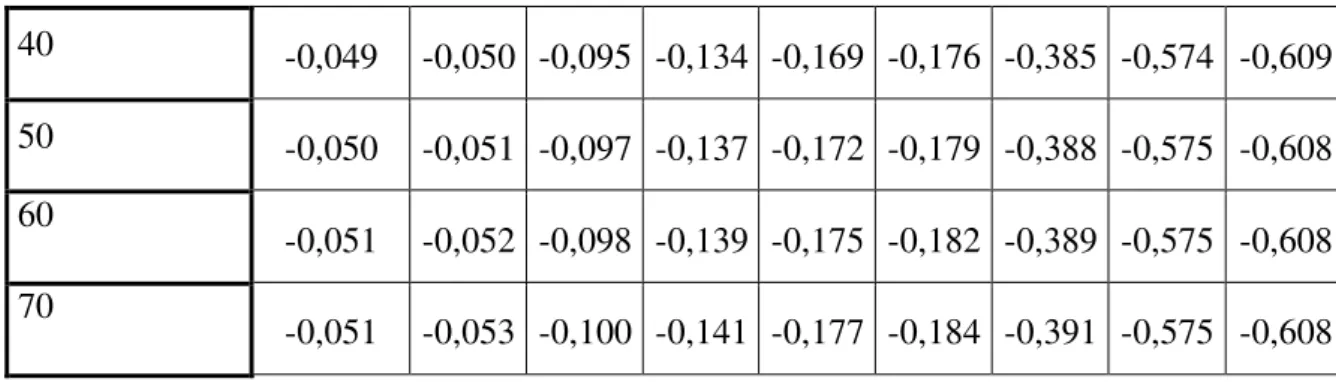
Tabela 4.4 – Tabela de convergência da pressão longitudinal no centro do duto
( ).
Posição x
NN 0,2 0,208 0,4 0,6 0,8 0,833 3,333 7,5 12,228
5 -0,026 -0,027 -0,052 -0,077 -0,101 -0,106 -0,332 -0,563 -0,603
10 -0,038 -0,039 -0,073 -0,105 -0,134 -0,140 -0,360 -0,571 -0,608
15 -0,041 -0,043 -0,081 -0,116 -0,147 -0,154 -0,370 -0,572 -0,608
20 -0,044 -0,046 -0,086 -0,122 -0,155 -0,161 -0,376 -0,573 -0,609
40 -0,049 -0,050 -0,095 -0,134 -0,169 -0,176 -0,385 -0,574 -0,609
50 -0,050 -0,051 -0,097 -0,137 -0,172 -0,179 -0,388 -0,575 -0,608
60
-0,051 -0,052 -0,098 -0,139 -0,175 -0,182 -0,389 -0,575 -0,608 70
-0,051 -0,053 -0,100 -0,141 -0,177 -0,184 -0,391 -0,575 -0,608
Tabela 4.5 – Tabela de convergência da pressão média.
Posição x
NN 0,2 0,208 0,4 0,6 0,8 0,833 3,333 7,5 12,228
5 -0,035 -0,066 -0,095 -0,096 -0,120 -0,124 -0,272 -0,348 -0,359
10 -0,066 -0,068 -0,113 -0,147 -0,173 -0,178 -0,310 -0,372 -0,382
15 -0,086 -0,088 -0,136 -0,169 -0,195 -0,200 -0,324 -0,381 -0,390
20 -0,099 -0,101 -0,149 -0,182 -0,208 -0,212 -0,331 -0,386 -0,394
30 -0,114 -0,116 -0,164 -0,197 -0,222 -0,227 -0,340 -0,391 -0,399
40 -0,123 -0,125 -0,173 -0,206 -0,231 -0,235 -0,345 -0,394 -0,402
50 -0,129 -0,131 -0,180 -0,212 -0,236 -0,241 -0,348 -0,396 -0,404
60
-0,134 -0,136 -0,184 -0,216 -0,241 -0,245 -0,351 -0,398 -0,405 70
-0,138 -0,140 -0,188 -0,220 -0,244 -0,248 -0,353 -0,399 -0,406
Tabela 4.6 – Tabela de convergência da temperatura longitudinal no centro do duto ( ).
Posição x
NN 0,2 0,208 0,4 0,6 0,8 0,833 3,333 7,5 12,228
5 1,0219 1,0211 1,0071 1,0024 1,0012 1,0011 1,0021 0,9780 0,2556
10 0,9998 0,9999 1,0000 1,0000 1,0000 1,0000 0,9992 0,9768 0,2553
15 1,0004 1,0004 1,0004 1,0003 1,0003 1,0003 0,9991 0,9764 0,2552
20 0,9999 0,9999 0,9999 0,9999 0,9999 0,9999 0,9988 0,9761 0,2551
30 0,9999 0,9999 0,9999 1,0000 1,0000 1,0000 0,9988 0,9760 0,2551
40 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 0,9988 0,9760 0,2551
50 1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 0,9987 0,9759 0,2551
60
1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 0,9987 0,9759 0,2551 70
1,0000 1,0000 1,0000 1,0000 1,0000 1,0000 0,9987 0,9759 0,2551
Tabela 4.7 – Tabela de convergência da temperatura média.
Posição x
NN 0,2 0,208 0,4 0,6 0,8 0,833 3,333 7,5 12,228
5 0,903 0,901 0,864 0,836 0,814 0,810 0,720 0,657 0,147
10 0,892 0,891 0,850 0,824 0,804 0,800 0,715 0,651 0,146
15 0,887 0,886 0,847 0,822 0,803 0,799 0,714 0,650 0,146
20 0,886 0,884 0,846 0,821 0,802 0,799 0,714 0,650 0,146
30 0,884 0,883 0,846 0,821 0,803 0,799 0,714 0,650 0,146
50 0,884 0,882 0,846 0,822 0,803 0,800 0,715 0,650 0,146 60
0,884 0,882 0,846 0,822 0,804 0,800 0,715 0,650 0,146
70
0,884 0,882 0,846 0,822 0,804 0,801 0,716 0,650 0,146
Em todas as tabelas é de fácil observação que para pequenos números de termos a convergência não é alcançada. Também é notório observar em regiões próximas a entrada do duto, a convergência é mais lenta e somente é alcançada para números de maiores termos de velocidade e pressão, já no final do duto a convergência é mais rápida devido aos filtros da velocidade e da pressão aplicados no problema. A taxa de convergência melhora ao longo do duto, a medida que se alcança o escoamento completamente
desenvolvido. A função , usada como filtro, representa o perfil de velocidade
completamente desenvolvido de ; assim ao se avançar o escoamento ao longo do
duto, a velocidade tende para , requerendo menos termo na expansão.
Por meio da figura (4.1) podemos observar o comportamento da velocidade longitudinal no centro do duto, onde se pode constatar que está de acordo as condições impostas. Nota-se que na entrada do duto a velocidade esta próxima de 1 (um), mas já no final do mesmo, onde a problema está desenvolvido, a velocidade tende para 1,5 (um virgula cinco), como predefinido, pois pela equação (3.19), com Y igual a 0 (zero), o valor
de vale 1,5.
Na figura 4.2 está ilustrado a comportamento da velocidade longitudinal media do problema proposto, onde este foi calculado para Reynolds igual a 300 e a equação usada foi a 3.52. O comportamento da velocidade media é quase constante, não sendo desta forma devido a singularidade da função.
Figura 4.2 – Comportamento da velocidade longitudinal média.
a) b)
Figura 4.3 – Comportamento da relação f.Re ao longo da componente X.
As figuras seguintes, figura 4.4, 4.5 e 4.6, tratam do perfil de velocidade no duto em diferentes posições axiais para o caso de Reynolds igual a 300.
a) b)
Figura 4.5 – Perfil de velocidade na posição axial (a) X=3,333 e (b) X=7,5.
Figura 4.6 – O perfil de velocidade completamente desenvolvido na posição 12,228
Os resultados mostram que à medida que se avança no duto, o perfil parabólico fica mais evidente, caracterizando o escoamento completamente desenvolvido.
a) b)
a) b)
Observa-se que o comportamento da pressão é inversamente proporcional a da velocidade, ou seja, quanto maior a velocidade menor é a pressão, como devido, e as condições estão de acordos com os impostos ao problema.
Figura 4.7 – Perfil de Pressão na posição axial (a) X=0,208 e (b) X=0,833.
Figura 4.9 – Perfil de pressão na posição 12,228.
Para a figura (4.10) observa-se que esta de acordo com as condições impostas, onde a temperatura no inicio do duto permanece em 1 (um), porém ao longo do duto ela decresce tendendo a 0 (zero). Isto implica que o desenvolvimento da temperatura quando
a) b)
Figura 4.10 – Comportamento da temperatura no centro do duto ao longo do mesmo para
Reynolds 300.
As figuras seguintes, figura 4.11, 4.12 e 4.13, tratam do perfil de temperatura no duto em diferentes posições axiais para o caso de Reynolds igual a 300.
a) b)
Figura 4.12 – Perfil de Temperatura na posição axial (a) X=3,333 e (b) X=7,5.
Os gráficos do perfil da temperatura atende as condições de contorno. Onde no início do canal a temperatura tende para 1, e esta no desenvolver do canal tende para 0. E é perceptível que o comportamento da temperatura se desenvolve bem mais rápido que a velocidade devido ao número de Prandtl ser menor que um.
Figura 4.14 – Comportamento do Nusselt ao longo da componente X, para Reynolds 300,
com destaque para o final do escoamento.
CAPÍTULO V
RESULTADOS E SUGESTÕES
Este trabalho no primeiro momento tratou de abordar as equações de Navier-Stokes juntamente com a equação de Poisson de forma simultânea, com o objetivo de determinar os campos de velocidade e de pressão, assim estudando parâmetros importantes da literatura; no segundo momento abordou a equação da energia para obtenção do campo de temperatura, onde este possibilitou analisar o comportamento do Nusselt. Estas equações foram resolvidas utilizando a técnica da transformação integral generalizada (G.I.T.T.), na forma primitiva, considerando o fluido Newtoniano, incompressível e propriedades físicas constantes.
dificuldade que teríamos se utilizássemos função corrente, contudo, vale ressaltar, que esta ultima proporciona a continuidade automaticamente.
O campo de temperatura comportou-se estável, seu desenvolvimento foi bastante satisfatório, com convergência para baixos números de autovalores, muito disto devido ao número de Prandtl ser menor que 1, o que possibilitou o desenvolvimento mais rápido para temperatura.
Os resultados obtidos para os parâmetros citados tiveram bom comportamento, onde o fator de atrito multiplicado por Reynolds convergiu para 23,91 onde a vasta literatura sobre o assunto mostra que este deve ficar próximo de 24, referente ao problema proposto. Já o número de Nusselt é validado pelo livro do KAKAÇ (1995) onde este relata que, com as condições iguais ao do presente trabalho, tende a convergir para 9,8698, onde obtivemos 9,88, para 70 autovalores.
Com tudo isto exposto, verifica-se que a Técnica da Transformação Integral Generalizada, que é utilizada neste trabalho, mostrou ser eficaz na solução do problema de um escoamento, simultâneo, bidimensional, permanente, considerando a velocidade, pressão e temperatura, mostrando também uma excelente concordância com outros trabalhos anteriores.
Como sugestões para futuros trabalhos:
a) Buscar resultados experimentais para a validação e ajuste da parte teórica
realizada nesse trabalho.
b) Estudar outras geometrias.
d) Rever uma solução numérica para a substituição da subrotina DBVPFD
REFERÊNCIAS BIBLIOGRÁFICA
ÇENGEL, A.Y. e CIMBALA J. M. Mecânica dos Fluidos, (2007). Fundamentos e Aplicações. Mc Graw Hill Editora. 6ª edição, São Paulo.
CORRÊIA E.J. CO A R.M. e ORLANDE H.R.B. 1997 “On the red ction of Computational Costs in Eigenfunctions Expansions of Multidimensional Diffusion roblems” International Jo rnal Numerical Method Heat & Fluid Flow, Vol. 7, pp. 675-695.
COTTA, R. M., 1993. Integral Transform in Computational Heat and Fuid Flow. CRC Press, Boca Raton, FL.
CO A R.M. 1993ª “A Re iew of the integral ransform Method In Nonlinear Heat and fl id Flow roblems” roc. of the 1st Ibero-American Congress of Mechenical Engineering, Madri, Espanha
IMSL library - MATH/LIB, (1989). Houston, Texas.
INCROPERA, FRANK P., DE Witt, DAVID P., BERGMAN, Theodore L., LAVINE,
Adrienne S., 2008, Fundamentos de Transferência de Calor e Massa, 6ª ed. LTC.
KAKAÇ, S. e YENNER, Y., 1995. Convective Heat Transfer. 2ª edição, CRC Press, Boca Raton, FL.
LEAL M.A. 1996 “Con ecção Nat ral em Ca idades para Regimes ermanentes e
Transientes – O Método da Transformação Integral” ese de Do torado
COPPE/UFRJ, Rio de Janeiro, RJ, Brasil.
LIMA J.A. 1995 “Sol ções das Eq ações de na ier-Stokes Médias para Escoamento t rb lento ia ransformação Integral” Dissertação de Mestrado CO E/ FRJ Rio de Janeiro, RJ, Brasil.
LIMA, J.A., 2000, “Escoamento Turbulento em Canais de Placas planas e paralelas:
Análise via Transformação Integral e Modelos Algébricos e K-L de rb lência”
Tese de Doutorado, CT/UFPB, João Pessoa, PB, Brasil.
MACÊDO E.N. Cotta R.M. e Orlande H.R.B. 1999 “Local Instantaneo s Filtering in
the Integral Transform Solution of Non-Linear Diff sion roblems”
Computational Mechanics, Vol. 23, pp. 524-532.
MACHADO H.A. 1998 “Sol ções em con ecção érmica com ropiedades ariá eis ia ransformação Integral” ese de Do torado EM/CO E Rio de Janeiro RJ Brasil.
MIKHAILOV, M. D. e ÖZISIK, M. N., (1984). Unified Analysis and Solutions of Heat and Mass Diffusion, John Wiley, New York.
EREIRA L.M. e érez G errero J.S. 2 2 “Na ier-Stokes Formulation Laminar Flow” in: Con ecti e Heat ransfer in D cts the integral transform Approach, Santos C.A.C., Quaresma J.N.N. e Lima J.A. (eds), E-Papers Serviços Editoriais, Rio de Janeiro, pp. 217-236.
ERREZ G ERRERO J.S. e Cotta R.M. 1996 “Bechmark Integral ransform Res lts
for Flow over a Backward-facing Step” Comp ter & Fl ids ol. 25 pp. 527-540.
Q ARESMA J.N.N. e Cotta R.M. 1997 “Integral ransform Method for Na ier-Stokes Equations i Steady Three-Dimensional Flow, Proceedings of the 10th International Symposium on Transport Phenomena (ISTP-10), Vol 1, pp. 281-287, Kyoto, Japan.
ERONESE J. . 2 8. “Análise do Escoamento Bidimensional de Fluidos Não -Newtonianos com Form lação em ariá eis rimiti as ia GI ”. Tese de Doutorado. UFPB, Abril.