La partie B, composée de deux chapitres, traite principalement de la formulation du modèle (Chapitre III) puis des aspects numériques associés (Chapitre IV). Puis sont présentés les différentes problématiques de caractérisation de Z.F et les tests qui apportent des informations pertinentes.
Introduction
Les deux matériaux provenant d'une fourniture de tôlerie, les essais cycliques seront réalisés par découpe. Nous présenterons ensuite les résultats des essais pour les deux matériaux en parallèle, en commençant par les essais de traction.
Essais de traction ` a diff´ erentes vitesses
De ce fait, la réponse du matériau dépend fortement de la vitesse de chargement. La formation de ces atmosphères nécessite donc suffisamment de temps pour que les impuretés se dispersent, rendant ce phénomène dépendant du temps (vieillissement) et de la température.

Essais de traction dans diff´ erentes directions pour le tantaletantale
Les données caractéristiques des courbes sont résumées dans le tableau I.4, Direction de contrainte Rm (MPa) Huit (%) At(%). L'hypothèse d'isotropie de comportement s'appuie sur un bon essai de traction « dialogue », essai de cisaillement (voir paragraphe V.2.1.3), ainsi que sur le choix communément fait dans la période de la littérature, et notamment au CEA (Robert, 2007), du comportement isotrope.

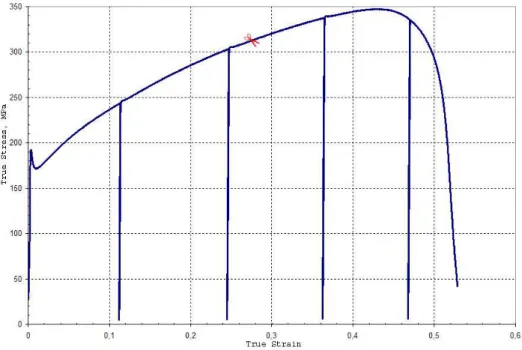
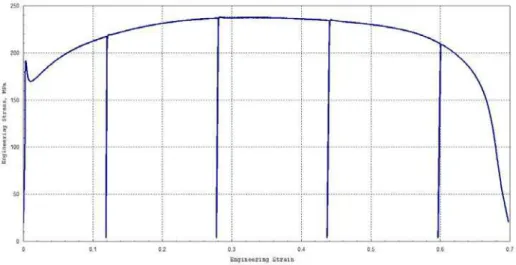
Essais de traction avec charge-d´ echarge
La contrainte thermique effective σatheff f est égale à la moitié de la taille du domaine élastique. L'effet de texture et de microplasticité très prononcée entraîne une diminution importante et rapide du module élastique.
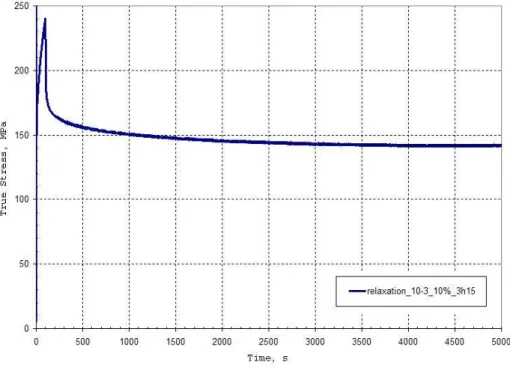
Essais de relaxation
En traçant la déformation visqueuse en fonction de la vitesse de déformation viscoplastique, on obtient : De ˙εvp = 10−3s−1 à ˙εvp = 2.10−6s−1 l'évolution de la déformation visqueuse en fonction de la vitesse de déformation viscoplastique linéaire (sur une échelle logarithmique), puis à partir de.
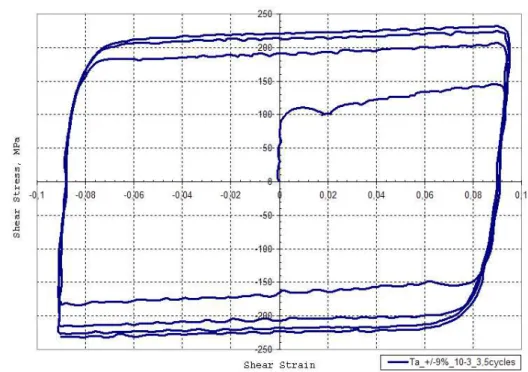
Essais de cisaillement cyclique
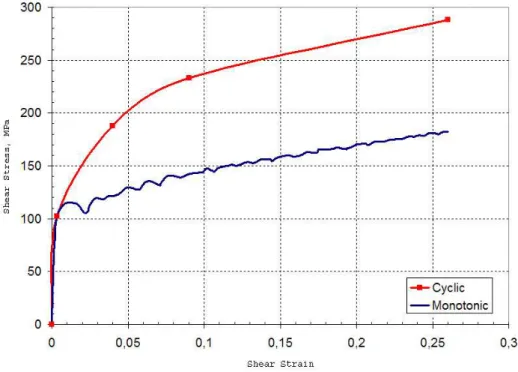
L'évolution de l'écrouissage cyclique en cisaillement ξ en fonction de la déformation plastique cumulée peut être représentée par le calcul de . En comparant la courbe de cisaillement monotone obtenue pour le premier quart de cycle de l'essai à 26% d'amplitude de déformation avec la courbe de consolidation cyclique, on obtient le graphique de la figure I. 39.

R´ ealisation de liaisons soud´ ees h´ et´ erog` enes par soudage laser
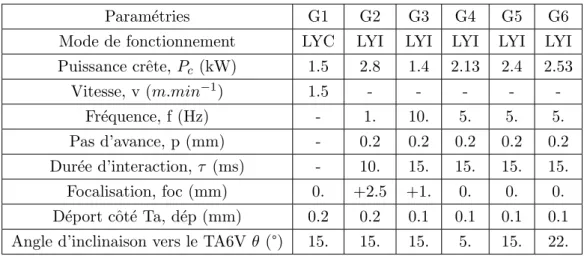
Les différents paramètres utilisés au cours de cette thèse sont résumés dans le tableau II.1 et le schéma de base du soudage laser est présenté dans la figure II.2. Ainsi, les éléments avec une valence supérieure à Ti stabilisent la configuration C.C et abaissent Tβ (voir Tableau II.3 et Figure II.3).
Identification des phases au sein de la Z.F
Les diffractogrammes des matériaux de base sont réalisés avec une anticathode Cu et représentés sur les figures II.12 et II.13. A partir de ce diffractogramme il est possible d'identifier les plans de diffraction comme pour cette figure II.14 pure. En superposant les diffractogrammes de TA6V et le masque (Figure II.16), on constate que certains pics se chevauchent, rendant difficile l'identification des phases Tiα et Tiβ au sein du Z.F.
On peut ainsi indexer l'ensemble du diffractogramme (Figure II.18) et mettre en évidence une augmentation du nombre de plans diffractés appartenant à la phase β (voir Figure II.15). Quoi qu'il en soit, l'analyse M.E.T de deux sections en bas (voir Figure II.19a) et au milieu de la bille (voir Figure II.19c) ne met pas en évidence la présence d'autres phases que Tiβ.

Probl´ ematique exp´ erimentale de caract´ erisation
Dans l'hypothèse où le comportement du joint soudé est intermédiaire entre celui des deux matériaux, dont nous reparlerons un peu plus loin (paragraphe II.4 et II.5.1), on se retrouve alors d'accord d'une part, que de lui. , et le sous-match d'autre part, celui du TA6V. Si le comportement du joint soudé n'est pas inférieur à celui de Ta, la réponse de l'échantillon sera la réponse de Ta telle qu'observée dans l'étude (Farre et al., 2002) (figure II.21). La comparaison entre la réponse globale d’une éprouvette Ta et celle de l’essai de joint soudé n’est pas présentée.
Cependant, malgré ces précautions, la localisation des déformations reste très forte dans Ta et la réponse globale est forcément très dépendante de ce matériau (cf. Figures II.22, II.23). L'évolution de la déformation locale au cours de l'essai dans la configuration de la coupe de rayon 1 mm est représentée sur la figure II.24.

Essais de flexion quatre points
Nous retraçons sur la figure II.31 l'évolution du module effectif en fonction de la fraction volumique. Une interprétation graphique de la détermination du champ de cisaillement est donnée dans la Figure II.35. Sur la figure II.44(c) il est possible de voir l'influence de l'hétérogénéité chimique de Z.F sur la propagation de la fracture.
La répartition des éléments au sein du Z.F est donnée par la microsonde W.D.S (Figure II.58). Ces trajectoires de localisation des déformations correspondent respectivement à la fissure et à la zone 2 de la figure II.70.

Essais d’indentation
Les résultats des mesures de module d'élasticité et de dureté pour ces 4 filiations sont présentés dans la figure II.84. Sur la figure II.87(b), le liseré noir côté TA6V (à droite sur la figure) représente le Z.A.T ayant subi une transformation martensitique. Les mesures du module élastique sont réalisées par méthode de vibration et sont résumées dans la figure II.94.
Les résultats des mesures de module d'élasticité et de dureté pour ces 3 filiations sont présentés dans les figures II.95 et II.96. Cette propriété est visible sur la figure II.98(b) et est liée à l'évolution de la dureté au sein du Z.F.

Essais de traction longitudinale
L'intervention de l'opérateur est alors nécessaire pour ajouter ou supprimer les points erronés de la figure II.110(a). De la même manière, il est possible de tracer les profils de déformation (voir figure II.119). Les champs de déformation au sein de la zone riche en Ta au milieu de la figure II.120(b) sont parmi les plus importants, reflétant l'influence de l'hétérogénéité chimique.
L'échantillon se brise à quelques millimètres de la zone de dépôt du micro-réseau comme on peut le voir sur la figure II.122. En conclusion, l'hétérogénéité semble être liée au caractère polycristallin du système Z.F.
Potentiel d’´ etat et relations d’´ etat
L'inégalité fondamentale fournit les principales relations d'état selon une approche classique (Germain, 1973) (équations III.5 et III.6), ainsi qu'une inégalité résiduelle représentant la somme des dissipations intrinsèques et thermiques (équations III.7). Dans l'hypothèse où l'élasticité n'est pas affectée par la plasticité mais uniquement par l'endommagement, la distribution du potentiel d'état sous la forme de l'équation III.13 est justifiée. Le potentiel d’état peut donc s’écrire en fonction des variables effectives dans le cas isotherme.
A l'aide des relations III.5, III.8, III.9 et III.10, les expressions des variables de force s'écrivent en fonction de l'endommagement sous la forme. Pour vérifier, a posteriori, l'expression de la distribution interne (équation III.11), il faut donner les équations de l'évolution des phénomènes dissipatifs.
Analyse des dissipations et relations compl´ ementaires
Une étude détaillée des fonctions de viscosité possibles est réalisée dans (Chaboche, 2007) et est résumée dans le tableau III.5 et la figure III.4. Les équations d'évolution des variables internes sont donc données, comme pour la plasticité indépendante du temps (équations III.45 à III.48), par,. Enfin, les équations d'évolution auront la même forme que celle obtenue dans le cas indépendant du temps (Équations III.45 à III.48) avec le multiplicateur viscoplastique imposé par le choix de la fonction viscosité.
Le choix du potentiel de dommage conduit à une dépendance au taux cumulé de déformation plastique (équation III.64). On obtient ainsi la loi d'évolution des dommages (équation III.64), qui s'écrit en fonction du multiplicateur viscoplastique.
Ecrouissage de nature isotrope ´
Cependant, grâce à la construction du modèle viscoplastique, la limitation de traînée n'apparaît pas dans le potentiel d'état, mais uniquement dans le potentiel de dissipation (équations III.13 et III.63). Cependant, les équations d'évolution des variables de flux sont écrites en dérivant le potentiel des dissipations par rapport aux variables duales (équations III.82 à III.85). Les équations d'évolution des variables de flux découlent du potentiel des dissipations par rapport aux variables duales et n'introduisent donc aucun terme supplémentaire (cf. équation III.96).
Les formulations les plus usuelles prennent la forme de l'équation III.98 proposée par Marquis (Marquis, 1979) ou III.99 issue de la théorie endochronique développée par Valanis (Valanis, 1980), (Watanabe et Atluri, 1986). L'étude paramétrique du modèle et l'identification seront décrites en détail dans les sections III.7 et V.2.
Synth` ese des ´ equations du mod` ele et application au cas de l’isotropie
Leurs expressions, en fonction du module élastique E et du coefficient de Poissonν, sont données dans les équations III.111 et III.112. Le potentiel viscoplastique est écrit pour le modèle de Norton (« Norton ») et le modèle de sinus hyperbolique (« sinh »). Les équations d'évolution qui en résultent sont exprimées sous la même forme quel que soit le modèle.
Nous avons développé le modèle dans un cadre général incluant l'anisotropie critère et l'anisotropie d'écrouissage, puis l'avons isolé au cas de l'isotropie totale. Un cas précis ne remplit pas cette dernière condition, c'est le cas de la contrainte planaire que nous étudierons dans le paragraphe suivant (III.5).
Traitement de la contrainte plane
L'équation III.126 n'est généralement pas prise en compte et donc la compatibilité des déformations selon la direction 3 n'est pas assurée. Pour mieux comprendre l'intérêt et les possibilités d'une telle approche, nous reprendrons les équations modèles dans le cas de l'isotropie totale et utiliserons la formulation proposée par Simo pour le stress du plan de traitement. Le sous-espace de contraintes plan SP est donc un sous-espace tridimensionnel de l'espace de contraintes S défini par l'équation III.138.
Cette spécification du modèle est traitée dans le cas de contraintes planes par une approche « mapping » proposée par Simo. On voit donc que le traitement des contraintes planes avec cette méthode permet d'élargir considérablement le potentiel d'un modèle isotrope dans le cas de l'anisotropie plastique du critère et de l'écrouissage.
G´ en´ eralisation aux transformations finies
J est souvent noté le jacobien de la transformation, c'est-à-dire le déterminant du gradient de la transformation F∼, J = det(F. On peut donc définir la mesure de déformation s', qui disparaît pour le mouvement d'un corps rigide, comme da ,. Le gradient de vitesse peut être décomposé en la somme de la vitesse de déformation D correspondant à la partie symétrique de L.
A chaque mesure de déformation correspond une mesure de contrainte conjuguée, on définit donc différents tenseurs de contraintes : le tenseur de Piola Kirchoff 2 (S. ~) in. L’un des principaux problèmes des grandes transformations, outre le choix de la mesure des déformations et des contraintes, réside dans le principe d’indifférence matérielle.