Un point important du problème élastique est la réussite de l'identification dans un cas anisotrope, ainsi que l'identification d'un matériau isotrope avec une erreur dans la loi de comportement correspondant à la symétrie cubique. Ce chapitre est consacré à la présentation du problème de l'identification de la distribution interne des modules élastiques en élastostatique linéaire.
Le probl`eme math´ematique
1Pour le problème de Neumann, l'existence est assurée si les forces extérieures sont auto-auto-. Le problème inverse peut idéalement être reformulé comme suit : Déterminer C avec la connaissance de ΛC.
Questions importantes et r´esultats existants
Ikehata a démontré [31], en utilisant la technique de Calderon [16], que les mesures sur la frontière déterminent complètement les perturbations des modules élastiques, ce qui équivaut à l'unicité du problème linéarisé. L'unicité du problème linéarisé dans le cas des plaques de Love-Kirchhoff vient d'être démontrée par Ikehata [32].
Caract´erisations de l’application DN
Les applications Energie et DN
Nous commencerons par montrer que la connaissance de l’application de Dirichlet-Neumann ΛC implique une connaissance de la consommation d’énergie. La démonstration mutuelle, lorsque l'on veut exprimer l'application Dirichlet-Neumann à partir de l'utilisation de l'énergie, semble plus difficile car elle doit être exprimée.
Formules de r´eciprocit´e
Si l’on considère uniquement les termes du premier ordre dans le développement de (1.5), on obtient l’expression suivante pour QδC(u0). Une application directe de ces équations consiste à démontrer l’unicité de la solution au problème d’identification [31, 58].
Propri´et´es de monotonie
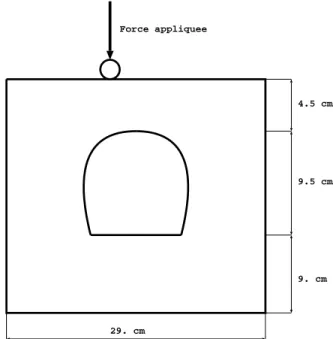
Compte tenu de la croissance de l’application C−→ QC et de l’hypothèse initiale C≤L on obtient d’une part pour tout corps v Des mesures de pénétration d'un poinçon cylindrique effectuées à charge constante en différents points du bord supérieur d'une plaque époxy (voir fig. 1.2) sont effectuées, représentées sur la figure 1.1.
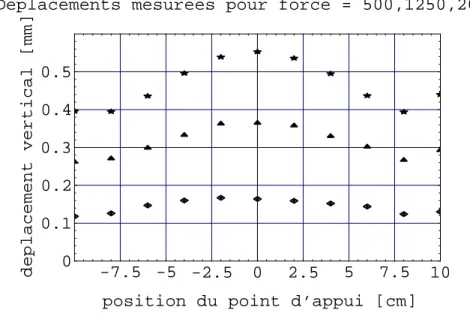
Application de DN et vibrations libres
On remarque que dans le cas plus général des corps à densité de masse inhomogène, le problème spectral inverse propose également de déterminer la densité de masse. Dans ce cas, le résultat précédent ne donne qu'une relation entre le problème d'identification élasto-statique et le problème spectral inverse correspondant à l'opérateur de Lam´e.
R´esultats d’unicit´e et de stabilit´e
Perte d’unicit´e dans l’´elasticit´e anisotrope
Ω(v◦Ψ−1)σL(u◦Ψ−1)nds En utilisant le fait que Ψ est l'identité à la frontière et en résolvant le problème élastique avec le tenseur d'élasticité de déplacement apparentCetvun, la relation précédente devient. Alors u◦Ψ−1 est la solution du problème élastique avec le tenseur d'élasticité eL car v◦Ψ−1 reste le déplacement apparent pour chaque déplacement apparent v et chaque déplacement différentiel Ψ.
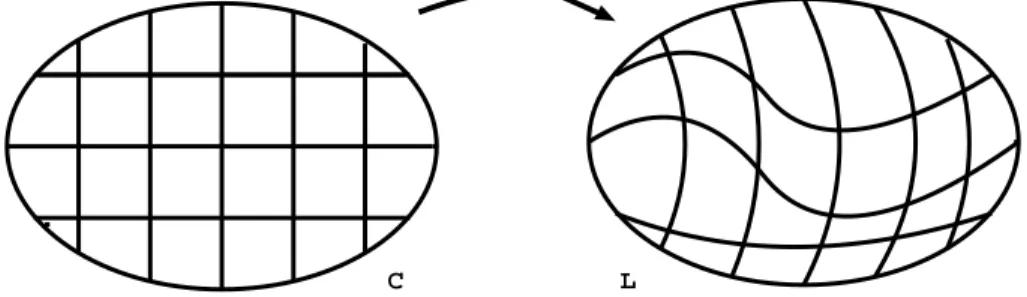
Discussion des r´esultats d’unicit´e
A partir de ces remarques concernant l'élasticité isotrope et de la technique utilisée pour la reconstruction numérique des modules élastiques dans les cas isotrope [18] et anisotrope [19], nous formulerons, sans démonstration, une conjecture identifiable d'élasticité anisotrope. Dans le cas de l'élasticité isotrope, les modules propres sont le module de déformation volumétrique et le module de cisaillement et les tenseurs propres correspondent à la direction sphérique et déviatorique de l'espace tenseur.
R´esultats de stabilit´e
Exemples 1D
Cela implique également la convergence des valeurs de l'état limite perturbé vers les valeurs de l'état limite non perturbé. Nous sommes bien conscients des difficultés qui surviennent lorsque l'on propose de reconstruire le coefficient d'une équation elliptique à partir des valeurs limites, ce qui est en réalité le problème d'identification auquel nous sommes confrontés. solution proposée.
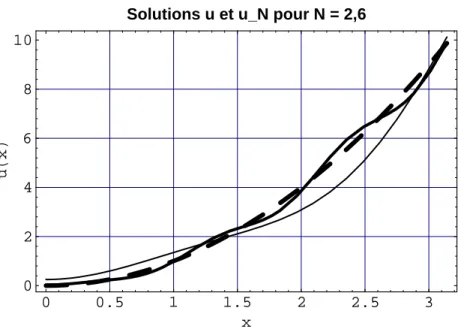
Equation de Fredholm
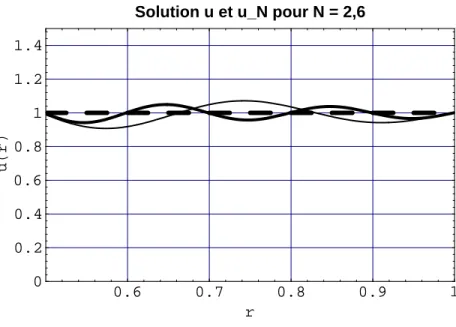
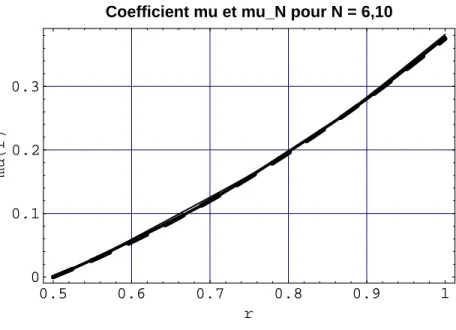
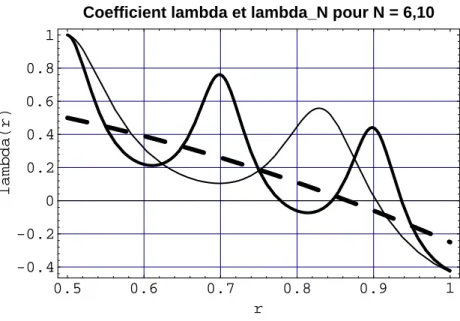
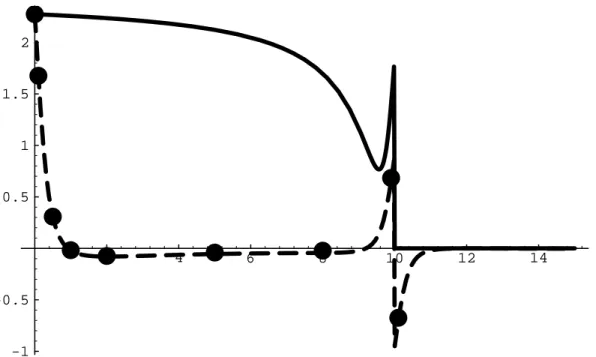
1.6 – Élasticité des sphères creuses : Convergence du déplacement suNr (traits continus N = 6.10) vers la solution ur (en tirets). Les équations (1.63) et (1.64), parfois appelées équations d'observation, ont la structure des équations intégrales de Fredholm du premier type, respectivement linéaires et non linéaires. 'dans l'inconnu δC.
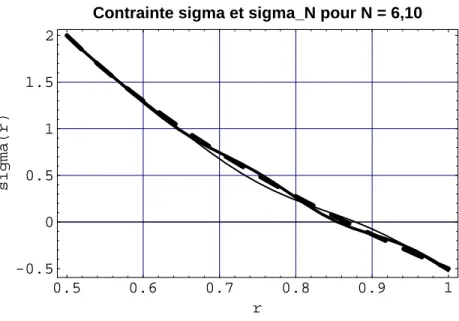
S´election des charges ` a appliquer
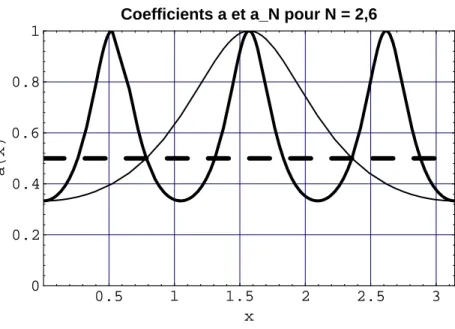
En utilisant le principe min-max (voir [21]), il en résulte que les meilleures puissances pour distinguer les distributions de tenseurs d'élasticité CetL sont les fonctions propres de D2 correspondant à la valeur propre la plus élevée21. Le calcul de la meilleure puissance discriminante entre deux distributions de tenseurs d'élasticité donnés se réduit donc à un problème de valeurs propres de la différence entre les inverses des cartes DN correspondant aux deux tenseurs d'élasticité.
Conclusion
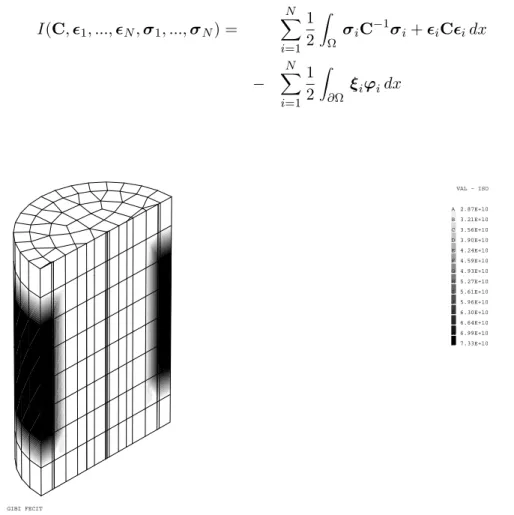
Dans ce chapitre, nous présentons en détail une approche originale pour résoudre le problème de l'identification des modules élastiques à partir d'un nombre limité de mesures simultanées de force-déplacement sur la frontière (Section 2.1). Le problème pratique d'identification peut être reformulé ainsi : Trouver la distribution interne des modules élastiques C(x) et N triplets de champs avec déplacements, déformations et contraintes, (ui(x),ǫi(x),σi( x)) i=1 ,N qui satisfait l'équation constitutive de Ω.

L’erreur en loi de comportement
- Elasticit´e isotrope
- Elasticit´e anisotrope
- Quelques remarques sur les propri´et´es math´ematiques de ELC 47
- Limitations de la m´ethode de reconstruction
Une brève discussion sur les propriétés de convexité de l’ELC sera faite plus tard. Une première étape dans la convexification de l’ELC sera de la placer sous forme relâchée.
Mod`ele analytique 1-D
Solutions analytiques aux probl`emes directs
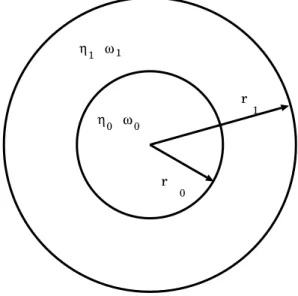
Il est clair que notre méthode fournit même les modules corrects dans ces cas, mais revenir à l’ensemble des modules élastiques est compliqué, voire impossible (voir Section 2.2.3). Les rayons des deux sphères sont r1 et tr0(r0 < r1), et les modules d'élasticité sont respectivement η1,ω1 dans la couche externe et η0,ω0 dans l'inclusion.
Probl`eme d’identification
La nouvelle valeur η0n+1 sera obtenue en minimisant l'expression de distribution ELC suivante pour r∈[0, r0]. En raisonnant sur la monotonie de la suite et la position du choix initial η00 par rapport à η0, on conclut que la convergence η0n−→ η0 ne dépend que des signes de f′ et (x f)′.
Conclusions
Dans notre cas, des calculs élémentaires montrent que le signe de f′ est déterminé par le signe de. La portée de la méthode est à la fois mathématique (car de nombreuses questions sont encore ouvertes d'un point de vue mathématique) et pratique, car la décomposition de l'ELC peut être utilisée dans d'autres problèmes d'identification (c'est-à-dire des problèmes spectraux inverses) ou d'optimisation d'élasticité.
Description des test num´eriques
Ces mesures ont été bruitées pour différents calculs de bruit blanc selon les formules suivantes. Les distributions des modules élastiques au début de la reconstruction étaient considérées comme constantes, leurs valeurs n'avaient pas d'influence particulière sur le résultat de la reconstruction.
R´esultats - Elasticit´e isotrope
Le bruit affecte à la fois la vitesse de descente des premières itérations et la valeur seuil pour un grand nombre d'itérations. Si la différence |E0−E1| grande, on observe une fluctuation du module calculé qui augmente avec le nombre d'itérations.
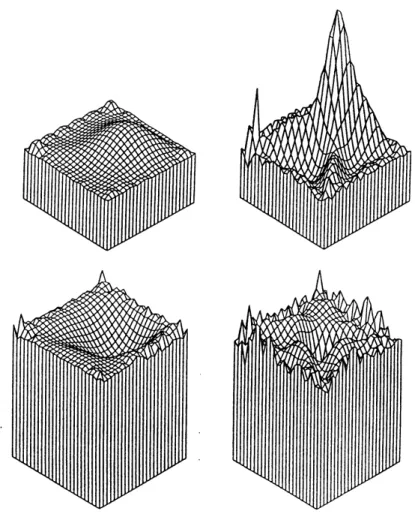
R´esultats - Elasticit´e ` a sym´etrie cubique
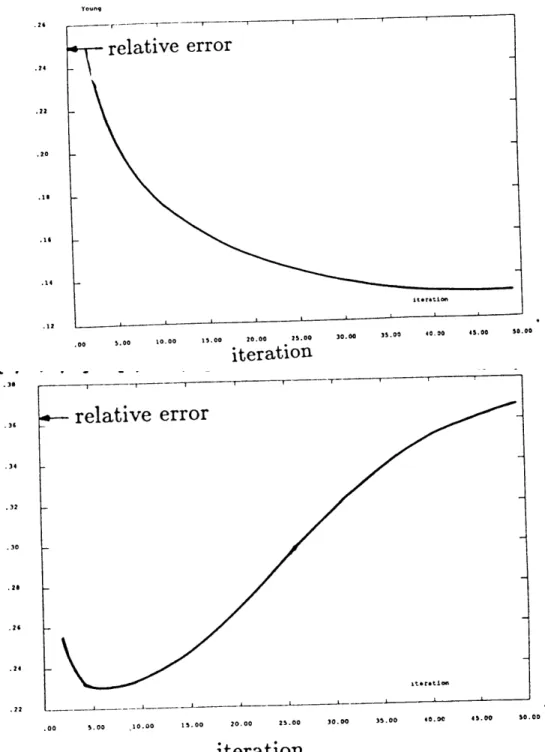
En poursuivant les itérations, les erreurs descendent en dessous de 10% pour le module de cisaillement. Tomber en dessous de 2 % - 3 % pour le module d'Young E et le coefficient de Poissonν. 3.10 – Erreur dans la constitution des distributions exponentielles du module d'Young avec (en haut) et sans bruit (en bas) (δE1/E0= 0,5).
Comparaison avec le probl`eme ´electrique
Dans ce passage, nous avons en fait libéré juste un degré de liberté supplémentaire, qui correspond à un module propre. L'instabilité rapportée par Kohn et McKenney doit probablement arriver au moment où les degrés de liberté correspondant aux distributeurs sont libérés.
Conclusion
Nous présentons ci-dessous l’expression complète des modules d’élasticité pour l’élasticité à symétrie isotrope et cubique. La symétrie cubique est entièrement caractérisée par 3 modules élastiques λ, µ et β reliés à Cˆ par.
Analyse spectrale et fonction de Green
La solution fondamentale permet de fournir une représentation intégrale de la frontière pour les déplacements à partir d'un champ de force donné. Disons un champ de force autour de ∂Ω, nous considérons l'unique solution du problème aux limites suivant.
Sur l’identification des fissures
Le principe des potentiels apparents est écrit pour la solution u d'un problème perturbé par un déplacement apparent v. Le même principe s'applique à la solution v du problème non perturbé avec déplacement apparent u.
Erreurs des calculs de reconstruction
- Etat de contrainte r´esiduelle
- Equation ´elastique lin´eaire
- Probl`eme d’identification des contraintes r´esiduelles
- M´ethode de l’´etat adjoint
Avec ces notes, l'équation constitutive de l'élasticité linéaire avec les contraintes restantes est écrite. L'étude de l'identification des modules élastiques conduit à imaginer une identification des contraintes résiduelles réalisée en deux étapes : la détermination du pseudotenseur d'élasticité C[σ] en chaque point du solide, puis l'identification de deo σo à partir de C[σ] .o.
Reconstruction des mesures des contraintes par rayons X
Introduction
Cheng et Finnie [17] ont reconstruit les contraintes résiduelles dans une plaque à partir de jauges de contrainte fixées sur un côté et enlevant des couches de matériau de l'autre côté. Gao et Mura [27] ont reconstruit numériquement les contraintes résiduelles en dehors de la zone plastiquement déformée à partir de mesures de déplacement de surface, en utilisant des formulations intégrales à la frontière.
G´en´eralit´es sur le probl`eme - Exemples
Les mesures sur une ligne tombant vers l'intérieur du corps sont-elles suffisantes pour remonter à la contrainte initiale sur cette ligne ?
Redistribution des contraintes - I
B.2 – Confinement plastique rectangulaire dans un demi-espace élastique Cet exemple montre que l'enlèvement de matière provoque une redistribution des contraintes, qui peut être très forte selon les cas. B.3 – Répartitions des contraintes résiduelles le long de l'axe : σxx (courbe continue), et σxxm mesurées (ligne pointillée) pour une demi-grade élastique avec inclusion plastique (sans enlèvement (I) et avec enlèvement de matière (II & III) ).
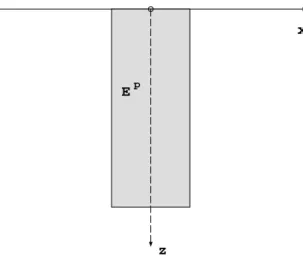
Redistribution des contraintes - II
Cet exemple montre que les informations issues des mesures sur une ligne de points ne sont pas suffisantes pour reconstituer la contrainte résiduelle initiale sur cette ligne.
Redistribution des contraintes - III
Reconstruction de la boule
Dans cet exemple nous avons procédé exactement comme Moore et Evans, l’avantage essentiel étant le problème unidimensionnel. Même si ce problème présente peu d'intérêt pratique, il permet de mettre en évidence les points principaux de la reconstruction : l'imbrication des problèmes et la solution claire du problème auxiliaire.
Reconstruction dans le cas du demi-espace
On voit que la résolution du problème auxiliaire sur chaque surface ∂Ωh fournit une relation entre le champ de contraintes mesuré σm et le champ de contraintes initial σ. Pour résoudre le problème auxiliaire, nous utilisons la solution du problème de Boussinesq-Cerruti (voir par exemple Johnson [36]).
Probl`eme bidimensionnel
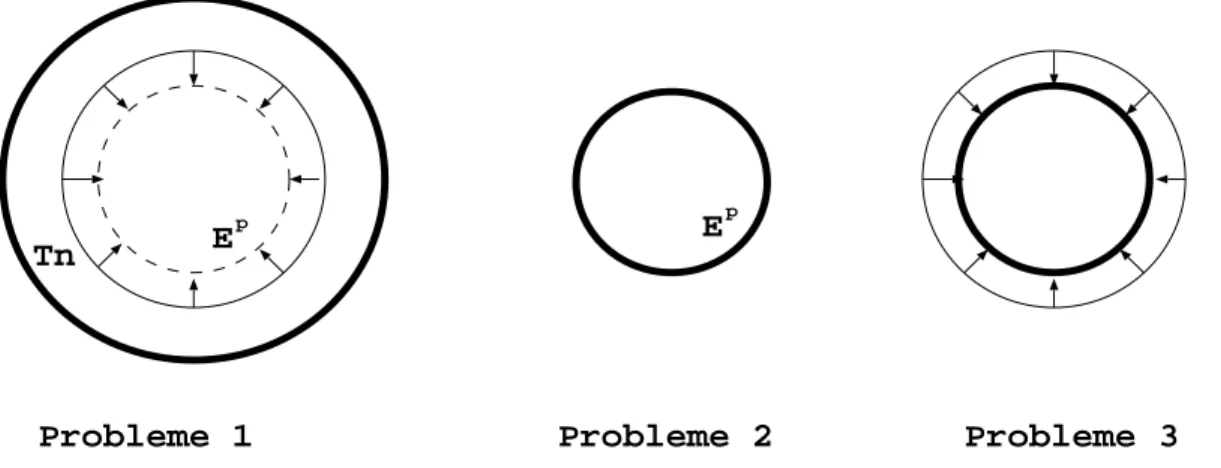
Le problème 3 est un problème purement élastique, tandis que les problèmes 1 et 2 font intervenir un champ de déformation inélastique (supposé identique dans les deux cas du fait de l'hypothèse de relaxation élastique) à l'origine du champ de contraintes résiduelles. A partir du champ de contraintes mesuré, les valeurs de la contrainte résiduelle initiale ont été calculées à l'aide des formules précédentes, puis les valeurs obtenues numériquement ont été comparées à la solution exacte.
Le probl`eme tridimensionnel
B.7 – Comparaison des contraintes résiduelles calculées (points) avec celles initiales (ligne pointillée) et mesurées (courbe pleine) le long de l'axe z. Reconstruction des mesures de contraintes aux rayons X 134. B.56). Pour la reconstruction du champ de contraintes résiduelles initiales σ il est nécessaire de connaître le champ de mesure complet σm à chaque interface.
G´eom´etrie arbitraire
Le champ de déplacement ut, solution du problème auxiliaire, satisfait (voir par exemple Kupradze [46]) une équation intégrale de surface singulière. Nous pouvons donner une expression intégrale de la contrainte de surface pour le problème auxiliaire.
Br`eve description d’un algorithme de r´esolution num´erique . 140
Ainsi, le champ de contraintes résiduelles initiales dans le volume balayé par l'enlèvement de matière est déterminé par des mesures de contraintes superficielles à chaque interface. Les données initiales sont alors clairement données par les conditions aux limites sur le solide avant enlèvement de matière (σn = 0).
Inclusion plastique dans un demi-espace
24] D.C.Dobson - Estimations de résolution et de stabilisation pour le problème de conductivité inverse linéarisé Inverse Problems, Vol.8, pp. 57] F.Murat - Contre-exemples pour divers problèmes où le contrôle intervient dans les coefficients Ann.Math.Pura e Appl., Vol.62, 1977, p.