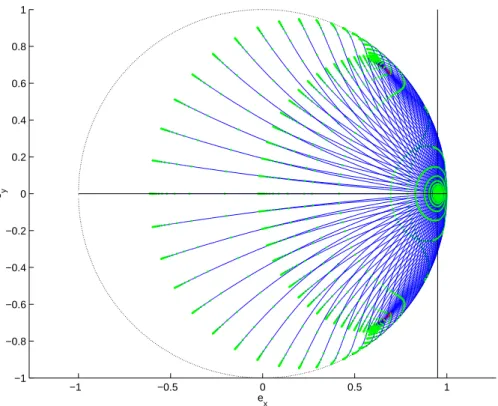
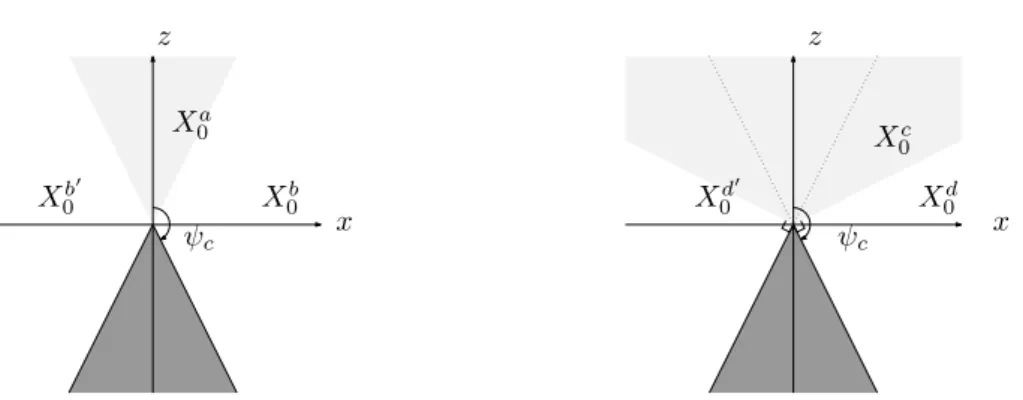La dernière coordonnée est la longitude, ce qui permet de localiser la position de l'objet sur l'ellipse. La présentation des résultats est organisée en deux chapitres : le premier est consacré au temps minimum, le second à la moyenne du problème de minimisation de l'énergie.
Contrˆ olabilit´ e
Dans le cas d’une décomposition en poussée dans le repère radial-orthoradial local, on a Dans le cas d'une seule poussée radiale, les crochets de longueur trois sont donnés en premier.
Extr´ emales en sous-riemannien avec d´ erive
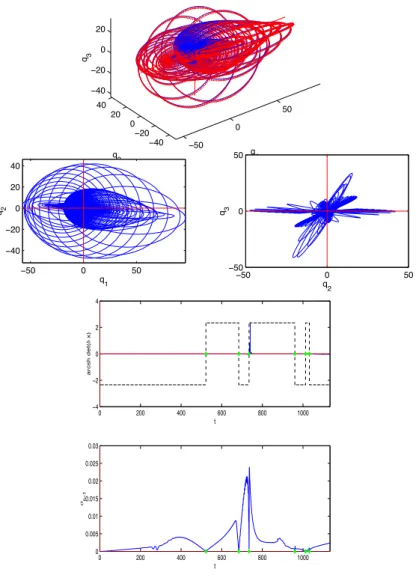
Nous analysons d’abord les extrêmes du cas multi-entrées (deux contrôles coplanaires, trois contrôles non coplanaires). Il existe des extrémales obtenues en concaténant deux extrémales d’ordre zéro.
Points conjugu´ es, cas r´ egulier
En l'absence de point conjugué le long de l'extremum de référence, il existe un voisinage ouvert V de la trajectoire (sans l'extremum initial) et deux applications lisses, g : V → R et uˆ : V → U, telles que pour tout (x , u) v V × U,. Les tests 1 (ou 2) et 3 sont complémentaires dans la mesure où le rang dans les deux premiers cas peut être évalué en évaluant à chaque instant la plus petite valeur singulière σn−1(t ) de la famille des corps de Jacobi, et où l'on se réduit à une équation scalaire dans le troisième.
Extr´ emales en mono-entr´ ee affine
Calculer une valeur singulière est meilleur en peu de temps, puisqu'on découple σn−1 des autres valeurs singulières, toutes nulles à l'origine, et donc responsables de la très faible taille du d'-déterminant du test 3 au voisinage de det= 0, déterminant dont l'ordre de grandeur est déterminé par le produit de ces valeurs singulières. Le déterminant et la plus petite valeur singulière des champs de Jacobi le long de l'extremum sont ensuite représentés. Comme dans le cas hyperbolique, un singulier d'ordre minimal passe par z0, mais la connexion avec un arc ±1 est impossible.
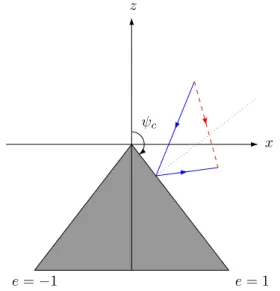
Enfin, nous décrivons les extrêmes singuliers associés à un contact d'ordre infini : H1 est identiquement nul le long de l'extrême. Comme nous le rappelons en 1.5, cette sous-classification des singuliers est directement liée à leur optimalité, puisque la condition d'ordre minimum jusqu'au signe est interprétée comme une condition de Legendre forte. L'application au transfert orbital est une conséquence de l'analyse de l'algèbre de Lie faite en 1.1 et est résumée ci-dessous dans le cas des deux directions de poussée pour lesquelles nous tenons la contrôlabilité en mode coplanaire (et en mode non coplanaire par une poussée hors de plan), à savoir la poussée tangentielle et la poussée orthoradiale.
Toutes les singularités sont elliptiques d'ordre minimal, et les contacts d'ordre deux sont paraboliques ou elliptiques, et non hyperboliques. Puisque les singularités elliptiques d'ordre minimal ne peuvent pas être des temps minimaux (cf. 1.5), nous en déduisons que les trajectoires optimales en mono-entrée tangentielle sont nécessairement bang-bang. Alors tous les singuliers non normaux sont d’ordre minimal en dehors des péricentres et des apocentres, et la vérification correspondante est valable.
Points conjugu´ es, cas singulier mono-entr´ ee affine
La transformée de Goh consiste alors à considérer un nouveau système ˙y = f(y, xn) contrôlé par xn. Puisque l'état adjoint est normalisé par |p(0)|= 1, nous donnons la définition du point conjugué dans le cas hyperbolique (ou elliptique) puis non normal sous la forme du test de rang correspondant sur les champs de Jacobi de linéarisés, associés avec la commande minimum au singulier. Nous considérons le problème de contrôle suivant avec des données périodiques : minimiser le Rlf fonctionnel.
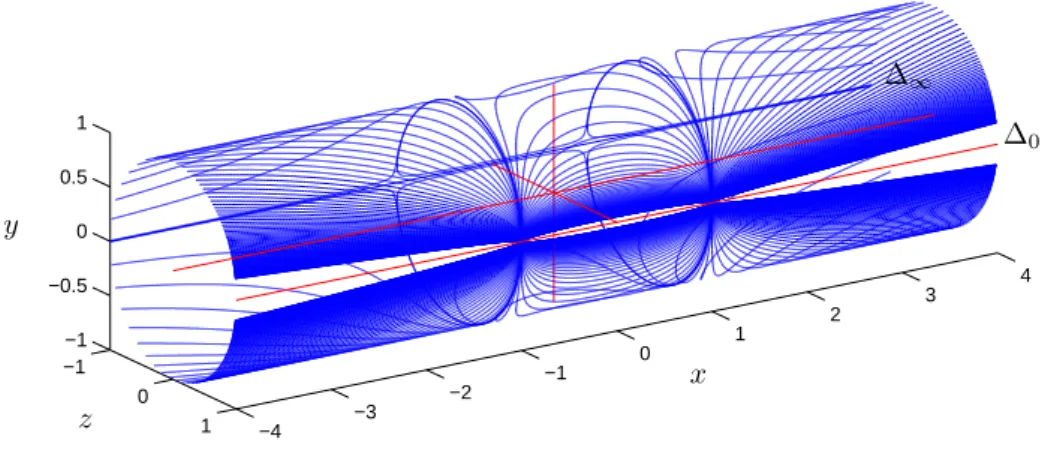
Nous nous intéressons à un système pour les grands temps, l dans [0, lf], tel que le petit paramètre ε= 1/lf. Plus précisément, on a une convergence uniforme sur l'intervalle de longueur 1/ε de la solution à la moyenne, avec la condition initiale étant la même, sous les hypothèses standards de [24], puisqu'on peut évidemment réécrire le système non moyenné précédent sous la forme Mais au lieu de faire la moyenne des extrema du temps minimum en utilisant le module de poussée comme petit paramètre, nous suivons [40, 42] et considérons la minimisation de la norme (ou énergie) de contrôle L2 dans un temps fini donné, sans contraintes sur le temps minimum. commande.
Notez qu'en raison des calculs de classement de 1,1, un tel système ne permet pas de dévier les extrêmes. Quant au casp=1 correspondant au problème important du transfert avec consommation minimale, on peut déduire des résultats de [46, 43] que l'existence ne peut persister sans restriction de contrôle. Les orbites du système, là encore paramétrées par la longitude, sont dérivées des précédentes par projection basée sur le domaine elliptique.
Probl` emes sous-riemanniens p´ eriodiques
Tant que ˙l =W2/P3/2 ne s'annule pas sur le domaine elliptique coplanaire (W = 1+excosl+eysinl), on peut reparamétrer les trajectoires par la longitude cumulée, l∈R , qu'il faut distinguer de la longitude∈ S1. On peut donc définir une métrique sur X, unique modulo la réduction gaussienne effectuée sur la forme carrée moyenne. Dans le cas du transfert, coplanaire tout d'abord, le résultat de la moyenne en coordonnées (P, ex, ey) est le suivant.
Il est également remarquable que les mêmes coordonnées soient toujours orthogonales au hamiltonien moyen en mono-entrée tangentielle [7, 38]. Le terme supplémentaire résultant de la moyenne de l'action de poussée hors plan est ensuite calculé explicitement en utilisant l'approximation précédente. L'hamiltonien complet de cinquième dimension a toujours le rang maximum et a la forme H+H1.
Le nouvel hamiltonien H1 est associé à un problème sous-riemannien en dimension trois, et finalement nous avons la proposition suivante [8]. L'hamiltonien H1 correspond au problème sous-riemannien défini en dimension trois par la distribution de contact. Dans ce qui suit, nous nous limitons à l’étude de la métrique riemannienne du problème coplanaire, en commençant par l’intégrabilité.
Int´ egrabilit´ e et courbure du moyenn´ e
La métrique g2 est une métrique de Clairaut-Liouville[27, 35], classiquement intégrable (d'où encore l'intégrabilité de l'ensemble du système en dimension trois). Nous vérifions que la nullité de la courbure transversale, évidemment nécessaire à la planéité de la métrique, est également suffisante. Si KV est nul, F peut être normalisé en sinψ et on obtient ag=dr2+r2(sin2ψdθ2+ dψ2), c'est-à-dire la métrique plate en coordonnées sphériques.
La courbure résultante diffère logiquement de la courbure sectionnelle, et le caractère non nul de la deuxième forme fondamentale se traduit par le fait que l'injection de Y = {r=c} 'S2 dans X n'est pas géodésique : les géodésiques de Y ne le sont pas. sur X (cela se voit par exemple en constatant que r2 n'est pas constant dès que pr0 est différent de zéro, c'est-à-dire dès qu'on a une géodésique qui n'est pas réduite à un point sur Y). Le caractère cyclique de la coordonnée θ nous invite à rechercher une surface de révolution de R3 sur laquelle la métrique planaire serait limitée à G(ϕ)dθ2+dϕ2. En d’autres termes, la courbure ne peut pas provenir uniquement de la surface, et la propriété remarquable suivante naît de la comparaison avec l’ellipsoïde.
La métrique Clairaut du transfert correspond à la métrique plate sur l'ellipsoïde étiré du demi-petit axe 1/√. La restriction du plan métrique0=dx2+dy2+dz2 à l'ellipsoïdeEµ de rotation de demi-grand axe unitaire et demi-petit axe 0<µ≤1 encastré dans R3 selon . En particulier, nous dérivons une homotopie qui permet de relier dans S2 la restriction de la métrique plate à celle du transfert, qui consiste en la transition continue de μ de 1 à 1/√.
Analyse dans les demi-plans m´ eridiens
Les géodésiques sur l'ellipsoïde pour chacune des deux métriques sont présentées sur la fig. A l'exception du séparateur en contact avec la limite du domaine à n = 0, l'anomalie moyenne est strictement positive le long des lignes géodésiques. Sur la gauche se trouvent les lignes géodésiques vers n'importe quelle destination pour les points de X0a, puisque X0 est marqué d'un astérisque par rapport à ces points.
A l'inverse, pour les points dans X0b (respectivement X0b0), l'existence est perdue pour les cibles telles que ψ≤ψ0−π(respectivement à droite, les contacts avec ∂X0 sont classés selon que le contact se produit avec {r= 0} pour les points initiaux en X0c, ou avec {e= 1} Deuxièmement, celles en X0f(x0, z0) pour lesquelles des géodésiques existent mais ne sont plus complètes à cause du contact avec le bord du demi-plan méridien.
Puisque le contact |e|= 1 coïncide avec une singularité pour la coordonnée polaire ψ= (1/c) les courbes e,c=p. Le contact avec l'arête parabolique est converti en coordonnées plates x=rsinψ,z=rcosψ par une réflexion. Les points en bordure du domaine forment une enveloppe pour la géodésique et sont interprétés (hormis l'origine) comme des points conjugués.
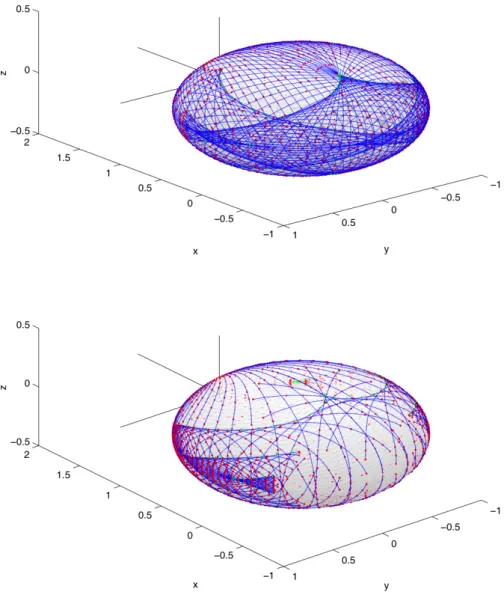
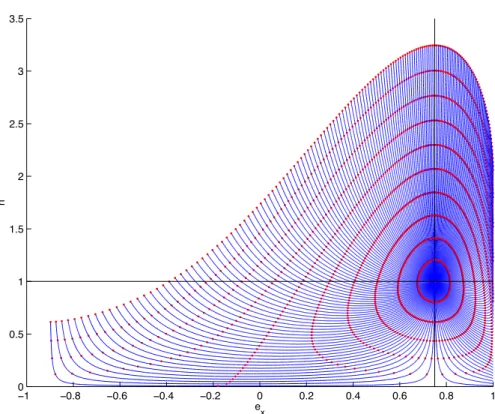
Points conjugu´ es, analyse globale
Dans le cas d'un transfert orbital, le défaut de surjectivité est mesuré par l'exponentielle, comme le montre la Fig. Le rayon d'injectivité de la métrique Clairaut associé au transfert coplanaire moyen est π/√. Le lieu conjugué est une déformation de l'astroïde obtenue en limitant la métrique plate à l'ellipsoïde à quatre sommets.
21] Contribution à l'étude du contrôle en temps minimum des transferts orbitaux, thèse de doctorat de l'Institut National Polytechnique de Toulouse, 2000. Tr´elat, Une approche géométrique du contrôle optimal de l'arc atmosphérique d'un avion-fusée, ESAIM Control Optimale. Application au problème du transfert orbital, thèse de doctorat Institut National Polytechnique de Toulouse, 2001.
Dujol, Contribution à l'étude du contrôle optimal des transferts orbitaux mono-entrée, Thèse de doctorat de l'Institut National Polytechnique de Toulouse, 2006. Haberkorn, Transfert orbital à faible poussée avec minimisation de la consommation : résolution par homotopie différentielle, Thèse de doctorat de l'Institut National Polytechnique de Toulouse, 2004. Contrôle optimal et transfert orbital en un temps minimal, Thèse de doctorat de l'Institut National Polytechnique de Toulouse, 2004. National Polytechnique de Toulouse, 1999.
Martinon, Solution numérique de problèmes de contrôle optimal par une méthode de continuation linéaire par morceaux, Thèse de doctorat de l'Institut National Polytechnique de Toulouse, 2005. Preda, Intégration d'une contrainte logique dans l'optimisation de problèmes de contrôle et solution par programmation mixte, Thèse de doctorat de l'Institut National Polytechnique de Toulouse, 2004.