The net external work done on a closed system will equal the change in energy of the system. It is critical that students practice using the concepts presented in this text by solving problems.
Review of fundamentals
Introduction
In general, memorizing the governing equations is a very poor means of developing the fundamental understanding needed to solve complex problems in any engineering discipline. It is strongly recommended that students develop the very important and versatile skill of solving problems from first principles based on the most general governing equations available.
Displacement, velocity and acceleration
- Displacement, velocity and acceleration as functions of time
- Acceleration and velocity as a function of displacement
To determine the velocity as a function of position, we must eliminate time from the expression for velocity. By applying the chain rule as shown in Equation (1.3), it was possible to obtain the velocity as a function of the acceleration directly, without solving for time.
Other important considerations
Therefore, the evaluation of derivatives or integrals becomes impossible, while the generality of the result is completely lost. Instead, students would simply ensure that all numerical values used were in standard SI units (kg, m, s) and then assume that the result would be in the required units.
Examples
- Exponential acceleration
- Velocity as a function of displacement
- Sinusoidal acceleration
- Acceleration as a function of displacement
- Linear acceleration with mixed initial conditions
Next, we integrate the definition of velocity to obtain an expression for position as a function of time. This is an expression for the displacement as a function of time, in terms of the known quantities v1,t1,t2andx2, as well as the given constant0andt0.

Problem set 0: Velocity and acceleration Question 1Question 1
A train applying its brakes will decelerate with an acceleration that varies as a function of the distance traveled according to the expression, . Determine the velocity of the train as a function of position if it was traveling at a speed of v0 when the brakes were first applied.
Vector kinematics
Vector arithmetic
- Vector addition
- Scalar multiplication
- Dot product
- Cross-product
Because the scalar cannot contribute to the direction of the vector (since it has no direction of its own), it simply increases the magnitude (or length) of the vector without affecting its direction. The direction of the cross product ggg=aaa×bbb is defined as being mutually perpendicular to aaa and bbb.

Unit vectors
- Cartesian coordinates
- Cylindrical coordinates
- Spherical coordinates
- Converting between coordinate systems
This position vector can be represented by rrrp/op/op/o, which denotes the vectorrrr describing the location of the point 'p' with respect to the origin and coordinate system 'o'. Recognize that the vector rrrp/up/up/o cannot change due to the change in unit vectors.

Time-derivatives
- Cartesian coordinates
- Cylindrical coordinates
- Spherical coordinates
- Normal-tangential coordinates
As with the cylindrical coordinate system, the velocity of a point can also be expressed as the time derivative of the position vector in the spherical coordinate system. We can then evaluate the time derivative of the unit vector eeerrrin spherical coordinates as,.

Relative motion
- Universality of relative motion equations
We express this in terms of the unit vectors eeexxx and eeexxx (at our particular moment when everything happens to be aligned). The acceleration of the point in space can also be expressed in terms of the velocity and acceleration of the moving reference frame. If we define the angular acceleration of the axes as αααaxaxax=ωωω˙˙˙axaxax, the above expression can be reduced to.
This is another extremely important result, and each of the terms in this equation has a special meaning. Taking the time derivative of this angular velocity through the application of the product rule and equation (2.7), then.

Examples
- Computing velocities
- Generalized coordinates
- Relative motion: bug on a disc
- Relative motion: bug on a wheel
- Angular velocity and axes of rotation
- Relative motion in three dimensions
- Constrained motion: bug on a ladder
- Constrained motion: Slotted crank
- Scotch yoke mechanism
- Crank-slider mechanism
- Crank-rocker mechanism
The moving axes are fixed to the disk, and the angular velocity of the disk is provided in the problem description. The term aaap/up/up/or represents the acceleration of the error relative to the moving frame (which is fixed to the disc). Again, since o is fixed to the disk, ωωωaxaxax is simply the angular velocity ω of the disk).
This term represents the acceleration of the error relative to the moving frame of reference. As always, the velocity of the bug vvvp/up/up/orrelative to a stationary observer can be given as,. The angular velocity of the ladder (to which our moving axes are attached)ωωωaxis-axis still unknown.
Because the moving coordinate system is fixed to the crank, ωωωaxaxax will be the same as the angular velocity of the crank ˙θθθ˙˙.

Problem-solving technique
The angular velocity of the rocker arm is also plotted as a function of θa Figure 2.40 below. The rotation of the rocker arm therefore changes sense, resulting in a periodic (but distinctly non-sinusoidal) motion. It is also typically easiest to choose the orientations of the moving unit vectors eeexxx, eeeyyy, and eeezzz.
Write down all the available information about each of the terms in the relative velocity equations. The scalar coefficients of each of the unit vectors on the left and right sides of the equation must be equal.
Problem set 1: Coordinate systems Question 1Question 1
Problem set 2: Relative motion Question 1Question 1
Determine the velocity and acceleration of the bug relative to a fixed observer at the instant shown, when the bug is a distance b from the center of the puck, at an angle θ to the direction of motion of the puck. When the crank rotates at a certain constant angular velocity ω, the pin on the slider is pushed at some linear speed due to its contact with the sides of the slot in the crank. Solve for the linear velocity of the slide and the acceleration of the pin with respect to the lever.
Express the results as functions of ω, the distance H between the crank's center of rotation and the rod, and the angle θ subtended between the crank and the horizontal. Show that the speed and acceleration of the insect when the insect is on the eeeyyy axis are .

Linear momentum
Conservation of linear momentum
- Definitions
- Implications of the law of conservation of linear momentum
- Newton’s three ‘Laws’
- Centre of mass
In contrast, an internal force is a force that acts between things that are all part of the system. Consequently, if a system is initially at rest, then C=0 and the center of mass of the system must always remain at rest. If we define the "system" here as the Earth and all that it contains, then both the keys and the Earth are part of the system.
Since we defined the system as the Earth and everything it contains, the air is also part of the system. However, the rocket body moves in one direction and the rest of the system (the exhaust plume) moves in the other direction.

Collisions
- Momentum and collisions
- Impulse
Since there is no interaction with anything outside the system, there are no external forces. It is very important to note here that the terminal velocity of the system (vvvccc)2 does not depend on the energy lost due to material deformation during the collision. It is also interesting to note that this result is identical to the result for the perfectly inelastic collision when the terminal velocity of the combined body Ci is zero.
The magnitude of the internal force FFF exerted by one body on the other will be a function of time during that small Δt, as illustrated in Figure 3.6. In fact, the shape of the function FFF(t) will depend strongly on the elasticity of the body.

Historical note: Origins of the conservation laws
Unfortunately, with only the change in momentum and the duration of the collision, it is impossible to determine the shape of the function FFF(t) or the maximum force to which the object was subjected. The first actual mention of a law of conservation of momentum is sometimes attributed to the philosopher and physician Abu Ali Al-Hussein ibn-Sina, who described a quantity he called impulse, defined as mass×velocity. Although somewhat incomplete (as discussed earlier), the first formal and rigorous mathematical definition of a law of conservation of momentum is typically credited to Sir Isaac Newton, as it appeared in his Philosophiæ Naturalis Principia Mathematicain 1687.
It is Galileo Galilei who is usually credited with the first observation of the conservation of energy during his pendulum experiments, although he did not explicitly propose a conservation law. Described by Albert Einstein as one of the greatest mathematicians who ever lived, Noether made significant contributions to physics and mathematics, and tragically died of complications following a relatively minor operation.
Examples
- Elastic collision
- Perfectly inelastic collision
- The jet engine: an “explosive” collision
- Centre of mass of a mixed system
- Centre of mass of a solid object
- Centre of mass and linear momentum
From our previous definition of the location of the center of mass for extended bodies, . So the center of mass of the stick is at the geometric center of the stick, as expected. Substituting this result into our previous expression for the center of mass of the entire system (and taking axaandxbas the locations of bugsAandB, respectively).
To simplify, the location of the center of mass of the system can be given as rc. Calculate the location of the center of gravity of this body if the density is uniform.

Problem set 3: Conservation of linear momentum Question 1Question 1
A 70 kg fisherman (who looks a lot like a bug, by the way) paddles his 50 kg, 2.5 m long canoe until the nose of the canoe just touches the pier. If the fisherman walks from his paddling position at the very back of the canoe to the front of the canoe, how far will he have to jump to get out of the canoe and onto the pier. Assume that the projectile is an aluminum sphere with a radius of 1 mm and a density of 3000 kg/m3 and that it is fired at 0.1% of the speed of light (which is 3 × 108 m/s) and assume that Arnold has a mass of 130 kg, what velocity the gun will pass to Arnold when fired.
On the other hand, the Boeing 747 is one of the largest and most successful commercial aircraft ever built, with a mass of approximately 5 × 105 kg and a typical cruising speed of 240 m/s. The spacecraft then disengage, leaving spacecraft A with a terminal velocity of 240 m/s eeexxx−60 m/s eeeyyy−8 m/s eeezzz.

External forces
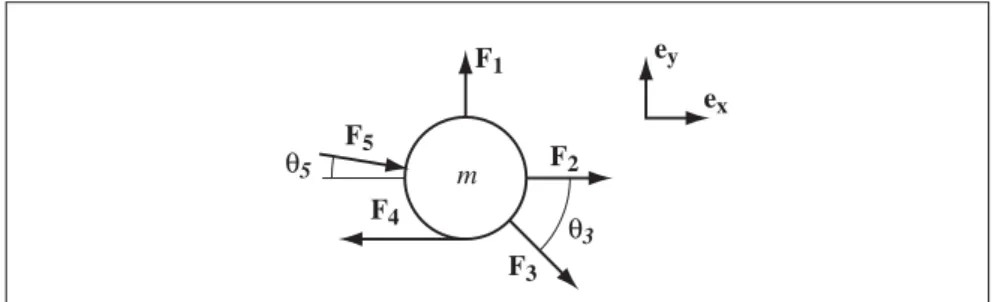
Free-body diagrams
- Hydrostatic pressure
- Buoyancy
The determination of the value of Yeast is often mistakenly attributed to the English scientist Henry Cavendish. The limits of integration must describe the extent of the gas column above the object. If we define the height of the object (or the distance between the object and, for example, the bottom of the gas tank), then the lower limit of the gas column will be 0.
The limits of the gas column above the object will therefore be given by the inequality 0