Estudo sobre o risco de mercado de uma carteira de opções através da análise de componentes principais

FUNDAÇÃO GETÚLIO VARGAS ESCOLA DE ECONOMIA DE SÃO PAULO

DANIEL KENDI OYA

ESTUDO SOBRE O RISCO DE UMA CARTEIRA DE OPÇÕES ATRAVÉS DA ANÁLISE DE COMPONENTES PRINCIPAIS

DANIEL KENDI OYA

ESTUDO SOBRE O RISCO DE UMA CARTEIRA DE OPÇÕES ATRAVÉS DA ANÁLISE DE COMPONENTES PRINCIPAIS

Dissertação apresentada à Escola de Economia da Fundação Getúlio Vargas (FGV/EESP) como requisito para obtenção do título de Mestre em Finanças e Economia Empresarial.

Orientador: Prof. Dr. Afonso de Campos Pinto

DANIEL KENDI OYA

ESTUDO SOBRE O RISCO DE UMA CARTEIRA DE OPÇÕES ATRAVÉS DA ANÁLISE DE COMPONENTES PRINCIPAIS

Dissertação apresentada à Escola de Economia da Fundação Getúlio Vargas (FGV/EESP) como requisito para obtenção do título de Mestre em Finanças e Economia Empresarial.

Data de aprovação:

___/___/_____

Banca Examinadora:

Prof. Dr. Afonso de Campos Pinto (Orientador)

FGV-EAESP

Prof. Dr. Ricardo Ratner Rochman FGV-EAESP

Oya, Daniel Kendi.

Estudo sobre o risco de uma carteira de opções através da análise de componentes principais / Daniel Kendi Oya. - 2006.

114 f.

Orientador: Afonso de Campos Pinto.

Dissertação (mestrado) - Escola de Economia de São Paulo.

1. Mercado de opções. 2. Administração de risco. 3. Análise de componentes principais. I. Pinto, Afonso de Campos. II. Dissertação (mestrado) - Escola de Economia de São Paulo. III. Título.

AGRADECIMENTOS

Agradeço ao meu orientador, Prof. Dr. Afonso de Campos Pinto, pelo apoio, pela orientação e pela confiança depositada neste trabalho, sem os quais não seria possível concluí-lo com sucesso.

Agradeço aos meus pais, pelo constante apoio e incentivo.

Agradeço à Luciana, pelos conselhos, sua ajuda ao longo do trabalho e compreensão por todos os momentos em que não pudemos estar juntos e por tornar este período muito menos árduo com seu companheirismo e carinho.

RESUMO

A presente dissertação tem como objeto de estudo a superfície de volatilidade implícita de opções européias da paridade Real / Dólar no mercado brasileiro. Este trabalho não tenta explicar as deformações ou os desvios da volatilidade implícita com relação à hipótese de volatilidade constante do modelo de Black & Scholes (1973), mas trata a volatilidade implícita como uma variável financeira interessante por si só, procurando analisar a dinâmica de sua superfície.

Para a análise desta superfície, o presente estudo propõe a utilização de uma ferramenta empregada em estudos empíricos de diversos ramos da ciência: a Análise de Componentes Principais – ACP (Principal Component Analysis).

As mudanças na superfície de volatilidade alteram o apreçamento das opções de uma carteira. Desta forma, constituem um fator de risco que precisa ser estudado e entendido para o desenvolvimento de estratégias de imunização e de técnicas de gerenciamento de risco, dentre elas o cálculo de Valor em Risco (V@R – Value at Risk).

De posse dos resultados obtidos com a análise de componentes principais da superfície de volatilidade implícita, o presente estudo tem por objetivo obter valores limite de variação desta volatilidade implícita, como forma de estimar as conseqüentes variações extremas nos valores de uma carteira de opções. Para tanto, baseia-se em estudos sobre a aplicação da análise de componentes principais da superfície de volatilidade implícita desenvolvidos por Alexander (2001). Estes estudos, por sua vez, são derivados de estudo sobre a dinâmica de curvas de volatilidade proposto por Derman (1999).

ABSTRACT

This dissertation is focused on the study of the implied volatility surface of european options on Real / US$ parity traded in the Brazilian market. This work doesn’t try to explain the deformations or deviations of the implied volatility from to the hypothesis of constant volatility of Black & Scholes (1973) model. This work treats the implied volatility observed in the market as an interesting variable by its own, trying to analyze the dynamic of that surface.

To analyze this surface, the present study proposes the use of a technique widely used to analyze empirical data: Principal Component Analysis.

The changes on the implied volatility surfaces alter the pricing of the options in a portfolio. Therefore changes in implied volatility are a risk factor that should be studied and analyzed for the development of immunization techniques and for risk management purposes, such as Value at Risk (V@R).

Using the output from the use of Principal Component Analysis on the implied volatility surface, the present study proposes a limit range of variation of the implied volatility as a way to estimate the limit range of variation of the price of an option portfolio. The technique used in this work to apply Principal Component Analysis on the implied volatility surface was developed by Alexander (2001). Her study was based on a study made by Derman (1999) where he proposed some models to explain the dynamic of the volatility surface.

To verify the effectiveness of the methodology proposed in this dissertation, the result was tested using criteria’s proposed on Basel committee of 1996.

1 Introdução ... 1

2 Revisão bibliográfica... 5

2.1 Modelo de Black & Scholes ... 5

2.2 As letras gregas – Delta, Gama, Vega, Teta e Rô... 8

2.2.1 Delta... 9

2.2.2 Teta ...10

2.2.3 Gama...11

2.2.4 Vega...11

2.2.5 Rô...12

2.2.6 Opções dentro do dinheiro, fora do dinheiro e no dinheiro ...12

2.3 Estrutura Temporal de Volatilidade Implícita (Sorriso) ...13

2.4 O Estudo da volatilidade dos ativos ...18

2.5 Sticky-Delta, Sticky Strike e Sticky Tree ...21

2.5.1 Sticky Strike ...22

2.5.2 Sticky Delta...24

2.5.3 Sticky Tree ...26

2.6 Análise de componentes principais ...29

2.6.1 Fundamentação matemática...30

2.7 Aplicação da análise de componentes principais à Estrutura a Termo de Volatilidade Implícita35 2.8 Modelos de cálculo de V@R ...43

2.8.1 Proposta para Basiléia II ...43

2.8.2 Cálculo de V@R para carteiras de opções ...44

2.8.3 Aproximação Delta-Gama-Vega-Teta...44

2.8.4 Utilização de ACP para cálculo de V@R ...46

3 Metodologia...47

3.1 Dados utilizados – amostra ...47

3.2 Carteira para teste retroativo de resultados (backtesting) ...51

3.3 ACP das diferenças da volatilidade em relação ao ATM ...52

3.4 Teste retroativo (Backtesting) dos resultados ...53

4 apresentação dos resultados...60

4.1 Aplicação de ACP para a estrutura a termo de volatilidade implícita...60

4.2 Variância explicada dos três componentes principais nas diversas carteiras...65

4.3 V@R calculado pela expansão de Taylor para riscos de delta, gama e teta somada a risco de variação de volatilidade calculada por ACP ...67

4.4 V@R calculado através da expansão de Taylor para riscos de delta, gama e teta ...72

4.5 V@R calculado pela expansão de Taylor para riscos de delta, gama, teta e vega ...74

4.6 V@R calculado pela expansão de Taylor para riscos de delta, gama e teta somado ao risco de variação de volatilidade sugerido pela Basiléia II...75

4.7 Influência da variação da volatilidade implícita nos parâmetros delta, gama e teta utilizados na expansão de Taylor ...80

5 Conclusão ...82

6 Bibliografia...84

7 Apêndice 1 – Resultados obtidos em todas as carteiras, em todos os métodos...90

1 INTRODUÇÃO

Em 1973, Fischer Black e Myron Scholes apresentaram um artigo propondo um modelo para o cálculo de preços teóricos de opções européias de ações sem dividendos. Este modelo é baseado em hipóteses rígidas e muitas vezes não observáveis no mercado. Deste então, muitos estudos têm sido feitos para relaxar estas hipóteses iniciais do modelo. No entanto, apesar de suas hipóteses, a fórmula de Black & Scholes (1973) e os desenvolvimentos posteriores elaborados por outros autores, são ainda amplamente empregada para o apreçamento de diversos tipos de opções sobre diversos ativos.

A evolução do mercado de opções no mundo das finanças, acompanhada pela diversificação e sofisticação de instrumentos tais como opções exóticas, gera a necessidade de estudos sobre estes instrumentos financeiros, de forma a tornar seu entendimento mais claro e simples. Instituições financeiras, em especial, têm grande necessidade de acompanhar estes estudos de forma a incorporar estes instrumentos em sua carteira de produtos oferecidos. Estes novos produtos, por sua vez, geram demandas de estratégias de imunização e também do cálculo dos riscos envolvidos na negociação dos mesmos.

O conceito de volatilidade implícita está muito ligado ao conceito de volatilidade histórica. A volatilidade histórica é a volatilidade que efetivamente realizada pelo ativo. Já a volatilidade implícita, segundo Alexander (2001), pode ser interpretada como a expectativa do mercado para a volatilidade futura do ativo.

Antes da grande queda da bolsa de 1987, a volatilidade implícita das opções de diferentes preços de exercício apresentava pouca variação, isto é, para um mesmo vencimento, opções com preços de exercício abaixo do preço do ativo eram apreçadas utilizando-se volatilidades implícitas muito semelhantes das opções com preço de exercício acima do preço do ativo. A esta relação entre a volatilidade implícita e o preço de exercício, o mercado atribui o nome de assimetria.

Após esta queda abrupta, os mercados começaram a apresentar uma assimetria negativa, como constatado por Das e Sundaram(1999), Rubinstein (1994) e Jackwerth e Rubinstein (1996), onde opções com preços de exercício abaixo do preço do ativo eram apreçadas com uma volatilidade superior em muitos pontos à volatilidade das opções com preço de exercício acima do preço do ativo. Este fenômeno é conhecido como Sorriso de Volatilidade Implícita ou Sorriso. Tal

denominação deve-se ao formato da curva de volatilidade implícita em função do preço de exercício que lembra um sorriso.

A relação tridimensional entre volatilidades implícitas, preços de exercício e prazo para o vencimento é chamada de estrutura a termo de volatilidade ou, ainda, superfície de volatilidade.

Para a análise desta superfície, o presente estudo propõe a utilização de uma ferramenta empregada em estudos empíricos de diversos ramos da ciência: a Análise de Componentes Principais – ACP (Principal Component Analysis).

A análise de componentes principais busca identificar os principais fatores, chamados componentes principais, que afetam a dinâmica de determinado conjunto de dados, através da redução da dimensionalidade do mesmo.

Os primeiros autores a utilizar a análise de componentes principais para entendimento da dinâmica do mercado financeiro foram Litterman e Scheinkman (1991), que aplicaram a técnica à estrutura temporal de taxas de juros de títulos norte americanos. Já com relação à aplicação específica da análise de componentes principais a estruturas de volatilidades implícitas de opções é possível encontrar diversos trabalhos, com destaque ao de Alexander (2001).

As mudanças na superfície de volatilidade alteram o apreçamento das opções de uma carteira. Desta forma, constituem um fator de risco que precisa ser estudado e entendido para o desenvolvimento de estratégias de imunização e de técnicas de gerenciamento de risco, dentre elas o cálculo de Valor em Risco (V@R – Value at

Risk).

De posse dos resultados obtidos com a análise de componentes principais da superfície de volatilidade implícita, o presente estudo tem por objetivo obter valores limite de variação desta volatilidade implícita, como forma de estimar as conseqüentes variações extremas nos valores de uma carteira de opções. Para tanto, baseia-se em estudos sobre a aplicação da análise de componentes principais da superfície de volatilidade implícita desenvolvidos por Alexander (2001). Estes estudos, por sua vez, são derivados de estudo sobre a dinâmica de curvas de volatilidade proposto por Derman (1999).

Os resultados obtidos serão também comparados àqueles obtidos a partir da aplicação das seguintes metodologias:

• proposta do acordo da Basiléia II, que propõe um critério para o cálculo do risco de uma carteira de opções através de um deslocamento proporcional da superfície de volatilidade;

• aproximação delta-gama-vega-teta, representada pela expansão de Taylor de segunda ordem da mudança do valor da carteira com relação a mudanças de preço do ativo base.

Serão utilizados como amostra, dados de volatilidade implícita de opções européias da paridade Real / Dólar, de janeiro de 2001 até março de 2006 negociadas na Bolsa de Mercadorias e Futuros (BM&F).

No próximo capítulo é apresentada a revisão bibliográfica dos modelos aqui aplicados. São apresentados trabalhos sobre o sorriso de volatilidade e posteriormente sobre a estrutura a termo da volatilidade implícita. Seguem-se uma apresentação sobre a teoria de análise de componentes principais, modelos de dinâmica de curva de volatilidade apresentados por Derman (1999) e finalmente a aplicação da análise de componentes principais na curva de volatilidade.

No capítulo três, a amostra utilizada e o tratamento dos dados são apresentados, bem como a metodologia adotada para o cálculo do ACP, do teste retroativo e do cálculo da eficiência do teste.

No capítulo quatro é realizada a apresentação e a análise dos resultados obtidos através da aplicação da metodologia descrita no capítulo três.

2 REVISÃO BIBLIOGRÁFICA

Nesta seção é inicialmente apresentado o modelo de Black & Scholes, com sua formulação e hipóteses, bem como os artigos que propõem a modificação e o aperfeiçoamento deste modelo. Posteriormente , são apresentadas as letras gregas – delta, gama, vega, teta e rô – e sua formulação de acordo com o modelo de Garman e Kohlhagen (1983). Em seguida, são apresentados os conceitos relacionados à estrutura temporal de volatilidade implícita , assim como os estudos já realizados na tentativa de explicação da formação do sorriso de volatilidade. Também são apresentados estudos sobre volatilidade histórica, estudos sobre expectativa de volatilidade e estudos sobre a diferença entre dados empíricos e dados observados pela aplicação do modelo de Garman e Kohlhagen. Além destes, são apresentadas abordagens que se utilizam de volatilidade estocástica, de modelos de jump diffusion

ou do processo de Lévy generalizado, bem como modelos que adaptam o apreçamento de opções exóticas e não líquidas ao sorriso de volatilidade. Finalmente – também relacionados ao estudo da volatilidade – são apresentados os modelos propostos por Derman (1999) para tentar explicar o comportamento do mercado – sticky delta, sticky strike e sticky tree.

Finalizando esta seção, é apresentado o modelo de análise de componentes principais, com suas vantagens e fundamentação matemática, bem como o estudo sobre a aplicação da análise de componentes principais à estrutura a termo de volatilidade. Também são apresentados modelos de cálculo de valor em risco (comumente chamados de modelos de value at risk – V@R) com ênfase ao cálculo

voltado a carteiras de opções. Por fim, apresentam-se estudos sobre a utilização da análise de componentes principais ao cálculo do V@R de uma carteira de opções.

2.1 Modelo de Black & Scholes

uma opção européia de ações sem dividendos. Este modelo apresenta muitas hipóteses:

• não há pagamentos de dividendos até o vencimento da opção;

• exercício é do tipo europeu isto é, somente no dia do vencimento da opção;

• mercado é eficiente isto é, as pessoas não podem prever consistentemente a direção do mercado ou de uma ação específica;

• mercado opera de forma contínua seguindo um processo de Itô;

• não existe custo de transação ou impostos;

• a taxa de juros se mantém constante durante a vida da opção e é conhecida;

• os investidores podem tomar emprestado ou emprestar à mesma taxa de juro livre de risco;

• os retornos dos ativos obedecem a uma distribuição lognormal;

• a volatilidade é constante ao longo do tempo independentemente do preço de exercício ou prazo de vencimento da opção.

Desde sua publicação, o modelo hoje conhecido por Black & Scholes tem sido alvo de muitos estudos que, na sua maioria, têm por objetivo propor e implementar modificações para relaxar algumas de suas hipóteses. Para ilustrar alguns exemplos, em 1973 Robert Merton propôs uma modificação para apreçar opções sobre ativos que pagam uma taxa de dividendos constante. Em 1976, Jonathan Ingersoll propôs um modelo relaxando a premissa de ausência de impostos e custos de transação. Em 1976, Merton incorporou a estrutura a termo de taxa de juros ao modelo, relaxando a hipótese de taxas de juros constantes. Em 1983, Garman & Kohhagen observaram que a fórmula desenvolvida por Merton (1973) poderia ser utilizada para apreçar opções européias de taxas de câmbio, sendo que esta fórmula é utilizada até hoje como padrão para conversão de volatilidades negociadas no mercado de balcão de opções de moedas para preços. Esta fórmula (a ser demonstrada posteriormente) será utilizada ao longo deste trabalho.

As fórmulas de Black & Scholes para os preços de opções de compra – call (c) – e

venda – put (p) – européias de ações sem dividendos são:

) ( . . ) (

.N d X e N d S

) ( . ) ( .

.e N d₂ S N d₁ X

p= −rT − − − (2)

onde: T T r K S d . ). 2 ( ) ln( 2 1 σ σ + +

= (3)

T d T T r K S d . . ). 2 ( ) ln( 1 2 2 σ σ σ − = − +

= (4)

onde:

S: preço da ação;

K: preço de exercício da opção; s: volatilidade da ação;

r: taxa livre de risco;

T: tempo para o vencimento;

A função N(x) é a função de probabilidade cumulativa de uma variável normal padronizada. Segundo Hull (1991), tal função pode ser aproximada pela função polinomial: ) ( ' ). . . . ( 1 )

(x a₁k a₂k2 a₃k3 N x

N = − + + ,quando x >= 0 (5)

) ( 1 )

(x N x

N = − − , quando x < 0 (6)

onde: x k . 1 1 α + =

a = 0,33267 a1 = 0,4361836 a2 = -0,1201676 a3 = 0,9373980

2 2 . 2 1 ) ( ' x e x N − Π

O modelo que é utilizado neste trabalho foi proposto por Garman e Kohlhagen (1983), segundo o qual os preços de opções de compra – call (c) – e venda – put (p)

– européias podem ser calculados como:

) ( . . ) ( .

.e . N d₁ X e N d₂

S

c= −rf T − −rT ₍₈₎

) ( . ) ( .

.e N d₂ Se . N d₁

X

p= −rT − − −rf T − ₍₉₎

T T r r K S d f . ). 2 ( ) ln( 2 1 σ σ + − +

= (10)

T d T T r r K S d f . . ). 2 ( ) ln( 1 2 2 σ σ σ − = − − +

= (11)

onde:

r: taxa de juros livre de risco doméstica; rf: taxa de juros livre de risco estrangeira.

2.2 As letras gregas – Delta, Gama, Vega, Teta e Rô

A fim de aprofundar o estudo sobre o sorriso de volatilidade, faz-se necessário o conhecimento de algumas derivadas parciais da equação de Black & Scholes que representam a sensibilidade do preço da opção a pequenas variações dos seus parâmetros. Estas derivadas são chamadas de gregas, sendo que as mais importantes são o delta, o gama, o vega, o teta e o rô.

Considerando-se:

S: preço da ação;

K: preço de exercício da opção; s: volatilidade da ação;

rf: taxa livre de risco;

T: tempo para o vencimento;

E, N(x), uma função de probabilidade cumulativa de uma variável normal

Assim, as letras gregas podem ser calculadas das maneiras apresentadas nas subseções seguintes.

2.2.1 Delta

O delta de uma opção é definido como a taxa de variação do preço (P) de uma

opção em relação ao preço do ativo objeto (S), _

     ∂ ∂

S P

. Pode ser descrito para uma

opção de compra de uma ação sem dividendos como:

) (d₁ N

C =

∆ (12)

onde:

d1: definido na equação (3);

?C: delta da opção de compra

Já para uma opção de venda, o delta pode ser definido por:

1 ) ( ₁ − =

∆_V N d (13)

onde:

d1: definido na equação (3);

?V: delta da opção de venda.

No caso da fórmula de Garman e Kohlhagen (1983) a opção de compra e de venda tem deltas respectivamente iguais a:

) ( . 1 .

d N e r T

C f

− =

∆ (14)

onde:

) 1 ) ( .( 1 . − =

∆_V e−rf T N d (15)

onde:

d1: definido na equação (10)

?V: delta da opção de venda.

2.2.2 Teta

O teta de uma opção representa a taxa de variação de seu valor (P) ao longo do

tempo (t), _

     ∂ ∂ t P

. Ela pode ser expressa para a fórmula de Garman e Kohlhagen

(1983) para opções de compra e venda européia, respectivamente, por:

) ( . . . ). ( . . . 2 . ). ( ' . 2 . . 1 .

1 _{r S N d e r X e N d}

T e d N

S r T rT

f T r C f f − − − − + − = σ

θ (16)

Onde:

d1 e d2: são definidos na equação (10)

?C: teta da opção de compra;

) ( . . . ). ( . . . 2 . ). ( ' . 2 . . 1 .

1 _{r S N d e r X e N d}

T e d N

S r T rT

f T r V f f − − − + − − = σ

θ (17)

Onde:

d1 e d2: são definidos na equação (10)

2.2.3 Gama

O gama de uma opção representa a taxa de variação de seu delta com relação ao

preço do ativo objeto (S),

    ∂ ∂ 2 2 S P

. O gama é o mesmo para opções de compra e

venda. Para a fórmula de Garman e Kohlhagen (1983) tem-se:

T S

e d N rf T

. .

). ( ' ₁ .

σ =

Γ (18)

Onde:

d1: é definido na equação (10)

G: é o gama da opção de compra e de venda.

2.2.4 Vega

O vega de uma opção representa a taxa de variação do valor da opção (P) com

relação a mudanças na volatilidade do ativo objeto

( )

     ∂ ∂ σ

P _{. O vega é o mesmo}

para opções de compra e venda, e segundo Garman e Kohlhagen (1983), é calculado de acordo com a seguinte fórmula :

T rf e d N T

S. . '( 1). .

−

=

Λ (19)

Onde:

d1: é definido na equação (10)

2.2.5 Rô

O rô representa a taxa de variação do valor da opção (P) com relação à taxa de

juros (rf), _

      ∂ ∂ f r

P _{, e pode ser descrito de acordo com Garman e Kohlhagen (1983),}

para opções de compra e venda, respectivamente:

) ( . . . 1 . d N S e T

rô_C =− rfT (20)

Onde:

d1: é definido na equação (10)

rôC: é o rô da opção de compra;

) ( . . . 1 . d N S e T

rô_V =− rfT − (21)

Onde:

d1: é definido na equação (10)

rôV: é o rô da opção de venda.

2.2.6 Opções dentro do dinheiro, fora do dinheiro e no dinheiro

Segundo Hull (1991), as opções podem ser classificadas conforme a relação entre o seu preço de exercício e o preço atual do ativo. Uma opção “dentro do dinheiro” – geralmente chamada pela sua sigla em inglês ITM (in the money) – é aquela que, no

caso de exercício imediato, proporciona a seu titular ou detentor um fluxo de caixa positivo. Para tanto, o preço do ativo deve ser maior que o preço de exercício, no caso de uma opção de compra. Já com relação à opção de venda, o preço do ativo deve ser inferior ao preço de exercício. As opções chamadas “no dinheiro” ou ATM

(at the money) são aquelas que, no caso de exercício imediato, produzem fluxo de

opção for maior que o preço do ativo para opções de compra e, analogamente, o preço de exercício for menor que o preço do ativo para opções de venda, as opções são ditas “fora do dinheiro” ou OTM (out of the money).

2.3 Estrutura Temporal de Volatilidade Implícita (Sorriso)

No modelo de Garman e Kohlhagen (1983), o preço de uma opção de câmbio é função do preço do ativo, do preço de exercício, do tempo para vencimento, das taxas de juros interna e externa, e da volatilidade dos retornos dos ativos. No mercado de câmbio da BM&F, as opções são negociadas pelo valor do seu prêmio, tornando a volatilidade o único parâmetro não observável diretamente no mercado.

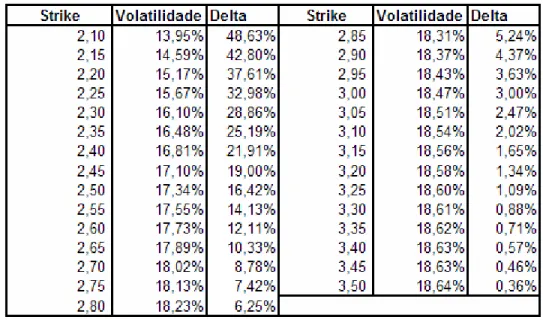
A volatilidade pela qual o prêmio teórico obtido através do modelo de Black & Scholes se iguala ao prêmio observado no mercado chama-se volatilidade implícita. Segundo Alexander (2001), a volatilidade implícita é uma previsão da volatilidade do processo. No caso da volatilidade do processo ser estocástica, então a volatilidade implícita pode ser entendida como a volatilidade média do preço do ativo que está implícita no prêmio de mercado da opção. No entanto, observa-se empiricamente que o mercado apreça, para um mesmo ativo, opções com volatilidades implícitas diferentes dependendo de suas características como preço de exercício ou prazo para o vencimento, independentemente da hipótese feita sobre a volatilidade do processo.

1, observam-se duas curvas de volatilidade em relação ao preço de exercício. A curva azul representa uma relação entre a volatilidade e o preço de exercício na qual é possível observar pouca inc linação. Já na curva rosa é possível observar uma grande inclinação negativa na relação entre a volatilidade e o preço de exercício (assimetria).

Comparação das curvas de volatilidade com e sem skew

13,95%

12,00% 11,50%

13,00% 14,10%

14,70% 15,50%

17,00%

14,00% 14,05%

14,10% 14,15%

14,20% 14,25%

9,00% 10,00% 11,00% 12,00% 13,00% 14,00% 15,00% 16,00% 17,00% 18,00%

70 80 90 100 110 120 130

Preços de exercício

Volatilidade

Curva com skew Curva sem skew

Gráfico 1: Gráfico ilustrativo da curva de volatilidade com e sem assimetria

Esta variabilidade de volatilidades implícitas para opções sobre o mesmo ativo, com mesmo vencimento mas com diferentes preços de exercício, é também observada para opções sobre o mesmo ativo, com mesmo preço de exercício mas com vencimentos diferentes. Dado o formato do gráfico que representa a relação entre as volatilidades implícitas e os preços de exercício para um mesmo vencimento, esta curva passou a ser conhecida pelos participantes de mercado financeiro e posteriormente pelo meio acadêmico como Sorriso de Volatilidade (Smile).

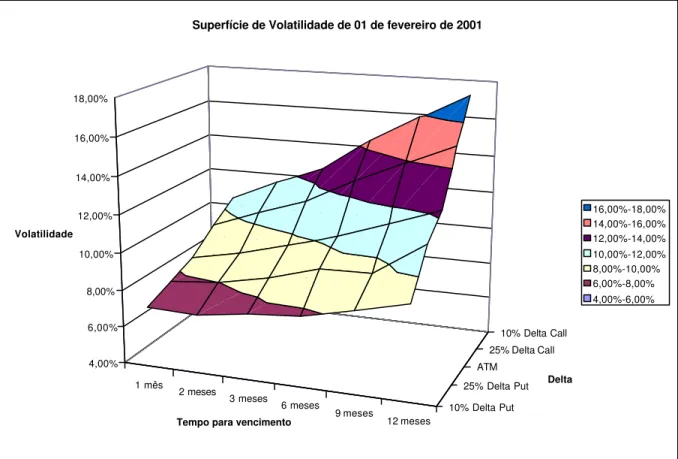
comportamento passado do ativo ou com a mudança de expectativa de volatilidade futura do ativo. Um exemplo de superfície de volatilidade é apresentada no gráfico 2.

Esta característica da superfície de volatilidade foi descrita por Das e Sundaram (1999), Rubinstein (1994) e Jackwerth e Rubinstein (1996).

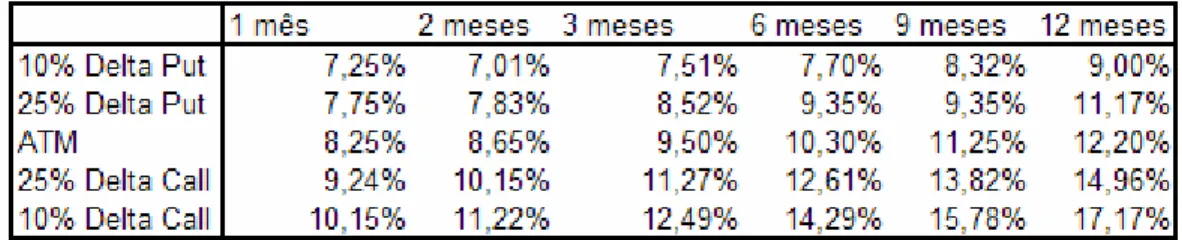
1 mês

2 meses _{3 meses}

6 meses

9 meses

12 meses

10% Delta Put 25% Delta Put

ATM

25% Delta Call 10% Delta Call

4,00% 6,00% 8,00% 10,00% 12,00% 14,00% 16,00% 18,00%

Volatilidade

Tempo para vencimento

Delta

Superfície de Volatilidade de 01 de fevereiro de 2001

16,00%-18,00% 14,00%-16,00% 12,00%-14,00% 10,00%-12,00% 8,00%-10,00% 6,00%-8,00% 4,00%-6,00%

Gráfico 2: Superfície de volatilidade apresentando assimetria e diferentes níveis de volatilidade

dependente do prazo de vencimento

Segundo Alexander (2005), grande parte das opções hoje negociadas no mercado de ações e câmbio utiliza a fórmula de Garman e Kohlhagen (1983). Mas, como visto anteriormente, as hipóteses sob as quais essa fórmula está baseada não são

justificadas empiricamente. Duas delas ajudam a exp licar a existência de assimetria para apreçar opções de diferentes preços de exercício:

Portanto, não é apropriado modelar-se o preço do ativo subjacente como um movimento browniano geométrico pois este modelo assume ditribuição normal e volatilidade constante.

Desta forma, por não se tratar de um movimento geométrico browniano, grandes mudanças de preços podem ser observadas empiricamente com uma freqüência maior do que aquela assumida no modelo de Garman e Kohlhagen. Assim, se a distribuição dos retornos é normal, mas a volatilidade é estocástica, ou se a volatilidade é constante, mas os retornos exibem caudas pesadas – ou se, de fato, as duas coisas ocorrem –, grandes oscilações de preço são mais prováveis de ocorrer que o previsto pela distribuição normal e, conseqüentemente , uma opção OTM (para o caso de opções de bolsa de valores) tem maior chance de se tornar ITM do que aquela assumida no modelo Garman e Kohlhagen.

Como conseqüência, o prêmio que se obtém utilizando Garman e Kohlhagen para uma opção de venda OTM, utilizando-se a volatilidade implícita da Put ATM, é

menor que o observado no mercado. Como foi dito anteriormente, o único parâmetro que pode ser alterado, e que não é observado diretamente no mercado, é a volatilidade. Assim, a volatilidade implícita das Put´s OTM é maior que a volatilidade

implícita das Put´s ATM. Desta forma vê-se que o mercado contesta a premissa de

volatilidade do ativo constante ao longo do tempo e ao longo dos preços de exercícios.

se observar no mercado diferentes tipos de sorrisos de volatilidade. Podem-se obPodem-servar aqueles simétricos, em que as opções de compra e opções de venda OTM têm volatilidades implícitas maiores que as opções ATM. Estes sorrisos de volatilidade são geralmente observados nos mercados de câmbio de países desenvolvidos. Sorrisos de volatilidade com assimetria negativa, em que opções de venda OTM têm volatilidade implícita maior que as ATM, que por sua vez têm volatilidades maiores que as opções de compra OTM. Este é o caso de opções de bolsa de valores. Esta assimetria pode ser positiva em alguns mercados como o de opções sobre a paridade Real / Dólar.

A assimetria pode ser explicada por diversas razões. No mercado de ações, por exemplo, uma queda de preços é uma má notícia para os acionistas. Assim, a assimetria negativa pode ser explicada pela demanda existente de proteção por parte destes investidores para put´s OTM. Desta forma, o mercado utiliza volatilidade

elevada para apreçar estas opções. E freqüentemente, como ressalta Alexander (2001), o mercado de ações torna-se muito mais turbulento (mais volátil) após uma grande queda de preço do que após uma elevação de preços de mesma magnitude. Assim, o prêmio de uma opção de compra ITM reflete o fato de que, se ocorrer uma grande queda de preço, a volatilidade do preço do ativo subjacente permanecerá elevada por algum tempo. Então, os prêmios de todas as opções aumentam em virtude do aumento da expectativa de volatilidade futura.

A assimetria positiva observada no mercado de opções sobre a paridade Real / Dólar negociadas na BM&F também pode ser explicada, como no caso da bolsa, pelo fato de uma alta do dólar representar má notícia para aqueles que possuem dívidas em dólar, ou para investidores estrangeiros que possuem investimentos no país. E, semelhante ao mercado de ações, uma alta do dólar em grande magnitude torna o mercado mais turbulento.

Este fenômeno de sorriso de volatilidade implícita está presente em diversos tipos de mercados: moedas, ações, commodities, juros, energia, etc. No mercado de

commodities, por exemplo, as quedas de preços são boas notícias, enquanto que os

assimetria do sorriso de volatilidade é inverso ao observado no mercado de ações. O mercado de juros, por sua vez, se aproxima mais do mercado de opções de moedas.

2.4 O Estudo da volatilidade dos ativos

Segundo Desterro (2003), o estudo da volatilidade dos ativos financeiros tem se tornado o ponto mais importante da teoria financeira moderna. O entendimento da volatilidade e da expectativa do mercado sobre ela é imprescindível tanto para controle de risco, quanto para a imunização de carteiras ou para o apreçamento de opções. Um investidor racional utiliza proposições de Markowitz (1959), Sharpe (1964) e Lintner (1965) para balancear seu perfil de aversão ao risco (e portanto de variância que aceita em sua carteira de investimentos) com o retorno esperado.

Muitos estudos foram realizados sobre a volatilidade histórica, ou seja, a volatilidade efetivamente realizada, calculada a partir do histórico dos retornos do preço do ativo objeto (Roll, 1977). Mas os dados históricos explicam de forma limitada a volatilidade futura, e existe no mercado uma expectativa de volatilidade futura que é aquela implícita nos preços das opções negociadas. Esta expectativa de volatilidade foi alvo de estudos de Dumas, Fleming, e Whaley (1998). Os autores utilizaram um modelo de GARCH e através de um teste fora da amostra, empírico, obtiveram bons resultados.

Mas muita literatura tem sido desenvolvida para tentar explicar as diferenças entre os dados empíricos que se observa no mercado e aqueles previstos pelo modelo de Black & Scholes. Jarrow e Rudd (1982) buscaram modelar o sorriso de volatilidade através da distribuição histórica dos retornos. Dupire (1984) empregou equações diferenciais estocásticas para tentar ajustar o sorriso observado no mercado.

assumem que a volatilidade é uma variável estocástica. Outros autores propõem a modelagem através de modelos de saltos descontínuos (jump diffusion), como

Merton (1976) e Prigent, Renault e Scaillet (2001). Outra abordagem consiste em utilizar modelos baseados no processo de Lévy generalizado (como o hiperbólico desenvolvido por Bibby and Sørensen em 1997).

No entanto, conforme apresentado por Das e Sundaran (1999) e Bakshi (1997), nenhum desses modelos de volatilidade estocástica ou saltos foi capaz de apresentar explicação completa para as anomalias.

Tendo como objeto de estudo a superfície de volatilidade implícita de opções européias da paridade Real / Dólar, este trabalho não tenta explicar as deformações ou os desvios da volatilidade implícita com relação à hipótese de volatilidade constante do modelo de Garman e Kohlhagen (1973), mas trata a volatilidade implícita como uma variável financeira interessante por si só, procurando analisar a dinâmica de sua superfície. Existem muitas razões que justificam esta abordagem. As volatilidades de Garman e Kohlhagen são amplamente utilizadas como parâmetro único para mapeamento entre preço, preço de exercício, taxa de juros e vencimentos. A análise deste parâmetro permite que tomadores de decisão de investimento e gestores de risco reduzam o número de informações necessárias para a tomada de decisão de investimento e análise de risco. Além disso, com o aumento da liquidez dos mercados de opção tanto em bolsa como em balcão, a volatilidade tem ganhado importância como alternativa de ativo financeiro fazendo com que muitas instituições desejem construir carteiras com exposições em gama e vega.

O exemplo deste interesse do mercado pela volatilidade implícita é a criação de índices de volatilidade implícita como o VIX (calculado pela CME1, reflete a volatilidade implícita dos ativos do S&P 500), VIMEX (calculado no Mercado Mexicano de Derivados refletindo a volatilidade implícita das ações da Bolsa do México), VXN (Calculado pelo CME, reflete a volatilidade implícita dos papéis do Nasdaq 100).

Do ponto de vista teórico, muitos modelos de mercado de volatilidade têm sido criados adaptando-se o apreçamento das opções, principalmente as exóticas e não líquidas, ao sorriso de volatilidade. Modelos inicialmente desenvolvidos para

mercado de taxas de juros por Milterse et al (1997) e Jamshidian (1997), foram aprimorados por Ledoit e Santa-Clara (1998) e Schönbucher (1999), entre outros. Estes modelos assumem que existem opções líquidas em número suficiente para que seus parâmetros sejam utilizados como dados de entradas em modelos de apreçamento de opções consistentes com o sorriso de volatilidade.

Um importante ponto a favor da modelagem da volatilidade implícita de Garman e Kohlhagen é de ordem pragmática: modelos complexos ganham em acurácia, mas perdem nas defasagens das atualizações, uma vez que ativos intensamente negociados requerem constantes atualizações dos preços teóricos. Desta forma modelos complexos têm a desvantagem da lentidão nas atualizações, como ressalta Desterro (2003).

A análise da dinâmica da volatilidade implícita deve refletir corretamente as suas movimentações, ou seja deve identificar e quantificar os choques e as mudanças da curva de volatilidade com o passar do tempo. Para a análise desta dinâmica, propõe-se neste trabalho a utilização da técnica de análipropõe-se de componentes principais (ACP). Esta técnica é comumente utilizada para a análise da estrutura a termo de taxas de juros (Litterman e Scheikman, 1991) e já foi aplicada para a análise da estrutura a termo de volatilidade. Avellaneda e Zhu (1997); Härdle e Schimidt (2000); Sylla e Villa (2000); são exemplos de aplicação desta técnica para a análise de opções ATM para diferentes prazos. Já Alexander (2001) aplicou a mesma técnica com outro enfoque, análise do sorriso para um determinado vencimento.

2.5 Sticky-Delta, Sticky Strike e Sticky Tree

Em 1999 Emanuel Derman apresentou um artigo propondo a explicação da curvatura existente na superfície de volatilidade do mercado de opções de S&P 500 após a grande queda da bolsa de 1987. Analisando mais de um ano de dados de opções do S&P 500 ele os separou em sete períodos diferentes onde alguns padrões de mudanças pareciam se manter constantes. Analisando estes dados ele propôs três diferentes modelos para tentar explicar o comportamento do mercado:

Sticky Delta, Sticky Strike e Sticky Tree.

Derman (1999) propõe a criação de um modelo descrevendo aquilo que não varia e excluindo sua influência. Assim ocorre na física e matemática, onde estes termos são chamados invariantes. No mercado de opções estas invariantes são comumente chamadas de sticky. Derman afirma que existem ao menos três abordagens sobre

qual variável no sorriso de volatilidade não varia. Segundo o autor existem duas abordagens baseadas em algum tipo de intuição de mercado ou senso comum e uma terceira com embasamento formal teórico. No entanto, o autor ressalta que, apesar de sua base teórica, esta visão não necessariamente é a correta.

Derman verificou a existência de uma correlação negativa entre a volatilidade de opções ATM e o valor do índice S&P 500. No entanto, uma mudança na volatilidade implícita de uma opção ao longo do tempo altera diretamente o seu apreçamento, conseqüentemente alterando o resultado financeiro obtido. Outro ponto a se destacar é o fato de que no mercado, quando se negocia uma opção de compra ou venda, o seu preço de exercício é fixo, ou seja, as opções negociadas não necessariamente são sempre ATM. Desta forma, a análise da dinâmica deve se concentrar nas opções existentes no mercado, ou seja, com preço de exercício fixo e não necessariamente ATM.

A dependência da volatilidade em relação ao nível de preço, dado um preço de exercício K, é muito importante para a definição da carteira de imunização e a

relações existentes entre mudanças no nível do ativo base e a volatilidade implícita do ponto de vista de um modelo de um fator (como explicado a seguir). Derman ainda ressalta que assim como mudanças estocásticas na volatilidade podem acontecer, a volatilidade ATM e a inclinação de sua curvatura podem mudar de maneira randômica, mesmo dentro de um regime em particular. Como as mudanças dentro destes regimes não são tão grandes, a sua análise pode ainda ser válida.

Para encontrarmos a melhor árvore que descreva a assimetria atual, é necessário saber como ele vai se comportar com a movimentação do ativo base.

A seguir são apresentadas em detalhes as proposições feitas por Derman (1999), respectivamente Sticky Strike, Sticky Delta, Sticky Tree, que são apresentados a

seguir.

2.5.1 Sticky Strike

Segundo Derman (1999), em uma tentativa fraca de preservar o modelo de Black and Scholes, alguns operadores acreditam que, independentemente do nível do ativo base, a volatilidade daquele preço de exercício será a mesma. O modelo que parte desta premissa é chamado sticky strike, pois a cada preço de exercício

deve-se construir uma determinada árvore binomial com volatilidade constante, ou deve-seja, cada opção é apreçada de forma independente.

Assim, quando o preço do ativo base sobe, a volatilidade das opções ATM cai, uma vez que mudam os preços de exercícios das opções ATM. O delta neste modelo é exatamente igual ao delta de Black and Scholes. Derman associou estas características a mercados que estão operando lateralmente, isto é, sem uma tendência definida. Matematicamente pode-se expressar esta característica como:

( )

( )(

)

K τ =σ − τ −

OndeσK

( )

uma opção de preço de exercício K e vencimento τ quando o preço do ativo base

vale S0 e sua volatilidade tem valor σ₀. O parâmetro b(t) é a inclinação da assimetria

expressa em pontos percentuais de volatilidade por ponto de preço de exercício e é positivo quando a assimetria é negativa.

Se o preço do ativo base muda, as volatilidades de preços de exercícios fixos não vão se modificar, mas a volatilidade do ATM (σ_ATM) vai subir se o preço do ativo

base cair e vice-versa. Vemos isso simplesmente substituindo K por S na equação

(22).

( )

( )(

)

ATM τ =σ − τ −

σ (23)

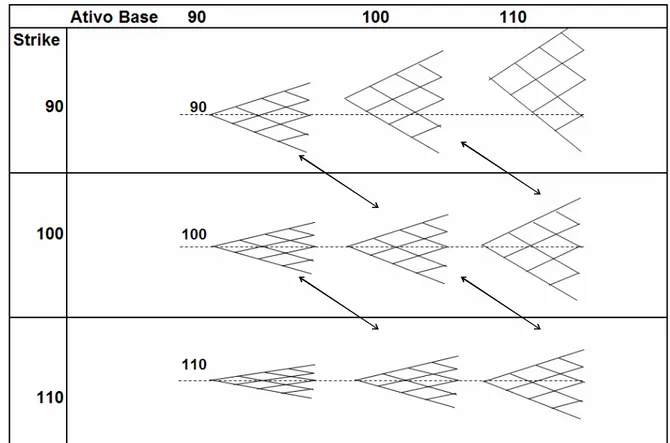
Figura 1: No modelo Sticky Strike, a coluna central demonstra as diferentes volatilidades para

Observa-se, na figura 1, que a volatilidade com que são apreçadas as diferentes opções não se altera com mudanças no nível de preço do ativo base, isto é, a volatilidade se mantém constante nas linhas da figura 1. Na coluna central, com o ativo base com preço 100, as opções de diferentes preços de exercício possuíam cada qual sua volatilidade implícita. Com a mudança do preço do ativo base para 110 ou para 90 (primeira e terceira coluna), a volatilidade implícita utilizada para se apreçar as opções de diferentes preços de exercício não muda.

2.5.2 Sticky Delta

A premissa de que o nível da volatilidade ATM atual se manterá constante à medida que o ativo base se move sustenta esta segunda proposição de Derman. Desta forma as opções com delta 50%, ou seja, ATM, permaneceriam com volatilidade constante, sendo este o motivo do nome sticky delta.

Este modelo é também chamado de sticky moneyness, pois a volatilidade também é

constante com respeito ao moneyness (relação entre o preço de exercício e o valor

do ativo base – K/S). O conceito de moneyness é equivalente ao delta de Garman e

Kohlhagen, pois depende das mesmas variáveis, K e S. Isto significa que o

moneyness determina a volatilidade local e esta terá uma determinada árvore

binomial com volatilidade constante. Ou seja, sticky moneyness é equivalente a

sticky delta.

Sticky Moneyness

( )

( )

S K b

K 

     − −

=σ τ

τ

σ (24)

Sticky Delta

( )

( )(

)

K τ =σ − τ −

E, para o caso de assimetria negativo, o delta das opções usando-se este modelo é maior que o delta Garman e Kohlhagen dado um mesmo preço de opção. Derman observou que este tipo de comportamento pode ser observado em mercados que exibem uma tendência.

Neste modelo a volatilidade do preço de exercício K vai subir com o nível de preço

do ativo base, mas a volatilidade do ATM será igual a inicial e independente do preço do ativo base.

Figura 2: No modelo Sticky Delta, a coluna central demonstra as diferentes volatilidades para

diferentes preços de exercício, cada qual com sua árvore binomial. À medida que ocorre uma variação no preço do ativo base, sua árvore de ATM se mantém constante, isto é, a árvore binomial do preço de exercício 110 quando o preço do ativo base está em 110 é a mesma que a árvore do preço de exercício 100 quando o preço do ativo base vale 100

110, quando o ativo base vale 110 é a mesma da volatilidade da opção de 100 quando o ativo base vale 100.

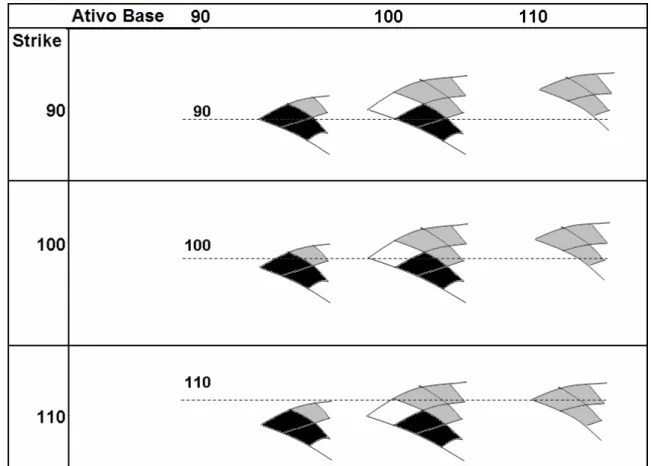
2.5.3 Sticky Tree

Em 1994 Derman e Kani propuseram a construção de uma única árvore para o ativo base de forma tal que ela seja consistente com os preços observados no mercado e as expectativas de volatilidade futura implícitas no mercado, chamada de árvore implícita. À volatilidade escolhida de forma a se adaptar a assimetria observada no mercado, dá-se o nome de volatilidade local, que varia tanto com o nível futuro de preço do ativo base como também com o tempo.

Este conceito contrasta-se com os apresentados nos dois itens anteriores, pois nestes cada opção demandava uma árvore diferente para o mesmo ativo base.

Este modelo é chamado sticky tree. Neste modelo a volatilidade local não é mais

constante. No entanto, existe uma única árvore para apreçar todas as opções que são determinadas pela assimetria da curva de volatilidade no momento.

Em um modelo de um fator para o cálculo de opção, o apreçamento é fruto das expectativas sobre a volatilidade instantânea futura. No caso de opções sobre índices de bolsas, assume-se que a volatilidade sobe quando o índice cai. Como conseqüência, as volatilidades locais para altos valores de índice têm menores volatilidades instantâneas.

Derman observou que o modelo de sticky tree é o mais adequado para mercados

com descontinuidades, principalmente com quedas abruptas (no caso do Índice S&P 500) sem que haja negócios no intervalo.

( )

( )(

)

( )

K τ σ τ τ

σ = − + + (26)

Onde:

( )

σK denota a volatilidade implícita calculada por Garman e Kohlhagen de uma

opção de preço de exercício K e vencimento τ quando o ativo base vale S0;

0

σ denota a volatilidade implícita inicial;

( )

b é a inclinação da assimetria expressa em pontos percentuais de volatilidade por

ponto de preço de exercício e é positivo quando a assimetria é negativa.

Assim, a volatilidade do preço de exercício fixo K vai cair quando o preço do ativo

base se valorizar e cair quando o preço do ativo base se desvalorizar e também:

( )

( )(

)

ATM τ =σ − τ −

σ (27)

onde:

( )

σATM denota a volatilidade implícita calculada por Garman e Kohlhagen de uma

opção ATM.

Figura 3: No modelo Sticky Tree, a coluna central demonstra a árvore que corresponde ao corrente

sorriso de volatilidade. À medida que o preço do ativo base se move, apenas desloca-s e para o nó referente ao valor atual do preço do ativo base.

Na figura 3, a coluna central identifica o estado inicial onde o mercado apreça diferentes opções, com diferentes volatilidades implícitas. No entanto, este modelo utiliza uma mesma árvore binomial, chamada árvore implícita, para apreçar todas as opções, de diferentes preços de exercício. Assim, quando o preço do ativo base se move, a mesma árvore é utilizada, apenas deslocando-se para o nó correspondente.

Resumidamente podemos apresentar os modelos propostos por Derman:

Modelo Volatilidade Preço de exercício Fixo

Volatilidade ATM Exposição Delta

(Considerando Skew Negativo)

Sticky Strike Independente do nível

de preço do ativo base Decai com a alta do preço do ativo base Igual ao Garman e Kohlhagen

Sticky Delta Sobe com a alta do

preço do ativo base

Independente do nível de preço do ativo base

Maior que o de Garman e Kohlhagen

Sticky Tree Cai com a alta de preço

do ativo base Cai duas vezes mais rápido com a

alta do preço do ativo base

Menor que o de Garman e Kohlhagen

No quadro observamos que o modelo Sticky Tree mantém a volatilidade implícita

constante para todos os preços de exercícios, a volatilidade implícita da opção ATM cai com a alta do preço do ativo base para ativos que apresentam uma assimetria negativa para a curva de volatilidade implícita e o delta equivale ao delta obtido através da fórmula de Garman e Kohlhagen. Já o modelo de Sticky Delta, a

volatilidade de uma opção de preço de exercício fixo sobe com a alta do preço do ativo base para ativos que apresentam assimetria negativa na sua curva de volatilidade implícita , a volatilidade implícita da opção ATM se mantém constante independente do nível do preço do ati vo base e o delta é maior que o delta obtido pela fórmula de Garman e Kohlhagen. No modelo Sticky Tree, a volatilidade de uma

opção de preço de exercício fixo cai com a alta do preço do ativo para ativos que apresentam uma assimetria negativa da curva de volatilidade implícita, a volatilidade da opção ATM cai duas vezes mais rápido com a alta do preço do ativo base e o delta é menor que o delta obtido através da fórmula de Garman e Kohlhagen.

2.6 Análise de componentes principais

A dinâmica da estrutura a termo da volatilidade implícita muito se assemelha à dinâmica da estrutura a termo de taxas de juros, uma vez que ambas apresentam alto grau de colinearidade entre os retornos. Estruturas a termo como as de taxas de juros de diferentes vencimentos exibem alto grau de correlação. Este tipo de característica é geralmente observado quando existem informações comuns a várias variáveis. No caso da taxa de juros, por exemplo, a taxa overnight impacta toda a

estrutura a termo. No caso da volatilidade implícita, variações do ativo base também altera toda a sua estrutura a termo.

A análise de componentes principais é um método de extração das principais fontes não correlacionadas de variação de um sistema multivariado. Ela reduz a dimensionalidade de um conjunto de dados que possui um grande número de variáveis colineares, preservando o máximo possível da variação presente no

conjunto original. Desta forma, como destaca Alexander (2001), apenas as fontes mais importantes de informação são utilizadas.

Em resumo, para diminuir a dimensionalidade de um conjunto de dados, faz-se uma transformação ortogonal dos dados originais para um novo conjunto de variáveis não-correlacionados, e que são ordenados de maneira que os primeiros contenham grande parte da variação presente em todas as variáveis originais. A esse novo conjunto de dados dá-se o nome de componentes principais. Alexander (2001) lembra que outra vantagem da metodologia é que a técnica constrói grandes matrizes de covariância positivas definidas. “Nesse caso, a vantagem da ACP não se encontra tanto na redução da dimensionalidade, mas na ortogonalização das variáveis. Dado que os componentes principais são ortogonais, então sua matriz de covariância não condicional é diagonal.”

Geralmente, somente os m-primeiros componentes principais são utilizados,

trazendo uma grande vantagem à análise de cenários.

Alexander (2001) também enfatiza o fato de que, na administração de risco, medidas de risco e os modelos de apreçamento geralmente precisam ser aplicados a vários cenários baseados nos movimentos de diversos fatores de risco. Isso torna sua execução muito complexa e computacionalmente pouco eficaz. Esse tipo de barreira costuma levar a elaboração de cenários simplistas, como no caso de análise de livros de opção, onde o risco de variações na volatilidade implícita (vega) costuma não ser contemplado ou utiliza-se uma movimentação paralela (e no caso da Basiléia II, movimentação proporcional ao nível da volatilidade).

2.6.1 Fundamentação matemática

Sendo X a matriz de p variáveis de dados estacionários e normalizados. De acordo

com Alexander (2001), os componentes principais de X e suas cargas fatoriais são

– o primeiro componente principal explique a maior parcela da variação total de X, o segundo compone nte explique a maior parcela da variação remanescente e assim por diante;

- os componentes principais não tenham correlação entre si.

Desta forma, a ACP tem como primeiro objetivo buscar uma função linear z₁=a₁′X

(primeiro componente principal) que possua a máxima variância.

Sendo V a matriz de covariância de X:

( )

var z =z′z =a′Va (28)

A resolução do problema se da pela maximização da variância de var

( )

1 1′a =

a . Utilizando-se de um escalar lagrangeano λ₁:

Max a₁′Va₁ −λ₁

(

)

Diferenciando com relação a a′₁:

0

1 1

1− a =

Va λ

1 1

1 a

Va =λ (29)

Da equação (29), acima, é possível observar que λ₁é um autovalor de V e a₁ é o

autovetor correspondente.

Substituindo (29) em (28) tem-se que:

( )

var z =a′λa =a′aλ

( )

var z =λ (30)

Desta forma, é possível observar que a maior variância é obtida com o maior autovalor de V.

O segundo componente principal é escolhido de forma a obter a maior variância, sujeito a não ser correlacionado com o primeiro componente principal.

Assim, a resolução do problema se dá pela maximização da variância de var

( )

sujeito a a₂′a₂ =1 e cov

(

)

Sendo cov

(

)

E utilizando-se dos escalares lagrangeanos λ₂ e θ:

Max a′₂Va₂−λ₂

(

) (

)

Diferenciando com relação a a′₂:

0

1 2 2

2− a − a =

Va λ θ (31)

Multiplicando todos os termos por a′₁:

0

1 1 2 2 1 2

1′Va −a′ a − a′a =

a λ θ

0

1 1′a =

a θ

0 =

θ (32)

2 2

2 a

Va =λ (33)

Como var

( )

Substituindo (33) em (34) tem-se que:

( )

var z =a′λ a =a′a λ =λ

Desta forma, é possível observar que a maior variância para o segundo componente principal, sujeito à restrição deste não ser correlacionado com o primeiro componente principal, é obtida com o segundo maior autovalor de V.

Os demais componentes principais são escolhidos de maneira análoga, sempre sujeitos a restrição de não serem correlacionados com os componentes principais anteriores.

Por resolução matricial:

V.A = A.?

Onde:

   

 

   

  = Λ

n

λ λ

λ

... 0 0

... ... ... ...

0 ... 0

0 ... 0

2 1

E A representa a matriz que contem os autovetores de V.

X a z_k = '_k

onde zk é o “k-ésimo” componente principal e ak é um autovetor de V

correspondente ao seu “k-ésimo” autovalor, λk. Desta forma, tem-se que:

X A Z = '

onde A é a matriz ortogonal cuja “k-ésima” coluna, a_k, é o “k-ésimo” autovetor de V e

contém as cargas fatoriais do “k-ésimo” componente principal.

Como observado por Santos (2005), os autovalores da matriz V representam a

variância dos dados originais projetada nos autovetores. A variância total dos dados originais é equivalente à somatória dos autovalores. Desta forma, é possível se observar que a variância explicada pelo “k-ésimo” componente principal é

representada por:

∑

Contudo a soma dos autovalores é p, isto é, o número de variáveis do sistema.

Kreinin et al (1998) sugerem a utilização do seguinte critério para escolha do número de componentes principais a ser utilizado: seja e* uma proporção aceitável de

variância não explicada dos diversos fatores de risco. Desta forma, escolhe -se um valor mínimo - h - de componentes principais, de forma a satisfazer a seguinte

inequação: * 1 ... ... 1 1 ε λ λ λ

λ _{> −}

+ +

+ +

p

Assim, os componentes principais j > h tem um efeito pequeno na explicação da

variância dado que sua variância explicada é pequena.

2.7 Aplicação da análise de componentes principais à Estrutura a Termo de Volatilidade Implícita

A análise da dinâmica da volatilidade implícita deve refletir corretamente as suas movimentações, ou seja, deve identificar e quantificar os choques e as mudanças da curva de volatilidade com o passar do tempo. A técnica de análise de componentes principais (ACP), comumente utilizada para a análise de estrutura a termo de taxas de juros (Litterman e Scheikman, 1991) pode ser aplicada para a análise da estrutura a termo de volatilidade. Avellaneda e Zhu (1997); Härdle e Schimidt (2000); Sylla e Villa (2000); são exemplos de aplicação desta técnica para a análise de opções ATM para diferentes prazos. Já Alexander (2001) aplicou a mesma técnica com outro enfoque, a análise do sorriso de volatilidade para um determinado vencimento.

O grande diferencial do artigo de Alexander (2001) é que a autora aplica o método de ACP utilizando a diferença entre a volatilidade das opções de preço de exercício fixo e a volatilidade das opções ATM como variável a ser modelada. A autora adota esta metodologia em detrimento da metodologia adotada pelos autores anteriores, que utiliza as variações diárias da volatilidade implícita. Ela demonstra que existem vantagens empíricas e teóricas para a utilização deste procedimento.

Teoricamente, a autora demonstra que os três cenários de movimentação da curva de volatilidade propostos por Derman (1999), quando analisados do ponto de vista de diferença de um preço de exercício fixo para um ATM, produzem resultados teoricamente mais robustos. A relação da diferença entre o preço de exercício fixo e o ATM e o preço do ativo base é a mesmo em todos os modelos de Derman (1999).

Assim, em mercados sem tendência (comumente chamado de lateral pelos seus participantes), Derman propõe a utilização do modelo de sticky strike, a seguir.

Sendo:

S: preço da ativo base;

S0: preço inicial do ativo base; K: preço de exercício da opção;

( )

σATM denota a volatilidade implícita calculada por Garman e Kohlhagen de uma

opção ATM.

( )

σK denota a volatilidade implícita calculada por Garman e Kohlhagen de uma

opção de preço de exercício K e vencimento τ quando o ativo base vale S0;

0

σ denota a volatilidade implícita inicial;

( )

b é a inclinação da assimetria expressa em pontos percentuais de volatilidade por

ponto de preço de exercício e é positivo quando a assimetria é negativa.

Tem-se:

( )

( )(

)

K τ =σ − τ −

σ (38)

( )

( )(

)

ATM τ =σ − τ −

σ

( )

( )

( )(

)

( )(

)

K τ −σ τ =σ − τ − −σ + τ −

σ

( )

( )

( )(

)

K τ −σ τ =− τ −

σ (39)

Já em mercados com tendência, Derman propõe a utilização do modelo de sticky

( )

( )(

)

K τ =σ − τ −

σ 0

( )

σATM =

( )

( )

( )(

)

σK − ATM = −b K−S −

( )

( )

( )(

)

K τ −σ τ =− τ −

σ (40)

Em mercados com descontinuidade:

( )

( )(

)

( )

K τ σ τ τ

σ = − + +

( )

( )(

)

ATM τ =σ − τ −

σ

( )

( )

( )(

)

( )

( )(

)

K τ −σ τ =σ − τ + + τ −σ + τ −

σ

( )

( )

( )(

)

( )( )

K τ σ τ τ τ

σ − =− + +2

( )

( )

( )(

)

K τ −σ τ =− τ −

σ (41)

É possível observa r, assim, que a diferença entre a volatilidade de preço de exercício fixo e a volatilidade do ATM se mantém constante em todos os modelos propostos por Derman:

( ) ATM

( )

( )(

)

K −σ τ =− τ −

σ _τ (42)

Desta forma, uma maneira de testar os modelos sticky propostas por Derman, seria

fazer um ACP sobre ∆

(

)

do ACP desta diferença deve demonstrar que somente o primeiro componente principal tem significância. Se ocorrer de encontrarmos outros componentes, de ordens maiores e significantes, será apropriado utilizar movimentos não paralelos de assimetria quando o ativo base se move.

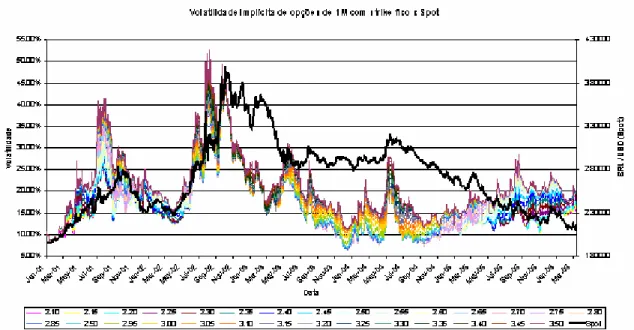
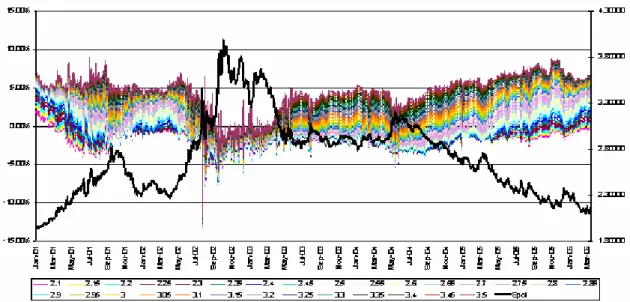
O gráfico 3 mostra tanto os valores de volatilidade implícita de opções com vencimento em um mês e preços de exercício que variam entre R$ 2,10 e R$ 3,50 (linhas coloridas, utilizando a escala da esquerda), quanto os valores da paridade Real / Dólar (em linha preta, utilizando a escala da direita) para o período de janeiro de 2001 até março de 2006. Observa-se que existe uma correlação positiva entre as volatilidades implícitas e o nível da paridade Real / Dólar. Já no gráfico 4, além dos valores da paridade Real / Dólar (linha preta, utilizando a escala da direita) é exibida também a diferença entre a volatilidade implícita de opções com um determinado preço de exercício e a volatilidade implícita das opções ATM com vencimento em um mês (linhas coloridas, utilizando a escala da esquerda). Observa-se que este último exibe menos correlação entre as diferenças de volatilidade e o valor do preço do ativo base e que as diferenças são, entre elas, mais correlacionadas e ordenadas do que as volatilidades em si.

Desta forma, os dados da diferença da volatilidade implícita dos diferentes preços de exercício em relação ao ATM, mostram-se estacionários e com baixa correlação em relação ao ativo base. Assim a aplicação da técnica de análise de componentes principais sobre esta diferença (que exige dados estacionários) torna -se possível para este conjunto de dados.

Gráfico 3: Gráfico da volatilidade implícita dos diferentes preços de exercício das opções da paridade Real / Dólar de um mês, associado ao gráfico da paridade do Real / Dólar. Pode-se notar grande correlação entre os gráficos.

Gráfico 4: Gráfico da diferença da volatilidade implícita dos diferentes preços de exercício em relação ao ATM das opções da paridade Real / Dólar de um mês, associado ao gráfico da paridade Real / Dólar. Pode-se observar que a correlação entre os dados diminui consideravelmente.

Gráfico 5: Gráfico da volatilidade implícita dos diferentes preços de exercício das opções da paridade Real / Dólar de três meses, associado ao gráfico da paridade do Real / Dólar. Pode-se notar grande correlação entre os gráficos.

Gráfico 7: Gráfico da volatilidade implícita dos diferentes preços de exercício das opções da paridade Real / Dólar de doze meses, associado ao gráfico da paridade do Real / Dólar. Pode-se notar grande correlação entre os gráficos.

Gráfico 8: Gráfico da diferença da volatilidade implícita dos diferentes preços de exercício em relação ao ATM das opções da paridade Real / Dólar de doze meses, associado ao gráfico da paridade Real / Dólar. Pode-se observar que a correlação entre os dados diminui consideravelmente.