Ordenação com autômatos celulares unidimensionais

(1)

UNIVERSIDADE PRESBITERIANA MACKENZIE

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM

ENGENHARIA EL´

ETRICA

Carlos Eduardo Profeta de Carvalho

ORDENAC

¸ ˜

AO COM AUT ˆ

OMATOS CELULARES

UNIDIMENSIONAIS

Disserta¸cão de Mestrado apresentada ao Programa de Pós-Gradua¸cão em Engenharia Elétrica da Universidade Presbiteriana Mackenzie, como parte das Exigências para Obten¸cão do Grau de Mestre em Engenharia Elétrica e Computa¸cão, na Área de Concen-tra¸cão em Engenharia da Computa¸cão.

Orientador: Pedro Paulo Balbi de Oliveira

(2)

(3)

(4)

AGRADECIMENTOS

Agrade¸co primeiramente a Deus por conduzir a minha vida e principalmente por dar discernimento para desenvolver esse projeto.

Agrade¸co aos meus pais Vitor Profeta de Carvalho e ´Aguida Maria Carvalho por me ensinarem o caminho que eu deveria andar e tamb´em por me apoiarem em todos os momentos de minha vida.

Agrade¸co `a minha esposa e companheira Fabiana Gouveia Martins de Carvalho por me apoiar e suportar incansavelmente durante essa jornada.

Aos colegas de curso especialmente Eduardo Lellis Queiros um grande amigo, Rafael, Taciano, Paulo e tamb´em `a Ana Carolina Lima por compartilhar conhecimento.

(5)

RESUMO

Autômatos celulares são sistemas complexos discretos e também sistemas computacio-nais totalmente distribu´ıdos, com processamento local arbitrariamente simples. Uma das computa¸cões que se pode realizar com autômatos celulares é a ordena¸cão de sequências numéricas. A ordena¸cão é um tema bastante relevante e utilizado amplamente na com-puta¸cão, como um de seus processos fundamentais. A presente pesquisa visou o desenvol-vimento de algoritmos de ordena¸cão baseados em autômatos celulares unidimensionais. Foram propostas duas novas versões, de raios 1 e 3, inspirados por caracter´ısticas de tra-balhos existentes na literatura. Em análise realizada, os autômatos celulares propostos apresentam vantagens com rela¸cão às abordagens que lhes deram origem.

(6)

ABSTRACT

Cellular automata are discrete complex systems and also fully distributed computational systems, with arbitrarily simple local processing. One of computations that can be made with cellular automata is sorting of numerical sequences. Sorting is a quite relevant topic and widely used in computing, as one of its fundamental processes. This research aimed at the development of sorting algorithms based on one-dimensional cellular automata. Two new versions with range 1 and 3 have been proposed, inspired by the characteristics of existing studies in the literature. In the analysis carried out, the proposed cellular automata have advantages over the approaches that originated them.

(7)

Sum´

ario

1 INTRODUC¸ ˜AO 1

2 AUT ˆOMATOS CELULARES 3

2.1 Autˆomatos celulares elementares . . . 5

3 ORDENAÇ ÃO EM AUT ÔMATOS CELULARES 8 3.1 Algoritmos de Gordillo e Luna . . . 8

3.1.1 Primeiro algoritmo de Gordillo e Luna . . . 9

3.1.2 Segundo algoritmo de Gordillo e Luna . . . 11

3.2 Algoritmos de Shakeri et al. (2008) . . . 12

3.2.1 Primeiro algoritmo de Shakeri et al. (2008) . . . 13

3.2.2 Segundo algoritmo de Shakeri et al. (2008) . . . 15

3.2.3 Terceiro algoritmo de Shakeri et al. (2008) . . . 16

3.3 Odd-even Transposition Sort em Autˆomatos Celulares: Algoritmo de Worsch e Nishio . . . 17

4 ODD-EVEN TRANSPOSITION SORT EM AC UTILIZANDO PROPAGAÇ ÃO DE SINAIS 22 4.1 AC utilizando propaga¸cão de sinais com r=1 . . . 25

4.2 AC utilizando propaga¸c˜ao de sinais com r=3 . . . 30

4.3 An´alises e compara¸c˜oes . . . 35

5 CONCLUS ˜OES 41

(8)

Lista de Figuras

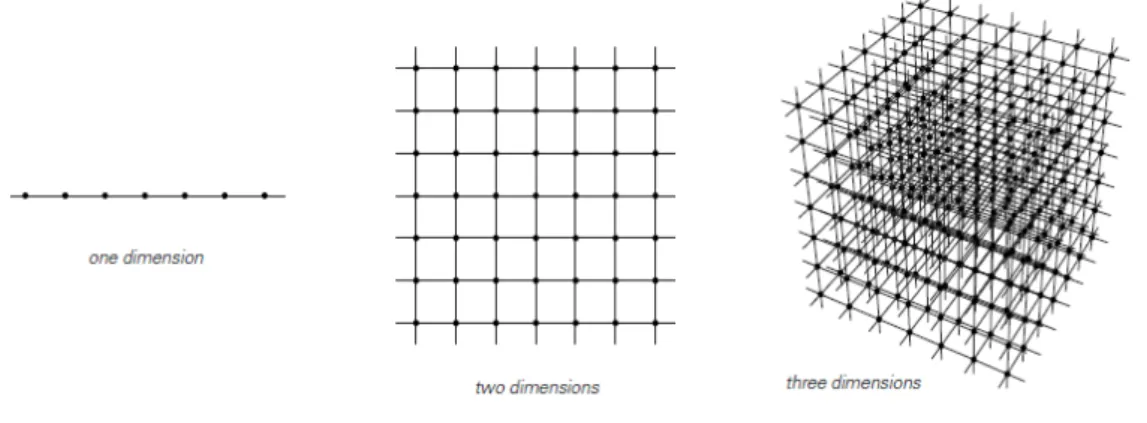
1 Dimens˜oes de um autˆomato celular (WOLFRAM, 2002a, p. 169). . . 3

2 Vizinhan¸ca de Moore (WEISSTEIN, 2013b). . . 4

3 Vizinhan¸ca de von Neumann (WEISSTEIN, 2013c). . . 5

4 Exemplo de transi¸c˜ao de estados em um autˆomato celular elementar. . . . 6

5 Exemplo de autômato celular unidimensional com condi¸cão de contorno periódica. . . 7

6 Condi¸c˜ao inicial das c´elulas Xi,Xi+1 e Xi−1. . . 10

7 Atualiza¸cão dos registradores de memória das células Xi, Xi+1 e Xi−1. . . . 10

8 Altera¸c˜ao do estado das c´elulas Xi e Xi+1. . . 10

9 Condi¸c˜ao inicial das c´elulas Xi,Xi+1 e Xi−1. . . 13

10 Conserva¸c˜ao do estado das c´elulas Xi e Xi+1. . . 14

11 Custo temporal de GL2 e SDFR3, de n= 0 a n= 50000. . . 17

12 Exemplo de ordena¸c˜ao utilizando o algoritmo OETS (HARWOOD, 2011). . 17

13 Ordena¸cão baseada na compara¸cão de números binários Worsch e Nishio (2010). . . 20

14 Comportamento dos n´umeros bin´arios nos registradores. . . 21

15 Compara¸c˜ao de c´elulas no AC de r= 1. . . 23

16 Dinˆamica dos ACs propostos neste trabalho. . . 24

17 Transi¸c˜oes de exemplo sendo aplicadas. . . 25

18 Simula¸c˜ao de ordena¸c˜ao do AC CP1. . . 29

19 Simula¸c˜ao de ordena¸c˜ao do AC CP2. . . 34

20 Custo temporal entre os ACs: GL2, SDFR3 e CP2. . . 35

(9)

Lista de Tabelas

1 Evolu¸c˜ao do AC GL1. . . 11

2 Evolu¸c˜ao do AC GL2. . . 12

3 Exemplo de execu¸c˜ao do AC SDFR1. . . 14

4 Transi¸c˜oes de estado de exemplo. . . 24

5 Transi¸c˜oes de estado do AC CP1. . . 26

6 Exemplo de ordena¸c˜ao para os elementos S={10,9, ...,6} de CP1. . . 28

7 Transi¸c˜oes de estado de CP2. . . 31

8 Exemplo de ordena¸c˜ao para os elementos S={17,16, ...,11} de CP2. . . . 33

9 Compara¸c˜ao entre os ACs de Gordillo e Luna (1994), Shakeri et al. (2008) e dos dois novos ACs. . . 36

10 Compara¸c˜ao de custo de mem´oria entre os ACs de Gordillo e Luna (1994), Shakeri et al. (2008) e dos dois novos ACs. . . 36

11 Ranking dos ACs considerando custo temporal e custo de processamento integralizado. . . 39

(10)

1 INTRODUC

¸ ˜

AO

Mitchell et al. (2005) descrevem os Autômatos Celulares (ACs) como sistemas com-plexos discretos que podem ser considerados sistemas totalmente distribu´ıdos computaci-onalmente e com processamento local bastante simples. Eles afirmam que a capacidade de compreender a forma como os ACs computam e como eles devem ser concebidos de modo a executar uma determinada tarefa computacional podem produzir um grande im-pacto sobre tecnologia da informa¸cão e teoria da computa¸cão, onde os ACs seriam um modelo completamente novo de computa¸cão, totalmente paralelo, descentralizado e lo-cal. Wolfram (1983) complementa que um AC é uma estrutura (ouarray) uniforme que consiste em uma variável discreta em cada célula. O estado de cada célula é alterado de acordo com o de suas células vizinhas no instante de tempo anterior, e todas as células são atualizadas de forma s´ıncrona regida por um conjunto de regras locais.

Uma das computa¸cões realizadas por autômatos celulares estudadas ao longo do tempo é a ordena¸cão (ousorting em inglês). Este tema é bastante relevante e utilizado no campo da computa¸cão como um dos seus problemas fundamentais e têm sido utilizado ampla-mente em vários dom´ınios. Diferentes abordagens de ordena¸cão têm sido apresentadas ao longo do tempo, sejam elas em série ou em paralelo. Nesta pesquisa serão apresentadas somente abordagens paralelas (WORSCH; NISHIO, 2010; SHAKERI et al., 2008).

Este trabalho aborda a utiliza¸cão de autômatos celulares na tarefa de ordena¸cão. Na li-teratura já existem algumas abordagens de algoritmos de ordena¸cão utilizando autômatos celulares, e o objetivo deste trabalho é propor novos algoritmos para obter ganho na quan-tidade de passos necessários para realizar ordena¸cão e também no custo de processamento com rela¸cão às propostas existentes. As pesquisas existentes sobre o assunto foram pro-postas por Gordillo e Luna (1994) que trabalham dois novos ACs com registradores de memória, Shakeri et al. (2008) que propuseram três abordagens com registradores de memória e Worsch e Nishio (2010) que apresentam ACs utilizando a técnica Odd-even Transposition Sort na ordena¸cão de números binários. Essas abordagens motivaram este trabalho no sentido de comparar e buscar melhorias para os algoritmos existentes.

(11)

O processo de agrupamento de dados classifica, sem qualquer conhecimento prévio, uma massa de dados em grupos ou clusters. Os clusters são claramente dissemelhantes aos demais grupos e seus objetos são altamente semelhantes aos outros objetos do cluster. Utilizando o exemplo do algoritmo de agrupamento, para realizar essa tarefa com ACs seria necessário apenas definir transi¸cões de estados com objetivo de agrupar células se-melhantes. Como o processo ocorre sem qualquer interferência externa, esse é um ponto a ser explorado na área de autômatos celulares (XU; CHEN; HE, 2005).

(12)

2 AUT ˆ

OMATOS CELULARES

Wolfram (1994) define autômatos celulares como modelos matemáticos elementares oriundos de sistemas naturais, formados em uma rede ou malha, com indiv´ıduos idênticos e discretos, em que cada célula assume valores sobre um conjunto finito, por exemplo, de valores inteiros. Os indiv´ıduos evoluem em espa¸cos de tempo discretos, e obedecem a regras determin´ısticas que regem os valores de cada célula baseado nos valores de sua vizinhan¸ca. A natureza discreta dos autômatos celulares igualmente permite a analogia com computadores digitais, pois os agentes podem ser considerados como computadores com processamento paralelo e de arquitetura simplificada (WOLFRAM, 1994).

Nos autômatos celulares o tempo é discreto e a cada itera¸cão, as células devem ter seu estado atualizado que é determinado pelo estado presente das células vizinhas da célula em questão. A fun¸cão que determina o estado de todas as células é chamada de regra local e o estado das células em um determinado instante é chamado de estado global do autômato ou simplesmente configura¸cão (SARKAR, 2000).

Para que a atualiza¸cão do estado de uma determinada célula seja realizada é necessário definir a estrutura do autômato celular. A seguir são apresentadas as dimensões e os tipos de vizinhan¸ca para um AC. Como pode ser visto na Figura 1, um AC pode possuir uma dimensão qualquer, tipicamente, uma ou duas dimensões. Os componentes de um autômato celular também podem ter várias formas como quadrangular, triangular ou hexagonal. Em geral, todas as células de um AC possuem a mesma forma, isto é, se a forma adotada para um determinado autômato celular for triangular, todas as suas células deverão ser triangulares.

(13)

De acordo com Packard e Wolfram (1985), dois tipos de vizinhan¸ca em autômatos celulares bidimensionais bastante utilizados são a de von Neumann e Moore, conhecidos também como vizinhan¸ca de cinco vizinhos e nove vizinhos, respectivamente.

Além de adotar o tipo de vizinhan¸ca do autômato celular, também é necessário definir o seu raio (ourange), ou seja, o alcance da vizinhan¸ca de cada célula para a atualiza¸cão de seu estado, usualmente denotado por r. As Figuras 2 e 3, representam respectiva-mente a vizinhan¸ca de Moore e von Neumann. Apesar de as figuras evidenciarem que as vizinhan¸cas seguem uma lógica de forma¸cão, pode-se também considerar vizinhan¸cas arbitrárias.

Figura 2: Vizinhan¸ca de Moore (WEISSTEIN, 2013b).

Na Figura 3 ´e poss´ıvel observar a vizinhan¸ca de von Neumann com r = 0, r = 1,

(14)

Figura 3: Vizinhan¸ca de von Neumann (WEISSTEIN, 2013c).

´

E preciso também especificar a quantidade de estados distintos que o autômato celular pode assumir, que pode ser representado por k. Em geral k é um número inteiro, no intervalo [0, k−1] e o autômato celular bináriok = 2 é a escolha mais simples a ser feita. Para autômatos celulares binários (comk = 2), geralmente a cor “branca” representa valor 0 e o valor 1 pela cor “preta”. Naturalmente os autômatos celulares com k > 2 podem ser representados com outras cores (WEISSTEIN, 2013a). As Figuras 2 e 3 ilustram o caso com k= 2 nas cores branca e preta.

Além do AC clássico, que foi definido acima, existe também o AC em Bloco, que de acordo com Wolfram (2002b) pode ser definido como um autômato celular que a cada itera¸cão atualiza um bloco de células ao invés de apenas uma célula, ou seja, as transi¸cões de estado se aplicam a blocos de células.

2.1 Autˆ

omatos celulares elementares

(15)

S ={0, ..., k −1}

ondeSé o alfabeto definido para o autômato celular eka quantidade de poss´ıveis estados. A vizinhan¸ca de um AC sempre são 2r+ 1 células, onderé o raio e essa vizinhan¸ca pode ser representada como (−r,−r+ 1, ..., r−1, r).

De acordo com Wolfram (1983), um autômato celular elementar é um AC unidimen-sional com dois valores poss´ıveis (S ={0,1}) em cada célula. Neste caso, a vizinhan¸ca é a própria célula e as adjacentes imediatas a ela à esquerda e à direita, ou seja, com raio

r= 1.

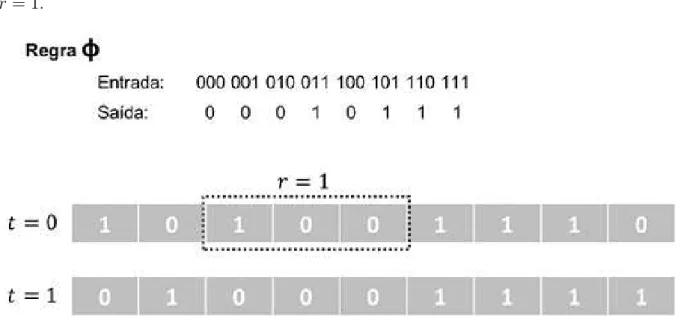
Figura 4: Exemplo de transi¸c˜ao de estados em um autˆomato celular elementar.

A Figura 4 mostra um exemplo de transi¸cão de estado baseada na regra φ comr = 1, onde a primeira linha apresenta os estados das células i, i−1 e i+ 1 no instante t = 0. Já a segunda linha exibe o estado das célulasi,i−1 e i+ 1 no instante t= 1 atualizados de acordo com a regra utilizada, ou seja, a Figura 4 exibe a configura¸cão inicial (t= 0) e final (t = 1) de autômato celular elementar baseado em uma regra (φ).

Para os autômatos celulares elementares existem 256 poss´ıveis regras de transi¸cão. Uma regra de transi¸cão pode ser demonstrada conforme a seguir:

xt_i+1 =φ(xt i−1, x

(16)

em que xt_i+1 é o estado da célula i no instante t+ 1 e φ representa a regra local que é aplicada na célulai.

Um outro ponto a ser considerado nos autômatos unidimensionais é a condi¸cão de contorno. Uma possibilidade é utilizar condi¸cão periódica, que pode ser definida por

i1 = in+1, onde i representa as c´elulas e n a quantidade de elementos do AC, ou seja, o

vizinho da direita da última célula é a primeira célula. Outra alternativa é a condi¸cão de contorno fixa, onde a primeira e a última células do reticulado não são vizinhas. Para os ACs com condi¸cão de contorno fixa, pode-se utilizar um estado quiescente (ou de background), que é aquele em que, se a vizihan¸ca da célula central é formada apenas por células do mesmo estado, o próximo estado se repete. E isso possibilita que as células do limite esquerdo e direito do reticulado fiquem em repouso, ou seja, células à esquerda da primeira célula e à direita da última célula.

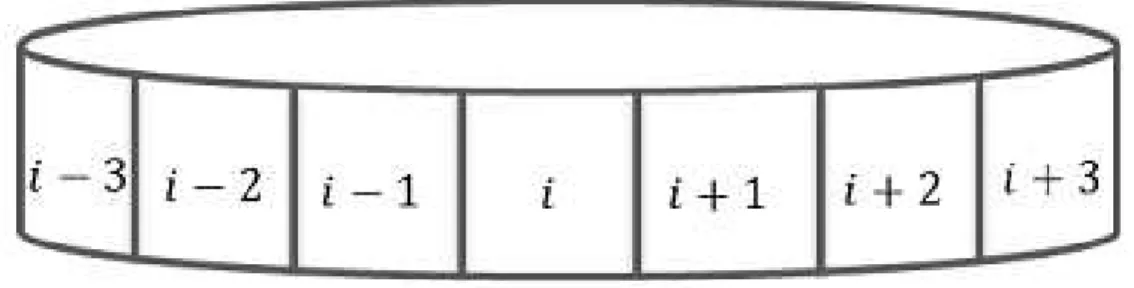
Conforme pode ser visto na Figura 5, a condi¸cão de contorno periódica em um AC unidimensional faz com que a última célula seja vizinha da primeira célula.

Figura 5: Exemplo de autômato celular unidimensional com condi¸cão de contorno periódica.

(17)

3 ORDENAC

¸ ˜

AO EM AUT ˆ

OMATOS CELULARES

Um algoritmo é uma série finita de instru¸cões que processam parâmetros de entrada e retornam uma sa´ıda. O processo de ordena¸cão é considerado como uma das opera¸cões fundamentais da ciência da computa¸cão, podendo ser utilizado como passos intermediários de diversos processos. Um algoritmo de ordena¸cão pode ser descrito como uma série de procedimentos que rearranjam uma sequência de itens em ordem crescente ou decrescente (BENIWAL; GROVER, 2013).

Alnihoud e Mansi (2010) apresentam algumas raz˜oes para os algoritmos de ordena¸c˜ao serem considerados como problema fundamental:

• A necessidade de classificar informa¸cões é inerente em diversas aplica¸cões.

• Muitos problemas de engenharia são encontrados quando um algoritmo de ordena¸cão é implementado.

• A ordena¸c˜ao geralmente faz parte de alguns algoritmos.

Embora o processo de ordena¸cão possa ser considerado como um problema já resol-vido, novos algoritmos e técnicas ainda são propostos na literatura. A seguir são apresen-tadas algumas implementa¸cões de ordena¸cão utilizando autômatos celulares. Para cada AC abordado na próxima se¸cão, será informada a quantidade necessária de passos de tempo para ordenar os elementos em perfeita ordem decrescente dada sua pior condi¸cão inicial, e.g., para a condi¸cão inicial S = {5,4,3,2,1} o AC X reordena os elementos em

S = {1,2,3,4,5} utilizando n+ 3 passos de tempo. A quantidade de passos de tempo ser´a considerada como custo temporal.

3.1 Algoritmos de Gordillo e Luna

(18)

A condi¸cão de contorno do AC de Gordillo e Luna não está expl´ıcita em Gordillo e Luna (1994), portanto a condi¸cão de contorno foi inferida como sendo fixa a partir do seguinte entendimento: como pode ser visto na próxima se¸cão, de forma global, a tarefa a ser realizada é ordenar os elementos de forma crescente através das transi¸cões de estado, sendo que, a medida que AC evolui, os maiores números devem ser deslocados para a direita e os menores para a esquerda do reticulado. Com base nisso, caso o AC possu´ısse condi¸cão de contorno periódica, os autores deveriam apresentar uma defini¸cão para o AC considerar as suas extremidades, pois em algum momento a primeira e última célula do reticulado seriam certamente comparadas. No entanto, em todo o trabalho de Gordillo e Luna (1994), não é sinalizado em momento algum qualquer defini¸cão a respeito de tratamento ou bloqueio das extremidades do reticulado.

3.1.1 Primeiro algoritmo de Gordillo e Luna

Gordillo e Luna (1994) apresentam dois algoritmos de ordena¸cão com autômatos ce-lulares. O primeiro AC é unidimensional, com vizinhan¸car = 1, processamento paralelo e o estado de cada célula pode ser qualquer número inteiro. Este AC será referenciado no restante do texto como “GL1”, e cada célula possui, além do conteúdo sujeito ao processo de ordena¸cão, dois registradores (direita e esquerda), e a cada itera¸cão, os estados dos registradores são atualizados conforme regra a seguir:

Sr i =     

1 Se Xi > Xi+1

0 Caso contr´ario

Sl i =     

1 Se (Xi < Xi−1 ∧ Xi ≤Xi+1) 0 Caso contr´ario

onde Xi representa o conte´udo da c´elula i, e Sil e Sir representam os registradores de

memória da esquerda e da direita da célulai, respectivamente. Na expressão acima Xi+1

é o conteúdo do vizinho da direita da célula i eXi−1 o do vizinho da esquerda.

Após a atualiza¸cão do estado dos registradores de memória, é aplicada a seguinte regra de transi¸cão para a célulaXi:

Xi =

            

Xi+1 Se (S_ir = 1 ∧ S_il+1 = 1)

Xi−1 Se (S

l

i = 1 ∧ Sir−1 = 1)

(19)

Conforme pode ser visto na regra de transi¸c˜ao acima, a c´elulaXi pode ter seu estado

alterado para Xi+1, Xi−1 ou Xi conforme os estados de seus registradores de memória e também de seus vizinhos. A seguir é apresentado como ocorre a atualiza¸cão de estado dos registradores e como a regra de transi¸cão é aplicada.

Figura 6: Condi¸c˜ao inicial das c´elulas Xi, Xi+1 eXi−1.

A Figura 6 exibe o estado inicial das células Xi, Xi+1 e Xi−1. O próximo passo é atualizar o valor dos registradores not1 conforme a regra informada anteriormente. Essa

atualiza¸c˜ao pode ser vista na Figura 7.

Figura 7: Atualiza¸cão dos registradores de memória das célulasXi, Xi+1 eXi−1.

Após atualizar os registradores de memória, a próxima etapa é, finalmente, alterar o estado das células conforme transi¸cão de estado descrita anteriormente.

Figura 8: Altera¸c˜ao do estado das c´elulasXi e Xi+1.

A Figura 8 mostra o estado das células após aplicada a regra de transi¸cão, que ocorre de acordo com os registradores Sl _e _Sr_{. Como pode ser visto na Figura 8, a célula} _X

i

recebeu o valor 1 e a c´elulaXi+1 o 4, mostrando uma troca de estados que contribui para

(20)

Gordillo e Luna (1994) afirmam que dada a pior condi¸cão inicial para ordena¸cão crescente dos elementos S = {n, ...,2,1}, esse algoritmo necessita de 2n−3 passos de tempo para ordenar todos os elementos. A Tabela 1 apresenta a evolu¸cão de GL1 para a pior condi¸cão inicial dos elementosS ={5,4, ...,1} para ordena¸cão crescente.

Tabela 1: Evolu¸c˜ao do AC GL1.

Passos Sl ₅ _Sr _Sl ₄ _Sr _Sl ₃ _Sr _Sl ₂ _Sr _Sl ₁ _Sr

1 0 5 1 0 4 1 0 3 1 0 1 1 1 2 0

2 0 5 1 0 4 1 0 1 1 1 3 0 0 2 0

3 0 5 1 0 1 1 1 4 0 0 2 1 1 3 0

4 0 1 1 1 5 0 0 2 1 1 4 0 0 3 0

5 0 1 0 0 2 1 1 5 0 0 3 1 1 4 0

6 0 1 0 0 2 0 0 3 1 1 5 0 0 4 0

7 0 1 0 0 2 0 0 3 0 0 4 1 1 5 0

Conforme pode ser visto na Tabela 1, os estados das células são alterados a cada itera¸cão conforme o valor dos registradoresSl _e_Sr _{de cada célula.}

3.1.2 Segundo algoritmo de Gordillo e Luna

O segundo algoritmo proposto por Gordillo e Luna (1994) é um AC unidimensional de processamento paralelo e com vizinhan¸ca r = 1.5, em que fazem parte da vizinhan¸ca o primeiro vizinho da esquerda e os dois primeiros da direita. Este AC será mencionado no restante do texto como “GL2”, e o estado de cada célula também pode ser qualquer número inteiro e cada célula também possui dois registradores (direita e esquerda). Para este AC, os estados dos registradores são atualizados conforme regra a seguir:

Sr i =     

1 Se (Xi > Xi+1 ∧ Xi+i ≤Xi+2)

0 Caso contr´ario

Sl i =     

1 Se (Xi < Xi−1 ∧ Xi ≤Xi+1) 0 Caso contr´ario

onde Xi representa a célula i, Sir é o registrador de memória da direita da célula i, e Sil

representa o registrador de memória da esquerda da célula i. Na expressão acima Xi+1

(21)

Após a atualiza¸cão do estado dos registradores de memória, é aplicada a seguinte regra de transi¸cão para a célulaXi:

Xi =

            

Xi+1 Se S_ir = 1

Xi−1 Se S

l i = 1 Xi Caso contr´ario

O comportamento deste AC é similar ao GL1 e possui funcionamento conforme as Figuras 6, 7 e 8. Deve ser notado na regra de transi¸cão acima que, mesmo a célula Xi

tendo raio r = 1.5, seu estado é alterado somente para os valores Xi+1, Xi−1 ou Xi, ou seja, Xi+2 é utilizado apenas como referência no processo, não participando diretamente

da ordena¸c˜ao. Este AC requer⌈3n

2 ⌉ −2 passos de tempo para ordenar todos os elementos

dada sua pior condi¸cão inicial. A Tabela 2 apresenta a evolu¸cão das células de GL2 para a pior condi¸cão inicial dos elementos S = {5,4, ...,1} para ordena¸cão crescente. A cada itera¸cão deste algoritmo, os estados das células são alterados conforme o valor de seus registradoresSl _e_Sr_.

Tabela 2: Evolu¸c˜ao do AC GL2.

Passos Sl ₅ _Sr _Sl ₄ _Sr _Sl ₃ _Sr _Sl ₂ _Sr _Sl ₁ _Sr

1 0 4 1 1 5 0 0 3 0 0 1 1 1 2 0

2 0 4 0 0 3 1 1 5 0 0 1 0 0 2 0

3 0 3 1 1 4 0 0 1 1 1 5 0 0 2 0

4 0 3 0 0 1 1 1 4 0 0 2 1 1 5 0

5 0 1 1 1 3 0 0 2 1 1 4 0 0 5 0

6 0 1 0 0 2 1 1 3 0 0 4 0 0 5 0

3.2 Algoritmos de Shakeri et al. (2008)

Em 2008 Shakeri et al. (2008) propuseram três autômatos celulares de ordena¸cão baseados no trabalho de Gordillo e Luna (1994); esses três ACs se diferenciam dos que lhes deram origem principalmente pelo fato de serem ACs em Bloco.

(22)

próxima se¸cão, de maneira global, o objetivo das transi¸cões de estado deste AC é realizar a ordena¸cão crescente deslocando os maiores números para a direita e os menores para a esquerda do reticulado. Com base nisso, caso o AC possu´ısse condi¸cão de contorno periódica, deveria existir uma defini¸cão para o AC contemplar as suas extremidades, pois em algum momento a primeira e última célula do reticulado seriam certamente compara-das. No entanto, em Shakeri et al. (2008) não é apresentado em momento algum qualquer informa¸cão a respeito de tratamento ou bloqueio das extremidades do reticulado.

3.2.1 Primeiro algoritmo de Shakeri et al. (2008)

O primeiro AC de Shakeri et al. (2008) que será citado como “SDFR1” no restante do texto, é um AC unidimensional de processamento paralelo, com vizinhan¸car= 1, que altera o estado de suas células conforme o critério a seguir:

Se (X_it₋1 < X

t

i ∧ X

t i > X

t i+1)

Ent˜ao{Xt+1

i =X

t

i+1 ∧ X

t+1

i+1 =X

t i}

Caso contr´ario{Xt+1

i =X

t

i ∧ X

t+1

i+1 =X

t i+1}

A regra de transi¸cão acima apresenta as condi¸cões para altera¸cão dos estados das célulasXi eXi+1, sendo Xi a célula em referência do AC, Xi+1 a primeira célula vizinha

`a direita, t o instante atual do AC e t+ 1 o pr´oximo instante.

Figura 9: Condi¸c˜ao inicial das c´elulas Xi, Xi+1 eXi−1.

(23)

Figura 10: Conserva¸c˜ao do estado das c´elulas Xi eXi+1.

Como pode ser verificado na Figura 10, o estado da c´elulaXi not0 ´e menor queXi+1

e maior que Xi−1, portanto nesse caso os estados das c´elulas Xi e Xi+1 s˜ao conservados not1.

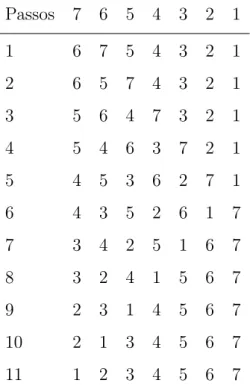
Tabela 3: Exemplo de execu¸c˜ao do AC SDFR1. Passos 7 6 5 4 3 2 1

1 6 7 5 4 3 2 1

2 6 5 7 4 3 2 1

3 5 6 4 7 3 2 1

4 5 4 6 3 7 2 1

5 4 5 3 6 2 7 1

6 4 3 5 2 6 1 7

7 3 4 2 5 1 6 7

8 3 2 4 1 5 6 7

9 2 3 1 4 5 6 7

10 2 1 3 4 5 6 7

11 1 2 3 4 5 6 7

A Tabela 3 exibe a evolu¸c˜ao de SDFR1 para a pior condi¸c˜ao inicial dos elementos

S = {7,6, ...,1}. O custo temporal para este autˆomato celular realizar a ordena¸c˜ao

(24)

3.2.2 Segundo algoritmo de Shakeri et al. (2008)

O segundo autômato celular proposto por Shakeri et al. (2008) é um AC unidimensi-onal de processamento paralelo, com raior= 1.5, fazendo parte da vizinhan¸ca o primeiro vizinho da esquerda e os dois primeiros da direita. Este AC será mencionado no restante do texto como “SDFR2”.

Assim como os ACs propostos por Gordillo e Luna (1994), este autômato celular utiliza registradores de memória para as células. O primeiro passo deste AC é determinar o valor do registrador S para cada célula conforme o procedimento a seguir:

Se [(X_it

−1 < X

t

i ∧ X

t i > X

t i+1)

∨ (X_it> X_it+1 ∧ X

t

i+1 < X

t i+2)]

Ent˜aoSi = 1

Caso contr´arioSi = 0

ondeXié o estado da célula em referência,Xi+1representa o estado do primeiro vizinho da

direita,Xi+2 o estado do segundo vizinho da direita, e Xi−1 o estado do primeiro vizinho da esquerda. Na express˜ao acimatindica o instante atual eSi representa o registrador da

célulaXi. Este Autômato Celular utiliza somente um registrador de memória e necessita

de⌈3n

2 ⌉−2 passos de tempo para realizar ordena¸c˜ao crescente da sua pior condi¸c˜ao inicial.

A equa¸c˜ao abaixo apresenta a regra de transi¸c˜ao deste AC:

Se (Si = 1 ∧ Si−1 = 0) Ent˜ao{Xt+1

i =X

t

i+1 ∧ X

t+1

i+1 =X

t i}

i =X

t

i ∧ X

t+1

i+1 =X

t i+1}

Para o procedimento acima,Si representa o registrador de memória da célulai eSi−1 o registrador da primeira célula a esquerda da célula i. O estado atual da célula i é representado porXt

(25)

3.2.3 Terceiro algoritmo de Shakeri et al. (2008)

O terceiro e último AC proposto por Shakeri et al. (2008) é um AC unidimensional de processamento paralelo com raio r = 2.5, sendo sua vizinhan¸ca as duas primeiras células da direita e as três primeiras células da esquerda. Este AC será referenciado como “SDFR3” no restante do texto.

O AC SDFR3 também trabalha com registradores de memória e a atualiza¸cão dos registradores se dá pela rela¸cão a seguir:

Se [(Xi−1 < Xi ∧ Xi > Xi+1)

∨ (Xi−3 < Xi−2 ∧ Xi−2 > Xi−1 ∧ Xi−1 > Xi ∧ Xi > Xi+1)

∨ (Xi−2 > Xi−1 ∧ Xi−1 > Xi ∧ Xi > Xi+1 ∧ Xi+1 < Xi+2)] Ent˜aoSi = 1

Caso contr´arioSi = 0

ondeSi representa o registrador da c´elulaieXi o estado atual da c´elulai. De acordo com

o estado das células vizinhas da célula i, o estadoSi é atualizado. Após os registradores

de memória serem atualizados, o procedimento abaixo é utilizado para atualizar o estado das células do AC.

Se (Si = 1 ∧ Si−1 = 0) Ent˜ao{Xt+1

i =X

t

i+1 ∧ X

t+1

i+1 =X

t i}

i =X

t

i ∧ Xt

+1

i+1 =X

t i+1}

De acordo com o procedimento acima, os estados das c´elulas i ei+ 1 s˜ao atualizados de acordo com os registradores Si e Si−1. Este AC requer ⌈n+

n

4⌉ −1 passos de tempo

para realizar ordena¸c˜ao crescente da sua pior condi¸c˜ao inicial.

(26)

Figura 11: Custo temporal de GL2 e SDFR3, de n = 0 an = 50000.

3.3 Odd-even Transposition Sort em Autˆ

omatos Celulares:

Al-goritmo de Worsch e Nishio

O algoritmo Odd-even Transposition Sort (OETS) opera com duas fases que se al-ternam (fase ´ımpar e fase par). Na fase par, elementos com ´ındice par (o segundo, o quarto, o sexto, etc.) são comparados com seu vizinho da direita. Por outro lado, na fase ´ımpar, elementos com ´ındice ´ımpar (o primeiro, o terceiro, o quinto, etc.) são comparados com seu vizinho da direita. Após a compara¸cão, o menor elemento assume a posi¸cão da esquerda e o maior a da direita. A Figura 12 apresenta um exemplo de execu¸cão do algoritmo Odd-even Transposition Sort iniciando na fase ´ımpar.

Figura 12: Exemplo de ordena¸c˜ao utilizando o algoritmo OETS (HARWOOD, 2011).

(27)

serão ordenados pelo algoritmo. A cada itera¸cão, os elementos são comparados com seu vizinho conforme indica¸cão das setas, onde o vizinho da esquerda sempre assume o menor e o da direita o maior número. Com isso, o algoritmo termina quando todos os elementos estão devidamente ordenados e não há mais trocas a serem realizadas. Neste caso, após oito itera¸cões, os oito elementos foram ordenados em ordem crescente.

Worsch e Nishio (2010) propuseram um autômato celular que tem como objetivo a or-dena¸cão de números binários. O AC apresentado por Worsch e Nishio (2010) utiliza o me-canismo de ordena¸cão do OETS na compara¸cão binária, sendo um AC unidimensional de processamento paralelo com raior= 1 e possuindo alfabetoS ={0,1,0h,1h,0i,1i,0|,1|,|0,|1}. Cada número binário a ser comparado é representado por w conforme a seguir:

w=w1· · ·wn =hx1y1z1| · · · hxnynzn|

onde wn é cada número que será comparado no AC, xn o primeiro elemento ou bit do

número, zn o último bit binário e yn os demais bits posicionados entre xn e zn.

O AC proposto por Worsch e Nishio (2010) trabalha com trˆes registradores conforme a seguir:

• Para os três registradores as células do meio são chamadas de L eR conforme pode ser visto na Figura 13. As células identificadas como L e R servirão de aux´ılio na compara¸cão de números binários conforme será descrito nos próximos parágrafos.

• O primeiro registrador chamado de lef t, irá assumir os valores do número binário

←_w−

i como pode ser visto Figura 13, j´a o segundo registrador chamado de right, ir´a

assumir os valores do n´umero bin´ario −→wi.

• O terceiro registrador chamado de comp realiza a compara¸c˜ao das c´elulas e pode assumir os valores =, < ou>.

A dinâmica deste AC é os bits serem movidos nos registradores lef te right em suas dire¸cões correspondentes ←w−i (esquerda) e −→wi (direita) e, após a compara¸cão, o menor

n´umero estar no registrador lef t e o maior no right. O comportamento do registrador

(28)

R.comp=             

< se R.right < L.lef t

= se R.right=L.lef t

> se R.right > L.lef t

ondeR.righté a célulaRdo registradorrighteL.lef ta célulaLdo registradorlef t. Para

os demais bits dos n´umeros que est˜ao sendo comparados, o valor do registrador R.comp

´e alterado da seguinte forma:

• Se a célula R.comp possui os valores >ou <, então seu valor não é alterado.

• No entanto, se a célula R.comp possui o valor =, então seu valor não é alterado conforme a regra citada acima para R.comp.

Outra informa¸cão importante é que R.comp e L.comp possuem sempre o mesmo conteúdo, ou seja, a regra acima se aplica também para L.comp. Já a célula R.lef t

tem seu valor alterado de acordo com a regra a seguir:

R.lef t=

            

R.right se R.comp ´e <

R.right se R.comp ´e =

L.lef t se R.comp ´e >

E a c´elula L.righttem seu valor alterado de acordo com a regra a seguir:

L.right=             

L.lef t se L.comp ´e <

L.lef t se L.comp ´e =

(29)

Figura 13: Ordena¸cão baseada na compara¸cão de números binários Worsch e Nishio (2010).

(30)

Figura 14: Comportamento dos n´umeros bin´arios nos registradores.

(31)

4 ODD-EVEN TRANSPOSITION SORT EM AC

UTI-LIZANDO PROPAGAC

¸ ˜

AO DE SINAIS

As pesquisas de Gordillo e Luna (1994), Shakeri et al. (2008) e Worsch e Nishio (2010) inspiraram este trabalho no sentido de buscar e propor novas abordagens de ordena¸cão de dados utilizando autômatos celulares unidimensionais. Neste trabalho são propostos dois autômatos celulares unidimensionais com fun¸cão de ordena¸cão de números inteiros utilizandoOdd-even Transposition Sort, sendo o primeiro AC de r= 1 e o segundor = 3. A motiva¸cão para o desenvolvimento dos ACs propostos nesse trabalho é realizar a ordena¸cão de números inteiros utilizando um autômato celular unidimensional de forma que seja realizado através de processamento paralelo e que seja mais eficiente que as abordagens existentes de ordena¸cão em AC unidimensional, ou seja, que possua um custo menor para ordenar n elementos. Observando os trabalhos de Gordillo e Luna (1994), Shakeri et al. (2008) e Worsch e Nishio (2010) procurou-se extrair as funcionalidades relevantes de cada trabalho e apresentar um novo AC que una essas caracter´ısticas em apenas um algoritmo.

Com base nisso, o conceito de registradores trabalhado por Gordillo e Luna (1994) e Shakeri et al. (2008) foi abstra´ıdo e culminou no uso de propaga¸cão de sinais, que são informa¸cões adicionais aos estados das células que auxiliam na tarefa de ordena¸cão. Já a técnica de OETS abordada por Worsch e Nishio (2010), foi utilizada neste trabalho para ordenar números inteiros ao invés de números binários.

(32)

Figura 15: Compara¸c˜ao de c´elulas no AC de r = 1.

(33)

Figura 16: Dinˆamica dos ACs propostos neste trabalho.

Para facilitar a compreensão do processo de propaga¸cão de sinais desse AC, foram criadas três transi¸cões de exemplo, mostradas na Tabela 4, em que i representa a célula central,i−1 a vizinha da esquerda e i+ 1 a da direita. Esse AC possui r= 1 e condi¸cão de contorno fixa.

Tabela 4: Transi¸c˜oes de estado de exemplo.

Transi¸c˜ao i−1 i i+ 1 i em t+ 1

1 . xi xi+1 xi >

2 xi−1 > xi xi+1 xi <

3 xi−1 < xi xi+1 xi >

(34)

Figura 17: Transi¸c˜oes de exemplo sendo aplicadas.

Como pode se verificar na Figura 17, a Transi¸cão 1 primeiramente é aplicada no número 4. De acordo com aTransi¸cão 1, quando a célula central for um número qualquer, sua vizinha esquerda for a extremidade esquerda do AC e à sua direita for um número qualquer, o seu estado no próximo passo será “xi >”, ou seja, o número 4 com o sinal>,

que é “4 >”. Já a Transi¸cão 2 é aplicada no número 3, pois sua vizinha da esquerda é uma célula com o sinal > e da direita um número qualquer, com isso seu estado no próximo passo será “xi <”, que é “3<”. Por fim, aTransi¸cão 3é aplicada no número 2,

pois sua vizinha da esquerda é uma célula com o sinal<e da direita um número qualquer, com isso seu estado no próximo passo será “xi >”, que é “2>”.

4.1 AC utilizando propaga¸c˜

ao de sinais com r=1

O primeiro AC proposto neste trabalho é um autômato celular de processamento paralelo e possui raior = 1. Este AC será referenciado como “CP1” no restante do texto.

(35)

elementos, se o algoritmo for executado 2n−1 passos, o autômato celular irá convergir. As transi¸cões de estado desse AC estão descritas na Tabela 5. Nesta tabela são apresentadas somente as transi¸cões ativas, nas demais transi¸cões, o estado da célula central não é alterado.

Tabela 5: Transi¸c˜oes de estado do AC CP1.

Transi¸c˜ao i−1 i i+ 1 i em t+ 1

1 . xi xi+1 xi >

2 . xi < # xi >

3 xi−1 > xi xi+1 xi <

4 xi−1 < xi xi+1 xi >

5 xi−1 xi . xi <

6 # xi > . xi <

7 xi−1 > xi xi+1 < xi <

8 xi−1 > xi xi+1 > xi <

9 # xi > xi+1 < M in(xi >, xi+1 <)<

10 xi−1 > xi < # M ax(xi−1 >, xi <)>

Pode-se verificar na Tabela 5, que as transi¸c˜oes de estado podem ser segregadas em trˆes grupos:

Inicializa¸cão: Compreende as transi¸cões 1, 2, 5 e 6. O grupo é de inicializa¸cão devido às serem caracterizadas por iniciar a propaga¸cão de sinais do AC, pois tratam as células que estão nas bordas, ou seja, na extremidade esquerda e direita.

Propaga¸cão de sinais: As transi¸cões 3, 4, 7 e 8 compõem esse grupo. O objetivo delas é realizar a propaga¸cão de sinais nas células que ainda não possuem nenhum sinal.

Compara¸cão: Grupo formado pelas transi¸cões 9 e 10. É responsável por realizar a compara¸cão dos números, deslocando o menor elemento para a célula da esquerda e o maior para a célula da direita.

(36)

direita. A expressãoi em t+ 1 deve ser entendida como o estado da célula ino próximo instante de tempo. Nas transi¸cões de estado, deve-se entender a nota¸cão utilizada para descrevê-las conforme a seguir:

- Estado que pode ser um n´umero inteiro qualquer: x

- Estado quiescente (ou de background): .

- Modificadores de estados originais: > e <

- Um estado qualquer: #

- O menor elemento dos argumentos: M in

- O maior elemento dos argumentos: M ax

Os sinais > e < são propagados pelas células a cada itera¸cão alterando os estados originais das células gerando novos estados. Esses sinais permitem que a ordena¸cão seja realizada em um AC unidimensional utilizando a técnica de OETS.

As transi¸c˜oes de estado apresentadas na Tabela 5 devem ser entendidas conforme a seguir:

Ex. transi¸c˜ao # 1 Se (xt_i

−1, x

t i, x

t

i+1) = (., xi, xi+1)

Ent˜aoxt_i+1 =xt_i >

−1, x

t i, x

t

i+1) = (#, xi >, .)

Ent˜aoxt_i+1 =xt_i <

(37)

Tabela 6: Exemplo de ordena¸c˜ao para os elementos S ={10,9, ...,6}de CP1.

t i i+ 1 i+ 2 i+ 3 i+ 4

t0 10 9 8 7 6

t1 10> 9 8 7 6<

t2 10> 9< 8 7 6<

t3 9< 10> 8> 7 6<

t4 9> 10> 8> 7< 6<

t5 9> 10> 7< 8> 6<

t6 9> 7< 10> 6< 8>

t7 7< 9> 6< 10> 8<

t8 7> 6< 9> 8< 10>

t9 6< 7> 8< 9> 10<

(38)

(39)

4.2 AC utilizando propaga¸c˜

ao de sinais com r=3

Já o segundo autômato celular proposto nesta pesquisa, também unidimensional e de processamento paralelo, possui r = 3. Este AC será citado no restante do texto como “CP2”

O crit´erio de parada de CP2 pode ser definido da seguinte forma: para um AC de n

elementos, o autômato celular irá convergir emn−1 passos para uma quantidade par de células en+ 1 para uma quantidade ´ımpar de células. A Tabela 7 exibe suas transi¸cões de estado. O funcionamento deste AC é bem semelhante ao CP1, diferenciando apenas o

(40)

Tabela 7: Transi¸c˜oes de estado de CP2.

Transi¸c˜ao i−3 i−2 i−1 i i+ 1 i+ 2 i+ 3 i em t+ 1

1 . . . xi xi+1 xi+2 xi+3 xi >

2 . . xi−1 > xi xi+1 xi+2 xi+3 xi >

3 . xi−2 > xi−1 xi xi+1 xi+2 xi+3 xi <

4 xi−3 > xi−2 > xi−1 < xi xi+1 xi+2 xi+3 xi < 5 xi−3 > xi−2 < xi−1 < xi xi+1 xi+2 xi+3 xi >

6 xi−3 < xi−2 < xi−1 xi xi+1 xi+2 xi+3 xi >

7 xi−3 < xi−2 > xi−1 > xi xi+1 xi+2 xi+3 xi <

8 xi−3 > xi−2 > xi−1 xi xi+1 xi+2 xi+3 xi <

9 xi−3 > xi−2 > xi−1 > xi xi+1 xi+2 xi+3 xi <

10 . . . xi < # # # xi >

11 . . xi−1 < xi < # # # xi >

12 # # # xi > . . . xi <

13 # # # xi > xi+1 > . . xi <

14 # # # xi > xi+1 > xi+2 < xi+3 < M in1(i, i+ 1, i+ 2, i+ 3) <

15 # # xi−1 > xi > xi+1 < xi+2 < # M in2(i−1, i, i+ 1, i+ 2)<

16 # xi−2 > xi−1 > xi < xi+1 < # # M ax1(i−2, i−1, i, i+ 1)>

17 xi−3 > xi−2 > xi−1 < xi < # # # M ax2(i−3, i−2, i−1, i)> 18 # # # xi > xi+1 > xi+2 < . M in1(i, i+ 1, i+ 2, i+ 3) <

19 # # xi−1 > xi > xi+1 < . . M in2(i−1, i, i+ 1, i+ 2)<

20 # xi−2 > xi−1 < xi < . . . M ax2(i−3, i−2, i−1, i)>

´

E possivel segregar as transi¸c˜oes de estado da Tabela 7 em quatro grupos:

Inicializa¸c˜ao: Transi¸c˜oes 1, 2 e 3.

Propaga¸c˜ao de sinais: Transi¸c˜oes 4, 5, 6, 7, 8 e 9.

Manuten¸c˜ao de extremidades: Transi¸c˜oes 10, 11, 12 e 13.

(41)

Somente o grupo de ’manuten¸cão de extremidades’ possui caracter´ıstica diferente das já apresentadas na Tabela 5; as transi¸cões desse grupo visam alterar o estado somente das células localizadas na extremidade esquerda ou direita.

A interpreta¸cão da Tabela 7 é semelhante à da 5, pois deve-se entender que cada linha é uma transi¸cão de estado da célulai, ondeirepresenta a célula em questão,i−1, i−2, i−3 os vizinhos da esquerda, e i+ 1, i+ 2, i+ 3 os da direita. Nas transi¸cões de estado, o que muda sãoM in1 o menor elemento dos argumentos,M in2 o segundo menor elemento,

M ax2 o segundo maior elemento e M ax1 o maior elemento dos argumentos. A seguir ´e apresentado um exemplo de transi¸c˜ao de estado para o AC der = 3 conforme a Tabela 7:

−3, x

t i−2, x

t i−1, x

t i, x

t i+1, x

t i+2, x

t i+3) =

(., ., xi−1 >, xi, xi+1, xi+2, xi+3) Ent˜aoxt_i+1 =xt_i >

Outro exemplo de transi¸c˜ao de estado para o AC de r = 3 conforme a Tabela 7 pode ser visto a seguir:

−3, x

t i−2, x

t i−1, x

t i, x

t i+1, x

t i+2, x

t i+3) =

(#,#, xi−1 >, xi >, xi+1 <, xi+2 <,#) Ent˜aoxt+1

i =M in2(i−1 t_{, i}t_{, i}

+ 1t, i+ 2t)<

A Tabela 8 exibe um exemplo de ordena¸c˜ao para a pior condi¸c˜ao inicial dos elementos

(42)

Tabela 8: Exemplo de ordena¸c˜ao para os elementosS ={17,16, ...,11} de CP2.

t i i+ 1 i+ 2 1 + 3 1 + 4 1 + 5 1 + 6

t0 17 16 15 14 13 12 11

t1 17> 16 15 14 13 12 11

t2 17> 16> 15< 14 13 12 11

t3 17> 16> 15< 14< 13 12 11

t4 14< 15< 16> 17> 13> 12> 11

t5 14> 15> 16> 17> 13> 12> 11<

t6 14> 15> 16> 17> 11< 12< 13>

t7 14> 15> 11< 12< 16> 17> 13<

t8 11< 12< 14> 15> 13< 16< 17>

t9 11> 12> 13< 14< 15> 16> 17<

(43)

(44)

4.3 An´

alises e compara¸c˜

oes

Após apresentados os ACs de Gordillo e Luna (1994), Shakeri et al. (2008) e Worsch e Nishio (2010) que inspiraram este trabalho, foi realizada uma compara¸cão entre o melhor AC de Gordillo e Luna (1994) “GL2”, de Shakeri et al. (2008) “SDFR3” e desta pesquisa, que é o “CP2”. O resultado desta compara¸cão pode ser visto na Figura 20, que exibe o custo temporal para realizar a ordena¸cão crescente da pior condi¸cão inicial den = 0 até

n= 50000. Esta compara¸cão é uma extensão da Figura 11.

Figura 20: Custo temporal entre os ACs: GL2, SDFR3 e CP2.

(45)

Tabela 9: Compara¸c˜ao entre os ACs de Gordillo e Luna (1994), Shakeri et al. (2008) e dos dois novos ACs.

AC Vizinhan¸ca Estados Registradores Tipo de AC Passos de tempo

GL1 3 n 2 Cl´assico 2n−3

GL2 4 n 2 Cl´assico ⌈3n÷2⌉ −2

SDFR1 3 n 0 AC em Bloco 2n−3

SDFR2 4 n 1 AC em Bloco ⌈3n÷2⌉ −2

SDFR3 6 n 1 AC em Bloco ⌈n+n÷4⌉ −1

CP1 3 3n 0 Cl´assico 2n−1

CP2 7 3n 0 Cl´assico n−1 ou n+ 1

Observe-se na Tabela 9 que os novos ACs possuem mais estados que os demais, isto é devido aos sinais “<” e “>”, pois o número 9 por exemplo pode ser “9”, “9 >” ou “9<”. Em contrapartida, os demais ACs – exceto o SDFR1 – necessitam de registradores de memória, que também constituem informa¸cões adicionais que auxiliam na tarefa de ordena¸cão.

A quantidade de estados se relaciona à quantidade de memória necessária para a execu¸cão do AC. A Tabela 10 exibe uma compara¸cão do custo de memória entre os ACs apresentados neste trabalho.

Tabela 10: Compara¸c˜ao de custo de mem´oria entre os ACs de Gordillo e Luna (1994), Shakeri et al. (2008) e dos dois novos ACs.

AC Custo de Mem´oria

GL1 3n

GL2 3n

SDFR1 n

SDFR2 2n

SDFR3 2n

CP1 3n

CP2 3n

(46)

que os utilizam – e nos ACs CP1 e CP2 os sinais “<” e “>”. Com base isso, os ACs GL1 e GL2 utilizam 3n, pois cada célula possui dois registradores. O SDFR2 e SDFR3 que possuem somente um registrador, têm custo de memória 2n, CP1 e CP2 possuem custo 3n por cada célula poder possuir os sinais “<” e “>”, e por fim, SDFR1 que Não possui registrador, apresenta custo de memórian.

Por outro lado, a vizinhan¸ca, registradores, tipo de AC e custo temporal influenciam diretamente no tempo de processamento do AC. Dessa maneira, uma forma emp´ırica de avaliar o custo de processamento dos ACs foi definida pela express˜ao

C =V ×M ×T ×P

onde C simboliza o custo de processamento, M os registradores de memória, V a vizi-nhan¸ca, T o tipo de AC e P a quantidade de passos. Vale observar que V ×M será a vizinhan¸ca efetiva, uma vez que se considera também os registradores na transi¸cão de estados para os ACs que fazem uso dos registradores. Este custo foi definido neste tra-balho como custo de processamento integralizado, que é uma medida para avaliar o custo temporal levando em conta o processamento em cada passo.

Para encontrar o custo de processamento C, é necessário observar os valores contidos na Tabela 9. Já que a variávelnnas expressões de custo da tabela representa a quantidade elementos a serem ordenados, considera-se aqui que o “Tipo de AC” deve ser contabilizado de acordo com o seguinte esquema de pontua¸cão:

AC Cl´assico: 1 // AC em Bloco: 2

Essa pontua¸cão é oriunda do AC Clássico atualizar somente uma célula a cada itera-cao, e o AC em Bloco – no caso desta pesquisa – duas células.

Deve-se considerar ainda a seguinte pontua¸c˜ao relativa aos “Registradores”: Nenhum registrador: 1

Um registrador: 2 Dois registradores: 3

(47)

Tal defini¸cão considera a quantidade de células que são alteradas a cada itera¸cão do AC, quais sejam, uma célula para o Clássico e duas para o AC em Bloco. A t´ıtulo de exemplo, a seguir obtemos o custo de processamento de GL1 comn = 5:

GL1 com n= 5 Vizinhan¸ca: 3

Registradores: Dois (custo 3) Tipo de AC: Cl´assico (custo 1) Quantidade de passos: 2n−3

C =V ×M×T ×P = 3×3×1×(2n−3) = 63

Abaixo segue-se outro exemplo de c´alculo do custo de processamento, no caso, o AC em Bloco SDFR2 comn = 5:

SDFR2 com n= 5 Vizinhan¸ca: 4

Registradores: Um (custo 2)

Tipo de AC: AC em Bloco (custo 2) Quantidade de passos: (⌈3n÷2⌉)−2

C =V ×M ×T ×P = 4×2×2×(⌈3n÷2⌉)−2 = 128

Como evidenciado nos dois exemplos de cálculo de custo processamento integralizado, o GL1, que necessita de 7 passos para realizar a ordena¸cão para 5 elementos, possui custo de processamento integralizado menor que o SDFR2, que necessita de 6 passos; ou seja, realizar menos passos não necessariamente implica menor custo de processamento integralizado. A Figura 21 ilustra o custo de processamento de todos os ACs, den = 0 a

(48)

Figura 21: Compara¸c˜ao do custo de processamento de n= 0 a n = 50000.

A Tabela 11 apresenta um ranking de todos os ACs abordados no trabalho, levando em considera¸c˜ao custo temporal e custo de processamento integralizado paran = 50000.

Tabela 11: Ranking dos ACs considerando custo temporal e custo de processamento integralizado.

Posi¸c˜ao Custo temporal Custo de processamento integralizado

1 CP2 CP1

2 SDFR3 CP2

3 GL2 e SDFR2 SDFR1

4 GL1 e SDFR1 GL1

5 CP1 GL2

6 SDFR2

7 SDFR3

(49)

Tabela 12: Complexidade assint´otica para a pior condi¸c˜ao inicial.

Algoritmo Complexidade

Bubble Sort O(n2

)

Selection Sort O(n2

)

Insertion Sort O(n2

)

Merge Sort O(n log n)

Quick Sort O(n2

)

Bucket Sort O(n2

) Quick Sort Paralelo O(n2

p )

Bubble Sort Paralelo O(n2

p )

Merge Sort Paralelo O(log n) Bucket Sort Paralelo O(log n)

CP2 O(n)

Como pode ser visto na Tabela 12, a complexidade do CP1 e CP2 é linear, sendo que os algoritmos clássicos em geral possuem complexidade quadrática e n log n para a pior condi¸cão inicial. O denominador p na complexidade dos algoritmos Quick Sort Paralelo e Bubble Sort Paralelo, representa a quantidade de processamentos que serão executados em paralelo.

(50)

5 CONCLUS ˜

OES

Pode-se concluir que um autômato celular realizar a tarefa de ordena¸cão em menos passos, pode não indicar o menor custo de processamento integralizado efetivo. A quanti-dade de passos é apenas uma variável do método de avalia¸cão de custo de processamento integralizado adotado neste trabalho. Esta afirma¸cão fica evidenciada na Tabela 11, que mostra o CP2 como sendo o primeiro AC noranking de quantidade de passos e o segundo quando refere-se ao custo de processamento integralizado. Já o CP1 que está na última coloca¸cão de quantidade de passos, fica em primeiro no ranking de custo de processa-mento integralizado. Outro ponto interessante é o SDFR3 ser o segundo em quantidade de passos e o último no ranking de custo de processamento integralizado.

Conclui-se tamb´em que os ACs propostos neste trabalho (CP1 e CP2) destacam-se na compara¸c˜ao com os demais ACs aqui apresentados, sendo CP2 o melhor AC quando avaliada o custo temporal, ou o segundo melhor no ranking de custo de processamento, e o CP1 o melhor no custo de processamento.

O fato do CP2 estar próximo do CP1 quando avaliado o custo de processamento integralizado, é um ponto relevante a ser investigado, seja na busca pela diminui¸cão da quantidade de passos mantendo a vizinhan¸ca e o tipo de AC clássico, ou aprimorando as transi¸cões de estado, no intuito de reduzir a quantidade e complexidade das transi¸cões.

Pode-se verificar que neste trabalho a quantidade de estados foi desconsiderada no cálculo do custo, devido a afetar somente a memória utilizada durante a execu¸cão do autômato celular.

Tanto nos trabalhos de Gordillo e Luna (1994) e Shakeri et al. (2008), como nos ACs propostos nesta pesquisa, os ACs trabalham com ordena¸cão de números inteiros. No entanto, os ACs propostos neste trabalho podem realizar a ordena¸cão de qualquer s´ımbolo, para o qual os sinais “>” e “<” tenham sentido em termos lexicográficos.

Como fruto desta pesquisa, foi publicado um artigo de Carvalho e de Oliveira (2015) apresentando os ACs propostos neste trabalho e seus resultados e discuss˜oes.

(51)

(52)

REFERˆ

ENCIAS BIBLIOGR ´

AFICAS

ALNIHOUD, J.; MANSI, R. An enhancement of major sorting algorithms. International Arab Journal of Information Technology, v. 7, n. 1, p. 55–62, 2010.

BENIWAL, S.; GROVER, D. Comparison Of Various Sorting Algorithms: A review. In: International Journal of Emerging Research in Management and Technology. India: Advanced Research International, 2013. v. 2, p. 83–86.

de Carvalho, C. E. P.; de Oliveira, P. P. B. Sorting with one-dimensional cellular automata using odd-even transposition. In: Advances in Intelligent Systems and Computing. (Proc. of WorldCIST’15 - 3rd World Conference on Information Systems and Technologies). [S.l.]: Springer: Heidelberg, 2015. A ser publicado.

GORDILLO, J. L.; LUNA, J. V. Parallel sort on a linear array of cellular automata. In: IEEE International Conference on Systems, Man, and Cybernetics. [S.l.: s.n.], 1994. v. 2, p. 1903–1907.

HARWOOD, A. Odd-even Transposition Sort. 2011. Dispon´ıvel em: < http://ww2.cs-.mu.oz.au/˜aaron/subjects/comp90025 2011 sm2/lectures/node111.html>.

MITCHELL, M.; GRAMSS, T.; BORNHOLT, S.; GROSS, M.; PELLIZZARI, T. Computation in cellular automata: A selected review. Wiley-VCH Verlag GmbH Co. KGaA, p. 95–140, 2005.

PACKARD, N.; WOLFRAM, S. Two-dimensional cellular automata. Journal of Statistical Physics, Kluwer Academic Publishers-Plenum Publishers, v. 38, n. 5-6, p. 901–946, 1985.

SAREEN, P. Comparison of sorting algorithms (on the basis of average case). International Journal of Advanced Research in Computer Science and Software Engineering, v. 3, p. 522–532, 2013.

(53)

SHAKERI, M.; DELDARI, H.; FOROUGHI, H.; REZVANIAN, A. Parallel Sorting On Linear Cellular Automata. In: Parallel and Distributed Processing Techniques and Applications. [S.l.: s.n.], 2008. p. 377–383.

WEISSTEIN, E. W. Cellular Automaton. MathWorld - A Wolfram Web Resource, 2013. Dispon´ıvel em: <http://mathworld.wolfram.com/CellularAutomaton.html>.

WEISSTEIN, E. W.Moore Neighborhood. MathWorld - A Wolfram Web Resource, 2013. Dispon´ıvel em: <http://mathworld.wolfram.com/MooreNeighborhood.html>.

WEISSTEIN, E. W.von Neumann Neighborhood. MathWorld - A Wolfram Web Resource, 2013. Dispon´ıvel em: < http://mathworld.wolfram.com/vonNeumannNeighborhood-.html>.

WOLFRAM, S. Statistical mechanics of cellular automata. Reviews of Modern Physics, American Physical Society, v. 55, p. 601–644, Jul 1983.

WOLFRAM, S. Computation theory of cellular automata. Communications in Mathematical Physics, Springer-Verlag, v. 96, n. 1, p. 15–57, 1984. ISSN 0010-3616. WOLFRAM, S. Cellular automata and complexity: collected papers. In: . Reading, MA: Addison-Wesley, 1994. p. 608.

WOLFRAM, S. A new kind of science. In: . Champaign, Ilinois, US, United States: Wolfram Media Inc., 2002. p. 169. ISBN 1579550088.

WOLFRAM, S. A new kind of science. In: . Champaign, Ilinois, US, United States: Wolfram Media Inc., 2002. p. 459. ISBN 1579550088.

WORSCH, T.; NISHIO, H. Real-time sorting of binary numbers on one-dimensional ca. In: Journ´ees Automates Cellulaires. [S.l.: s.n.], 2010. p. 214–225.