Problemas de minimização com singularidades

(1)

Universidade Federal de Minas Gerais Instituto de Ciˆencias Exatas Departamento de Matem´atica

Problemas de minimizac¸˜ao com singularidades

Leonel Giacomini Delatorre

(2)

(3)

Universidade Federal de Minas Gerais Instituto de Ciˆencias Exatas Departamento de Matem´atica

Problemas de minimizac¸˜ao com singularidades

Leonel Giacomini Delatorre

Dissertação apresentada ao Departamento de Matemática do Instituto de Ciências Exa-tas da Universidade Federal de Minas Gerais, como requisito parcial para a obtenção de t´ıtulo de Mestre em Matemática.

Orientador: Prof. Dr. Ronaldo B. Assunc¸˜ao

(4)

xii + 72 páginas. Dissertação (Mestrado) — Universidade Federal de Minas Gerais, Instituto de Ciências Exatas, Departamento de Ma-temática

1. Operador laplaciano com singularidades. 2. Problemas de minimizac¸˜ao em esferas. 3. Desigualdade de Caffarelli-Kohn-Nirenberg.

(5)

(6)

(7)

(8)

(9)

Agradecimentos

Agradec¸o primeiramente `a Deus por ter permitido concluir esta etapa.

Aos meus pais Maximino e Marivete por estarem sempre presentes, apesar da distância, con-fiando em minhas decis ões, sempre acreditando em minha capacidade, quando eu mesmo du-vidava. Agradeço a vocês pelo amor, carinho e compreensão. À minha irmã Luana, que desde pequenina, teve que aceitar, assim como meus pais, minha ausência em momentos importan-tes. Amo muito vocês!

Aos meu familiares, tios, primos, av ós, padrinhos, que sempre torceram por mim, agradeço pelas oraç ões e pelo apoio.

Aos meus grandes amigos Alexandre, Daniela, Katiéle, Leticia, Marline e Thanise, que estive-ram sempre ao meu lado. Agradeço por compreenderem minha ausência e por serem amigos verdadeiros. Em particular, a amiga e professora Alice Kozakevicius, por estar sempre pre-sente, com dicas, comentários e, claro, uma palavra amiga.

Ao orientador, professor Ronaldo Brasileiro Assunção, agradeço pela oportunidade e pela dedicação e paciência com que transmitiu seus conhecimentos.

Aos membros da comissão examinadora, professores Marcos Montenegro e Ezequiel Rodri-gues Barbosa, agradeço por compartilharem sua experiência, bem como pelas sugest ões e contribuiç ões, sempre pertinentes.

Aos professores e funcionários da UFMG agradeço pela dedicação, apoio e prontidão. Em par-ticular, agradeço ao Professor Paulo César Carrião, pelas dicas e sugest ões, e à Professora Ana Cristina Vieira, pelo voto de confiança.

Aos meus amigos e colegas de mestrado Luciana, Natália, S´ılvia, Willian, Amanda, Guilherme, Charles, Luiza, Flávia, entre outros, agradeço pela companhia, pelas risadas, pela força. Vocês foram fundamentais nesta etapa! Em particular, agradeço a Daiane, amiga e colega de graduação e de mestrado, por todo o apoio nos momentos de dificuldades que tivemos, e não foram pou-cos.

Ao Conselho Nacional de Desenvolvimento Cient´ıfico e Tecnol ´ogico - CNPq, pelo aux´ılio fi-nanceiro.

(10)

(11)

Resumo

Esta dissertação trata de resultados de existência de soluç ões de energia m´ınima para as se-guintes classes de equaç ões el´ıpticas semilineares degeneradas definidas emRN_:

−div|x|−2a∇u= |x|−bp|u|p−2u, x ∈RN_, _(P1)

e

−div

|x|−2a∇u+λ|x|−2(1+a)u= |x|−bp|u|p−2u, x ∈RN_; _λ_∈R_. _(P2)

ConsideramosN>_{3, os parˆametros 0}6_a6₍_N₋₂₎_/2,_a6_b6_a₊_1,_λ_∈R_{e envolvendo}

o expoente cr´ıtico de Hardy-Sobolevp = p(a,b):= _N₋₂₊2N₂₍_b₋_a₎. Procuramos soluç ões para os problemas (P1) e (P2) no espaço de Sobolev D1,2_a ₍RN₎ _{e demonstramos vers ões do lema de}

concentração e compacidade para obtermos resultados de existência de soluç ões.

Palavras-chave Operador laplaciano com singularidades; problemas de minimizac¸˜ao em esfe-ras; desigualdade de Caffarelli, Kohn e Nirenberg.

Abstract

This work is concerned with existence results of ground state solutions for the following class of degenerate semilinear elliptic equations defined onRN_:

−div|x|−2a∇u= |x|−bp|u|p−2u, x ∈RN_, _(P1)

e

−div|x|−2a∇u+λ|x|−2(1+a)u= |x|−bp|u|p−2u, x ∈RN_; _λ_∈R_. _(P2)

We consider the case N > _{3, the parameters 0} 6 _a 6 (N−2)/2, a 6 _b 6 _a+1, λ ∈ R

and involving the critical exponent of Hardy-Sobolevp = p(a,b) := 2N

N−2+2(b−a). We look for solutions of the problems (P1) and (P2) in the Sobolev spaceD1,2_a ₍RN₎_{and we prove versions}

of a Concentration-Compactness Lemma to obtain existence results.

Key-words Laplacian operator with singularities; minimization problems on spheres; Caffarelli-Kohn-Nirenberg inequality.

(12)

(13)

Nota¸c ˜oes

:= igualdade por definic¸˜ao

R+ _{conjunto dos n ´umeros reais positivos}

x= (x1, . . . ,xN) elemento deRN

|x|= ∑N_i₌₁x2_i1/2

norma do elementox∈RN

Bρ(x) bola aberta de raioρe centro emx ∈RN

ωN volume da bolaBρ(x)emRN

NωN ´area da superf´ıcie esf´erica∂Bρ(x)emRN

p′ := p

p−1 expoente conjugado de p

p(a,b):= 2N

N−2+2(b−a) expoente cr´ıtico de Hardy-Sobolev

∇u(x):= ∂u(x)

∂x1 , . . . ,

∂u(x)

∂xN

gradiente da func¸˜aou

div(u1(x), . . . ,uN(x))

:= ∂u1(x)

∂x1

+· · ·+∂uN(x)

∂xN divergente do campo

(u1(x), . . . ,uN(x))

∆_u(x):=div

∇u(x)

= N

∑

i=1

∂2u(x)

∂x2 i

operador laplaciano

X∗ espac¸o dual do espac¸oX

Lp₍_RN₎ _{espac¸o de Lebesgue}

|u|_p:= Z

RN|u(x)|

p_d_x1/p _{norma no espac¸o de Lebesgue}_Lp₍_RN₎

D₍RN₎ _{espaço das funç ões teste}

D1,2₍RN₎

:=nu∈L2∗₍_RN₎_; ∂u ∂xi ∈ L

2₍_RN₎_,_i₌_{1, ...,}_No _{espac¸o de Sobolev}

D1,2_a ₍RN₎ _{completamento do espac¸o} D₍RN₎ _com

relac¸˜ao ao produto interno(·|·) (u|v):=R

RN|x|

−2a_∇_u_{· ∇}_{v dx} _{produto interno no espac¸o}_D1,2 a (RN)

kuk:=R RN|x|

−2a_|∇

u|2dx1/2 norma no espac¸o de SobolevD1,2_a ₍RN₎ H1₍_Ω₎

:=nu∈L2(Ω);_∂∂_xu_i ∈ L2(Ω),i=1, ...,No espac¸o de Hilbert

H1

0(Ω) espac¸o de Hilbert com trac¸o nulo, definido como o fecho deC∞

0(Ω)emH1(Ω)

D_r

:=

u∈D1,2₍RN₎_: _u _{é radial}_} _{espaço das funç ões radiais}

S(a,b) inf_u_∈D1,2_a (RN₎

||x|−bu|_p=1

|x|

−a_∇_u

2

S(a,b,λ) inf_u_∈D1,2_a (RN)

||x|−bu_|_p=1

|x|

−a_∇

u

2

2+λ

|x|

−(1+a)

u

2

(14)

un→uq.t.p. emX convergˆencia em quase todo ponto deX

C0₍Ω) espaço das funç ões reais cont´ınuas

Ck₍Ω) espaço das funç ões reaisk-vezes continua-mente diferenciáveis

C∞

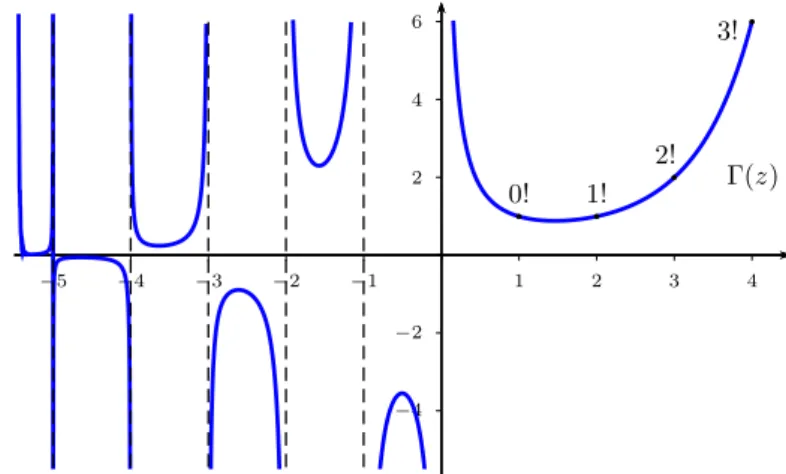
0 (RN) espaço das funç ões infinitamente diferen-ciáveis e de suporte compacto emRN Γ(z):=

Z ∞ 0 t

z−1_e−t_dt _{func¸˜ao gama}

B(y,z) = Γ_Γ(₍y_y)₊Γ(_zz₎) func¸˜ao beta

(15)

Sum´ario

Resumo . . . ix

Abstract. . . ix

Notac¸ ˜oes . . . xi

1 Métodos variacionais em equa¸c ões el´ıpticas 1 1.1 Soluç ões fracas e pontos cr´ıticos de funcionais . . . 1

1.2 Técnicas de minimização para problemas com compacidade . . . 3

1.3 Técnicas de minimização para problemas sem compacidade . . . 6

1.4 A identidade de Pohozaev e o resultado de Br´ezis e Nirenberg . . . 11

1.5 Resultados principais . . . 13

2 Sequências minimizantes paraS(a,b) 19 2.1 Invariância de sequências minimizantes por dilataç ões . . . 19

2.2 Lemas t´ecnicos. . . 20

2.3 Lema de concentrac¸˜ao e compacidade paraS(a,b) . . . 27

2.4 Demonstrac¸˜ao do Teorema 1.11 . . . 38

3 Sequências minimizantes paraS(a,b,λ) 45 3.1 Invariância de sequências minimizantes por dilataç ões . . . 45

3.2 Lema de concentrac¸˜ao e compacidade paraS(a,b,λ). . . 47

A Apêndice 63 A.1 Espaços de Funç ões . . . 63

A.2 Func¸ ˜oes gama e beta . . . 64

A.3 Resultados auxiliares . . . 65

A.4 Desigualdade de Caffarelli, Kohn e Nirenberg . . . 66

A.5 Definiç ões e resultados de Análise Funcional . . . 67

Bibliografia 69

(16)

(17)

-1- M´etodos variacionais em equa¸c ˜oes el´ıpticas

1.1 Solu¸c ˜oes fracas e pontos cr´ıticos de funcionais

O objetivo principal desta dissertação é demonstrar resultados de existência de soluç ões para uma classe de equaç ões diferenciais el´ıpticas semilineares definidas em todo o espaço, en-volvendo singularidadestanto no operador quanto na não linearidade e expoentes cr´ıticos de Hardy-Sobolev. Nas seç ões iniciais deste cap´ıtulo, baseadas no livro de Badiale e Serra [3], apresentamos alguns resultados básicos sobre minimização de funcionais visando contextua-lizar e descrever as maiores dificuldades para demonstrar os teoremas principais enunciados na última seção, baseados no artigo de Wang e Willem [19].

Começamos apresentando uma breve introdução ao estudo de problemas el´ıpticos semi-lineares através da aplicação de métodos variacionais. Equaç ões el´ıpticas semisemi-lineares são equaç ões em que a não linearidade envolve a função inc ógnita mas não suas derivadas. Essa classe de equaç ões é a primeira generalização não linear de equaç ões el´ıpticas lineares e surge em uma grande variedade de contextos em geometria, f´ısica e engenharia. Alguns exemplos de equaç ões semilineares incluem−∆u = f(x,u), que representam estados estacionários da equação não linear do calorut−∆u = f(x,u)ou da equação não linear da ondautt−∆u =

f(x,u). Nesses casos,udenota a função inc ógnita, f representa a não linearidade dada e∆u é o operador laplaciano.

Os métodos variacionais constituem um ramo do Cálculo das Variaç ões que visam o desen-volvimento de resultados e técnicas de minimização de funcionais e têm se mostrado bastante apropriados para estudar equaç ões el´ıpticas semilineares em geral.

A abordagem variacional para o estudo de equaç ões el´ıpticas semilineares é baseada na noção de solução fraca. No lugar de apresentar uma discussão geral desse conceito, nesta dissertação fazemos uma descrição dessa noção apenas para algumas classes de problemas semilineares. Começamos com um problema que também servirá de exemplo para diversos casos, lembrando que as definiç ões dos espaços de funç ões envolvidos estão no Apêndice.

SejaΩ⊂RN_{um conjunto aberto e limitado, em que}_N >_{3, seja}_q_: Ω→R_{uma func¸˜ao tal}

queq∈ L∞(Ω)e seja f: R_→R_{uma função cont´ınua verificando a condição de crescimento}

|f(t)|6_a+b|t|p−1_, _∀_t_∈_R _(1.1)

em quea,b ∈ R+ _{são constantes,} _p _∈ ₍_{2, 2}∗_] _{é um parâmetro e 2}∗ ₌ ₂_N_/₍_N₋₂₎ _{denota o}

expoente cr´ıtico de Sobolev. Suponhamos que devemos determinar uma func¸˜aou: Ω→R_tal

que

 



−∆_u+q(x)u= f(u), x∈ Ω_,

u(x) =0, x∈ ∂Ω_. (1.2)

(18)

Esse problema consiste de uma equação el´ıptica semilinear e uma condição de fronteira que especifica os valores da função inc ógnita na fronteira do dom´ınio e é chamado de problema homogêneo de Dirichlet.

Uma solução clássicado problema (1.2) é uma função u ∈ C2₍Ω)que verifica as equaç ões em (1.2) para todox ∈Ω¯_{. Outra noção de solução pode ser obtida da seguinte forma:}

multipli-camos a equação diferencial em (1.2) por uma funçãov∈C1

0(Ω)e integramos sobre o dom´ınio

Ω_{. Usando a f ´ormula de Green (}_A.9_{) e o fato de que a integral na fronteira se anula, pois}_v_tem

suporte compacto, resulta que seu é uma solução clássica do problema (1.2), então

Z

Ω∇u· ∇v dx+

Z

Ωq(x)uv dx=

Z

Ω f(u)v dx, ∀v ∈

C1

0(Ω). (1.3)

Observamos que a f órmula (1.3) faz sentido mesmo quando u não é de classe C2₍Ω¯); é suficiente queu∈C1₍Ω¯). Observamos também que as hip óteses sobre as funç õesuevpodem ser enfraquecidas: para que as integrais sejam finitas, é suficiente que u,v ∈ L2(Ω) e que

∂u/∂xi, ∂v/∂xi ∈ L2(Ω)para 16i6N. A partir disso, também não é necessário que a função

qseja cont´ınua; basta queq∈ L∞(Ω). Isso motiva a seguinte definic¸˜ao.

Defini¸cão 1.1. Sejam q ∈ L∞(Ω)e f ∈ C₍Ω). Uma solução fraca do problema (1.2) é uma funçãou∈ H₀1(Ω)tal que

Z

Ω∇u· ∇v dx+

Z

Ωq(x)uv dx=

Z

Ωf(u)v dx, ∀v∈ H

1

0(Ω). (1.4)

Observamos que se u é uma solução clássica do problema (1.2), então u ∈ C2₍Ω¯); logo,

u ∈ H1(Ω). Como u é cont´ınua em ¯Ω _e _u(x) = 0 para x ∈ ∂Ω_{, então} _u ∈ H₀1(Ω). Além disso, como vale a equação (1.3) e já que o espaçoC1

0(Ω)é denso emH01(Ω), fixada uma função

v ∈ H₀1(Ω)podemos escolher uma sequˆencia(vn)n∈N ⊂ C₀1(Ω)tal quevn→ vfortemente em

H₀1(Ω). Fazendo n → ∞_{, obtemos que vale a igualdade (}_1.3_{) para toda} _v ∈ H₀1(Ω), que é a equação (1.4). Portanto, uma solução clássica é solução fraca.

Suponhamos agora que temos uma soluc¸˜ao fracaudo problema (1.2) e queu ∈ C2₍Ω¯). Se

q ∈ C₍Ω), entãou é uma solução clássica. De fato,u ∈ H1

0(Ω)∩C2(Ω¯)implica queu(x) = 0 sex ∈ ∂Ω_{no sentido clássico. Usando uma função} _v ∈ C1

0(Ω)na f ´ormula (1.4), segue-se que vale a igualdade (1.3). Usando novamente a f ´ormula de Green (A.9) para reagrupar os termos, obtemos

Z

Ω(−

∆u+q(x)u− f(u))v dx =0, ∀v∈C1

0(Ω).

Como o espac¸oC1

0(Ω)é denso emL2(Ω), vemos que−∆u+q(x)u= f(u)q.t.p. emΩeu(x) = 0 em∂Ω_{. E como por hip ótese}_u∈ C2₍Ω), essas relaç ões valem em todos os pontos do dom´ınio eu é uma solução clássica.

(19)

1.2. Técnicas de minimização para problemas com compacidade 3

ent˜aou(x) = 0 para todox∈ ∂Ω_{. Outra vantagem, mais fundamental ainda, ´e que a}

demons-tração da existência de solução é completamente separada da questão da regularidade. Assim, podemos nos concentrar inicialmente em demonstrar um resultado de existência, que é o as-sunto principal desta dissertação, e apenas posteriormente considerar a questão da classe de diferenciabilidade da solução. Essa segunda parte é conhecida como questão da regularidade e, embora extremamente importante no estudo de equaç ões el´ıpticas, não será considerada neste trabalho; para mais detalhes, citamos os livros de Brézis [6, Caps. 8 e 9] e de Evans [11, Cap. 6]. Agora mostramos que as soluç ões fracasestão relacionadas com pontos cr´ıticos de funcio-nais associados ao problema (1.2). SejaF: R _→ R_{uma função definida por}_F₍_t_{) =}Rt

0 f(s)ds. Definimos o funcionalJ: H1₀(Ω)→R_por

J(u):= 1

2 Z

Ω|∇u|

2_dx₊1 2

Z

Ωq(x)u

2_dx₋Z

ΩF(u)dx,

usualmente denominado funcional de energia associado ao problema (1.2). Usando os resulta-dos de cálculo em espaços de Banach é poss´ıvel mostrar que o funcionalJ é diferenciável em

H₀1(Ω)e que a aplicaçãoJ′: H₀1(Ω)→(H₀1(Ω))∗ _{é tal que}

J′(u)v= Z

Ω∇u· ∇v dx+

Z

Ωq(x)uv dx−

Z

Ω f(u)v dx, ∀v∈ H

1

0(Ω). (1.5)

A partir dessa equação, vemos a conexão entre soluç ões fracas e pontos cr´ıticos: a funçãou é solução fraca para o problema (1.2) se, e somente se,u é ponto cr´ıtico do funcionalJ. Outra ma-neira de expressar esse fato é a seguinte: a equação de Euler-Lagrange associada ao funcional

J é a equação diferencial do problema (1.2).

Encerramos esses comentários mencionando que a condição de crescimento (1.1) é essencial para que o funcional de energia J esteja bem definido em H₀1(Ω). De fato, se f(t) tem um crescimento superior a|t|2∗−1_{, então}_F₍_t₎_{tem crescimento superior a}_|_t_|2∗_{; e como} _H1

0(Ω)n˜ao est´a imerso emLp(Ω)quandop >2∗, a integral deF(u)que aparece em uma das parcelas do

funcionalJpode divergir para algumas func¸ ˜oesu∈ H1 0(Ω).

1.2 T´ecnicas de minimiza¸c˜ao para problemas com compacidade

(20)

Um conceito útil na determinação de m´ınimos globais de funcionais é o de convexidade. Um funcionalJ: H₀1(Ω)→R _{é convexo se para todo}_u_,_v _∈_H1

0(Ω)e para todot∈ [0, 1], vale a desigualdade J(tu+ (1−t)v)6_tJ₍_u_{) + (}₁₋_t₎_J₍_v₎_{. Dizemos que o funcional}_J _{´e estritamente}

convexo se a desigualdade anterior ´e estrita.

Um resultado clássico em Análise garante que se J: H₀1(Ω)→R_{é um funcional cont´ınuo e}

convexo, entãoJ é fracamente semicont´ınuo inferiormente. Em particular, para toda sequência

(uk)k∈N ⊂ H₀1(Ω) e convergente fracamente para u ∈ H₀1(Ω), vale a desigualdade J(u) 6 lim infk→∞J(uk).

Um funcional cont´ınuo e convexo não possui necessariamente um m´ınimo, mesmo que seja limitado inferiormente. Um exemplo clássico é a funçãog:R_→R_{definida por}_g₍_x₎_:₌_exp₍_x₎

que é cont´ınua, convexa, limitada inferiormente mas que não atinge o ´ınfimo. Uma hip ótese adicional normalmente usada para garantir a existência de m´ınimo global é a de coercividade. Um funcional J: H1

0(Ω)→ Ré coercivo se para toda sequência(uk)k∈N ⊂ H1₀(Ω), a condição

kukk →∞implica queJ(uk)→∞.

Com essas hip ´oteses, consideramos um funcional I: X → R _{definido em um espac¸o de}

Banach reflexivo X e definimos m = infu∈XI(u). Seja(uk)k∈N ⊂ X uma sequência minimi-zante, isto é, uma sequência tal que I(uk) → mquandok → ∞. A coercividade do funcional

I garante que a sequência (uk)k∈N ⊂ X é limitada. Como X é um espaço reflexivo, o Teo-rema A.6 de Banach-Alaoglu garante a existência de uma subsequência, ainda denotada da mesma forma, tal queuk ⇀ ufracamente emX. Pela semicontinuidade inferior fraca deI, ob-temos I(u)6 _{lim inf}_k_→∞I(uk) =m. Portanto, I(u) =meu é um m´ınimo global do funcional

I. Isso demonstra o seguinte resultado.

Proposi¸c˜ao 1.2. Seja X um espa¸co de Banach reflexivo e seja I: X → R _{um funcional cont´ınuo,} convexo e coercivo. Ent˜ao I possui um ponto de m´ınimo global.

Uma aplicação desse resultado para demonstrar a existência de solução de um problema el´ıptico semilinear é apresentada a seguir.

Proposi¸cão 1.3. Seja Ω ⊂ RN _{com N} > ₃ _{um dom´ınio aberto e limitado. Suponhamos que q} ∈ L∞(Ω)verifica a condi¸cão q(x) > 0 q.t.p. emΩe seja f: R _→ R_{uma fun¸cão cont´ınua tal que vale} a desigualdade (1.1). Se f(t)t 6 ₀ _e (f(t)− f(s))(t−s) 6 ₀ _{para todo t}_,_s ∈ R_{, então para todo} h∈ L2₍_Ω₎_{o problema}

 



−∆_u+q(x)u= f(u) +h(x), x ∈Ω_,

u(x) =0, x ∈∂Ω (1.6)

possui uma ´unica solu¸c˜ao.

A demonstrac¸˜ao consiste em verificar que o funcional J: H₀1(Ω)→R_{definido por}

J(u):= 1

2 Z

Ω|∇u|

2_dx₊ 1 2

Z

Ωq(x)u

2_dx₋Z

ΩF(u)dx−

Z

(21)

1.2. Técnicas de minimização para problemas com compacidade 5

´e cont´ınuo, convexo e coercivo. ComoH1

0(Ω)é um espaço de Banach reflexivo, podemos apli-car a Proposição1.2ao funcional J. Para mais detalhes, consulte o livro de Badiale e Serra [3, Theorem 1.6.6].

Como exemplos de funç ões f verificando as hip óteses da Proposição 1.3, temos f(t) = −|t|p−2_t_com_p_∈₍_{1, 2}∗_]_ou _f₍_t_{) =}₋_arctan₍_t₎_.

A hip ótese f(t)t 6_{0 previne a existência de soluç ões não triviais no caso em que}h(x) =0. De fato, nesse caso qualquer soluçãouda equação diferencial é tal quekuk2₌ R

Ω f(u)u dx60,

ou seja,u(x) := 0. A hip ótese(f(t)− f(s))(t−s) é usada para se mostrar a convexidade do funcional J. Observamos que a hip ótese de convexidade na Proposição 1.2 é usada apenas para deduzir a semicontinuidade inferior fraca a partir da continuidade do funcional J. Um resultado mais geral é a seguinte versão do Teorema de Weierstrass, cuja demonstração segue as mesmas linhas da argumentação apresentada anteriormente.

Proposi¸c˜ao 1.4. Seja X um espa¸co de Banach reflexivo e seja I: X → R _{um funcional fracamente} semicont´ınuo inferiormente e coercivo. Ent˜ao I possui um ponto de m´ınimo global.

Esse resultado é um dos pontos de partida do método direto do cálculo das variaç ões. Ob-servamos que retirando a hip ótese sobre a monotonicidade de f perdemos a convexidade do funcional de energia; porém ainda é poss´ıvel mostrar a semicontinuidade inferior fraca do fun-cional e aplicar a Proposição1.4. Nesse caso, obtemos um resultado de existência mas não de unicidade de soluç ões. Para mais detalhes, consulte [3, Theorem 2.1.11].

Consideramos agora um exemplo de problema cujo funcional de energia associado não é limitado inferiormente, o que impossibilita o uso da Proposição1.2ou da versão do Teorema de Weierstrass. Sejap∈R_{tal que 2}< p<2∗e procuramos uma funçãousolução do problema

 



−∆_u+q(x)u= |u|p−2_u_, _x_∈ _Ω_,

u(x) =0, x∈ ∂Ω_. (1.7)

Claramente o problema (1.7) admite a solução trivialu(x) := 0, o que causa uma dificuldade extra. Uma forma de demonstrar a existência de soluç ões não triviais é o uso de minimização em esferas. Um resultado relacionado com esse problema é o seguinte.

Proposi¸cão 1.5. SejaΩ⊂RN _{um dom´ınio aberto e limitado, seja p}_∈ ₍_{2, 2}∗₎_{e seja q}_∈ _L∞₍Ω)tal que q(x)>₀_{q.t.p. em}Ω_{. Então o problema}₍_1.7₎_{possui pelo menos uma solu¸cão não trivial e não negativa.}

Como ´e usual nesses tipos de problemas, munimos o espac¸o de HilbertH₀1(Ω)com o pro-duto escalar

(u|v):= Z

Ω∇u· ∇v dx+

Z

Ωq(x)uv dx (1.8)

(22)

O funcional de energia associado a esse problema, cuja equação de Euler-Lagrange associ-ada é a equação diferencial do problema (1.7), é J: H₀1(Ω)→R_{, definido por}

J(u):= 1

2 Z

Ω|∇u|

2_dx₊1 2

Z

Ωq(x)u

2_dx₋ 1

p

Z

Ω|u|

p_dx

= 1

2kuk 2₋ 1

p|u|

p p.

Esse funcional é diferenciável e observamos que J não é limitado inferiormente, pois fixada uma funçãou 6= 0, temos queJ(tu) = (t2_/2₎_k_u_k2₋₍_tp_/_p₎_|_u_|p

p → −∞quandot → ∞, j´a que

p>2.

Uma forma de tentar aplicar as ideias anteriores para resolver esse problema é usar a ho-mogeneidade das duas parcelas que definem o funcionalJ. Uma delas tem grau 2 e a outra tem graup; essa diferença dos graus de homogeneidade desempenha um papel central na técnica conhecida como minimização em esferas.

O primeiro passo consiste em eliminar a não limitação do funcional J estabelecendo um v´ınculo adequado no qual o funcional é limitado. Uma escolha conveniente é uma esfera no espaçoLp(Ω). Fixadoβ>0, definimos o conjunto

Eβ :=

u∈ H₀1(Ω): Z

Ω|u|

p_dx₌ _β _.

Dessa forma, o funcional J restrito à esfera Eβ tem a forma J(u) = (1/2)kuk2−(β/p), de modo que fica limitado inferiormente. Para verificar que o funcionalJassim restrito tem ponto cr´ıtico, devemos garantir que existe uma funçãou∈ Eβtal quemβ :=infv∈Eβkvk

2 ₌_k_u_k2_{. Em} seguida, escolhendo um m últiplo conveniente dessa funçãou, obtemos uma solução fraca do problema (1.7). Os detalhes da demonstração encontram-se em [3, Subseção 2.3.1].

A hip ótese principal usada na argumentação precedente é sobre o crescimento subcr´ıtico da não linearidade. Para p < 2∗, a imersão H1

0(Ω) ֒→ Lp(Ω) é compacta e isso permite ga-rantir que a sequência minimizante para o funcional possui uma subsequência que converge em Lp(Ω). Isso finalmente permite concluir que existe uma função que minimiza o funcional

J restrito à esferaEβ. No caso de problemas em que a não linearidade tem crescimento cr´ıtico, isto é, quando p = 2∗, a compacidade da imersão falha e o argumento não se aplica. Mais ainda, existem problemas que não possuem solução não trivial. Esse caso é tratado com mais detalhes na seção seguinte e é um dos pontos centrais da dissertação.

1.3 T´ecnicas de minimiza¸c˜ao para problemas sem compacidade

(23)

1.3. Técnicas de minimização para problemas sem compacidade 7

problemas sem compacidade. A dificuldade principal para resolver esses problemas se apre-senta através da possibilidade de existirem sequências minimizantes para o funcional de ener-gia que podem ser limitadas mas que não possuem subsequências convergentes nos espaços de funç ões naturalmente associados aos problemas. Esses problemas são bem mais dif´ıceis de resolver do que os problemas da seção anterior.

Para exemplificar um caso t´ıpico de problema sem compacidade, consideramos a não linea-ridade homogênea f(t) =|t|p−2_t_com_p_∈ ₍_{2, 2}∗₎_{, isto é, com crescimento ainda subcr´ıtico mas} com dom´ınio Ω = RN_{; em outro exemplo também tratamos da não linearidade homogênea}

cr´ıtica f(t) =|t|2∗−2_t_{através do método de minimização em esferas.} Consideramos inicialmente o problema

 



−∆_u+q(x)u= |u|p−2_u_, _x_∈_RN_,

u∈ H1₍_RN₎ (1.9)

em que p ∈ (2, 2∗) e N > _{3. A condição} _u ∈ H1(RN₎ _{é uma forma t´ıpica de substituir as}

condição de fronteira homogênea dos problemas anteriores. De fato, podemos interpretá-la como uma forma de expressar uma condição do tipo u(x) → 0 quando |x| → +∞, que é naturalmente associada à equação. Vale ressaltar queu ∈ H1(R1₎_{não implica que}_u_{se anula}

no infinito. Frequentemente a condiçãou ∈ H1(R1)juntamente com o fato de que uresolve a equação diferencial implicam queu(x) → 0 no infinito, mas isso deve ser demonstrado em cada caso.

O fato de que o dom´ınio do problema é todo o espaçoRN_{sugere que devemos ter ausência}

de compacidade. Sem entrar nos detalhes agora, que serão tratados nos cap´ıtulos seguintes, suponhamos que o problema (1.9) tem uma solução u 6= 0 que minimiza algum funcional. Como o problema é invariante por translaç ões, para todo y ∈ RN _{a sequência} ₍_u_k₎_k_∈_N _⊂ H1(RN₎_{definida por}_u_k₍_x_{) =}_u₍_x₊_ky₎_{é uma sequência minimizante limitada que não possui}

subsequˆencia convergente emLp(RN₎_{para nenhum valor de}_p_{. Assim, o problema possui uma}

sequência minimizante limitada que não converge. A razão para isso é a invariância deRN _por

translaç ões, o que torna a imersãoH1(RN₎֒→Lp(RN)não compacta para qualquerp.

Hip óteses usuais sobre a função cont´ınuaq: RN _→ R _{que permitem resolver o problema}

são infx∈RNq(x) > 0 e lim_|_x_|→_∞q(x) = +∞. Por outro lado, com essas hip óteses, se u ∈ H1(RN₎_{então uma integral da forma}R

RNq(x)u2dxpode divergir. Isso significa que n˜ao

pode-mos trabalhar diretamente com o espaço de funç õesH1(RN₎_{. Assim, consideramos o seguinte}

subespac¸oX⊂ H1₍_RN₎_{, definido por}

X:=

u ∈H1(RN₎_:

Z

RNq(x)u

2_dx_<₊_∞ _.

(24)

do problema (1.9) é uma funçãou∈Xtal que

Z

RN∇u· ∇v dx+

Z

RNq(x)uv dx=

Z

RN|u|

p−2_{uv dx}_, _∀_v _∈_X_. _(1.10)

Usando as hip óteses sobre a funçãoqpodemos verificar queXestá imerso continuamente emH1(RN₎_{e, portanto, também em}_Lp₍RN₎_{para todo}_p_∈_[_{2, 2}∗_]_{. Mais ainda, é poss´ıvel}

verifi-car que a imers˜aoX֒→ Lp(RN₎_{´e compacta para todo} _p_∈ _[_{2, 2}∗₎_{. Dessa forma, os argumentos}

de compacidade descritos no final da seção1.2 podem ser aplicados e obtemos um resultado de existência de solução fraca e não negativau∈ Xpara o problema (1.9). Essa solução verifica a condição (1.10). A etapa final da demonstração do resultado de existência consiste em veri-ficar que essa condição continua válida para toda função teste v ∈ H1(RN₎_{. Dessa maneira,}

obtemos o seguinte resultado de existência, cuja demonstração encontra-se no livro de Badiale e Serra [3, Sec. 3.2].

Proposi¸c˜ao 1.6. Seja q ∈ C0₍RN₎_{uma fun¸c˜ao tal que}_inf

x∈RNq(x) > 0 elim|_x_|→∞q(x) = +∞e

seja p∈(2, 2∗). Ent˜ao o problema(1.9)possui uma solu¸c˜ao fraca u>₀_.

Observamos que a dificuldade principal desse tipo de problema, o ponto em que a ausência de compacidade se apresenta, é mostrar que uma sequência minimizante converge em um sen-tido suficientemente forte para que seja poss´ıvel fazer a passagem ao limite no termo não linear. No caso exemplificado, a compacidade pode ser restaurada pela escolha adequada do espaço

X. Em outras situaç ões, por exemplo usando hip óteses distintas sobre a funçãoq, isso não pode ser feito e é o que torna os problemas mais dif´ıceis. A estratégia então é analisar cuidadosa-mente as sequências minimizantes, de forma a tentar classificar os poss´ıveis comportamentos dessas sequências. Em seguida, tentamos eliminar todas essas possibilidades com a excessão de uma delas, exatamente aquela que permite recuperar a compacidade e concluir a demonstração de existência de soluç ões fracas para os problemas.

Esse tipo de argumentação é um exemplo de uma teoria bastante refinada que visa a classifi-cação de todos os poss´ıveis comportamentos de sequências de soluç ões aproximadas, tais como as sequências minimizantes. A teoria foi desenvolvida por Lions [14,15] e um dos principais resultados é o lema de concentração e compacidade, ferramenta crucial usada nesta dissertação. A seguir apresentamos um exemplo da aplicação desse princ´ıpio em um problema envol-vendo uma não linearidade com crescimento cr´ıtico. Consideramos o problema

 



−∆_u=|u|2∗₋₂

u, x∈RN_,

u∈D1,2₍RN₎_,

(1.11)

em que N > _{3. Formalmente, soluç ões do problema (}_1.11_{) são pontos cr´ıticos do funcional} J: D1,2₍RN₎_→R_{definido por}

J(u):= 1

2 Z

RN|∇u|

2_dx₋ 1 2∗

Z

RN|u|

(25)

1.3. Técnicas de minimização para problemas sem compacidade 9

A escolha do espaçoD1,2₍RN₎_{se deve ao fato de que não é conveniente considerar o funcional} J como definido em H1(RN₎_{, já que nesse espaço a primeira parcela da integral de} _J _{não é o}

quadrado de uma norma, o que imp ˜oe s´erias dificuldades.

Sabemos que a imersãoD1,2₍RN₎֒→ _L2∗(RN₎_{é cont´ınua mas não é compacta, nem mesmo}

em um sentido local, como veremos a seguir. Claramente, como estamos considerando todo o espaçoRN_{, existe a ausência de compacidade devido à invariância por translaç ões. Entretanto,}

no caso do problema (1.11) existe uma dificuldade ainda mais séria, que surge da invariância do problema por dilataç ões, como descrito a seguir. Sejav∈C∞

0(RN)uma função fixada; então

v∈D1,2₍RN₎_{. Para}_t_∈R+_{, definimos a dilatac¸˜ao}

vt(x):=t(N−2)/2v(tx).

Então a funçãovtverifica as seguintes propriedades:

Z

RN|∇vt|

2_dx₌Z

RN|∇v|

2_dx_, _∀_t _∈_R+

e

Z

RN|vt|

2∗_dx₌Z RN|v|

2∗_dx_, _∀_t _∈_R+ .

Da primeira propriedade conclu´ımos quevt ⇀0 fracamente emD1,2(RN)set →0 ou set → +∞; combinando essas convergências fracas para a função nula com a segunda propriedade, conclu´ımos que a sequência (vt)t∈N ⊂ L2

∗

(RN₎_{n˜ao possui subsequˆencia convergente. Isso}

acontece exatamente pela presenc¸a do expoente cr´ıtico de Sobolev 2∗ =2N/(N−2).

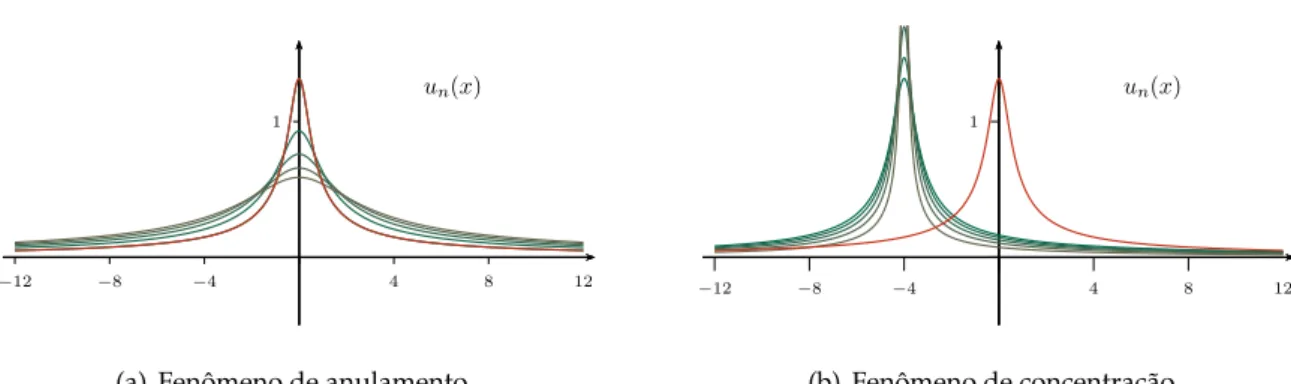
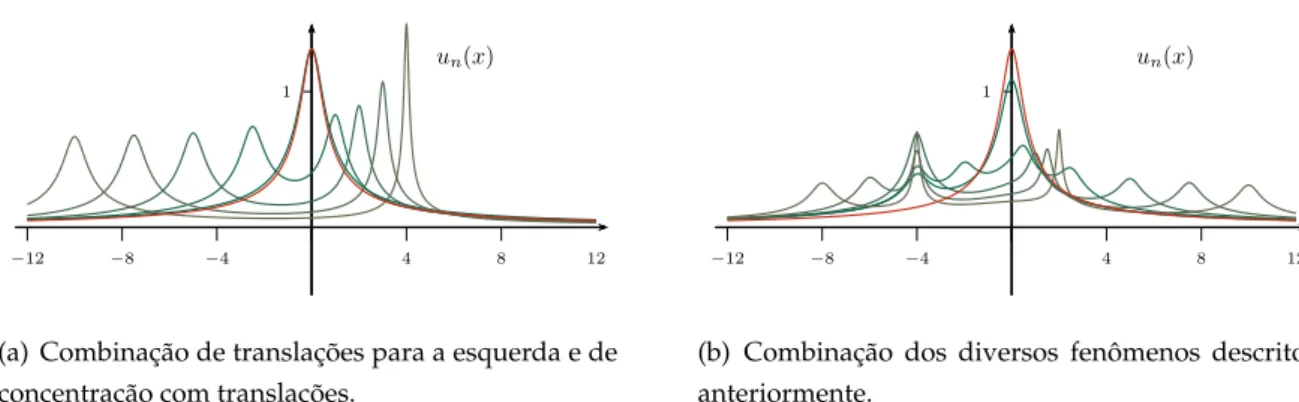
Em relação a essa discussão informal, reconhecemos agora que a ausência de compacidade não se deve simplesmente em decorrência da invariância das sequências minimizantes por translaç ões no espaçoRN_{, mas também devido à invariância por dilataç ões. De fato, supondo}

quev(0) 6= 0, vemos que se t → 0 as func¸ ˜oes vt ∈ C∞₀(RN) tendem a zero uniformemente, enquanto que a integralR

RN|vt|2 ∗

dxmantém-se constante. Dizemos que nesse caso há perda de compacidade por anulamento. Por outro lado, vemos que set →+∞_{as funç ões}_v_t ∈C∞

0 (RN) tendem a zero fora da origem evt(0)→ +∞, enquanto que a integralRRN|vt|2

∗

dxnovamente mantém-se constante. Dizemos que nesse caso há perda de compacidade por concentração.

Em outros termos, podemos dizer que set → 0 a “massa” devida `a integral envolvendo

|vt|2 ∗

espalha-se por todo o espac¸o e set →∞_{a “massa” concentra-se na origem.}

Consequen-temente, em ambos os casos há perda de massa na passagem ao limite e não há convergência forte no espaçoL2∗(RN₎_{. Esses fen ômenos acontecem em todos os problemas envolvendo}

cres-cimento cr´ıtico, at´e mesmo em dom´ınios limitados.

(26)

de compacidade pela invariância do problema por translaç ões. Dessa forma, trabalhamos no subespaço

D_r_:₌

u∈D1,2₍RN₎_: _u_{´e radial} _.

Proposi¸cão 1.7. O problema(1.11)possui uma solu¸cão não negativa e não trivial u∈D_r_.

Apresentamos apenas as linhas gerais da demonstração. Para mais detalhes, referimos aos cap´ıtulos seguintes da monografia, onde generalizaç ões do problema (1.11) são estudadas mais cuidadosamente.

Para garantir a existência de solução para o problema (1.11) procuramos minimizar o fun-cional Jna esfera unitária deL2∗₍_RN₎_{. Para isso, devemos garantir que o ´ınfimo}

S:= inf u∈D1,2₍_RN₎

|u|₂∗=1

kuk2 (1.13)

é atingido por uma funçãou∈D1,2₍RN₎_{. O valor}_S_{é denominado melhor constante de Sobolev}

e ´e a maior constante positiva tal que

S

Z

RN|u|

2∗

dx2/2

∗

6

Z

RN|∇u|

2_dx_, _∀_u_∈_D1,2₍_RN₎_.

Devido `a desigualdade de Sobolev, que ´e um caso particular da desigualdade (A.7) de Caffa-relli, Kohn e Nirenberg, sabemos queS>0.

Para analisar as sequências minimizantes, a ideia inicial é verificar que existe uma sequência minimizante que seja radial, isto é, uma sequência(vk)k∈N ⊂ Drtal que vk > 0,|vk|2∗ = 1 e

kvkk → S. Em seguida usamos a invariância do problema por dilataç ões e obtemos uma nova sequência minimizante(uk)k∈N ⊂DrparaSformada por funç ões não negativas e uma função

u ∈ D_r_{tamb´em n˜ao negativa e tais que}R

|x|<₁|uk|

2∗_dx ₌ _1/2,R

|x|>1|uk|2 ∗

dx = 1/2, e com as convergˆencias fracasuk ⇀ uemD1,2(RN)e em L2

∗

(RN₎_{e com a convergˆencia}_u_k₍_x₎ _→ _u₍_x₎

q.t.p. emRN_.

A pr óxima etapa consiste em definir quantidades que registram as poss´ıveis perdas de massa tanto na origem quanto no infinito. Esta é a parte principal da argumentação e está relacionada com o lema de concentração e compacidade. De fato, constitui o esforço para se obter informação sobre o anulamento ou a concentração da sequência minimizante(uk)k∈N ⊂

D1,2₍RN₎_{obtida na etapa anterior. Para isso definimos os valores}

ν0:= lim R→0+

lim sup k∈N

Z

|x|<_R

|uk|2 ∗

dx, ν∞ := lim

R→+∞

lim sup k∈N

Z

|x|>R|uk| 2∗_dx_,

µ0:= lim R→0+

lim sup k∈N

Z

|x|<_R

|∇uk|2dx

, µ∞ := lim

R→+∞

lim sup k∈N

Z

|x|>R|∇uk| 2_dx_.

Esses valores s˜ao tais queν0, ν∞ ∈ [0, 1/2]e, al´em disso, quandok → ∞a massa original de

(27)

1.4. A identidade de Pohozaev e o resultado de Br´ezis e Nirenberg 11

parte que se concentra no infinito, isto ´e, 1=R RN|u|2

∗

dx+ν0+ν∞. Tamb´em vale um resultado

similar para o quadrado da norma deD1,2₍RN₎_{, isto ´e,}_S ₌ R

RN|∇u|2dx+µ0+µ∞. Por fim,

temos as desigualdades fundamentais para a argumentac¸˜aoSν₀2/2∗ 6_µ₀_e_S_ν2/2_∞ ∗ 6_µ∞.

A etapa seguinte consiste em verificar queRRN|u|2

∗

dx=1 e queν0=ν∞ =0. Dessa forma,

mostramos que existe uma func¸˜ao minimizante para a melhor constante de SobolevS. Mas pela semicontinuidade fraca da norma, temos que

kuk26_{lim inf}

k∈N kukk 2₌ _S_.

Pela definição de S, resulta que kuk2 ₌ _S_{. Logo, o ´ınfimo} _S _{é atingido e} _u _{é uma função} minimizante. Finalmente, usando um m últiplo conveniente da funçãouobtemos uma solução para o problema (1.11).

Encerramos esta seção mencionando que é fato bem conhecido que as soluç ões do pro-blema (1.11) são conhecidas explicitamente e podem ser escritas como m últiplos de

U(x):= c

(1+|x|2₎(N−2)/2, c:= (N(N−2))

(N−2)/4_,

que verifica a equac¸˜ao diferencial

−∆U(x) =SU2∗−1(x), x∈RN_.

De forma geral, todas as soluç ões dessa equação diferencial formam a fam´ılia de funç ões

Ut,y(x):= t(N−2)/2U(t(x−y)),

em quey ∈ RN _e_t _∈ R+_{. Notamos que essa fam´ılia de funç ões é obtida a partir da função}_U

através de translaç ões e dilataç ões. Além disso, temos queUt,y ∈ L2 ∗

(RN₎_,_∇_U_t,y _∈ _L2₍RN₎_e kUt,yk2 =|Ut,y|2

∗

2∗ =SN/2.

1.4 A identidade de Pohozaev e o resultado de Br´ezis e Nirenberg

Se tentamos resolver um problema semelhante ao problema (1.11) em um dom´ınio limitado

Ω⊂RN_{, a saber, se consideremos o problema}

 



−∆u=|u|2∗−2_u_, _x_∈ _Ω_,

u=0 x∈ ∂Ω_, (1.14)

(28)

um dom´ınio Ω ⊂ RN _{com fronteira} _∂Ω _{diferenciável é um conjunto} estrelado em relação à origem seν(x)·x > 0 para todox ∈∂Ω, em queν(x)denota o vetor normal unitário exterior

a∂Ωemx.

Proposi¸cão 1.8. Suponhamos que Ω ⊂ RN _{é um conjunto aberto, limitado, com fronteira} _∂Ω dife-renciável e estrelado em rela¸cão à origem, em que N>₃_{. Então o problema}

    

   

−∆_u=|u|2∗₋₂

u, x∈Ω_,

u>0 x∈Ω,

u=0 x∈∂Ω_,

(1.15)

n˜ao tem solu¸c˜ao em H1 0(Ω).

A demonstração desse resultado é baseada em um resultado de regularidade, que afirma que qualquer solução fracau ∈ H₀1(Ω)do problema (1.15) é de classeC2(Ω)e de uma identi-dade integral, devida a Pohozaev, que enunciamos a seguir.

Proposi¸c˜ao 1.9. Seja f: R _→ R _{uma fun¸c˜ao cont´ınua e seja F}₍_t_{) =} Rt

0 f(s)ds. Suponhamos que

Ω⊂RN _{é um conjunto aberto e limitado, em que N}>₃_{. Se u}∈C2(Ω)é uma solu¸cão do problema

 



−∆_u= f(u), x∈ Ω_,

u= 0 x∈ ∂Ω_, (1.16)

ent˜ao vale a identidade

N−2 2

Z

Ω|∇u|

2_d_x₋_NZ

ΩF(u)dx=−

1 2

Z

∂Ω

∂u

∂ν

2

ν(x)·xdσ. (1.17)

A igualdade (1.17) é conhecida como identidade de Pohozaev. Para a demonstração desse resultado, consulte o livro de Badiale e Serra [3, Theorem 3.4.26, pag. 137] ou o livro de Am-brosetti e Malchiodi [1, Theorem 8.30, pág. 136]. Como consequência direta da Proposição1.9

vemos que seΩ⊂RN _{é estrelado em relação à origem, então toda solução do problema (}_1.16₎

verifica a desigualdade

N

Z

ΩF(u)dx−

N−2 2

Z

Ωu f(u)dx

>_0.

Em particular, se f(u) =|u|p−2_u_{, ent˜ao devemos ter}

N

p − N−2

2

Z

Ω|u|

p_d_x _>_0,

e, se u > 0, então p < 2N/(N−2) = 2∗. Esses comentários implicam que o expoente 2∗ é

(29)

1.5. Resultados principais 13

Em contraste com a Proposição1.8, que é um resultado de não existência de solução, Brézis e Nirenberg demonstraram em [7] que adicionando uma perturbação de ordem inferior ao pro-blema (1.15) podemos recuperar a existência de solução positiva no caso de qualquer dom´ınio limitadoΩ⊂ RN _{para perturbaç ões convenientemente escolhidas. Mais precisamente,}

consi-deramos o problema

    

   

−∆_u(x)−λu(x) =u2∗−1(x) x ∈Ω_,

u(x)>₀ x ∈Ω_,

u∈ H₀1(Ω)

(1.18)

em queN > _3,Ω ⊂ RN _{é um conjunto aberto e limitado com fronteira}_∂Ωe o espaço H1 0(Ω) é equipado com a normakuk := (R

Ω|∇u|2dx)1/2. As soluç ões fracas do problema (1.18) são

pontos cr´ıticos do funcionalJ: H₀1(Ω)→R_{definido por}

J(u):= 1

2 Z

Ω|∇u|

2_dx₋ λ 2

Z

Ω|u|

2_dx₋ 1 2∗

Z

Ω|u|

2∗

dx.

Apresentamos agora alguns comentários sobre o intervalo de variação para o parâmetroλ

da perturbac¸˜ao linear. Para isso, denotamos porλ1 o primeiro autovalor do operador laplaci-anoL[u]:= −∆u(x)emH1

0(Ω), isto ´e,

λ1:= inf u∈H1

0(Ω)

u(x)6≡0 Z

Ω|∇u|

2_dx

Z

Ω|u|

2_dx . (1.19)

É fato conhecido que λ1 > 0 e que λ1 é atingido, isto é, existe solução para o problema

−∆u(x) =λ1u(x).

Usando novamente a Proposição1.9, seΩ_{for um dom´ınio estrelado em relação à origem,}

então o problema (1.18) não possui solução se λ 6 _{0. Dessa forma, para obtermos resultados}

de existência de soluç ões para o problema (1.18) devemos considerar valores positivos paraλ.

Proposi¸cão 1.10. Se N > ₄_{, então o problema}₍_1.18₎_{tem uma solu¸cão para todo}_λ ∈ (0,λ1), em que

λ1´e o primeiro autovalor definido em(1.19).

Se N = 3, ent˜ao existeλ0 = λ0(Ω)comλ0 ∈ [0,λ1)e tal que o problema(1.18)tem solu¸c˜ao se,

e somente se,λ ∈ (λ0,λ1). Em particular, no caso em queΩ´e a bola unit´aria, temosλ0 = λ1/4e o

problema(1.18)tem solu¸c˜ao se, e somente se,λ∈(λ1/4,λ1).

Para a demonstração, consulte o artigo original de Brézis e Nirenberg [7] ou o livro de Ambrosetti e Malchiodi [1, Theorem 11.6, pág. 180].

1.5 Resultados principais

(30)

singularidades tanto no operador quanto na não linearidade e expoentes cr´ıticos de Hardy-Sobolev. A referência básica é o trabalho de Wang e Willem [19].

Mais especificamente, estudamos resultados de existência de soluç ões de energia m´ınima, conhecidas na literatura como soluç ões “ground state”, para equaç ões el´ıpticas degeneradas definidas emRN _{da forma geral}

−div(A(x)∇u) = f(x,u), (x∈RN₎_, _(1.20)

em queA:RN _→R _{é uma função não negativa que pode ser ilimitada ou se anular em alguns}

pontos. Essa classe de equaç ões generaliza alguns exemplos apresentados nas seç ões anteriores e surgem no estudo de ondas estacionárias em equaç ões anisotr ópicas de Schr ödinger. Como prot ótipos para estes tipos de problemas, consideramos as equaç ões

−div|x|−2a∇u=|x|−bp|u|p−2u, (x∈RN₎ _(1.21)

e

−div|x|−2a∇u+λ|x|−2(1+a)u=|x|−bp|u|p−2u, (x∈RN_,_λ_∈R₎_. _(1.22)

Seguindo algumas das ideias desenvolvidas previamente, procuramos soluç ões para os problemas (1.21) e (1.22) no espaço reflexivo D1,2_a ₍RN₎_{, definido como o completamento do}

espaço das funç ões testeD₍RN₎_{com relação ao produto interno}₍_·_,_·₎_:D1,2_a ₍RN₎_×D1,2_a ₍RN₎_→ R_{definido por}

(u,v):= Z

RN|x|

−2a_∇

u· ∇v dx

e com a correspondente norma definida por

kuk:= (u,u)1/2 = Z

RN|x|

−2a_|∇

u|2_dx1/2_.

ConsideramosN > _{3, os parˆametros}_a_e_b_{tais que}

06_a6(N−2)/2, a6_b6_a+1 (1.23)

e o expoente cr´ıtico de Hardy-Sobolev

p= p(a,b):= 2N

N−2+2(b−a). (1.24)

Utilizando a desigualdade (A.7) estabelecida por Caffarelli, Kohn e Nirenberg, esses pro-blemas permitem formulaç ões variacionais para os parâmetros nos intervalos especificados e, principalmente, podemos formular os seguintes problemas de minimização com restriç ões. Consideramos

S(a,b):= inf u∈D1,2_a (RN)

||x|−bu|_p=1

|x|

−a_∇

u

2

(31)

1.5. Resultados principais 15

para o problema (1.21) e

S(a,b,λ):= inf u∈D1,2_a ₍RN)

||x|−bu|_p=1

|x|

−a_∇_u

2

2+λ

|x|

−(1+a)

u

2

2 (1.26)

para o problema (1.22). Conforme vimos anteriormente, demonstrar existência de soluç ões para os problemas (1.21) e (1.22) é equivalente a demonstrar que os valoresS(a,b)eS(a,b,λ)

s˜ao atingidos.

A desigualdade (A.7) de Caffarelli, Kohn e Nirenberg (TeoremaA.3) garante que para os pa-rˆametros especificados em (1.23) e (1.24), existe uma constante positivaC ∈ R+_independente

deutal que

_Z

RN|x|

−bp

|u|pdx

2/p

6_C

Z

RN|x|

−2a

|∇u|2dx, u∈D1,2_a ₍RN₎_. _(1.27)

Assim, a constanteS(a,b)´e positiva.

Como podemos antecipar, a principal dificuldade no estudo dos problemas (1.21) e (1.22) é a ausência a priori de compacidade das sequências minimizantes, já que ambos os proble-mas estão definidos em todo o espaçoRN _{e envolvem o expoente cr´ıtico} _p₍_a_,_b₎_{. Portanto, as}

sequências minimizantes são invariantes por translaç ões e por dilataç ões.

Para um breve hist órico do problema (1.21), mencionamos que Lieb [13] demonstrou a existência de funç ões minimizantes, isto é, de funç ões que realizam o ´ınfimo S(a,b)no caso

a = 0 e 0 < b < 1. Além disso, Chou e Chu [10] demonstraram o mesmo resultado quando a 6 _b < _a+_{1. Ambos mostraram também que}_S(_a_,_a+₁) _{nunca é atingido. Em particular,}

o valorS(0, 1)que corresponde à desigualdade de Hardy nunca é atingido. O caso a = 0 e 0< b< _{1 também foi estudado por Lions [}₁₅_{] em dom´ınios não limitados. O primeiro}

resul-tado, relativo ao problema (1.21), ´e enunciado a seguir.

Teorema 1.11. Sejam N > ₃_,₀ 6 _a < (N−2)/2, a+b > 0, a 6 _b < 1+a e p = p(a,b). Seja

(un)_n∈N ⊂D 1,2

a (RN)uma sequˆencia minimizante para S(a,b)verificando

|x|

−b

un

p=1,

|x|

−a_∇

un

2

2→S(a,b).

Então existe uma sequência(tn)_n∈N ⊂]0,∞[tal que a sequência de dilata¸cões((un)_t_n)n∈N ⊂D1,2_a (RN)

definidas por(un)tn(x):=t

(N−2(1+a))/2

n un(tnx)possui uma subsequˆencia convergente. Em particular,

existe uma fun¸c˜ao minimizante para S(a,b).

(32)

a = b depende de uma estimativa diferente, pois p(a,a) = 2∗ = 2N/(N−2)e existe uma dilatação duplamente invariante. O método utilizado por Wang e Willem [19] é diferente da-quele utilizado por Lions [15], pois avalia quantitativamente a não compacidade de sequências minimizantes.

A seguir, enunciamos dois resultados relativos ao problema (1.22).

Teorema 1.12. Sejam N > ₃_,₀ 6 _a < (N−2)/2, a 6 _b< 1+a, p = p(a,b)e−S(a,a+1) <

λ<₀_{. Seja}(_u_n)

n∈N ⊂D 1,2

a (RN)uma sequˆencia minimizante para S(a,b,λ)satisfazendo

|x|

−b_u n

p=1,

|x|

−a_∇_u n

2

2+λ

|x|

−(1+a)

un

2

2 →S(a,b,λ).

Então existe uma sequência(tn)n∈N ⊂]0,∞[tal que a sequência de dilata¸cões((un)tn)n∈N ⊂D

1,2 a (RN)

(N−2(1+a))/2

existe uma fun¸c˜ao minimizante para S(a,b,λ).

Teorema 1.13. Sejam N > ₃_,₀ 6 _a < (_N−₂)_/2_{e p} = _p(_a_,_b)_{. Seja}(_u_n)

n∈N ⊂ D1,2a (RN)uma

sequˆencia minimizante para S(a,b,λ)satisfazendo

|x|

−b

un

p=1,

|x|

−a_∇

un

2

2+λ

|x|

−(1+a)

un

2

2 →S(a,b,λ).

Suponhamos que vale um dos grupos de hip´oteses a seguir: 1. a <b< a+1e0<λ, ou

2. 0<a =b e₀<λ≪₁.

Então existe uma sequência(tn)n∈N ⊂]0,∞[tal que a sequência de dilata¸cões((un)tn)n∈N ⊂D

1,2 a (RN)

(N−2(1+a))/2

existe uma fun¸c˜ao minimizante para S(a,b,λ).

Para demonstrar o Teorema1.12verificamos que as sequˆencias minimizantes paraS(a,b,λ)

são relativamente compactas a menos de dilataç ões quandoa6_b<a+1 e−S(a,a+1)<λ<

0. O caso a = b = 0 e −S(0, 1) < _λ < _{0 foi resolvido por Lions ([}₁₄_{]). Para demonstrar o}

Teorema1.13, em que consideramos o caso λ > 0, novamente tratamos de forma diferente os

casosa<b<a+1 ea=b. Ao contr´ario do valorS(a,b), paraS(a,b,λ)comλ6=0 n˜ao se sabe

se existem soluç ões expl´ıcitas para o problema (1.22). O método aqui utilizado apresenta uma abordagem uniforme para ambos os problemas.

Vale mencionar que Chou e Chu demonstraram em [10] que a solução do problema (P1) é radialmente simétrica. Além disso, Catrina e Wang estudaram em [9] o problema (P1) para o parâmetro a definido no intervalo −∞ < a < (N−2)/2 e demonstraram, entre outros

resultados, o caso em que ocorre a quebra de simetria [9, Theorem 1.3]. Esse resultado afirma que existea06 0 e uma func¸˜aoh(a)definida paraa6 a0, satisfazendoh(a0) = a0,a <h(a)<

a+1 para a < _a₀_{, e}_a+₁−_h(_a) → _{0 quando} −_a → ∞_{, de forma que para qualquer} (_a_,_b)_,