Auto-organização e formação de padrão em sistemas físicos e biológicos.

(1)

DOI: http://dx.doi.org/10.1590/1806-9126-RBEF-2015-0022 Licenc¸a Creative Commons

Auto-organiza¸

c˜

ao e forma¸

c˜

ao de padr˜

ao em sistemas f´ısicos

e biol´

ogicos

Self-organization and pattern formation in physical and biological systems

Jefferson A.R. da Cunha∗1, Ladir Cˆandido1, Andr´e L.A. Penna2,3, Fernando A. Oliveira3

1

Instituto de F´ısica, Universidade Federal de Goi´as, Goiˆania, GO, Brasil 2

Universidade de Bras´ılia, Bras´ılia, DF, Brasil 3

International Center for Condensed Matter Physics, Bras´ılia, DF, Brasil

Recebido em 15 de dezembro de 2015. Revisado em 11 de janeiro de 2016. Aceito em 17 de janeiro de 2016

Neste trabalho apresentamos uma breve discussão sobre a descri¸cão matemática do fenômeno forma¸cão de padrão em sistemas biológicos, observando os modelos matemáticos de dinâmica de popula¸cões. Listamos vários exemplos de sistemas f´ısicos, qu´ımicos e biológicos que exibem este fenômeno enfatizando, em cada um, os parâmetros principais envolvidos em seu entendimento. Mostramos que, no caso das popula¸cões, o fenômeno padrão pode ser modelado ao modificarmos a equa¸cão de Fisher-Kolmogorov, considerando uma intera¸cão não-local para o termo de competi¸cão. Apresentamos um estudo anal´ıtico e numérico da equa¸cão de Fisher-Kolmogorov com difusão e analisamos o papel dos termos de crescimento, difusão e competi¸cão na forma¸cão dos padrões.

Palavras-chave:Dinâmica de popula¸cões, Forma¸cão de padrão, Fisher-Kolmogorov, Intera¸cões não locais.

In this work we present a brief discussion of the mathematical description of pattern formation phenomena in biological systems through the mathematical models of population dynamics. We present some examples of physical, chemical and biological systems which exhibit this phenomena. For each system we show the main parameters that describe the patterns. We show that in the case of population, patterns can be described when we modify the Fisher-Kolmogorov equation, considering a non-local interaction for the competition term. We present an analytical and numerical study of the Fisher-Kolmogorov equation with diffusion and we analyze the role of growth, diffusion and competition term in the pattern formation. Keywords:Population dynamics, Pattern formation, Fisher-Kolmogorov, nonlocal interactions.

1. Introdu¸c˜ao

O desenvolvimento cient´ıfico e tecnológico vivido pela sociedade, em certos momentos, se deu por meio da tentativa de desvendar determinados mecanismos responsáveis por fenômenos encontrados na natu-reza. Um desses fenômenos que sempre atraiu grande aten¸cão da comunidade cient´ıfica, é o fenômeno de forma¸cão de padrão. Este fenômeno se caracte-riza pelo processo no qual um estado espacial de um determinado sistema, inicialmente homogêneo e estável, evolui para um novo regime, agora sem esta homogeneidade espacial. Neste novo regime o

∗_Endere¸_{co de correspondˆ}_{encia: jeffadriany@gmail.com.}

sistema esbo¸ca um tipo de estrutura espacial que chamamos de padr˜ao [1].

Consideremos um sistema termodinâmico onde não existam trocas de matéria ou energia. Nes-tas condi¸cões este sistema pode obedecer as leis básicas da termodinâmica de equil´ıbrio, onde suas variáveis macroscópicas são invariantes no tempo e homogêneas no espa¸co. Neste sistema em equil´ıbrio, se houver troca de energia ou matéria com o meio, o sistema pode se organizar em estruturas com dinâmicas próprias que caracterizam o fenômeno de “forma¸cão de padrão”, caso em que as variáveis

(2)

Neste texto analisamos alguns sistemas f´ısicos, qu´ımicos e biológicos que apresentam os fenômenos de auto-organiza¸cão e forma¸cão de padrão. Des-crevemos como alguns sistemas se auto-organizam formando padrões, e, para cada sistema, quais os parâmetros envolvidos neste processo. Uma vez compreendido e listado alguns exemplos de auto-organiza¸cão e forma¸cão de padrão, mostramos como este fenômeno pode ser modelado matematicamente em um sistema biológico constitu´ıdo de um coletivo qualquer de indiv´ıduos de uma popula¸cão descritos pela equa¸cão de Fisher-Komogorov.

2. Auto-organiza¸cão e forma¸cão de padrão

Na literatura cient´ıfica, encontramos inúmeros traba-lhos teóricos e experimentais sobre auto-organiza¸cão e forma¸cão de padrão em sistemas f´ısicos, qu´ımicos e biológicos [1–13]. É interessante observar a riqueza de sistemas encontrados na natureza, que exibem for-mas diferentes do mesmo fenômeno. Abaixo, apresen-tamos uma breve descri¸cão de alguns destes sistemas já bem estabelecidos e estudados pela comunidade cient´ıfica.

2.1. Cristalizac¸˜ao de Wigner

Existem vários sistemas f´ısicos que se organizam apresentando uma ordem espacial, ou seja, formando um padrão. A cristaliza¸cão de Wigner é um dos exemplos mais simples que exibem este fenômeno. Como ilustrado na Fig. 1, no cristal de Wigner elétrons são depositados sobre uma fina camada de Hélio que por sua vez é colocada sobre um substrato. Estes elétrons estão presos na superf´ıcie do Hélio na dire¸cão vertical devido a intera¸cão destes com o substrato. Na horizontal os elétrons interagem entre si via um potencial coulombiano.

No estudo deste sistema definimos o parˆametro Γ =_hU_i/_hK_i, sendo_hU_i a m´edia da energia

poten-Figura 1: Rede triangular peri´odica de el´etrons formando um cristal de Wigner bidimensional.

cial de intera¸cão entre elétrons e _hK_i a média da energia cinética [14, 15]. Segundo o critério de Lind-mann [14, 15], para Γ_≪1 os elétrons encontram-se em um regime totalmente desordenado vagando em uma dinâmica randômica pela superf´ıcie do Hélio. Já para Γ_≫1 os elétrons se auto-organizam em um regime cristalino, distribu´ıdos em uma rede trian-gular periódica, como apresentado na Fig. 1. Agora para Γ _≈ 1 temos uma situa¸cão em que os dois regimes coexistem. É interessante observar que Γ é o parâmetro de ordem que determina o surgimento da estrutura de padrão neste sistema.

2.2. Convecção de Rayleigh-Bénard

Na conveçcão de Rayleigh-Bénard temos uma fina camada de óleo que é aquecida lentamente a partir de sua superf´ıcie inferior. Se a diferen¸ca de tempera-tura ∆T =Ti−Ts, da parte inferior e superior da

lˆamina de ´oleo, for menor que um certo valor cr´ıtico

Tc, ent˜ao temos um fluxo de calor homogˆeneo da

parte de baixo do ´oleo para sua superf´ıcie em um processo convectivo normal.

Como ilustrado na Fig. 2, se a diferen¸ca de tempe-ratura ∆T exceder o valor cr´ıtico Tc, agora teremos

uma conveçcão no óleo, que em algumas regiões ocorre da parte inferior do l´ıquido para a superf´ıcie, e em outras regiões da parte superior da lâmina para baixo. Na superf´ıcie da lâmina, veremos a forma¸cão de “telhas” em formato hexagonal por onde circula o óleo. Nestas “telhas” hexagonais, teremos o seguinte comportamento para o fluxo de óleo: no centro do hexágono temos um fluxo que sobe, e nas laterais um fluxo em sentido contrário, que sai da superf´ıcie

Figura 2:Convecção de Rayleigh-Bénard em óleo com

(3)

e vai para a região inferior da lâmina. Esta nova dinâmica convectiva caracteriza o surgimento do que conhecemos como forma¸cão de padrão [1, 2]. Para este sistema é importante observar a existência de um estado inicial estável no qual, alterando um de-terminado parâmetro, que no caso da conveçcão de Rayleigh-Bénard é o valor de ∆T, teremos a perda desta estabilidade espacial favorecendo o surgimento da forma¸cão de padrão.

2.3. Instabilidade do impressor

Este fenômeno é uma instabilidade morfológica de origem hidrodinâmica conhecida como Instabilidade do Impressor [16, 17]. Neste sistema, consideramos um rolo molhado por um l´ıquido que gira com certa velocidade angular ω. Na interface da camada de l´ıquido com o ar do ambiente, forma-se uma região cuja morfologia apresenta forma¸cão de padrão es-pontânea, como observado na Fig. 3, quando a velo-cidade angular do cilindro possui determinado valor cr´ıticoωc, ou um valor acima deste.

2.4. O modelo de Turing

Em 1952, Alan Turing prop˜oe um mecanismo que representa uma grande contribui¸c˜ao para os

estu-Figura 3: Franjas de formação de padrão no experimento da instabilidade do impressor [16]. Painel A, foto das franjas de padrão e painel B aparato experimental utilizado.

dos sobre a morphogeneses [7, 10], o processo no qual um zigoto adquire forma e se torna um em-brião. Turing sugere um modelo de rea¸cão-difusão, onde sob certas condi¸cões, popula¸cões podem inte-ragir e se difundir de alguma maneira produzindo padrões heterogêneos estáveis. No modelo de Tu-ring, os padrões são resultados das taxas de rea¸cão e difusão das substâncias qu´ımicas que estão envol-vidas no processo, não levando em conta nenhum outro mecanismo externo. As equa¸cões do modelo de Turing, são usualmente escritas como

∂U(~r, t)

∂t = DU∇

2_U₍_{~r, t}_{) +}_f₍_{U, V}₎

∂V(~r, t)

∂t = DV∇

2_V₍_{~r, t}_{) +}_g₍_{U, V}₎_. ₍₁₎

Neste conjunto de equa¸cões, U e V representam substâncias qu´ımicas que podem se difundir e reagir. As fun¸cões f e g são os termos de rea¸cão, não-lineares, que são escolhidos de acordo com o sistema.

2.5. Reac¸˜oes de Belouzov-Zhabotinsky

Outro sistema qu´ımico muito famoso é a rea¸cão de Belousov-Zhabotinsky. Neste caso padrões espaciais e temporais surgem de rea¸cões oscilantes onde a concentra¸cão dos reagentes envolvidos oscilam no tempo gerando padrões. Assim como no modelo de Turin este sistema pode ser modelado por um conjunto de equa¸cões de rea¸cão-difusão semelhantes as equa¸cões de dinâmica de popula¸cões de Lotka-Volterra [1].

2.6. Padrões em populações

As popula¸cões também se organizam formando padrões. Um conjunto de bactérias, pássaros, ro-edores, peixes e outros animais, em determinadas condi¸cões também podem exibir padrões espaciais ou temporais [18].

Como bem conhecido na literatura, a sincro-niza¸cão do piscar de vaga-lumes apresenta um padrão temporal, onde estes insetos piscam de forma s´ıncrona para atrair a fêmea da espécie. O fenômeno de sincroniza¸cão também pode ser observado em diapasões ou pêndulos e é bem descrito pelo modelo de fases de Kuramoto.

(4)

Figura 4: Figura de padrão em uma colônia de pássaros disputando espaço para construir seus ninhos. Adaptado de: http://cftc.cii.fc.ul.pt/PRISMA.

a chance de preda¸cão por outros animais. Caso o terreno para seus ninhos fosse infinito, ou mesmo se não existisse intera¸cão entre estes pássaros, não ter´ıamos esta figura de padrão.

Outro exemplo, visualizado na Fig. 5, apresenta os ninhos das Tilápias encontrados no fundo do rio. Elas se agrupam em uma colônia e como cada uma tenta defender seu espa¸co, seus ninhos ficam equidistantes em rela¸cão às vizinhas. Nesta disputa por espa¸co as bordas dos ninhos exibem formatos hexagonais, pentagonais ou quadrados. Observando de longe a colônia de Tilápias exibe uma figura t´ıpica de padrão.

3. Equa¸c˜ao de Fisher-Kolmogorov

Como discutido anteriormente as popula¸cões também se organizam formando padrões espaciais.

Figura 5: Padrão observado em uma colônia de Tilápias. Adaptado de:http://cftc.cii.fc.ul.pt/PRISMA.

Um aspecto importante na dinâmica de popula¸cões para a forma¸cão de padrão é a intera¸cão entre os constituintes deste sistema. Como nos exemplos ci-tados as colônias de popula¸cões em uma competi¸cão por espa¸co e suprimentos podem se organizar exi-bindo estruturas espaciais.

Do ponto de vista da predi¸cão do número ou den-sidade de indiv´ıduos de uma popula¸cão ao longo do tempo e espa¸co, temos vários modelos matemáticos muito bem estabelecidos na literatura. Estes mode-los descrevem muito bem como é o crescimento, com-peti¸cão, difusão, migra¸cão e intera¸cão entre espécies. Diante deste cenário podemos nos questionar: será que podemos modelar a forma¸cão de padrão de uma colônia via uma equa¸cão de dinâmica de popula¸cões? A resposta é sim e nas próximas se¸cões mostraremos que este fenômeno pode ser modelado modificando a forma como ocorre a competi¸cão entre seus cons-tituintes.

3.1. Equação de Fisher-Kolmogorov com interação local

Uma forma geral de descrever a taxa de varia¸cão de uma densidade populacional u(x, t), que pode migrar de uma região para outra, se difundir em um meio, crescer e competir por espa¸co ou recursos é através da equa¸cão de Fisher-Kolmogorov com termo convectivo [21, 22]

∂u(x, t)

∂t = −v

∂u(x, t)

∂x +D

∂2u(x, t)

∂x2

+ au(x, t)₋bu2(x, t). (2)

Nesta equa¸c˜ao a densidade populacional u(x, t) muda no tempo obedecendo os seguintes proces-sos:

i)A popula¸c˜ao pode evoluir em um fluxo migrat´orio com velocidadev dado pelo termo

−v∂u(x, t)

∂x (3)

ii)A medida` que uma popula¸c˜ao cresce a densidade

u(x, t) se difunde no espa¸co com uma taxa D. Este comportamento dos indiv´ıduos de uma colˆonia ´e dado pelo termo

D∂

2_u₍_{x, t}₎

(5)

iii) O processo de crescimento em um contexto malthusiano ocorrem com uma taxa a e s˜ao des-critos pelo termo

au(x, t) (5)

iv) A competi¸cão dos constituintes de um determi-nada popula¸cão, que ocorrem com uma frequência

b, ´e dado pelo termo de Verhust

−bu(x, t)_·u(x, t) (6)

As competi¸cões entre os constituintes de uma po-pula¸cão, no modelo de Fisher-Kolmogorov, Eq. (6), são do tipo local no sentido em que os indiv´ıduos interagem com seus vizinhos apenas quando estão no mesmo ponto, não sendo assim intera¸cões de médio ou longo alcance. Isso se assemelha a uma intera¸cão de caro¸co duro, em que uma part´ıcula apenas percebe a outra quando estão no mesmo ponto do espa¸co. Como neste tipo de intera¸cão os indiv´ıduos não percebem seus vizinhos a uma de-terminada distância esta equa¸cão de dinâmica de popula¸cões não é capaz de descrever a forma¸cão de padrão em uma colônia [23–26].

3.2. Equação de Fisher-Kolmogorov com interação não-local

De acordo com a se¸cão anterior a forma usual da equa¸cão de Fisher-Kolmogorov, Eq. (2), não é ca-paz de descrever a forma¸cão de padrão em sistemas biológicos. Para que isso aconte¸ca, devemos rees-crever o termo de competi¸cão, introduzindo uma não-localidade na intera¸cão entre indiv´ıduos.

Como discutido por vários autores [21, 22, 24–28], uma intera¸cão não-local no termo de competi¸cão

−bu(x, t)_·u(x, t) pode ser escrita considerando a densidadeu(x, t) na posi¸cãox e somando o produto desta com as demais densidades que estão a uma distância β. Isso equivale a dizer que cada indiv´ıduo da colônia vai interagir com todos os vizinhos que se encontram a uma determinada distância β. Para um sistema de tamanho L, devemos substituir a intera¸cão local pela não-local como:

−bu(x, t)_·u(x, t)_{−→ −}bu(x, t)_·

Z

L

fβ(x−x′)u(x′, t)dx′ (7)

Considerando apenas o termo difusivo, a nova equa¸cão com não-localidade é escrita como

∂u(x, t)

∂t = D

∂2u(x, t)

∂x2 +au(x, t) +

− bu(x, t)

Z

L

fβ(x−x′)u(x′, t)dx′.(8)

Esta equa¸cão é conhecida como Equa¸cão de Fisher-Kolmgorov Generalizada (EFKG). Neste formato, os constituintes de uma determinada colônia têm suas intera¸cões pesadas pela fun¸cão fβ(x−x′) que

é uma distribui¸cão chamada “fun¸cão influência”, ca-racterizada pelo alcance β normalizada no dom´ınio

L

Z

L

fβ(x)dx= 1. (9)

Neste modelo cada indiv´ıduo interage com todos seus vizinhos que estão dentro de um determinado raio β e esta intera¸cão é pesada pela fun¸cão in-fluência fβ(x−x′), diferentemente da antiga

for-mula¸cão local em que as competi¸cões se davam em um mesmo pontox. A fun¸cão influência de intera¸cão, pode assumir diversas formas. Podemos utilizar dis-tribui¸cões gaussianas, delta de Dirac, fun¸cões de Heaviside ou mesmo uma distribui¸cão de Laplace. Esta escolha depende do tipo de intera¸cão a ser modelado.

3.3. Limites da função influência

´

E relatado em alguns trabalhos [4, 23–25] e será analisado nesta se¸cão, que a forma¸cão de padrão observada em uma densidade populacional esta-cionáriau(x), para uma dada fun¸cão de distribui¸cão

fβ(x−x′), tem os seguintes comportamentos: i) Se o alcance da intera¸cão competitiva entre os indiv´ıduos for muito curtoβ _→0, isso corresponde a uma fun¸cão de distribui¸cão bem localizada, do tipo delta

fβ(x−x′) =δ(x−x′). (10)

Para esse caso o termo de competi¸c˜ao pode ser escrito como

bu(x, t)

Z

L

δ(x₋x′₎_u₍_x′_{, t}₎_dx′₌_bu2₍_{x, t}₎_. ₍₁₁₎

(6)

ii) A não-localidade deixará de existir para o li-mite oposto, se o alcance da intera¸cão competitiva for grande, β _→ L/2. Para este valor de β, ob-servando as condi¸cões de contorno, as intera¸cões são pesadas e contadas entre ₋L/2 atéL/2 igual-mente para todos os pontos. Neste caso a fun¸cão influência é constante e pode ser retirada para fora da integral e o que resta do termo de intera¸cão é apenas o produto de u(x, t) com uma constante. Com isso a competi¸cão entre termos deixa de exis-tir e novamente não teremos forma¸cão de padrão. Este comportamento pode ser melhor compreendido resolvendo a EFKG numericamente.

iii) Os processos difusivos também têm um pa-pel muito importante na forma¸cão de padrão nos sistemas biológicos, por exemplo em uma colônia de bactérias. Se tivermos uma constante de difusão muito grande, essa dinâmica dominará a competi¸cão entre os indiv´ıduos do sistema, fazendo com que a distribui¸cão inicial de bactérias u(x) se torne rapi-damente homogênea ao longo do espa¸co, não dando tempo para que o sistema se organize em uma es-trutura, não formando assim uma figura de padrão. Como observado nos itens anteriores, a fun¸cão de distribui¸cão fβ(x−x′) deve ter um alcance β

não muito pequeno nem muito grande, para que possamos ter forma¸cão de padrão. Desta forma, fun¸cões adequadas com as caracter´ısticas desejadas, serão, distribui¸cões do tipo gaussianas, Heaviside ou mesmo Laplacianas, desde que obede¸cam os requisi-tos anteriores.

4. An´alise perturbativa na EFKG

Podemos fazer um estudo anal´ıtico na EFKG in-troduzindo uma pequena perturba¸cão na solu¸cão de u(x, t) que não exibe padrão. As solu¸cões que não exibem padrões são homogêneas no espa¸co e constantes, u(x, t) = u0. As solu¸cões que exibem padrões são caracterizado pelo surgimento de on-das com comprimento e frequência bem definidos na solu¸cão de u(x, t). Impondo que u(x, t) = u0 na EFKG teremos u0 = a/b, sendo a a constante de crescimento e b o termo de competi¸cão. Nesta análise perturbativa, devemos imaginar que o es-tado estacionário homogêneo terá uma pequena flu-tua¸cão temporal. Se esta flutua¸cão for amplificada no tempo, a solu¸cão final estacionária será deslocada da solu¸cão homogêneau0 dando origem à forma¸cão de padrão no sistema [4, 25]. Matematicamente este

comportamento pode ser dado por

u(x, t) =u0+εeikxeϕ(k)t. (12)

Nesta equa¸cão,εé a amplitude da perturba¸cão os-cilante considerada muito pequena, ié a unidade imaginária (i2 = ₋1), k é o número de onda no espa¸co de Fourier e ϕ(k) é a quantidade de maior interesse nesta análise, conhecida como taxa de cres-cimento da forma¸cão de padrão, que pode depender do número de onda k. Notamos que se a taxa de crescimento da forma¸cão de padrãoϕ(k) for menor que zero, esta perturba¸cão se extinguirá no tempo, não deslocando a solu¸cão homogênea para um estado de forma¸cão de padrão. Mas se ϕ(k) for maior que zero, alguns modos perturbativos são amplificados, propiciando assim, o surgimento deste fenômeno. Desta forma, nossa análise perturbativa se dará no sentido de verificar em quais condi¸cões os modos de perturba¸cão serão ou não amplificados gerando forma¸cão de padrão, ou seja, estaremos interessados em verificar para quais condi¸cões dos parâmetros da EFKG a taxa ϕ(k) é positiva ou negativa.

Substituindo a Eq. (12) na Eq. (8), desprezando termos de segunda ordem na amplitude deε, intro-duzindo a transforma¸c˜ao de vari´aveis z = x₋x′

e considerando que a fun¸c˜ao influˆencia obedece as seguintes propriedades

fβ(x−x′) =fβ(x′−x) (13)

e _Z

L

fβ(x′)dx′ = 1 (14)

encontramos a seguinte rela¸c˜ao de dispers˜ao

ϕ(k) =₋Dk2₋a_Fc{fβ(z)} −iaFs{fβ(z)}. (15)

Nesta equa¸c˜ao_Fc{fβ(z)}e Fs{fβ(z)}s˜ao as

tran-formadas de Fourier cosseno e seno da fun¸c˜ao in-fluˆenciafβ(z),

Fc{fβ(z)} = Z

L

fβ(z) cos(kz)dz

Fs{fβ(z)} = Z

L

fβ(z) sin(kz)dz. (16)

Observamos que a Eq. (15) ´e composta por uma parte real e uma parte imagin´aria

γ(k) =_Re_{ϕ(k)_}=₋Dk2₋a_Fc{fβ(z)} (17)

e

(7)

A evolu¸c˜ao temporal da densidade populacional

u(x, t) ´e observada no espa¸co real. Podemos verificar como esta evolu¸c˜ao temporal ocorre pela Eq. (12), tomando apenas sua parte real

u(x, t) = a

b +εcos(kx)e

γt_. ₍₁₉₎

Com isso devemos impor que nossa taxa de forma¸cão de padrão seja real. Observado esse detalhe, sempre restringiremos nossa análise à parte real da fun¸cão

ϕ(k) que denotamos por γ(k),

γ(k) =₋Dk2₋a Z

L

fβ(z) cos(kz)dz. (20)

Como estamos interessados em verificar em que con-junto de valores dos parâmetros da Eq. (8) a taxa de forma¸cão de padrão é positiva, devemos escolher uma fun¸cão influência para realizar a transformada de Fourier e encontrarγ(k). Podemos come¸car nosso estudo anal´ıtico escolhendo a distribui¸cão mais sim-ples, que é uma distribui¸cão de Heaviside,

fβ(z) =

1

2β[Θ (β−z) Θ (β+z)]. (21)

Nesta equa¸cão, β é o alcance da fun¸cão influência, que é normalizada no dom´ınioLdo sistema (0< β < L). Resolvendo a integral da Eq. (20), para a fun¸cão influência de Heaviside, Eq. (21), encontramos a seguinte expressão para a taxa real γ(k)

γ(k) =₋Dk2₋asin(kβ)

kβ . (22)

Na Fig. 6 mostramos como é o comportamento da taxa de crescimento da forma¸cão de padrãoγ(k) para alguns valores da constante de difusãoD. Nota-mos que para valores pequenos da difuão,D= 0.001,

γ(k) apresenta regiões positivas, mas para valores maiores, D = 1.0, este comportamento deixa de existir. Isso é fisicamente aceitável uma vez que os processos difusivos tendem a levar um determinado sistema a um regime espacialmente homogêneo e isotrópico, ou seja, impossibilitando que determi-nadas regiões sejam privilegiadas, o que poderia caracterizar o fenômeno forma¸cão de padrão.

5. Solu¸c˜ao num´erica da EFKG

Considere a EFKG com difus˜ao em uma dimens˜ao

∂u(x, t)

∂t = D

∂2u(x, t)

∂x2 +au(x, t) +

− bu(x, t)

Z

L

fβ(x−x′)u(x′, t)dx′(23).

Figura 6: Taxa de crescimento da formação de padrão

γ(k), para uma função influêcia Heaviside. A constante de crescimento vale a = 3.0 e o comprimento de interação

β= 4.0. Neste gráfico a medida que a constante de difusão aumenta, a taxaγ(k)deixa de ter valores positivos. Esta equa¸cão pode ser resolvida utilizando um método numérico apropriado, para uma determi-nada fun¸cão influênciafβ(x−x′), uma distribui¸cão

inicial u(x, t= 0) e condi¸cões de contorno definidas. Para um sistema de tamanho L, podemos ter di-versos tipos de distribui¸cões iniciaisu(x) para nossa popula¸cão. Podemos considerar uma distribui¸cão constante em todos os pontos,u(x) =cte, ou mesmo um único ponto da distribui¸cão diferente de zero,

u(x₋x0) = δ(x−x0). Considerando uma distri-bui¸c˜ao de indiv´ıduos tipo gaussiana, teremos

u(x) = Γ exp

"

−(x−x0)

2

2σ2

#

. (24)

Nesta equa¸cão Γ é um fator de normaliza¸cão, x0 é o ponto onde a distribui¸cão está centrada e σ é a dispersão da distribui¸cão. Impondo que u(x) seja normalizada no intervalo [0, L], o fator de norma-liza¸cão Γ será dado por

1 Γ =

q π/2σ

erf

_x

0

√

2σ

−erf

_x

0−L

√

2σ

. (25)

A fun¸cão influência escolhida é uma distribui¸cão, também gaussiana, dada por

fβ(x−x′) = Λ exp "

−(x−x

′₎2

2β2

#

. (26)

Considerando condi¸c˜oes de contorno peri´odicas

u(0, t) = u(L, t), a normaliza¸c˜ao de fβ(x−x′) ´e

constante e ´e dada por

1 Λ =

q

π/2β erf √L

2β !

(8)

Para resolver a EFKG numericamente, conside-ramos um sistema de tamanho L = 1.0 e aplica-mos condi¸c˜oes de contorno peri´odicasu(x= 0, t) =

u(x = L, t). Em cada evolu¸cão temporal usamos uma distribui¸cão gaussiana de part´ıculas, Eq. (24), centrada em x0 = 0.5, com dispersão σ = 0.04. Em todos os cálculos usamos os incrementos espa-ciais e temporais ∆x e ∆t iguais a ∆x= 3_×10−3 e ∆t = 1_×10−3_{. A evolu¸cão temporal de} _u₍_{x, t}₎

é feita até t = 180 e os estados estacionários são encontrados utilizando a condi¸cão:

|u(x, t+ ∆t)₋u(x, t)_|< δ, (28)

com δ= 1_×10−12_.

Na Fig. 7, apresentamos a solu¸cãou(x, t) com as intera¸cões pesadas por uma fun¸cão gaussiana, com

β = 0.01 (A), β = 0.15 (B) e uma taxa de difus˜ao

D = 1_×10−4_{, em unidades arbitr´}_{arias. Nesta} fi-gura podemos observar como ocorre a forma¸cão de padrão de uma distribui¸cão gaussiana de part´ıculas.

Figura 7: Solução numérica da EFKG para uma função in-fluência gaussiana. No painel A o comprimento de interação valeβ = 0.01 e no painel B,β = 0.15. O coeficiente de difusão em ambos os casos valeD= 1×10−4.

No primeiro gráfico (A) as intera¸cões são pesadas igualmente e o efeito não-local não se manifesta. Quandoβ = 0.15 os efeitos não-locais se fazem pre-sentes na dinâmica do sistema, que se organiza em estruturas periódicas bem definidas. Na Fig 7 (B), para t = 0 as part´ıculas estão mais concentradas no centro do sistema, mas para tempos maiores,

t= 180, o sistema apresenta uma distribui¸cão osci-lante no espa¸co, caracterizando uma estrutura de forma¸cão de padrão.

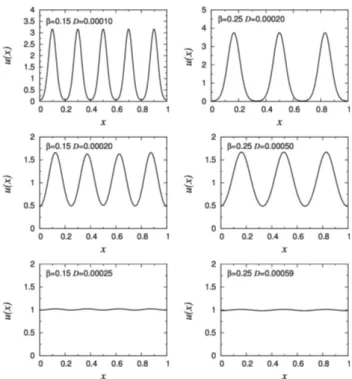
Os estados estacionários u(x) são mostrados na Fig. 8, para β= 0.15 eβ = 0.25 e vários valores do coeficiente de difusãoD. Nestes gráficos, podemos verificar a influência da difusão nas estruturas de forma¸cão de padrão. Fixando β = 0.15, para va-lores pequenos da difusão os estados estacionários apresentam padrão. Mas quando elevamos o coefici-ente de difusão, notamos que para D= 2.5_×10−4

os picos de padrão já se tornam negligenciáveis. O mesmo comportamento ocorre para β = 0.25, onde notamos que as estruturas bem definidas de forma¸cão de padrão são completamente amortecidas paraD= 5.9_×10−4_{. Este comportamento ilustra} bem a relevância dos processos difusivos em sistemas

(9)

biológicos, que vem sendo intensamente estudados nos últimos anos por vários autores.

6. Conclus˜ao

No presente texto realizamos uma revisão dos aspec-tos principais envolvidos no surgimento do fenômeno forma¸cão de padrão, do ponto de vista da dinâmica de popula¸cões. Apresentamos vários exemplos de sistemas f´ısicos, qu´ımicos e biológicos que apresen-tam auto-organiza¸cão seguindo dos padrões, ou mesmo sistemas que exibem padrões sem auto-organiza¸cão. Verificamos que para cada sistema exis-tem parâmetros espec´ıficos que governam o surgi-mento dos padrões. Para uma popula¸cão o aspecto central na forma¸cão dos padrões são o espa¸co onde está confinado a popula¸cão e principalmente as in-tera¸cões. Mostramos que para modelar matemati-camente este fenômeno, é necessário modificar a equa¸cão de Fisher-Kolmogorov, que é um modelo dinâmico geral, e introduzir um termo não-local nas intera¸cões. Apresentamos um estudo anal´ıtico perturbativo e também solucionamos a EFKG nume-ricamente e mostramos como os processos difusivos influenciam a forma¸cão de padrões e a importância da não-localidade nas intera¸cões na descri¸cão deste fenômeno.

Referˆencias

[1] M.C. Cross and P.C. Hohenberg, Rev. Mod. Phys. 65, 851 (1993).

[2] P. Berge and M. Dubois, Phys. Rev. Lett.32, 1041 (1974).

[3] D. Binks and W. van de Water, Phys. Rev. Lett. 78, 4043 (1997).

[4] M.G. Clerc, D. Escaff and V.M. Kenkre, Phys. Rev. E72, 056217 (2005).

[5] B. Legawiec and A.L. Kawczynski, J. Phys. Chem. A101, 8063 (1997).

[6] P.C. Fife, J. Chem. Phys.64, 554 (1976).

[7] T. Leppanen, M. Karttunen, R.A. Barrio and K. Kaski, Braz. J. Phys.34, 368 (2004).

[8] S. Genieys, V. Volpert and P. Auger, Mathematical Modelling of Natural Phenomena1, 65 (2006). [9] K.A. Dahmen, D.R. Nelson and N.M. Shnerb,

Jour-nal of Mathematical Biology41, 1 (2000).

[10] T. Leppanen, M. Kartunen, K. Kaski, R. Barrio and L. Zhang, Phys. D168, 35 (2002).

[11] R. Hoyle, Pattern Formation an Introduction to Methods (Cambridge University Press New York, 2006).

[12] E. Ben-Jacob, G. Deutscher, P. Garik, N.D. Gol-denfeld and Y. Lareah, Phys. Rev. Lett. 57, 1903 (1986).

[13] E. Ben-Jacob, O. Schochet, A. Tenenbaum, I. Cohen, A. Czir´ok and T. Vicsek, Nature368, 46 (1994). [14] J.A.R da Cunha and L. Cˆandido, Phys. Rev. B71,

1 (2005).

[15] J.A.R. da Cunha and L. Cˆandido, Braz. J. Phys. 36, 682 (2006).

[16] H.Z. Cummins, L. Fourtune and M. Rabaud, Phys. Rev. E47, 1727 (1993).

[17] R.L. Santos, U. Agero and J.M.A. Figueiredo, Phys. Rev. E77, 66310 (2008).

[18] J.D. Murray,Mathematical Biology I: An Introduc-tion (Springer-Verlag Berlin Heidelberg, 2002). [19] E.P. Odum,Systems Ecology. An Introduction (Jon

Wiley and Sons, New York, 1983).

[20] E.P. Odum, Fundamentos de Ecologia (Funda¸c˜ao Calouste Gulbenkian, Lisboa, 1988), 6ª ed.

[21] J.A.R. da Cunha, G.R. Resende, A.L.A. Penna, R. Morgado and F.A. Oliveira, Act. Phys. Pol. B 40, 1473 (2009).

[22] J.A.R. Cunha, A.L.A. Penna, M.H. Vainstein, R. Morgado and F.A. Oliveira, Phys. Lett. A 373, 661 (2009).

[23] M.A. Fuentes, M.N. Kuperman and V.M. Kenkre, Phys. Rev. Lett. 15, 91 (2003).

[24] V.M. Kenkre, Phys. A242, 342 (2004).

[25] M.A. Fuentes, M.N. Kuperman and V.M. Kenkre, J. Phys. Chem. B108, 10505 (2004).

[26] S. Gourley, J. Math. Biol.41, 272 (2000).

[27] J. A.R. Cunha, A.L. A. Penna and F.A. Oliveira, Phys. Rev. E83, 015201 (2011).