Percolação convencional, percolação correlacionada e percolação por invasão num suporte multifractal

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIˆENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE FÍSICA TE ÓRICA E EXPERIMENTAL PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

PERCOLAC

¸ ˜

AO CONVENCIONAL, PERCOLAC

¸ ˆ

AO

CORRELACIONADA E PERCOLAC

¸ ˜

AO POR

INVAS ˜

AO NUM SUPORTE MULTIFRACTAL

DARLAN ARA ´UJO MOREIRA

Orientador: Prof. Dr. LIACIR DOS SANTOS LUCENA

Co-orientador: Prof. Dr. GILBERTO CORSO

Disserta¸cão de mestrado apresentada ao Departamento de F´ısica Teórica e Experimental da Universidade Federal do Rio Grande do Norte como requisito parcial à obten¸cão do grau de MESTRE em FÍSICA.

(2)

(3)

Agradecimentos

Agrade¸co aos meus pais e `a minha querida Juliana.

Agrade¸co ao Prof. Liacir dos Santos Lucena por ter aceitado ser meu orientador e por me incentivar bastante.

Ao Prof. Gilberto Corso por seus coment´arios precisos e valiosos sobre a pesquisa e a disserta¸c˜ao.

Ao Prof. Joaquim Elias e ao Prof. Roosewelt Soares por me ajudarem a com-preender melhor alguns aspectos deste trabalho.

Ao amigo Antˆonio Soares pela ajuda com alguns recursos materiais. Aos companheiros de curso pelas horas de convivˆencia.

Aos funcionários do Departamento de F´ısica que são pessoas muito prestativas, em especial a Celina, que é uma funcionária muito dedicada.

`

(4)

Resumo

Nesta disserta¸cão estudamos o problema da percola¸cão num suporte geométrico mul-tifractal, em suas diferentes versões, e analisamos a conexão deste problema com a per-cola¸cão convencional e com o formalismo dos fenômenos cr´ıticos.

(5)

Abstract

In this work we have studied the problem of percolation in a multifractal geome-tric support, in its diﬀerent versions, and we have analysed the conection between this problem and the standard percolation and also the connection with the critical phenomena formalism.

(6)

´Indice

AGRADECIMENTOS

i

RESUMO

ii

ABSTRACT

iii

INTRODUC

¸ ˜

AO

1

FRACTAIS

4

1.1

Introdu¸c˜ao

. . . 4

1.2

Defini¸c˜ao e Propriedades

. . . 4

1.2.1

Defini¸c˜ao

. . . 4

1.2.2

Ausˆencia de Escala T´ıpica

. . . 5

1.2.3

Auto-Similaridade

. . . 6

1.2.4

Dimens˜ao e Dimens˜ao Fractal

. . . 9

1.2.5

Auto-Afinidade

. . . 11

1.3

Categorias de Fractais

. . . 12

1.3.1

Fractais Determin´ısticos

. . . 12

1.3.2

Fractais Aleat´orios

. . . 24

1.4

Dimens˜ao Fractal

. . . 27

1.4.1

Dimens˜ao Topol´ogica

. . . 28

1.4.2

Dimens˜ao de Minkowski-Bouligand

. . . 29

1.4.3

Dimens˜ao de Hausdorﬀ-Besicovitch

. . . 31

(7)

1.5.1

Introdu¸c˜ao

. . . 32

1.5.2

Arvore Bronquial

´

. . . 33

1.5.3

Membranas Celulares

. . . 33

1.5.4

Movimento Browniano

. . . 33

2

O MULTIFRACTAL

35 2.1

Introdu¸c˜ao

. . . 35

2.2

O Conjunto Multifractal

Q

mf . . . 35

2.3

Distribui¸c˜ao de ´

Areas

. . . 37

2.4

Espectro Multifractal do Objeto

Q

mf . . . 38

2.5

Densidade dos monofractais de

Q

mf . . . 42

3

PERCOLAC

¸ ˜

AO

45 3.1

Introdu¸c˜ao

. . . 45

3.2

Percola¸c˜ao por S´ıtios

. . . 46

3.2.1

Conceito

. . . 46

3.2.2

Fenˆomenos Liminares, Leis de Escala e Universalidade

. 47 3.2.3

Algoritmos para Determina¸c˜ao de

p

c

.

. . . 50

3.3

Percola¸c˜ao por Liga¸c˜ao

. . . 53

3.4

Percola¸c˜ao em Outras Redes

. . . 53

3.5

Propriedades Estruturais

. . . 54

3.5.1

Dimens˜ao Fractal do Aglomerado Percolante

. . . 54

3.5.2

Distˆancia M´ınima e Dimens˜ao Qu´ımica

. . . 56

3.5.3

Sub-estruturas fractais

. . . 57

3.6

Percola¸c˜ao por Invas˜ao

. . . 59

3.6.1

A Fenomenologia

. . . 59

3.6.2

O Modelo

. . . 59

3.6.3

Variantes da Percola¸c˜ao Invasiva

. . . 60

(8)

4

PERCOLAC

¸ ˜

AO NO MULTIFRACTAL

63

4.1

Introdu¸c˜ao

. . . 63

4.2

As Redes

. . . 63

4.3

Escalonamento de Sistemas de Tamanho Finito

. . . 65

4.4

Percola¸c˜ao Convencional na

Rede N˜

ao Regular

. . . 69

4.5

Percola¸c˜ao na

Rede Correlacionada

. . . 75

4.6

Percola¸c˜ao por Invas˜ao

. . . 78

CONCLUS ˜

OES

80 A

CRIANDO FRACTAIS

82 A.1

Criando Fractais Utilizando Recursividade

. . . 82

A.1.1

Conjunto de Cantor

. . . 82

A.1.2

Curva de Koch

. . . 83

A.1.3

Triˆangulo de Sierpinski

. . . 83

A.1.4

Curva Drag˜ao

. . . 84

A.1.5

Deslocamento do Ponto M´edio

. . . 85

A.1.6

Superf´ıcie Fractal

. . . 86

A.1.7

Um Fractal Auto-Afim

. . . 88

(9)

Lista de Figuras

1.1 Seqüência de transforma¸cões de similaridade sobre um triângulo P1P2P3. (a) O objeto, (b) após uma mudan¸ca de escala, (c) objeto anterior após uma rota¸cão (eixo de rota¸cão na origem) e (d) objeto anterior após uma

transla¸c˜ao. . . 8

1.2 Aplica¸cão de uma mudan¸ca de escala a uma região do fractal de Sierpinski. A parte que sofreu a mudan¸ca de escala é idêntica ao todo. . . 8

1.3 Aplica¸cão de uma mudan¸ca de escala a uma região do fractal de Sierpinski. A parte ampliada não foi detalhada durante o processo de constru¸cão e, portanto, o objeto deixa de ser auto-similar nesta escala. . . 9

1.4 Exemplos de objetos com dimens˜oesd= 1, d= 2 e d= 3. . . 10

1.5 Parte de um triângulo de Sierpinski utilizado no cálculo da dimensão fractal. 11 1.6 Uma transforma¸cão de afinidade aplicada a um c´ırculo. . . 12

1.7 Um fractal auto-afim. . . 12

1.8 Cinco primeiros passos da cria¸c˜ao de um conjunto de Cantor. . . 13

1.9 Cinco primeiros passos da cria¸c˜ao de uma curva de Koch. . . 15

1.10 Os quatro primeiros passos da cria¸c˜ao de um floco de neve de Koch. . . 16

1.11 Os quatro primeiros passos da cria¸cão do inverso do floco de neve de Koch. 18 1.12 Os quatro primeiros passos da cria¸cão de uma curva dragão. . . 19

1.13 N´ıveis 10 e 14 da cria¸c˜ao de uma curva drag˜ao. . . 19

1.14 Os três primeiros passos da cria¸cão de um triângulo de Sierpinski. . . 20

(10)

1.16 Conjuntos de Julia preenchidos obtidos com a fun¸c˜ao f(z) = z2₊_c _para

c =₋1 e c= 0.6i. . . 23

1.17 Fractal de Mandelbrot para f(z) =z2₊_c_{. . . 24}

1.18 Figura obtida atrav´es de DLA. . . 25

1.19 Dois primeiros passos da cria¸cão de uma curva através da técnica de deslo-camento do ponto médio. Linha tracejada: passo anterior. Linha pontil-hada: δym. . . 27

1.20 A Direita` : Curva criada através da técnica de deslocamento do ponto médio para n = 6. A Esquerda: Utiliza¸cão da curva para a cria¸cão do perfil de` uma montanha. . . 27

1.21 Um superf´ıcie fractal produzida por uma algoritmo semelhante ao do deslo-camento do ponto m´edio vista de duas posi¸c˜oes diferentes. . . 28

1.22 Caixas fechadas de lado ₂1n cobrindo um quadrado de lado 1. Na figura n = 2. . . 30

2.1 Dois primeiros passos da cria¸c˜ao do conjuntoQmf com ρ= _rs = 2₃. . . 37

2.2 Passos 2, 3 e 4 da cria¸c˜ao do conjunto Qmf com ρ= s_r = 2₃. . . 37

2.3 ObjetoQmf constru´ıdo at´e o n´ıvel n= 10 paraρ= 1₂. . . 40

2.4 Dois objetos Qmf para n = 10 e ρ = 1₂. A esquerda:` em destaque o subconjunto k= 3. A direita:` em destaque o subconjunto k= 5. . . 41

2.5 ObjetoQmf constru´ıdo at´e o n´ıvel n= 10 paraρ= 2₃. . . 41

2.6 Dois objetos Qmf para n = 10 e ρ = 2₃. A esquerda:` em destaque o subconjunto k= 3. A direita:` em destaque o subconjunto k= 5. . . 42

2.7 Espectro multifractal deQmf para n= 1000 e (s, r) = (1,2) . . . 42

2.8 Espectro multifractal deQmf para n= 1000 e (s, r) = (2,3) . . . 43

2.9 Espectros de objetosQmf para diversos (s, r). . . 43

(11)

3.2 Esquema ilustrativo de um sistema artificial para o qual o modelo de per-cola¸cão se aplica. S´ıtios pretos, células condutoras, s´ıtios brancos, células isolantes. . . 47 3.3 Exemplos de s´ıtios ocupados para rede 64_×64 e p = 0.59. Aglomerado

percolante est´a em verde. . . 48 3.4 CurvasRL×ppara diversos tamanhosLde sistema. Quanto maior o valor

de L mais a curva se aproxima da fun¸cão escada de Heavyside. . . 49 3.5 Algoritmo Fogo na Floresta aplicada a uma rede 5×5 comp= 0.4. . . 51 3.6 Curva do tempo de propaga¸cão como uma fun¸cão deppara uma rede 64_×64. 51 3.7 Ilustra¸cão do método de Hoshen-Kopelman . . . 52 3.8 Exemplos de rede 30_×30 de liga¸cões. A direita:` p = 0.5. A esquerda:`

p= 0.2 . . . 53 3.9 Exemplos de outros tipos de rede. A esquerda: rede triangular.` A direita:`

rede hexagonal (colméia). . . 54 3.10 Ilustra¸cão da aplica¸cão do algoritmo de queima. . . 57 3.11 Menor caminho entre dois s´ıtios de uma rede 64_×64. . . 57 3.12 Modelagem de um meio poroso. A direita: Representa¸cão idealizada de`

um meio poroso. Cada poro é conectado por gargantas estreitas a outros quatro vizinhos. A esquerda: Modelo representativo do meio poroso.` . . . 60 3.13 Quatro primeiros passos de um invasão . . . 61 4.1 A esquerda: Objeto` Qmf constru´ıdo com os parâmetros n = 6, r = 2 e

s= 1. A direita:` Rede não regularproveniente da rela¸cão de vizinhan¸ca entre os retângulos de Qmf. Cada c´ırculo preto é um s´ıtio oriundo de um retângulo (de seu centro) conforme descrito no texto. . . 64 4.2 A esquerda: Objeto` Qmf constru´ıdo com os parâmetros n = 4, r = 3 e

(12)

4.3 Colapso de dados deRL para dados expostos na Fig. (3.4). Rede quadrada 64_×64. Os parˆametros cr´ıticos estimados foram pc = 0.5933±0.0005 e

ν = 1.33±0.02 . . . 70 4.4 Colapso de dados de P_∞ para um multifractal criado com ρ = s/r = 1.

Os valores estimados foram pc = 0.5932±0.0001, β = 0.139±0.002 e

ν = 1.34±0.02 . . . 71 4.5 Colapso de dados deP_∞na dire¸c˜ao vertical para arede n˜ao regularcriada

com ρ = s/r = 1/2. Os valores estimados foram pc = 0.5258±0.0001,

β = 0.145_±0.002 e ν = 1.35_±0.02 . . . 72 4.6 Colapso de dados de P_∞ na dire¸c˜ao horizontal para a rede n˜ao regular

criada com ρ = s/r = 1/2. Os valores estimados foram pc = 0.5257± 0.0001,β = 0.148_±0.002 e ν = 1.42_±0.02 . . . 74 4.7 Colapso de dados deP_∞na dire¸c˜ao vertical para arede n˜ao regularcriada

com ρ = s/r = 1/5. Os valores estimados foram pc = 0.5250±0.0001,

β = 0.177±0.001 e ν = 1.48±0.02 . . . 74 4.8 Colapso de dados de P_∞ na dire¸c˜ao horizontal para a rede n˜ao regular

(13)

Lista de Tabelas

3.1 Valores depc da percola¸c˜ao por s´ıtio para diversos tipos de redes regulares. 55 3.2 Dimens˜oes fractais associadas com sub-estruturas[20] pertencentes ao

aglomerado percolante. . . 58 4.1 Parˆametros cr´ıticos calculados para diversos valores ρ = s/r. Eles foram

obtidos a partir do colapso de curvas atrav´es da rela¸c˜ao de escala para P_∞

na dire¸cão vertical na rede não regular. . . 73 4.2 Parâmetros cr´ıticos calculados para diversos valores ρ = s/r. Eles foram

na dire¸cão horizontal na rede não regular. . . 73 4.3 Parâmetros cr´ıticos calculados para diversos valores ρ = s/r. Eles foram

na dire¸c˜ao vertical na rede correlacionada. . . 76 4.4 Parˆametros cr´ıticos calculados para diversos valores ρ = s/r. Eles foram

na dire¸cão horizontal na rede correlacionada. . . 77 4.5 Dimensão fractal calculada para percola¸cão narede correlacionadapara

diversos valores ρ=s/r. Eles foram obtidos da rela¸cão M(L)∝Ldf, onde M(L) é a área do aglomerado percolante pertencente a uma rede de lado L. 77 4.6 Dimensão fractal do aglomerado obtido através de percola¸cão por invasão

narede correlacionadapara diversos valoresρ=s/r. Eles foram obtidos da rela¸cão M(L) _∝ Ldf, onde M(L) é a área do aglomerado percolante

(14)

Introdu¸

c˜

ao

A descri¸cão de objetos naturais através da geometria é uma técnica tão velha quanto a própria geometria. Tradicionalmente isto envolve o uso de linhas euclidianas, retângulos, cubos, esferas e tudo o mais. Mas a natureza não é restrita as formas euclidianas. Há um pouco mais de 20 anos Benoit B. Mandelbrot[1] observou:

Nuvens não são esferas, montanhas não são cones, as linhas costeiras dos pa´ıses não são c´ırculos, as cascas das árvores não são polidas, nem o raio viaja em linha reta.

(15)

Os fractais serão alvo do primeiro cap´ıtulo desta disserta¸cão. Nele discutiremos sua defini¸cão formal, alguns conceitos subjacentes que ajudarão a compreende-los melhor, alguns métodos de constru¸cão ricamente exemplificados, algumas defini¸cões de dimensão fractal e exemplos de onde podemos encontrar fractais na natureza.

Com a cria¸cão em 1982 por Mandelbrot desta nova área do conhecimento, muitos conjuntos matemáticos tidos como estranhos (e não estudados pelos matemáticos por este fato) e objetos naturais foram caracterizados e estudados como fractais. O estudo na área aprofundou-se de tal forma que foram descobertos outros objetos naturais e conjuntos matemáticos que não se poderiam caracterizar como apenas um fractal e sim como a união de muitos fractais. A estes deram o nome de multifractais.

No segundo cap´ıtulo desta disserta¸cão vamos descrever um objeto multifractal proposto por G. Corso e colaboradores[3]. Nele nós apresentaremos detalhes da con-stru¸cão e das propriedades deste objeto. As rela¸cões de vizinhan¸ca existentes entre os elementos deste multifractal serão utilizadas para o estabelecimento de duas redes que serão utilizadas para estudos de percola¸cão no cap´ıtulo quatro.

(16)

A percola¸cão será o assunto do terceiro cap´ıtulo. Nele descreveremos seus con-ceitos, discutiremos os tipos de percola¸cão existentes e suas conexões com a teoria dos fractais. Nele ainda apresentaremos alguns algoritmos que são utilizados para estudos no assunto.

No quarto cap´ıtulo relatamos os resultados da aplica¸cão de conceitos de percola¸cão ao multifractal de Corso. Alguns dos resultados foram obtidos através da aplica¸cão de uma técnica conhecida porescalonamento de sistemas de tamanhos finitos à dados prove-nientes de simula¸cões numéricas. Neste cap´ıtulo apresentamos ainda análises dos resulta-dos obtiresulta-dos.

Percola¸cão é um assunto que tem ajudado a unifica¸cão de um novo campo do conhecimento intitulado Sistemas Complexos. É bem verdade que este campo tem surgido do englobamento do conhecimento de várias áreas, mas é só das ciências ditas exatas que ele tem se desenvolvido de um ponto de vista quantitativo.

(17)

CAP´ITULO 1

FRACTAIS

1.1 Introdu¸

c˜

ao

Nas últimas décadas, uma ampla faixa de estruturas complexas de interesse de cien-tistas, médicos e engenheiros tem sido quantitativamente descrita utilizando-se da idéia de uma dimensão fractal: uma dimensão que caracteriza de uma maneira única a forma geométrica em estudo. Essa dimensão está associada à simetria que o objeto exibe quando sofre mudan¸cas de escala: ele sempre parece o mesmo.

O conceito de dimensão fractal ajudou a explicar muitas coisas que eram conside-radas mistérios matemáticos. Um simples exemplo foi a explica¸cão do motivo pelo qual o comprimento da costa de um pa´ıs depende da régua utilizada. Isto deve-se ao fato da costa ser um fractal.

Neste cap´ıtulo discorreremos sobre os fractais, suas propriedades, métodos de constru¸cão e cálculo de sua dimensão. Daremos vários exemplos de fractais e da maneira particular como cada um é criado. Encerraremos com a apresenta¸cão de alguns exemplos de fractais encontrados na natureza.

1.2 Defini¸c˜

ao e Propriedades

1.2.1 Defini¸

c˜

ao

(18)

por Benoit Mandelbrot em 1975 e tem origem na palavra latinafractusque significa que-brado. A defini¸cão formal para fractal, que foi criada por Mandelbrot[1], não pode ser entendida sem que haja compreensão da no¸cão de dimensão:

Um fractal é, por defini¸cão, um conjunto para o qual a dimensão de Hausdorff-Besicovitch (ver se¸cão 1.4.3) excede, estritamente, a dimensão topológica (ver se¸cão 1.4.1).

Conjuntos fractais exibem propriedades interessantes e intrigantes, o que lhes ren-deu durante muitos anos a alcunha de objetos monstros. A principal propriedade res-ponsável por isso é a de que alguns fractais são cont´ınuos em todos os pontos e nenhum destes pontos possui derivada. As propriedades aceitas como sendo gerais aos fractais são a ausência de escala t´ıpica, auto-similaridade (que é a responsável pela ausência de escala) e dimensão fractal. Há outras propriedades, que podem estar ou não presentes nos fractais, como por exemplo, auto-afinidade. Trataremos destas quatro propriedades em seguida.

1.2.2 Ausˆ

encia de Escala T´ıpica

A escala caracter´ıstica para medidas no corpo humano é o cent´ımetro. Como exem-plo, podemos citar a estatura média do brasileiro, que é 170 cm. A escala caracter´ıstica para as distâncias interestaduais é o quilômetro. A distância Natal-Fortaleza é de aprox-imadamente 540 km. A distância Natal-Maceió é de aproxaprox-imadamente 570 km. Existem objetos que não possuem uma escala t´ıpica, ou seja, é poss´ıvel encontrar medidas de seus componentes em todas as escalas. Os conjuntos fractais exibem esta propriedade. A costa de um pa´ıs é um exemplo de conjunto sem escala t´ıpica.

Lewis Fry Richardson era um pacifista e matemático que tentou calcular a probabi-lidade de dois pa´ıses entrarem em guerra como fun¸cão do comprimento de suas fronteiras. Em 1961 ele relatou que se deparou com o problema de que as medidas dos comprimentos das fronteiras mudavam de acordo com a escala adotada. Richardson conseguiu encontrar uma rela¸cão matemática que expressaria a forma como a medida mudaria. A rela¸cão era

(19)

onde F é um prefator constante e positivo, D é uma segunda constante, no m´ınimo, igual a unidade, Lé comprimento da fronteira e G o tamanho da “régua” adotada. Nas próprias palavras de Richardson, oDé uma “caracter´ıstica” da fronteira e pode-se esperar ter alguma correla¸cão positiva com uma imediata percep¸cão visual da irregularidade da fronteira. Richardson calculou os seguintes valores para D: D = 1.14 para a fronteira entre Portugal e Espanha, D = 1.15 para a fronteira terrestre da Alemanha, D = 1.13 para a costa Australiana. Mandelbrot cita este trabalho no seu artigo intitulado Quão longa é a costa britânica? [8] no qual chegou à conclusão de que o D calculado por Richardson é, na verdade, a dimensão de similaridade daquelas curvas.

1.2.3 Auto-Similaridade

(20)

nas dire¸cões horizontais e verticais, mesmo os segmentos de linhas curvas serão ampli-ados pelo mesmo fator. Este fator é chamado fator de escala. A transforma¸cão entre os objetos é chamada transforma¸cão de similaridade. Essencialmente, transforma¸cões de similaridade são composi¸cões envolvendo uma mudan¸ca de escala, uma rota¸cão e/ou uma transla¸cão. Outras opera¸cões são evetualmente utilizadas, como por exemplo, a reflexão. As três primeiras transforma¸cões de similaridade citadas neste parágrafo podem ser rep-resentadas como se segue. Considere-se um objeto especificado pelas linhas que ligam em seqüência os três pontos P1 = (x1, y1), P2 = (x2, y2) e P3 = (x3, y3). Uma opera¸cão de mudan¸ca de escalaS :_ℜ2 _{→ ℜ}2 _{se aplica a cada ponto individualmente:}

P′

i =S(Pi) (1.2)

x′

i= sxi (1.3)

y′

i =syi, (1.4)

ondesé o fator de escala associado com a opera¸cão de mudan¸ca de escalaS,s >1 dá uma amplia¸cão. s <1 dá uma redu¸cão. Uma rota¸cão aplicada aP′

i = (x′i, yi′) d´aPi′′= (x′′i, yi′′).

P′′

i =R(Pi′) (1.5)

x′′

i =x′icos(θ)−y′isen(θ) (1.6)

y′′

i =x′isen(θ) +y′icos(θ) (1.7) Isto descreve uma rota¸c˜ao R : ℜ2 _{→ ℜ}2 _{no sentido anti-hor´ario de} _P′

i em torno da origem do sistema de coordenadas por um ˆangulo θ. Uma transla¸c˜ao T : _ℜ2 _{→ ℜ}2 _de

P′′

i = (x′′i, yi′′) por um deslocamento (Tx, Ty) ´e definida por

P′′′

i =T(Pi′′) (1.8)

x′′′

i =x′′i +Tx (1.9)

y′′′

i =y′′i +Ty, (1.10)

o que d´a como resultado o pontoP′′′

(21)

Figura 1.1: Seqüência de transforma¸cões de similaridade sobre um triângulo P1P2P3. (a) O objeto, (b) após uma mudan¸ca de escala, (c) objeto anterior após uma rota¸cão (eixo de

rota¸cão na origem) e (d) objeto anterior após uma transla¸cão.

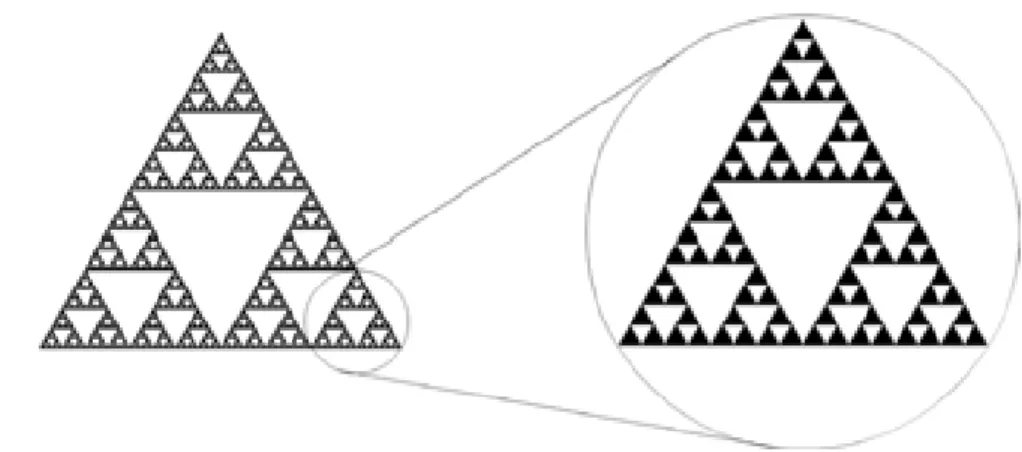
Dado o parágrafo anterior pode-se concluir que auto-similaridade é a propriedade que alguns objetos possuem de, após sofrerem transforma¸cões de similaridade, manterem a forma original, ou, em outras palavras, o objeto parece o mesmo após sofrer tais trans-forma¸cões. Um exemplo de uma estrutura auto-similar é o triângulo de Sierpinski (Fig. (1.2)). Aplicando-se uma mudan¸ca de escala a uma região do fractal, observa-se que essa região é idêntica ao todo. Note que a auto-similaridade existe considerando-se a

Figura 1.2: Aplica¸c˜ao de uma mudan¸ca de escala a uma regi˜ao do fractal de Sierpinski. A

parte que sofreu a mudan¸ca de escala ´e idˆentica ao todo.

(22)

exibido na Fig. (1.3).

Figura 1.3: Aplica¸c˜ao de uma mudan¸ca de escala a uma regi˜ao do fractal de Sierpinski. A

parte ampliada n˜ao foi detalhada durante o processo de constru¸c˜ao e, portanto, o objeto deixa

de ser auto-similar nesta escala.

Tipos de auto-similaridade

Na auto-similaridade geométrica, que foi descrita acima, partes do objeto são exata-mente uma cópia menor do objeto inteiro. Dizemos então que as partes são geometrica-mente similares ao todo. Há uma classe de conjuntos cujas partes reproduzem o todo, mas não de forma exata e sim estat´ıstica, isto é, as partes possuem os mesmos valores para certas propriedades estat´ısticas do todo. Dizemos então que o conjunto é estatisticamente auto-similar. Este tipo de auto-similaridade é mais comum na natureza do que o primeiro tipo.

1.2.4 Dimens˜

ao e Dimens˜

ao Fractal

(23)

um ponto naquele conjunto. Assim, um plano euclidiano (X =ℜ2_{) é bidimensional pois é} necessário um par de números, (x, y), para se especificar qualquer ponto dele. Mas esta é apenas uma das defini¸cões de dimensão (oriunda da álgebra linear). Descreveremos aqui a no¸cão de dimensão de similaridade, que aplicaremos aos objetos fractais apresentados em seguida, e na se¸cão 1.4 descreveremos com mais detalhes outras defini¸cões.

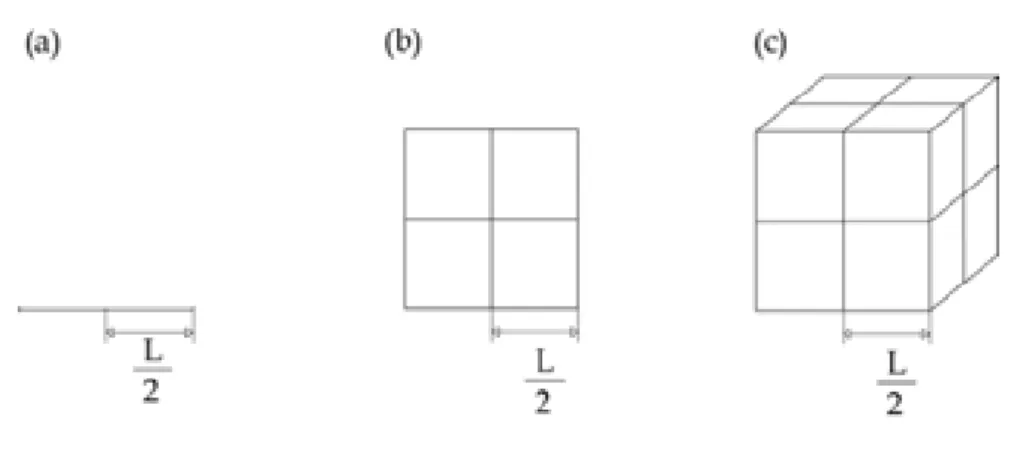
Dimens˜aodde um conjunto pode ser definida como sendo a forma como o n´umero

M de objetos que compõem o conjunto muda com sua dimensão linear L. Considerando-se uma pequena parte do conjunto de tamanho linear igual abL (b <1), então M(bL) é modificado em seu valor por um fatorbd_:

M(bL) =bdM(L) (1.11)

Na Fig. (1.4) vemos exemplos de objetos com dimens˜oes inteiras. O objeto (a) de

Figura 1.4: Exemplos de objetos com dimens˜oes d= 1,d= 2e d= 3.

Fig. (1.4) possui dimens˜aod= 1 porque

M

_L

2

= 1

2M(L), (1.12)

no caso em questãob= 1₂. Já o objeto (c) da mesma figura possui dimensãod= 3, pois,

M

_L

2

= 1

8M(L) = ₁

2 3

M(L). (1.13)

(24)

Figura 1.5: Parte de um triângulo de Sierpinski utilizado no cálculo da dimensão fractal.

(1.11) n´os obtemos

d=

logM(bL)_M(L)

log(b) . (1.14)

Na Fig. (1.5) observa-se queb= 1

2, M(L) = 27 e M _L

2

= 9. Substituindo estes valores na Eq.(1.14) obtˆem-se

d= log ₉

27

log1 2

= 1.5849... (1.15)

1.2.5 Auto-Afinidade

Uma transforma¸c˜ao w:_ℜ2 _{→ ℜ}2 _{da forma}

w(x1, x2) = (ax1+bx2+e, cx1+dx2+f), (1.16) onde a, b, c, d, e e f são números reais, é chamada uma transforma¸cão de afinidade (bidimensional)[10]. Na Fig. (1.6) temos um exemplo de transforma¸cão aplicada a um c´ırculo. A transforma¸cão em questão é

w(x, y) = (2x, y). (1.17)

Alguns fractais após sofrerem certas transforma¸cões de afinidade permanecem com o mesmo aspecto, isto é, a transforma¸cão de afinidade não altera sua forma. Dizemos então que este fractal exibe auto-afinidade. Na Fig. (1.7) temos um exemplo de um fractal autoafim constru´ıdo até certo passo. Note que para que uma parte do conjunto represente o todo é necessário aplicar diferentes mudan¸cas de escala para os eixosxey.

(25)

Figura 1.6: Uma transforma¸c˜ao de aﬁnidade aplicada a um c´ırculo.

Figura 1.7: Um fractal auto-aﬁm.

de fun¸cão auto-afim aleatória é a fun¸cão h(t) de um movimento Browniano unidimen-sional, onde hrepresenta a posi¸cão da part´ıcula e trepresenta o tempo.

1.3 Categorias de Fractais

1.3.1 Fractais Determin´ısticos

(26)

Em seguida veremos alguns exemplos de sistemas de fun¸cões iteradas e suas pro-priedades. Para que um verdadeiro fractal seja criado, é necessário que este processo não termine nunca, o que significa que os fractais são objetos limites. Veremos, também, objetos fractais determin´ısticos gerados por outros processos, como o conjunto de Julia.

Conjunto de Cantor

O conjunto de Cantor é obtido tomando-se um segmento de reta de comprimento 1, isto é, tomando-se um conjunto T0 = {[0,1]} , dividindo-o em três partes iguais e retirando-se a parte central, então, obtêm-se o conjunto T1 = {[0,1₃]∪[2₃,1]}. Repete-se então este procedimento para os intervalos que surgirem, continuando o processo ad infinintum. Na Fig. (1.8) pode-se observar os 5 primeiros passos na cria¸cão do conjunto de cantor. O comprimento total do conjunto, depois de n itera¸cões, é dado por

Figura 1.8: Cinco primeiros passos da cria¸c˜ao de um conjunto de Cantor.

ln =

2 3

n

, (1.18)

o n´umero de segmentos de reta ´e dado por

Nn = 2n, (1.19)

ent˜ao o comprimento de cada segmento ´e

ǫn =

ln

Nn =

1 3

n

(27)

A dimens˜ao de similaridade para este conjunto pode facilmente ser calculada. Vamos fazˆe-lo com o aux´ılio do n´ıveln= 2. Neste casoM(L) = 4, comb= 1

3 temosM(bL) = 2. Substituindo estes valores na Eq. (1.14) obtemos

d= log ₂

4

log1₃ =

log (2)

log(3) = 0.6309... (1.21)

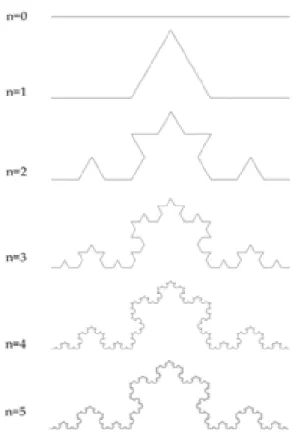
Curva de Koch

A curva de Koch é uma curva matemática e um dos mais antigos fractais conheci-dos. Ele apareceu pela primeira vez num artigo intitulado “Une méthode géométrique élémentaire pour l’étude de certaines questions de la théorie des courbes plane” em 1906 pelo matemático sueco Helge Von Koch. Neste artigo Koch mostrou que a curva em questão era continua em todos os pontos e não diferenciável, também, em todos os pon-tos. A curva de Koch é um dos fractais determin´ısticos mais comuns. O processo de cria¸cão come¸ca com uma única linha. Divide-se a linha em três trechos iguais, retira-se o trecho central (como no processo de cria¸cão do conjunto de Cantor) e insere-se dois seg-mentos de reta, de mesmo comprimento do trecho retirado, nas extremidades dos trechos restantes, de tal maneira que suas extremidades se unam e eles formem um ângulo de 60o _{entre si. Repete-se indefinidamente este procedimento em cada segmento de reta do} novo objeto criado. Na Fig. (1.9) vemos os 5 primeiros passos da cria¸cão de uma curva de Koch. Em cada itera¸cão o comprimento desta curva é incrementada por um fator 4₃. Assim sendo o comprimento depois den intera¸cões será dado por

ln =

4 3

n

, (1.22)

o número de segmentos de reta depois de n itera¸cões é

Nn = 4n, (1.23)

assim sendo, o comprimento de cada segmento ´e

ǫn =

(28)

Figura 1.9: Cinco primeiros passos da cria¸c˜ao de uma curva de Koch.

Vamos utilizar o n´ıvel 1 para c´alculo de similaridade, para b = 1₃, M(L) = 4 e

M(bL) = 1, obtemos

d= log ₁

4

log1₃ =

log (4)

log(3) = 1.261859... (1.25) Floco de Neve de Koch

O floco de Neve de Koch, também conhecido por estrela de Koch ou ilha de Koch é obtido aplicando-se o processo de cria¸cão da curva de Koch a um triângulo equilátero de lado L0 = 1. Na Fig. (1.10) pode-se observar quatro passo da cria¸cão de um floco de neve de Koch. Ele possui as mesmas propriedades da curva de Koch, isto é, é cont´ınuo em todos os pontos e não diferenciável em todos eles. Seja Nn o número de lados, Ln o comprimento dos segmentos de retas existentes no conjunto e ln o per´ımetro, então

(29)

Figura 1.10: Os quatro primeiros passos da cria¸c˜ao de um floco de neve de Koch.

Ln = ₁

3 n

= 3−n _(1.27)

ln =NnLn = 3 ₄

3 n

(1.28) Vamos agora calcular a área delimitada pelo objeto fractal. No n´ıvel n existem Nn (Eq. (1.26)) lugares onde serão inseridos triângulos equiláteros de lado 1

3Ln, onde Ln é tamanho de um segmento do fractal, dado pela Eq. (1.27). Então, sendo An a área delimitada pelo objeto no n´ıvel npodemos afirmar que

An+1=An+Nn△

Ln 3

, (1.29)

sendo_△= _△(x) a fun¸cão que dá a área do triângulo equilátero

△(x) = x 2√₃

4 , (1.30)

ondex´e o lado do triˆangulo. Substituindo os valores apropriados na Eq. (1.29) obtemos

An+1=An+ 3·4n

L2 n 32

√

3

4 , (1.31)

que pode ser reescrita como

An+1 =An+

3·4n√₃

4·32_·₉n. (1.32)

Como a área do triângulo original é△(1) =A0 =

√

3

4 podemos reescrever a Eq. (1.32) da seguinte forma

An+1 =An+ 1 3

₄ 9

n

(30)

Temos ent˜ao

A1 =A0+ 1 3

₄ 9

0

A0. (1.34)

A2 =A1+ 1 3

₄ 9

1

A0 =A0+ 1 3

₄ 9

0

A0+ 1 3

₄ 9

1

A0. (1.35)

A3 =A2+ 1 3 4 9 2

A0 =A0+ 1 3 4 9 0

A0+ 1 3 4 9 1

A0+ 1 3 4 9 2

A0. (1.36) Da Equa¸c˜oes 1.34, 1.35 e 1.36 podemos inferir que

An =A0

1 +1 3 n i=0 ₄ 9 i . (1.37)

O termo n_i=04₉i na Eq. (1.37) pode ser encarado como a soma dos termos de uma progressão geométrica (P.G) com termo iniciala1= 1 e razãoq= 4₉. Sabemos que a soma dos termos de uma P.G infinita é dada por

S_∞ = a1

1−q. (1.38)

Assim sendo, para o fractal, que existe realmente apenas paran_{→ ∞} temos

∞ i=0 ₄ 9 i = 1

1₋4 9

. (1.39)

Substituindo a Eq. (1.39) na Eq. (1.37) (comn→ ∞) n´os obtemos lim

n→∞An =

8

5A0. (1.40)

Temos agora mais uma estranha propriedade deste fractal. Um per´ımetro infinito (pois limn→∞ln =∞) delimita uma área finita. Por ser apenas a união de três curvas de Koch, a dimensão de similaridade deste conjunto é a mesma da curva, isto é, d = log(

1 4)

log(1 3)

= log(4)

log(3) = 1.261859...

Inverso do Floco de Neve de Koch

(31)

Figura 1.11: Os quatro primeiros passos da cria¸c˜ao do inverso do floco de neve de Koch.

que os n´ıveis novos deverão retirar área do triângulo equilátero original e não acrescentar. O per´ımetro, número e tamanho dos segmentos de reta possuem valores idênticos aos do fractal floco de neve. A área delimitada pelo per´ımetro claramente é diferente. O processo para o cálculo da área também é o mesmo. Se repetirmos todos os passos descritos na se¸cão anterior chegaremos a equa¸cão seguinte ao invés da Eq. (1.37)

An =A0

1₋1 3

n

i=0

4 9

i

. (1.41)

Paran_{→ ∞} obtemos

A_∞ = 2

5A0. (1.42)

A dimensão de similaridade deste conjunto é idêntica à dimensão fractal do Floco de Neve de Koch.

Curva Drag˜ao

(32)

Fig. (1.13) vemos os n´ıveis 10 e 14. A linha pontilhada é o estágio anterior, isto é, é a

Figura 1.12: Os quatro primeiros passos da cria¸c˜ao de uma curva drag˜ao.

curva base. Note que os triângulos não são constru´ıdos todos de um mesmo lado da curva base. Determinando-se um sentido nesta, note que os triângulos são constru´ıdos de forma alternada, ora à esquerda, ora à direita desta. Em cada n´ıvel o comprimento da curva é

Figura 1.13: N´ıveis 10 e 14 da cria¸c˜ao de uma curva drag˜ao.

incrementado em √2. Assim o comprimento da curva no n´ıvel n ser´a dado por

ln = _√

2nl0. (1.43)

O comprimento dos segmentos ser´a dado por

ǫn =

ln 2n = 2

−n2l

0 (1.44)

(33)

Triˆangulo de Sierpinski

O triângulo de Sierpinski existe desde o século XII em algumas catedrais, mas foi o matemático polonês Waclaw Sierpinski[17] (1882-1969) que o introduziu formalmente ao grupo dos conjuntos matemáticos estranhos, no ano de 1916. Sua constru¸cão é feita da seguinte forma. Inicia-se com um triângulo equilátero de lado 1. Retira-se um triângulo equilátero de lado 1₂ de tal maneira que restarão outros três triângulos de lado 1₂. Então este processo é repetido em cada triângulo que tiver surgido. Em cada n´ıvel da cria¸cão, o número de triângulos é igual a

Nn = 3n (1.45)

A área de cada triângulo que compõe o conjunto é, no n´ıvel n,

△n = ₁

2 2n

△0, (1.46)

onde _△0 é a área do triângulo equilátero inicial (de lado 1). A área total do conjunto depois de n passos é

An = 3n ₁

2 2n

A0. (1.47)

O conjunto fractal existe paran_{→ ∞}ent˜ao lim

n→∞An = 0. (1.48)

A Eq. (1.48) revela que este conjunto existe, mas possui densidade nula, outra estranha propriedade de alguns fractais. Na Fig. (1.14) podemos observar os trˆes primeiros passos

Figura 1.14: Os três primeiros passos da cria¸cão de um triângulo de Sierpinski.

(34)

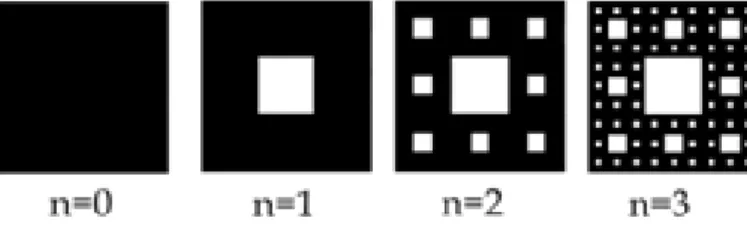
Tapete de Sierpinski

Este conjunto é uma varia¸cão do triângulo de Sierpinski. Ele é criado a partir de um quadrado de lado 1. Retira-se do centro um quadrado de lado 1

3. Dessa forma passa a existir 8 quadrados dos quais retira-se de seus respectivos centros um quadrado de lado 1

9. E assim por diante. Na Fig. (1.15) podemos ver os três primeiros passos na cria¸cão de uma tapete de Sierpinski. O número quadrados de lado 1₃n no n´ıvelné igual a

Figura 1.15: Os trˆes primeiros passos da cria¸c˜ao de um tapete de Sierpinski.

Nn = 8n. (1.49)

A ´area de cada quadrado no n´ıveln ´e dada por n =

₁ 3

2n

0 (1.50)

A área total então é

An =

8 9

n

A0, (1.51)

assim, quandon→ ∞ teremos

lim n→∞

An = 0, (1.52)

ou seja, a área total deste conjunto é zero. Assim como o triângulo de Sierpinski, este fractal também possui densidade nula, juntando-se assim ao grupo dos conjuntos com estranhas propriedades.

Vamos agora calcular a dimens˜ao de similaridade deste fractal. Para isto vamos nos utilizar do n´ıveln= 1.Para este n´ıvel temos M(L) = 8 e, parab = 1

3, temos M(bL) = 1. Substituindo na Eq. (1.14) obtemos

d= log ₁

8

log1₃ =

log (8)

(35)

Conjuntos de Julia

Em 1918 o matemático frânces Gaston Julia publicou um trabalhou que permaneceu esquecido até os anos 1980, quando os computadores puderam visualizar sua cria¸cão. Para facilitar o entendimento da idéia de Julia vamos definir três conceitos importantes: métrica, órbita e conjunto limitado.

Defini¸cão 1.3.1.1 Um espa¸co métrico (X, d)é um espa¸co X junto com uma fun¸cão real

d:_{X × X →}R_{, que mede a “distˆancia” entre o par de pontos} _{x, y} _{∈ X}_{. Exige-se que} _d obede¸ca aos seguintes axiomas:

• d(x, y) =d(y, x)∀x, y∈ X

• 0< d(y, x)<_{∞ ∀}x, y_{∈ X}, x=y • d(x, x) = 0_∀x_{∈ X}

• d(x, y)≤d(x, z) +d(z, y)∀x, y, z∈ X

Defini¸cão 1.3.1.2 Uma órbita _W de um número z _{∈ X} sobre uma fun¸cão f :_{X × X} é o conjunto W ={f(z), f(f(z)), f(f(f(z))), ...}.

Defini¸cão 1.3.1.3 Seja S _{⊂ X} um subconjunto de um espa¸co métrico (_X, d). S é limi-tado se há um ponto a_{∈ X} e um número real R >0 tal que d(a, x)< R_∀x_∈S.

O conjunto de Julia preenchido é definido como o conjunto de pontos z ∈C_para os quais a órbita sobre uma fun¸cão f(z)_→ C _{é limitada, e o conjuto de J´}_{ulia simples é} a fronteira entre o conjunto composto por todos os pontos z com órbitas limitadas e o conjunto composto por todos os pontosz com órbitas não-limitadas.

Vamos dar um exemplo de como desenhar um conjunto de J´ulia. Seja a fun¸c˜ao

(36)

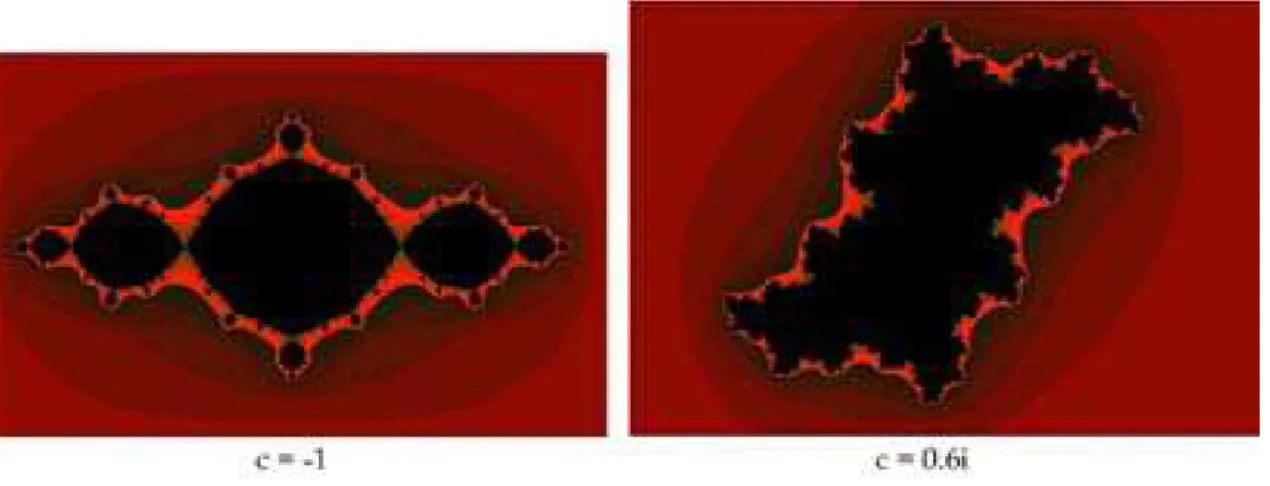
determinante fosse alcan¸cada. Para evitar que o sistema fique iterando para sempre num ponto que possui órbita limitada, deve-se limitar o número de itera¸cões máximas da fun¸cão e considerar que qualquer ponto cujas itera¸cões tenham atingido este número de vezes é um ponto de órbita limitada. A cor atribuida a este ponto é então preta. Observe que para cadacum conjunto de pontos será encontrado e existem valores decpara o quais não existem pontos com órbitas limitadas e existemc para o quais existem órbitas limitadas e o conjunto, no entanto, não forma um fractal. Por exemplo, parac = 0, o conjunto de pontos cuja órbita é limitada forma um c´ırculo. Na Fig. (1.16) vemos dois conjuntos de Julia.

Figura 1.16: Conjuntos de Julia preenchidos obtidos com a fun¸c˜aof(z) =z2₊_c _para_c₌₋₁ ec= 0.6i.

Fractal de Mandelbrot

(37)

se deseja determinar se possui órbita limitada ou não. Na Fig. (1.17) vemos um conjunto de Mandelbrot preenchido paraf(z) =z2₊_c_{. O conjunto de Mandelbrot simples reside} na fronteira do conjunto dos elementos com órbita limitada com o conjunto dos elementos com órbita não limitada e ele que dá, como já dissemos, todos os valores para os quais o conjunto de Julia é conectado.

Figura 1.17: Fractal de Mandelbrot para f(z) =z2₊_c_.

1.3.2 Fractais Aleat´

orios

ALD (Agrega¸c˜ao Limitada por Difus˜ao)

(38)

la¸cos (a não ser em escalas reduzidas). A figura que surge no plano tem dimensão fractal aproximadamente igual a 1.7 (ver Fig. (1.18). No espa¸co tridimensional ela tem dimensão de aproximadamente 2.5.

Figura 1.18: Figura obtida atrav´es de DLA.

M. Matsushita e Hiroshi Fujikawab [12] em 2002 estudaram o crescimento de uma colônia de bactérias da espécie Bacillus subtilis. Eles mostraram que ela crescia bidimensionalmente e auto-similarmente em placas de ágar-ágar (material encontrado em algas vermelhas utilizado na produ¸cão de hidrogel para cultivo de microorganismos) em um meio concentrado de nutrientes. Eles obtiveram dimensão fractal D = 1.73±0.02, muito próximo do valor atribuido ao modelo de DLA bidimensional.

A estrutura dada pelo algoritmo DLA está presente em muitos lugares na natureza. A razão disto, como nos mostra H. E. Stanley num artigo editado por A. Bunde e Shlomo Havlin[20], é em primeiro lugar o fato de que o fenômeno de agrega¸cão baseado na cam-inhada aleatória corresponde à equa¸cão de Laplace (∇2_Π(_{r, t}_{) = 0) para a probabilidade} Π(r, t) de que a caminhada esteja na posi¸cão(r) no tempot. Em segundo lugar, há uma ampla faixa de fenômenos que aparentemente nada possuem em comum com caminhada aleatória. Entre eles destacamos o fenômeno dos “Dedos Viscosos”, para o qual a pressão

(39)

podem ser modelados por DLA. Eles pertecem ao que se chama classe de universalidade do DLA. Em seguida veremos dois exemplos de DLA em colˆonias de microorganismos.

Em 1993 Matsuura e Miyazama[13] mostraram que uma colônia de fungos As-pergillus oryzae quando cultivada num meio com escassez de alimentos cresce exatamente com a aparência de uma figura criada por DLA. Na experiência, quem se difundia não era o fungo, mas o alimento, e onde o alimento encostava, favorecia o crescimento dos fungos naquele ponto.

Deslocamento do Ponto M´edio

Pode-se gerar imagens de paisagens terrestres através da utiliza¸cão de fractais. Um dos mais simples fractais utilizado para esta fun¸cão é criado através do algoritmo intitulado “Deslocamento do Ponto Médio”. Este algoritmo funciona da seguinte forma. Inicia-se com um segmento de reta de comprimentol0. Determina-se a coordenada do ponto médio (xm, ym). Adiciona-se a ym um número aleatório δym que pertence ao intervalo [−l0, l0]. O segmento é então repartido em dois e estes são esticados até encontarem no ponto cor-respondente ao deslocamento do ponto médio. O segundo passo consiste na aplica¸cão da mesma regra aos dois segmentos que surgiram. Desta vez o deslocamento do ponto médio será feito por um valorδym aleatório pertecente ao intervalo [−l₂0,l₂0]. Generalizando, os deslocamentos deverão ser dados, para o n´ıveln, por um número aleatório pertencente ao intervalo

δym ∈

−₂l0_n, l0

2n

. (1.54)

Na Fig. (1.19) vemos os dois primeiros n´ıveis na cria¸cão de um fractal através da técnica de deslocamento do ponto médio. E na Fig. (1.20) vemos uma curva criada até o sexto n´ıvel.

(40)

Figura 1.19: Dois primeiros passos da cria¸cão de uma curva através da técnica de deslocamento

do ponto m´edio. Linha tracejada: passo anterior. Linha pontilhada: δym.

Figura 1.20: A Direita` : Curva criada através da técnica de deslocamento do ponto médio para

n= 6. A Esquerda` : Utiliza¸cão da curva para a cria¸cão do perfil de uma montanha.

utilizada no plano para a produ¸c˜ao de superf´ıcies fractais.

1.4 Dimens˜

ao Fractal

Dimensão fractal é o nome dado a cada elemento do conjunto de números que podem caracterizar os fractais. Esses números são importantes porque definem a conexão dos conjuntos fractais com os dados reais, e eles podem ser medidos aproximadamente através de experiências.

(41)

Figura 1.21: Um superf´ıcie fractal produzida por uma algoritmo semelhante ao do

desloca-mento do ponto m´edio vista de duas posi¸c˜oes diferentes.

no in´ıcio deste cap´ıtulo.

1.4.1 Dimens˜

ao Topol´

ogica

A dimensão topológica descreve como pontos que compõem o conjunto são conectados. O valor da dimensão topológica é sempre um inteiro. Por defini¸cão o ponto tem dimensão topológica 0. Como a uma curva pode ser separada por um ponto, diz-se que ela tem dimensão topológica 1. Uma superf´ıcie pode ser separada por uma curva, então diz-se que ela tem dimensão topológica 2. Um volume pode ser separado por um plano, possui, portanto, dimensão topológica igual a 3. Este conceito vem da defini¸cão de equivalência topológica. Dois objetos são topologicamente equivalentes quando um pode ser obtido do outro através de algumas opera¸cões permitidas (esticar certos segmentos, encurvar outros, etc). Sob este ponto de vista, a curva de Koch e um segmento de reta são equivalentes. Assim, objetos topologicamente equivalentes possuem mesma dimensão topológica.

Há muitas defini¸cões de dimensão que recaem na dimensão topológica. Vamos descrever a dimensão de cobertura. Para seu cálculo nós primeiro encontramos o menos número de conjuntos necessários para cobrir todas as partes de um objeto. Esses conjuntos podem precisar se sobrepor. Se cada ponto do objeto é coberto por não mais que G

(42)

coberto com o menor número de c´ırculos de raio finito poss´ıveis, cada ponto no plano irá ser coberto por não mais do que 3 c´ırculos. Como 3₋1 = 2, dizemos que a dimensão de cobertura do plano é 2.

1.4.2 Dimens˜

ao de Minkowski-Bouligand

Seja X _{o espa¸co (e.g} R_, R2 _ou _C_{) que contém o conjunto fractal} _F_{, isto é,} _{F ⊂} _X_. Digamos queB(x, ǫ) denota bolas de raioǫ centradas emxtal quex_∈X_{. Vamos definir} o inteiroN(F, ǫ) como sendo o menor número de bolas fechadas de raioǫnecessárias para cobrir o conjunto_F. Formalmente escrevemos

N(_F, ǫ) =M in(M _∈N_{) :}_{F ⊂} M

n=1

B(x, ǫ). (1.55)

A no¸cão intuitiva por trás da dimensão fractal é a de que o conjunto_Ftem uma dimensão fractalD se

N(_F, ǫ)_≈Cǫ−D_, _(1.56)

onde o s´ımbolo ”_≈”est´a sendo utilizado com o seguinte significado. Sejam f(ǫ) e

g(ǫ) duas fun¸cões reais da variável positiva e real ǫ. Então f(ǫ) ≈ g(ǫ) significa

limǫ→0{lnf(ǫ)/lng(ǫ)}= 1. Escrevendo o D da Eq. (1.56) obtemos

D≈ lnN(F, ǫ)−lnC

ln1_ǫ . (1.57)

Note que o termo lnC/ln1_ǫ tende a zero quando ǫ → 0. Definimos ent˜ao dimens˜ao fractal da seguinte forma:

Defini¸c˜ao 1.4.2.1 Se

D = lim ǫ→0

ln (N(_F, ǫ)) ln1

ǫ

existe, então D é chamado dimensão fractal de F.

Se fizermos ǫ=ǫn =crn, onde c >0 e 0< r <1, na Defini¸c˜ao 1.4.2.1 chegamos a

D= lim n→∞

⎧ ⎨ ⎩

ln (N(_F, ǫn)) ln1

ǫn

⎫ ⎬

⎭. (1.58)

(43)

Teorema 1.4.2.1 SejaF um conjunto fractal pertencente ao conjuntoRm_{. Cobre-se}_Rm com caixas quadradas de ladoǫn, como exemplificado na Fig. (1.22) para ǫn = ₂1n, n= 2

e m= 2. Nn(F) denota o n´umero de caixas de lado ₂1n que intercepta o conjunto F. Se

D = lim n→∞

⎧ ⎨ ⎩

ln (N(F, ǫn)) ln_ǫ1

n

⎫ ⎬ ⎭

existe, então D é a dimensão fractal do conjunto _F.

Figura 1.22: Caixas fechadas de lado 1

2n cobrindo um quadrado de lado1. Na ﬁgura n= 2.

Vamos ver alguns exemplos de cálculo de dimensão fractal utilizando o Teorema 1.4.2.1. Vamos iniciar com um quadrado. Seja o conjunto _⊂R2_{. Considerando-se os lados do} quadrado como sendo de tamanho unitário, o número de quadrados de tamanho ǫn = ₂1n

que interceptam todo o conjunto ´eNn = 4n. Assim sendo

D = lim n→∞

⎧ ⎨ ⎩

ln (Nn)) ln_ǫ1

n

⎫ ⎬

⎭= limn→∞

ln 4n ln 2n

= 2. (1.59)

Agora vamos calcular a dimensão fractal do tapete de Sierpinski(ver se¸cão 1.3.1). Seja o conjunto ⊂ R2_{, é poss´ıvel mostrar que o o n´}_{umero de quadrados de lado} _ǫ

n = ₃1n

que interceptam o conjunto para n= 1 é igual a N1 = 8. Paran = 2 esse número é

N2 = 64. Generalizando, o n´umero de quadrados de lado ǫn = ₃1n que interceptam o

conjunto fractal ´e dado porNn( ) = 8n. Assim sendo temos

D = lim n→∞

⎧ ⎨ ⎩

ln (Nn)) ln_ǫ1

n

⎫ ⎬

⎭= limn→∞

ln 8n ln 3n

(44)

1.4.3 Dimens˜

ao de Hausdorff-Besicovitch

Vamos definir esta dimensão apenas para subconjuntos do espa¸co métrico (_Rm_{, d}_). A dimensão fractal de Hausdorff-Besicovitch de um subconjunto limitado de_Rm _{é outro} número real que pode ser utilizado para caracterizar a complexidade de tais conjuntos. Vamos a algumas defini¸cões que nos ajudarão na compreensão da dimensão fractal de Hausdorff-Besicovitch.

Defini¸cão 1.4.3.1 Seja A ⊂Rm _{tal que} _Rm ₌ _{_x_|_x_{= (}_x₁_{, ..., x}_n₎_{, x}_i _∈R_} _para _m_{∈ N}_. A métrica d do espa¸co métrico (Rm_{, d}₎_{é definida como sendo}

d(x, y) =

n

i=1

(xi−yi)2.

Vamos agora definir o ´ınfimo de um subconjunto_{X ⊂}R_.

Defini¸c˜ao 1.4.3.2 inf(x _{∈ X}) = maior limite inferior de x. Em outras palavras, a= inf(x∈ X) fornece a≤x para todox∈ X.

De forma similiar definimos o supremo.

Defini¸c˜ao 1.4.3.3 sup(x ∈ X) = menor limite superior de x, isto ´e, b=sup(x ∈ X) fornece b_≥x para todox_{∈ X}.

Utilizando a Defini¸cão 1.4.3.3 vamos agora definir a no¸cão de diâmetro de um subconjunto

U ⊂Rm_.

Defini¸c˜ao 1.4.3.4 diam(_U)=sup_{d(x, y)_|x, y_{∈ U}}

Defini¸c˜ao 1.4.3.5 Um subconjunto U ⊂ Rm _{´e dito ser aberto desde que para qualquer}

x_{∈ U} exista uma pequena bola Bξ(x) ={y ∈ Rm|d(x, y)< ξ} de raioξ e centrada em x, tal queBs(x)⊂ U.

Sejam ξ es reais positivos, vamos definir a fun¸c˜ao

hs_ξ(A) = inf _∞

i=0

(45)

O ´ınfimo é extendido sobre todas as coberturas abertas de A para o qual o conjunto coberturaUi tem diâmetro menor que ξ. Esta soma pode ser finita ou infinita. Quando nós decrementamos ξ, a classe de coberturas permiss´ıveis de A é reduzida. Todavia, o ´ınfimo cresce e então aborda o limiteξ _{→ ∞}o qual pode ser finito ou infinito. Escrevemos

ent˜ao

hs(A) = lim ξ→0h

ξ

s(A) (1.61)

O valor hs₍_A_{) ´e chamado medida}_s_{-dimensional de Hausdorﬀ.}

Teorema 1.4.3.1 Sejamum inteiro positivo. SejaAum subconjunto limitado do espa¸co métrico(Rm_{, d}_{). Seja} _hs₍_A₎ _{a fun¸cão de} _p_∈_[0_,_∞_] _{definida acima. Então, há um ´}_unico número real DH ∈[0, m] tal que

hs(A) = ⎧ ⎨ ⎩

∞ se p < DH e p∈[0,∞] 0se p > DH e p∈[0,∞]

(1.62)

O número DH é o chamado dimensão fractal de Hausdorff-Besicovitch.

Como deve ter ficado claro, não é uma tarefa fácil trabalhar com esta defini¸cão e por isso não é comum encontrar procedimentos experimentais para medi¸cão de dimensão que utilizem ela por base.

1.5 Fractais na Natureza

1.5.1 Introdu¸

c˜

ao

Estrutura auto-similares or auto-afins com caracter´ısticas semelhantes aos fractais discutidos acima podem ser encontrados em muitos lugares na natureza[7], da escala astronômica à escala microscópica. Os exemplos incluem aglomerados de galáxias, as crateras lunares, a distribui¸cão de terremotos e a estrutura de linhas costeiras, montanhas e nuvens.

(46)

materiais, fractais aparecem em pol´ımeros, géis, agrega¸cões, eletrodeposi¸cão, interfaces rugosas e superf´ıcies.

1.5.2 Arvore Bronquial

´

A respira¸cão é um tipo de processo realizado através de uma interface. Na interface dos alvéolos há a troca por difusão de gás carbônico pelo oxigênio. Como o organismo precisa de muito oxigênio se faz necessário uma grande área para que mais e mais alvéolos possam realizar a troca. Objetos fractais têm uma área superficial muito larga. De fato eles são compostos quase que inteiramente por superf´ıcies[7]. No pulmão, a estrutura bronquial é compostas por ramifica¸cões autosimilares[16],o que faz com que a área total do pulmão seja aproximadamente igual a área de uma quadra de tênis[7].

1.5.3 Membranas Celulares

Membranas revestem células vivas, bem como partes internas destas. Paumgastner et ali[14] mediram a área da superf´ıcie total de tais membranas com o aux´ılio de fotografias obtidas por microscopia eletrônica. O que eles observaram foi o seguinte. Ampliando certas regiões onduladas, mais ondula¸cões eram observadas e consequentemente a área total da superf´ıcie era incrementada. Logo eles perceberam que a membrana era um objeto auto-similar. Eles encontraram então que as dimensões fractais associadas ao perfil da membrana do ret´ıculo endoplasmático, com o perfil da membrana externa e interna da mitocondria são respectivamente 1.72, 1.09 e 1.54.

1.5.4 Movimento Browniano

(47)

(48)

CAP´ITULO 2

O MULTIFRACTAL

2.1 Introdu¸

c˜

ao

Os fractais aumentaram de uma forma espantosa nossa capacidade de descrever a natureza. Entretanto, há muitos fenômenos em F´ısica, Qu´ımica e Geologia que requerem a generaliza¸cão do conceito de fractal para incluir estruturas intricadas. Essas estruturas geralmente são compostas por vários fractais sendo necessário um conjunto de números para caracteriza-las. Esse conjunto é chamado espectro multifractal. Um exemplo de um multifractal é o já apresentado fractal criado por agrega¸cão limitada por difusão (DLA) (ver se¸cão 1.3.2). Considerando-se o conjunto como um todo, a figura de DLA possui apenas uma dimensão fractal, mas considerando-se todos os s´ıtios que possuem iguais probabilidades de serem o elemento agregador da part´ıcula caminhante, temos uma série de conjuntos, cada qual com sua própria dimensão fractal.

2.2 O Conjunto Multifractal

Q

mf

Chamaremos o conjunto multifractal que ser´a objeto de nossa an´alise de conjunto

Qmf. Ele foi proposto originalmente por G. Corso e colaboradores[3]. Antes de defini-lo vamos enumerar algumas de suas propriedades.

1. Qmf é um conjunto multifractal, o que significa que Qmf tem um número infinito de subconjuntos k com dimensão fractal Dk própria.

(49)

3. A união de todos os subconjuntosk forma um conjunto quadrado deR2_. 4. O algoritmo para a constru¸cão deQmf tem apenas um parâmetro ρ. 5. Quandoρ= 1 o conjunto Qmf degenera numa rede quadrada.

6. O objeto Qmf exibe auto-afinidade ou auto-similaridade dependendo da regi˜ao do conjunto.

7. O algoritmo para constru¸cão deQmf é simples e facilmente implementável em um computador.

Vamos descrever o processo de cria¸cão do conjunto Qmf. Vamos definir como unidade elementar do conjunto multifractal o retângulo. O multifractal é um conjunto de retângulos que por sua vez são subconjuntos deR2_{. Os fractais que compõem o conjunto}

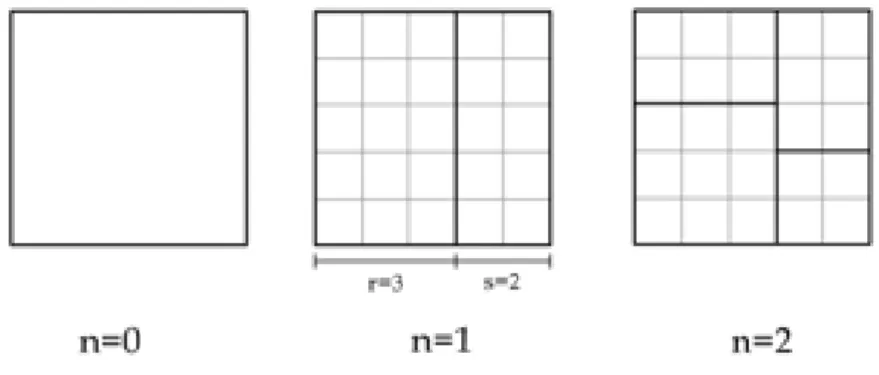
Qmf são os subconjuntos compostos por retângulos de mesma área. O conjunto Qmf é criado através de itera¸cão, é portanto um IFS (ver se¸cão 1.3.1). Em cada passo um retângulo é dividido de forma a dar origem a dois retângulos. Os cortes são realizados segundo determinadas regras. Vamos a elas.

No passo n = 0 temos um retângulo de lados iguais com comprimento L. Es-colhemos um parâmetro ρ que caracterizará o multifractal. ρ deve obedecer a condi¸cão 0< ρ <1 , onde

ρ= s

r, (2.1)

(50)

Fig.(2.1) paraρ= s_r = 2₃. Para o passon= 3 (bem como para todos os n´ıveis ´ımpares) os cortes s˜ao verticais e o lado que fica com a parte maior ´e alternado, ora para a esquerda, ora para a direita (ver Fig. (2.2)).

Figura 2.1: Dois primeiros passos da cria¸c˜ao do conjuntoQmf comρ= s_r = 2₃.

Figura 2.2: Passos 2, 3 e 4 da cria¸c˜ao do conjunto Qmf com ρ= s_r = 2₃.

2.3 Distribui¸

c˜

ao de ´

Areas

O cálculo da distribui¸cão das áreas dos retângulos que compõem o multifractal é um passo importante para o cálculo do espectro multifractal do conjunto, que será realizado na próxima se¸cão.

No n´ıvel n= 1 temos dois retˆangulos de ´area r/(s+r) = 1/(1 +ρ) e s/(s+r) =

ρ/(1 +ρ) (em unidades deL2_{), ent˜ao, claro que} 1

1 +ρ+ ρ

(51)

No n´ıvel n = 2 temos quatro retângulos, um com área (ρ/(1 +ρ))2, dois com áreas

ρ/(1 +ρ)2 _{e um com área (1}_/_{(1 +}_ρ₎₎2_{. A soma delas é então} _ρ

1 +ρ

2 + 2

₁ 1 +ρ

ρ

1 +ρ

+

₁ 1 +ρ

2

= 1. (2.3)

No n´ıveln= 3 temos 8 retângulos com a seguinte distribui¸cão de áreas:

1 1 +ρ

3 + 3

ρ

1 +ρ

1 1 +ρ

2 + 3

ρ

1 +ρ

2 1 1 +ρ

+

ρ

1 +ρ

3

= 1 (2.4) No n´ıveln= 4 temos 16 retângulos com a seguinte distribui¸cão de área:

_ρ

1 +ρ

4 +4

_ρ

1 +ρ

3 ₁ 1 +ρ

+6

_ρ

1 +ρ

2 ₁ 1 +ρ

2 +4

_ρ

1 +ρ

1 1 +ρ

3 +

₁ 1 +ρ

4 = 1.

(2.5) Observando as Eq. (2.2) à (2.5) podemos inferir que a distribui¸cão de áreas é binomial (em unidades de L2_):

A= n

k=0

C_nk

_ρ

1 +ρ

k ₁ 1 +ρ

n−k =

_{1 +}_ρ 1 +ρ

n

= 1, (2.6)

ondeCk

n ´e o coeficiente binomial, dado por

C_nk = n!

k!(n−k)!. (2.7)

Como pode-se deduzir da Eq. (2.6), construindo-se o conjuntoQmf at´e o n´ıvelnexistir˜ao

n+ 1 subconjuntos compostos por retˆangulos com ´areas iguais.

2.4 Espectro Multifractal do Objeto

Q

mf

Para realizar o cálculo do espectroDk, isto é, o cálculo da dimensão fractal associada a cada um dos k subconjuntos X, vamos utilizar o Teorema 1.4.2.1 com uma ligeira modifica¸cão:

D(X) = lim ǫ→0

logN(_X) log (1

ǫ)

= lim L→∞

logN(_X)

logL (2.8)

(52)

lado L = (r+s)n2. Dessa forma o lado das caixas quadradas utilizadas no c´alculo ser´a

ǫ= 1 e a área de cada retângulo que faz parte do monofractal dará o número de quadrados necessários para cobri-lo. Como podemos extrair da Eq. (2.6) a área dos retângulos do

k-´essimo conjunto do n´ıvel n´e dada por

ρ

1 +ρ

k 1 1 +ρ

n−k

, (2.9)

este valor, relembrando, está em unidades de L2_{. Como estamos considerando que} _L₌ (s+ r)n2 temos que o número de quadrados de lado ǫ = 1 necessários para cobrir um

retângulo dok-éssimo conjunto, isto é, sua área, é igual a

Ak =

ρ

1 +ρ

k 1 1 +ρ

n−k

(s+r)n22. (2.10)

Pode-se mostrar ainda que _1+ρρ = s

s+r e que 1 1+ρ =

r

s+r. Substituindo estas express˜oes em 2.10 n´os obtemos

Ak = _s

s+r

k _r

s+r

n−k

(s+r)n,

donde tiramos, ap´os simplifica¸c˜ao,

Ak =skrn−k. (2.11)

Como existem Ck

n retângulos no k-éssimo conjunto do multifractal de n´ıvel n, podemos afirmar que o número de quadrados de lado ǫ = 1 necessários para cobrir o conjunto fractalk do n´ıvel né igual a:

Nk =CnkAk =Cnkskrn−k. (2.12) Combinando estas informa¸cões nós chegamos ao valor da dimensão fractal do k-éssimo conjunto:

Dk = lim n→∞

logCk nskrn−k log (s+r)n2

(53)

de mesma área, células quadradas. Desta maneira o objeto é formado por um simples subconjunto com dimensão

D= lim n→∞

log (1 + 1)n log (1 + 1)n2

= 2 (2.14)

Este resultado ´e esperado uma vez que neste caso particular Qmf degenera em uma rede quadrada que tem dimens˜ao 2.

Na Fig. (2.3) temos um objeto multifractal que foi constru´ıdo at´e o n´ıvel n = 10 comρ= s_r = 1₂. Na Fig. (2.4) temos em destaque dois monofractais do objeto multifractal exibido na Fig. (2.3), s˜ao eles o subconjuntok= 3 e o subconjunto k = 5.

Figura 2.3: Objeto Qmf constru´ıdo at´e o n´ıvel n= 10 para ρ= 1₂.

Na Fig. (2.5) temos um objeto multifractal que foi constru´ıdo at´e o n´ıvel n = 10 comρ= s_r = 2₃. Na Fig. (2.6) temos em destaque dois monofractais do objeto multifractal exibido na Fig. (2.5), s˜ao eles o subconjuntok= 3 e o subconjunto k = 5.

(54)

Figura 2.4: Dois objetosQmf para n = 10e ρ= 1₂. A esquerda:` em destaque o subconjunto

k= 3. A direita:` em destaque o subconjunto k= 5.

Figura 2.5: Objeto Qmf constru´ıdo at´e o n´ıvel n= 10 para ρ= 2₃.

o n´umero k e faz a curva parecer mais densa. Na Fig. (2.8) vemos o espectro deDk para

(55)

Figura 2.6: Dois objetosQmf para n = 10e ρ= 2₃. A esquerda:` em destaque o subconjunto

k= 3. A direita:` em destaque o subconjunto k= 5.

Figura 2.7: Espectro multifractal de Qmf para n= 1000 e(s, r) = (1,2)

2.5 Densidade dos monofractais de

Q

mf

(56)

Figura 2.8: Espectro multifractal de Qmf para n= 1000 e(s, r) = (2,3)

Figura 2.9: Espectros de objetos Qmf para diversos(s, r).

disto é simples. A área de cada retângulo do k-éssimo conjunto do n´ıvel né dada por

(57)

com p= ρ/(1 +ρ) e q=q/(1 +ρ) (ver Eq. (2.9)). Esta área é dada em unidades deL2_, ou seja, da área total do multifractal. A área total dos retângulos existentes nok-éssimo conjunto do n´ıveln para um certo ρ(que está impl´ıcito em qe p) é dada por

fn(k) =Cnkpkqn−k (2.16) Como a Eq. (2.16) é dada em unidades de L2_{, o seu valor corresponde à fra¸cão da área} total do multifractal ocupada pelo monofractal. Sabemos que para valores grandes de n, a distribui¸cão binomial aproxima-se da distribui¸cão gaussiana

fn(k) = 1

√

2πnpqe

−12

k−np √_npq

2

. (2.17)

Da Eq. (2.17) podemos retirar duas conclusões sobre a densidade dos multifractais. A primeira é a que o monofractal de maior densidade é o da posi¸cão

k=np=n

ρ

1 +ρ

=n

s s+r

. (2.18)

A segunda conclusão é a respeito da densidade dos monofractais no limite n _{→ ∞}. O valor associado com a maior densidade é dado por

f(np) = √ 1

2πnpq. (2.19)

(58)

CAP´ITULO 3

PERCOLAC

¸ ˜

AO

3.1 Introdu¸

c˜

ao

O conceito da percola¸cão está relacionado com questões que surgem quando se con-sidera a conectividade geométrica em objetos da natureza. Em tese, pode ser de qualquer tipo de objeto. Um tipo de questão t´ıpica envolvida com a percola¸cão é a que se refere à estrutura dos aglomerados (conjunto de objetos conectados)[20]. Como eles se comportam com a mudan¸ca de um parâmetro geométrico do sistema? Na se¸cão 3.2 discutiremos esta questão com mais detalhes.

A percola¸cão está presente de diversas formas na natureza e em dispositivos criados pelo homem. Na biologia o conceito de percola¸cão aplica-se, por exemplo, ao espalhamento de epidemias[30]. A questão importante que esse conceito ajuda a responder é: qual a concentra¸cão cr´ıtica de indiv´ıduos sadios numa determinada rede para que a doen¸ca não se propague? Na qu´ımica o conceito aplica-se ao fenômeno de polimeriza¸cão, onde pequenas moléculas podem formar moléculas maiores através da ativa¸cão da liga¸cão entre elas. Se a probabilidade de ativa¸cão pé maior que a probabibilidade cr´ıtica, uma rede de liga¸cão, que se espalha por todo o sistema, é obtida. Isto acontece, por exemplo, no cozimento do ovo. Ao fornecermos calor, aumentarmos o valor de p e portanto as liga¸cões vão se formando até que exista uma grande estrutura conectada que atravessa todo o sistema. O ovo torna-se um gel com propriedades elásticas semelhantes às das gelatinas.

(59)

mes-mos.

3.2 Percola¸

c˜

ao por S´ıtios

3.2.1 Conceito

Seja uma rede quadrada comN_×N s´ıtios. Considera-se que cada s´ıtio pode assumir uma dentre duas propriedades. Digamos que ele possui probabilidadepde estar ocupado, e probabilidade 1−pde estar vazio. Na Fig (3.1) vemos exemplos de redes 5×5 parcialmente ocupadas. Observe que há a forma¸cão de aglomerados, isto é, conjunto de s´ıtios unidos pelas primeiras vizinha¸cas. No caso em que p = 0.6 observe que há três aglomerados, um com 10 s´ıtios e que atravessa toda a rede de um lado a outro, um com 4 s´ıtios e outro com apenas um s´ıtio. O tipo de modelo que acabamos de descrever é chamado

Figura 3.1: Exemplos de redes ocupadas com diferentes valores dep. Os aglomerados foram

coloridos de acordo com o seu tamanho.

(60)

estará conduzindo, ou não estará conduzindo. Isto depende apenas do valor de p. Para baixos valores dep, o sistema claramente não conduz. Para altos valores dep, o sistema conduz. Então surge a questão, qual o valor de p para o sistema come¸ca a conduzir? O

Figura 3.2: Esquema ilustrativo de um sistema artiﬁcial para o qual o modelo de percola¸c˜ao

se aplica. S´ıtios pretos, c´elulas condutoras, s´ıtios brancos, c´elulas isolantes.

sistema só conduz quando a corrente elétrica percola através do sistema, isto é, ela pode atravessar de um lado do sistema. O menor valor de p para o qual o sistema percola é chamado limiar de percola¸cão. Este valor separa duas fases distintas: a fase isolante da fase condutora. Neste sentido podemos dizer que o sistema sofre uma transi¸cão de fase, e como o parâmetro que regula a transi¸cão é um dado sobre caracter´ısticas geométricas do sistema (propor¸cão de elementos condutores em meio a elementos isolantes) dizemos que trata-se de uma transi¸cão de fase geométrica. Além da percola¸cão por s´ıtios, há inúmeros outros tipos de percola¸cão. São exemplos, a percola¸cão por liga¸cão, a percola¸cão de longo alcance, entre outras.

(61)

Figura 3.3: Exemplos de s´ıtios ocupados para rede64×64ep= 0.59. Aglomerado percolante est´a em verde.

s˜ao ditos pertencentes a uma classe de universalidade.

O primeiro trabalho que sugere a existência de universalidade nos fenômenos naturais foi produzido por Guggeheim [21]. Neste trabalho ele relata que as curvas de coexistência de oito fluidos distintos se ajustariam a uma só curva se o expoente cr´ıtico

β associado ao parˆametro de ordem dos fluidos fosse 1/3. Os fluidos utilizados por ele foramN e,Ar, Kr,Xe, N2, O2,CO eCH4.

Uma razão pela qual a percola¸cão é interessante é porque ela exibe fenômeno de liminaridade [28]. Se tra¸carmos a probabilidade RL de achar o aglomerado percolante para uma rede de tamanhoL_×L como uma fun¸cão dep (probabilidade de ocupa¸cão da rede), vamos encontrar que no limite em que L_{→ ∞},RL tende para uma fun¸cão escada de Heavyside, em outras palavras, quandop→ pc há uma descontinuidade genu´ına que separa duas diferentes fases macroscópicas: “sem aglomerado percolante” e a outra “com aglomerado percolante”. Essa mudan¸ca de fase é algo relevante, uma vez que uma suave mudan¸ca no parâmetro de controle microscópico p provoca uma mudan¸ca brusca num relevante parâmetro macroscópicoRL. Na Fig. (3.4) podemos ver que a medida em que aumentamos o tamanho do sistema,RL tende para a fun¸cão escada de Heavyside.