Método de Projeções Ortogonais

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM MATEM´

ATICA

APLICADA E ESTAT´ISTICA

Francin´ario Oliveira de Araujo

M´etodo de Proje¸c˜

oes Ortogonais

(2)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM MATEM´

ATICA

APLICADA E ESTAT´ISTICA

M´etodo de Proje¸c˜

oes Ortogonais

Francin´ario Oliveira de Araujo

Orientador

_{: Prof. Dr. Nir Cohen}

Coorientador

_{: Prof. Dr. Roberto Hugo Bielschowsky}

(3)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM MATEM´

ATICA

APLICADA E ESTAT´ISTICA

M´

etodo de Proje¸

c˜

oes Ortogonais

Francin´ario Oliveira de Araujo

Disserta¸cão de Mestrado apresentada ao Programa de P´ os-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Uni-versidade Federal do Rio Grande do Norte (PPGMAE-UFRN) como parte dos requisitos necessários para obten¸cão do t´ıtulo de Mestre em Matemática Aplicada e Estat´ıstica. Orientador: Prof. Dr. Nir Cohen

Coorientador: Prof. Dr. Roberto Hugo Bielschowsky

(4)

(5)

(6)

Dedicat´

oria

“Este trabalho ´e dedicado a minha m˜

ae, Maria Nazar´e, meus irm˜

aos Francimario e

Franklinario e minha noiva Ja´ıra, por terem sempre me apoiado e me ensinado as coisas que

(7)

Agradecimentos

Primeiro agrade¸co a Deus por estar comigo durante toda minha vida, sempre colocando pessoas boas em meu caminho, ´otimos amigos e excelentes professores que contribu´ıram bastante na minha vida tanto pessoal quanto acadˆemica.

Aos professores Nir Cohen e Roberto Hugo B. pela orienta¸c˜ao e co-orienta¸c˜ao, e pela confian¸ca depositada em mim, acreditando na minha capacidade. Obrigado por ter feito conhecer os problemas inversos, por terem sido meus professores no mestrado, por me aconselhar e me ajudar a trilhar meu caminho profissional.

A minha mãe Maria Nazaré pelo apoio, pela confian¸ca, por sua dedica¸cão e por ter sido pai e mãe para mim e meu irmãos.

Aos meus irm˜aos Francimario e Franklinario e minha noiva Ja´ıra por ter sempre me apoiado. A toda minha fam´ılia em especial: As Minhas tias Meyre e Ana Selma e minha av´o Esmeraldina que sempre torceram por mim e me incentivaram a continuar.

A todos os professores do Programa PPGMAE que contribu´ıram bastante para minha forma¸c˜ao. Ao professor Pledson (UFRN) pelos conselhos na disciplina de semin´ario e pelo incentivo.

Aos meus grandes amigos da gradua¸c˜ao Moises, Aparecida e Camila que sempre me incentivaram a continuar e por tudo que eles me ensinaram.

Aos meus colegas de mestrado do PPGMAE, em especial Felipe e Kaline (“cabe¸cão”), pois eles me ajudaram bastante em toda minha trajetória acadêmica no programa PPGMAE, sempre prontos para me ajudar.

Aos meus colegas Elvis, Aldemir, Ivanildo e H´erica pelos momentos de descontra¸c˜ao.

Ao meu amigo Manassés, que além de grande amigo ele também é colega de trabalho, pelas dicas na disserta¸cão e na defesa.

(8)

Resumo

O problema abordado nesta disserta¸cão é a prova da propriedade de limita¸cão para os iterados de um algoritmo iterativo emℜd _{que aplica em cada passo uma proje¸c˜}_{ao ortogonal sobre uma reta em}_ℜd_,

inde-xada em uma fam´ılia de retas dada (possivelmente infinita) e permitindo ordem arbitrária na aplica¸cão das várias proje¸cões. Este problema foi abordado em um artigo de Bàràny et al. em 1994, que encontrou uma condi¸cão necessária e suficiente para o caso d = 2 e analisou também o caso d > 2 sob algumas condi¸cões técnicas. Porém, este artigo usa argumentos intuitivos não triviais e nas suas demonstra¸cões nos parece faltar rigor. Nesta disserta¸cão detalhamos e completamos as demonstra¸cões do artigo de Barány, fortalecendo e clareando algumas de suas proposi¸cões, bem como propiciando pontos de vista complementares em alguns aspectos do artigo em tela.

(9)

Abstract

The problem treated in this dissertation is to establish boundedness for the iterates of an iterative algo-rithm in ℜd _{which applies in each step an orthogonal projection on a straight line in} _ℜd_{, indexed in a}

(possibly infinite) family of lines, allowing arbitrary order in applying the projections. This problem was analyzed in a paper by B`ar`any et al. in 1994, which found a necessary and sufficient condition in the cased= 2, and analyzed further the case d >2, under some technical conditions. However, this paper uses non-trivial intuitive arguments and its proofs lack sufficient rigor. In this dissertation we discuss and strengthen the results of this paper, in order to complete and simplify its proofs.

(10)

Sum´

ario

1 Introdu¸c˜ao 10

1.1 Descri¸c˜ao do Problema . . . 10

2 Uma breve introdu¸cão ao método de proje¸cões 12 2.1 O problema geral . . . 12

2.2 Uma visão geral de alguns métodos de proje¸cões . . . 13

2.2.1 O m´etodo de Kaczmarz . . . 14

2.2.2 O m´etodo da relaxa¸c˜ao de Agmon, Motzkin e Schoenberg . . . 14

2.2.3 A generaliza¸cão do método de proje¸cões para conjuntos convexos . . . 15

2.2.4 Problemas n˜ao convexos . . . 16

2.2.5 Outra formula¸c˜ao para o problema de viabilidade convexa . . . 17

2.2.6 Uma abordagem para equa¸c˜oes n˜ao lineares . . . 18

2.3 Aplica¸c˜oes . . . 18

2.3.1 Reconstru¸c˜ao de imagens a partir de proje¸c˜oes . . . 19

2.3.2 Tomografia computadorizada . . . 19

2.3.3 O problema da fase . . . 20

2.4 Estrutura da Disserta¸c˜ao . . . 20

3 Fam´ılia de Retas no Plano 21 3.1 Propriedade da Proje¸c˜ao Limitada . . . 21

3.2 O Teorema Original . . . 23

3.3 O resultado principal . . . 25

3.4 Demonstra¸c˜ao do Teorema 3.1 . . . 27

4 Fam´ılia de Retas emRd ₄₀ 4.1 Situando o Problema de proje¸c˜ao Limitada comd >2 . . . 40

4.2 Consequˆencias da propriedade da proje¸c˜ao limitada em retas emℜd _{. . . .} ₄₁

(11)

9

5 Considera¸c˜oes Finais 54

5.1 Conclus˜ao . . . 54 5.2 Trabalhos Futuros . . . 55

A Resultados Da Geometria Euclidiana Plana 56

B Resultados de ´Algebra Linear 58

C Trajet´oria Ortogonal 61

D Conjuntos Convexos e Abertos 62

E Resultados de C´alculo 65

(12)

Cap´ıtulo 1

Introdu¸

c˜

ao

No artigo [4], Bàràny et al. apresentam alguns resultados interessantes a respeito do método de proje¸cões ortogonais sobre um número infinito de retas emℜd_, ₍_d_∈_N_{). O artigo é matematicamente}

denso e sua leitura é dif´ıcil. Suas demonstra¸cões são intuitivas e as vezes falta o rigor necessário. Neste trabalho detalhamos estas demonstra¸cões e acrescentamos novas observa¸cões e nova intui¸cão para o entendimento do problema.

1.1 Descri¸

c˜

ao do Problema

Sejam d∈N dado,Lum conjunto de retas em ℜd _{e um ponto}_x

0∈ ℜd. Gera-se uma sequˆencia de pontosxn∈ ℜd, da seguinte maneira

xn+1=Pjnxn (1.1)

ondePjné a proje¸cão ortogonal sobre uma das retas deL, arbitrariamente escolhida (ver o apêndice B).

O problema é verificar que a sequência (xn)∞n=1 gerada desta maneira é necessariamente limitada. Este problema foi solucionado por Aharoni et al. em [2], quandoLé uma fam´ıliafinitade subespa¸cos afins em ℜd_{. Meshulam e Bargury deram outras demonstra¸c˜}_{oes para o mesmo problema em [86], [6]}

respectivamente. Bargury tamb´em considerou o caso de reflex˜oes emℜd _{e proje¸c˜}_{oes com relaxa¸c˜}_{ao (ver}

[27]) emℜ2_.

Em 1991, B`ar`any et al. [4] generalizaram o resultado de Aharoni et al. [2] para uma fam´ıliainfinita

de retas, obtendo a condi¸cão necessária e suficiente para a limita¸cão da sequência (xn)∞n=1 em ℜ2; além disto, uma condi¸cão apenas necessária, e outra apenas suficiente, para a mesma limita¸cão emℜd_{, d >}_2.

Neste trabalho detalhamos e aprofundamos os teoremas de B`ar`any et al. [4].

O problema descrito acima surgiu dentre a teoria geral de m´etodos de proje¸c˜oes. DadosQ1, Q2, ..., Qn

(13)

1.1 Descri¸

c˜

ao do Problema

11

de um pontox0∈ ℜd qualquer, por

xn+1=Pjnxn (1.2)

ondePjn´e a proje¸c˜ao ortogonal sobre um dos conjuntosQipara (i= 1,2, ..., n). Como descrevemos, este

método geral e suas várias generaliza¸cões têm várias aplica¸cões. Normalmente, supõe-se que os conjuntos

Qi são convexos, fechados e ∩Qi 6= ∅ (condi¸cão de viabilidade) e procura-se provar a convergência

(xn)→x∗, ondex∗ ∈ ∩Qi. Por´em, se∩Qi =∅, como em nosso problema, apenas pode-se esperar, no

melhor dos casos, provar que a sequˆencia (xn)∞n=1 ´e limitada.

Oproblema de viabilidadepara os conjuntosQipara (i= 1,2, ..., n) consiste no estudo de

algorit-mos para encontrar um ponto na interse¸cão∩Qi. Os algoritmos de proje¸cão são normalmente estudados

(14)

Cap´ıtulo 2

Uma breve introdu¸

c˜

ao ao m´

etodo de

proje¸

c˜

oes

2.1 O problema geral

Historicamente, as primeiras aplica¸cões do método de proje¸cões foram feitas sobre conjuntos Qi dos

seguintes tipos:

1. Hiperplano: conjunto de pontosx∈ ℜd _{tal que}

ha, xi=b (2.1)

2. Semiespa¸co: conjunto de pontos x∈ ℜd _{tal que}

ha, xi ≤b (2.2)

3. “Hiper fatia”: conjunto dosx∈ ℜd _{que pertencem `a interse¸c˜}_{ao entre semiespa¸cos paralelos}

b−ǫ≤ ha, xi ≤b+ǫ (2.3)

coma∈ ℜn _e_b_{∈ ℜ}_.

(15)

2.2 Uma vis˜

ao geral de alguns m´

etodos de proje¸

c˜

oes

13

Entre os primeiros trabalhos mencionamos Kaczmarz [71] que usou a ordem c´ıclica (ver [27]) de proje¸c˜oes

P1, P2, ..., Pn, P1, P2, ..., Pn, ...

emℜd_{e Von Neumann [70] que considerou duas proje¸c˜}_{oes sobre subespa¸cos fechados no espa¸co de Hilbert.}

O m´etodo para hiperplanos era usado para resolver sistemas linearesAx=b, de modo similar aos m´etodos de Gauss-Seidel e Jacobi.

Quando queremos resolver um sistema linear Ax=b, se A é invert´ıvel, então a solu¸cão do sistema será x=A−1_b_{. Mas, existem v´}_{arias situa¸c˜}_{oes em que a matriz}_A_{“dificulta” a resolu¸c˜}_{ao do sistema, ou} seja,Anão é invert´ıvel ou de grande porte ou mal condicionada, e/ou não-simétrica.

Existem v´arias t´ecnicas para tentar resolver tais problemas, como por exemplo: m´ınimos quadrados

emétodos iterativos, incluindo o método de proje¸cões. Sugerimos a leitura do livro [53].

Em 1971, Tanabe [104] mostra que o método de proje¸cões funciona bem para sistemas singulares ou não singulares. Ele também determina o espa¸co formado pelo conjunto solu¸cão, caso exista.

Para aprofundamento neste assunto sugerimos a leitura dos artigos: [100], [9], [94], [23], [8], [28] e [29], [72] e [14].

Para outros tipos de abordagens veja [27], [10], [62], [74], [40], [41] e [101]. Para ver várias consi-dera¸cões práticas sobre implementa¸cão, [57], [59], [61], [43], [44], [76] e [82].

O artigo de Censor [27] descreve alguns procedimentos para determinar a ordem da sequência de proje¸cões, ou seja, a escolha dejn na equa¸cão (1.2). A ordem c´ıclica é a mais popular entre elas.

2.2 Uma vis˜

ao geral de alguns m´

etodos de proje¸

c˜

oes

Nesta se¸cão, vamos rever alguns métodos de proje¸cões. As informa¸cões sobre cada método aqui apresentado, estão organizadas da seguinte maneira: (1) o problema o qual ele é utilizado para resolver, (2) formula¸cão do algoritmo, (3) uma interpreta¸cão geométrica e (4) comentários e referências.

Subse¸c˜ao

Nome

Natureza

Restri¸c˜oes

2.2.1 Kaczmarz

Equa¸c˜ao linear

_h

a

i

, x

i

=

b

i

2.2.2 Agmon et al.

Inequa¸c˜ao linear

_h

a

i

, x

i ≤

b

i

2.2.3 Gubin et al.

Conjuntos convexos

x

_{∈ ∩}

Q

Tabela 2.1: Os métodos de proje¸cões da se¸cão 2.2

(16)

2.2 Uma vis˜

ao geral de alguns m´

etodos de proje¸

c˜

oes

14

2.2.1 O m´

etodo de Kaczmarz

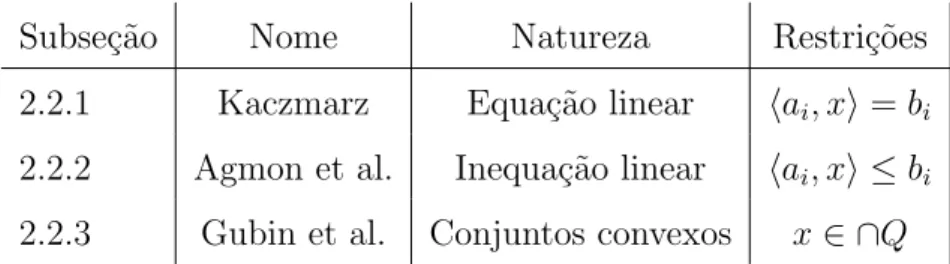
O problema. hai, xi=bi, i∈M (ou seja, (2.1)), assumindo que a solu¸cão existe. O método. Iniciando emx(0)_{∈ ℜ}d _{qualquer. O passo geral é dado por}

x(k+1)₌_x(k)₊_λ

k

bik−

aik, x

(k)

kaikk

2 aik

Tipo de controle. Quase c´ıclico.

Interpreta¸c˜ao geom´etrica. Dadox(k)_{e o hiperplano}_H

ik=

x∈ ℜd_;_h_a

ik, xi=bik , determinado

pela equa¸c˜ao haik, xi=bik, encontramos x

(k+1)_{baixando uma perpendicular de} _x(k) _{na reta}_H

ik. Para

o relaxamento unitário, λk = 1 e para todo k ≥0,x(k+1) é a proje¸cão ortogonal dex(k) paraHik, ver

figura (2.1).

Figura 2.1: O m´etodo de Kaczmarz.

Comentários e referências. O método foi originalmente estudado por Kaczmarz [71] que provou a convergência com o relaxamento unitário, para sistemas quadrados não singulares. Foi denotado por ART (algebraic reconstruction technique) por Gordon et al. [49], na reconstru¸cão de imagem a partir de proje¸cões, ver também Herman et al. [60]. Tanabe [104] estudou o método para matrizes em geral. A rela¸cão com métodos SOR foi estudada por Elfving et al. [11]. McCormick [85] investigou o método em espa¸co de Hilbert e deu uma extensão para equa¸cões não-lineares. Veja também [12], [42], [105], [67], [3] e [83].

2.2.2 O m´

etodo da relaxa¸

c˜

ao de Agmon, Motzkin e Schoenberg

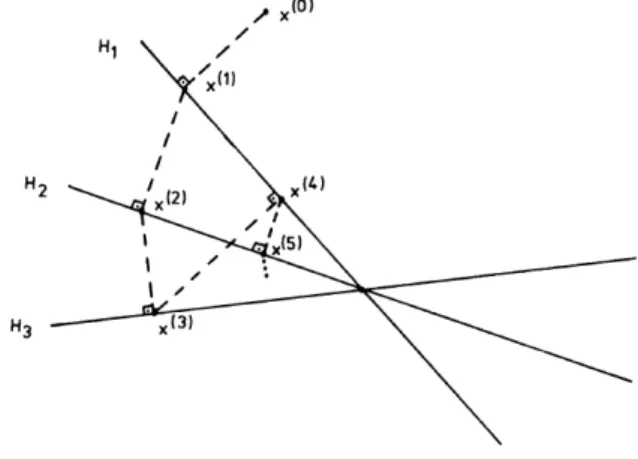
O problema:

Encontrar x∈ ℜd _{tal que}_h_a

i, xi ≤bi para todo i∈M (2.4)

(17)

2.2 Uma vis˜

ao geral de alguns m´

etodos de proje¸

c˜

oes

15

M´etodo:

Iniciando em x(0)_{∈ ℜ}d _{qualquer. O passo geral ´e dado por}

x(k+1)₌_x(k)₊_c(k)_a

ik

onde,

c(k)=min 0, λk

bik−

aik, x

(k)

kaikk

2

!

Controle: Quase c´ıclico.

Interpreta¸c˜ao geom´etrica: Dadox(k)_{e o semiespa¸co} _L

ik=

x∈ ℜd_;_h_a

ik, xi ≤bik , determinado

pela inequa¸c˜aohaik, xi ≤bik, sex

(k)_∈_L

ik ent˜aox

(k+1)₌_x(k)_{, se}_x(k)_∈_/ _L

ik ent˜aox

(k+1)_{encontra-se na} reta perpendicular aHik que passa emx

(k)_{, onde}_H

ik´e o semiespa¸co limitado porLik. Para a relaxa¸c˜ao

unit´aria,x(k+1) _{´e a proje¸c˜}_{ao ortogonal de} _x(k)_sobre_L

ik. Ver figura (2.2).

Figura 2.2: O método de Agmon, Motzkin and Schoenberg com relaxa¸cão unitária.

Coment´ario e referˆencias

Agmon [1] e Motzkin et al. [87] publicaram o método em 1954. Na década de 70 esse método foi amplamente estudado por Goffin [45], [46], [47], [48] que também estabeleceu sua rela¸cão com a otimiza¸cão por subgradiente (ver, por exemplo, [92]). Um resumo da literatura pode ser encontrada em [37]. Generaliza¸cões podem ser vistas em [88] para controles não-c´ıclicos.

2.2.3 A generaliza¸

c˜

ao do m´

etodo de proje¸

c˜

oes para conjuntos

convexos

(18)

2.2 Uma vis˜

ao geral de alguns m´

etodos de proje¸

c˜

oes

16

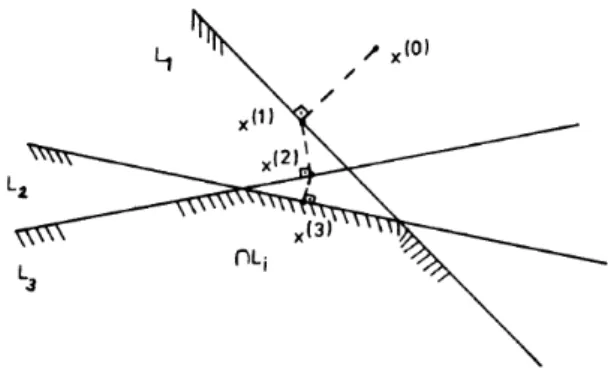
Problema: Dada uma fam´ılia (Qi)i∈M de conjuntos convexos e fechados deℜd com∩i∈MQi 6=∅,

encontrar um pontox∈ ∩i∈MQi. Este é o problema de viabilidade convexa. Método: Iniciando dex(0)_{∈ ℜ}d _{qualquer. O passo geral é dado por:}

x(k+1)₌_x(k)₊_λ

k

PQik(x

(k)₎

−x(k) ondePQ(x) representa a proje¸c˜ao ortogonal de xsobre o conjuntoQ.

Controle: Quase c´ıclico.

Interpreta¸cão geométrica: Para o relaxamento unitário, λk = 1 e para todo k ≥ 0, x(k+1) é a

proje¸c˜ao ortogonal de x(k) _{sobre o conjunto}_Q

ik, ver figura (2.3).

Figura 2.3: O m´etodo das proje¸c˜oes ortogonais sucessivas

Comentários e referências: Ao escolherQicomo o hiperplano ou meio plano, os métodos da se¸cão

(2.2.1) ou (2.2.2) s˜ao obtidos, respectivamente.

2.2.4 Problemas n˜

ao convexos

Quando os conjuntos Qk não são todos convexos, o método de proje¸cões não tem convergência

garantida, mesmo quando o problema é viável, ou seja,∩Qi6=∅. A aplica¸cão no problema da fase é do

tipo

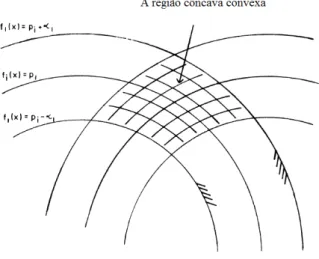
fi(x) =pi, i∈M

ondefi:ℜn → ℜs˜ao fun¸c˜oes convexas, ou melhor

pi−ǫi≤fi(x)≤pi+ǫi

(19)

2.2 Uma vis˜

ao geral de alguns m´

etodos de proje¸

c˜

oes

17

2.2.5 Outra formula¸

c˜

ao para o problema de viabilidade convexa

O problema de viabilidade convexa pode tamb´em ser escrito como

encontrar x∈ ℜd tal que gi(x)≥0, para todo i∈M (2.5)

ondegi(x) s˜ao convexas. Uma forma de abordagem para (2.5) seria considerar conjuntos convexos

Qi=x∈ ℜd;gi(x)≤0 , i∈M (2.6)

e buscar um ponto comum, ou seja, umxque pertence a∩i∈MQi. Esse problema, por sua vez, poderia,

em princ´ıpio, ser abordado pelo m´etodo da se¸c˜ao (2.2.3).

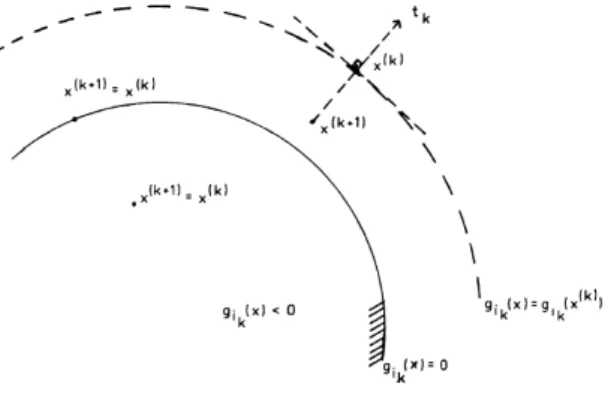
Censor et al. [20] descreveram uma variante que resolve (2.5), efetuando, a cada passo, um movimento em uma dire¸cão determinada pelo gradiente (ou subgradiente, caso a fun¸cão não seja diferenciável) da fun¸cãogik calculada na atual itera¸cãox

(k)_.

M´etodo: iniciando com x(0)_{∈ ℜ}d _{qualquer, onde o passo ´e dado por}

x(k+1)₌

  

x(k)_, _se _g

ik(x

(k)₎_≤₀

x(k)₋_λ

k gik(x(

k)₎

ktkk2 tk cc

ondetk ∈∂gik(x

(k)_{), ´e qualquer subgradiente de}_g

ik em x

(k)_{, ver, por exemplo [93].}

Controle: C´ıclico.

Interpreta¸cão geométrica: Em uma itera¸cão t´ıpica, a fun¸cãogik(x

(k)₎_≤ _{0 ´e tomada de acordo} com um controle c´ıclico. Sex(k)_{satisfaz a desigualdade} _g

ik(x

(k)₎_≤_{0 então nenhum movimento é feito,} caso contrário, um movimento é feito na dire¸cão oposta ao (sub)gradiente degikemx

(k)_{, ver figura (2.4).}

Figura 2.4: Passo t´ıpico do m´etodo CSP para o caso convexo.

(20)

2.3 Aplica¸

c˜

oes

18

2.2.6 Uma abordagem para equa¸

c˜

oes n˜

ao lineares

Existe uma abordagem equivalente por fun¸cões não lineares. Considerando um sistema de equa¸cões

fi(x) =pi, i∈M (2.7)

onde fi : ℜd → ℜ e M = {1,2, ..., m}, e utilizando argumentos semelhantes, podemos substituir esse

sistema por um problema de viabilidade n˜ao-linear da seguinte forma

encontrar um x∈ ℜd _{tal que p}

i−ǫi≤fi(x)≤pi+ǫi, i∈M (2.8)

ondeαi s˜ao tolerˆancias apropriadas.

Sefi(x) são fun¸cões convexas para todos osi∈M, então (2.8) representa um problema de viabilidade

convexa-cˆoncava mista, ver figura (2.5). Tal abordagem foi dada em Censor et al. em [26], para o problema da tomografia por emiss˜ao computadorizada, onde um determinado modelo discretizado do problema leva a um sistema enorme e esparso como (2.8). Ver, por exemplo, Budinger et al. [16].

Uma extensão do método c´ıclico de proje¸cões por subgradiente para o caso não convexo foi formulada por Censor et al. [26].

Figura 2.5: O problema de viabilidade convexa-cˆoncava para resolver equa¸c˜oes

n˜ao-lineares.

2.3 Aplica¸

c˜

oes

(21)

2.3 Aplica¸

c˜

oes

19

2.3.1 Reconstru¸

c˜

ao de imagens a partir de proje¸

c˜

oes

Problemas na deteçcão de sinais e recupera¸cão de imagens às vezes podem ser reformulados como um problema de viabilidade convexa (convex feasibility problem), ou seja, consistem em encontrar um ponto na interse¸cão de uma fam´ılia finita de conjuntos convexos e fechados. A reconstru¸cão de imagens a partir de proje¸cões é um procedimento de extrema utilidade em muitos campos cient´ıficos.

Os algoritmos de proje¸cão, tanto os baseados em conjuntos convexos quanto os demais, têm sido muito utilizados na área de processamento de imagens. O método de proje¸cões em conjuntos convexos, “POCS” (Projections Onto Convex Sets), é um poderoso algoritmo de restaura¸cão de imagens que utiliza informa¸cões a priori das mesmas, como conjuntos de restri¸cões, a fim de solucionar o problema, ver [98]. O uso de “POCS” para solu¸cão de sistemas lineares através de proje¸cões ortogonais iterativas entre os hiperplanos descritos por cada equa¸cão é também chamado de algoritmo de Row-Action Projection, RAP, ou Algebraic Reconstruction Technique, ART, que foi inicialmente desenvolvido por Kaczmarz [71].

Sugerimos a leitura de [32], [103], [91], [98], [97], [68], [73] e [89].

2.3.2 Tomografia computadorizada

A tomografia computadorizada (Computerized Tomography) tornou-se uma ferramenta indispensável em hospitais e cl´ınicas, e influenciou modelos afins nas áreas de testes indestrut´ıveis e s´ısmica. Matema-ticamente, o modelo principal é a inversão da transformada (linear) de Radon, ou adapta¸cões da mesma para incluir o efeito da atenua¸cão. Portanto, em princ´ıpio, o modelo da tomografia é linear (Ax =b). Porém, o problema é de grande porte e mal condicionado, de modo que métodos adaptados para matrizes de grande porte (e esparsas) devem ser utilizados. Veja [104], [61].

No modelo tomogr´afico, as proje¸c˜oes 2−D de tomografia computadorizada de um objeto 3−D

(seja o modelo PET ou SPECT) são obtidas com medidas registradas externamente em vários ângulos de referência. A partir destas proje¸cões 2−D, os dados originais do objeto 3−D devem ser reconstru´ıdos utilizando-se técnicas apropriadas. Várias técnicas e algoritmos estão dispon´ıveis hoje em dia, permitindo a reconstru¸cão da imagem a partir das proje¸cões obtidas. O método de inversão direta (retro-proje¸cão ou back-projection) é usado apenas para problemas simples de resolu¸cão baixa, embora hoje em dia esteja ficando mais viável com o avan¸co da computa¸cão. Métodos que utilizam conceitos da estat´ıstica são bastante populares e reduzem o problema mal-condicionado a um problema de otimiza¸cão com melhor condicionamento. Mencionamos aqui o método ML (maximal likelihood), EM/OS-EM/GEM/RAMLA (minimum expectation, ou máxima verossimilhan¸ca, e suas generaliza¸cões) e métodos Bayesianos. Veja [97], [58], [63] e [64].

(22)

2.4 Estrutura da Disserta¸

c˜

ao

20

Ver [49], [65], [59] e [107].

A técnica é semelhante à do método de Gauss-Seidel (GS). O custo computacional por itera¸cão é aproximadamente igual ao dos métodos de gradiente. Para imagens avaliadas continuamente, GS é usado por ter uma convergência melhor. Além disso, GS é bem adequado para segmenta¸cão quando a imagem deve ser discretizada. Veja [97].

Para maior aprofundamento do assunto, sugerimos a leitura dos artigos: [99], [90], [34], [35], [107], [31], [102], [75], [96], [78], [95], [77] e [108].

2.3.3 O problema da fase

No problema da fase (phase retrieval) procura-se uma fun¸cão real f(x), que representa a escala de cinza de uma imagem, a partir de|T(u)|, ondeT(u) é a transformada de Fourier def(x). Este problema é importante na astronomia, e foi tratado por Fienup usando vários esquemas de proje¸cão. Veja [39] e [7].

Um problema similar ocorre em microscopia eletrˆonica. Neste caso, dado f(x) complexa, queremos recuperarf(x) a partir de|f(x)|e|T(u)|, ver [84].

2.4 Estrutura da Disserta¸

c˜

ao

A presente disserta¸cão encontra-se dividida em cinco cap´ıtulos e um apêndice. Nosso trabalho será dividido em quatro partes: No Cap´ıtulo 2 expusemos uma revisão de conceitos importantes do método de proje¸cões.

No Cap´ıtulo 3, vamos mostrar que, uma fam´ılia de retas L no plano, sem pares de retas paralelas, tem a propriedade da proje¸cão limitada se, e somente se, o conjunto formado pelos pontos de interse¸cão entre duas retas quaisquer está contido em um disco limitado.

No Cap´ıtulo 4, vamos mostrar que se uma fam´ılia de retas L em ℜd _(d_>_{2) tem a propriedade de}

proje¸cão limitada, então F(u) é limitada e satisfaz as seguintes condi¸cões

|(F(u)−F(v))(u−v)| ≤c|u−v|2,∀u, v∈T

onde F(u) é a proje¸cão ortogonal da origem na reta que tem dire¸cão u ∈ T, onde T é um conjunto simétrico da esferaSd−1 _onde_F₍_u_{) está definida; e}

Z

Γ

F(u)·du= 0 (2.9)

para toda curva suave e fechada Γ⊂T. Reciprocamente, seT =Sd−1_,_F _∈_C1 _e_F _{satisfaz (2.9), ent˜ao} a fam´ıliaLpossui a propriedade da proje¸c˜ao limitada.

(23)

Cap´ıtulo 3

Fam´ılia de Retas no Plano

Neste cap´ıtulo, investigamos a propriedade de proje¸c˜ao limitada emℜd_,₍_d_≥_{2) na se¸c˜}_{ao 3.1 e depois}

enunciamos e provamos um resultado de Bàràny et al. [4] sobre a caracteriza¸cão desta propriedade em

ℜ2_{nas se¸c˜}_{oes 3.2 e 3.3. Nossa demonstra¸c˜}_{ao na se¸c˜}_{ao 3.3 ´e mais detalhada e rigorosa que a demonstra¸c˜}_ao na vers˜ao original.

3.1 Propriedade da Proje¸

c˜

ao Limitada

Queremos caracterizar sistemas Θ de proje¸cões sobre retas em ℜ2_{, cujos iterados ficam limitados} a um disco de raio r fixo, independentemente da ordem na qual se escolhe as proje¸cões. Nesta se¸cão, iniciamos uma discussão que vale emRd_{, para todo}_d_≥_2.

Defini¸cão 3.1 (Sequência Uniformemente Limitada) Seja Θuma fam´ılia de aplica¸cõesPi:ℜd→

ℜd_{. Dizemos que}_Θ_{´e uniformemente limitada em} _x

0∈ ℜd, se existet∈ ℜ+ tal que

kPkPk−1· · ·P1(x0)k ≤t

para todok∈N e todos Pk, Pk−1,· · · , P1∈Θ.

Defini¸c˜ao 3.2 (Conjunto Invariante) Seja Θ como definido em 3.1. Um conjunto W ⊂ ℜd _{´e dito}

invariante para Θ, se P w∈W para todo P∈Θe para todo w∈W.

Uma maneira de construir um conjunto invariante (o chamado “minimal”) em torno de um conjunto (n˜ao necessariamente invariante)W0seria considerar

(24)

3.1 Propriedade da Proje¸

c˜

ao Limitada

22

Proposi¸c˜ao 3.1 Dada uma fam´ılia Lde subespa¸cos afins1 _em _ℜd _{e um ponto}_x

0∈ ℜd, denotemos por Θ =Pi:ℜd−→li , ondePi representa a proje¸c˜ao ortogonal dex0 sobre a reta li. (ver o apˆendice B).

As seguintes afirma¸c˜oes s˜ao equivalentes

(i) Cada sequência de proje¸cõesPi1, Pi2,· · · , Pik,· · · aplicada em x0 é limitada.

(ii) A fam´ılia Θ´e uniformemente limitada emx0.

(iii) O conjunto invariante Θ(x0)´e limitado.

Demonstra¸c˜ao.

Nossa demonstra¸cão segue o contorno geral da demonstra¸cão original ( Bárány et al. [4] proposi¸cão 1 ), porém é mais clara. As implica¸cões (ii)⇒(iii)⇒(i) são bem diretas e falta só mostrar (i)⇒(ii). Seja

C = sup{kPn...P1x0k} ≤ ∞ ondePi s˜ao proje¸c˜oes emL, n∈N.

Queremos mostrar que C <∞, supondo (i). Iniciamos escolhendo uma sequˆencia (yi)∞i=1 que atinge

C, ou seja,

yi=Rix0 kyik →C

quandoi7→ ∞eRié um produto de proje¸cões emL. Defina também a sequência associada (xi)∞i=1 por

xn =Rnxn−1 n= 1,2, ...

Usando a propriedade contrativa dosPi (kPi(x)k ≤ kxk), e portanto, dosRn, temos

kynk ≤ kyn−xnk+kxnk=kRnx0−Rnxn−1k+kxnk ≤ kx0−xn−1k+kxnk

≤ kx0k+kxn−1k+kxnk ≤3A

ondeA=supkxnk. Por hipótese,A <∞já quex1, x2, ...., xné uma subsequência de uma sequência de

proje¸c˜oes da fam´ılia Θ, definida a partir dex0. PortantoC≤3A <∞.

Conforme Bárány et al. [4], vamos definir a propriedade da proje¸cão limitada.

Defini¸cão 3.3 (Propriedade da Proje¸cão Limitada) Dizemos que uma fam´ılia L possui a propri-edade da proje¸cão limitada, quando a fam´ılia L satisfaz uma das condi¸cões equivalentes da proposi¸cão 3.1.

Note que a propriedade da proje¸cão limitada é independente da escolha do ponto x0, já que para toda sequência finita de proje¸cões emL

kPk· · ·P1(x0)−Pk· · ·P1(y0)k ≤ kx0−y0k.

1_{Dizemos que o conjunto}_W ₌_a₊_U _{´e um subespa¸co afim de}_ℜd_{, se}_a_{∈ ℜ}d_e_U _{⊂ ℜ}d_{for um subespa¸co}

(25)

3.2 O Teorema Original

23

Na an´alise desta propriedade vale apenas a propriedade contrativa das proje¸c˜oes Pl. Assim, este

resultado generaliza às proje¸cões sobre conjuntos convexos (e não apenas às proje¸cões sobre conjuntos afins).

3.2 O Teorema Original

Dado uma reta qualquer l ∈ ℜd_{, denotemos por} _F₍_l₎ _{∈ ℜ}d _{o ponto de menor norma na reta} _l_{, ou}

seja,F(l) =Pl(O) (a proje¸c˜ao ortogonal da origem eml).

Lema 3.1 Se L´e uma fam´ılia de conjuntos afins emℜd _{com a propriedade da proje¸c˜}_{ao limitada, ent˜}_ao

o conjuntoF(L) ={F(l), l∈L}´e limitado em ℜd_. Demonstra¸c˜ao.

Argumentamos por contradi¸c˜ao. Seja u1, u2, ..., un, ... uma sequˆencia tal que kF(un)k → +∞, e

forma-se a sequˆencia de iterados

xn=Pn...P1x0

comx0 qualquer. O fato queF(un) =Pn(O) minimiza a norma emln, implica portanto

kxnk ≥ kF(un)k → ∞

o que é uma contradi¸cão à propriedade da proje¸cão limitada.

A limita¸cão deF(L) é suficiente, mas não necessária para garantir a propriedade da proje¸cão limitada (ver figura 3.2). O corolário 3.1 mais adiante mostra a condi¸cão necessária e suficiente.

Lema 3.2 Se l1, l2 são retas em ℜd com ponto de interse¸cão ξ, então os iterados xn do método de

proje¸c˜oes entrel1 el2 convergem para ξ.

Demonstra¸c˜ao.

Este é o caso particular dos teoremas obtidos por Von Neumann [70] e Kaczmars [71], e pode ser verificado facilmente poiskxk+1−ξk=cos(α)kxk−ξk, ondeαé o ângulo entre l1 el2

Caso as retasl1, l2∈ ℜdnão se interceptem, então a sequência de iteradosxndo método de proje¸cões

converge para pontos que torna as retas mais pr´oximas.

Corol´ario 3.1 Seja L uma fam´ılia de retas em ℜ2_{, que n˜}_{ao possui retas paralelas. Seja} _Ω _{o conjunto}

(26)

3.2 O Teorema Original

24

Demonstra¸c˜ao.

Suponha por contradi¸c˜ao que existamξ1, ξ2, ξ3, ...∈Ω comkξik 7−→ ∞. Sejax0 qualquer, e defina

xn= (Pn,1Pn,2)k

n

xn−1

ondePn,1Pn,2 s˜ao as duas proje¸c˜oes nas duas retas ln,1, ln,2 ∈L que se interceptam emξn; escolhemos

kn>>1 tal quekxn−ξnk ≤1, argumentando pelo lema 3.2.

Assim,kxnk ≥ kξnk − kxn−ξnk ≥ kξnk −1→ ∞, implicando na perda da propriedade da proje¸c˜ao

limitada.

Figura 3.1:

Ilustrando a situa¸cão onde a fam´ılia não possui a propriedade de proje¸cão limitada.

Agora vamos dar um contra-exemplo para a rec´ıproca do lema 3.1. Tomemos

L=nl(θ); 0≤θ≤π₄o

onde para cada θ6= 0,l(θ) é a reta com inclina¸cãotg(θ) que passa na origem, el(0) é a reta horizontal que passa em (0,−4).

(27)

3.3 O resultado principal

25

O conjunto Ω seria ilimitado. Conforme o corolário 3.1, a limita¸cão de Ω é uma condi¸cão necessária para a propriedade da proje¸cão limitada. De fato, Bárány et al. [4] (teorema 1) mostra que é também suficiente.

A demonstra¸cão deste resultado em Bárány et al. [4] é intuitiva e informal. A seguir, fornecemos uma demonstra¸cão formal e um novo ponto de vista sobre o problema: a propriedade Lipschitz da fun¸cão

F(u), e a maneira mon´otona na qual as retasl(θ) interceptam grandes c´ırculos.

3.3 O resultado principal

Precisamos das seguintes defini¸c˜oes.

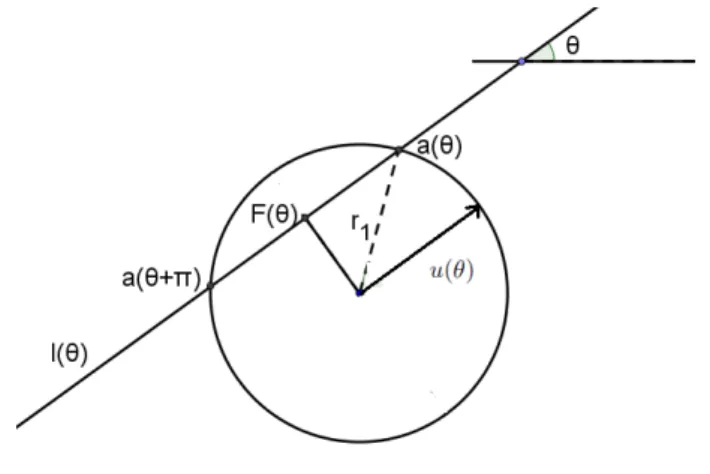
Dada uma fam´ıliaLde retas no plano, sem pares de retas paralelas, sejar1>0 tal quekF(l)k ≤r1, para todol∈L(a condi¸c˜ao necess´aria do lema 3.1). Para cada reta l∈L, denotemos por

1. θ=θ(l), o ânguloθ da retalcom o eixo x, onde (0≤θ < π). A fun¸cãoθ(l) é bem definida uma vez que não existem retas paralelas; além disso, os ângulosθeθ+πdescrevem a mesma reta. Ver figura 3.3.

Conforme definimosθ, vamos denotar por

u(θ) =

  cos(θ)

sen(θ)



 e v(θ) =u′(θ) =



 −sen(θ)

cos(θ)

 .

2. W ={θ(l);l∈L}, o conjunto de dire¸cões emL. Sem perda de generalidade, mediante rota¸cão no sentido horário, podemos supor que 0∈W ⊂[0, π).

3. Wc=W∪ {W +π} ⊂[0,2π). Em especial, passamos a descreverF(l) porF(θ), com dom´ınio em

c

W, de forma queF(θ) =F(θ+π), ondeθ∈W.

4. Pelo lema 3.1, cadal(θ) intercepta a circunferˆenciaB(0, r) em exatamente dois pontos, que podem ser escritos como

a±(θ) =F(θ)±x(θ)u(θ), x(θ)≥0 (θ∈W).

Observando que formalmentea±(θ) =a∓(θ+π) (j´a que trata-se da mesma reta), seria equivalente

definir:

5. a(θ) =a+(θ) =F(θ) +x(θ)u(θ),(θ∈Wc), comF(θ), x(θ) satisfazendo para todoθ∈W

  

F(θ) = F(θ+π)

(28)

3.3 O resultado principal

26 Figura 3.3:

A figura est´a ilustrando as defini¸c˜oes feitas acima.

Teorema 3.1 Seja L uma fam´ılia de retas no plano, que n˜ao possui pares de retas paralelas. Seja

W ={θ(l);l∈L} eWc=W ∪ {W+π} ⊂[0,2π). As seguintes afirma¸c˜oes s˜ao equivalentes:

(a) A fam´ıliaLpossui a propriedade de proje¸c˜ao limitada.

(b) O conjuntoΩdo corol´ario 3.1 ´e limitado.

(c) A fun¸c˜ao F :Wc→ ℜ2 _{´e Lipschitz} 2_{, ou seja,}

|F(θ1)−F(θ2)| ≤k min{θ1−θ2, θ2−θ1+ 2π}

para0≤θ2≤θ1<2π.

(d) Se r >0 é tal queΩ⊂B(0, r), então a:cW →S1 _{como definida no item (5), é mon´}_{otona (lembre}

que 0∈W).

O Teorema 1 de Bàràny et al. afirma a equivalência entre os itens (a) e (b) do teorema 3.1 e sua demonstra¸cão segue a seguinte cadeia de implica¸cões (a) ⇒ (b) ⇒ (c) ⇒ (d) ⇒ (a), onde o passo (d)⇒(a) é bastante complicado.

Para evitar a complica¸cão (d) ⇒(a) apresentamos aqui uma demonstra¸cão que segue as seguintes implica¸cões (a)⇒(b)⇔(c)⇒(a). Além disso, o lema 3.4 mostra a implica¸cão (b)⇒(d), já que uma 2_{Dado que} _F₍_θ_{) e} _a₍_θ_{) podem ser tratados como fun¸c˜}_{oes peri´}_{odicas de per´ıodo 2}_π_{, é mais natural} pensar tudo em S1_{. Seja} _f_W ₌ _{₍_cos₍_θ₎_{, sen}₍_θ_));_θ_∈_W_}_{, bem como} _F_e _: _f_W _⊂ _S1 _{→ ℜ}_{, definida por}

e

(29)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

27

fun¸cão real cont´ınua f(x) sobre um conjunto conexo, é injetiva se, e somente se, f(x) é estritamente monótona. Assim a implica¸cão (d)⇒(a) não será abordada aqui.

A implica¸c˜ao (a)⇒(b) ´e garantida pelo lema 3.1.

3.4 Demonstra¸

c˜

ao do Teorema 3.1

Nesta se¸cão, demonstraremos o teorema 3.1, em vários lemas, de modo a facilitar o entendimento do mesmo. Vamos iniciar mostrando a equivalência entre os itens (b) e (c) do teorema 3.1.

Lema 3.3 O conjunto Ωno corolário 3.1 é limitado se, e somente se, a fun¸cãoF :Wc→ ℜé Lipschitz.

Bàràny et al. [4], mostram apenas (b)⇒(c). De fato, essa implica¸cão seria suficiente.

Demonstra¸c˜ao.

Para a demonstra¸cão direta desse lema, vamos usar a ideia de Bàràny et al. [4]. Nossa hipótese é que Ω é limitado, digamos, Ω⊂B2₌_B₍₀_{, r}_{2) e temos que mostrar que}_F₍_θ_{) é Lipschitz.}

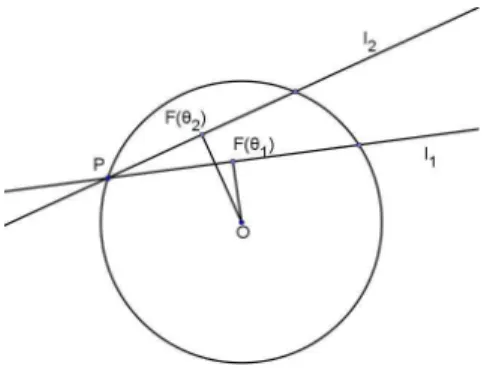
Sejam l1,l2 ∈L duas retas quaisquer, nas dire¸c˜oes θ1, θ2, respectivamente e denotemos por{P} =

l1∩l2. Por hip´otesekPk ≤r2. Observe a figura 3.4.

Figura 3.4:

Ilustrando a pior das situa¸cões, ou seja, quando o ponto P está na fronteira deB2_. Ora, o lema A.3 do apêndice garante a existência de uma circunferência de diâmetro kOPk ≤ r2 que passa pelos pontos P, O, F(θ1), F(θ2). Com isso vamos obter a circunferência de centroZ que está ilustrada na figura 3.5.

Da figura 3.5 podemos tirar o triângulo isósceles formado pelos pontosZ, F(θ1), F(θ2). onde a altura desse triângulo referente à baseF(θ1)F(θ2) também é bissetriz do ânguloF(θ1)ZFb (θ2). Logo, pelo lema A.1 do apêndice, o ânguloF(θ1)ZFb (θ2) é o dobro do ânguloF(θ2)P Fb (θ1); para melhor entendimento observe a figura 3.6.

Na figura 3.6, α= (θ2−θ1); com isso vamos obter a seguinte rela¸c˜ao

|sen(θ2−θ1)| =

kF(θ2)−F(θ1)k

2

kOPk

2

(30)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

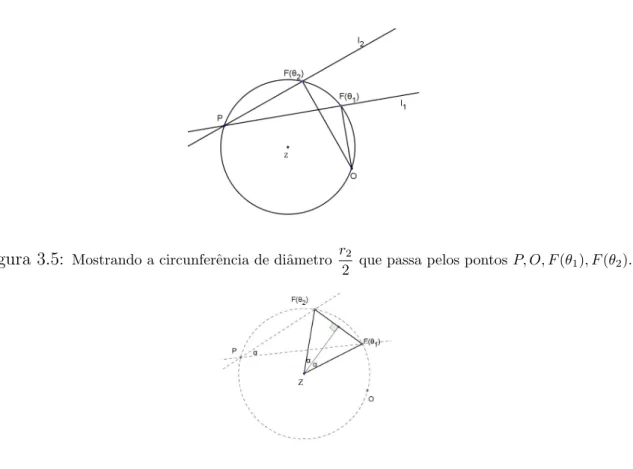
28 Figura 3.5:

Mostrando a circunferˆencia de diˆametro r2

2 que passa pelos pontosP, O, F(θ1), F(θ2).

Figura 3.6:

Ilustrando a situa¸c˜ao descrita acima.

Juntando (3.1) com a desigualdade|sen(x)| ≤ |x|, obtemos

kF(θ2)−F(θ1)k ≤r2|sen(θ2−θ1)| ≤r2|θ2−θ1| Portanto podemos concluir que, F(θ) ´e Lipschitz com constantek=r2.

Agora vamos argumentar a rec´ıproca. Como a fam´ılia Lnão possui retas paralelas, então todo par de retas li, lj ∈L possui um ponto em comum. Denotemos por{P}=li∩lj, nosso objetivo é mostrar

que existeA >0, tal quekOPk ≤A.

Nossa hipótese é que F(θ) é Lipschitz com constante k, e temos que mostrar que o conjunto Ω (do corolário 3.1) é limitado. Para isso tomemos duas retas quaisquer li, lj ∈ L nas dire¸cões θi e θj

(31)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

29 Figura 3.7:

Ilustrando a situa¸c˜ao descrita acima.

Pelo lema A.3 do apˆendice, existe uma circunferˆencia que passa pelos pontos F(θi), F(θj), Pi,j e O

que tem por diâmetrokOPi,jk, ondePi,jé o ponto de interse¸cão entre as duas retas dadas. Como mostra

a figura 3.8.

Figura 3.8:

Mostrando a circunferˆencia que passa pelos pontosF(θi), F(θj), Pi,j e O.

Como na equa¸c˜ao (3.1), temos

|sen(θj−θi)|= k

F(θj)−F(θi)k

kOPi,jk

.

Vamos considerar dois casos:

1. 0≤θj−θi≤

π

2.

kOPi,jk=k

F(θj)−F(θi)k

|sen(θj−θi)| ≤

k |θj−θi|

|sen(θj−sen(θi))|

=k

senx(x)

≤ kπ2 para 0< x=θj−θi, j´a que

x

sen(x) ´e crescente em [0,

π

2]. 2. π

2 ≤θj−θi< π.

kOPi,jk=k

F(θj)−F(θi)k

|sen(θj−θi)|

= kF(θj)−F(θi+π)k

|sen(θj−(θi+π))| ≤

k |θj−(θi+π)|

|sen(θj−(θi+π))|

=k

_senx₍_x₎

≤kπ₂

para−π

2 ≤x=θj−(θi+π)<0, j´a que

x

sen(x) ´e decrescente em [−

π

(32)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

30

Pelo lema E.1 do apˆendice conclu´ımos que, a interse¸c˜ao entre pares de retas deL vai estar contida em um discoD2_{, de raio menor ou igual a} kπ

2 .

Como a fam´ıliaLpode estar definida em qualquer subconjuntoW de [0, π), então para continuarmos nossas demonstra¸cões, vamos estender a fam´ıliaLpara uma fam´ıliaLe completa, ou seja, a fam´ıliaLeestá definida em todo intervalo [0,2π). Vamos fazer essa extensão de modo que F : [0,2π] → ℜ ainda seja Lipschitz e com a mesma constante. Vale lembrar que esse artif´ıcio foi usado na demonstra¸cão da parte principal do teorema 1 (versão original do artigo) por Bàràny et al. [4]. Porém eles não mostram como é feita tal extensão.

Vamos construirLeda seguinte forma. Sejaθ0qualquer ângulo em (0, π) tal que não existel∈Lcom dire¸cãoθ0(lembre que 0, π∈Wc) eW ⊂[0, π). Defina agora

(a) θ−0 =sup{W∩[0, θ0)}. (b) θ+0 =inf{Wc∩(θ0, π]}.

temos então que, 0≤θ−0 ≤θ0≤θ+0 ≤π. Dado queF(θ) é Lipschitz, observe que, seθn→θ−0 (θn→θ+0), entãoF(θn) é uma sequência de Cauchy. Portanto, podemos definir:

(c) Fe−= lim θ→θ−

0

F(θ). (d) Fe+= lim

θ→θ+₀

F(θ).

Seθ₀−=θ+₀, pela propriedade LipschitzF−=F+ e portanto ´e suficiente aumentar a reta

l(θ) ={F++ru0, r∈ ℜ} u0=u(θ0).

Caso contr´ario, vamos completar o “cone” formado pelas retasl(θ0−), l(θ+0) por retas que passam pelo pontoξ=l(θ−0)∩l(θ+0), com ˆanguloθno intervalo [θ0−, θ+0]. Ver figura 3.9.

(33)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

31

As equa¸c˜oes dessas retas s˜ao dadas por

l(θ) ={ξ+ru(θ);r∈ ℜ}

paraθ−₀ ≤θ≤θ₀+. Do mesmo jeito que fizemos em 1-5 na se¸c˜ao 3.3 paraL, podemos definirWf= [0, π),

c f

W = [0,2π), bem como as extens˜oesFe: [0,2π)→ ℜe_ea: [0,2π)→ ℜ. Podemos resumir o completamento para a fam´ıliaLe no lema 3.4, a seguir.

Lema 3.4 Se as retas de L indexadas por w∈W ⊂[0, π), se interceptam no interior de um disco D, de raio r2, ent˜ao seu completamento Le ´e uma fam´ılia de retas, indexadas em[0, π), tal que:

(i) Todo par de retas deLe se intercepta em D.

(ii) Fe(θ)´e Lipschitz com a mesma constante e Fe(θ+π) =Fe(θ).

(iii) _ea: [0,2π)→∂D ´e cont´ınua e bijetora (1-1 sobre∂D).

(iv) Por todo ponto fora do disco D passa uma ´unica reta deL.

Demonstra¸c˜ao.

(i) Tomemos um “cone” qualquerC(θ0), formado pelas retasl(θ−0) el(θ+0). Escolha uma retal(θ)∈L, denotemos{P+}=l(θ)∩l(θ0+) e{P−}=l(θ)∩l(θ−0). Ver figura 3.10.

Figura 3.10:

Ilustrando a situa¸c˜ao acima.

Isto ignora uma possibilidade como a da figura 3.11.

Isto ´e imposs´ıvel poisl(θ) seria paralela a uma reta no “cone”, e a fam´ıliaLe n˜ao pode possuir retas paralelas.

Sabendo que Ω⊂D, então na pior das situa¸cões, os pontosP+ eP−vão pertencer a fronteira deD.

Com isso, a reta l(θ) vai cortar todas as retas do “cone”C(θ0) no segmento P+P−. Portanto, todo par

de retas da fam´ıliaLe se intercepta emD.

(34)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

32 Figura 3.11:

Quanto o item (iii), a continuidade de _ea(θ), segue da continuidade de Fe(θ), uma vez que, para 0≤θ <2π

e

a(θ) =Fe(θ) +

r

r2 1−

eF(θ)

2

u(θ).

Figura 3.12:

Além disso, _ea(θ) é injetiva para 0≤θ <2π, pois não pode haver duas retas deLe se interceptando fora deD. Para ver que_ea([0,2π)) =∂D, dado que _ea(θ) é injetiva, basta checar que lim

θ→2π−ea(θ) =ea(0). Isto decorre da defini¸c˜ao deea(θ), pois: lim

θ→π+ea(θ) = lim_θ→π−ea(θ) =ea(π) e lim_θ→₀+ea(θ) =ea(0) asseguram que

lim

θ→2π−ea(θ) =ea(0) .

Para ver o item (iv), suponha r > r1 e defina a fun¸c˜ao ear(θ) = Fe(θ) +x(θ)u(θ), com x(θ) = r

r2₋

eF(θ)2. Ou seja, da mesma forma como anteriormente, mas com respeito a um discoDrde raio

r > r1, de modo quekear(θ)k=r. Pelo mesmo argumento de antes,ear(θ) ´e cont´ınua, 1-1 e sobre∂Dr.

Consequentemente, isto nos garante uma ´unica reta de Le passando por cada ponto dos c´ırculos de raior > r1.

(35)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

33

basta considerarmos o caso no qualLe ´e uma fam´ılia de retas completa, ou seja, indexada em 0≤θ < π, satisfazendo os itens (i−iv) do lema 3.4.

Assim com Bàràny et al. [4], a ideia dessa demonstra¸cão consiste em construir curvas ortogonais (ver o apêndice (C)) a todas as retas da fam´ıliaLe come¸cando com pontos suficientemente distantes, de modo que:

1. Cada uma destas curvasGé fechada, simples (ou seja, sem auto-interse¸cão) e delimita a fronteira de uma região convexa HG.

2. HG ´e um conjunto invariante para as proje¸c˜oes ortogonais sobre as retas deLe.

Pelo lema 3.4, todo ponto fora do disco D está em única reta de Le, de modo que, se z ∈ ℜ2₋_D_. Portanto, existe um único par θ, x(θ) tal que

z(θ) =F(θ) +x(θ)u(θ) =ξ(θ)v(θ) +x(θ)u(θ) (3.2) ondev(θ) =u′(θ) eξ(θ) =hF(θ), v(θ)i.

SeF(θ) e x(θ) forem diferenciáveis, então a curvaz(θ)∈(ℜ2₋_D_{) seria ortogonal às retas de} _L_e _se: 0 =Dz′(θ), u(θ)E=Dξ′(θ)v(θ) +ξ(θ)v′(θ) +x′(θ)u(θ) +x(θ)u′(θ), u(θ)E=x′(θ)−ξ(θ) dado quehu(θ), v(θ)i= 0. PeloTeorema Fundamental do Cálculoobter´ıamos:

x(θ) =x(0) +

Z θ

0

ξ(t)dt. (3.3)

O fato deF(θ) =ξ(θ)v(θ) n˜ao ser, necessariamente, diferenci´avel, complica um pouco os argumentos. Ainda assim, podemos considerar, para x(0) =x0 suficientemente grande, a curva z: [0,2π]→ ℜ2 dada por,

z(θ) =ξ(θ)v(θ) + x0+

Z θ

t=0

ξ(t)dt

!

u(θ). (3.4)

Lembrando queF(θ) é Lipschitz e está definida em [0,2π], então existe Φ>0 tal que, kF(θ)k ≤Φ, para todo θ ∈ [0,2π]. Assim, podemos afirmar que

Z θ 0

ξ(t)dt

≤ 2πΦ. O lema 3.5 nos dir´a que

x0> r2+ Φ(2π+ 1) já é “suficientemente grande” para manter z(θ) fora deD e quez(θ) é uma curva Lipschitz e fechada, ver figura 3.13.

Lema 3.5 z(θ)´e Lipschitz para0≤θ≤2π ez(0) =z(2π). Sex0> r2+ Φ(2π+ 1), ent˜ao kz(θ)k> r2.

Demonstra¸c˜ao.

Sabemos que ξ(θ) =hF(θ), v(θ)i´e Lipschitz, pois F(θ) e v(θ) s˜ao Lipschitz e limitadas. Portanto,

z(θ) ´e Lipschitz. Al´em disso, temosF(θ) =F(θ+π) e v(θ+π) =−v(θ); consequentemente

(36)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

34 Figura 3.13:

para 0≤θ≤π. Em particular tem-se

Z 2π

0

ξ(t)dt=

Z π

0

ξ(t)dt+

Z π

0

ξ(t+π)dt= 0.

Segue que:

z(2π) =ξ(2π)v(2π) +

x0+

Z 2π

0

ξ(t)dt

u(2π) =ξ(0)v(0) +x0u(0) =z(0) ou seja, z(θ) ´e fechada.

Para concluir a demonstra¸c˜ao do lema 3.5 falta mostrar que min{kz(θ)k: 0≤θ <2π} > r2. Se

x > r2+ Φ(2π+ 1). De fato, usando a desigualdade triangular

kz(θ)k =

ξ(θ)v(θ) + x0+ Z θ

0

ξ(t)dt

!

u(θ)

≥ kx0u(θ)k −

ξ(θ)v(θ) + Z θ

0

ξ(t)dt

!

u(θ)

> k(r2+ Φ(2π+ 1))u(θ)k −

ξ(θ)v(θ) + Z θ

0

ξ(t)dt

!

u(θ)

≥ r2+ Φ(2π+ 1)− kξ(θ)v(θ)k+

Z θ 0

ξ(t)dt)dt

!

u(θ)

!

≥ r2+ Φ(2π+ 1)−(Φ + 2Φπ) =r2

Como desejado. Em resumo o lema 3.5 garante que a curva z(θ) é Lipschitz e fechada. Além disso, se tomarmosx0> r2+ Φ(2π+ 1), então a trajetóriaz(θ) não intercepta o discoD.

Queremos investigar o comportamento da curva z(θ) (0 ≤ θ ≤ 2π) em torno de um ponto z(θ0), usando um sistema local de coordenadas em torno deste ponto, definido pela base ortonormal {u0, v0} emℜ2_com_u

0=u(θ0) ev0=u ′

(θ0). Denotemos por ∆θ=θ−θ0, e de maneira geral, ∆f =f(θ)−f(θ0) para toda fun¸c˜aof(θ).

Temos

u(θ) = cos(∆θ)u0+sen(∆θ)v0

(37)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

35

com as expans˜oes conhecidas de Taylor de ordem 2 (ver [30]).

sen(∆θ) ≈ ∆θ+O(∆θ3₎

cos(∆θ) ≈ 1−∆θ

2

2 +O(∆θ 4₎

assim obtemos

∆u= (u(θ)−u(θ0)) ≈

−∆θ

2

2 +O(∆θ 4₎

u0+ ∆θ+O(∆θ3)v0 ∆v= (v(θ)−v(θ0)) ≈ −∆θ+O(∆θ3)u0+

−∆θ

2

2 +O(∆θ 4₎_v

0

Usando a parametriza¸c˜ao descrita na equa¸c˜ao (3.2) temos

∆z = ξ(θ)v(θ) +x(θ)u(θ)−ξ(θ0)v(θ0)−x(θ0)u(θ0) =ξ(θ)∆v+x(θ)∆u+ ∆ξv0+ ∆xu0 onde ∆z=z(θ)−z(θ0), ∆ξ=ξ(θ)−ξ(θ0) e ∆x=x(θ)−x(θ0).

Temos ent˜ao a representa¸c˜ao local

∆z = α(∆θ)u0+β(∆θ)v0 com

α(∆θ) = h∆z, u0i=ξ(θ)h∆v, u0i+x(θ)h∆u, u0i+ ∆x = ξ(θ)−∆θ+O(∆θ3)+x(θ)

−∆θ

2

2 +O(∆θ 4₎

+ ∆x β(∆θ) = h∆z, v0i=ξ(θ)h∆v, v0i+x(θ)h∆u, v0i+ ∆ξ

= ξ(θ)

−∆θ

2

2 +O(∆θ 4₎

+x(θ)∆θ+O(∆θ3)+ ∆ξ

Por outro lado, usando (3.4) e o teorema do valor intermedi´ario aplicado na fun¸c˜ao cont´ınua ξ(θ), temos

∆x=x(θ)−x(θ0) =

Z θ

0

ξ(t)dt−

Z θ0

0

ξ(t)dt=

Z θ

θ0

ξ(t)dt=ξ(θ∗)∆θ

paraθ∗_∈_[_θ

0, θ], e tamb´em

−2πΦ≤

Z θ

0

ξ(t)dt=ξ(β∗₎_θ_≤₂_π_Φ

comβ∗_∈_[0_{, θ}_{]. Consolidando os resultados obtidos acima, podemos afirmar o seguinte.}

Lema 3.6 Paraxosuficientemente grande, existeǫ >0tal que, o seguinte vale para todoθcom|∆θ|< ǫ:

∆z = α(∆θ)u0+β(∆θ)v0

de modo que,

−3x₂0 ≤ α_∆(∆_θ2θ) ≤ −1 (3.5)

−2x0 ≤

β(∆θ)

(38)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

36

Demonstra¸c˜ao.

Dado que ξ(θ) ´e Lipschitz, sejak1 tal que

ξ(θ)−ξ(θ′) ≤ k1

θ−θ′

Observe que a igualdadeα(∆θ) descrita acima nos diz que:

α(∆θ) = ξ(θ) −∆θ+O(∆θ3)+x(θ)

−∆θ

2

2 +O(∆θ

4₎_{+ ∆}_x

≤ ξ(θ) −∆θ+O(∆θ3₎_{+ (}_x

0−2πΦ)

−∆θ

2

2 +O(∆θ 4₎

+ξ(θ∗_)∆_θ

= (ξ(θ∗)−ξ(θ)) ∆θ+−x₂0 +πΦ∆θ2+O(∆θ3)

≤ k1∆θ2+−x₂0 +πΦ∆θ2+O(∆θ3)

≤

−1₂x0+ [k1+πΦ]

∆θ2+O(∆θ3) por outro lado, de forma an´aloga podemos obter o seguinte:

α(∆θ) ≥

−1₂x0−[k1+πΦ]

∆θ2+O(∆θ3) logo,

−1

2x0−[k1+πΦ]

∆θ2₊_O_(∆_θ3₎_≤_α_(∆_θ₎_≤

−1

2x0+ [k1+πΦ]

∆θ2₊_O_(∆_θ3₎ _(3.7) Fazendo desenvolvimento an´alogo paraβ(∆θ), vamos obter:

β(∆θ) = ξ(θ)

−∆θ

2

2 +O(∆θ

4₎₊_x₍_θ₎_∆_θ₊_O_(∆_θ3₎_{+ ∆}_ξ

≤ Φ₂ |∆θ|+ (x0+ 2πΦ)∆θ+k1|∆θ|+O(∆θ2)≤

x0+ (2π+ 1

2)Φ +k1

|∆θ|+O(∆θ2) por outro lado, podemos escrever:

β(∆θ) ≥

x0−(2π+1

2)Φ−k1

|∆θ|+O(∆θ2) logo,

x0−(2π+ 1

2)Φ−k1

|∆θ|+O(∆θ2₎ _≤ _β_(∆_θ₎_≤

x0+ (2π+ 1

2)Φ +k1

|∆θ|+O(∆θ2_{) (3.8)} Fa¸ca x0>2

1 +k1+ (π+1 4)Φ

eǫtal que, para todo|∆θ|< ǫ, tenhao(∆θ2₎_<_∆_θ2_{. Observe} que isso nos garante (3.5) e (3.6) a partir de (3.7) e (3.8).

O lema 3.6 nos garante que para |∆θ| < ǫ, onde ǫ > 0 ´e pequeno, a proje¸c˜ao ortogonal do vetor

(39)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

37

Lema 3.7 Para x0∈ ℜ suficientemente grande, a reta l⊥θ0 ={z(θ0) +λv(θ0);λ∈ ℜ}, ortogonal a lθ0 e

contendo z(θ0), ´e tangente em z(θ0) a curva G, parametrizada porz(θ), no sentido que z(θ) =z(θ0) +

α(∆θ)u0+β(∆θ)v0 com

lim ∆θ→0

α(∆θ)

β(∆θ) = 0.

Demonstra¸c˜ao.

De (3.5) e (3.6), sek∆θk 6= 0 ´e suficientemente pequeno, ent˜ao

|∆θ|

x0 ≤

α_β(∆_(∆θ_θ)₎

≤x0|∆θ| pelo teorema do confronto temos, lim

∆θ→0

α(∆θ)

β(∆θ) = 0.

A partir do lema 3.7, apesar dez(θ) não ser, necessariamente, uma parametriza¸cão diferenciável da curva fechada que a define, ainda assim podemos pensar nas curvas obtidas como ortogonais aLe.

Lembrando que estamos denotando porHG a componente conexa e limitada definida por uma das

cur-vas ortogonais (ver o apêndice (C)) aLe, estamos em condi¸cões de concluir a demonstra¸cão da propriedade da proje¸cão limitada deLe.

Lema 3.8 Para x0 suficientemente grande, HG é convexa. Além disto, é invariante sob proje¸cões

orto-gonais por Le.

Para a demonstra¸cão que o conjunto HG é convexo, nossa ideia é mostrar primeiro que existe um

hiperplano suporte local para cada ponto da curvaG(ver a defini¸cão D.5 no apêndice). Feito isso, vamos usar o teorema do hiperplano suporte local D.3 do apêndice para mostrar que o conjuntoHG é convexo.

Já a demonstra¸cão da segunda parte desse lema é mais direta.

Demonstra¸c˜ao.

SejaGuma curva parametrizada porz(θ), constru´ıda a partir dex0suficientemente grande e fixo, de modo a valerem os lemas 3.6 e 3.7. Considere agora, para cada 0≤θ≤2π, os semiplanos definidos por

(40)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

38 Figura 3.14:

Agora vamos definir o seguinte conjunto.

HG = \

0≤θ≤2π

H_θ− (3.9)

O lema 3.7 nos garante que:

hz−z(θ), u(θ)i ≤0 (3.10) parak∆θk=kθ0−θk< δ, comδ >0 suficientemente pequeno ex0 suficientemente grande. Isso mostra que para todo 0≤θ≤2πo semiplanoH_θ−é localmente um hiperplano suporte local da curvaG. O lema 3.5 garante que a curvaGé fechada, além disso o interior deHG é não vazio. Portanto, o teorema D.3,

do hiperplano suporte local no apˆendice, garante que o conjuntoHG ´e convexo.

Agora, vamos mostrar que se tomarmos p ∈ HG, ent˜ao a proje¸c˜ao ortogonal de p em uma reta

qualquer l(θ)∈ Le ainda pertence ao conjuntoHG. Denotemos por Pθ(p) a proje¸c˜ao ortogonal dep na

retalθ∈Le.

Para ver que, dado p ∈ HG, tem-se tamb´em quePθ(p) ∈ HG, veja que a reta ortogonal a lθ que

contém o ponto p∈H_θ−∩H_θ−₊_π permanecerá emH_θ−∩H_θ−₊_π. Vale dizer, quePθ(p) cairá no segmento

(41)

3.4 Demonstra¸

c˜

ao do Teorema 3.1

39 Figura 3.15:

Agora podemos mostrar a parte principal deste cap´ıtulo que ´e a implica¸c˜ao (c)⇒(a) do teorema 3.1.

Lema 3.9 Se F :Wc→ ℜ2 _{´e Lipschitz, ent˜}_{ao a fam´ılia}_L_e _{possui a propriedade da proje¸c˜}_{ao limitada.}

Demonstra¸c˜ao.

Para x fixo e bastante grande, o lema 3.8 garante que o conjunto HG ´e invariante para todas as

proje¸cões em Le. Além disso, o lema 3.5 mostra que a curva z(θ) é limitada, e assim o interior Gx é

também limitado. Portanto, toda sequência de proje¸cões come¸cando em um pontozqualquer emGxfica

(42)

Cap´ıtulo 4

Fam´ılia de Retas em

R

d

Neste cap´ıtulo, vamos fazer uma extens˜ao do corol´ario 3.1 para uma fam´ılia de retas em ℜd _com

(d >2). A situa¸cão aqui é mais complicada. Primeiro, não é razoável estipular a interse¸cão de cada par de retas. Segundo, a monotonia dea(θ) mensionada no lema 3.4 não faz mais sentido.

4.1 Situando o Problema de proje¸

c˜

ao Limitada com

d >

2

Come¸camos esta se¸cão com um exemplo, de uma fam´ılia de retasLemℜ3_{, onde}_L_{possui a propriedade} da proje¸cão limitada, porémF(θ) não é Lipschitz.

Exemplo 4.1 Seja L uma fam´ılia de retas em ℜ3_{, onde todas as retas de} _L _est˜_{ao no plano} _z _{= 0} _e

passam pela origem. Pelo lema 3.1 Lpossui a propriedade da proje¸c˜ao limitada. Agora vamos construir uma fam´ılia Le a partir de L da seguinte forma: retiramos uma reta qualquer l ∈L e a colocamos em outro plano paralelo, digamosz=a.

Afirmamos que a fam´ılia Le também possui a propriedade da proje¸cão limitada. Ao projetarmos na reta l destacada, é o mesmo que projetarmos na original e fazémos z = a. Vice-versa, se P ∈ l, sua proje¸cão em qualquer outra reta é a mesma obtida a partir da reta que lhe é paralela e foi destacada de

L. Portanto, a cada sequência no novo sistema Le corresponde uma sequência de proje¸cões emL, cujos iterados ou bem coincidem, ou então diferem de (0,0, a). Isto significa que Le herda a propriedade da proje¸cão limitada deL.

(43)

4.2 Consequˆ

encias da propriedade da proje¸

c˜

ao limitada em retas em

_ℜ

d

41

F(θ) =

  

0 se l ∈ L

(0,0, a) se l ∈/ L

Isso significa queF(θ) é descont´ınua, logo não é Lipschitz.

Bàràny et al. em [4] acrescentam a condi¸cão de suavidade aF(θ), que não foi necessária para o caso

d = 2. Até acreditamos que ela não seja necessária, no caso analisado por Bàràny et al. em [4], mas deixaremos isso para um trabalho futuro.

4.2 Consequˆ

encias da propriedade da proje¸

c˜

ao

limi-tada em retas em

_ℜ

d

Seja L uma fam´ılia de retas em ℜd ₍_{d >} _{2). Assim como no caso do plano, cada reta} _l _∈ _L _vai

ser dada pela sua dire¸cão, que pode seru∈Sd−1 _(ou₋_u_∈_Sd−1_{) e pelo vetor} _F₍_u₎_∈_l _{mais pr´}_oximo à origem, ou seja, F(u) é a proje¸cão ortogonal da origem O em l. Além disso, vamos supor que F(u) está definida em um subconjunto simétrico T ⊂ Sd−1 _{que assumimos ser fechado. (isso é um pouco} mais do que assumir que L não contém retas paralelas). Podemos afirmar que, F(u) tem as seguintes propriedades;

F(u) = F(−u) ∀u∈T (4.1)

hu, F(u)i = 0 ∀u∈T (4.2)

As igualdades (4.1) e (4.2) são garantidas pelo modo que F(u) foi definido. SeL tem a propriedade da proje¸cão limitada, então, pelo lema 3.1,F(u) é limitada. Além disso, vamos enunciar mais algumas condi¸cões sobre a fun¸cãoF(u), a serem consideradas em alguns momentos deste cap´ıtulo.

|hF(u)−F(v), u−vi| ≤ cku−vk2,∀u, v∈T (4.3)

kF(u)−F(v)k ≤ cku−vk,∀u, v∈T (4.4)

Z

Γ

F(u)·du = 0, para todas as curvas suaves f echadasΓ⊂T (4.5)

Observa¸cão 1 Devemos observar que (4.4) implica em (4.3). A equa¸cão (4.4) diz que a fun¸cãoF(u)é Lipschitz. A equa¸cão (4.3) diz que a fun¸cão F(u)é Lipschitz direcional. A equa¸cão (4.5) sugere pensar emF(u) como um campo conservativo emT ⊂Sd−1_.

Nesta se¸c˜ao, vamos mostrar que para toda fam´ılia de retas L em ℜd _{que possui a propriedade da}

(44)

4.2 Consequˆ

encias da propriedade da proje¸

c˜

ao limitada em retas em

_ℜ

d

42

Teorema 4.1 Se uma fam´ılia de retasLtem a propriedade da proje¸cão limitada, então F(u)satisfaz a condi¸cão (4.3). Além disso, seF(u)satisfaz a condi¸cão (4.3), então as sequências de proje¸cões alternadas entre quaisquer pares de retas deL são uniformemente limitadas.

Demonstra¸c˜ao.

Vamos iniciar mostrando que, se uma fam´ılia de retasLtem a propriedade da proje¸c˜ao limitada, ent˜ao

F(u) satisfaz a condi¸cão (4.3). Nessa demonstra¸cão, nossa contribui¸cão será detalhar a argumenta¸cão feita por Bàràny et al. em [4]. Dado duas retas lu, lv ∈ L, com dire¸cões u, v ∈ Sd−1 respectivamente

escolhidas de modo que hu, vi ≥ 0 (uma vez que u ∈ Sd−1 _e ₋_u _∈ _Sd−1 _{definem a mesma reta). A} sequência de proje¸cões ortogonais alternadas entre lu elv vai aproximar a distância entre as duas retas.

Sejam p ∈ lu e q ∈ lv, pontos que realizam a distˆancia entre as retas lu e lv, como no lema B.2 no

apˆendice.

kp−qk=dist(lu, lv)

observe a figura 4.1.

Figura 4.1:

Ilustrando a sequˆencia de proje¸c˜oes entre as duas retas emℜd_.

Pelo lema B.2 no apˆendice vamos obter:

p = F(u)− hF(u), vi

1 +hu, viu+

hF(v), ui+hF(u), vi

1− hu, vi2 u (4.6)

Os dois primeiros termos da equa¸cão (4.6) são limitados, pelo fato queF(u) é limitado. Enquanto o ´

ultimo termo ´e limitado se, e somente se, existec∈ ℜ, c >0 tal que

|hF(v), ui+hF(u), vi|

1− hu, vi2 ≤

c

de modo equivalente

(45)

4.2 Consequˆ

encias da propriedade da proje¸

c˜

ao limitada em retas em

_ℜ

d

43

portanto

|hF(v), ui+hF(u), vi| ≤ c1|1− hu, vi| (4.7) Como, kuk=kvk= 1, temos que

1

2ku−vk 2

=1

2hu−v, u−vi= 1 2(kuk

2

−2hu, vi+kvk2) =1

2(2−2hu, vi) = 1− hu, vi ou seja,

1

2ku−vk 2

= 1− hu, vi (4.8)

al´em disto, dehF(u), ui=hF(v), vi= 0

hF(u), vi+hF(v), ui = − hF(u)−F(v), u−vi (4.9) substituindo (4.8), (4.9) em (4.7), podemos concluir que

|hF(u)−F(v), u−vi| ≤c₂1ku−vk2

ou seja,F(u) satisfaz a condi¸c˜ao (4.3) como quer´ıamos demonstrar.

Agora vamos mostrar a rec´ıproca. Para isso, devemos observar que a conta acima pode ser revertida, no sentido que, dadas duas dire¸c˜oes quaisqueru, v∈Sd−1_{, com}_h_{u, v}_{i ≥}_{0, se a condi¸c˜}_{ao (4.3) vale, ent˜ao}

kp(u, v)k=

F(u)−

hF(u), vi

1 +hu, viu+

hF(v), ui+hF(u), vi

1− hu, vi2 u

permanece uniformemente limitado. Veja que, por (4.3), (4.7) ekuk=kvk= 1, tem-se que

hF(v), ui+hF(u), vi

1− hu, vi2

≤ c1 2

|1− hu, vi|

1− hu, vi2 ≤

c1 2

1

|1 +hu, vi| ≤c (4.10)

As equa¸cões (4.6) e (4.10) nos garantem que a distância entre os pontos mais próximos de duas retas

lu elvquaisquer tˆem uma cota uniforme, dado que basta supor quehu, vi ≥0 em (4.6). Como sequˆencias

de proje¸cões alternadas entre as retasluelv têmpu eqv como pontos de acumula¸cão, isto nos garante a

rec´ıproca.

Agora vamos mostrar que se L tem a propriedade da proje¸c˜ao limitada e F(u) ∈C1 _em _T_{, ent˜ao}

F(u) satisfaz (4.5).

Teorema 4.2 Suponha que Ltem a propriedade da proje¸c˜ao limitada. Se F(u)∈C1 _em_T_{, ent˜}_ao_F₍_u₎

satisfaz a condi¸c˜ao (4.5).

(46)

4.2 Consequˆ

encias da propriedade da proje¸

c˜

ao limitada em retas em

_ℜ

d

44

Nossa contribui¸cão na demonstra¸cão do teorema 4.2, será detalhar a argumenta¸cão feita por Bárány et al. em [4], principalmente na parte final da demonstra¸cão feita por eles. Para estabelecer a condi¸cão (4.5), vamos tomar u(t),0 ≤ t ≤ 1, uma parametriza¸cão suave da curva Γ de modo que u(0) = u(1). Consideremos também uma curva ortogonal a fam´ılia L (ver no apêndice (C)) que passa em z0 ∈ ℜd, dada por;

z(t) =F(u(t)) +x(t)u(t) (4.11) Iniciando dez(0) =z0 comx(0) =x0grande o suficiente. Pela defini¸cão (C.2 no apêndice),z(t) será a trajetória ortogonal ao longo da fam´ılia de retaslu(t)∈Lse a dire¸cão dez(t) for ortogonal alu(t)para todot∈[0,1], ou seja,

hz˙(t), u(t)i= 0 para todot∈[0,1]. Portanto

0 =hz˙(t), u(t)i=

_∂F

∂u(u(t))·u˙(t) + ˙x(t)u(t) +x(t) ˙u(t), u(t)

=

_∂F

∂u(u(t))·u˙(t), u(t)

+hx˙(t)u(t) +x(t) ˙u(t), u(t)i

Em resumo, dado queku(t)k= 1 ehu˙(t), u(t)i= 0, chegamos a

∂F

∂u(u(t))·u˙(t), u(t)

+ ˙x(t) = 0 (4.12)

Vamos fazer uma rela¸cão entre a equa¸cão (4.12) e a derivada da equa¸cão (4.2). DerivandohF(u(t)), u(t)i= 0, obtemos

0 =

_∂F

∂u(u(t))·u˙(t), u(t)

+hF(u(t)),u˙(t)i

logo,

_∂F

∂u(u(t))·u˙(t), u(t)

= − hF(u(t)),u˙(t)i (4.13) De (4.12) e (4.13), obtemos

˙

x(t) = hF(u(t)),u˙(t)i (4.14) Sabemos que F(u) e ˙u(t) são cont´ınuas e limitadas. Portanto, podemos aplicar oteorema funda-mental do cálculona equa¸cão (4.14), com isso vamos obter

x(t) =x(0) +

Z t

y=0h

F(u(y)),u˙(y)i ·dy=x(0) +

Z

Γt

F(u)·du

onde Γt= Γ|[0,t]. Em particular, temos

x(1) =x(0) +

Z

Γ