Avaliação e correções de testes de hipóteses em modelos de sobrevivência com fração de cura

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exatas e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

La´ıs Helen Loose

Avalia¸c˜

ao e corre¸c˜

oes de testes de hip´

oteses em

modelos de sobrevivˆ

encia com fra¸c˜

ao de cura

(2)

La´ıs Helen Loose

Avalia¸c˜

ao e corre¸c˜

oes de testes de hip´

oteses em

modelos de sobrevivˆ

encia com fra¸c˜

ao de cura

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Orientadora:

Prof

a

_{. Dr}

a

_{. Dione Maria Valen¸ca}

Coorientador:

Prof. Dr. F´abio Mariano Bayer

(3)

La´ıs Helen Loose

Avalia¸c˜

ao e corre¸c˜

oes de testes de hip´

oteses em

modelos de sobrevivˆ

encia com fra¸c˜

ao de cura

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica

Aprovado em: / /

Banca Examinadora:

Profa_{. Dr}a_{. Dione Maria Valen¸ca} Departamento de Estat´ıstica - UFRN

Orientadora

Prof. Dr. F´abio Mariano Bayer Departamento de Estat´ıstica - UFSM

Coorientador

Prof. Dr. Marcelo Bourguignon Pereira Departamento de Estat´ıstica - UFRN

Examinador Interno

Prof. Dr. Francisco Cribari Neto Departamento de Estat´ıstica - UFPE

(4)

Loose, Laís Helen.

Avaliação e correções de testes de hipóteses em modelos de sobrevivência com fração de cura / Laís Helen Loose. - Natal, 2016.

vi, 72f: il.

Orientadora: Profa. Dra. Dione Maria Valença. Coorientador: Prof. Dr. Fábio Mariano Bayer.

Dissertação (Mestrado) - Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Matemática Aplicada e Estatística.

1. Análise de sobrevivência. 2. Fração de cura. 3. Melhoramentos inferenciais. 4. Bootstrap. 5. Correção em testes de hipóteses. I. Valença, Dione Maria. II. Bayer, Fábio Mariano. III. Título.

Catalogação da Publicação na Fonte

(5)

Dedicat´

oria

Ao meus pais, Sidio e Haidi, com muito amor.

(6)

Agradecimentos

`

A minha orientadora, Dione Maria Valen¸ca, pela disponibilidade, paciência, com-prometimento, dedica¸cão e clareza na orienta¸cão. Obrigada por todos os ensinamentos e por acreditar que seria poss´ıvel realizar esse trabalho.

Ao meu coorientador, Fábio Mariano Bayer, pelas valiosas sugestões, pela disponi-bilidade, comprometimento e por ser o exemplo de professor, pesquisador e pessoa que és. Obrigada pelo incentivo, pelos conselhos, por me acompanhar desde a gradua¸cão e ter contribu´ıdo significativamente na minha forma¸cão acadêmica e pessoal.

A minha fam´ılia e amigos, por entenderem minha ausência e mesmo longe estarem sempre torcendo por mim. Em especial aos meus pais, pelos ensinamentos e exemplos de honestidade, perseveran¸ca e for¸ca. Obrigada por respeitarem minhas decisões, pelo apoio incondicional, por vibrarem a cada conquista e pelo amor sem fim. Aos meus irmãos Lu´ıs e Léo, por suprirem minha ausência e por todo apoio.

Ao meu namorado Moizés e sua fam´ılia, por todos os momentos em fam´ılia que me proporcionaram mesmo longe do RS. Em especial ao Moizés, além de meu namorado, tornou-se meu amigo, meu companheiro de estudo, com quem compartilhei muitas horas de estudos durante a realiza¸cão desse trabalho. Obrigada por toda paciência, amor e carinho.

Aos meus amigos Jhonnata e Felipe, pela acolhida em Natal, por todas as horas de estudos e pelos momentos de descontra¸cão. Obrigada pela amizade e carinho de vocês. Aos colegas do PPGMAE, pelos estudos, pelas discussões acadêmicas, pelas brin-cadeiras e risadas.

Aos professores do PPGMAE, pelos ensinamentos, apoio e aten¸c˜ao. Aos participantes da banca examinadora pelas sugest˜oes.

`

A CAPES pelo apoio financeiro.

(7)

Resumo

Os modelos de sobrevivência tratam do estudo do tempo até a ocorrência de um evento de interesse. Em algumas situa¸cões, uma propor¸cão da popula¸cão pode não estar mais sujeita à ocorrência do evento. Nesse contexto, surgiram os modelos com fra¸cão de cura. Dentre os modelos que incorporam uma fra¸cão de curados um dos mais conhecidos é o modelo de tempo de promo¸cão. No presente trabalho abordamos infe-rências em termos de testes de hipóteses no modelo de tempo de promo¸cão assumindo a distribui¸cão Weibull para os tempos de falha dos indiv´ıduos suscet´ıveis. Os testes de hipóteses nesse modelo podem ser realizados com base nas estat´ısticas da razão de verossimilhan¸cas, gradiente, escore ou Wald. Os valores cr´ıticos dos testes são obtidos através de aproxima¸cões válidas em grandes amostras, que podem conduzir a distor¸cões no tamanho do teste em amostras de tamanho finito. Nesse sentido, o presente trabalho propõe corre¸cões via bootstrap para os testes mencionados e Bartlett bootstrap para a estat´ıstica da razão de verossimilhan¸cas no modelo tempo de promo¸cão Weibull. Por meio de simula¸cões de Monte Carlo comparamos o desempenho em amostras finitas das corre¸cões propostas com os testes usuais. Os resultados numéricos obtidos evidenciam o bom desempenho das corre¸cões propostas. Ao final do trabalho é apresentada uma aplica¸cão a dados reais.

Palavras-chave: análise de sobrevivência, fra¸cão de cura, melhoramentos inferen-ciais,bootstrap, corre¸cão em testes de hipóteses.

(8)

Abstract

Survival models deals with the modelling of time to event data. In certain situa-tions, a share of the population can no longer be subjected to the event occurrence. In this context, the cure fraction models emerged. Among the models that incorpo-rate a fraction of cured one of the most known is the promotion time model. In the present study we discuss hypothesis testing in the promotion time model with Weibull distribution for the failure times of susceptible individuals. Hypothesis testing in this model may be performed based on likelihood ratio, gradient, score or Wald statistics. The critical values are obtained from asymptotic approximations, which may result in size distortions in finite sample sizes. This study proposes bootstrap corrections to the aforementioned tests and Bartlett bootstrap to the likelihood ratio statistic in Weibull promotion time model. Using Monte Carlo simulations we compared the finite sample performances of the proposed corrections in contrast with the usual tests. The nume-rical evidence favors the proposed corrected tests. At the end of the work an empinume-rical application is presented.

Keywords: Survival analysis, cure fraction, inferential improvement, bootstrap, improvement in hypothesis testing

(9)

Sum´

ario

1 Introdu¸c˜ao 1

1.1 Objetivos . . . 3

1.2 Descri¸c˜ao dos cap´ıtulos . . . 3

2 Modelos de sobrevivência com fra¸cão de cura e modelo de tempo de promo¸cão Weibull 4 2.1 Introdu¸cão à análise de sobrevivência . . . 4

2.1.1 Fun¸cão de sobrevivência e fun¸cão risco . . . 5

2.1.2 Censura . . . 6

2.1.3 Modelos param´etricos . . . 6

2.2 Modelos com fra¸c˜ao de cura . . . 7

2.2.1 Formula¸c˜ao do modelo . . . 8

2.2.2 Verossimilhan¸ca para o modelo de tempo de promo¸c˜ao . . . 10

2.3 Modelo de tempo de promo¸c˜ao Weibull . . . 11

3 Testes de hip´oteses e melhoramentos inferenciais em pequenas amos-tras 14 3.1 Estat´ısticas de teste . . . 14

3.2 Melhoramentos inferenciais em testes de hip´oteses . . . 16

3.2.1 Corre¸c˜ao bootstrap usual . . . 17

3.2.2 Corre¸c˜ao de Bartlett bootstrap para a estat´ıstica LR . . . 18

3.2.3 Bootstrap para dados com censura . . . 19

3.3 Testes de hip´oteses em modelos de sobrevivˆencia . . . 21

4 Resultados num´ericos 22

5 Aplica¸c˜ao 32

6 Considera¸c˜oes finais 36

(10)

Referˆencias Bibliogr´aficas 37

A Demonstra¸c˜oes 43

A.1 Obten¸cão do logaritmo da fun¸cão de verossimilhan¸ca do modelo de tempo de promo¸cão Weibull . . . 43 A.2 Obten¸cão do vetor escore . . . 44

B Valores fixados para os parˆametros nas simula¸c˜oes 46

C Aspectos computacionais 48

C.1 Simula¸c˜oes . . . 48 C.2 Aplica¸c˜ao . . . 61

(11)

Cap´ıtulo 1

Introdu¸c˜

ao

O tempo até a ocorrência de um evento de interesse, também conhecido como tempo de vida, tempo até a falha ou tempo de sobrevivência, é a variável de estudo em análise de sobrevivência (LAWLESS, 2003). Os modelos usuais de sobrevivência são amplamente conhecidos e discutidos na literatura, sendo baseados na suposi¸cão de que o evento de interesse irá ocorrer em todos os indiv´ıduos do estudo, desde que acompanhados tempo suficiente (LAWLESS, 2003; COX; OAKES, 1984; COLLETT, 2015).

No entanto, esses modelos usuais podem ser inadequados quando uma propor¸cão da popula¸cão não estiver mais sujeita ao evento de interesse, ou seja, parte da popula¸cão estiver “curada”. Modelos que tratam desta abordagem são chamados de modelos de fra¸cão de cura. Os primeiros modelos para esse tipo de situa¸cão foram propostos por Boag (1949) e Berkson e Gage (1952) no contexto de tempo de sobrevivência de pacientes com câncer, considerando mistura de distribui¸cões. Esses modelos ficaram conhecidos como modelos de mistura padrão, pois são baseados na mistura de duas distribui¸cões, uma para a sobrevivência dos indiv´ıduos não curados e a outra uma distribui¸cão degenerada, a qual permite tempos infinitos para os curados. Para mais detalhes sobre modelos de mistura ver Maller e Zhou (1996).

O modelo de mistura parece atraente e intuitivo. No entanto, apresenta alguns inconvenientes. Na presen¸ca de covariáveis ele não apresenta estrutura de riscos pro-porcionais, caracter´ıstica desejada quando utilizada inferência clássica (MATELUNA, 2014; YAKOVLEV; TSODIKOV, 1996). Outra abordagem na classe dos modelos de fra¸cão de cura com a estrutura de riscos proporcionais é o modelo de tempo de pro-mo¸cão. Este modelo foi apresentado por Yakovlev et al. (1993), estendido por Chen, Ibrahim e Sinha (1999) e incorporado como caso particular em uma forma unificada juntamente com o modelo de mistura padrão, por Rodrigues et al. (2009). Este modelo,

(12)

2

mais complexo que o modelo de mistura padrão, tem caracter´ısticas adequadas para explicar o mecanismo biológico envolvido em estudo de portadores de câncer. Também se adequa a outras aplica¸cões e atende à caracter´ıstica de riscos proporcionais.

Diferentes abordagens têm sido apresentadas no contexto de estima¸cão dos parâ-metros nesses modelos, sob o ponto de vista clássico e bayesiano (MALLER; ZHOU, 1996; CHEN; IBRAHIM; SINHA, 1999; IBRAHIM; CHEN; SINHA, 2005; FONSECA; VALEN ¸CA; BOLFARINE, 2013). A estima¸cão dos parâmetros no presente trabalho é baseada nos estimadores de máxima verossimilhan¸ca (EMV). Sob condi¸cões de regulari-dade esses estimadores possuem proprieregulari-dades de consistência e normaliregulari-dade assintótica (SEVERINI, 2000). Após a estima¸cão pontual, outro aspecto importante na modela-gem são os testes de hipóteses sobre os parâmetros do modelo. Entre as estat´ısticas de teste conhecidas na literatura para realiza¸cão de testes de hipóteses temos: (i) a estat´ıstica da razão de verossimilhan¸cas (LR) (NEYMAN; PEARSON, 1928), (ii) es-tat´ıstica Wald (W) (WALD, 1943), (iii) eses-tat´ıstica escore de Rao (S) (RAO, 1948) e (iv) a estat´ıstica gradiente (G) (TERRELL, 2002).

Estes testes são baseados em estat´ısticas cuja distribui¸cão assintótica sob a hipó-tese nula é a qui-quadrado e são denominados testes assintóticos de primeira ordem (CORDEIRO; CRIBARI-NETO, 2014). Desta forma, os valores cr´ıticos são prove-nientes de aproxima¸cões válidas em grandes amostras. Contudo, essas aproxima¸cões podem ser pobres em pequenas amostras, acarretando consideráveis distor¸cões da pro-babilidade do erro tipo I (tamanho) dos testes (CRIBARI-NETO; CORDEIRO, 1996; CORDEIRO; CRIBARI-NETO, 2014).

Nas estat´ısticas (i) e (iv), conforme Carneiro (2012), verifica-se consideráveis distor-¸cões da probabilidade do erro tipo I no modelo de tempo de promo¸cão Weibull. Nesse sentido, torna-se evidente a necessidade de melhoramentos inferenciais em pequenas amostras, por meio de ajustes anal´ıticos ou numérico computacionais.

(13)

1.1 Objetivos 3

CYSNEIROS; CRIBARI-NETO, 2013; CRIBARI-NETO; QUEIROZ, 2014).

Outra alternativa às corre¸cões bootstrap usuais é a corre¸cão de Bartlett bootstrap

para a estat´ıstica da razão de verossimilhan¸cas, introduzida por Rocke (1989), em que o fator de corre¸cão de Bartlett (LAWLEY, 1956) é determinado pelo métodobootstrap. Essa corre¸cão se torna uma boa alternativa à determina¸cão anal´ıtica do fator de cor-re¸cão de Bartlett, que em alguns modelos podem ser custosas ou imposs´ıveis de serem obtidas (CORDEIRO; CRIBARI-NETO, 2014; LOOSE; BAYER; PEREIRA, 2015).

1.1 Objetivos

Neste sentido, o objetivo geral do presente trabalho é avaliar e melhorar as infe-rências via testes de hipóteses em amostras de tamanho finito no modelo de tempo de promo¸cão Weibull. Para alcan¸car este objetivo geral, pontuamos os seguintes objetivos espec´ıficos:

• revisar o estado da arte no que tange corre¸c˜oes de testes de hip´oteses viabootstrap

e Bartlett bootstrap, em especial em modelos de sobrevivˆencia;

• avaliar os testes de hipóteses da razão de verossimilhan¸cas, escore, Wald e gradi-ente no modelo de tempo de promo¸cão Weibull. Salienta-se que os desempenhos das estat´ısticas Wald e escore ainda não foram investigados no modelo de tempo de promo¸cão Weibull;

• melhorar os testes de hip´oteses por meio de corre¸c˜oes bootstrap e Bartlett boots-trap;

• avaliar numericamente via simula¸c˜oes de Monte Carlo as corre¸c˜oes propostas;

• aplicar a dados reais os melhoramentos inferenciais propostos.

1.2 Descri¸c˜

ao dos cap´ıtulos

(14)

Cap´ıtulo 2

Modelos de sobrevivˆ

encia com

fra¸c˜

ao de cura e modelo de tempo

de promo¸c˜

ao Weibull

Neste cap´ıtulo é apresentada uma introdu¸cão aos conceitos básicos de análise de sobrevivência e do modelo de fra¸cão de cura, considerando a abordagem unificada proposta em Rodrigues et al. (2009).

2.1 Introdu¸c˜

ao `

a an´

alise de sobrevivˆ

encia

A análise de sobrevivência é caracterizada por um conjunto de técnicas estat´ısticas que têm como principal objetivo o estudo do tempo de vida, ou tempo até a ocorrência de um evento de interesse. Por exemplo, tempo até a morte de um paciente, tempo até a falha de um componente eletrônico, tempo até a recidiva de uma doen¸ca, tempo até a falência de uma empresa, entre outras ocorrências, são objetivo de estudo em análise de sobrevivência. Sendo a variável resposta conhecida na literatura como tempo de vida ou tempo de falha (LAWLESS, 2003; COX; OAKES, 1984; COLLETT, 2015; COLOSIMO; GIOLO, 2006).

Seja T a variável aleatória cont´ınua não-negativa que corresponde ao tempo até a ocorrência de um evento de interesse, f(t) a fun¸cão densidade e F(t) a fun¸cão distri-bui¸cão acumulada. Em análise de sobrevivência são frequentemente utilizadas duas outras fun¸cões: a fun¸cão de sobrevivência e a fun¸cão risco, apresentadas a seguir.

(15)

2.1 Introdu¸cão à análise de sobrevivência 5

2.1.1 Fun¸c˜

ao de sobrevivˆ

encia e fun¸c˜

ao risco

A fun¸cão de sobrevivência para a variável aleatóriaT é dada por (LAWLESS, 2003):

S(t) = P(T > t) = Z ∞

t

f(u)du= 1−F(t), para t >0. (2.1)

Esta fun¸cão representa a probabilidade de um indiv´ıduo sobreviver pelo menos até o tempo t. Note que S(t) é monótona decrescente com as seguintes propriedades:

i) S(0) = 1

ii) limt→∞S(t) = 0.

A fun¸c˜ao risco ou taxa de falha de T ´e dada por

h(t) = lim ∆t→0+

P(t < T ≤t+ ∆t|T > t)

∆t . (2.2)

Esta fun¸cão especifica a taxa de falha instantânea no tempo t (LAWLESS, 2003). As fun¸cões de densidade, sobrevivência e taxa de falha estão relacionadas. Essa rela¸cão é dada por

f(t) = −dS(t)

dt , h(t) = f(t)

S(t) =

−dlogS(t)

dt .

Nota-se que conhecendo uma delas as demais podem ser obtidas diretamente. A primeira rela¸cão vem da defini¸cão (2.1), sendo fácil a verifica¸cão e a segunda vem de (2.2). A demonstra¸cão é dada a seguir:

h(t) = lim ∆t→0+

P(t < T ≤t+ ∆t|T ≥t) ∆t

= lim ∆t→0+

1 ∆t

P(t < T ≤t+ ∆t)

P(T > t)

= lim ∆t→0+

1 ∆t

F(t+ ∆t)−F(t)

S(t)

= 1

S(t)∆limt→0+

F(t+ ∆t)−F(t) ∆t

= 1

S(t)F

′₍_t_{) =} f(t)

(16)

2.1 Introdu¸cão à análise de sobrevivência 6

2.1.2 Censura

Em dados de sobrevivência a principal caracter´ıstica observada é a presen¸ca de censura, vista como uma ocorrência apenas parcial da resposta (COX; OAKES, 1984). A censura surge quando algum acontecimento impede que a ocorrência do evento de interesse seja observada para um indiv´ıduo. Isso pode ocorrer pela morte do indiv´ıduo, pela mudan¸ca de cidade ou, até mesmo, porque o estudo terminou antes que o evento de interesse tenha sido observado (LAWLESS, 2003; COX; OAKES, 1984).

A censura nos dados é a principal razão para o desenvolvimento dos modelos de sobrevivência (LAWLESS, 2003). Nos casos em que não há censura, métodos usuais como modelos de regressão ou modelos lineares seriam aplicáveis.

Há diferentes tipos de censura, sendo que o mais utilizado e também considerado nesse trabalho é a censura à direita. Caracteriza-se pela ocorrência da falha após o tempo registrado, ou seja, o tempo do in´ıcio do estudo até a ocorrência do evento de interesse é maior que o tempo registrado (COLLETT, 2015; LAWLESS, 2003). Entre os mecanismos de censura à direita conhecidos na literatura o mais comum na prática é o de censura aleatória. Este caracteriza-se por interrup¸cões aleatórias no acompanhamento dos indiv´ıduos (LAWLESS, 2003). Neste mecanismo assume-se que os tempos de censura também são variáveis aleatórias. Quando a distribui¸cão da censura não envolve parâmetros de interesse, diz-se que a censura é não informativa (COLLETT, 2015).

2.1.3 Modelos param´

etricos

A seguir são apresentadas duas distribui¸cões usadas frequentemente na análise de dados de sobrevivência, que serão consideradas neste trabalho.

Distribui¸c˜ao Weibull

A distribui¸cão Weibull é uma generaliza¸cão da distribui¸cão exponencial. Dentre os modelos paramétricos, possivelmente é o mais utilizado na modelagem de dados de tempo de vida (LAWLESS, 2003).

A fun¸cão densidade de probabilidade de uma variável aleatória T com distribui¸cão Weibull é dada por

f(t) = a

bat

a−1_exp

−

t b

a

, t≥0, (2.3)

(17)

2.2 Modelos com fra¸c˜ao de cura 7

A fun¸cão de sobrevivência e fun¸cão risco são dadas por

S(t) = exp − t b a

e h(t) = a

bat a−1_.

Distribui¸c˜ao valor extremo

Na análise de dados de sobrevivência muitas vezes é conveniente trabalhar com o logaritmo dos dados (COLOSIMO; GIOLO, 2006). A distribui¸cão valor extremo está relacionada com a distribui¸cão Weibull, de tal forma que se T tem distribui¸cão Weibull(a,b), Y = log(T) tem distribui¸cão valor extremo com parâmetros µ= log(b) e

σ= 1

a. A fun¸cão densidade de probabilidade da variável aleatória Y é dada por

f(y) = 1

σ exp

y−µ σ −exp

y−µ σ

,

em quey eµ∈R eσ > 0,µ eσ são parâmetros de posi¸cão e escala, respectivamente. A fun¸cão de sobrevivência é dada por

S(y) = exp

−exp

y−µ σ

.

2.2 Modelos com fra¸c˜

ao de cura

Os modelos clássicos de análise de sobrevivência têm como caracter´ıstica fun¸cão de sobrevivência própria, ou seja, limt→∞S(t) = 0, (ver Se¸cão 2.1.1, propriedade ii).

Fun¸cões de sobrevivência que não satisfazem essa propriedade são ditas impróprias, caracterizando os modelos com fra¸cão de cura, também chamados de modelos de longa dura¸cão (CHEN; IBRAHIM; SINHA, 1999; RODRIGUES et al., 2009).

Na prática, a presen¸ca de imunes na popula¸cão pode ser identificada através do gráfico de Kaplan-Meier (KAPLAN; MEIER, 1958), que estima de forma não para-métrica a fun¸cão de sobrevivência teórica. Um indicativo da presen¸ca de imunes nos dados pode ser a ocorrência de um grande número de observa¸cões censuradas no fim do estudo, desde que o acompanhamento seja feito por um tempo suficientemente grande (MALLER; ZHOU, 1996). Desta forma, a curva de Kaplan-Meier vai se estabilizar em um valor maior que zero.

(18)

promo¸c˜ao como casos particulares.

2.2.1 Formula¸c˜

ao do modelo

SejaM uma variável aleatória que denota o número de causas ou riscos competindo para a ocorrência de um particular evento de interesse, com distribui¸cão de probabi-lidade pm = Pθ(M = m), sendo θ o parâmetro da distribui¸cão e m = 0,1,2, . . .. SejamZk, k= 1, . . . , m, variáveis aleatórias independentes com fun¸cão de distribui¸cão

F(t) = 1−S(t), independente deM, representando o tempo até a ocorrência do evento devido àk-ésima causa.

O número de causas competindo para a ocorrência do evento M e o tempo de ocorrência para cada causa (Zk) são não observáveis. Apenas pode-se observar o menor tempo entre todas as causas, T = min{Z0, Z1, . . . , ZM}, definido como o tempo até a ocorrência do evento. A variávelZ0 é tal que P(Z0 =∞) = 1, pois quandoM = 0 não existem causas ou riscos para a ocorrência do evento.

A fun¸cão de sobrevivência da variável aleatória T, denotada por Sp(t), é dada por

Sp(t) = P(T > t)

=P(T > t,M = 0) +P(T > t,M ≥1)

=P(T > t|M = 0)P(M = 0) +P(T > t|M ≥1)P(M ≥1)

=p0+

∞

X

m=1

pmS(t)m, (2.4)

em queP(T > t|M = 0) = 1,P(M = 0) =p0eS(t) representa a fun¸cão de sobrevivên-cia dos indiv´ıduos suscept´ıveis à ocorrênsobrevivên-cia do evento, caracterizada por ser própria. Logo, é fácil ver que Sp(t) é imprópria, ou seja, limt→∞Sp(t) = p0 >0, sendo p0 > 0 interpretado como a fra¸cão de curados (RODRIGUES et al., 2009).

Seja{am}uma sequˆencia de n´umeros reais. Se

A(s) =a0 +a1s+a2s2+· · ·

converge para s ∈ [0,1], então define-se A(s) como a fun¸cão geradora de sequências {am} (FELLER, 1960).

Rodrigues et al. (2009) mostram que:

Sp(t) = A(S(t)) =

∞

X

m=0

(19)

em queA(·) é a fun¸cão geradora de sequências {pm}.

Ainda, conforme Rodrigues et al. (2009) a equa¸c˜ao (2.4) pode tamb´em ser escrita como

Sp(t) =p0+ (1−p0)Sp∗(t), (2.5)

em queS∗

p(t) = P∞

m=1p∗mS(t)m ep∗m =

pm 1−p0

.

As fun¸c˜oes de subdensidade e de risco do modelo s˜ao dadas, respectivamente, por:

fp(t) =−

∂Sp(t)

∂t =f(t)

∞

X

m=1

mpm[S(t)]m−1 e hp(t) =

fp(t)

Sp(t)

.

A seguir s˜ao apresentados dois casos particulares do modelo unificado que se dife-renciam pela distribui¸c˜ao assumida paraM.

Modelo de mistura

No modelo de mistura assume-se que M tem distribui¸cão Bernoulli com parâmetro 1−θ, em que p0 =θ, p1 = 1−θ epn = 0 paran ≥2 (RODRIGUES et al., 2009). Ba-seada na equa¸cão (2.4) ou em (2.5), a sobrevivência do modelo de mistura apresentado por Berkson e Gage (1952) é dada por

Sp(t) = θ+ (1−θ)S(t),

em que θ representa a propor¸cão de curados. As fun¸cões de subdensidade e de risco são dadas por

fp(t) = (1−θ)f(t) e hp(t) = f(t)

(1−θ)

θ+ (1−θ)S(t).

Modelo de tempo de promo¸c˜ao

Neste modelo assume-se que M tem distribui¸cão Poisson com parâmetro θ. Base-ada na equa¸cão (2.4), a sobrevivência do modelo tempo de promo¸cão apresentado em Yakovlev et al. (1993) e Chen, Ibrahim e Sinha (1999) é dada por

(20)

em que S(t) é a fun¸cão de sobrevivência dos tempos Zk, k = 1, . . . , M, caracterizada por ser própria. Logo, é fácil ver que Sp(t) é imprópria, com limt→∞Sp(t) = exp(−θ), sendo p0 = exp(−θ) a fra¸cão de curados. As fun¸cões de subdensidade e de risco são dadas, respectivamente, por

fp(t) = θf(t) exp(−θF(t)) e hp(t) = θf(t). (2.7)

2.2.2 Verossimilhan¸ca para o modelo de tempo de promo¸c˜

ao

Para obten¸cão da fun¸cão de verossimilhan¸ca, supomos uma amostra com n indi-v´ıduos e para cada indiv´ıduo i, i = 1, . . . , n, e consideramos as seguintes variáveis associadas:

• Mi: variável aleatória discreta não observável com fun¸cão de probabilidade

Pθ(Mi =mi) =

e−θ_θmi

mi!

, em que θ ´e um vetor de parˆametros desconhecidos;

• Zij, i = 1, . . . , n, j = 1 =, . . . , mi: são variáveis aleatórias independentes e iden-ticamente distribu´ıdas (i.i.d.) que representam o tempo que a causaj, noi-ésimo indiv´ıduo, leva para provocar o evento de interesse, com fun¸cão de distribui¸cão

F(z|λ) e sobrevivˆencia S(z|λ) = 1 −F(z|λ), sendo λ o vetor de parˆametros associados ao modelo.

• Yi = min{Ti, Ci}: tempo observado para o indiv´ıduo i, sendo Ci o tempo de censura, considerada aleat´oria, n˜ao informativa e independente de Ti, e Ti = min{Zi0,Zi1, . . . , ZiMi};

• δi: indicador da censura, ou seja, se Yi =Ti, δi = 1, e se Yi =Ci,δi = 0;

• xi = (xi1, xi2, . . . , xip)⊤: vetor de covariáveis associado aoi-ésimo indiv´ıduo; • X: a matrizn×p que contém os vetores de covariáveis.

O conjunto dos dados completos é denotado por Dc = (n,y,δ,M,X), em que y= (y1, . . . , yn)⊤ são os tempos observados, δ = (δ1, . . . , δn)⊤, M = (M1, . . . , Mn)⊤, X = (x1, . . . , xn)⊤. O conjunto dos dados observáveis é denotado por D= (n,y,δ,X).

As covariáveis podem ser inclu´ıdas através do parâmetro associado à fra¸cão de cura

(21)

2.3 Modelo de tempo de promo¸c˜ao Weibull 11

Seja φ = (β⊤,λ⊤)⊤ _{o vetor de parˆametros desconhecidos. Pode-se mostrar (ver}

Carneiro (2012)), que a fun¸cão de verossimilhan¸ca em rela¸cão aos dados completos é dada por

L(φ;Dc) = n Y

i=1

[mif(yi|λ)]δi[S(yi|λ)]mi−δipθi(mi).

O logaritmo da fun¸c˜ao de verossimilhan¸ca ´e dado por

ℓ(φ;Dc) = n X

i=1

[δilog(mi) +δilog(f(yi|λλλ)) + (mi−δi) log(S(yi|λλλ)) + log(pθi(mi))].

Como existem variáveis latentes, na prática utiliza-se uma verossimilhan¸ca mar-ginal, obtida através do somatório nas variáveis Mi. A fun¸cão de verossimilhan¸ca marginal é dada por

L(φ;D) = n Y

i=1

[fp(yi|λλλ,θ)]δi[Sp(yi|λλλ, θ)]1−δi.

O logaritmo da fun¸c˜ao de verossimilhan¸ca marginal ´e dado por

ℓ(φ;D) = n X

i=1

δilog[fp(yi|φ)] + (1−δi) log[Sp(yi|φ)]. (2.8)

As demonstra¸c˜oes desses resultados podem ser verificadas, por exemplo, em Car-neiro (2012).

2.3 Modelo de tempo de promo¸c˜

ao Weibull

Neste modelo assume-se que os tempos de falha dos indiv´ıduos suscet´ıveis seguem uma distribui¸cão Weibull(a, b), como apresentada em (2.3). Em análise de sobrevi-vência, por razões computacionais, é comum reparametrizar a distribui¸cão Weibull. Um dos trabalhos que utiliza reparametriza¸cões é Fonseca, Valen¸ca e Bolfarine (2013). Neste trabalho consideramos a reparametriza¸cão dada a seguir:

ρ= log(a) e γ =−alog(b),

(22)

Considerando essa reparametriza¸cão, as fun¸cões de densidade de probabilidade e sobrevivência são dadas, respectivamente, por:

f(t) =eρteρ−1exp(γ−teρeγ) e S(t) = exp(−teρeγ).

Como consequência, temos a fun¸cão de sobrevivência de longa dura¸cão (2.6) dada por

Sp(t) = exp{−θ[1−exp(−te ρ

eγ)]}. (2.9)

De (2.7) temos a subdensidade dada por

fp(t) =θeρte ρ₋₁

exp(γ−teρ

eγ_{) exp{−}_θ_[1₋_exp(−_teρ

eγ_)]} _(2.10)

e a fun¸c˜ao risco do modelo dada por

hp(t) = θeρte ρ₋₁

exp(γ−teρ

eγ₎_.

Considerando uma amostra com n indiv´ıduos, seja D = (n,y,δ,X) o conjunto dos dados observ´aveis e φ = (β⊤,λ⊤)⊤ _{o vetor de parˆametros, em que} _λ _{= (}_{ρ, γ}_).

Substituindo (2.9) e (2.10) em (2.8) e incluindo covariáveis através da rela¸cão θi = exp(xi⊤β), o logaritmo da fun¸cão de verossimilhan¸ca do modelo de tempo de promo¸cão

é dado abaixo (ver demonstra¸cão no Apêndice A):

ℓ(φ;D) = n X

i=1

δi[xi⊤β+γ+ρ+ log(ye

ρ₋₁ i )−y

eρ i e

γ

]−exp(xi⊤β)[1−exp(−ye

ρ i e

γ )].

(2.11)

O vetor escore é obtido derivando (2.11) em rela¸cão ao vetor de parâmetrosφ, dado a seguir:

U(φ) = ∂ℓ(φ;D)

∂φ =

      

∂ℓ(φ;D)

∂β ∂ℓ(φ;D)

∂ρ ∂ℓ(φ;D)

∂γ        =   

Uβ(φ)

Uρ(φ)

Uγ(φ)   

(p+2)×1 =

n X

i=1

(23)

em que X∗

i =   

xi 0 0

0 1 0

0 0 1

  

(p+2)×3

é uma matriz e si(φ) é o vetor de dimensão 3×1

dado por (si1(φ), si2(φ), si3(φ))⊤, sendo

si1(φ) =δi−θi[1−exp(−ye ρ i eγ)],

si2(φ) =δi[1 +eρlog(yi)(1−ye ρ

i eγ)]−θiexp(ρ+γ−ye ρ i eγ)ye

ρ

i log(yi) e

si3(φ) =δi(1−ye ρ

i eγ)−θiexp(γ−ye ρ i eγ)ye

ρ i .

A obten¸cão do vetor escore pode ser verificada no Apêndice A. As estimativas de máxima verossimilhan¸ca são obtidas a partir da solu¸cão do seguinte sistema:

    

Uβ(φ) = 0,

Uρ(φ) = 0,

Uγ(φ) = 0.

A solu¸cão deste sistema não possui forma fechada, sendo necessário o uso de algorit-mos de otimiza¸cão não-linear para encontrar as estimativas de máxima verossimilhan¸ca. Neste trabalho utiliza-se o método quasi-Newton BFGS (PRESS et al., 1992).

A matriz de informa¸cão observada J(φ) é dada pelo negativo da segunda derivada da fun¸cão de log-verossimilhan¸ca (2.11), dada a seguir:

J(φ) =−∂

2_ℓ₍_φ_;_D₎

∂φ∂φ⊤ =−

       

∂2_ℓ₍_φ_;_D₎

∂β∂β⊤

∂2_ℓ₍_φ_;_D₎

∂β∂ρ

∂2_ℓ₍_φ_;_D₎

∂β∂γ ∂2_ℓ₍_φ_;_D₎

∂ρ∂β⊤

∂2_ℓ₍_φ_;_D₎

∂ρ2

∂2_ℓ₍_φ_;_D₎

∂ρ∂γ ∂2_ℓ₍_φ_;_D₎

∂γ∂β⊤

∂2_ℓ₍_φ_;_D₎

∂γ∂ρ

∂2_ℓ₍_φ_;_D₎

∂γ2         .

(24)

Cap´ıtulo 3

Testes de hip´

oteses e

melhoramentos inferenciais em

pequenas amostras

Após a estima¸cão dos parâmetros do modelo, em geral, realizam-se testes a fim de determinar se hipóteses feitas sobre esses parâmetros são suportadas por evidências ob-tidas a partir de dados amostrais. A seguir descrevemos os testes de hipóteses baseados nas estat´ısticasLR,W,S eG, uma breve revisão sobre melhoramentos inferenciais em testes de hipóteses, as propostas de corre¸cões consideradas nesse trabalho e algumas referências que discutem a validade dos testes em modelos de sobrevivência.

3.1 Estat´ısticas de teste

Seja o vetor de parˆametros φ= (ν⊤,τ⊤)⊤_{, em que} _ν _{= (}_ν

1, . . . , νq)⊤ representa o vetor de parâmetros de interesse eτ = (τ1, . . . , τs)⊤ o vetor de parâmetros de pertur-ba¸cão. Suponha que o interesse esteja em testar

H0 :ν =ν0 versus H1 :ν 6=ν0,

em queν0 ´e um vetor de constantes especificado de dimens˜ao q.

O estimador de máxima verossimilhan¸ca sob H0 (restrito) é denotado por φe = (ν0⊤,τe⊤)⊤ e o estimador de máxima verossimilhan¸ca irrestrito φb = (νb⊤,bτ⊤)⊤. Seja

ℓ(φ) = ℓ(ν,τ) o logaritmo da fun¸c˜ao de verossimilhan¸ca de ν e τ. Conforme Cor-deiro (1992), podemos particionar o vetor escore U(φ), a matriz informa¸c˜ao de Fisher

K(φ) e sua inversa K(φ)−1 _{da mesma maneira que particionamos} _φ_{, sendo} _U₍_φ₎⊤ ₌

(25)

3.1 Estat´ısticas de teste 15

(Uν(φ)⊤, Uτ(φ)⊤),

K(φ) = Kν ν(φ) Kν τ(φ)

Kτ ν(φ) Kτ τ(φ)

!

e K(φ)−1 = K

ν ν

(φ) Kν τ

(φ)

Kτ ν

(φ) Kτ τ

(φ) !

.

Considerando essas parti¸cões as estat´ısticas da razão de verossimilhan¸cas, Wald, escore e gradiente são escritas conforme segue:

LR= 2[ℓ(_bν,τ_b)−ℓ(ν0,τe)],

W = (ν_b−ν0)⊤[K

ν ν_(b

φ)]−1(ν_b−ν0),

S=Uν(φe)⊤K ν ν

(φe)Uν(φe),

G=Uν(φe)⊤(νb−ν0),

sendoKν ν

= Kν ν −Kν τKτ τ−1Kν τ⊤

−1

. Note que quando ν e τ s˜ao ortogonais, Kν ν

=

K−1

ν ν.

Sob condi¸cões de regularidade usuais e sob a hipótese nula, as quatro estat´ısti-cas apresentadas são assintoticamente equivalentes, possuindo aproximadamente dis-tribui¸cão χ2

q em grandes amostras, em que q é o número de parâmetros testados na hipótese nula (SEVERINI, 2000; CASELLA; BERGER, 2002; VARGAS; FERRARI; LEMONTE, 2014).

Um importante trabalho no contexto de testes de hipóteses é Buse (1982), o qual apresenta interpreta¸cões geométricas dos testes baseados nas estat´ısticas RV, W e S. No mesmo sentido, recentemente Montoril (2010) apresenta a interpreta¸cão geométrica também para o teste baseado na estat´ıstica G.

(26)

3.2 Melhoramentos inferenciais em testes de hip´oteses 16

Os testes de hipóteses são realizados com base em valores cr´ıticos obtidos a partir de aproxima¸cões válidas em grandes amostras. Nesse sentido, o uso destes testes em pequenas amostras pode acarretar consideráveis distor¸cões na probabilidade do erro tipo I. Essas distor¸cões podem ser reduzidas através de melhoramentos inferenciais (CRIBARI-NETO; QUEIROZ, 2014; VARGAS; FERRARI; LEMONTE, 2014). A seguir são apresentados os procedimentos utilizados no presente trabalho baseados em métodos numérico computacionais para corre¸cões em testes de hipóteses.

3.2 Melhoramentos inferenciais em testes de hip´

o-teses

Melhoramentos inferenciais em testes de hipóteses têm recebido grande destaque na comunidade acadêmica nos últimos anos, sendo desenvolvidos em diferentes mode-los, via ajustes anal´ıticos ou numérico computacionais. Duas importantes referências sobre melhoramentos inferenciais em pequenas amostras são Cribari-Neto e Cordeiro (1996) e Cordeiro e Cribari-Neto (2014). Esses trabalhos abordadam corre¸cões como a de Bartlett, por exemplo, a qual foi proposta por Bartlett (1937) e posteriormente generalizada por Lawley (1956), obtida de forma anal´ıtica. A ideia dessa corre¸cão é considerar uma transforma¸cão na estat´ıstica de teste, baseada em um fator de corre¸cão, a qual leva a uma melhor aproxima¸cão da distribui¸cão da estat´ıstica corrigida pela dis-tribui¸cão qui-quadrado. Também são abordadas outras corre¸cões como a tipo Bartlett, Bartlett bootstrap e bootstrap.

Dentre os trabalhos desenvolvidos considerando corre¸cões em testes de hipóteses temos Cysneiros e Cordeiro (2002), no qual é obtida a corre¸cão tipo Bartlett para a estat´ıstica escore, em nota¸cão matricial, na classe dos modelos não-lineares da fam´ılia loca¸cão e escala, além da aproxima¸cãobootstrap para a distribui¸cão nula das estat´ısticas escore e razão de verossimilhan¸cas. Em Cysneiros e Ferrari (2006) é obtida a corre¸cão de Bartlett para a estat´ıstica da razão de verossimilhan¸cas modificada para testar dispersão variável no modelo não-linear da fam´ılia exponencial. Cysneiros et al. (2010) propõem corre¸cões anal´ıticas para a estat´ıstica escore, bem como a versão bootstrap

(27)

melhoramentos inferenciais no contexto de dados com censura. Cribari-Neto e Queiroz (2014) consideram no modelo de regressão beta versões ajustadas da estat´ıstica razão de verossimilhan¸cas já propostas na literatura por Ferrari e Pinheiro (2011), e corre¸cões via bootstrap para as estat´ısticas razão de verossimilhan¸cas, escore e Wald. Vargas, Ferrari e Lemonte (2014) nos modelos lineares generalizados apresentam a corre¸cão de Bartlett para as estat´ısticas razão de verossimilhan¸cas e escore, e derivam o fator de corre¸cão tipo Bartlett para a estat´ıstica gradiente, além de versões bootstrap para as quatro estat´ısticas já mencionadas no presente trabalho. Recentemente Loose, Bayer e Pereira (2015) propõem a corre¸cão Bartlett bootstrap no modelo de regressão beta inflacionado, comparando com a estat´ıstica usual e ajustes anal´ıticos via Skovgaard (SKOVGAARD, 1996) já propostos na literatura para o modelo por Pereira e Cribari-Neto (2014). Cabe destacar que não há trabalhos que abordam corre¸cões em testes de hipóteses no modelo com fra¸cão de cura, em especial no modelo tempo de promo¸cão Weibull.

Todos os trabalhos mencionados avaliam o desempenho dos testes usuais e de suas versões corrigidas. Em todos os casos os testes corrigidos são menos distorcidos que os testes usuais. Cabe ainda destacar que os desempenhos das corre¸cões anal´ıticas ou via métodos numérico computacionais são muito semelhantes. Em geral as corre¸cões numérico computacionais apresentam desempenhos iguais ou até superiores às corre¸cões anal´ıticas.

Nesse sentido, corre¸cões via métodos numérico computacionais são alternativas viá-veis para melhoramentos inferenciais em pequenas amostras, quando há dificuldades anal´ıticas impeditivas ou muito custosas, como no modelo aqui considerado. A seguir são apresentados os dois métodos de corre¸cão em testes de hipóteses considerados no presente trabalho.

3.2.1 Corre¸c˜

ao

bootstrap

usual

Uma das op¸cões de melhoramento inferencial em testes de hipóteses é a corre¸cão

(28)

aleat´o-3.2 Melhoramentos inferenciais em testes de hip´oteses 18

ria observada a distribui¸c˜ao emp´ırica da estat´ıstica de teste de interesse (CORDEIRO; CRIBARI-NETO, 2014; CRIBARI-NETO; QUEIROZ, 2014). Para maiores detalhes ver Davison e Hinkley (1997).

Conforme Cribari-Neto e Queiroz (2014) o esquema bootstrap pode ser descrito baseado nos seguintes passos:

1. Seja y a amostra observada. Calcular a estat´ıstica de teste de interesse (dentre as apresentadas na Se¸c˜ao 3.1), denotada por ξ(y).

2. Gerar a amostra bootstrap y∗

b do modelo, substituindo os parˆametros do modelo pelas estimativas sob H0, obtidos com base na amostra original y.

3. Estimar o modelo usando y∗

b e calcular a estat´ısticaξb∗ =ξ(y∗b). 4. Repetir os passos 2 e 3 um n´umeroB grande de vezes.

5. Calcular o quantil de interesse ξ∗

1−α, com base na distribui¸c˜ao emp´ırica das B realiza¸c˜oes da estat´ıstica ξ∗

b, obtidas usando os passos do item 2 at´e 4.

6. Realizar o teste utilizando a estat´ıstica ξ(y) calculada no item 1 junto com o valor cr´ıtico de bootstrap, ξ∗

1−α, obtido no item 5. A região de rejei¸cão é definida com base no quantilξ∗

1−α, sendo a hip´otese nula, H0, rejeitada quando a estat´ıstica ´e maior que o quantil estimado, ou seja, ξ(y) > ξ∗

1−α. Ou ainda, em termos de p-valor aproximado por bootstrap:

p∗ = PB

b=1I{ξ∗ b>ξ(y)}

B ,

em que

I{ξ∗

b>ξ(y)} = (

1, se ξ∗

b > ξ(y), 0, c.c.

H0 ´e rejeitada se p∗ _{´e menor que um valor} _α _selecionado.

3.2.2 Corre¸c˜

ao de Bartlett

bootstrap

para a estat´ıstica

LR

(29)

(BARTLETT, 1937), onde o fator de corre¸cão é obtido via métodobootstrap (EFRON, 1979).

Rocke (1989) descreve a obten¸c˜ao da corre¸c˜ao de Bartlett bootstrap utilizando o valor esperado de LR estimado diretamente da amostra observada y = (y1, . . . , yn)⊤ utilizando reamostrasbootstrap.

Conforme Loose, Bayer e Pereira (2015) esse procedimento pode ser descrito pelos seguintes passos:

1. Gerar sob H0 B reamostras bootstrap (y∗

1, . . . ,y∗B) do modelo, substituindo os parˆametros do modelo pelas estimativas sob H0 usando a amostra original.

2. Obter a estat´ıstica LR bootstrap (LR∗b_{) para cada pseudo amostra} _y∗

b, com b = 1, . . . , B. Calculada da seguinte forma:

LR∗b = 2{ℓ(φb∗b;y∗b)−ℓ(φe

∗b ;y∗b)},

em que φb∗b ´e o EMV de φ irrestrito e φe∗b ´e o EMV sob H0.

3. Calcular a estat´ıstica LR corrigida, dada por:

LRB =

LR×q LR∗ ,

em que LR∗ ₌ 1

B

B P b=1

LR∗b_.

Rocke (1989) afirma que a corre¸cão de Bartlett bootstrap tem vantagens computa-cionais comparadas ao esquema bootstrap usual, de tal forma que com B = 100 em geral tem-se resultados equivalentes ao método bootstrap usual com B = 700. Ainda, Bayer e Cribari-Neto (2013) afirmam que valores de B maiores que 200 conduzem a melhoramentos neglig´ıveis para a corre¸cão de Bartlett bootstrap.

3.2.3 Bootstrap

para dados com censura

(30)

são obtidas do vetor (Yi, δi), i = 1, . . . , n, reamostrado com reposi¸cão. Akritas (1986) apresenta uma discussão das duas abordagens.

Um dos poucos trabalhos que abordam reamostragem em dados com censura à di-reita com o objetivo de melhoramentos inferenciais em testes de hipóteses é Barreto, Cysneiros e Cribari-Neto (2013). Alternativamente, utilizam bootstrap paramétrico para a obten¸cão das reamostras. As amostras bootstrap são constru´ıdas baseada na distribui¸cão associada à amostra original, utilizando os estimadores dos parâmetros dessa distribui¸cão. Sendo que a quantidade de censura das amostrasbootstrap é preser-vada, ou seja, as reamostras tem a mesma quantidade de censura da amostra original. O presente trabalho considera a mesma abordagem de Barreto, Cysneiros e Cribari-Neto (2013). As reamostras são geradas pelo métodobootstrap paramétrico, buscando preservar a quantidade de censura da amostra original nas amostrasbootstrap. A seguir é descrito o procedimento de reamostragem proposto, para o modelo considerado neste estudo, baseado no método bootstrap paramétrico.

Reamostragem bootstrap no modelo tempo de promo¸c˜ao Weibull

Seja φe = (eβ⊤,λe⊤)⊤ _{o EMV de} _φ _sob _H

0 e λ = (ρ, γ)⊤. A matriz das vari´aveis regressoras permanece constante, sendo a mesma da amostra original. As amostras

bootstrap s˜ao geradas considerando o algoritmo dado a seguir:

1. Gerar ocorrˆencias de m∗

i da distribui¸c˜ao Poisson com m´edia θei = exp(x⊤i βe). 2. Dado m∗

i >0, gerar zi∗1, . . . , z∗im∗

i iid da distribui¸c˜ao Weibull(ea,eb), sendo a=e ρ _e

b = exp(−γ/eρ_).

3. Obter os tempos de falha por t∗

i = min{zi∗1, . . . , zim∗ ∗ i}.

4. Gerar c∗

i aleatoriamente de uma distribui¸cão uniforme, U(0,u), sendo utal que a propor¸cão de censura da amostra original é conservada.

5. Obter os tempos observados por:

yi∗ = (

max{c∗

1, . . . , c∗n}, se m∗i = 0, min{t∗

i, c∗i}, se m∗i >0.

6. Associar a cada tempo observado o indicador de falha δ∗

i, dado por:

δ∗_i = (

1, se y∗

i =t∗i, 0, se y∗

(31)

3.3 Testes de hip´oteses em modelos de sobrevivˆencia 21

Considerando os passos 1 a 6, obt´em-se o conjunto dos dados da b-´esima amostra

bootstrap, denotado por D∗

b = (n,y∗b,δ

∗

b,X), em que y∗b = (y∗1, . . . , yn∗). Cabe destacar, que a proposta para gera¸cão das amostras bootstrap aqui apresentada para o modelo em estudo é pioneira em modelos de fra¸cão de cura, podendo ser generalizada para outros modelos dessa classe.

As corre¸cões bootstrap e Bartlett bootstrap são realizadas conforme os passos dos algoritmos apresentados nas Sub-se¸cões 3.2.1 e 3.2.2. A amostrabootstrap gerada, D∗

b, ´e aplicada nos passos correspondentes nos algoritmos, sendo o modelo dado em (2.11).

3.3 Testes de hip´

oteses em modelos de sobrevivˆ

en-cia

As inferências baseadas nas estat´ısticas de teste apresentadas na Se¸cão 3.1 depen-dem de resultados assintóticos, os quais estão relacionados à teoria assintótica dos es-timadores de máxima verossimilhan¸ca. A seguir são apresentadas algumas referências que evidenciam a validade dos resultados para os modelos de sobrevivência.

Um dos primeiros trabalhos a analisar com detalhes as propriedades assintóticas do estimador de máxima verossimilhan¸ca do modelo com fra¸cão de cura, com distribui¸cão exponencial associada aos tempos de falha, foi Ghitany e Maller (1992). Posterior-mente, Maller e Zhou (1996) apresentam demonstra¸cões da normalidade assintótica do estimador de máxima verossimilhan¸ca e resultados para testes em grandes amostras, considerando o modelo paramétrico exponencial com covariáveis, censura (não infor-mativa) e fra¸cão de cura. Conforme Maller e Zhou (1996), o desenvolvimento teórico para outras distribui¸cões se dá de forma análoga ao modelo exponencial.

No contexto dos modelos Weibull com fra¸cão de cura, segundo Paes (2007) as propriedades do estimador de máxima verossimilhan¸ca podem ser vistas como uma extensão da teoria desenvolvida para modelos lineares generalizados (MCCULLAGH; NELDER, 1989). Ainda Paes (2007) descreve com detalhes os resultados assintóticos para modelos Weibull com fra¸cão de cura apresentados por Ghitany, Maller e Zhou (1994).

(32)

Cap´ıtulo 4

Resultados num´

ericos

Para avaliar os desempenhos em pequenas amostras dos testes razão de verossimi-lhan¸cas (LR), gradiente (G), escore (S) e Wald (W), as versões corrigidas porbootstrap, respectivamente,LRb,Gb,Sb eWb e do teste baseado na razão de verossimilhan¸cas cor-rigida via Bartlett bootstrap (LRB), foi realizado um estudo de simula¸cão. O número de réplicas de Monte Carlo foi 5000 e para as corre¸cões bootstrap foram considera-das B = 1000 reamostras bootstrap. Os tamanhos amostrais utilizados foram iguais a

n= 30, 50, 100. Toda a implementa¸cão computacional foi desenvolvida na linguagem R (R Development Core Team, 2014), sendo que para a estima¸cão dos parâmetros do modelo foi utilizada a fun¸cãooptim, considerando o método BFGS com primeiras deri-vadas anal´ıticas. Para os testes Wald e escore foi considerada a informa¸cão observada, já que a informa¸cão de Fisher nesse modelo é imposs´ıvel de ser obtida, conforme já descrito no Cap´ıtulo 2. A matriz de informa¸cão observada foi obtida através da aproxi-ma¸cões numéricas no R, fornecida pelo optim. Ainda, a parametriza¸cão utilizada noR se dá em termos do logar´ıtmo deT, dessa forma utiliza-se a distribui¸cão valor extremo apresentada em 2.1.3 (CARVALHO et al., 2011).

Da mesma forma que em Carneiro (2012), a matriz das variáveis regressoras é gerada a partir de distribui¸cões de Bernoulli(pb), compb em torno de 0,5, e considerada constante durante todas as réplicas de Monte Carlo. Nas simula¸cões, a fim de avaliar o impacto do aumento do número de parâmetros de perturba¸cão, foram consideradas quatro (p = 4) e seis (p = 6) covariáveis. Para p = 4, foram geradas para cada i = 1,2, . . . , n, xi1, xi2, xi3 e xi4 de forma independente, de distribui¸cões de Bernoulli, com probabilidades de sucesso (pb) 0,49, 0,5, 0,51 e 0,52, respectivamente. Analogamente, para p= 6, foram geradas xi1, xi2, xi3, xi4, xi5 e xi6 de distribui¸cões de Bernoulli, com probabilidades de sucesso (pb) 0,48, 0,49, 0,5, 0,51, 0,52 e 0,53, respectivamente.

Os valores de Mi são gerados da distribui¸cão Poisson com média θi = exp(x⊤i β).

(33)

23

Os valores de β são fixados de tal forma que, combinados com a matriz das variáveis regressoras, a média da fra¸cão de cura seja em torno de 10% e 30%. Para os indiv´ıduos não imunes (Mi > 0) foi gerada uma amostra de tamanho mi (zik;k = 1, . . . mi) da distribui¸cão Weibull(a,b), em que a = 2 e b = 4. Os tempos de falha são obtidos por ti = min{zik;k = 1, . . . mi}. As censuras são geradas aleatoriamente de uma distribui¸cão uniforme, U(0,u), sendo que o valor de u afeta inversamente a propor¸cão de censuras da amostra. Após gerada a censuraci, os tempos observados são dados por

yi = min{ti, ci}. A cada tempo observado ´e associado o indicador de falha, δi = 1 se

ti ≤ci eδi = 0 seti > ci . QuandoMi = 0, o tempo observado recebe max{ci, . . . , cn}, (valor suficientemente grande), e o indicador de falhas recebe zero. Os valores fixados nas simula¸cões paraβ e u são descritos no Apêndice B.

Assim como Fonseca, Valen¸ca e Bolfarine (2013) e Carneiro (2012), para definir o percentual de censuras entre os curados e a propor¸c˜ao de censuras com rela¸c˜ao ao total de indiv´ıduos suscet´ıveis ao evento, consideramos os seguintes eventos: A = curados,

Ac _{= não curados,} _C _{= censurados ou imunes. A partir desses eventos definimos a} propor¸cão de censuras dentre os não curados, denotada porpc1, dada a seguir:

pc1 =

(C∩Ac₎ #Ac ,

em que # denota a quantidade de indiv´ıduos no conjunto. A propor¸c˜ao de censurados ou imunes ´e dada por

pc2 =

#C

#(A∪Ac₎.

Em aplica¸cões a dados reais a quantidadepc2 é vista como o percentual de censuras da popula¸cão. Ainda em Fonseca, Valen¸ca e Bolfarine (2013) é apresentada uma rela¸cão entre pc1 e pc2, que é dada por

pc2 =pc1(1−p0) +p0,

em quep0 representa a propor¸c˜ao de imunes.

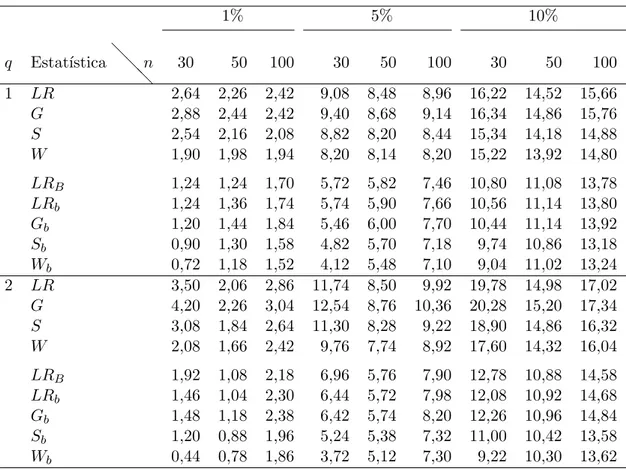
Os resultados para a avalia¸cão da taxa de rejei¸cão nula dos testes estão apresentados nas Tabelas 4.1 a 4.6. Foi considerado o modelo de tempo de promo¸cão Weibull, n´ıveis nominais iguais a 1%, 5% e 10%. As três combina¸cões dep0 epc1 usadas para as simu-la¸cões implicam propor¸cões de censuras na popula¸cão (pc2) iguais a 19%, 37%, 51%. Para as Tabelas 4.1 e 4.4, a propor¸cão de imunes ou fra¸cão de curados fixada foi de

(34)

24

Tabela 4.1: Taxas de rejei¸c˜ao nula (%) para H0 :β1 =. . . =βq = 0, comp = 4, 10% de fra¸c˜ao de cura e 10% censura, (pc2 = 19%), considerando os diferentes tamanhos amostrais e n´ıveis nominais.

1% 5% 10%

q Estat´ıstica❅_❅

❅n 30 50 100 30 50 100 30 50 100

1 LR 1,84 1,58 1,30 7,20 7,02 6,16 13,70 12,88 11,20

G 1,90 1,84 1,30 7,28 7,28 6,18 13,50 13,26 11,26

S 2,04 1,18 1,34 7,56 6,36 6,12 13,76 12,28 11,30

W 1,56 1,12 1,28 6,92 6,16 6,06 13,30 12,18 11,14

LRB 0,86 0,90 1,00 4,42 5,08 5,40 9,10 10,04 9,86

LRb 0,94 1,02 1,22 4,46 5,18 5,44 9,02 10,24 9,92

Gb 0,98 1,00 1,16 4,52 5,14 5,46 9,02 10,14 9,92

Sb 0,82 0,98 1,14 4,40 4,84 5,46 8,74 10,26 9,96

Wb 0,90 0,94 1,14 4,46 4,82 5,46 8,92 10,30 9,92

2 LR 2,38 1,82 1,44 8,74 7,42 6,68 15,40 13,54 11,76

G 2,56 2,16 1,56 8,94 7,58 6,86 15,36 13,96 11,92

S 2,54 1,70 1,46 8,98 7,32 6,58 15,76 13,30 11,68

W 1,90 1,52 1,30 8,22 6,94 6,38 14,86 12,74 11,54

LRB 0,94 1,18 0,92 5,34 5,38 5,34 10,16 10,40 10,12

LRb 1,06 1,22 1,04 5,38 5,46 5,40 10,08 10,42 10,14

Gb 1,04 1,28 1,10 5,30 5,40 5,44 10,08 10,60 10,12

Sb 0,96 1,06 1,16 5,12 5,42 5,34 9,78 10,62 10,28

Wb 0,96 1,16 1,18 5,28 5,46 5,42 9,90 10,58 10,28

pc2 = 19% (percentual de censuras da popula¸c˜ao). Nas Tabelas 4.2 e 4.5 foram fixados

p0 = 10% e pc1 = 30%, (pc2 = 37%). Ainda, para as Tabelas 4.3 e 4.6, foram fixados

p0 = 30% e pc1 = 30%, (pc2 = 51%).

(35)

25

taxas de rejei¸c˜ao nula para 13,54%, 13,96%, 13,30% e 12,74%, respectivamente, LR,

G, S e W. Já os testes baseados nas corre¸cões propostas mantém as taxas de rejei¸cão próximas aos n´ıveis nominais, apresentando no mesmo cenário, taxas de rejei¸cão iguais a 10,40%, 10,42%, 10,60%, 10,62% e 10,58%, respectivamente, para LRB, LRb, Gb, Sb eWb.

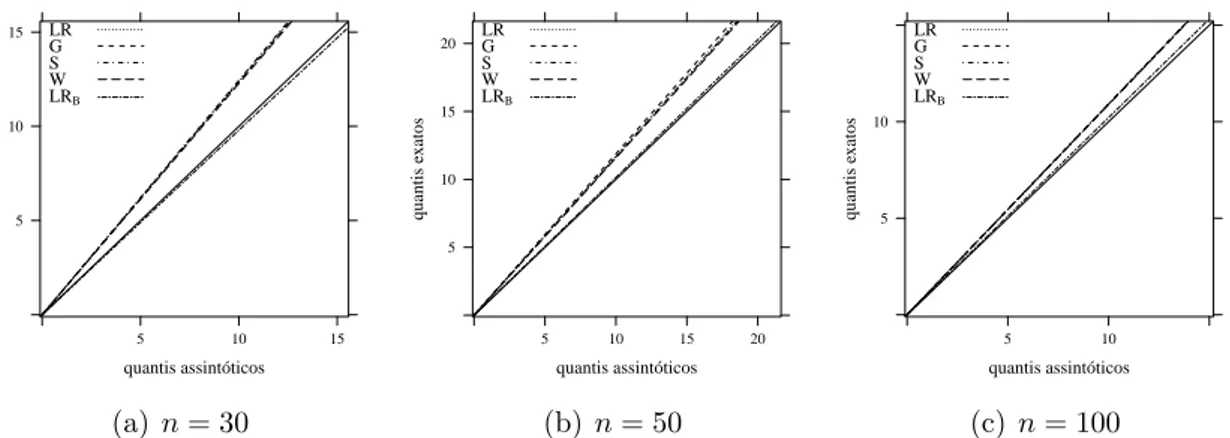
A Figura 4.1 apresenta os gráficos QQ-plot (quantil exato versus quantil assintó-tico), considerando os diferentes tamanhos amostrais, q = 1 e a mesma configura¸cão de censura da Tabela 4.1. Observando a Figura 4.1, nota-se que a estat´ıstica corrigida por Bartlettbootstrap apresenta distribui¸cão mais próxima da distribui¸cão nula de re-ferência, χ2

q. Já as estat´ısticas usuais, para o tamanho amostral n = 30, apresentam distribui¸cões muito próximas entre si, mas longe da distribui¸cão nula de referência, quando comparadas com LRB. A medida que o tamanho amostral aumenta as distri-bui¸cões das estat´ısticas usuais tornam-se mais próximas à de referência.

quantis assintóticos quantis e xatos 5 10 15

5 10 15

LR G S W LRB

(a) n= 30

quantis assintóticos quantis e xatos 5 10 15 20

5 10 15 20

LR G S W LRB

(b)n= 50

quantis assintóticos quantis e xatos 5 10 5 10 LR G S W LRB

(c) n= 100

Figura 4.1: Gr´afico quantil-quantil considerando 10% de fra¸c˜ao de cura e 10% censura,

q= 1 e diferentes tamanhos amostrais.

Na Tabela 4.2 são apresentadas as taxas de rejei¸cão nula para o cenário com per-centual de censura na popula¸cão de 37%, com 4 covariáveis, considerando q = 1, 2. Verifica-se, assim como na Tabela 4.1, que os testes baseados nas corre¸cões propostas apresentam menores distor¸cões de tamanho quando comparadas às usuais. Por exem-plo, paran= 30, n´ıvel de 10%, tem-se taxas de rejei¸cão nula muito próximas aos n´ıveis nominais (10,16%, 10,14%, 10,04%, 9,92% e 9,98%, respectivamente para LRB, LRb,

Gb, Sb e Wb). J´a as estat´ısticas usuais se mostram mais liberais, apresentando taxas de rejei¸c˜ao de 15,36%, 15,10%, 15,32% e 14,66%, respectivamente, para LR, G, S e

(36)

26

1% 5% 10%

❅n 30 50 100 30 50 100 30 50 100

1 LR 2,72 2,82 1,42 8,88 10,10 6,28 15,36 17,32 12,24

G 2,74 3,06 1,46 8,86 10,32 6,30 15,10 17,30 12,32

S 2,88 2,40 1,38 8,92 8,82 6,08 15,32 16,12 11,90

W 2,22 1,96 1,30 8,16 8,72 6,04 14,66 16,26 11,94

LRB 1,06 1,14 0,92 5,22 5,66 4,96 10,16 10,90 10,28

LRb 1,22 1,22 1,02 5,14 5,84 4,94 10,14 11,08 10,20

Gb 1,12 1,00 0,96 5,22 5,62 4,92 10,04 10,70 10,08

Sb 1,22 1,30 1,00 5,08 5,90 4,72 9,92 10,78 10,02

Wb 1,22 1,22 1,04 5,16 5,78 4,86 9,98 10,90 10,10

2 LR 2,30 2,66 3,02 8,98 10,36 10,78 16,70 17,52 18,00

G 2,44 3,00 3,18 9,32 10,76 11,26 16,62 17,64 17,74

S 2,58 3,24 3,54 9,44 10,34 10,52 16,66 17,00 17,92

W 1,78 1,86 2,64 7,76 8,84 9,90 15,72 16,06 17,36

LRB 0,68 0,98 1,26 4,04 5,18 5,66 8,96 11,34 11,00

LRb 0,66 1,26 1,64 4,08 5,50 5,92 9,18 11,46 11,38

Gb 0,64 1,16 1,48 4,04 5,42 5,76 9,22 11,20 11,18

Sb 0,80 1,44 1,74 4,28 6,12 6,24 9,32 11,76 11,74

Wb 0,76 1,20 1,50 4,20 5,52 5,96 9,08 11,60 11,50

acarreta em aumento das distor¸cões dos testes usuais. Ainda, à medida que o tamanho amostral aumenta, os resultados dos testes usuais são ainda mais distorcidos (q = 2). Esse resultado não é esperado, no entanto, está de acordo com os resultados obtidos por Carneiro (2012), no qual é considerado o mesmo modelo e configura¸cões aqui apresen-tadas. Esse comportamento at´ıpico pode ser justificado, possivelmente, por problemas numéricos, que em amostras maiores ocorrem com maior frequência. Os testes basea-dos nas corre¸cões propostas mesmo quando q = 2 apresentam bom desempenho, com as menores distor¸cões.

(37)

27

1% 5% 10%

❅n 30 50 100 30 50 100 30 50 100

1 LR 2,20 2,24 1,54 8,36 8,56 6,20 14,16 14,98 11,24

G 2,40 2,82 1,62 8,34 9,42 6,40 14,30 15,86 11,48

S 2,18 1,62 1,28 8,24 7,14 5,90 14,12 13,46 11,14

W 1,32 1,46 1,16 7,28 6,76 5,70 13,20 13,48 10,90

LRB 0,90 0,98 1,06 4,82 5,14 5,00 9,46 10,12 9,96

LRb 0,80 1,22 1,22 4,90 5,42 5,14 9,48 10,24 10,06

Gb 0,76 1,10 1,16 4,86 5,28 5,06 9,26 10,10 9,98

Sb 0,84 1,14 1,14 4,88 5,16 5,14 9,66 9,98 9,90

Wb 1,04 1,18 1,14 5,18 5,22 5,18 10,00 10,14 9,88

LR 2,48 2,26 2,32 9,12 9,04 9,88 15,12 16,82 17,06

G 2,92 3,04 2,98 9,68 10,54 10,82 15,50 18,18 18,04

S 2,12 1,40 1,64 8,06 6,92 8,34 14,40 13,68 15,14

W 1,30 0,90 1,42 6,90 6,48 8,06 13,54 12,94 14,88

LRB 0,78 0,82 1,08 4,66 5,10 5,70 9,98 10,20 11,70

LRb 0,82 1,04 1,28 4,78 5,24 5,92 9,94 10,42 12,04

Gb 0,72 1,08 1,20 4,44 4,96 5,78 9,52 9,98 11,86

Sb 0,92 1,02 1,28 4,64 5,32 5,70 9,72 10,20 11,70

Wb 1,04 1,00 1,28 5,14 5,48 5,76 10,16 10,50 11,78

8,56%, 9,42%, 7,14% e 6,76%. As respectivas corre¸cões propostas apresentam taxas de rejei¸cão nula de 5,14%, 5,42%, 5,28%, 5,16% e 5,22%. Ou seja, as corre¸cões propostas apresentam menores distor¸cões quando comparadas aos testes usuais, com taxas de rejei¸cão próximas aos n´ıveis nominais. Ao aumentar o número de restri¸cões (q= 2), os desempenhos dos testes em geral apresentam resultados ainda mais distorcidos quando comparados a q = 1. Ainda cabe destacar que o aumento do tamanho amostral não melhora o desempenho dos testes quando considerado q = 2. As corre¸cões propostas mesmo com o aumento do número de restri¸cões apresentam as taxas de rejei¸cão nula próximas aos n´ıveis nominais.

(38)

28

1% 5% 10%

❅n 30 50 100 30 50 100 30 50 100

1 LR 2,78 2,20 1,50 9,00 7,80 6,68 15,54 13,78 12,62

G 2,88 2,22 1,50 9,24 7,90 6,76 15,68 13,82 12,68

S 2,50 2,22 1,46 8,84 7,90 6,52 15,48 13,66 12,70

W 2,32 2,12 1,42 8,62 7,78 6,40 15,28 13,52 12,58

LRB 1,58 1,32 1,10 5,48 5,72 5,40 10,86 10,40 10,90

LRb 1,46 1,36 1,24 5,28 5,76 5,52 10,36 10,56 11,02

Bb 1,22 1,38 1,20 5,08 5,74 5,62 10,46 10,60 11,02

Sb 1,20 1,14 0,96 4,90 5,50 5,44 9,84 10,44 11,00

Wb 0,80 1,08 0,94 4,16 5,46 5,40 9,30 10,56 11,00

2 LR 3,04 1,90 2,04 9,94 7,94 7,30 17,10 13,86 12,98

G 3,40 2,00 2,10 10,36 7,94 7,54 17,50 13,96 13,08

S 2,78 2,04 1,92 9,50 8,02 7,32 16,64 13,80 12,82

W 2,20 1,78 1,80 8,86 7,76 7,10 16,02 13,64 12,62

LRB 1,80 1,36 1,36 6,80 5,84 6,30 12,32 10,70 11,48

LRb 1,44 1,22 1,44 5,92 5,58 6,10 11,14 10,28 11,40

Bb 1,30 1,18 1,48 5,82 5,48 6,18 10,70 10,12 11,44

Sb 0,86 1,02 1,34 4,84 5,24 5,68 9,14 9,46 10,74

Wb 0,38 0,80 1,26 3,58 4,78 5,64 7,82 9,48 10,88

de 37%. Em rela¸cão às corre¸cões propostas, os resultados indicam bom desempenho na maioria das configura¸cões, com distor¸cões menores que os testes usuais. Durante o estudo de simula¸cão verificou-se o percentual médio de censura nas amostrasbootstrap, sendo poss´ıvel constatar que as corre¸cões apresentam maiores distor¸cões quando o per-centual médio de censura nas amostrasbootstrap não foi o mesmo da amostra original. Dessa forma, salienta-se a importância de, em aplica¸cões, preservar a quantidade de censura da amostra original.

(39)

pa-29

1% 5% 10%

❅n 30 50 100 30 50 100 30 50 100

1 LR 2,64 2,26 2,42 9,08 8,48 8,96 16,22 14,52 15,66

G 2,88 2,44 2,42 9,40 8,68 9,14 16,34 14,86 15,76

S 2,54 2,16 2,08 8,82 8,20 8,44 15,34 14,18 14,88

W 1,90 1,98 1,94 8,20 8,14 8,20 15,22 13,92 14,80

LRB 1,24 1,24 1,70 5,72 5,82 7,46 10,80 11,08 13,78

LRb 1,24 1,36 1,74 5,74 5,90 7,66 10,56 11,14 13,80

Gb 1,20 1,44 1,84 5,46 6,00 7,70 10,44 11,14 13,92

Sb 0,90 1,30 1,58 4,82 5,70 7,18 9,74 10,86 13,18

Wb 0,72 1,18 1,52 4,12 5,48 7,10 9,04 11,02 13,24

2 LR 3,50 2,06 2,86 11,74 8,50 9,92 19,78 14,98 17,02

G 4,20 2,26 3,04 12,54 8,76 10,36 20,28 15,20 17,34

S 3,08 1,84 2,64 11,30 8,28 9,22 18,90 14,86 16,32

W 2,08 1,66 2,42 9,76 7,74 8,92 17,60 14,32 16,04

LRB 1,92 1,08 2,18 6,96 5,76 7,90 12,78 10,88 14,58

LRb 1,46 1,04 2,30 6,44 5,72 7,98 12,08 10,92 14,68

Gb 1,48 1,18 2,38 6,42 5,74 8,20 12,26 10,96 14,84

Sb 1,20 0,88 1,96 5,24 5,38 7,32 11,00 10,42 13,58

Wb 0,44 0,78 1,86 3,72 5,12 7,30 9,22 10,30 13,62

râmetros verificou-se que as distor¸cões dos testes usuais são ainda maiores. Em rela¸cão às corre¸cões propostas, foi poss´ıvel verificar que todas possuem bons resultados, em todos os cenários considerados, com pequena diferen¸ca do n´ıvel nominal quando essa ocorre. Dessa forma, qualquer versão corrigida é recomendável. Por vantagens compu-tacionais poderia ser considerada a estat´ıstica da razão de verossimilhan¸cas corrigida por Bartlettbootstrap (LRB).

(40)

30

1% 5% 10%

❅n 30 50 100 30 50 100 30 50 100

1 LR 2,72 2,00 2,24 9,52 8,22 8,08 16,14 14,34 14,44

G 3,16 2,08 2,54 9,80 8,44 8,56 16,32 14,38 14,80

S 2,60 1,70 1,88 8,68 7,74 7,52 15,34 14,04 13,90

W 2,06 1,50 1,70 8,18 7,62 7,38 15,10 14,00 13,68

LRB 1,10 0,98 1,62 5,28 5,40 6,84 10,26 11,30 12,70

LRb 1,08 1,16 1,72 5,34 5,58 6,96 10,28 11,20 12,86

Gb 1,12 1,12 1,92 5,18 5,56 7,20 10,40 11,16 12,94

Sb 0,90 1,04 1,50 5,02 5,18 6,52 9,64 10,94 12,46

Wb 0,82 0,98 1,44 5,10 5,24 6,50 9,72 11,08 12,34

2 LR 3,26 2,50 1,84 11,38 8,42 8,06 18,72 14,74 14,40

G 4,00 2,68 2,20 12,50 8,66 8,60 19,72 14,80 14,98

S 2,44 2,24 1,58 9,98 8,10 7,12 16,76 14,18 13,46

W 1,74 1,84 1,38 8,56 7,60 6,86 15,94 13,86 13,20

LRB 1,20 1,18 1,46 5,36 5,88 6,50 11,14 10,30 12,20

LRb 1,04 1,28 1,52 5,12 5,78 6,60 10,94 10,40 12,34

Gb 1,20 1,34 1,62 5,36 5,76 6,84 11,06 10,50 12,54

Sb 0,92 1,18 1,18 4,46 5,56 5,96 9,94 10,18 11,70

Wb 0,94 1,18 1,20 4,38 5,52 5,80 9,66 10,22 11,62

Tabela 4.7: Taxas de rejei¸c˜ao n˜ao nula (%) para H0 :β1 = 0 eH1 :β1 =δ, com p= 4, considerando o tamanho amostral n= 50 e n´ıvel nominal 5%.

Estat´ıstica❅_❅

❅δ −1,5 −1,0 −0,5 0,5 1,0 1,5

LR 95,86 78,90 33,72 12,88 62,80 96,50

G 95,56 77,44 33,18 11,00 58,76 95,38

S 94,22 75,74 31,56 16,90 69,36 97,56

W 95,56 78,20 32,96 16,74 69,12 97,48

LRB 96,30 80,42 35,96 14,46 65,80 97,14

LRb 96,28 80,74 36,40 14,66 66,10 97,18

Gb 96,10 80,26 36,30 12,96 63,16 96,64

Sb 94,68 78,02 33,92 18,28 71,64 97,98

(41)

31

(42)

Cap´ıtulo 5

Aplica¸c˜

ao

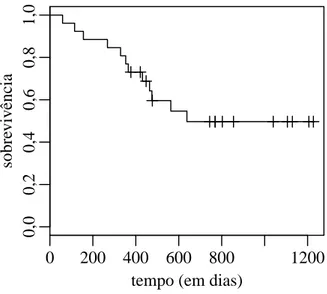
Este cap´ıtulo apresenta uma aplica¸cão a dados reais dos testes apresentados e das corre¸cões propostas. Os dados utilizados correspondem a um estudo realizado pela cooperativa de oncologia Ocidental, publicado por Edmonson et al. (1979), em que um ensaio aleatorizado foi feito para comparar dois tratamentos para câncer de ovário em 26 pacientes. Estes dados, clássicos na literatura em análise de sobrevivência, estão dispon´ıveis com o nome ovarian no pacote survival (THERNEAU; GRAMBSCH, 2000) no R (R Development Core Team, 2014).

A base de dados apresenta o tempo (em dias) das pacientes até a morte ou censura, o indicador da censura, a idade, a presen¸ca ou não de doen¸ca residual, o tipo de tratamento, e uma medida de performance, em que 1 é a melhor.

tempo (em dias)

sobre

viv

ência

0 200 400 600 800 1200

0,0

0,2

0,4

0,6

0,8

1,0

Figura 5.1: Kaplan-Meier dos dados referente ao tempo até a morte de pacientes com câncer de ovário.

(43)

33

A Figura 5.1 apresenta o gráfico de Kaplan-Meier, que estima a curva de sobre-vivência com base nestes dados. Pode-se notar que há um indicativo da presen¸ca de imunes nos dados, através da alta presen¸ca de censura à direita no fim do estudo e pelo Kaplan-Meier, que se estabilizou em um valor em torno de 0,53. Nessa situa¸cão os modelos com fra¸cão de cura são adequados.

Em rela¸cão às caracter´ısticas dos indiv´ıduos, foram consideradas 4 covariáveis (fa-tores): idade (x1 = −1 se a paciente tem menos de 60 anos, e 1 em caso contrário); doen¸ca residual (x2 = 1 se a paciente tem presen¸ca de doen¸ca residual, 0 em caso contrário); tipo de tratamento (x3 = 1 para o tratamento do grupo 1, 0 para o grupo 2) e medida de performance (x4 = 1 para a melhor performance, e 0 para a pior).

Dessa forma, o modelo tempo de promo¸cão Weibull foi ajustado, com o objetivo de avaliar o efeito das covariáveis consideradas no estudo sobre a fra¸cão de cura. As covariáveis foram inclu´ıdas no modelo através do parâmetro θ, por meio da rela¸cão

θi = exp(x⊤i β).

Inicialmente foram consideradas todas as covariáveis no modelo, associadas à fra¸cão de cura, dada por

p0i = exp[−exp(β1x1i+β2x2i+β3x3i+β4x4i)].

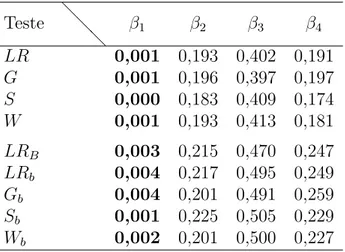
Após a estima¸cão dos parâmetros foram realizados testes de hipóteses para verificar a significância dos parâmetros associados a cada covariável. As hipóteses consideradas foram

H0 :βj = 0 versus H1 :βj 6= 0, (5.1)

para j = 1, . . . ,4. Da mesma forma que nas simula¸c˜oes, foram considerados p = 4 e

q= 1, sendo 5 o número de parâmetros de perturba¸cão em todos os testes realizados. Os testes foram realizados considerando o n´ıvel de significância de 5%, sendo a hi-pótese nula rejeitada se p-valor < 0,05. Na Tabela 5.1 são apresentados os p-valores associados aos testes de hipóteses realizados considerando as estat´ısticas usuais, corri-gida (LRB) e os testes corrigidos. São destacados em negrito os p-valores que rejeitam a hipótese nula.