UNIVERSIDADE ESTADUAL DE MARING ´
A
CENTRO DE CIˆ
ENCIAS EXATAS
DEPARTAMENTO DE MATEM ´
ATICA
PROGRAMA DE P ´
OS-GRADUAC
¸ ˜
AO EM MATEM ´
ATICA
(Mestrado)Um Estudo Sobre Grafos Divisores de Zero
JULIO CESAR MORAES PEZZOTT
Orientadora: Irene Naomi Nakaoka
Um Estudo Sobre Grafos Divisores de Zero
JULIO CESAR MORAES PEZZOTT
Disserta¸c˜ao apresentada ao Programa de P´os-Gradua¸c˜ao em Matem´atica do Departamento de Matem´atica, Centro de Ciˆencias Exatas da Univer-sidade Estadual de Maring´a, como requisito par-cial para obten¸c˜ao do t´ıtulo de Mestre em Ma-tem´atica.
´
Area de concentra¸c˜ao: ´Algebra
Orientadora: Profa. Dra. Irene Naomi Nakaoka
Agradecimentos
Agrade¸co `a minha fam´ılia, que sempre me apoiou. Em especial, `a minha esposa Claudia, aos meus pais e aos meus irm˜aos.
Agrade¸co `a minha orientadora Profa. Dra. Irene Naomi Nakaoka pela paciˆencia, sabedoria e dedica¸c˜ao na realiza¸c˜ao deste trabalho.
Aos professores do Departamento de Matem´atica da UEM por contribu´ırem com minha forma¸c˜ao.
Aos meus amigos e colegas de mestrado. `
Resumo
Dado um anel comutativo com identidade R, o grafo divisor de zero de R, denotado por Γ(R), ´e o grafo cujos v´ertices s˜ao os divisores de zero n˜ao nulos deR e dois v´ertices distintos
Abstract
Given a commutative ring with identityR, the zero-divisor graph ofR, denoted by Γ(R), is the graph whose vertices are the nonzero zero-divisors ofR and two distinct vertices xand
vi
´Indice de Nota¸c˜oes
∅ conjunto vazio
|X| cardinalidade do conjunto X
X∗ X\ {0}
X (Y X ´e um subconjunto pr´oprio de Y X ⊆Y X ´e um subconjunto de Y
X×Y produto direto de X por Y Im(f) imagem da fun¸c˜ao f ker(f) n´ucleo da fun¸c˜ao f
(x) ideal gerado pelo elemento x
U(R) conjunto dos elementos invert´ıveis do anel R D(R) conjunto dos divisores de zero do anel R Id(R) conjunto dos ideais do anel R
Spec(R) conjunto dos ideais primos do anel R √
I ideal radical do ideal I
N il(R) {r∈R : rn = 0,para algumn∈N} (nilradical de R)
J(R) radical de Jacobson do anel R V ar(I) variedade do ideal I
M in(R) conjunto dos primos minimais do anel R ass(I) conjunto dos primos associados do ideal I Ass(R) conjunto dos primos associados do anel R
(I :x) quociente do ideal I por x
Ann(x) {r∈R : rx= 0} (anulador de x)
Ann(I) {r∈R : rI ={0}}(anulador de I)
char(R) caracter´ıstica do anel R
G= (V, E) grafo com conjunto de v´ertices V e conjunto de arestas E
vii
d(u, v) distˆancia de ua v diam(G) diˆametro do grafo G
Km grafo completo de ordem m
Km,n grafo bipartido completo com conjunto de v´ertices V =V1∪V2 (uni˜ao disjunta) tal que |V1|=m e |V2|=n
ω(G) cardinalidade do maior clique no grafoG Cn n-ciclo
gr(G) cintura do grafo G
χ(G) n´umero crom´atico por v´ertices deG
e(v) max{d(v, x) : x∈V} (excentricidade do v´erticev)
rad(G) raio do grafo G Cen(G) centro do grafo G
Sum´
ario
´Indice de Nota¸c˜oes vi
Introdu¸c˜ao ix
1 Preliminares 1
1.1 An´eis comutativos . . . 1
1.1.1 An´eis Artinianos e an´eis Noetherianos . . . 4
1.1.2 Decomposi¸c˜ao prim´aria de um ideal . . . 6
1.1.3 Sobre os divisores de zero de um anel . . . 8
1.2 Grafos . . . 13
1.2.1 Grafos planares . . . 18
2 Grafos divisores de zero 22 2.1 O grafo divisor de zero . . . 22
2.2 Colora¸c˜oes de Beck . . . 29
2.3 Quando Γ(R) possui um v´ertice adjacente aos demais v´ertices . . . 38
2.4 Grafos completos e grafos estrela . . . 40
2.5 Grafos divisores de zero r-partidos completos . . . 44
2.6 Ciclos e cintura . . . 57
2.7 Raio, centro e n´umero de domina¸c˜ao . . . 61
Introduc
¸˜
ao
O conceito de grafo divisor de zero surgiu na literatura matem´atica com o artigo “Coloring of commutative rings” [11], publicado por Istvan Beck em 1988. O autor definiu um grafo tomando como v´ertices os elementos de um anel comutativo e colocando que dois v´ertices distintos seriam adjacentes se o produto entre eles resultasse no elemento neutro da adi¸c˜ao. Beck estudou colora¸c˜oes de v´ertices desse grafo. Mais resultados sobre esse tema foram obtidos por D. D. Anderson e M. Nasser e publicados, em 1993, no artigo “ Beck’s Coloring of Commutative Rings ” [4].
Em 1999, no artigo “ The zero-divisor graph of a commutative ring ”[6], D. F. Anderson e P. S. Livingston apresentaram uma defini¸c˜ao de grafo divisor de zero um pouco diferente da defini¸c˜ao de Beck. Tais autores mantiveram a condi¸c˜ao dada por Beck para que dois v´ertices fossem adjacentes; no entanto, passaram a considerar como v´ertices apenas os divisores de zero n˜ao nulos do anel. A partir desse artigo, a maioria dos matem´aticos que trataram do tema assumiram a defini¸c˜ao de D.F. Anderson e P.S. Livingston como a defini¸c˜ao de grafo divisor de zero.
Nos trˆes artigos acima citados, algumas rela¸c˜oes entre um anel e seu grafo divisor de zero foram explicitadas e alguns resultados mostraram que propriedades acerca dos an´eis poderiam ser deduzidas a partir do seu grafo divisor de zero. Desse modo, o grafo divisor de zero se apresentava como uma ferramenta auxiliar para o estudo das propriedades alg´ebricas dos an´eis.
isomorfis-Introdu¸c˜ao xi
mos de an´eis. Tais rela¸c˜oes tamb´em foram estudadas por S. Akbari e A. Mohammadian em [2]. Neste mesmo artigo, estes autores apresentaram um estudo sobre colora¸c˜oes de arestas. Cintura, planaridade e grafos divisores de zeror-partidos completos s˜ao temas abordados por S. Akbari, H. R. Maiamani e S. Yassemi em [1]. Em [20], s˜ao explicitadas algumas rela¸c˜oes entre o conjunto dos divisores de zero e o grafo divisor de zero de um anel. T. G. Lucas, em [19], estudou quest˜oes referentes ao diˆametro de um grafo divisor de zero. Raio, centro e n´umero de domina¸c˜ao s˜ao temas tratados por S. P. Redmond em [22]. Este ´ultimo autor introduziu ainda, em [23], o conceito de grafos divisores de zero de an´eis n˜ao comutativos, tema esse que n˜ao ser´a explorado aqui.
Nesta disserta¸c˜ao, apresentaremos um estudo sobre grafos divisores de zero de an´eis co-mutativos. Veremos quais informa¸c˜oes acerca de um anel podem ser obtidas a partir de seu grafo divisor de zero e destacaremos algumas propriedades desse grafo no que diz res-peito aos seguintes temas: conexidade, diˆametro, raio, centro, tamanho, cintura, n´umero de domina¸c˜ao, colora¸c˜oes de v´ertices e forma (grafos completos e grafos r-partidos completos).
Cap´ıtulo 1
Preliminares
Neste cap´ıtulo, apresentaremos alguns conceitos e resultados da Teoria de An´eis Comu-tativos e da Teoria de Grafos necess´arios ao estudo que faremos no pr´oximo cap´ıtulo. N˜ao demonstraremos aqui todos os resultados enunciados. No entanto, para cada resultado n˜ao demonstrado, indicaremos um texto no qual sua demonstra¸c˜ao pode ser encontrada. Os pr´e-requisitos para leitura desta disserta¸c˜ao s˜ao os t´opicos b´asicos de Grupos, An´eis e M´odulos.
1.1
An´
eis comutativos
Iniciamos este t´opico com algumas nota¸c˜oes e conven¸c˜oes. Dados os conjuntos X e Y, escrevemos X ⊆ Y se X ´e um subconjunto de Y. Se X ´e um subconjunto pr´oprio de Y, escrevemos X(Y. Se X ´e um conjunto finito, denotamos a cardinalidade deX por |X|.
Em todo o texto, os an´eis ser˜ao an´eis comutativos com identidade. A identidade do anel ser´a denotada por 1 e o elemento neutro da adi¸c˜ao por 0, com 1 6= 0. Quando X for um subconjunto de um anel, denotamos o conjuntoX\ {0}por X∗.
Dado um anel R, indicamos o conjunto de todos os ideais desse anel por Id(R). Dados
I ∈ Id(R) e a ∈ R, escrevemos a para indicar o elemento a+I do anel quociente R/I. O conjunto dos elementos invert´ıveis de R´e representado por U(R).
A interse¸c˜ao de todos os ideais maximais de um anel R ´e um ideal chamado Radical de Jacobson, o qual denotamos por J(R). O Radical de Jacobson pode ser caracterizado pelo seguinte resultado:
1.1 An´eis comutativos 2
Um anel R ´e local quando possui um ´unico ideal maximal M. Neste caso, R/M ´e um corpo, chamado de corpo residual de R. O seguinte resultado nos d´a condi¸c˜oes para que um anel seja local.
Proposi¸c˜ao 1.2. ([7], p´ag. 4) Sejam R um anel e M ∈Id(R)\ {R}.
(i) Se R\M =U(R), ent˜ao R ´e um anel local e M ´e seu ´unico ideal maximal;
(ii) Se R\U(R) ´e um ideal, ent˜ao R ´e um anel local com ideal maximalR\U(R);
(iii) Se M ´e um ideal maximal e 1 +m∈U(R) para todom ∈M, ent˜ao R ´e local.
Denotamos o conjunto dos ideais primos de R por Spec(R). Usaremos neste texto o seguinte resultado envolvendo ideais primos.
Proposi¸c˜ao 1.3. ([7], p´ag.8) Sejam P, P1, . . . , Pn∈Spec(R) e I, I1, . . . , Ir ∈Id(R).
(i) Se I ⊆Sni=1Pi, ent˜ao I ⊆Pi para algum i∈ {1, . . . , n};
(ii) Se Trj=1Ij ⊆P, ent˜ao Ij ⊆P, para algum j ∈ {1, . . . , r}, .
Dado I ∈ Id(R)\ {R}, o conjunto V ar(I) = {P ∈ Spec(R) : I ⊆ P} ´e chamado de
variedade do ideal I. O seguinte teorema caracteriza esse subconjunto do Spec(R).
Teorema 1.4. ([24], p´ag. 53) Dado I ∈Id(R)\ {R}, V ar(I)´e n˜ao vazio e admite elemento minimal em rela¸c˜ao `a inclus˜ao de conjuntos.
Os elementos minimais de V ar(I) s˜ao chamados de primos minimais de I. Os primos minimais do ideal nulo {0} s˜ao chamados tamb´em de primos minimais de R. Desse modo, temos que P ∈ Spec(R) ´e um primo minimal de R se, e somente se, n˜ao existe outro ideal primo contido propriamente emP.
O conjunto dos primos minimais de R ´e representado por M in(R). Na hip´otese da pr´oxima proposi¸c˜ao, temos um anel R com M in(R) finito.
Proposi¸c˜ao 1.5. Seja R um anel tal queM in(R)´e finito, digamos M in(R) = {P1, . . . , Pk}.
Ent˜ao, para cada j ∈ {1, . . . , k}, existe um elemento yj ∈( k \
i=1
i6=j
1.1 An´eis comutativos 3
Demonstra¸c˜ao: Dado Pj ∈ M in(R), temos que Pi * Pj, para todo i ∈ {1, . . . , k} \ {j}. Desse modo, para cada i 6= j, podemos escolher xi ∈ Pi \Pj. Assim, podemos considerar
yj =x1. . . xj−1xj+1. . . xk. Do fato de Pj ser um ideal primo segue que yj ∈( k \
i=1
i6=j
Pi)\Pj. ⊓⊔
Dado I ∈ Id(R), o conjunto √I = {r ∈ R : existen ∈ Z∗
+tal quern ∈ I} ´e um ideal, chamado de ideal radical de I. Claramente vemos que I ⊆√I.
O idealp{0}={r ∈R : existen∈Z∗
+tal quern = 0}´e denotado porN il(R) e chamado denilradical de R. Um elemento r∈ N il(R) recebe o nome de nilpotente e o menor inteiro positivontal que rn = 0 ´e chamado de´ındice de nilpotˆencia de r. Um anelR ´e ditoreduzido seN il(R) ={0}. Caso contr´ario, R ´e n˜ao reduzido.
A pr´oxima proposi¸c˜ao nos d´a uma rela¸c˜ao entre o nilradical, os ideais primos e os primos minimais de um anelR:
Proposi¸c˜ao 1.6. ([24], p´ag. 52 e p´ag. 54) Em um anel R, s˜ao verdadeiras as seguintes
igualdades: N il(R) = \ P∈Spec(R)
P = \
P∈M in(R)
P.
Um elemento a ∈ R ´e idempotente quando a2 = a. Encerramos esta se¸c˜ao com dois resultados envolvendo elementos deste tipo.
Lema 1.7. Seja R um anel. Se a∈R∗ ´e idempotente, ent˜ao R=Ra⊕R(1−a).
Demonstra¸c˜ao: Dado r ∈ R, podemos escrever r = r+ra−ra = ra+r(1−a). Assim,
R = Ra+R(1−a). Agora, tomemos x ∈ Ra∩R(1−a). Ent˜ao existem r, s∈ R tais que
x=ra=s(1−a) =s−sa. Multiplicando pora em ambos os lados dessa ´ultima igualdade e usando o fato quea´e idempotente, obtemos x=ra=ra2 = (ra)a= (s−sa)a=sa−sa2 =
sa−sa= 0, donde Ra∩R(1−a) = {0}. Portanto, R =Ra⊕R(1−a). ⊓⊔
Lema 1.8. Se R ´e um anel local, ent˜ao seus ´unicos elementos idempotentes s˜ao 0 e 1.
Demonstra¸c˜ao: Seja R um anel local com ideal maximal M e seja a ∈ R tal que a2 = a. Se a ∈ U(R), ent˜ao existe b ∈ R tal que ab = 1. Neste caso, temos que 1 = ab = a2b =
1.1 An´eis comutativos 4
um anel pertence a algum ideal maximal. Mas notemos que M = J(R). Segue da Pro-posi¸c˜ao 1.1 que 1−a ∈ U(R). Logo, existe x ∈ R tal que x(1−a) = 1. Assim, como 1 = 12 = x2(1−a)2 = x2(1−2a+a2) = x2(1−2a+a) = x2(1−a) = x[x(1−a)] = x,
obtemos que 1−a= 1, donde vem que a= 0. ⊓⊔
1.1.1
An´
eis Artinianos e an´
eis Noetherianos
Nesta se¸c˜ao, apresentaremos as defini¸c˜oes de an´eis Artinianos e an´eis Noetherianos e alguns resultados b´asicos envolvendo tais an´eis. Come¸camos com a seguinte defini¸c˜ao:
Defini¸c˜ao 1.9. Seja C um conjunto parcialmente ordenado por uma rela¸c˜ao (respectiva-mente, ).
(a) Dizemos que C satisfaz acondi¸c˜ao de cadeia descendente (c.c.d.) (respect.,condi¸c˜ao de cadeia ascendente (c.c.a.)) se, para cada fam´ılia (Si)i∈N de elementos deC que satisfaz
S0 S1 S2 . . .Si . . . (respect., S0 S1 S2 . . .Si . . .), existir k ∈N tal que Sk =Sk+i, para todo i∈N. Neste caso, dizemos que a cadeia estaciona.
(b) Dizemos que C satisfaz `a condi¸c˜ao minimal (respect., condi¸c˜ao maximal) se todo sub-conjunto n˜ao vazio deC admite um elemento minimal (respect., maximal), com respeito `a (respect., ).
O pr´oximo resultado nos diz que as condi¸c˜oes (a) e (b) dadas na defini¸c˜ao anterior s˜ao equivalentes.
Proposi¸c˜ao 1.10. ([24], p´ag. 47) SejaC um conjunto parcialmente ordenado por(respect.,
por ). Ent˜ao C satisfaz a c.c.d (respect., c.c.a) se, e somente se, C satisfaz a condi¸c˜ao
minimal (respect., condi¸c˜ao maximal).
1.1 An´eis comutativos 5
Defini¸c˜ao 1.11. SejaM umR-m´odulo. Dizemos queM ´eArtiniano (respect.,Noetheriano) se o conjunto de seus subm´odulos, ordenado por ⊇ (respect., ⊆), satisfaz `a condi¸c˜ao de ca-deia descendente (respect., condi¸c˜ao de caca-deia ascendente) ou, equivalentemente, `a condi¸c˜ao minimal (respect., condi¸c˜ao maximal).
Um anelR´e Artiniano (respect., Noetheriano) seR, visto como umR-m´odulo, ´e Artiniano (respect., Noetheriano), isto ´e, se o conjunto de seus ideaisId(R), ordenado por⊇(respect.,
⊆), satisfaz `a condi¸c˜ao de cadeia descendente (resp., condi¸c˜ao de cadeia ascendente) ou, equivalentemente, `a condi¸c˜ao minimal (respect., condi¸c˜ao maximal).
O resultado a seguir destaca uma propriedade dos an´eis Noetherianos.
Proposi¸c˜ao 1.12. ([24], p´ag. 146) Sejam R um anel Noetheriano e I ∈Id(R). Ent˜ao, R/I ´e um anel Noetheriano.
A pr´oxima proposi¸c˜ao apresenta v´arias propriedades de um anel Artiniano. Antes de enunci´a-la, precisamos saber que um ideal I ´e dito nilpotente quando existe um inteiro positivo n tal que In={0}.
Proposi¸c˜ao 1.13. ([7], p´ag. 163 e 164) SejamR um anel Artiniano e I ∈Id(R). Ent˜ao:
(i) Todo ideal primo de R ´e maximal;
(ii) N il(R) = J(R);
(iii) R tem somente um n´umero finito de ideais maximais;
(iv) N il(R) ´e nilpotente.
O teorema a seguir descreve a estrutura dos an´eis Artinianos.
Teorema 1.14. (Estrutura de An´eis Artinianos) ([7], p´ag. 90) Um anel Artiniano
R ´e de maneira ´unica (a menos de isomorfismo) um produto direto finito de an´eis locais
Artinianos.
1.1 An´eis comutativos 6
Teorema 1.15. ([24], p´ag. 166) Um anelR ´e Artiniano se, e somente se, R ´e Noetheriano
e todo ideal primo de R ´e maximal.
1.1.2
Decomposi¸c˜
ao prim´
aria de um ideal
Nesta se¸c˜ao, definiremos o que ´e uma decomposi¸c˜ao prim´aria minimal de um ideal e apresentaremos alguns conceitos e resultados relacionados ao assunto. Para isso, precisamos da seguinte defini¸c˜ao:
Defini¸c˜ao 1.16. SejaQ∈Id(R)\ {R}. Dizemos queQ´e umideal prim´ario se dadoab∈Q, tivermos a∈Q oub ∈√Q.
Se Q ´e um ideal prim´ario de R, ent˜ao √Q = P ´e um ideal primo ([24], p´ag. 63). Mais ainda: qualquer outro ideal primo que cont´emQdeve conterP, ou seja,P ´e o ´unico elemento minimal deV ar(Q). Neste caso, dizemos que Q´e um ideal P-prim´ario.
Estamos agora em condi¸c˜oes de definir o que ´e um ideal decompon´ıvel e o que ´e uma decomposi¸c˜ao prim´aria minimal de um ideal.
Defini¸c˜ao 1.17. Dizemos que I ∈ Id(R)\ {R} admite uma decomposi¸c˜ao prim´aria se I
pode ser escrito como uma interse¸c˜ao finita de ideais prim´arios. Neste caso, dizemos queI ´e um ideal decompon´ıvel .
Defini¸c˜ao 1.18. Seja I um ideal decompon´ıvel e seja I = Tni=1Qi uma decomposi¸c˜ao prim´aria de I, com √Qi = Pi, para i ∈ {1, . . . , n}. Dizemos que tal decomposi¸c˜ao ´e uma
decomposi¸c˜ao prim´aria minimal deI quando as condi¸c˜oes (a) e (b) dadas a seguir s˜ao satis-feitas:
(a) Pi 6=Pj, se i6=j;
(b) Para todo j ∈ {1, . . . , n}, n \
i=1
i6=j
Qi *Qj.
1.1 An´eis comutativos 7
prim´arias minimais distintas. Ou seja, podemos ter Tni=1Qi = I = Tmi=1Ti duas decom-posi¸c˜oes prim´arias minimais de um ideal I, com Ti ∈ {/ Q1, . . . , Qn} ([24], p´ag. 74). No entanto, seI ´e um ideal decompon´ıvel, podemos garantir a seguinte unicidade:
Teorema 1.19. (Unicidade da Decomposi¸c˜ao Prim´aria) ([24], p´ag. 70)
Sejam Tni=1Qi = I = Tmi=1Ti duas decomposi¸c˜oes prim´arias minimais de I tais que
√
Qi =Pi e
√
Ti =Ui. Ent˜ao, n=m e {P1, . . . , Pn}={U1, . . . , Um}.
SejamI um ideal decompon´ıvel eI =Tni=1Qi uma decomposi¸c˜ao prim´aria minimal de I, com √Qi =Pi, para i ∈ {1, . . . , n}. Pelo Teorema 1.19, os ideais P1, . . . , Pn n˜ao dependem da escolha da decomposi¸c˜ao prim´aria minimal deI. Estes ideais P1, . . . , Pn s˜ao chamados de
primos associados de I e o conjunto formado por eles ´e denotado porass(I).
A pr´oxima proposi¸c˜ao afirma que os primos minimais de um ideal decompon´ıvel I coin-cidem com os elementos minimais do conjuntoass(I).
Proposi¸c˜ao 1.20. ([24], p´ag. 72) Seja I ∈ Id(R)\ {R} um ideal decompon´ıvel de R e seja P ∈ Spec(R). Ent˜ao P ´e um primo minimal de I se, e somente se, P ´e um elemento minimal deass(I). Comoass(I)´e finito, temos queV ar(I)admite apenas um n´umero finito de elementos minimais.
Existem an´eis que possuem ideais pr´oprios n˜ao decompon´ıveis (temos um exemplo em ([24], p´ag. 76)). O pr´oximo teorema destaca o fato de que em an´eis Noetherianos, todos os ideais distintos do pr´oprio anel s˜ao decompon´ıveis.
Teorema 1.21. ([24], p´ag. 78) SeR´e um anel Noetheriano, ent˜ao todo idealI ∈Id(R)\{R} ´e decompon´ıvel.
Por este ´ultimo teorema, temos que seR´e um anel Noetheriano, ent˜ao o ideal nulo{0}de
R ´e decompon´ıvel. Logo, M in(R) ´e finito, pois pelo Teorema 1.20, V ar({0}) possui apenas um n´umero finito de elementos minimais. Provamos assim a seguinte proposi¸c˜ao:
Proposi¸c˜ao 1.22. Se R ´e um anel Noetheriano, ent˜ao R possui apenas um n´umero finito
1.1 An´eis comutativos 8
1.1.3
Sobre os divisores de zero de um anel
Nesta se¸c˜ao, destacaremos alguns resultados sobre o conjunto de divisores de zero de um anel. Em um primeiro momento, apresentaremos resultados v´alidos para an´eis quaisquer. Ao final da se¸c˜ao, restringiremos nosso estudo aos an´eis Noetherianos e aos an´eis finitos.
Defini¸c˜ao 1.23. Seja R um anel. Dado a ∈R, dizemos que a´e um divisor de zero quando existe b ∈ R∗ tal que ab = 0. Denotamos o conjunto dos divisores de zero do anel R por
D(R).
Conv´em enfatizarmos aqui alguns fatos conhecidos acerca dos divisores de zero:
(1) Por defini¸c˜ao, 0∈D(R);
(2) Sabemos que nem sempre D(R) ´e um ideal; por exemplo, D(Z6) = {0,2,3,4}, mas 2 + 3 = 5∈/ D(R);
(3) Dado a ∈ D(R), seja b ∈ R∗ tal queab = 0; ent˜ao, ar ∈D(R), para todo r ∈R, pois
(ra)b=r(ab) = 0;
(4) Pelos itens (2) e (3), temos que se D(R) n˜ao ´e ideal, ent˜ao existem a, b ∈ D(R) tais que a+b /∈D(R).
Veremos, ainda nesta se¸c˜ao, casos em que D(R) ´e um ideal. A pr´oxima proposi¸c˜ao nos garante que, em tais casos, D(R) deve ser necessariamente um ideal primo.
Proposi¸c˜ao 1.24. Em um anel R, se D(R) ´e um ideal, ent˜ao D(R) ´e ideal primo.
Demonstra¸c˜ao: Suponhamos que D(R)∈ Id(R). Como 1 ∈/ D(R), temos que D(R)6= R. Tomemosab∈D(R). Ent˜ao existe c∈R∗ tal que (ab)c= 0. Se bc6= 0, ent˜ao a∈D(R). Se
bc= 0, ent˜aob∈D(R). Logo,D(R) ´e um ideal primo deR. ⊓⊔
O pr´oximo resultado nos d´a uma caracteriza¸c˜ao do conjunto dos divisores de zero e nos mostra uma importante rela¸c˜ao entre este conjunto e o conjunto dos primos minimais.
1.1 An´eis comutativos 9
(i) D(R) ´e uma uni˜ao de ideais primos de R;
(ii) S
P∈M in(R)P ⊆D(R).
Analisemos agora a rela¸c˜ao entre D(R) e N il(R). Facilmente podemos mostrar que a inclus˜aoN il(R)⊆ D(R) ´e verdadeira, qualquer que seja o anel R. Em alguns casos, ocorre a igualdade N il(R) = D(R) (por exemplo, se R = Z8). Por´em, n˜ao podemos garantir que tal igualdade ´e verdadeira para qualquer anel R. Por exemplo, para R = Z2 ×Z2, temos
D(R) = {(0,0),(1,0),(0,1)} e N il(R) = {(0,0)}. Os dois pr´oximos resultados apresentam algumas condi¸c˜oes sob as quais a igualdadeD(R) = N il(R) ocorre.
Proposi¸c˜ao 1.26. Em um anel R, se {0} ´e um ideal prim´ario, ent˜ao D(R) =N il(R).
Demonstra¸c˜ao: Dadoa∈D(R), existeb ∈R∗ tal queab= 0 ∈ {0}. Como {0}´e prim´ario,
devemos ter a ∈ N il(R) ou b ∈ {0}. Como b 6= 0, temos que a ∈ N il(R), donde segue a
igualdade D(R) =N il(R). ⊓⊔
Proposi¸c˜ao 1.27. Seja R um anel tal que todo ideal primo ´e maximal. Ent˜ao, temos que
D(R) =N il(R) se, e somente se, D(R)´e um ideal (primo).
Demonstra¸c˜ao: Se D(R) = N il(R), ent˜ao D(R) ∈ Spec(R), pela Proposi¸c˜ao 1.24. Reci-procamente, suponhamos que D(R) ∈ Spec(R). Dado Q ∈ M in(R), segue da Proposi¸c˜ao 1.25 que Q⊆D(R). Como todo ideal primo de R ´e maximal, devemos ter D(R) =Q, para todoQ∈M in(R). Da proposi¸c˜ao 1.6 vem que N il(R) = T
Q∈M in(R)Q=D(R). ⊓⊔
A pr´oxima proposi¸c˜ao caracteriza o conjunto dos divisores de zero de um anel reduzido.
Proposi¸c˜ao 1.28. Seja R um anel reduzido.
(i) Ent˜ao, S
P∈M in(R)P =D(R);
1.1 An´eis comutativos 10
Demonstra¸c˜ao: (i) Pela Proposi¸c˜ao 1.25, j´a temos que S
P∈M in(R)P ⊆ D(R). Da Pro-posi¸c˜ao 1.6 e do fato deR ser reduzido, obtemos as igualdades:
\
P∈M in(R)
P = \
P∈Spec(R)
P =N il(R) = {0}. (1.1)
Dado x ∈ D(R), existe y ∈ R∗ tal que xy = 0. Assim, xy = 0 ∈ P, para todo primo
minimal P. Ent˜ao, para cada P ∈ M in(R), x ∈ P ou y ∈ P. Se para todo primo minimal
P, tiv´essemos x /∈ P, ter´ıamos y ∈ P, para todo P ∈ M in(R), donde ter´ıamos que y ∈
T
P∈M in(R)P, o que contradiz (1.1). Logo, existe pelo menos um primo minimal P tal que
x∈P. Temos assim a inclus˜ao D(R)⊆S
P∈M in(R)P e o resultado est´a provado. (ii) Sabemos por (i) que S
P∈M in(R)P = D(R). Assim, supondo que R possui um ´unico primo minimalP, de (1.1) obtemosD(R) =P =N il(R) ={0}, o que contradiz o fato deR
n˜ao ser um dom´ınio de integridade. ⊓⊔
Dados x ∈ R e I ∈ Id(R), o conjunto (I : x) = {r ∈ R : rx ∈ I} ´e um ideal de R, chamado de ideal quociente deI por x. O ideal {r ∈R : rI ={0}}´e denotado por Ann(I) e chamado de anulador de I. J´a o ideal {r ∈ R : ra = 0} ´e chamado de anulador de a e denotado porAnn(a).
Proposi¸c˜ao 1.29. ([18], p´ag. 4) Sejam R um anel e C ={Ann(a) : a∈R∗}. Se C admite
um elemento maximalI, ent˜ao I ´e um ideal primo de R.
Demonstra¸c˜ao: Seja I = Ann(a), a ∈ R∗. Dado bc ∈ I, vamos supor que b /∈ I. Ent˜ao
ab6= 0. Notemos que I =Ann(a) ⊆Ann(ab). Por hip´otese, I ´e um elemento de C. Ent˜ao
I = Ann(a) = Ann(ab). Como bc ∈ Ann(a), temos 0 =a(bc) = (ab)c, donde obtemos que
c∈Ann(ab). Assim,c∈Ann(a) = I e, portanto,I ´e um ideal primo. ⊓⊔
Vejamos agora duas proposi¸c˜oes acerca do conjunto dos divisores de zero de um anel Noetheriano. A primeira considera o caso em que tal conjunto ´e um ideal. A segunda relaciona os divisores de zero com os primos associados do ideal nulo.
1.1 An´eis comutativos 11
Proposi¸c˜ao 1.31. ([24], p´ag. 155 e p´ag. 156) Sejam R um anel Noetheriano. Ent˜ao:
(i) D(R) =S
P∈ass({0})P;
(ii) Dado P ∈ Spec(R), temos que P ∈ ass({0}) se, e somente se, existe a ∈ R tal que P =Ann(a).
Definiremos agora o que ´e um ideal primo associado de um anel qualquerR. Na sequˆencia, mostraremos uma rela¸c˜ao entre tais ideais e o conjunto dos divisores de zero em um anel Noetheriano.
Defini¸c˜ao 1.32. SejaR um anel qualquer. Dizemos queP ∈Spec(R) ´e um primo associado de R quando existe a ∈ R tal que P = Ann(a). O conjunto dos primos associados de R ´e denotado porAss(R).
Observa¸c˜ao 1.33. Se R ´e um anel Noetheriano, do item (ii) da Proposi¸c˜ao 1.31 vem que
ass({0}) =Ass(R). Pelo item (i) deste mesmo resultado, obtemos que D(R) = S
P∈Ass(R)P. A pr´oxima proposi¸c˜ao trata do conjunto dos divisores de zero em um anel Artiniano local.
Proposi¸c˜ao 1.34. Seja R um anel local Artiniano que n˜ao ´e um dom´ınio. Ent˜ao:
(i) todo elemento de R ´e invert´ıvel ou nilpotente;
(ii) D(R) ´e o ´unico ideal maximal de R.
Demonstra¸c˜ao: (i) Seja M o ´unico um ´unico ideal maximal de R. Sendo R Artiniano, todo ideal primo de R ´e maximal. Assim, M ´e tamb´em o ´unico ideal primo de R. Da Proposi¸c˜ao 1.6 segue queN il(R) =T
P∈Spec(R)P =M. Sabemos que, em um anel qualquer, todo elemento n˜ao invert´ıvel pertence a algum ideal maximal. Desse modo, dador /∈U(R), devemos terr ∈M, donde obtemos que todo elemento de R ´e invert´ıvel ou nilpotente.
(ii) Pelo item (i), temos queN il(R) =M ´e o ´unico ideal maximal deR. Dadox∈D(R), comox /∈U(R), segue quex∈M =N il(R), donde vem queD(R)⊆N il(R). Como sempre ocorre N il(R) ⊆ D(R), obtemos a igualdade D(R) = N il(R). Logo, D(R) ´e o ´unico ideal
1.1 An´eis comutativos 12
Vejamos agora alguns resultados acerca dos divisores de zero em an´eis finitos. A pro-posi¸c˜ao enunciada a seguir classifica os elementos de um anel finito.
Proposi¸c˜ao 1.35. ([17], p´ag. 8) SeR´e um anel finito, ent˜ao cada elemento deR´e invert´ıvel
ou divisor de zero.
A pr´oxima proposi¸c˜ao nos d´a uma condi¸c˜ao necess´aria e suficiente para que um anel finito seja local.
Proposi¸c˜ao 1.36. Seja R um anel finito. Ent˜ao R ´e local se, e somente se, todo elemento
deR n˜ao invert´ıvel ´e nilpotente. No caso em que R´e local, temos que D(R)´e o (´unico) ideal maximal de R.
Demonstra¸c˜ao: Suponhamos que todo elemento a ∈ R n˜ao invert´ıvel ´e nilpotente. Afir-mamos que R \ N il(R) = U(R). De fato, se x /∈ U(R), ent˜ao x ∈ N il(R), ou seja,
x /∈ R\N il(R). Disso resulta a inclus˜ao R\N il(R) ⊆U(R). ´E f´acil ver que se x ∈U(R), ent˜ao x /∈ D(R). Como N il(R) ⊆ D(R), temos que x /∈ N il(R) e disso resulta a outra inclus˜aoR\N il(R)⊇U(R) e a igualdade desejada. Pelo item (i) da Proposi¸c˜ao 1.2, temos queR ´e anel local cujo ideal maximal ´e N il(R).
A rec´ıproca e a segunda afirma¸c˜ao do enunciado seguem da Proposi¸c˜ao 1.34, utilizando
o fato de que todo anel finito ´e Artiniano. ⊓⊔
O pr´oximo resultado trata da caracter´ıstica de um anel local finito.
Proposi¸c˜ao 1.37. Seja R ´e um anel local finito. Ent˜ao existem um n´umero primo p e
inteiros n˜ao negativos n, t, k tais que:
(i) A caracter´ıstica de R ´epn (char(R) =pn);
(ii) D(R) com a opera¸c˜ao de adi¸c˜ao do anel ´e um p-grupo, de modo que |D(R)|=pt;
(iii) |R|=pk.
1.2 Grafos 13
isto ´e, p1∈ D(R). Agora, pela demonstra¸c˜ao da Proposi¸c˜ao 1.36, D(R) = N il(R) e, ent˜ao, existe n ∈ N tal que (p1)n = 0 e (p1)n−1 6= 0, ou seja, pn1 = 0 e pn−11 6= 0. Portanto,
char(R) = pn.
(ii) SendoD(R) um ideal, temos queD(R) ´e um subgrupo deR (Rvisto como um grupo com a opera¸c˜ao de adi¸c˜ao). Como char(R) =pn, temos que pna = 0, para todo a∈ R. Em particular, sez ∈D(R), ent˜ao pnz = 0. Assim, a ordem de z, denotada por o(z), divide pn, ou seja, o(z) = pm, para algum inteiro n˜ao negativo m. Logo, D(R) ´e um p-grupo. Disso segue que|D(R)|=pt, para algum inteiro n˜ao negativo t.
(iii) ComoR/D(R) ´e um corpo finito, sua cardinalidade ´e uma potˆencia de algum primo. Pelo item (ii), |D(R)| = pt. Como |R/D(R)| = |R|/|D(R)|, devemos ter |R| = pk, para
algum inteiro positivok. ⊓⊔
Encerramos este cap´ıtulo com um teorema que nos d´a uma rela¸c˜ao entre as cardinalidade deR e de D(R) no caso em que R ´e finito.
Proposi¸c˜ao 1.38. Seja R um anel finito. Ent˜ao |R| ≤ |D(R)|2.
Demonstra¸c˜ao: Seja a∈D(R)∗. Ent˜ao Ann(a)⊆D(R) e, da´ı,|Ann(a)| ≤ |D(R)|.
Consi-deremos agora o homomorfismo sobrejetorf :R →(a) deR-m´odulos dado por f(x) =ax. ´E claro queker(f) =Ann(a) e, assim, R
Ann(a) ∼= (a), donde
|R|
|Ann(a)| =|(a)| ≤ |D(R)|. Portanto,
|R| ≤ |Ann(a)||D(R)| ≤ |D(R)|2. ⊓⊔
1.2
Grafos
Nesta se¸c˜ao, introduziremos t´opicos b´asicos da Teoria de Grafos necess´arios ao estudo dos grafos divisores de zero, tais como conexidade, diˆametro, colora¸c˜oes, ciclos, cintura, grafos
r-partidos completos, raio, centro, conjuntos dominantes e planaridade. Iniciamos com a defini¸c˜ao de grafo.
Defini¸c˜ao 1.39. Sejam V um conjunto e E um subconjunto de {{u, v} : u, v ∈ V}. Um
1.2 Grafos 14
elemento de E ´e chamado de aresta. Se V ´e um conjunto finito, dizemos que n = |V| ´e a
ordem do grafoG= (V, E) e a denotamos por|G|.
Quando n˜ao houver d´uvidas, vamos nos referir ao grafo G = (V, E) apenas por G. Po-demos, em alguns casos, escrever V(G) e E(G) para indicar, respectivamente, o conjunto de v´ertices e o conjunto de arestas de um grafoG.
Um v´ertice v ∈V ´e adjacente a um v´ertice u∈ V se {u, v} ∈E. O grau do v´ertice v ´e definido por deg(v) = |{u : {u, v} ∈ E}|. Uma aresta {u, v} ∈ E ´eincidente aos v´ertices u
ev.
Se V′ ⊆ V e E′ ⊆ {{u, v} : u, v ∈ V′,{u, v} ∈ E}, dizemos que G′ = (V′, E′) ´e um
subgrafo de G e escrevemos G′ ⊆ G. E se, para todos u, v ∈ V′, {u, v} ∈ E implicar que
{u, v} ∈E′, ent˜ao dizemos queG′´e umsubgrafo induzido. Neste caso, escrevemosG′ =G[V′].
Sejam G1 = (V1, E1) e G2 = (V2, E2) grafos. Dizemos que G1 e G2 s˜ao isomorfos, e escrevemos G1 ≃ G2, quando existe uma bije¸c˜ao ϕ : V1 −→ V2 tal que {u, v} ∈ E1 se, e somente se, {ϕ(u), ϕ(v)} ∈ E2, para todos u, v ∈ V1. Segue diretamente da defini¸c˜ao de isomorfismo quedeg(v) = deg(ϕ(v)), para todo v ∈V1.
Umcaminho em um grafoG= (V, E) ´e uma sequˆencia de v´ertices v0, v1, . . . , vk, distintos dois a dois, tal que {vi, vi+1} ∈ E, para todo i = 0, . . . , k−1. Neste caso, denotamos tal caminho porv0v1· · ·vk e dizemos que o n´umerok ´e o comprimento do caminho.
Um subgrafo de ordem k ≥ 3 de G da forma G′ = (V′, E′), com V′ = {v1, v2, . . . , vk} e
E′ = {{v
1, v2},{v2, v3}, . . . ,{vk−1, vk}, {vk, v1}} ´e um ciclo de comprimento k. Denotamos tal ciclo por v1v2· · ·vkv1. Um k-ciclo, denotado por Ck, ´e um grafo que ´e um ciclo de comprimentok quando visto como subgrafo de G.
Dizemos que um grafo G = (V, E) ´e conexo se existe um caminho ligando quaisquer dois v´ertices distintos. Dados u, v ∈ V, com u 6= v, a distˆancia de u a v ´e definida por
d(u, v) = min{k : existe um caminho de u av de comprimentok} e convencionamos que
d(v, v) = 0, para todo v ∈ V. O diˆametro de um grafo conexo G ´e denotado por diam(G) e definido por diam(G) = sup{d(u, v) : u, v ∈ V, u 6= v}. A cintura de G, denotada por
gr(G), ´e definida como o comprimento do menor ciclo em G; se G n˜ao cont´em ciclos, ent˜ao
1.2 Grafos 15
Proposi¸c˜ao 1.40. ([16], p´ag. 8) Todo grafo G contendo um ciclo satisfaz
gr(G)≤2·diam(G) + 1.
Dado um grafo G= (V, E), dizemos que um subconjuntoS de V domina o grafo G (ou queS ´e um conjunto dominante de G) quando todo v´ertice de V pertence ao conjunto S ou ´e adjacente a algum v´ertice desse conjunto. Podemos ver que o pr´oprio conjunto V sempre dominaG.
Dizemos que S ⊆ V ´e um conjunto dominante minimal de G quando S domina G e os demais conjuntos dominantes deGpossuem cardinalidade maior ou igual a cardinalidade de
S. Quando a cardinalidade de um conjunto dominante minimal de um grafoG´e um n´umero inteiro n˜ao negativon, dizemos que n ´e o n´umero de domina¸c˜ao (ou n´umero dominante) de
Ge escrevemos γ(G) =n.
A seguir, damos um exemplo que ilustra alguns dos conceitos dados neste cap´ıtulo.
Exemplo 1.41. Consideremos o grafo conexoG= (V, E), com V ={a, b, c, d, e} e
E ={{a, b},{b, c},{b, e},{c, d},{d, e}},
dado na Figura 1.1. O grafoH = (V′, E′) tal queV′ ={b, c, d, e}eE′ ={{b, c},{c, d},{d, e}}
´e um subgrafo de G, mas n˜ao ´e um subgrafo induzido por V′, uma vez que {b, e} ∈ E\E′
(Figura 1.2).
Figura 1.1: Grafo G do Exemplo 1.41 Figura 1.2: Grafo H do Exemplo 1.41
Podemos ver que h´a dois caminhos distintos entre os v´ertices b e e, a saber, be e bcde. Por defini¸c˜ao, temos que d(b, e) = 2. A maior distˆancia entre dois v´ertices de G ´e 3, que ´e a distˆancia entre a e d. Da´ı, diam(G) = 3. O grafo G cont´em o 4-ciclo bcdeb e n˜ao possui outros ciclos. Logo,gr(G) = 4.
O subconjunto A ={a, c, e} deV ´e um conjunto dominante de G. Tamb´em, B = {b, d}
1.2 Grafos 16
Antes de apresentarmos mais algumas defini¸c˜oes, devemos nos lembrar que uma parti¸c˜ao de um conjunto n˜ao vazio qualquer X ´e uma cole¸c˜ao {Xλ}λ∈Λ de subconjuntos n˜ao vazios de X, dois a dois disjuntos, tal que S
λ∈ΛXλ = X. Neste caso, cada elemento da cole¸c˜ao
{Xλ}λ∈Λ ´e uma parte da parti¸c˜ao de X.
Dado um inteiro positivo r, dizemos que um grafo G´e r-partido se existe uma parti¸c˜ao deV emr subconjuntos tal que v´ertices pertencentes a uma mesma parte dessa parti¸c˜ao n˜ao s˜ao adjacentes. Dizemos que G = (V, E) ´e um grafo r-partido completo se G ´e r-partido e se para quaisquer dois v´erticesu ev que est˜ao em partes distintas da parti¸c˜ao, tivermos que
{u, v} ∈E.
Para o casor= 2, um grafor-partido ´e chamado de grafobipartido. J´a um grafor-partido completo recebe o nome de bipartido completo e ´e denotado por Km,n, onde m =|V1| ≥ 1 e
n=|V2| ≥1. Os grafos da forma K1,n s˜ao chamados de grafos estrela.
Na Figura 1.3, vemos representado o grafo bipartido completo K3,3.
Figura 1.3: Grafo bipartido completo K3,3
Um grafoG´e um grafo nulo seV =∅. Dizemos que o grafoG´ecompleto com n v´ertices se|V|=n e {u, v} ∈E, para todos u, v ∈V, com u6=v. Denotamos tal grafo por Kn. Na Figura 1.4, temos o grafo completoK5 representado de dois modos distintos.
Figura 1.4: Duas representa¸c˜oes distintas de K5
1.2 Grafos 17
A cardinalidade do maior clique de G´e denotada por ω(G). Se Gpossui um clique infinito, escrevemos ω(G) =∞.
Uma k-colora¸c˜ao dos v´ertices de um grafo G ´e uma fun¸c˜ao f : V → {1,2, . . . , k}. Colo-candoVi =f−1(i), parai∈ {1, . . . , k}, temos queV1, V2, . . . , Vk´e umak-parti¸c˜ao deV. Uma
k-colora¸c˜ao f ´e pr´opria se v´ertices adjacentes possuem imagens distintas pela f. O n´umero crom´aticoχ(G) ´e o menor inteiro positivoktal que existe umak-colora¸c˜ao de v´ertices pr´opria deG. Dado um grafo G, sempre temos queχ(G)≥ω(G).
Proposi¸c˜ao 1.42. Se G = (V, E) ´e um grafo r-partido, ent˜ao G possui uma r-colora¸c˜ao pr´opria de seus v´ertices.
Demonstra¸c˜ao: Sejam V1, . . . , Vr as r partes deV que tornamG um grafo r-partido. De-finamos f : V → {1, . . . , r} por f(x) = k, se x ∈ Vk. Ent˜ao, se {x, y} ∈ E, devemos ter
f(x)6=f(y), pois se f(x) = f(y) = k, ter´ıamosx, y ∈Vk e n˜ao poder´ıamos ter xadjacente a
y. Logo,f ´e uma colora¸c˜ao pr´opria dos v´ertices G, donde χ(G) ´e finito. ⊓⊔
Seja G = (V, E) um grafo conexo com diˆametro finito. A excentricidade de um v´ertice
v ∈ V ´e o n´umero e(v) = sup{d(v, x) : x ∈ V}. O raio de G ´e o n´umero rad(G) =
min{e(v) : v ∈V,}. Um v´erticev ∈V ´e ditocentral see(v) =rad(G). O subgrafo induzido pelo conjunto dos v´ertices centrais deG´e ocentro do grafoG, o qual denotamos porCen(G).
Exemplo 1.43. Nas Figuras 1.5 e 1.6, representamos os grafos G1 e G2, destacando os v´ertices do centro com uma cor mais clara e os v´ertices que n˜ao est˜ao no centro com uma cor mais escura. Notemos querad(G1) = rad(G2) = 2.
Figura 1.5: Grafo G1 do Exemplo 1.43 Figura 1.6: GrafoG2 do Exemplo 1.43
1.2 Grafos 18
Proposi¸c˜ao 1.44. Seja G= (V, E) um grafo conexo e finito. Temos querad(G) = diam(G)
se, e somente se, G=Cen(G).
Demonstra¸c˜ao: Se |G| = 1, o resultado ´e imediato. Analisemos o caso em que |G| ≥ 2. Inicialmente, vamos supor que rad(G) = diam(G). Dado x ∈ V, tomemos y ∈ V \ {x} tal que e(x) = d(x, y). Como rad(G)≤e(x) = d(x, y)≤sup{d(u, v) : u, v ∈V} =diam(G) =
rad(G), temos que e(x) =rad(G) e, assim, x∈V(Cen(G)). Logo,G=Cen(G).
Supomos agora que G =Cen(G). Sabemos que rad(G) ≤ diam(G). Tomemos x, y ∈ V
tais que d(x, y) =diam(G). Como x∈V(Cen(G)), temos que e(x) =rad(G). Desse modo,
diam(G) =d(x, y)≤sup{d(x, u) : u∈V}=e(x) = rad(G). Logo, rad(G) =diam(G). ⊓⊔
1.2.1
Grafos planares
Introduziremos aqui o conceito de grafo planar e apresentaremos alguns resultados en-volvendo esse tipo de grafo. Dentre tais resultados, destacamos o Teorema de Kuratowski-Harary-Tutte-Wagner, o qual fornece uma condi¸c˜ao necess´aria e suficiente para que um grafo seja planar.
Embora o estudo de grafos planares n˜ao se restrinja apenas aos grafos finitos, vamos assumir nesta se¸c˜ao que todos os grafos s˜ao finitos.
Defini¸c˜ao 1.45. Dizemos que um grafo G ´e um grafo planar se for poss´ıvel desenh´a-lo em um plano de modo que suas arestas n˜ao se interceptem, exceto possivelmente nos v´ertices aos quais s˜ao ambas incidentes. Caso contr´ario, G´e dito n˜ao planar.
Notemos que tal defini¸c˜ao ´e intuitiva, pois n˜ao explicitamos aqui o que significa, em termos matem´aticos, desenhar no plano. O leitor interessado em uma defini¸c˜ao mais rigorosa de grafo planar pode consultar ([16], cap´ıtulo 4). Vejamos agora um exemplo.
1.2 Grafos 19
Figura 1.7: K4 com interse¸c˜ao de arestas Figura 1.8: K4 sem interse¸c˜ao de arestas
Dois exemplos importantes de grafos n˜ao planares s˜ao apresentados a seguir.
Teorema 1.47. ([10], p´ag. 200) Os grafos K5 (Figura 1.4) e K
3,3 (Figura 1.3) n˜ao s˜ao
planares.
Nosso intuito agora ´e enunciar o Teorema de Kuratowski-Harary-Tutte-Wagner. Um dos conceitos que aparecem no enunciado deste teorema ´e o conceito de subcontra¸c˜ao. Numa tentativa de compreendermos melhor tal conceito, apresentamos as seguintes defini¸c˜oes.
Defini¸c˜ao 1.48. SejaG= (V, E) um grafo e sejae={a, b} ∈E. Dado q /∈V, consideremos o conjuntoF1 ={{q, x} : {a, x} ∈E ou {b, x} ∈E}. Denotemos porF2o conjunto formado pelas arestas do grafo G[V \ {a, b}].
(a) O grafo G′ = (V′, E′) que tem V′ = (V \ {a, b})∪ {q} e E′ = F
1 ∪F2 ´e chamado de uma contra¸c˜ao elementar de G pela aresta e. Denotamos tal grafo G′ por G·e.
(b) Dizemos que um grafo G′ ´e uma contra¸c˜ao elementar de G quando G′ = G·e, para
alguma aresta e deG.
Defini¸c˜ao 1.49. Dado um inteiro n ≥ 1, dizemos que uma sequˆencia finita de grafos
G0, G1, . . . , Gn ´e uma sequˆencia de contra¸c˜oes elementares quando Gi+1 for uma contra¸c˜ao elementar deGi, para cada i∈ {0, . . . , n−1}.
A partir de tais defini¸c˜oes, podemos definir o que ´e uma contra¸c˜ao e uma subcontra¸c˜ao de um grafo.
1.2 Grafos 20
Exemplo 1.51. ConsideremosG0,G1,G2eG3os grafos dados, respectivamente, nas Figuras 1.9, 1.10, 1.11 e 1.12. Podemos ver que G1 =G0·g,G2 =G1·h e G3 =G2·j. Temos ent˜ao queG0, G1, G2, G3 ´e uma sequˆencia de contra¸c˜oes elementares e G3 ´e uma contra¸c˜ao de G0. Em tais figuras, destacamos com uma cor mais clara o v´ertice de Gi+1 que n˜ao ´e v´ertice de
Gi, para cada i∈ {0,1,2}.
Figura 1.9: Grafo G0 do Exemplo 1.51 Figura 1.10: Grafo G1 do Exemplo 1.51
Figura 1.11: Grafo G2 do Exemplo 1.51 Figura 1.12: Grafo G3 do Exemplo 1.51
Estamos em condi¸c˜oes de enunciar o Teorema de Kuratowski-Harary-Tutte-Wagner, que nos d´a uma condi¸c˜ao necess´aria e suficiente para que um grafo seja planar.
Teorema 1.52. (Kuratowski-Harary-Tutte-Wagner)([10] p´ag. 200 e p´ag. 201) Um
grafo G´e planar se, e somente se, n˜ao cont´em uma subcontra¸c˜ao isomorfa a K3,3 ou a K5.
Destacamos que se G cont´em K5 ou K
3,3 como subgrafo, ent˜ao G n˜ao ´e planar, pelo teorema anterior e pela defini¸c˜ao de subcontra¸c˜ao (Defini¸c˜ao 1.50).
1.2 Grafos 21
Logo H, J, K5 ´e uma sequˆencia de contra¸c˜oes elementares, donde obtemos que K5 ´e uma contra¸c˜ao deH. Pelo Teorema 1.52, H n˜ao ´e planar.
Figura 1.13: Grafo H do Exemplo 1.53 Figura 1.14: Grafo J do Exemplo 1.53
Figura 1.15: K5 ≃J·j (Exemplo 1.53)
Encerramos este cap´ıtulo com um resultado que nos apresenta mais uma caracter´ıstica de um grafo planar.
Proposi¸c˜ao 1.54. ([13] p´ag. 232) Todo grafo planar cont´em um v´ertice de grau menor ou
Cap´ıtulo 2
Grafos divisores de zero
Neste cap´ıtulo, apresentaremos alguns resultados sobre grafos divisores de zero de an´eis comutativos. Nosso objetivo ´e descrever algumas propriedades desses grafos e destacar algu-mas rela¸c˜oes entre o anel e o seu grafo divisor de zero.
Dividimos o cap´ıtulo em oito se¸c˜oes. Na primeira, daremos a defini¸c˜ao de grafo divisor de zero e apresentaremos alguns exemplos e alguns resultados b´asicos que tratam da conexidade, do diˆametro e do tamanho desse grafo. Na se¸c˜ao seguinte, exibiremos alguns resultados obtidos por Istvan Beck sobre colora¸c˜ao de v´ertices de um grafo divisor de zero. Na terceira se¸c˜ao, veremos uma condi¸c˜ao necess´aria e suficiente para que um grafo divisor de zero possua um v´ertice adjacente aos demais v´ertices. Os grafos divisores de zero que s˜ao grafos completos e os que s˜ao grafos estrela ser˜ao estudados na se¸c˜ao 4. Na quinta se¸c˜ao, apresentaremos resultados sobre grafos divisores de zero r-partidos completos, r ≥ 2. Na se¸c˜ao seguinte, faremos um breve estudo acerca dos ciclos e da cintura de um grafo divisor de zero. Na se¸c˜ao 7, estudaremos algumas quest˜oes referentes ao raio, ao centro e ao n´umero de domina¸c˜ao de um grafo divisor de zero. Encerraremos o cap´ıtulo com uma se¸c˜ao cujos resultados visam determinar quando que um grafo divisor de zero ´e planar.
2.1
O grafo divisor de zero
2.1 O grafo divisor de zero 23
v´ertices, mas os elementos de R que n˜ao s˜ao divisores de zero s˜ao adjacentes apenas ao elemento 0.
Nesta disserta¸c˜ao, n˜ao usaremos a defini¸c˜ao dada por Beck, mas a defini¸c˜ao de grafo divisor de zero apresentada por D. F. Anderson e P. S. Livingston em [6]. Veremos que o grafo definido por tais autores pode ser visto como um subgrafo do grafo de Beck: o subgrafo induzido pelo conjunto dos divisores de zero n˜ao nulos do anel. Vejamos ent˜ao a defini¸c˜ao de grafo divisor de zero.
Defini¸c˜ao 2.1. O grafo divisor de zero de um anel R, denotado por Γ(R), ´e o grafo dado pelo par
Γ(R) = (V(Γ(R)), E(Γ(R)))
em que V(Γ(R)) =D(R)∗ eE(Γ(R)) = {{x, y} : x, y ∈V(Γ(R)), x6=y e x.y = 0}.
De tal defini¸c˜ao temos que Γ(R) ´e um grafo nulo se, e somente se, R ´e um dom´ınio de integridade. Para evitar que Γ(R) seja um grafo nulo, vamos supor implicitamente que R
n˜ao ´e um dom´ınio de integridade.
Dado um grafoG, se existir um anelRtal que Γ(R) = G, diremos queGpode ser realizado como Γ(R).
Na sequˆencia desta se¸c˜ao, daremos alguns exemplos e alguns resultados b´asicos acerca da conexidade, do diˆametro e do tamanho do grafo divisor de zero. Destacaremos ainda algumas rela¸c˜oes entre isomorfismos de grafos e isomorfismos de an´eis.
Comecemos ent˜ao apresentando alguns exemplos de grafos divisores de zero. Para n˜ao sobrecarregarmos a nota¸c˜ao, em algumas situa¸c˜oes, omitimos as barras dos elementos de um anel quociente.
Exemplo 2.2.Consideremos os an´eisR=Z4eS = Z
2[x]
(x2). Ent˜aoD(R)
∗ ={2}eD(S)∗ ={x}
e seus respectivos grafos divisores de zero s˜ao dados por:
Figura 2.1: Γ(Z4) Figura 2.2: Γ Z
2[x]
(x2
2.1 O grafo divisor de zero 24
Exemplo 2.3. Dados R = Z9, S = Z3[x]
(x2) = {0,1,2, x, x+ 1, x+ 2,2x,2x + 1,2x+ 2} e
T = Z2 ×Z2 temos que D(R)∗ = {3,6}, D(S)∗ = {x,2x} e D(T)∗ = {(0,1),(1,0)}. Os grafos divisores de zero de tais an´eis s˜ao:
Figura 2.3: Γ(Z9) Figura 2.4: Γ Z
3[x]
(x2)
Figura 2.5: Γ(Z2×Z2)
Exemplo 2.4. Sejam R = Z6, S = Z8, T = Z
2[x]
(x3) e V =
Z4[x]
(2x,x2
−2). Ent˜ao D(R)
∗ ={2,3,4},
D(S)∗ ={2,4,6}, D(T)∗ ={x, x2, x2+x} e D(V)∗ ={2, x, x+ 2} e seus respectivos grafos
divisores de zero s˜ao:
Figura 2.6: Γ(Z6) Figura 2.7: Γ(Z8)
Figura 2.8: ΓZ2[x]
(x3
)
Figura 2.9: Γ Z4[x]
(2x,x2−2)
Observa¸c˜ao 2.5. Os Exemplos 2.2, 2.3 e 2.4 nos mostram que an´eis n˜ao isomorfos podem ter grafos divisores de zero isomorfos (por exemplo, Z6 e Z8 s˜ao an´eis n˜ao isomorfos, mas ambos possuem K1,2 como grafo divisor zero). Logo, n˜ao podemos garantir que an´eis que possuem grafos divisores de zero isomorfos s˜ao isomorfos. No entanto, podemos mostrar que an´eis isomorfos sempre ter˜ao seus respectivos grafos divisores de zero isomorfos. ´E o que nos diz nosso primeiro resultado acerca dos grafos divisores de zero.
Teorema 2.6. Se dois an´eis s˜ao isomorfos, ent˜ao seus respectivos grafos divisores de zero
2.1 O grafo divisor de zero 25
Demonstra¸c˜ao: Sejam R eS an´eis isomorfos e seja f :R −→S um isomorfismo entre tais an´eis. Afirmamos que f(D(R)∗) ⊆ D(S)∗. De fato, dado x ∈ D(R)∗, existe y ∈ D(R)∗ tal
quexy = 0. Assim, 0 =f(0) =f(xy) =f(x)f(y). Como ker(f) ={0}, temos quef(x)6= 0 e f(y) 6= 0, donde obtemos que f(x) ∈ D(S)∗. Portanto, f(D(R)∗) ⊆ D(S)∗. Logo, faz
sentido considerarmos a aplica¸c˜ao
α=f|D(R)∗ : D(R)∗ −→ D(S)∗
x 7−→ f(x).
Vamos mostrar que α induz um isomorfismo de grafos. Claramente, α ´e injetora. Agora, dado z ∈ D(S)∗, temos que existe w ∈ D(S)∗ tal que zw = 0, ou seja, {z, w} ∈ E(Γ(S)).
Sendo f bijetor e f(0) = 0, existem x, y ∈ R∗ tais que f(x) = z e f(y) = w. Assim,
f(xy) = f(x)f(y) = zw = 0. Como f ´e injetor, segue que xy = 0, donde, x ∈ D(R)∗ e α
´e sobrejetora. Logo, α ´e bijetora. Facilmente podemos verificar que {x, y} ∈ E(Γ(R)) se, e somente se, {α(x), α(y)} ∈E(Γ(S)). Portanto, Γ(R)≃Γ(S). ⊓⊔
Conv´em mencionarmos aqui que, sob algumas condi¸c˜oes, a rec´ıproca do teorema anterior ´e verdadeira. No entanto, n˜ao explicitaremos nem faremos aqui um estudo sobre tais condi¸c˜oes. O leitor interessado neste assunto pode consultar [6] e [17].
No pr´oximo exemplo, mostramos que K3 pode ser realizado como Γ(R).
Exemplo 2.7. Consideremos os an´eisR= Z2[x,y]
(x2,xy,y2) ={0,1, x, y, x+ 1, y+ 1, x+y, x+y+ 1}
eS= F4[x]
(x2
) ={0,1, α, α
2, x, αx, α2x,1 +x,1 +αx,1 +α2x, α+x, α+αx, α+α2x, α2+x, α2+
αx, α2+α2x}, onde F
4 ={0,1, α, α2}´e um corpo com 4 elementos, com α2 =α+ 1. N˜ao ´e dif´ıcil ver queD(R)∗ ={x, y, x+y} e D(S)∗ ={x, αx, α2x}. Os grafos divisores de zero de
R e S podem ser vistos nas Figuras 2.10 e 2.11.
Figura 2.10: ΓZ2[x,y]
(x,y)2
Figura 2.11: ΓF4[x]
(x2)
2.1 O grafo divisor de zero 26
Considerando os an´eis T = Z4[x]
(2,x)2 = {0,1,2,3, x, x+ 1, x+ 2, x+ 3} e W =
Z4[x]
(x2+x+1) =
{0,1,2,3, x, x+ 1, x+ 2, x+ 3,2x,2x+ 1,2x+ 2,2x+ 3,3x,3x+ 1,3x+ 2,3x+ 3}, temos queD(T)∗ ={2, x, x+ 2} e D(W)∗ ={2,2x,2x+ 2}. Ambos os an´eis possuem tamb´em K3
como grafo divisor de zero.
Observa¸c˜ao 2.8. Em [11] e em [5], os autores mostraram que, a menos de isomorfismos, os an´eis dos Exemplos 2.2, 2.3, 2.4 e 2.7 s˜ao os ´unicos que possuem como grafo divisor de zero, respectivamente, K1, K2, K
1,2 e K3. N˜ao apresentaremos neste texto como que tais autores chegaram a tais conclus˜oes, mas usaremos mais adiante essa classifica¸c˜ao.
Destacamos agora que os grafos divisores de zero dados nos exemplos anteriores s˜ao todos conexos. O pr´oximo teorema nos garante que a conexidade ´e, na verdade, uma caracter´ıstica de todos os grafos divisores de zero. Este mesmo teorema afirma ainda que o diamˆetro de um grafo divisor de zero n˜ao pode ser maior do que 3.
Teorema 2.9. ([6]) Para todo anel R, Γ(R) ´e conexo e diam(Γ(R))≤3.
Demonstra¸c˜ao: Sejam x, y ∈D(R)∗ distintos. Se xy = 0, ent˜aod(x, y) = 1. Ent˜ao, vamos
supor que xy 6= 0 e analisar os poss´ıveis casos. Se x2 = 0 e y2 = 0, ent˜ao x(xy) = 0 e (xy)y = 0 e temos x(xy)y um caminho de comprimento dois, donde d(x, y) = 2. Se x2 = 0 e y2 6= 0 ent˜ao existe b ∈ D(R)∗ \ {x, y} tal que by = 0. Se bx = 0, temos que xby ´e um
caminho de comprimento dois. Sebx 6= 0, ent˜ao x(xb)y´e um caminho de comprimento dois. Analogamente, podemos mostrard(x, y) = 2 no caso em que x2 6= 0 e y2 = 0.
Suponhamos agora quexy6= 0, x2 6= 0 ey2 = 0. Temos que existem6 a, b∈D(R)∗\ {x, y}
tais que ax =by = 0. Se a =b, o caminho xay tem comprimento dois. Suponhamos a6= b. Se ab = 0, temos xaby um caminho de comprimento trˆes e, assim, d(x, y) = 3. Se ab 6= 0, temosx(ab)yum caminho de comprimento dois, donded(x, y) = 2. Logo,diam(Γ(R))≤3. ⊓⊔
J´a vimos, nos Exemplos 2.2, 2.3 e 2.4, grafos divisores de zero com diˆametros 0, 1 e 2, respectivamente. No pr´oximo exemplo, exibimos um anelR tal que diam(Γ(R)) = 3.
2.1 O grafo divisor de zero 27
que Ann(2)∩Ann(3) = {0}. Logo, n˜ao podemos ter d(2,3) = 2. Pelo teorema anterior,
d(2,3) = 3 e, assim, diam(Γ(Z12)) = 3. Na Figura 2.12, temos Γ(Z12).
Figura 2.12: Γ(Z12)
Com este ´ultimo exemplo, temos que, para cada d∈ {0,1,2,3}, existe um anelR tal que
diam(Γ(R)) = d. Em [2] e em ([17], p´ag. 49), o leitor pode encontrar condi¸c˜oes necess´arias e suficientes para que tenhamosdiam(Γ(R)) =d, para cada d∈ {0,1,2,3}. N˜ao exploraremos tal assunto aqui.
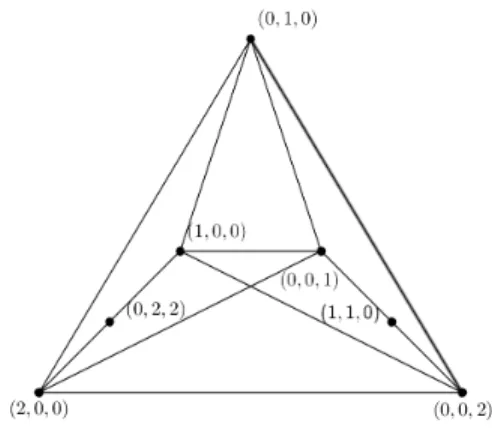
Vamos determinar agora quais s˜ao os grafos com 4 v´ertices que podem ser realizados como Γ(R). Pelo Teorema 2.9, temos que a conexidade ´e uma condi¸c˜ao necess´aria para que um grafo seja um grafo divisor de zero. A menos de isomorfismos, os ´unicos grafos conexos com 4 v´ertices s˜ao os dados na Figura 2.13:
Figura 2.13: Grafos conexos com 4 v´ertices (a menos de isomorfismo)
Dentre estes 6 grafos, apenas os 3 primeiros podem ser realizados como Γ(R). De fato, consideremos os an´eis R = Z25 e S = Z3 × Z3. Temos que D(R)∗ = {5,10,15,20} e
D(S)∗ = {(0,1),(1,0),(0,2),(2,0)}. Seja F
4 = {0,1, α, α2} um corpo com 4 elementos. Consideremos o anel
T =Z2×F4 ={(0,0),(0,1),(0, α),(0, α2),(1,0),(1,1),(1, α),(1, α2)}.
2.1 O grafo divisor de zero 28
Figura 2.14: Γ(Z25) Figura 2.15: Γ(Z3×Z3) Figura 2.16: Γ(Z2×F4)
Vamos mostrar agora que o grafo Gcom v´ertices {a, b, c, d}e arestas {a, b},{b, c},{c, d}
n˜ao pode ser realizado como Γ(R). De fato, suponhamos que exista um anelR comD(R)∗ =
{a, b, c, d} e somente os produtos nulos ab = 0, bc = 0 e cd = 0 entre os elementos de R∗.
Como (a+c)b = ab+cb = 0, temos que a +c ∈ D(R) = {0, a, c, b, d}. Afirmamos que
a+c=b. De fato, notemos que a+c=a implicac= 0 e que se a+c=c, ent˜ao a= 0. Se
a+c = d, temos db = 0, mas esta rela¸c˜ao n˜ao ocorre em R∗. Por fim, se a+c = 0, ent˜ao
0 = (a+c)d=ad+cd=ad, o que tamb´em n˜ao ocorre. Logo, devemos ter a+c=b.
Analogamente, como (b +d)c = bc+dc = 0, temos que b +d ∈ D(R)∗. Procedendo
como acima, obtemos queb+d =c. Assim, b =a+c=a+b+d, donde a+d= 0. Logo,
bd=b(−a) = −(ab) = 0, o que ´e um absurdo. Para os outros dois grafos conexos com quatro v´ertices, a demonstra¸c˜ao ´e an´aloga.
Encerramos este cap´ıtulo com um importante resultado acerca do tamanho do grafo divisor de zero.
Teorema 2.11. ([6]) Seja R um anel que n˜ao ´e um dom´ınio de integridade. Ent˜ao Γ(R)´e finito se, e somente se, R ´e finito. Em particular, se1≤ |Γ(R)|<∞, ent˜ao R ´e finito e n˜ao ´e corpo.
Demonstra¸c˜ao: Suponhamos Γ(R) finito. Ent˜ao, D(R)∗ ´e finito e, como R n˜ao ´e um
dom´ınio de integridade, D(R)∗ ´e tamb´em n˜ao vazio. Logo, existem x, y ∈ D(R)∗ tais que
xy = 0. Seja I = Ann(x). Ent˜ao I ⊆ D(R) e, assim, I ´e finito. Dado r ∈ R, temos que
ry ∈ I, pois xy = 0 implica ryx= 0. Se R fosse infinito, existiria z ∈ I com J = {r ∈ R :
ry=z} infinito. Assim, para quaisquer r, s∈J, ter´ıamos (r−s)y=ry−sy=z−z = 0 e, ent˜ao, Ann(y) =I seria infinito, o que ´e uma contradi¸c˜ao. Logo, R ´e finito.
2.2 Colora¸c˜oes de Beck 29
2.2
Colora¸c˜
oes de Beck
Apresentaremos aqui alguns resultados expostos por Istvan Beck, em seu artigo “Coloring of commutative rings” [11], sobre colora¸c˜oes de v´ertices. Dentre esses resultados, destacamos os Teorema 2.21 e o Teorema 2.24. O primeiro apresenta algumas condi¸c˜oes necess´arias e suficientes para que um grafo divisor de zero tenha n´umero crom´atico finito. O segundo elenca algumas propriedades de um anel que possui um grafo divisor de zero com n´umero crom´atico finito.
J´a mencionamos neste texto que a defini¸c˜ao de grafo divisor de zero dada por Beck difere da defini¸c˜ao que adotamos aqui. No entanto, nesta se¸c˜ao, manteremos a Defini¸c˜ao.2.1.
Para iniciarmos, devemos dizer que um elemento r∈R ´e um elemento finito de um anel
R se o ideal gerado por r ´e finito. Na sequˆencia, apresentamos alguns lemas que nos d˜ao condi¸c˜oes para que um grafo divisor de zero tenha um clique infinito.
Lema 2.12. ([11]) Seja R um anel que possui um n´umero infinito de elementos finitos.
Ent˜aoΓ(R) cont´em um clique infinito.
Demonstra¸c˜ao: Sejam x1, x2, . . . , xn, . . .elementos finitos distintos dois a dois de R. Como (x1) ´e um ideal finito e x1xi ∈(x1), para todo i∈N, existem infinitos ´ındicesa21, a22, a23, . . . tais que
x1xa21 =x1xa22 =x1xa23 =. . . .
Vamos considerar ent˜ao a sequˆencia {xa2n}n∈N e denotar xa21 = xa2. Sabemos que
xa2xa2i ∈ (xa2), para todo i ∈ N. Sendo (xa2) um ideal finito, existem infinitos ´ındices
a31, a32, a33, . . . , a3n, . . . tais que
xa2xa31 =xa2xa32 =xa2xa33 =. . . .
Consideremos agora a sequˆencia {xa3n}n∈N. Denotando xa31 = xa3 e repetindo o processo,
obteremos uma sequˆenciax1, xa2, xa3, . . ., a qual denotamos pory1, y2, y3, . . . , yn, . . ., tal que
yiyj =yiyk, quandoj > i e k > i.
2.2 Colora¸c˜oes de Beck 30
yjyk =yjyr, temos que
zijzkr = (yi−yj)(yk−yr) =yiyk−yiyr−yjyk+yjyr = 0.
Desse modo, z1,2z3,4 = z1,2z3,5 = 0. Como z3,4 6= z3,5, ent˜ao z3,4 6= z1,2 ou z3,5 6= z1,2. Sez3,4 6= z1,2, temos o clique {z1,2, z3,4}. Se z3,5 6=z1,2, o clique obtido ´e {z1,2, z3,5}. Vamos assumir que z3,5 6=z1,2 e que, portanto, Γ(R) possui o clique {z1,2, z3,5}.
Notemos agora que z6,7, z6,8, z6,9 s˜ao dois a dois distintos. Logo, um deles n˜ao pertence ao conjunto {z1,2, z3,5}. Supondo que z6,9 ∈ {/ z1,2, z3,5}, temos o clique {z1,2, z3,5, z6,9}. Pros-seguindo desse modo, obteremos um clique infinito de Γ(R). ⊓⊔
Lema 2.13. ([11]) Seja I um ideal finito de R. Ent˜ao Γ(R) cont´em um clique infinito se, e somente se, Γ(R/I) cont´em um clique infinito.
Demonstra¸c˜ao: Suponhamos que Γ(R) possui um clique infinito C. A imagem C de C
pela proje¸c˜ao canˆonica de R em R/I ´e um clique de Γ(R/I). Como I ´e finito, devemos ter
C infinito. Logo, Γ(R/I) cont´em um clique infinitoC.
Reciprocamente, consideremos {xi}i∈N um clique infinito de Γ(R/I). Ent˜ao, para todo
i6=j, xixj ∈I. Como I ´e finito, o conjunto dos produtos {xixj}i6=j ´e finito. Para o elemento
x1, existem ´ındicesa2, a22, a23, . . . , a2n, . . . tais que
x1xa2 =x1xa22 =x1xa23 =. . . .
Repetindo o racioc´ınio utilizado na demonstra¸c˜ao do Teorema 2.12, chegaremos que Γ(R)
possui um clique infinito. ⊓⊔
Lema 2.14. ([11]) Se Rcont´em um elemento nilpotente que n˜ao ´e finito, ent˜aoΓ(R)cont´em um clique infinito.
Demonstra¸c˜ao: Por hip´otese, existe x ∈ N il(R) tal que o ideal (x) ´e infinito. Mas x ∈ N il(R) implica que existe n ∈ N tal que xn = 0. A demonstra¸c˜ao ser´a feita por indu¸c˜ao sobre n. Como (x) ´e infinito, temos x 6= 0. Logo, iniciamos a demonstra¸c˜ao considerando
2.2 Colora¸c˜oes de Beck 31
Sex2 = 0, ent˜ao dadosax, bx∈(x), teremos (ax)(bx) = 0. Assim, Γ(R) possui um clique infinito, a saber, o subgrafo induzido pelo ideal (x).
Suponhamos n ≥3 e que o resultado seja verdadeiro para qualquer elemento nilpotente n˜ao finito de R cujo ´ındice de nilpotˆencia seja menor do que n. Tomemos y = x2. Ent˜ao
yn−1 = (x2)n−1 = xn−2 e, como n ≥ 3, temos 2n−2 ≥ n. Da´ı, yn−1 = 0. Se (y) ´e infinito, o resultado segue da nossa hip´otese de indu¸c˜ao. Vamos supor ent˜ao que (y) ´e finito. Neste caso, (x)/(y) ´e infinito e o subgrafo induzido por (x)/(y) ´e um clique infinito deR/(y). Como (y) ´e finito, segue do Lema 2.13 que Γ(R) possui um clique infinito. ⊓⊔
Exemplo 2.15. Em Z4[x], o elemento 2 ´e nilpotente com ´ındice de nilpotˆencia igual a 2. Como o ideal (2) ´e infinito, segue do lema anterior queZ4[x] possui um clique infinito.
Consideremos agora um anel R tal que N il(R) ´e infinito. Se todo elemento de N il(R) ´e finito, o Lema 2.12 nos garante que Γ(R) possui um clique infinito. Se algum elemento de
N il(R) n˜ao ´e finito, tamb´em obtemos que Γ(R) possui um clique infinito: basta aplicarmos o Lema 2.14. Provamos assim o seguinte resultado:
Lema 2.16. ([11]) Se N il(R)´e infinito, ent˜ao Γ(R) tem um clique infinito.
O pr´oximo lema trata de um anel reduzido R cujo grafo divisor de zero n˜ao possui um clique infinito.
Lema 2.17. ([11]) Se R ´e um anel reduzido tal que Γ(R) n˜ao cont´em um clique infinito, ent˜aoR satisfaz a condi¸c˜ao de cadeia ascendente (c.c.a.) sobre ideais da formaAnn(a), com a∈R∗.
Demonstra¸c˜ao: Seja R um anel reduzido. Vamos supor que exista uma cadeia
Ann(a1)(Ann(a2)(. . .
que n˜ao estaciona. Sejaxi ∈Ann(ai)\Ann(ai−1),i= 1,2, . . .. Ent˜ao, para todon ≥2, temos
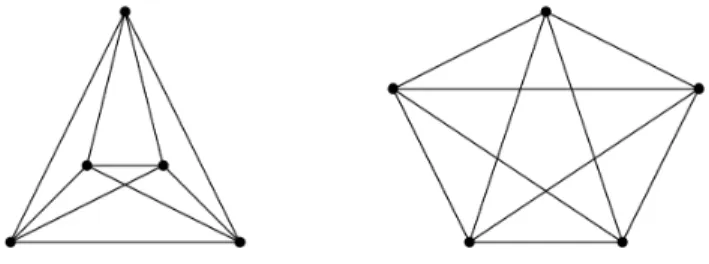
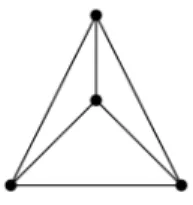
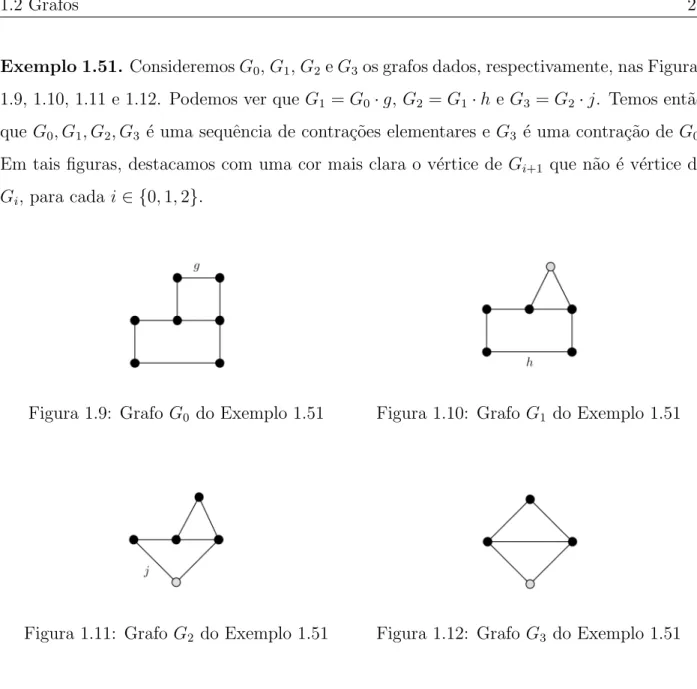

 Figura 2.5: Γ(Z 2 × Z 2 ) Exemplo 2.4](https://thumb-eu.123doks.com/thumbv2/123dok_br/17009374.764986/35.918.130.819.102.831/figura-γ-z-figura-γ-figura-γ-exemplo.webp)