Pions in Isospin Dense Media
M. Loewe
Facultad de F´ısica, P. Universidad Catolica de Chile, casilla 306, Santiago 22, Chile
and C. Villavicencio
Instituto de F´ısica, Universidade Federal do Rio de Janeiro, CP: 68528, Rio de Janeiro, RJ 21945-970, Brasil
Received on 6 December, 2006
The thermal and density corrections, in terms of the isospin chemical potentialµI, to the mass of the pions,
the decay constant and different condensates are studied in the framework of theSU(2)low energy effective chiral Lagrangian at finite temperature in the two phases: The first phase|µI|<mand the second phase|µI|>m,
beingmthe tree-level pion mass. As a function of temperature forµI=0, the mass remains quite stable, starting
to grow for very high values of T, confirming previous results. However, there are interesting corrections to the mass and the other observables mentioned when both effects (temperature and chemical potential) are simultaneously present. At zero temperature theπ±should condense whenµI=±mπ. At finiteT, the condensed pion acquires a thermal mass in such a way that a mixture, like in a superfluid, of a condensed and normal phase appears.
Keywords: Isospin chemical potential; Temperature; Pion superfluidity
In the last years, the pion condensation effect due to a dense isospin media has been a matter of study in a great variety of frameworks, specially in the description of the physics in-side compact stars and relativistic heavy-ion collisions. An isospin dense media (for positive isospin chemical potential) involves more u quarks baryon-charge than the d quarks , so in hadronic degrees of freedom, the media will contain more positive charged pions than negative ones. The oppo-site occurs with negative isospin chemical potential, which is the case in the core of neutron stars, where densities are big enough to condense the negative charged pions. Pion and kaon condensates are relevant at the cooling process period
The introduction of in-medium processes via isospin chem-ical potential has been studied first at zero temperature [ 1, 2] in both phases at tree level. Many works at zero and finite temperature study the effect of pion condensation for isospin dense media principally in the frame of NJL [ 3], lattice QCD [4] and in other frames [5].
All the works confirm that a pion gas, with chemical poten-tial greater than the pion mass, change to a superfluid phase, where one of the charged pions condense in a second order phase transition.
Chiral Perturbation theory (χPT) is an appropriate theory for such scenario, since is a QCD low-energy theory, which includes only the pseudo-goldstone modes. It is also simple in this frame to introduce isospin chemical potential as an exter-nal vector current. The different observables, such as masses, decay constants and currents can be easily extracted.
This proceeding contribution is based on the articles [ 6] for the masses and decay constants in the first phase, [7] for the masses in the second phase and [8] for the analysis of the con-densates in the two phases.
I. CHIRAL PERTURBATION THEORY
In the low-energy description where only pion degrees of freedom are relevant, let us consider the most general chiral invariant Lagrangian, ordered in a series of powers of the ex-ternal momentum. The pions will be coupled with exex-ternal fieldsSχ[U;s,p,v,a], where the external sourcess=s0(x) +
sa(x)τap=p0(x)+pa(x)τav
µ=12vaµ(x)τaandaµ=12aaµ(x)τa,
are the scalar, pseudo-scalar, vector and axial-vector external fields sources, respectively, beingτa the Pauli matrices (see
[9] for all the generalities ofχPT). The field matrixUcontain the pion fields and is defined asU=U¯1/2exp{iπaτa/f}U¯1/2, where ¯U is the vacuum expectation value of the fields and f the pion decay constant at tree level. In the case of massive pions at finite isospin chemical potential, we replaces=M, p=0,vµ=12µIδµ0τ3andaµ=0, whereMis the current quark
mass-matrix anduµis the four velocity.
Four our analysis we also need to extract the different cur-rents of the theory defined as the functional derivative of the Action with respect to the external sources:
Vµa=
δS
δva µ
=1
2q¯γµτ
aq, Aa µ=
δSχ
δaa µ
=1
2q¯γµγ5τ
aq,
Jap=δSχ
δpa=q¯γ5τ
aq, −J0
s =
δSχ
δs0 =−qq¯ ,
being the vectorial, axial, pseudo-scalar and scalar currents. In this way, the different condensates are defined as the vac-uum expectation value of the currents0|J|0and the decay constants from the PCAC relation saturating the axial current with a soft pion0|A|π ∼fπ.
For radiative corrections we need the chiral Lagrangian up to
O
(p4)in the Weinberg momentum power counting and ex-pand the chiral Lagrangian in powers of pion fields consider-ing that the expectation valueπ2 ∼P2.correc-tions we only need the Dolan-Jackiw propagator, defined as
DDJ(p) =
dk 0 2πiηlim→0
D(k0+iη,p)−D(k0−iη,p) k0−p0−iε
+nB(p0)
D(p0+iε,p)−D(p0−iε,p)
(1) After expanding the chiral Lagrangian and currents for one-loop calculations, following the prescriptions of χPT of the power counting, we can perform radiative corrections. In the case of the condensates the procedure is direct in both phases, since it is only needed to calculate the vacuum expectation value of the currents. Nevertheless, the identification of the masses and decay constants is not as simples as in the sec-ond phase, since there occurs a mixing of the charged fields. We use the prescription in [1] to extract the pion masses, as the poles of the determinant of the propagator matrix in rest frame, i.e. the solution of|D−1(p0)|=0.
II. CONDENSED PHASE
A common feature of all approaches in the second phase is the fact that the physical pion states do not correspond any-more to the usual pion charged states. In fact as we will see, theπ±states will mix in a non trivial way. The result of this
mixture produces and extremely cumbersome propagator, a matrix 2×2, so we need to define some criteria how to handle this propagator, according to the value of the chemical poten-tial, for computing radiative corrections.
For|µI|>mthere is a symmetry breaking. The vacuum
expectation value that minimizes the potential is ¯U=c+iτ˜1s, wherec≡m2/µ2
I ands≡(1−m4/µ4I)1/2as was obtained in
[1]. This non-trivial vacuum will produce as a result a mixing of the charged fields. Thus the pseudo-fields that appears in the Lagrangian are not any more the physical ones. A direct consequence is that the propagator matrix for charged pions is not diagonal. In momentum space it is
˜
D= i
[p4−p2µ2
Is2−4µ2Ic2p
2 0]
p2 −2i|µ
I|cp0
2i|µI|cp0 p2−µ2Is
2
(2) where ˜Di j≡Di j=3with respect the degrees of freedom of the quasi-fields ˜π1and ˜π2. Here we useµI=−|µI|as it is the case
in the core of neutron stars. The main difficulty with this ma-trix propagator is that it is very cumbersome to integrate the different loop corrections. This fact motivated us to proceed in a systematic way, through an expansion in a new appropri-ate smallness parameter, namelyswhen|µI| ∼mandcwhen
|µI| ≫m.
It is not difficult to realize that the different vertices which appear in our Lagrangian will correspond to different powers ofcorsdepending on the case. Although it could appear as a trivial correction, we will keep only the zero order in our calculations. As we will see, this procedure is not trivial at all and provide us with interesting information about the behav-ior of the pion masses as function of temperature and isospin chemical potential.
If we scale all the parameters with|µI|in all structures, it is
possible to expand the propagator in powers ofsnfor|µI| ∼m
andcnwhen|µI| ≫m.
In χPT the natural scale parameter is Λχ=4πf.
Usu-ally Λχ is compared with the tree level pion mass defining
in this way the smallness parameter for perturbative expan-sions α = (m/4πf)2. Now, since |µ
I|>m in the second
phase, we will re-define the perturbative expansion parame-ter asα′= (µI/4πf)2
After the renormalization procedure, the divergent terms and the scale factor that will appear in the loops calculation due to dimensional regularization and the
L
4terms will can-cel. Finally the renormalized self-energy will get the formΣ|µI|≫m = µ
2
Iα′
∑
n=0
σ(nc)
p |µI|
; T |µI|
+σlog
n
p |µI|
lnc
cn,
Σ|µI|∼m = µ
2
Iα′
∑
n=0σ(ns)
p |µI|
; T |µI|
s2n. (3)
where the functionsσ’s are dimensionless. The logarithmic terms in the high chemical potential region appears by the can-cellation of the divergences with theχPT counter-terms of the coupling constants. The limit of the theory isµI<mρ since
higher resonances must be considered.
A similar expansion is performed to the radiative correc-tions of the condensates. With all this in mind we can pro-ceed to calculate perturbative correction to the different ob-servables we are interested on.
III. MAIN RESULTS
In this section we only will show a graphical description of the different observables extracted from the procedures men-tioned above. The specifications and details of them can be founded in [6, 7, 8]
A. Condensates
In the first phase, the only non-vanishing condensates are the chiral condensate 0|qq¯ |0 and the isospin number density nI=0|12q†τ3q|0. When the isospin chemical potential is greater than the pion mass, due to the parity breaking, two more condensates appear, the pion conden-sateπ=0|iq¯γ5τ3q|0and the axial charge density
Q
A=0|1 2q
†γ
5τ2q|0. It is interesting to note that in terms of the vacuum expectation value of the currents form a basis in the isospin space:
0|Vµ|0 = nIδµ0e3, 0|Aµ|0 =
Q
Aδµ0e2,0.95 1 1.05 1.1 ΜImΠ
0.8 0.85 0.9 0.95 1
q
q
q
q
T0.5mΠ
T0.3mΠ
T0
(a)
2 2.2 2.4 2.6 2.8 3
ΜImΠ
0.1 0.125 0.15 0.175 0.2 0.225 0.25
q
q
q
q
T0.9mΠ
T0.5mΠ
T0
(b)
FIG. 1: Chiral condensate at finite temperature and isospin chemi-cal potential in (a) the transition region and (b) the high chemical potential region.
independent of the sign of the chemical potential. In the first phase start to decrease with temperature. In the second phase, however, it is affected directly by the chemical potential, be-ing this effect enhanced by the temperature as can be seen in Figure 1.a. For high values of chemical potential, the decrease will be more smooth due to logarithmic terms described in the last section as can be seen in Figure 1.b.
The isospin number density change it sign with respect to the chemical potential sign. It vanishes at zero temperature and for finiteT start to develop a similar behavior of the chiral condensate in the first and near the transition point (Figure 2.a). Nevertheless, for higher values of the chemical potential it presents an abruptly change due to the logarithmic terms. Moreover, it present a crossover in the isothermal lines as can be seen in Figure 2.a.
The pion condensate, will appear in the second phase and start growing with the chemical potential. It start to diminish by the action of the thermal bath as shows Figure 3.a. It is expected since at certain temperature, the condensed pion will acquire a thermal mass , a superfluid phase coexisting massive an condensedπ−pion. In Figure 3.b. we can see again that the
logarithmic terms change their behavior, starting to decrease with the chemical potential.
The axial charge density is one of the less studied conden-sates. It is interesting to note that for a certain temperature it change the sign near the phase transition point as can be seen in figure 4. For high values of the chemical potential, the isothermal lines start to approximate again and negative part start to grow to zero (figure 4.b). Again, the responsible of this change in the behavior is the ‘lnc’ term.
It is important to remark that in the second phase, the re-lation between the chiral condensate and the pion condensate
0.6 0.8 1 1.2 1.4
ΜImΠ
-2 -1.5 -1 -0.5 0
nI
mΠ fΠ
2
T mΠ T 0.7mΠ T 0
(a)
2 2.2 2.4 2.6 2.8 3
ΜImΠ
-1.85 -1.8 -1.75 -1.7 -1.65 -1.6 -1.55
nI
mΠ
fΠ
2
T0.8mΠ
T0.6mΠ
T0
(b)
FIG. 2: Isospin number density condensate at finite temperature and isospin chemical potential in (a) the transition region and (b) the high chemical potential region.
1 1.02 1.04 1.06 1.08
ΜImΠ
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
Π
1
q
q
T0.9mΠ
T0.5mΠ
T0
(a)
2 2.2 2.4 2.6 2.8 3
ΜImΠ
0.86 0.88 0.9 0.92 0.94 0.96
Π
1
q
q
T0.9mΠ
T0.5mΠ
T0
(b)
FIG. 3: Pion condensate at finite temperature and isospin chemical potential in (a) the transition region and (b) the high chemical poten-tial region.
sqq¯ +cπ=0 (5)
AICD condensate
0.5
1
1.5 TmΠ
1.01
1.015 1.02
ΜImΠ
-0.2 0
0.2
QA
mΠfΠ
2
0.5
1
1.5 TmΠ
-0 0
(a)
AICD condensate
0.5
1
1.5 TmΠ
2.2 2.4
2.6 2.8
3
ΜImΠ
-1.5 -1
-0.5 0
QA
mΠfΠ2
0.5
1
1.5 TmΠ
-1. -1 -0
0
(b)
FIG. 4: Axial charge density at finite temperature and isospin chem-ical potential in (a) the transition region and (b) the high chemical potential region.
B. Masses
In the first phase the only quantities that are affected di-rectly with the chemical potential at zero temperature are the charged pion masses.
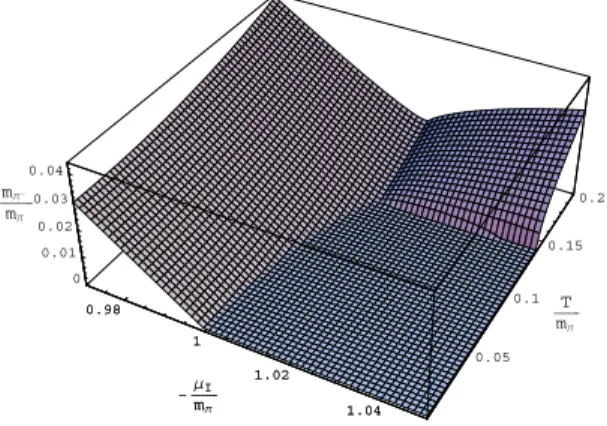
One of the most interesting results, of course is the π−
mass, since it will condense in the second phase (if we change the sign of the chemical potential, theπ+will condense). As
we can see in figure 5, the mass at zero temperature vanishes when the chemical potential reach the pion mass and remains in a condensed state. When the temperature start to grow, the condensation critical value of the chemical potential start to grow. For a certain critical temperatureTc≈20MeV, the
neg-ative pion acquire again a mass. Here is the superfluid phase where massive and condensed negative pions coexist. In the high chemical potential region, theπ−will be of
O
(c2).In the case of the other masses, near the transition point mπ+decreases, as in the tree-level approximation, and this
be-havior is enforced with temperature. In this regionmπ0 grows with both parameters (see figure 6.a). Formπ0 in this region, it increases monotonically both with temperature and chemi-cal potential.mπ+, as the temperature and the chemical
poten-tial rise, becomes asymptotically close tomπ0as was expected (see figure 6.b). In contrast with the first region, theπ+mass grows with temperature and a crossover occurs somewhere in the intermediate region of the chemical potential values.
0.98
1
1.02
1.04
ΜI
mΠ
0.05 0.1
0.15 0.2
T
mΠ 0
0.01 0.02 0.03 0.04
mΠ
mΠ
0.98
1
1.02
1.04
ΜI
mΠ
FIG. 5: mπ−at finite temperature and isospin chemical potential in
the transition region.
0.9 0.95 1 1.05 1.1
ΜImΠ 1
1.2 1.4 1.6 1.8 2
mΠ mΠ
mΠomΠ
T0.8mΠ T0.6mΠ T0
(a)
1.7 1.8 1.9 2 2.1 2.2
ΜImΠ 1.7
1.8 1.9 2 2.1 2.2 2.3 2.4
mΠ mΠ
mΠ0mΠ
T0.8mΠ T0.6mΠ T0
(b)
FIG. 6:mπ0andmπ+at finite temperature and isospin chemical po-tential in (a) the transition region and (b) the high chemical potential region.
C. Decay constants
Here we will give a description of the decay constants only in the first phase. Due to the mixing of the charged pions in the second phase, it is not simple to identify which is the physical pion field. Also the LSZ reduction formula must be generalized. This will developed in a future work.
0.2 0.4 0.6 0.8 1 TmΠ
0.95 0.96 0.97 0.98 0.99 1
fΠ
fΠ
ΜI0.8mΠ ΜI0.5mΠ ΜI0
(a)
0.2 0.4 0.6 0.8 1
TmΠ 0.95
0.96 0.97 0.98 0.99 1
fΠ
0
fΠ
ΜI0.8mΠ ΜI0.5mΠ ΜI0
(b)
FIG. 7: (a) fπ±and (b) fπ0as a function of temperature and finite
isospin chemical potential in the first phase.
with the charged pions decay constant:
0|A±µ(0)|π∓(p)=i(pµ±µIδµ0)fπ±∓inIδµ0
0|A0µ(0)|π0(p)=ipµfπ0 (6) where fπ+= fπ−. The temperature and isospin chemical
po-tential dependence of the decay constants in the first phase can be seen in figure 7.
We can see that it behaves like the chiral condensate in the first phase where the influence of the chemical potential is stronger for fπ0. This similarity with the chiral condensate is not surprising since they are related by the G-MOR relation which is valid at finite temperature. In fact for finite isospin chemical potential and Temperature, the G-MOR relation will be modified as
¯
m2πf¯π2=−1
2(mu+md)qq¯ (7)
beingmuandmdthe light quark masses and ¯mπ= 13(mπ++
mπ−+mπ0)and ¯fπ= 1
3(fπ++fπ−+fπ0), the average value of the masses and decay constants.
IV. CONCLUSIONS
Here we show an analysis of the development of the masses,decay constants and condensates of a pion gas in a dense isospin media within a thermal bath in the frame ofχPT. By calculating the negative-charged pion mass we can see the transition from the normal phase to a superfluid phase where initially, at zero temperature, this pion will condense and their mass vanishes. A pion con densate will appear and it will be the order parameter to the superfluid phase. The negative pion mass in the second phases, appears for values of the temper-ature over a critical tempertemper-atureTc≈20MeV, turning in to
a superfluid phase with partially condensed pa particles and partially with a thermal mass. Nevertheless this is a scheme dependant result predicted byχPT, but such temperatures co-incides with temperatures reached by the core of a neutron star from their born and initial cooling process.
Except for the charged pion masses, all the other quantities depend on the isospin chemical potential only at finite tem-perature in the first phase. In the second phase, two quanti-ties present a crossover between the limits near the transition region and for high isospin chemical potential: the positive charged pion mass and the isospin number density. In general all quantities change drastically with the logarithmic terms in the asymptotic limit whenµ→∞. All this results agree with lattice results [4].
It is interesting to remark again that the relation in ( 5) is preserved, and modifications to the PCAC (equation 6) and the G-MOR relation (equation 7). The last two are only valid in the first phase and will be future work the behavior of the decay constants in the second phase, as well as the modified PCAC and G-MOR relations.
Acknowledgments: The work of M.L. has been supported by Fondecyt (Chile) under grant No.1010976. C. V. acknowl-edges support from Conicyt
[1] J. B. Kogut and D. Toublan, Physical Review D 64, 034007 (2001).
[2] D. T. Son and M. A. Stephanov, Phys. Rev. Lett.86, 592 (2001); K. Splittorff, D. Toublan, J.J.M. Verbaarschot, Nucl. Phys. B 620, 290 (2002).
[3] J. B. Kogut and D. Toublan, Phys. Lett B 564, 212 (2003) [arXiv:hep-ph/0301183];
M. Frank, M. Buballa, and M. Oerttel, Phys. Lett. B562, 221 (2003) [arXiv:hep-ph/0303109];
A. Barducci, R. Casalbuoni, Giulio Pettini, and L. Ravagli, Phys. Rev. D69, 096004 (2004) [arXiv:hep-ph/0402104];
A. Barducci, R. Casalbuoni, G. Pettini, and L. Ravagli, Phys. Rev. D71, 01601 (2005) [arXiv:hep-ph/0410250];
A. Barducci, R. Casalbuoni, G. Pettini, and L. Ravagli, Phys. Rev. D72, 056002 (2005) [arXiv:hep-ph/0508117];
Lianyi He and Pengfei Zhuang [arXiv:hep-ph/0501024] L. y. He, M. Jin, and P. f. Zhuang, Phys. Rev. D71, 116001 (2005) [arXiv:hep-ph/0503272].
D. Ebert and K. G. Klimenko, Eur. Phys. J. C46, 771 (2006) [arXiv:hep-ph/0510222].
[4] J. B. Kogut, D. K. Sinclair, and D. Toublan, Phys. Lett. B514, 77 (2001);
J. B. Kogut, and D. K. Sinclair, Phys. Rev. D66, 014508 (2002); J. B. Kogut, and D. K. Sinclair, Phys. Rev. D66, 034505 (2002); J. B. Kogut, D. K. Sinclair, and D. Toublan, Nucl. Phys. B642, 181 (2002);
J. B. Kogut, D. K. Sinclair, and D. Toublan, Phys. Rev. D68, 054507 (2003).
[5] J. B. Kogut, Misha A. Stephanov, and D. Toublan, Phys. Lett. B 464, 183 (1999) [arXiv:hep-ph/9906346];
J. B. Kogut, Misha A. Stephanov, D. Toublan, J. J. M. Ver-baarschot, and A. Zhitnitsky, Nucl. Phys. B582, 477 (2000) [arXiv:hep-ph/0001171];
A. Barducci, G. Pettini, L. Ravagli, and R. Casalbuoni, Phys.
Lett. B564, 217 (2003) [arXiV:hep-ph/0304019];
S. Shu and J. R. Li, J. Phys. G 31, 459 (2005) [arXiv:hep-th/0501226]. Zhao Zhang and Yu-xin Liu [arXiv:hep-ph/0603252]
[6] M. Loewe and C. Villavicencio, Phys. Rev. D67, 074034 (2003) [arXiv:hep-ph/0212275].
[7] M. Loewe and C. Villavicencio, Phys. Rev. D70, 074005 (2004) [arXiv:hep-ph/0404232].
[8] M. Loewe and C. Villavicencio, Phys. Rev. D71, 094001 (2005) [arXiv:hep-ph/0501261].