INTERAÇÃO DE VAN DER WAALS NO COMPLEXO HÉLIO- ANTIHIDROGÊNIO A PARTIR DO ESPECTRO ROVIBRACIONAL SANDRO FRANCISCO DE BRITO

(1)

Universidade de Brasília

Instituto de Química

Programa de Pós-Graduação em Química

INTERAÇÃO DE VAN DER WAALS NO COMPLEXO

HÉLIO-ANTIHIDROGÊNIO A PARTIR DO ESPECTRO ROVIBRACIONAL

SANDRO FRANCISCO DE BRITO

Orientador : Prof. Dr. HEIBBE CRISTHIAN B.DE OLIVEIRA

Bras´ılia, DF

(2)

Universidade de Brasília

Instituto de Química

Programa de Pós-Graduação em Química

INTERAÇÃO DE VAN DER WAALS NO COMPLEXO

HÉLIO-ANTIHIDROGÊNIO A PARTIR DO ESPECTRO ROVIBRACIONAL

SANDRO FRANCISCO DE BRITO

Orientador : Prof. Dr. HEIBBE CRISTHIAN B.DE OLIVEIRA

Dissertaç ão apresentada ao programa de p ós-graduç ão do Instituto de Qu´ımica da Universidade de Bras´ılia como requisito parcial para obtenç ão do t´ıtulo de mestre.

(3)

FOLHA DE APROVAÇÃO

Comunicamos a aprovaç ão da Defesa de Dissertaç ão de Mestrado do (a) aluno (a)Sandro

Fran-cisco de Brito, matr´ıcula no_14/0194436_{, intitulada}_{“Interaç ão de van der Waals no complexo H élio}

- Antihidrog ˆenio a partir do espectro rovibracional”, apresentada no (a) Audit ´orio Verde do Instituto de Qu´ımica (IQ) da Universidade de Bras´ılia (UnB) em 27 de julho de 2016.

Prof. Dr. Heibbe Cristhian Benedito de Oliveira Presidente de Banca (IQ/UnB)

Prof. Dr. Clodoaldo Valverde Membro Titular (UEG)

Prof. Dr. Wiliam Ferreira da Cunha Membro Titular (IF/UnB)

Prof. Dr. Luciano Ribeiro Membro Suplente (UnuCET-UEG)

(4)

(5)

Agradecimentos

(6)

Resumo

Nesta dissertaç ão ser ão estudas as propriedades din âmicas entre mat éria e antim áteria, especifi-camente para o sistema h élio-antihidrog ênio, tais propriedades foram calculadas utilizando a curva de energia potencial obtida por Strasburgeret al(2002, Phys. Rev. Lett. 88(16) 163201). Com esse intuito a equaç ão de Schr ödinger nuclear para este sistema foi resolvida numericamente e as suas soluç ões combinadas com soluç ões da equaç ão da energia rovibracional para sistemas diat ômicos. Desta forma foram calculadas pela primeira vez na literatura as constantes espectrosc ópicas ωe, ωexe, ωeye, αe e

γe. Utilizou - se quatro formas anal´ıticas para representar o potencial efetivo: Rydberg, Rydberg

defor-mada, polin ômio em coordenadasBond Ordere Bond Ordemdeformado, todos os potenciais s ão de sexto grau. Foram ajustadas com boa precis ão as curvasab initio, bem como obtivemos valores muito pr óximos para as constantes espectrosc ópicas, independentemente da funç ão utilizada. Observou-se que o sistema h élio-antihidrog ênio possui apenas um único n´ıvel de vibraç ão (ν = 0), com tr ês n´ıveis rovibracionais (J = 0,1 e2) para todas as formas anal´ıticas empregadas no trabalho, indicando que existe uma ligaç ão extremamente fraca que, portanto, s ó faz sentido essa ligaç ão em temperaturas muito baixas. É importante destacar que essas propriedades foram calculadas pela primeira vez na literatura e podem servir de comparaç ão com estudos experimentais futuros acerca das propriedades espectrosc ópicas para o sistema diat ômico h élio-antihidrog ênio.

(7)

Abstract

The matter and antimatter properties of helium with antihydrogen were investigated within Born-Oppenheimer approximation using the potential energy curva calculated by Strasburger et al (2002, Phys. Rev. Lett. 88(16) 163201). We have solved the nuclear Schr ¨odinger equation for this system, combined the solutions with a diatomic rovibrational energy equation and determined for the first time, the spectroscopic constants and rovibrational energies as well. Namely, we have evaluatedωe, ωexe,

ωeye,αeandγe. We used four different analytical forms to represent the effective potential: Rydberg,

deformed Rydberg, Bond Order polynomial and deformed Bond Order. We fitted the ab initio curves accuratelly and the spectroscopic constants values are very close independently of the function used. We found that helium-antihidrogen system has only one bound vibration level(ν = 0) with three rotational levels (j= 0,1and2) for all analytical forms, indicating extremely weak binding and existence would be reasonable only at very low temperatures.

(8)

Lista de S´ımbolos, Abreviaturas e Acr ˆonimos

γe,αe Constantes de acoplamento rovibracional

ωexe Contribuiç ão anarm ônica de primeira ordem

ωeye Contribuiç ão anarm ônica de segunda ordem

cj Coeficientes de expans ˜ao

ωe Contribuiç ão harm ônica

λj Constante de normalizac¸ ˜ao

λ Peso associado a ordem da perturbac¸ ˜ao

~ _{Constante de Planck reduzida}

h Constante de Planck

B Constante de rotac¸ ˜ao caracter´ıstica do sistema

Be Constante rotacinal de equil´ıbrio

Bν Constante rotacinal com correc¸ ˜ao vibracional

ζ Descreve se os potenciais s ˜ao de curto ou longo alcance no potencial de Morse

Tij Elementos da matriz energia cin ´etica

Vij Elementos da matriz dos potenciais

Sij Elementos da matrizoverlap

ˆ

Te(r) Energia cin ´etica dos el ´etrons

ˆ

Tn(R) Energia cin ´etica dos n ´ucleos

De Energia de dissociac¸ ˜ao

ν Frequ ência de radiaç ão

fi(R) Func¸ ˜oes de base conhecidas

φ(r_;R₎ Funç ão de onda eletr ônica

θ(R₎ Func¸ ˜ao de onda nuclear

ψ(r_,R₎ _{Func¸ ˜ao de onda completa}

VBO₍_R₎ _{Func¸ ˜ao de coordenadas}_{Bond Order}

VdBO₍_R₎ _{Func¸ ˜ao de coordenadas}_{Bond Order}_deformada

VRyd₍_R₎ _{Func¸ ˜ao de coordenadas}_Rydberg

VdRyd₍_R₎ _{Func¸ ˜ao de coordenadas}_Rydberg_deformada

F(R₎ Func¸ ˜ao de onda em coordenadas nucleares unidimensionais ˆ

H Hamiltoniano total qu ˆantico

H Hamiltoniano total cl ´assico ˆ

HCM Hamiltoniano do centro de massa

Ym

J (θ, φ) Harm ˆonicos esf ´ericos

ˆ

Hint Hamiltoniano de coordenadas internas

δij Matriz identidade

H Matriz Hamiltoniana

(9)

J N ´umero qu ˆantico rotacional

υ N ´umero qu ˆantico vibracional

ηAB Ordem de ligac¸ ˜ao

ˆ

L Operador momento angular

ρ Par âmetro que denota dist ância entre átomos

d Par âmetro de deformaç ão da funç ão exponencial

wk Pesos associados ao pontoRkna malha de quadraturas

ˆ

Vnn(R) Potencial de interaç ão dos n úcleos

ˆ

Vee(r) Potencial de interaç ão dos el étrons

ˆ

Vne(r,R) Potencial de interaç ão dos n úcleos e el étrons

ˆ

V Termo de perturbac¸ ˜ao

Vm(R) Potencial de Morse

He Atomo de H ´elio´

H Anti-hidrog ˆenio

ABO Aproximac¸ ˜ao de Born-Oppenheimer

CEP Curva de energia potencial

GSA Generelized Simulated Anneling

CERN Organizac¸ ˜ao Europeia para pesquisa Nuclear

F ermilab Fermi Laborat ´orio de Aceleradores Nacional

DV R Representaç ão da Vari ável Discreta

(10)

Lista de Tabelas

3.1 Tabela de par ˆametros otimizados para todas as CEPs do sistemaHe−H. . . 23 3.2 Constantes espectrosc ´opicas rovibracionais para o sistemaHe−H calculadas usando

Eq.(79) atrav és do m étodo DVR. Todos os valores est ão apresentados emcm−1_{. . . .} ₂₆

3.3 N´ıveis de energias rovibracionais para o sistemaHe−H (emcm−1_{) obtidos da soluc¸ ˜ao}

(11)

Lista de Figuras

1.1 Comparaç ão entre a estrutura do átomo de hidrog ênio usual e seu correspondente for-mado por antipart´ıculas, o anti-hidrog ênio . . . 1 1.2 Curva de energia potencial ab initio para o sistema h élio anti-hidrog ênio. Esta curva foi

calculada por Strasburger e Chojnacki . . . 4

2.1 Sistema de coordenadas moleculares para uma estrutura que representa um sistema qualquer. . . 6 2.2 N ´ucleos que representam um sistema de coordenadas fixos. . . 12

3.1 Comparaç ão entre CEP obtida por Strasburgeret ale CEP Ryd6, juntamente com erro ponto-a-ponto do ajuste. . . 23 3.2 Comparaç ão entre CEP obtida por Strasburgeret ale CEP dRyd6, juntamente com erro

ponto-a-ponto do ajuste. . . 24 3.3 Comparac¸ ˜ao entre CEP obtida por Strasburgeret al e CEP BO6, juntamente com erro

ponto-a-ponto do ajuste. . . 24 3.4 Comparac¸ ˜ao entre CEP obtida por Strasburgeret ale CEP dBO6, juntamente com erro

(12)

Sum´ario

Agradecimentos . . . i

Resumo . . . ii

Abstract . . . iii

S´ımbolos Abreviaturas e Acr ˆonimos . . . iv

Lista de Tabelas . . . vi

Lista de Figuras . . . vii

1 Introdução 1 2 Fundamentação Te órica 6 2.1 O Problema Molecular . . . 6

2.2 Formas Anal´ıticas . . . 10

2.2.1 Polin ˆomios em coordenadas Bond Order Generalizada . . . 10

2.2.2 Polin ˆomios em coordenadas f´ısicas de Rydberg . . . 11

2.3 Equaç ão de Schr ödinger Nuclear . . . 11

2.4 M étodo da Representaç ão da Vari ável Discreta . . . 15

2.5 Propriedades Espectrosc ´opicas Rovibracionais . . . 18

2.5.1 Espectro Rotacional . . . 18

2.5.2 Espectro Vibracional . . . 19

2.5.3 Espectro Rovibracional . . . 20

3 Resultados e Discuss ˜oes 22

4 Conclus ˜oes e Perspectivas 31

Referˆencias Bibliogr´aficas 32

(13)

Cap´ıtulo 1

Introduc¸˜ao

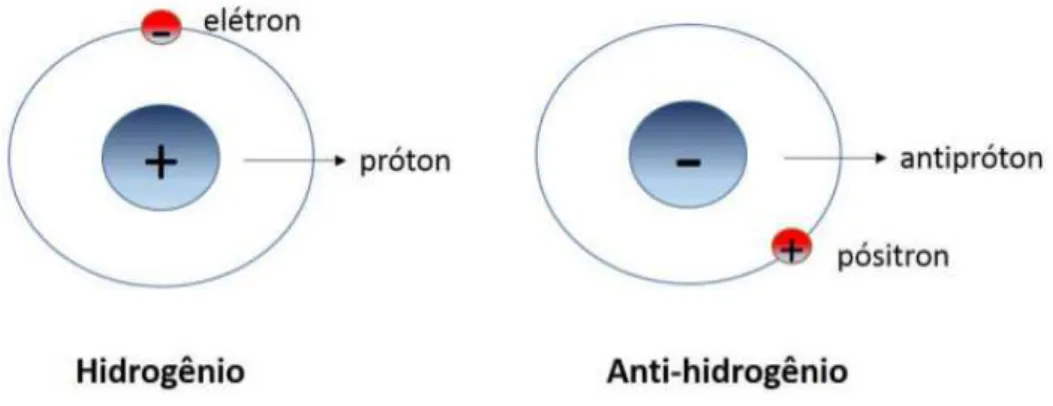
A produç ão artificial de antim áteria no CERN [1] e Fermilab [2] no final da d écada de 1990 atraiu de forma sistem ática o interesse da comunidade cient´ıfica com o intuito de buscar compreender sua natureza ainda misteriosa. A s´ıntese de átomos de antihidrog ênio [3] em 2002 foi uma experi ência que permitiu aos cientistas investigarem de forma mais profunda a interaç ão entre mat éria e antimat éria, sendo esse tema de interesse atual especialmente no que diz respeito ao estudo das diferenças entre ambas, e porque mat éria é t ão mais abundante na natureza do que a antimat éria. O sistema formado por antimat éria mais simples, analogamente aos átomos que estamos habituados a estudar é o átomo de anti-hidrog ênio nos anos recentes muito progresso tem ocorrido nas pesquisas destes sistemas em regimes ultrafinos, como a primeira demonstraç ão de confinamento de anti-hidrog ênio em armadilhas magn éticas [4] e a s´ıntese destes átomos usando a t écnicacusp trap[5]. A estrutura do anti-hidrog ênio é pictoricamente representada na Figura 1.1, em que o n úcleo do sistema possui carga negativa, sendo denominado de antipr óton e no lugar do el étron h á um p ósitron (det ém a massa do el étron por ém com carga positiva).

Figura 1.1: Comparaç ão entre a estrutura do átomo de hidrog ênio usual e seu correspondente formado por antipart´ıculas, anti-hidrog ênio.

(14)

estados mais baixos em que pudessem pemanecer ligados [6]. Este quadro tem se modificado com recentes avanços do ALPHA collaboration reportando o confinamento de átomos de anti-hidrog ênio por mais de 1000 segundos e indicando que a maioria dos átomos confinados alcançavam o estado fundamental [7].

O modelo padr ão da f´ısica de part´ıculas prev ê que o anti-hidrog ênio deve ter os mesmos n´ıveis de energia que o hidrog ênio, sendo que, essa hip ótese basea-se em postulados do Teorema CPT(”conjunç ão de carga”, ”paridade”e ”invers ão de tempo”) [8]. A quebra da teoria CPT est á sendo amplamente es-tudada [9] [10]. Estudos como o de Hori et al [11] bem como os de Kobayashiet al [12] no campo da espectroscopia s ão realizados de forma intensa para verificar quebra de simetria do teorema CPT, isto é, realizar medidas espectrosc ópicas comparando o anti-hidrog ênio com o hidrog ênio. Portanto, observa - se claramente a import ância das previs ões espectrosc ópicas em estudos te óricos acerca da interaç ão entre mat éria e antimat éria que busquem auxiliar na interpretaç ão das medidas experimetais.

Em um trabalho realizado por Strasburger e Chojnacki [13], foi determinado um conjunto de energias eletr ônicas para diferentes dist âncias internucleares em um conjunto de interaç ões entre um átomo de antihidrog ênio (H) com h élio no estado fundamental utilizando a aproximaç ão de Born-Oppenheimer. Levando em consideraç ão a simetria do sistema átomo-anti átomo, bem como os fatores que influenciam a interaç ão neste sistema, usou-se a teoria da perturbaç ão nos estudos realizados pelos autores, pois é uma teoria aplicanda nestes sistemas deste à d êcada de 70 [14].Os autores utilizaram um Hamiltoniano com perturbaç ão de primeira ordem, na seguinte forma:

ˆ

H = ˆH(0)+λV .ˆ (1.1)

A equaç ão (1.1) mostra o termoHˆ(0)_{, que denota o Hamiltoniano n ão perturbado, e}_V_ˆ _representa

o termo de perturbaç ão, usado para corrigir a energia de correlaç ão do sistema (Ecorr), que cont êm

todas as interaç ões interat ômicas, tal que:

ˆ

H(0)= ˆHA+ ˆHB. (1.2)

O potencial de perturbaç ão é completamente explicitado com as seguintes condiç ões; A representa o átomo, B representa o anti- átomo,NA denota o n úmero de el étrons eNB representa o n úmero de

p ósitrons. Ent ão o potencial é dado como:

ˆ

V = ZAZB

R − NA X i=1 ZB riB + NB X j=1 ZA rjA − NA X i=1 NB X j=1 1 rij , (1.3)

em queZAeZB s ão as cargas do sistema. Na representaç ão do potencial foram utilizadas unidades

at ˆomicas.

A energia total do sistema ter ´a a forma:

E=E(0)+λE(1). (1.4)

(15)

proprie-dades dos átomos isolados. A correç ão de primeira ordem(E(1)_{) é dada como,} _E(1) ₌ _h_ψ(0)_|_V_ˆ_|_ψ(0)_i_,

podendo ser facilmente obtida com as funç ões de onda dos átomos isolados, ψA eψB. A funç ão de

onda n ão perturbada n ão necessita de antissimetrizaçao j á que as esp écies s ão distinguiv éis. Assim a componente de trocaE(1) _{n ão estar á presente neste tipo de sistema, sendo semelhante ao produto de}

Hartree.

A funç ão de onda empregada por Strasburger e Chojnacki no trabalho é composta por part´ıculas le-ves, que denotam uma combinaç ão linear de funç ões gaussianas explicitamente correlacionadas como uma aproximaç ão, baseando-se em resultados muito precisos para mat éria ordin ária [15] e sistemas positr ônicos [16]. Para um sistema formado por um conjunto de Npart´ıculas o formato da funç ão de onda é:

ψ=

k

X

I=1

CIAeˆ

PN i=1−α

(I)

i (ri−R(iI)) 2₋PN

i>jβ (I)

ij (ri−rj)_Θ

I. (1.5)

Na funç ão de onda dada pela equaç ão (1.5),Nrepresenta o n úmero de part´ıculas leves do sistema, ˆ

A ´e o operador antissimetrizador, que garante as trocas das part´ıculas indistingu´ıveis do sistema,ΘI ´e

a funç ão de spin, os expoentesα(_iI),β(_ijI)s ão os par âmetros de variaç ão n ão-linear, bem como o termo de coordenadaR(I)

i .

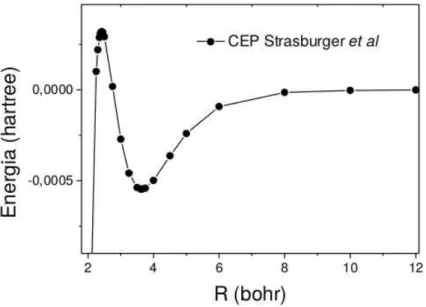
A curva de energia potencial (CEP) no trabalho de Strasburger e Chojnacki foi calculada variacional-mente para o sistema h élio-antihidrog ênio, cuja dist ância de equil´ıbrio ére= 3,63a0. A curva descrita

por Strasburger e Chojnacki possui um m ´aximo em 2,42a0, como representado pela Figura 1.2,

(16)

Figura 1.2: Curva de Energia Potencial ab initio para o sistema h ´elio-antihidrog ˆenio. Esta curva foi calculada por Strasburger e Chojnacki.

Devido à controv érsia sobre a exist ência da barreira de potencial na interaç ão deste sistema, foi in-vestigada no presente trabalho apenas o poss´ıvel estado fracamente ligado do sistema ”diat ômico”He− H, que encontra-se bem localizado no m´ınimo da CEP com propriedades de um sistema de van der Waals. O m´ınimo na curva seria produzido por forças de dispers ão, possibilitando a exist ênica do sis-tema molecular em baixas temperaturas. O objetivo principal deste trabalho é calcular as propriedades rovibracionais dentro do intervalo na CEP de Strasburger e Chojnacki para dist âncias maiores que2,4 bohr (regi ão que caracteriza o poço potencial), é necess ário resolver a equaç ão de Schr ödinger do sis-tema, isto é, estudar o comportamento dos n úcleos e dos el étrons (ou n úcleo antiprot ônico e p ósitron). A CEPab initioobtida por Strasburgeret alfoi ajustada utilizando quatro formas anal´ıticas,Bond Order, Rydberg e suas respectivas vers ões deformadas: d-Bond Order e d-Rydberg, todas de grau 6. Os par âmetros foram ajustados utilizando os m étodo h´ıbridos como Gradiente Simplex [21], Levenberg-Marquardt[22] [23] eGeneralized Simulated Annealing(GSA)[24]. Ap ós a execuç ão dos ajustes, foram avaliadas as constantes espectrosc ópicas rovibracionais relacionadas à contribuiç ão harm ônica (ωe), a

contribuiç ão anarm ônica de primeira ordem(ωeχe) e de segunda ordem (ωeγe) bem como as constantes

de acoplamento rovibracionais (αe, γe) e as energias rovibracionais atrav és das soluç ões da equaç ão de

Schr ödinger nuclear obtidas com o do M étodo da Representaç ão da Vari ável Discreta DVR (do ingl ês

Discrete Variable Representation) [25], [26]. A metodologia aqui empregada consiste na combinaç ão das energias rovibracionais, obtidas atrav és da resoluç ão da equaç ão de Schr ödinger nuclear com uma equaç ão espectrosc ópica (expans ão de Dunham [27]) para energias rovibracionais em sistemas diat ômicos. É importante enfatizar que esta metodologia foi empregada com sucesso na descriç ão es-pectrosc ópica de outros sistemas diat ômicos como o ´ıon molecularH₂+ e a mol éculaCl2em diversos

estados eletr ˆonicos.

(17)

(18)

Cap´ıtulo 2

Fundamentação Te órica

2.1 O Problema Molecular

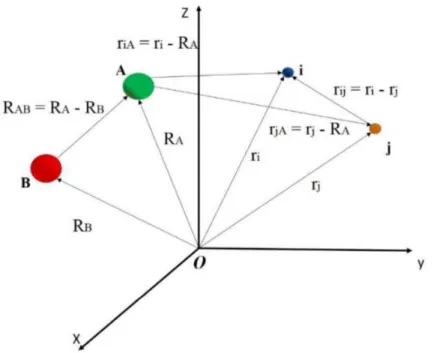
Para descrever a din âmica de um sistema poliat ômico composto porMn úcleos eNel étrons, deve-se levar em consideraç ão a resoluç ão da equaç ão de autovalor de Schr ödinger para o estado estacion ário deste sistema. Considerando um sistema genericamente representado por dois n úcleos e dois el étrons em coordenadas moleculares, como o ilustrado pela Figura 2.1.

Figura 2.1: Sistema de coordenadas moleculares para uma estrutura que representa um sistema qual-quer.

Este sistema de coordenadas moleculares tem como objetivo descrever queriA ´e a dist ˆancia entre

oi- ésimo el étron e oA- ésimo n úcleo,RAB é a dist ância entre oA- ésimo e oB- ésimo n úcleos erij s ão

as dist âncias entre osi- ésimo ej- ésimo el étrons.

(19)

independente do tempo, denotada por:

ˆ

Hψ(r_,R_{) =}_Eψ₍r_,R₎_. (2.1)

onde, ψ(r_,R₎_{representa a funç ão de onda completa, descrevendo as propriedades din âmicas deste} sistema molecular. O operador Hamiltaniano (Hˆ) molecular, n ão-relativ´ıstico e independente do tempo

´e denotado como:

ˆ

H =− ~

2

2me N X i=1 ∇2 i− ~2 2 M X A=1 ∇2 A MA + 1 4πǫ0

M X A=1 M X B>A

ZAZB

RAB

+ 1 4πǫ0

N X i=1 N X j>i e2 rij − 1

4πǫ0

M X A=1 N X i=1

ZAZBe2

riA

, (2.2)

Neste operadorMA é a raz ão entre a massa do n úcleo e a massa do életron,e é a carga elementar

do el étron,ZAeZB s ão as cargas referentes aos n úcleos A e B,~ é dado como a constante de Planck

dividida por2π. Escrevendo o Hamiltoniano em unidades at ˆomicas, teremos:

ˆ

H =−

N

X

i=1

∇2i − M

X

A=1

∇2

A

2MA

+ M X A=1 M X B>A

ZAZB

RAB + N X i=1 N X j>i 1 rij − M X A=1 N X i=1

ZAZB

riA

. (2.3)

Denotando a equaç ão (2.3) de forma mais simplificada em termos da notaç ão de Born-Oppenheimer,

ˆ

H = ˆTe(r) + ˆTn(R) + ˆVnn(R) + ˆVee(r) + ˆVne(r,R), (2.4)

Todos os termos da equaç ão (2.4) em unidades at ômicas, s ão apresentados de forma explicitida como:

Operador energia cin ética dos el étrons:Tê(r) =−₂1PNi=1∇2i.

Operador energia cin ´etica dos n ´ucleos:Tˆn(R) =−PMA=1

∇2_A

2MA. Interaç ão eletrost ática dos n úcleos:Vˆnn(R) =PMA=1

PM

B>AZRAABZB. Interaç ão eletrost ática dos el étrons:Vêe(r) =PNi=1

PN

j>ir1ij.

Interaç ão eletrost ática entre n úcleos e el étrons:Vˆne(r,R) =−PMA=1

PN

i=1 ZrAiAZB.

Explicitamente a equaç ão que deve ser resolvida para demonstrar a din âmica do sistema em estudo é dada por:

" − N X i=1 ∇2 i − M X A=1 ∇2 A

2MA

+ M X A=1 M X B>A

ZAZB

riA

#

ψ(r_,R_{) =}_Eψ₍r_,R₎_. _(2.5)

Em mec ânica qu ântica, em um dos seus teoremas temos a afirmativa que, caso um hamiltoniano seja separ ável sua autofunç ão total pode ser escrita como um produto das autofunç ões individuais para cada termo do hamiltoniano, sendo o autovalor total a soma dos autovalores individuais. Esse teorema por ém n ão pode ser aplicado em tal situaç ão, na resoluç ão da equaç ão (2.5), pois o termo de interaç ão n úcleo el étronVˆne(r,R)impede o desacoplamente dos movimentos nucleares e eletr ônicos, e assim,

(20)

Considerando que a equaç ão (2.5) s ó pode ser resolvida para sistemas monoeletr ônicos, para sis-temas maiores, como o diat ômico, devem ser feitas aproximaç ões para conhecer sua soluç ão. Portanto uma maneira muito utilizada para resoluç ão deste problema encontra-se na aproximaç ão de Born-Oppenheimer (ABO). Essa aproximaç ão leva em consideraç ão a ideia f´ısica de que a massa do pr óton é maior que a massa do el étron e, portanto, um n úcleo movimenta-se mais lentamente que os el étrons.

Sendo assim, os el étrons ajustam seu movimento rapidamente ao movimento dos n úcleos. Logo, usando a expans ão adiab ática, pode-se considerar que variaç ões na funç ão de onda eletr ônica justam-se de maneira quajustam-se instant ânea a mudanças em coordenadas nucleares. Pela expans ão adiab ática a funç ão de onda total pode ser escrita como:

ψ(r_,R_{) =}_φ₍r_;R₎_θ₍R₎_. _(2.6)

Nessa equaç ãoφ(r_;R₎denota a funç ão de onda eletr ônica que depende explicitamente de coorde-nadas eletr ônicas e parametricamente de coordecoorde-nadas nucleares e θ(R₎descreve a funç ão de onda nuclear, que s ó depende de coordenadas nucleares.

A equaç ão (2.5) pode ser reescrista de acordo com a aproximaç ão adiab ática com a seguinte forma:

"

−

N

X

i=1

∇2i − M

X

A=1

∇2

A

2MA

+ M X A=1 M X B>A

ZAZB

riA

#

φ(r_;R₎_θ₍R_{) =}_Eφ₍r_;R₎_θ₍R₎_. (2.7)

Distribuindo os termos, obtemos:

−

N

X

i=1

∇2i[φ(r;R)θ(R)]− M

X

A=1

∇2

A[φ(r;R)θ(R)]

2MA

+ M X A=1 M X B>A

ZAZB

RAB

[φ(r_;R₎_θ₍R_)]+

+ N X i=1 N X j>i

φ(r_;R₎_θ₍R₎

rij − M X A=1 N X i=1

ZAZB

riA

φ(r_;R₎_θ₍R_{) =}_Eφ₍r_;R₎_θ₍R₎_, (2.8)

´

E necess ário explicitar o laplaciano em coordenadas nucleares na equaç ão (2.8), para obter a se-guinte relaç ão:

∇2A[φ(r;R)θ(R)] = (∇2Aφ(r;R)θ(R) + 2∇Aφ(r;R)∇Aθ(R) +φ(r;R)(∇2Aθ(R)), (2.9)

Pode-se considerar fisicamente que a funç ão de onda eletr ônica sofre variaç ões adiab áticas em relaç ão a coordenada nuclear (R). Portanto: ∇2Aφ(r;R) ≈ 0 e ∇Aφ(r;R)∇Aθ(R) ≈ 0. Logo, a

aproximaç ão de Born-Oppenheimer (ABO) é considerada da seguinte forma:

∇2A[φ(r;R)θ(R)]≈φ(r;R)(∇2Aθ(R)), (2.10)

(21)

de coordenadas eletr ônicas e param êtricas de coordenadas nucleares e assim dividindo toda equaç ão porφ(r_;R₎_θ₍R_{), obtem-se:}

− 1

2φ(r_;R₎

N

X

i=1

∇2_iφ(r_;R₎₋ 1

θ(R₎

M

X

A=1

∇2

Aθ(R)

2MA

+ M X A=1 M X B>A

ZAZB

RAB + N X i=1 N X j>i 1 rij − M X A=1 N X i=1 ZA riA

=E, (2.11)

Rearranjando a equac¸ ˜ao (2.11), obtemos:

− 1

θ(R₎

M

X

A=1

∇2

Aθ(R)

2MA

+ M X A=1 M X B>A

ZAZB

RAB

−E= 1

2φ(r_;R₎

N

X

i=1

∇2

iφ(r;R)+ M X A=1 N X i=1 ZA riA − N X i=1 N X j>i 1 rij . (2.12)

A igualdade torna-se verdadeira quando os dois lados da equaç ão s ão uma constante que depen-dam de R. Definiremos essa constante como−ε(R).

Desta forma, s ão obtidas duas equaç ões desacopladas, que s ão:

− 1

θ(R₎

M

X

A=1

∇2

Aθ(R)

2MA

+ M X A=1 M X B>A

ZAZB

RAB

−E=−ε(R), (2.13)

e

1 2φ(r_;R₎

N

X

i=1

∇2iφ(r;R) + M X A=1 N X i=1 ZA riA − N X i=1 N X j>i 1 rij

=−ε(R). (2.14)

Multiplicando a equaç ão (2.13) porθ(R₎e a equaç ão (2.14) por−φ(r_;R_{), tem-se que:}

" −1 2 M X A=1 ∇2

Aθ(R)

MA + M X A=1 M X B>A

ZAZB

RAB

−E

#

θ(R_{) =}₋_ε₍_R₎_θ₍R₎_, (2.15)

e " −1 2 N X i=1

∇2iφ(r;R)− M X A=1 N X i=1 ZA riA + N X i=1 N X j>i 1 rij #

φ(r_;R_{) =}_ε₍_R₎_φ₍r_;R₎_. (2.16)

Rearranjando a equac¸ ˜ao (2.15), encontramos:

" −1 2 M X A=1

∇2Aθ(R)

MA + M X A=1 M X B>A

ZAZB

RAB

+ε(R)

#

θ(R_{) =}_Eθ₍R₎_, _(2.17)

onde chama-se a soma abaixo de ”curva de energia potencial”, curva que descreve como os n úcleos se movem sob a aç ão de um campo produzido por el étrons.

V(R) =

M X A=1 M X B>A

ZAZB

RAB

+ε(R). (2.18)

" −1 2 M X A=1 ∇2

Aθ(R)

MA

+V(R)

#

(22)

Observando a equaç ão (2.16), desacopla-se o movimento eletr ônico do movimento nuclear utili-zando a ABO, sendo esta equaç ão definida como equaç ão de Schr ödinger eletr ônica estacion ária o seu conjunto de soluç ões fornece as energias eletr ônicas para cada configuraç ão nuclear. O evento ex-traordin ário que devemos notar é o fato do conjunto de autovalores dados pela equaç ão de Schrodinger eletr ônica, ou seja, suas energiasε(R)serem usados para calcular a equaç ão de autovalores nuclear (2.17), esta equaç ão descreve os movimentos de rotaç ão, vibraç ão e translaç ão.

2.2 Formas Anal´ıticas

Na construç ão do trabalho foram utilizadas quatro funç ões anal´ıticas para descrever a curva ab initiopara o sistemaHe−H, de tal forma que essas curvas descrevam um ajuste com o menor erro poss´ıvel na obtenç ão das propriedades de interesse. As curvas s ão: Bond Order de grau 6, Rydberg generalizada de grau 6 e suas correspondentes formas deformadas de mesmo grau.

2.2.1 Polin ˆomios em coordenadas Bond Order Generalizada

O conceito de ordem de ligaç ão (BO) fora introduzido em estudos te óricos pelo qu´ımico Linus Pauling, ajustando esse conceito como um par âmetro para classificar a força de ligaç ão de sistemas diat ômicos, sendo ent ão a ordem de ligaç ão dessas estruturas representadas, como:

ηAB =e

−βAB(R−Re)_ρ, _(2.20)

em que:

ρ= (RAB−Re). (2.21)

A coordenadaRABdenota a dist ância entre o átomo A e B, comResendo a dist ância de equil´ıbrio e

βABum par âmetro que relaciona a força de interaç ão entre os átomos da estrutura diat ômica. Tomando

essa definiç ão quando a dist ância de equil´ıbrio é igual a separaç ão entre os átomos, ou seja,RAB =

Re, a ordem da ligaç ão torna-se igual a unidade, assim ηAB = 1. Se separarmos os átomos que

participam da ligaç ão com uma dist ância que tenda ao infinito, a ordem da ligaç ão tender á a zero, caso os átomos se aproximem, a ordem da ligaç ão ir á aumentar at é o limite estabelecido pela relaç ão;

e−_β_AB₍_R−_R_e₎

ρ. Portanto as interaç ões at ômicas que s ão descritas pelo modeloBond Order encontram-se em um intervalo que varia de zero at é o valor limite dee−_β_AB(R−_R_e)_ρ

A funç ão de coordenadas Bond Order é definida como uma combinaç ão linear de exponenciais, denotadas como:

VBO₍_R_{) =} N

X

j=1

cjηj (2.22)

(23)

separaç ão interat ômica que leva a uma condiç ão de equil´ıbrio.

Adicionadamente, foi utilizada no ajuste da CEP a func¸ ˜ao anal´ıtica deformada das coordenadas BO deformadas (dBO) de grau 6, dada como:

VdBO₍_R_{) =}

6

X

i=1

ci(expd(−βρ))i, (2.23)

em que

expd(−βρ) = [1−dβρ]

1

d. (2.24)

A equaç ão (2.24) representa a funç ão d-exponencial, uma generalizaç ão da funç ão exponencial convencional de acordo com a definiç ão de Euler baseada na termo-estat´ıstica de Tsallis. No caso particular em que d aproxima-se de zero a funç ão exponencial de Euler é recuperada. O polin ômio

Bond Order é de grau 6, eρ= (R−Re),ci,β e d s ão par âmetros ajust áveis.

2.2.2 Polin ˆomios em coordenadas f´ısicas de Rydberg

Neste trabalho utilizou-se para descrever uma CEP a funç ão de Rydberg, que é denotada explicita-mente na forma:

VRyd₍_R_{) =}₋_D e " 1 + 6 X i=1

ci(R−Re)i

#

e−_c_i₍_R−_R_e₎

. (2.25)

O potencial (2.25) denotaDecomo a energia de dissociaç ão do um sistema diat ômico, ci s ão os

coeficientes ajust áveis, R é denota a separaç ão intermolecular eRe é a separaç ão de equil´ıbrio

(com-primentos de ligaç ão). A forma deformada deste potencial, a funç ão d-Rydberg, é mostrada como:

VdRyd₍_R_{) =}₋_D e " 1 + 6 X i=1

ci(R−Re)i

#

[1−dc1(R−Re)]

1

d. (2.26)

Todos os par ˆametros foram ajustados utilizando os m ´etodos GSA [24], Gradiente Simples [28] e Levenberg Marquardt [22] [23].

2.3 Equação de Schr ödinger Nuclear

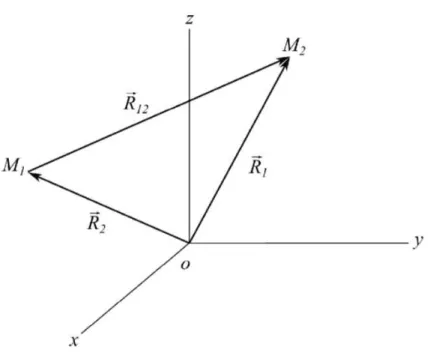
Considerando o m étodo utilizado para se resolver a parte nuclear da equaç ão de Schr ödinger em um sistema gen érico como o representado pela Figura 2.2, em queM1eM2representam as massas

nucleares em suas respectivas posiç õesR₁ R₂_{, dado um refer ência fixa. J á} R₁₂_{denota a dist ância} entre os n úcleos 1 e 2.

(24)

Figura 2.2: N ´ucleos que representam um sistema de coordenadas fixos.

realizado se dedica a descever um sistema de dois corpos e o Hamiltoniano cl ´assico desse sistema pode ser escrito como:

H = 1

2M1

P₁P₁₊ 1 2M2

P₂P₂₊_V₍R₎_. (2.27)

O operador acima descreve as energias cin éticas dos n úcleos 1 e 2, respectivamente, e V(R₎ denota a interaç ão dos dois n úcleos. Buscando tornar o sistema com resoluç ão mais simples, é poss´ıvel escrever as energias cin éticas em termos da posiç ão do centro de massa e a posiç ão do n úcleo 2 em relaç ão ao n úcleo 1, tal como:

R_CM₌ M1R1+M2R2

M1+M2

, (2.28)

e

R₁₂₌R₂₋R₁_. (2.29)

Considerando a relaç ão do momento linear, substituindo as relaç ões (2.28) e (2.29) em (2.27) o operador Hamiltoniano cl ássico em funç ão das coordenadas do centro de massa, e tomando as cor-respond ências entre as vari áveis que descrevem a din âmica de um sistema na mec ânica cl ássica e os operadores hermitianos na mec ânica qu ântica a nova relaç ão ser á representada por:

ˆ

H =− 1 2M∇

2

CM−

1 2µ∇

2

12+V(R12). (2.30)

Ap ós realizadas um conjunto de operaç ões, nota-se que surge naturalmente a massa reduzida do sistema formado por dois corposµ= M1M2

M1+M2

(25)

funç ão do centro de massa e da dist ância relativa entre os n úcleos, de forma que pode-se definir.

ˆ

HCM ≡ −

1 2M∇

2

CM,

ˆ

Hint≡ −

1 2µ∇

2

12+V(R).

O Hamiltoniano do centro de massa (HˆCM) descreve o movimento de translac¸ ˜ao, enquanto que o

Hamiltoniano de coordenadas internas (Hînt) indica os movimentos de vibraç ão e rotaç ão no n úcleo.

A equaç ão de Schr ödinger que leva em consideraç ão os Hamiltonianos do centro de massa e dos movimentos de coordenadas internas é dada por:

[ ˆHCM+ ˆHint]θ(RCM,R) =Eθ(RCM,R). (2.31)

Assim, pela equaç ão (2.31) pode-se notar claramente que essa equaç ão é separ ável, e por esse argumento existe uma soluç ão do tipo,θ(R_CM_,R_{) =}_η₍R_CM₎_ϕ₍R_{). Com a utilizaç ão da separaç ão de} vari áveis obt êm-se duas equaç ões desacopladas:

ˆ

HCMη(RCM) =−

1 2M∇

2

CMη(RCM) =Etransη(RCM), (2.32)

e

ˆ

Hintϕ(R) =

− 1

2µ∇

2

12+V(R)

ϕ(R_{) =}_E_int_ϕ₍R₎_. _(2.33) A equaç ão (2.33) é a equaç ão de Schr ödinger para uma part´ıcula livre cujas soluç ões dependem das condiç ões de contorno e descreve o movimento de translaç ão do sistema diat ômico regido pela posiç ão do centro de massa. Supondo que este sistema n ão esteja sujeito a forças externas, pode-se considerar queEtrans= 0. Assim, a energia total ser á obtida exclusivamente pela equaç ão (2.33) que descreve os

movimentos de vibraç ão e rotaç ão. O potencialV(R₎em (2.33) é dito de força central, isto é, depende apenas das dist âncias entre as part´ıculas interagentes de modo que é invariante à orientaç ão espacial a qual o di átomo encontra-se, tendo portanto simetria esf érica. A simetria do potencial indica que deve-se modificar o sistema de coordenadas do laplaciano∇2

12para coordenadas esf ´ericas, reescrevendo a

equaç ão (2.33), obtemos a seguinte equaç ão:

− 1

2µ

"

∂2

∂R2 +

2 R

∂ ∂R−

ˆ

L2

R2 −2µV(R)

#

ϕ(R_{) =}_E_int_ϕ₍R₎_, _(2.34)

em queLˆ2 é o operador momento angular ao quadrado. Pela equaç ão (2.34) pode-se observar que a vibraç ão e a rotaç ão est ão desacopladas, de forma que podemos separar a funç ão de onda em que a parte radial que est á em funç ão de (R) e outra parte, angular, que est á em funç ão de (θ eφ). Logo, podemos escrever a funç ãoϕ(R₎como o produto de duas funç ões na forma:

ϕ(R_{) =}_ψ₍R₎_Ym

(26)

reconhecendo que,

ˆ

L2Ym

J (θ, φ) =J(J+ 1)YJm(θ, φ). (2.36)

A func¸ ˜aoYm

J (θ, φ)na equaç ão (2.36) denota os harm ônicos esf éricos, e a partir das equaç ões (2.35)

e (2.36), pode-se expressar a equaç ão de Schr ödinger nuclear unidimensional, como segue:

− 1

2µ

d2_ψ₍_R₎

dR2 +

2 R

dR

dR−

J(J+ 1)ψ(R₎

R2 −2µV(R)ψ(R)

=Eintψ(R). (2.37)

Buscando denotar uma simplificaç ão para equaç ão de Schr ödinger nuclear unidimensional, faremos a seguinte substituiç ão: F(R_{) =}R_ψ₍R_{), e finalmente chega-se a relaç ão:}

− 1

2µ

d2_F₍_R₎

dR2 +

_J₍_J_{+ 1)}

2µR2 +V(R)

F(R_{) =}_E_int_F₍R₎_, (2.38) ou

− 1

2µ

d2_F₍_R₎

dR2 +Vef(R)F(R) =EintF(R). (2.39)

O potencial efetivoVef(R) = J₂(_µJR+1)2 +V(R)formado pela curva de energia potencial unidimensi-onal e da correç ão de distorç ão centr´ıfuga determinada pelo estado rotaciunidimensi-onal. A equaç ão (2.39) é a equaç ão de Schr ödinger nuclear radial na qual o sistemaHe−H se reduziu e que deve ser resolvida para determinarmos completamente a funç ão de onda nuclear. A equaç ão (2.39) n ão possui soluç ão anal´ıtica, logo, é necess ário utilizar m étodos de aproximaç ão para denotar uma soluç ão, e para propor soluç ões usaremos o m étodo de Rayleigh-Ritz.

O m étodo variacional de Rayleigh-Ritz é aplicado para determinar o valor esperado de observ áveis f´ısicas no contexto da mec ânica qu ântica. Uma forma de caracterizar o m étodo de maneira breve, é multiplicar a equaç ão (2.38) porF∗

(R₎e integra-se em todo espaço acess´ıvel ao sistema aplicando as condiç ões de contorno. Em seguida, aproximamos a funç ão de onda exataF(R₎por funç ões conheci-das, isto é, fazemos uma combinaç ão linear denfunç ões de base conhecidas,fi(R):

F(R_{) =}

n

X

j=1

cjfi(R), (2.40)

sendo oscj o conjunto de coeficientes da expans ˜ao a serem determinados. Com este procedimento

troca - se o problema de se determinar quais funç ões F(R₎satisfazem a equaç ão diferencial de se-gunda ordem com coeficientes vari áveis, equaç ão (2.39), por um problema de encontrar um conjunto de coeficientescj, que denota a resoluç ão de um problema alg ébrico. A partir desse m étodo pode-se

resolver o problema tranformando a (2.39) por uma equac¸ ˜ao matricial, tal que:

Hc₌ESc_. (2.41)

(27)

autovalores ece matriz coluna dos coeficientes. Os elementos destas matrizes sao dados por:

Tij =

1 2µ

Z ∞

0

Z ∞

0

df∗

i(R)

dR

dfi(R)

dR dR, (2.42)

Vij =

Z ∞

0

f∗

i(R)Vef(R)fi(R)dR, (2.43)

e

Sij=

Z ∞

0

f∗

i(R)(R)fi(R)dR. (2.44)

Neste trabalho, cada elemento deHser á numericamente avaliado atrav és do M édoto da Representaç ão da Vari ável Discreta (DVR). Utilizando-se funç ões de bases ortonormais de modo queS₌I_{, ser á a} ma-triz identidade, isto éSij=δij.

2.4 Método da Representação da Variável Discreta

O m étodo DVR, que teve como um de seus pioneiros Light et al [29], se apresenta como uma ferramenta extremamente poderosa para resolver problemas qu ânticos tanto para estados estacion ários como para estados dependentes do tempo. Neste trabalho, o m étodo DVR foi aplicado na obtenç ão dos autovalores e autofunç ões da equaç ão de Schr ödinger radial satisfazendo o princ´ıpio variacional. O m étodo DVR é baseado na expans ão da funç ão de onda em um conjunto de bases ortonormaisφi(Ri);

i= 1,2, ..., Ne a utilizaç ão de regras de quadraturas gaussianas para computar as integrais envolvidas [30]. Estas funç ões de base tem a seguinte propriedade:

φj(Rk) =δjk(j, k= 1,2, ..., n), (2.45)

As funç ões de base cont´ınuas s ão indexadas em valores discretos das vari áveis em um grade de pontos no espaço com coordenadasRk (quadratura gaussiana). Sendo queRk representa os pontos

da quadratura gaussiana em que as funç ões de base ser ão avaliadas. Caso seja expandida a soluç ão

F(R_i₎como uma combinaç ão de funç ões de baseφi(R), logo:

F(R₎_≈

N

X

j=1

cjφj(R), (2.46)

ondecjs ão os coeficientes da expans ão a serem determinados, e as funç ões representam a discretizaç ão

da vari ´avelR.

Portanto as funç ões discretizadas s ão obtidas a partir de um conjunto de funç ões cont´ınuas primiti-vas, que s ão conhecidas, associando a estas uma quadratura gaussiana.

Pode-se escreverφj(R)como a projeç ão deφjsobreRna notaç ão de Dirac:

(28)

inserindo a relac¸ ˜ao de completeza, dada por:

n

X

i=1

|iihi|= 1, (2.48)

na equac¸ao (2.47), obt ˆem-se:

φj(R) = n

X

i=1

hR|fiihfi|φji, (2.49)

As integrais dos elementos da matrizhfi|φjipodem ser calculadas utilizando quadraturas

gaussia-nas,

hfi|φji ≈ n

X

k=1

wkf

∗

i(Rk)φj(Rk), (2.50)

em que wk s ˜ao os pesos associados ao pontoRk na malha de quadraturas. Substituindo (2.50) em

(2.51), obt ˆem - se:

φj(R) = n X i=1 n X k=1

fi(R)wkf

∗

i(Rk)φj(Rk). (2.51)

Como as funç ões de baseφj(Rk)s ão ortogonais, ent ão:

φj(R) =wj n

X

i=1

fi(Rk)f

∗

i(Rk), (2.52)

Assim, escolhendo um pontoR_jqualquer dentro da malha das quadraturas, teremos que:

φj(Rj) =wj n

X

i=1

fi(Rk)f

∗

i(Rk), (2.53)

Considerando que as funç ões de base escolhidas est ão normalizadas podemos afirmar que:

n

X

i=1

fi(Rj)f

∗

i(Rj) = 1, (2.54)

de modo que o peso associado `a cada ponto da quadratura ´e:

wj=

1

Pn

i=1fi(Rj)fi∗(Rj)

. (2.55)

No entanto, as funç ões de base n ão est ão normalizadas e, portanto, ser á mecess ário normaliz á -las, expressando a seguinte substituiç ão, por:

¯

φj(R) =λjφj(R), (2.56)

em que λj é a constante de normalizaç ão de modo que hφ¯j|φ¯ji = 1, ou melhor, λj2hφ¯j|φ¯ji = 1.

(29)

λ2j n

X

i=1

wkφ

∗

j(Rk)φj(Rk) = 1. (2.57)

De acordo com a equaç ão (2.45) as funç ões primitivas s ão ortonormais, assim poderemos conside-rar que (2.57) ser á:

λ2jwj= 1, (2.58)

ou

λj=

1

w12

j

. (2.59)

Substituindo a constante de normalizaç ão, equaç ão (2.59) conjuntamente com a equaç ão (2.52) na equaç ão (2.56), obteremos a funç ão de base discreta e normalizadaφ¯j(R):

¯

φj(Rj) =wj

1 2

n

X

i=1

fi(Rk)f

∗

i(Rk), (2.60)

Desta maneira o conjunto que descreve a soluç ão da equaç ão de Schr ödinger na equaç ão (2.46) utilizando as funç ões de bases discretizadas (2.60) é denotado como:

F(R₎_≈

n

X

j=1

cjφ¯j(Rj), (2.61)

Substituindo (2.61) em (2.43), e utilizando os conceitos de quadratura gaussiana, teremos a seguinte equac¸ ˜ao:

Vij= n

X

k=1

φ∗

i(Rk)Vef(Rk)φ

∗

j(Rk)wk, (2.62)

ondeφ∗

j(Rk) =δjk. Portanto a matriz energia potencialVtorna-se diagonal sendo este resultado uma

das principais caracter´ısticas do m étodo DVR. Sendo ent ão R_k _{os pontos da quadratura gaussianan} que s ão os valores esperados da matriz composta pelos elementos:

Rij =hfi|Rˆ|φji. (2.63)

A matriz energia cin ética T _{pode ser calulada atrav és de quadraturas gaussianas com um} con-junto de pontos igualmente espaçados, tomando esses pontos pertencentes a um certo intervalo [a,b], teremos que:

Ri=a+

b−a

N i, (2.64)

(30)

Tij= N−₁

X

n=1

hRi|Tˆ|fnihfn|Rii. (2.65)

Considerando a soma anal´ıtica sobre todos os ´ındices n, os elementos ser ˜ao:

Tij =

1 2µ

1 (b−a)2

π2

2

 

1

sin2hπ(j−_k) 2N

i−

1

sin2hπ(j+k) 2N

i 

, (2.66)

parai6=j, e:

Tij=

1 2µ

1 (b−a)2

π2

2 2N2

3 − 1

sin2_πi

N

!

, (2.67)

parai=j. Portanto o DVR diagonaliza o potencial da matriz hamiltoniana, e permite que os elemen-tos da matriz de energia cin ética sejam obtidos analiticamente por express ões simples dadas pelas equaç ões (2.66) e (2.67).

2.5 Propriedades Espectrosc ´opicas Rovibracionais

Vimos anteriormente que a equaç ão de Schr ödinger é separada em uma parte eletr ônica e ou-tra nuclear por meio da aproximaç ão de Born-Oppenheimer e que est á última pode ser largamente simplificada para sistemas diat ômicos. Nesta simplificaç ão conseguimos desacoplar o movimento translacional regido pelo centro de massa, dos movimentos internos. Os movimentos internos, por sua vez, s ão descritos pela vibraç ão e rotaç ão do sistema de dois corpos. Usualmente utilizam-se duas aproximaç ões para tratar estes movimentos, s ão elas: aproximaç ão do oscilador harm ônico para vibraç ões, e aproximaç ão do rotor r´ıgido para rotaç ões. Experimentalmente estas aproximaç ões justificam-se ao observar que o espectro rotacional encontra-se em geral na regi ão de micro-ondas e o espectro vibracional na regi ão do infravermelho [32].

2.5.1 Espectro Rotacional

A rotaç ão de sistemas diat ômicos pode ser aproximada por um sistema ideal denominado ro-tor r´ıgido, a qual assume que a revoluç ão de uma mol écula de massa reduzida µ ocorre com uma separaç ão internuclear fixa igual à dist ância de equil´ıbrioRe. Quando se resolve a equaç ão de Schr

¨odin-ger para um rotor r´ıgido as energias permitidas nesse tipo de sistema s ˜ao denotadas da seguinte forma:

EJ =~2

J(J+ 1)

2I , (2.68)

em que, J = 0,1,2, ..., p e I = µRe2 é o momento de in ércia do sistema denotado. A diferença de

energia entre dois n´ıveis rotacionais ´e dada por:

(31)

ou

∆E= h

2

4π2_I(J+ 1). (2.70)

Levando em conta os termos de frequ ência, atrav és da condiç ão de frequ ência de Bohr∆E =hν, teremos:

ν= 2B(J+ 1), (2.71)

em queB =h/8π2_I _{´e a constante rotacional caracter´ıstica do sistema em estudo. De acordo com a}

equaç ão (2.71) nota-se que o modelo de um rotor r´ıgido para sistemas diat ômicos prev ê que o espec-tro rotacional consiste em uma s érie de linhas igualmente espaçadas com separaç ões2B cm−1 _[33].

Contudo, em sistemas caracterizados por serem diat ômicos n ão s ão verdadeiramente um rotor r´ıgido devido vibraç ões simult âneas, ainda que de pequena amplitude. Consequentimente o espaçamento das linhas espectrais de rotaç ão n ão ser ão exatamente constantes.

2.5.2 Espectro Vibracional

O modelo vibracional de um sistema diat ômico poder á ser aproximado pelo modelo do oscilador harm ônico qu ântico. As soluç ões permitidas das equaç ão de Schr ödinger para o oscilador harm ônico s ão restringidas a valores discretos dados por:

Eυ=hc

υ+1 2

ωe, (2.72)

em queυ= 0,1,2,3, ..., peωe é a frequ ência vibracional fundamental. A diferença de energia entre dois

n´ıveis adjacentes ´e dada como:

∆E=Eυ+1−Eυ, (2.73)

ou

∆E=hcωe. (2.74)

Como

os sucessivos estados de energia do oscilador harm ônico s ão separados pela mesma energia, este modelo prediz que o espectro vibracional consiste em apenas uma linha espectral cuja frequ ência é dada porωe. Esta aproximaç ão s ó é v álida nos estados vibracionais mais baixos, pois para dist âncias

internucleares fora da separaç ão de equil´ıbrio, o espaçamento entre os n´ıveis se aproxima cada vez mais devido à anarmonicidade da curva de energia potencial.

(32)

Vm(R) =De(1−e

−_ζ(R−_R_e)₎2_, _(2.75)

em queDedenota a energia de dissociaç ão eζdetermina se o potencial é de curto ou de longo alcance.

Fazendo uma expans ão em s érie de Taylor, o termo exponencial da equaç ão (2.75) em torno deR=Re

e utilizando uma aproximac¸ ˜ao em primeira ordem, obtemos:

Vm(R) =Deζ2(R−Re)2. (2.76)

Utilizando esse potencial na equaç ão de Schr ödinger para o oscilador harm ônico, obteremos os seguintes autovalores emcm−1_:

Eυ=

υ+1 2

ωe−

υ+1 2

2

ωeχe+

υ+1 2

3

ωeγe+... (2.77)

em queωeχeeωeγes ão denotadas de constantes anarm ônicas de vibraç ão do sistema diat ômico. Com

essa correç ão o espaçamento entre os n´ıveis diminui quando os estados vibracionais est ão mais ele-vados. Para estados vibracionais pr óximos da dist ância de equil´ıbrio, o espaçamento é muito pr óximo aos descritos pela equaç ão (2.74), j á que as correç ões anarm ônicas s ão pequenas se comparadas à

ωe.

2.5.3 Espectro Rovibracional

As aproximaç ões descritas pelo oscilador harm ônico qu ântico e rotor r´ıgido, permitem tratar o pro-blema dos movimentos internos separadamente. No entanto, os movimentos vibracionais e rotacionais n ão ocorrem de maneira independente, dando origem a uma estrutura fina nas bandas vibracionais.

Se os movimentos est ão acoplados uma maneira mais simples para estudar o espectro rovibracional seria utilizar o modelo do oscilador harm ônico conjuntamente com o modelo do rotor r´ıgido, conside-rando que o hamiltoniano do sistema diat ônico é composto pelas duas contribuiç ões, ou seja:

ˆ

Hrov= ˆHvib+ ˆHrot. (2.78)

Pela equaç ão (2.78), tem-se que os autovalores descritos pelo hamiltoniano rovibracional s ão a soma dos autovalores individuais de cada hamiltoniano separado, o que pode-se denotar como:

Erov(υ, J) =

υ+1 2

ωe+J(J+ 1)Be, (2.79)

em queBe=~2/2hcIe ´e a constante rotacional de equil´ıbrio. O acoplamento rovibracional surge quando

o sistema encontra-se em rotaç ão, por ém a dist ância internuclearR−Resofre flutuaç ões que dependem

da funç ão de onda vibracional e do n úmero qu ânticoυ. PortantoBepossui uma depend ência deυque

pode ser expressa como uma perturbac¸ ˜ao, que quando expandida em torno de υ+1₂

, obtemos:

Bυ=Be−

υ+1 2

αe+

υ+1 2

2

(33)

em queBυ é a correç ão vibracional da constante rotacional,αeeγes ão denominadas constantes de

acoplamento rovibracionais [34].

A energia rovibracional de um determinado n´ıvel(υ, J), deve levar em consideraç ão todas as contribuiç ões vibracionais (harm ônicas e anarm ônicas) e rotacionais(r´ıgidas e n ão r´ıgida). A nova relaç ão que deve ser escrita para expressar todas as contribuiç ões, é dada como:

Eυ,J =

υ+1 2

ωe−

υ+1 2

2

ωeχe+

υ+1 2

3

ωeγe+...

+

"

Be−

υ+1 2

αe+

υ+1 2

2

γe+...

#

J(J+ 1) +... (2.81)

Nesta dissertaç ão, as constantes espectrosc ópicas foram calculadas combinando as energias rovi-bracionaisEυ,J obtidas apartir da soluç ão da equaç ão de Schr ödinger nuclear com a equaç ão (2.81).

Desta combinaç ão, é obtido um sistema de equaç ões fechadas para constantes espectrosc ópicas,tal como:

ωe=

1

24[14(E1,0−E0,0)−93(E2,0−E0,0) + 23(E3,0−E1,0)]

ωeχe=

1

4[13(E1,0−E0,0)−11(E2,0−E0,0) + 3(E3,0−E1,0)]

ωeγe=

1

6[3(E1,0−E0,0)−3(E2,0−E0,0) + 3(E3,0−E1,0)] (2.82)

αe=

1

8[−12(E1,1−E0,1) + 4(E2,1−E0,1) + 4ωe−23αe]

γe=

1

(34)

Cap´ıtulo 3

Resultados e Discuss ˜oes

Nesta seç ão ser ão apresentados os resultados das propriedades din âmicas do sistemaHe−H, cu-jas energias lept ônicas (el étron e p ósitron) foram obtidas por Strasburger e Chojnacki [13]. Os autores calcularam um conjunto de energias lept ônicas para diferentes dist âncias internucleares para interaç ão

He−H utilizando a aproximaç ão de Born-Oppenheimer. Esse trabalho os autores utilizaram como funç ão de onda para part´ıculas leves uma combinaç ão linear de funç ões gaussianas explicitamente correlacionadas como uma aproximaç ão, baseando-se em resultados muito precisos para mat éria or-din ária [15] e sistemas positr ônicos [16] . No trabalho de Strasburger e Chojnacki foi calculada variaci-onalmente a CEP, para o sistemaHe−H cuja dist ância de equil´ıbrio ére= 3,63a0. Na Figura 1.2 foi

apresentada a CEP obtida pelos autores mostrando um barreira na regi ão repulsiva da CEP. Segundo os autores, este m áximo poderia ser explicado pela leve predomin ância da repuls ão eletrost ática entre o átomo e o anti- átomo perante às forças atrativas. Em [13] Strasburgeret alchamou a atenç ão para a possibilidade de existir um estado fracamente ligado na regi ão pr óxima a 3.64a0 e que se trata de

um estado excitado para este sistema e que a relaxaç ão seria suprimida pela barreira na CEP. Conse-quentemente, esta barreira diminuiria a taxa de aniquilaç ão el étron-p ósitron de modo que este sistema pode apresentar um tempo de vida relativamente longo para ser detectado. De fato, esta possibilidade pode ser bem razo ável quando se observa que nos experimentos de geraç ão e aprisionamento de an-tihidrog ênio (H), estes est ão imersos em um ambiente de h élio l´ıquido ultraresfriado e que um fator limitante ao tempo de vida dos anti- átomos est á nas colis ões com gases formados por átomos usuais, como o h élio.

O interesse deste trabalho é investigar as propriedades din âmicas do sistemaHe−H, na regi ão da CEP que viabiliza a exist ência de um poss´ıvel estado ligado. Para isto, constru´ımos o potencial efetivo da equaç ão de Schr ödinger nuclear (2.39) ajustando a CEP ab initio de Strasburger et alutilizando quatro diferentes formas anal´ıticas:Bond Order(BO), d-Bond Order(dBO),Rydberg(Ryd) e d-Rydberg

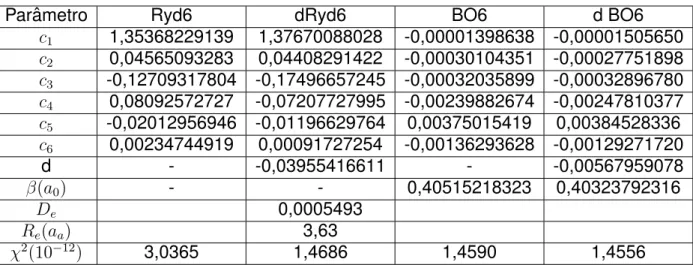
(dRyd), todas de grau 6. Utilizou-se os m étodos h´ıbridos Gradiente Simplex, Levenberg-Marquardt e Generalized Simulated Anneling(GSA) para otimizar os par âmetros das funç ões anal´ıticas que est ão apresentados na Tabela 3.1.

(35)

sistema He−H com as funç ões Ryd6, dRyd6, BO6 e dBO6. A energia de dissociaç ão é dada em hartree e a dist ância de equil´ıbrio est á em raio de bohr, sendo fixadas durante o ajuste.

Par ˆametro

Ryd6

dRyd6

BO6

d BO6

c

1

1,35368229139

1,37670088028

-0,00001398638

-0,00001505650

c

2

0,04565093283

0,04408291422

-0,00030104351

-0,00027751898

c

3

-0,12709317804

-0,17496657245

-0,00032035899

-0,00032896780

c

4

0,08092572727

-0,07207727995

-0,00239882674

-0,00247810377

c

5

-0,02012956946

-0,01196629764

0,00375015419

0,00384528336

c

6

0,00234744919

0,00091727254

-0,00136293628

-0,00129271720

d

-

-0,03955416611

-

-0,00567959078

β(a

0

)

-

0,40515218323

0,40323792316

D

e

0,0005493

R

e

(a

a

)

3,63

χ

2

(10

−12

)

3,0365

1,4686

1,4590

1,4556

Tabela 3.1: Tabela de par ˆametros otimizados para todas as CEPs do sistemaHe−H.

As figuras de 3.1-3.4 mostram as curvas ajustadas com os par ˆametros otimizadas na Tabela 3.1. Nessas figuras s ˜ao demonstrados os erros ponto-a-ponto.

(36)

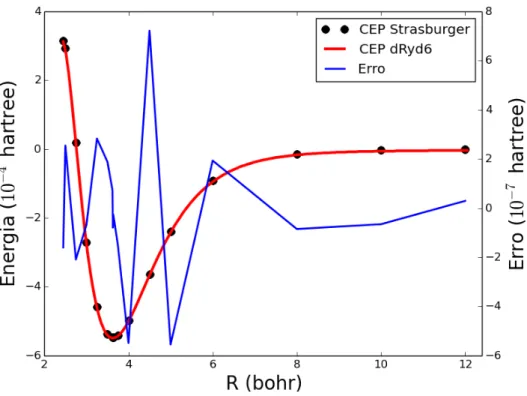
Figura 3.2: Comparac¸ ˜ao entre CEP obtida por Strasburger et ale CEP dRyd6, juntamente com erro ponto-a-ponto do ajuste.

(37)

Figura 3.4: Comparac¸ ˜ao entre CEP obtida por Strasburger et ale CEP dBO6, juntamente com erro ponto-a-ponto do ajuste.

As CEPs ajustadas pelos par ˆamentros otimizados na Tabela 3.1 s ˜ao comparadas aos pontosab initiode Strasburgeret al(SCEP) nas Figuras 3.1-3.4, para os potenciais Ryd6, dRyd6, BO6 e dBO6 respectivamente. Analizando todas as figuras bem como a Tabela 3.1 nota-se que o erro χ2 _para

qualquer uma das formas anal´ıticas ´e da ordem de 10−₇

Hartree, indicando uma boa concord ˆancia entre a CEP ajustada e a calculada por Strasburgeret al. Pelas Figuras apresentadas, os desvios que indicam os m ´aximos e m´ınimos encontrados para as energiasab initioe as energias ajustadas foram de8,37×10−7₍₈_,₆₃_×₁₀−4_{) Hartree para dBO6. Enquanto os desvios para BO6, dRyd6 e Ryd6 foram:}

8,09×10−7₍₂_,₀₀_×₁₀−8_),₇_,₂₁_×₁₀−7₍₂_,₆₉_×₁₀−8_{) e}₈_,₂₅_×₁₀−7₍₂_,₀₅_×₁₀−8_{) Hartree, respectivamente.}

Todos os ajustes aqui apresentados forneceram uma excelente descriç ão para as curvas de energia potencial que buscam denotar a interaç ão do sistema He−H, pois os desvios est ão abaixo do erro qu´ımico aceit ável (abaixo de 1 kcal/mol ou 0,0015 Hartree) em todas as regi ões da CEP calculada tanto nas zonas harm ônicas quanto nas zonas anarm ônicas (assint ótica, atrativa e repulsiva). Por uma an álise mais sofisticada observa-se que os ajustes que envolvem as funç ões deformadas (dRyd6 e dBO6) foram ligeiramente superiores. Podemos justificar esse fato comparando a soma doscj para as

formas das funç ões dBO6 e BO6, j á que a soma desses coeficientes deve ser igual à dissociaç ãoDe=

5,493×10−₄

Hartree, e os resultados foram deDe= 5,47081×10

−₄

para dBO6 eDe= 6,45998×10

(38)

par âmetro ddas funç ões deformadas dRyd6 e dBO6 s ão razoavelmente pequenos: -0.03955416611 e -0.00567959078, respectivamente. Contudo as funç ões deformadas s ão extremamente sens´ıveis ao par âmetrod.

As constantes espectrosc ópicas rovibracionais obtidas atrav és das soluç ões da Equaç ão de Schr ödin-ger nuclear, via Eq.(2.79) ser ão apresentadas na Tabela 3.2 para todas as formas analit´ıcas estudadas. Para calcular estas constantes utilizou-se a massa do anti-hidrog ênio como sendo igual à massa do hidrog ênio comum, com o intuito de se determinar a massa reduzidaµdo sistemaHe−H. Os valores dessas massas foram de 4,00386 a.m.u para o átomo de h élio e 1,008132 a.m.u para o anti-hidrog ênio, retirados da refer ência [34].

Tabela 3.2: Constantes espectrosc ópicas rovibracionais para o sistema He−H calculadas usando Eq.(79) atrav és do m étodo DVR. Todos os valores est ão apresentados emcm−₁

.

Potencial

ω

e

ω

e

χ

e

ω

e

γ

e

α

e

γ

e

B

e

Ryd6

105,77

36,16

6,12

10,68

2,87

5,674

dRyd6

105,51

36,05

6,11

10,65

2.86 5,674

BO6

107,70

37,00

6,24

10,62

2,85

5,674

dBO6

106,63

36,54

6,18

10,67

2,87

5,674

Na Tabela 3.2 podemos observar que os valores obtidos para as constantesωe,ωeχe,ωeγe,αeeγe,

est ão relativamente pr óximas para todas as funç ões anal´ıticas empregadas neste estudo.

Devido ao fato da energia de dissociaç ão e a dist ância de equil´ıbrio serem fixadas nos potenciais Rydberg e Rydberg deformada, seus ajustes expressaram valores ligeiramente melhores que os resul-tados obtidos usando BO6, pois este potencial apresenta o valor da energia de dissociaç ão como um par âmetro que n ão pode ser fixado, assim, apresenta valores n úmericos relativamente maiores para frequ ência fundamental ωe e para primeira correç ão anarm ônica ωeχe. Devido a fraca interaç ão do

sistema He−H, sua CEP tem um aspecto ”raso”, no sentido de que as correç ões anarm ônicas cor-respondem a uma fraç ão consider ável sobre a aproximaç ão harm ônica. Notemos, por exemplo, que os valores de ωeχeeωeγecalculados usando a funç ão Ryd6 correspondem a valores ditos altos quando

comparados a sistemas que s ão considerados ligados, nos quais essas constantes s ão muito menores que estes valores aqui apresentados. O valor deBefoi obtido usando a equaç ão (2.71) e substituindo

a massa reduzida e a dist ˆancia de equil´ıbrio do parHe−H.

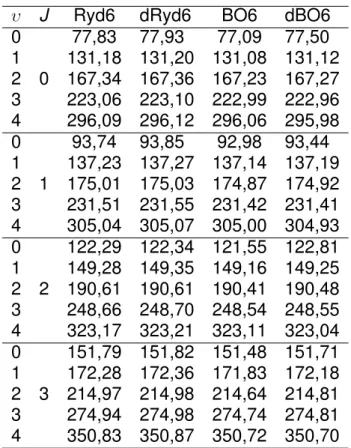
Na Tabela 3.3 est ão listadas o conjunto de energias rovibracionais obtidas atrav és da soluç ão da equaç ão de Schr ödinger nuclear com o n úmero qu ântico vibracional (υ) variando de 0 a 4, e o n úmero qu ântico rotacionalJ variando entre 0 e 3. Pode-se verificar pela Tabela 3.3 que, independentemente da forma anal´ıtica empregada, apenas um n´ıvel vibracional, o estado fundamental (υ= 0), e dois n´ıveis rotacionaisJ = 0,1encontram-se abaixo do limite de dissociaç ãoDe= 120,03cm−1. Esse fato indica

que o sistemaHe−H é formado por uma interaç ão de van der Waals.

(39)

Tabela 3.3: N´ıveis de energias rovibracionais para o sistemaHe−H (emcm−1_{) obtidos da soluc¸ ˜ao da}

equaç ão de Schr ödinger nuclear pelo m étodo DVR para os potenciais Ryd6, d-Ryd6, BO6 e dBO6.

υ

J

Ryd6

dRyd6

BO6

dBO6

0 77,83

77,93

77,09

77,50

1 131,18

131,20

131,08

131,12

2

0 167,34

167,36

167,23

167,27

3 223,06

223,10

222,99

222,96

4 296,09

296,12

296,06

295,98

0 93,74

93,85

92,98

93,44

1 137,23

137,27

137,14

137,19

2

1 175,01

175,03

174,87

174,92

3 231,51

231,55

231,42

231,41

4 305,04

305,07

305,00

304,93

0 122,29

122,34

121,55

122,81

1 149,28

149,35

149,16

149,25

2

2 190,61

190,61

190,41

190,48

3 248,66

248,70

248,54

248,55

4 323,17

323,21

323,11

323,04

0 151,79

151,82

151,48

151,71

1 172,28

172,36

171,83

172,18

2

3 214,97

214,98

214,64

214,81

3 274,94

274,98

274,74

274,81

4 350,83

350,87

350,72

350,70

fundamental, j á foram reportados na literatura estados excitados ligados. De acordo com o teorema CPT, todas as propriedades da antimat éria devem ser iguais à mat éria usual correspondente. Pode-mos, pois, apresentar a ideia de que se para mat éria usual o sistema He−H encontra-se ligado em seus estados excitados, ent ão o sistemaHe−Htamb ém pode estar ligado em algum estado excitado. No trabalho de Jonsellet al[17], os autores realizaram um estudo sobre o processo colisional entre

He−Hpartindo da CEP de Strasburger e Chojnacki. Levaram em conta os estados fracamente ligados com tempo de vida relativamente longo, cuja amplitude encontra-se quase que totalmente dentro do poço, pr óximo de2,42a0. Verificaram ent ão que para n úmero qu ânticos rotacionaisJ ≤3, o sistema

He−H suporta estados ligados. Os resultados apresentados na Tabela 3.3 denotam n´ıveis rovibracio-nais ligados nos casos em queυ= 0eJ = 0e assim concordam com dados apresentados por Jonsell

et al. A t´ıtulo de comparaç ão, as energias obtidas neste trabalho atrav és do m étodo DVR e os n´ıveis obtidos por Jonsellet al foram: 3,5221×10−4 _{hartree e} ₃_,₀₄₃_×₁₀−4 _{hartree para}_J _{= 0}

respectiva-mente. Uma diferenc¸a significativa aparece quando ´e consideradoJ = 3, em nosso trabalho obtemos 6,92×10−₄

que esta fora do limite da ligac¸ ˜ao e 5,39×10−₄

Hartree que est á abaixo da energia de dissociaç ão.

(40)

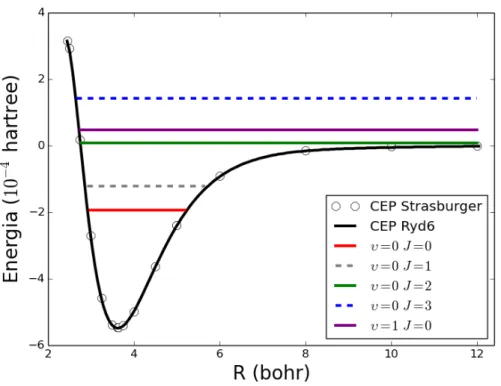
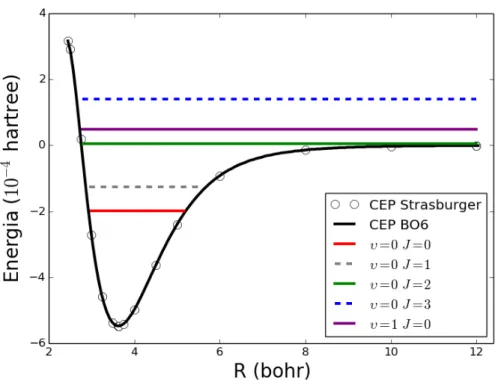
Figura 3.5: N´ıveis de Energia Rovibracionais para o sistemaHe−H com a forma anal´ıtica Ryd6.

(41)

Figura 3.7: N´ıveis de Energias Rovibracionais para o sistemaHe−H com a forma anal´ıtica BO6.

Figura 3.8: N´ıveis de Energias Rovibracionais para o sistemaHe−H com a forma anal´ıtica dBO6.

(42)

mol éculas diat ômicas heteronucleares. O m´ınimo da CEPab initioassemelha-se a estruturas que inte-ragem por forças dispersivas como mol éculas de van der Waals. Caso seja considerado, por exemplo, a interaç ão do sistemaHe−Hecomo um sistema diat ômico fraco, sua forma dim érica somente é formada

`a temperatura de10−₃

K [35]. O sistemaHe2apresenta energia de dissociac¸ ˜aoDe= 3,4728×10

−₅

Ha

comRe= 5,61a0[34], demonstrando que o sistemaHe−Hest ´a por uma ordem de grandeza mais

for-temente ligado (De= 5,5469×10

−4_{Hartree e}_R

e= 3,63a0). Poc¸os de potencial com um leve m´ınimo,

como os sistemasHe−H eHe−He, s ão denominados de mol éculas de van der Waals devido sua baixa energia de interaç ão. Isto leva a crer que exista um estado ligado para este sistema descrito pelas energias rovibracionais obtidas neste trabalho. Adicionalmente, é importante enfatizar que a interaç ão

(43)

Cap´ıtulo 4

Conclus ˜oes e Perspectivas

Neste trabalho foram determinas pela primeira vez na literatura as energias e constantes espec-trosc ópicas rovibracionais para interaç ão He−H usando a CEP ab initio obtida por Strasburger e Chojnacki [13]. Quatro formas anal´ıticas foram utilizadas para ajustar os pontos ab initio do poten-cial interat ômico e os par âmetros foram otimizados utilizando os m étodos h´ıbridosGradiente Simplex,

Levenberg - MarquardteGeneralized Simulated Annealing (GSA). O procedimento de ajuste foi consi-derado satisfat ório embasando-se no erro ponto-a-ponto n ão superou o erro qu´ımico aceit ável (abaixo de 1 kcal/mol∼0,0015 hartree) em todas as regi ões da CEP obtida.

As constantes espectrosc ópicas aqui obtidas apresentaram valores muito pr óximos para todas as formas anal´ıticas empregadas com diferença m áxima que n ão passou de7%paraωe,13%paraωeχe,

8% para ωeγe, 2% paraαe e 1% paraγe, quando utilizou-se a func¸ ˜ao Bond Order de grau 6. Estas

pequenas diferenças mostram que os ajustem apresentam qualidade similar. A exist ência de estados ligados é poss´ıvel para os n´ıveis rovibracionais,υ= 0eJ = 0,1. Esta interaç ão se assemelha aquelas que ocorrem com mol éculas de van der Waals com baixa energia de dissociaç ão e dist ância internu-clear relativamente grande. A precis ão das propriedades din âmicas apresentadas neste trabalho est ão intimamente ligadas à qualidade da CEPab initiode Strasburgeret al, a qual é considerada de altam-mente precisa. Desta forma acredita-se que os resultados obtidos possam servir de comparaç ão com estudos futuros acerca das propriedades espectrosc ópicas para o sistema diat ômicoHe−H.

Como perspectivas futuras pretendemos confrontar estes resultados utilizando outra metodologia para a determinaç ão de constantes espectrosc ópicas, tais como o m étodo de Dunham [27]. Este m étodo é baseado em f órmulas derivadas da teoria da perturbaç ão, no qual o potencial (funç ão anal´ıtica)