Blind multipath MIMO channel parameter
estimation using the Parafac decomposition
Carlos E. R. Fernandes
†, G´erard Favier
∗, and Jo˜ao C. M. Mota
† †Dpto de Eng. de Teleinform´atica ∗Laboratoire I3S / CNRS Universidade Federal do Cear´a Universit´e de Nice Sophia Antipolis Campus do Pici, Bloco 723, C.P. 6005 B.P. 121, 2000 route des Lucioles
60455-760 Fortaleza, Brazil 06903 Sophia Antipolis Cedex, France Email: estevao@gtel.ufc.br, mota@gtel.ufc.br Email: favier@i3s.unice.fr
Abstract—In this paper, we consider the problem of estimating the physical parameters that describe a multipath MIMO com-munication channel model characterized by specular reflections due to remote scatterers. Using the impulse response channel coefficients, we introduce a channel model based on a 3rd-order tensor structure that admits a Parafac decomposition with rank equal to the number of propagation paths. The alternating least squares (ALS) algorithm is used to estimate the channel spatial and temporal signatures and the multipath parameters are then extracted by means of MUSIC-like subspace algorithms, enabling us to recover the transmit and receive angles as well as the path propagation delays of the MIMO channel, without ambiguities. Computer simulation results are shown to illustrate the performance of the proposed ALS-MUSIC estimation algorithm.
I. INTRODUCTION
In mobile radiocommunication systems, signals are often transmitted through multiple propagation paths, characterized by specular reflections, troposphere refractions and scattering due to physical objects placed in the environment. In such a multipath propagation scenario, the wavefronts may reach the receive antennas with different delays, spreading the energy of the signals over the time and causing intersymbol interference (ISI), which induces capacity and performance limitations in wireless communication systems. To ensure a correct infor-mation recovery, it is necessary to reduce or suppress the effects of ISI, which generally requires the knowledge of the transmission channel. Several linear and nonlinear equalization methods make use of known sequences embedded in the transmitted signals in order to estimate the channel coefficients [1]. This supervised approach may be very bandwidth costly in the context of time-varying channels.
The channel identification problem has been often addressed using high-order output statistics (HOS), which gave rise to several non-supervised (blind) approaches. Blind methods have also been proposed for the single user case based only on second order statistics (SOS), exploiting subspace properties of multiple output channels corresponding to the use of receive antenna arrays or oversampling (cf. [2], [3] among others). Classical methods are available in the literature for estimating channel coefficients based on a given channel model [2], [3].
This work was partially supported by the CAPES agency of the Brazilian federal government.
More recently, HOS-based tensor channel identification methods have been introduced for the memoryless MIMO case, including the blind identification of over-complete mix-tures (BIOME) method [4] and a family of fourth-order-only blind identification (FOOBI) algorithms [5], both mak-ing use of joint-diagonalization techniques. While skippmak-ing prewhitening, these techniques treat the identification problem as two separate optimization stages, so that the MIMO channel coefficients are extracted from an initial estimate based on an eigenvalue decomposition (EVD). On the other hand, a single-step least squares (SS-LS) algorithm was introduced in [6] and extended to the case of convolutive MIMO channels proposing a solution based on a sole minimization stage, making use of the 4th-order output cumulant redundancies and avoiding any kind of preprocessing [7], [8]. Finally, a HOS-based frequency domain framework for MIMO system identification using tensor decompositions has also been developed, including the case of convolutive MIMO channels [9], [10], [11].
In this paper, we focus on the problem of blind multipath channel parameter estimation, assuming that the impulse re-sponse of the convolutive MIMO channel model has been previously estimated. Our main contribution consists in intro-ducing a channel model based on a 3rd-order tensor structure that admits a Parallel Factor (Parafac) decomposition. Few papers in the literature have exploited the multipath structure of the channel using a tensor formalism as in [12], where, unlike our proposition, the length of the total observation interval must be long enough to ensure variations of the path attenuations and a training sequence is used to estimate the temporal signature of the channel.
Another original contribution of this paper is the proposition of a new parametric multipath estimation procedure. The alternating least squares (ALS) algorithm is used to obtain the spatial and temporal channel signatures using the estimated channel coefficients. The physical parameters that characterize the multiuser radio channel are extracted by means of MUSIC-like subspace algorithms, enabling us to recover transmit and receive angles, propagation delays and path attenuations without the trivial ambiguities associated with the Parafac decomposition. This method will be referred to as the ALS-MUSIC algorithm.
This paper is organized as follows: after a brief recall of the Parafac decomposition, we present in section II the multipath MIMO channel model and introduce a Parafac formalism to treat the multipath channel as a tensor formed from its physical parameters; in section III, we propose a method for multipath parameter estimation using the ALS algorithm and MUSIC-like subspace algorithms; in section IV, we provide computer simulations results illustrating the performance of the proposed method. Conclusions are drawn in section V.
Brief recall of the Parafac decomposition
Let us consider a 3rd-order tensor T, of dimensions I×J×K and rank equal to F, with scalar representation given byti,j,k=Ff=1aifbjfckf, wherei∈[1, I],j∈[1, J]
and k ∈ [1, K]. The rank of T is defined as the minimum numberF of factors needed to decomposeti,j,k in the above
form. The Parafac decomposition consists in decomposing T into a sum of F rank-one tensors, each one being written as an outer product of 3 vectors:
T =
F
f=1
A·f◦B·f◦C·f. (1)
The matrices A∈ CI×F,B ∈ CJ×F and C ∈CK×F with
entriesaif,bjf andckf are called Parafac components [13].
Uniqueness is a main feature of the Parafac decomposition. The decomposition is said to be essentially unique if any set of matrices{A¯,B¯,C¯} satisfying (1) is such thatA¯ =AΛ1Π,
¯
B = BΛ2Π and C¯ = CΛ3Π, where Λ1, Λ2 and Λ3 are
diagonal scaling matrices satisfying Λ1Λ2Λ3 = Iand Π is
anF×F permutation matrix. In the case of a 3rd-order tensor, a sufficient uniqueness condition was established by Kruskal [14], stating that the Parafac decomposition of a 3rd-order tensor, with rankF >1, is essentially unique if
kA+kB+kC≥2(F+ 1), (2)
where kX denotes the k-rank of matrix X, defined as the largest integer kX for which any set of kX columns of X is linearly independent.
II. MULTIPATHMIMOCHANNEL MODEL
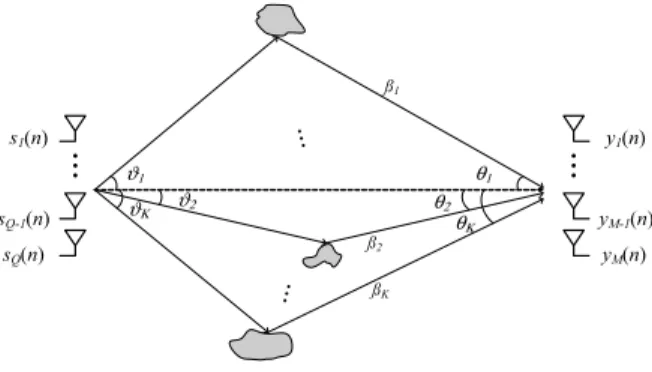
Let us consider a multiple-input multiple-output (MIMO) wireless communication system with Q transmit and M re-ceive sensors disposed in uniform linear arrays (ULA) of antennas with half wavelength spacing. It is assumed that the transmit array is placed at the far-field of the receive array and specular multipath propagation is due to remote scatterers, as shown in fig. 1, so that the link between each transmit and each receive antenna can be represented by a superposition of K plane waves, associated with K scatterers, located far apart each other. The location of the scatterers determines the directions of departure (DOD)ϑk and the directions of arrival
(DOA)θkof thekth path. The elevation angles are assumed to
be negligible and are therefore disregarded. We also assume that the transmitted signals are narrowband with respect to the array aperture so that the signals over the kth path are
...
...
.
.
.
. . .
ß1
ß2 ßK
s1(n)
sQ-1(n)
sQ(n)
y1(n)
yM-1(n)
yM(n) θ1
θ2
θΚ
ϑ1
ϑ2
ϑΚ
Fig. 1. Multipath propagation scenario.
subject to a single attenuation factor βk ∈ C, and have the
same relative propagation delayτk∈R, which is expressed in
multiples of the symbol period. We utilize a known real-valued pulse shape filter g(ℓ), with finite temporal support equal to L+ 1 symbol periods, so that g(ℓ) = 0, for ℓ /∈[0, L]. The multipath delay spread profile is assumed to be finite with a known maximum path delay τmax, which is larger than
the inverse of the coherence bandwidth so that the channel is frequency-selective. Finally, we assume that the channel is stationary over one time-slot composed ofN symbol periods.
The equivalent baseband signal at the output of the mth receive antenna, sampled at the symbol rate, is written as ym(n) =xm(n) +υm(n), where the noiseless part xm(n)is
given by:
xm(n) = Q
q=1 K
k=1 βka
′
q(ϑk)am(θk) L
ℓ=0
g(ℓ−τk)sq(n−ℓ), (3)
withβkbeing the complex fading gain associated with thekth
path anda′
q(ϑk)andam(θk)denoting the spatial responses of
the transmit and receive antennasqandmassociated with the kth path, respectively. The non-measurable complex-valued discrete input signals sq(n) are assumed to be stationary,
ergodic and mutually independent with symmetric distribution, zero-mean and non-zero kurtosis γ4,sq = c4,sq(0,0,0). The additive noiseυm(n)is assumed Gaussian and independent of
the input signals, zero-mean with unknown spatial correlation. From (3), we get xm(n) =Qq=1Lℓ=0hmq(ℓ)sq(n−ℓ),
m∈[1, M], the channel coefficientshmq(ℓ)being defined as:
hmq(ℓ) K
k=1
βka′q(ϑk)am(θk)g(ℓ−τk),∀ ℓ∈[0, L], (4)
andhmq(ℓ) = 0 elsewhere.
A. The multipath MIMO channel as a tensor model
Let us define: ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ A
R m,k =am(θk), m∈[1, M]
AT
q,k =a
′
q(ϑk), q∈[1, Q]
G
ℓ+1, k =g(ℓ−τk), ℓ∈[0, L].
b
k =βk k∈[1, K],
(5)
AR∈CM×K
,AT∈CQ×K
,G∈R(L+1)×K
,b∈CK×1, and
F=GDiag(b) ∈C(L+1)×K,
(6)
where the operator Diag(·)forms a diagonal matrix from its vector argument.
Note that (4) is the scalar notation of the 3rd-order tensor H ∈CM×Q×(L+1)with rankK and Parafac componentsA
R,
ATandF. A similar tensor channel model has been proposed
in [12], assuming a block-fading multipath channel. In that case, the signals received during multiple successive time-slots can be arranged in a Parafac model, and training sequences are used to estimate signals and channel parameters.
B. Uniqueness condition
Using the Kruskal Theorem, we derive the following suffi-cient condition for the uniqueness of the Parafac decomposi-tion ofH:
kAR+kAT+kF ≥2K+ 2. (7)
Considering the transmit and receive ULA arrays with half wavelength spacing and no elevation angle, the array ele-ment responses are defined as am(θk)ej π(m−1) cosθk and
a′
q(ϑk)ej π(q−1) cosϑk. Therefore, the spatial signature
ma-trices AR andAT have a Vandermonde structure. We further
assume that the generating vectors ofARandAThave distinct
nonzero elements1. Under this condition, it was shown in
[15] that a Vandermonde matrix is full k-rank and hence: kAR=rAR = min(M, K)andkAT=rAT = min(Q, K).
In addition, we assume that the real-valued pulse shape filter g(ℓ)is known and all path delays τk are distinct, k∈[1, K].
Rayleigh fading is assumed so that the gains βk are modeled
as complex random variables with independent real and imag-inary parts driven from a continuous Gaussian distribution. Under these conditions, matrixF=GDiag(b)is also ensured
to be full k-rank, and hencekF=rF= min(L+ 1, K). Due to the above considerations, the condition (7) yields:
min(M, K) + min(Q, K) + min(L+ 1, K)≥2K+ 2 (8)
so that, when min(M, Q, L+ 1) > K, the above condition becomes K ≥ 2, meaning that in this case at least two propagation paths are necessary to ensure uniqueness.
III. BLIND MULTIPATH CHANNEL PARAMETER ESTIMATION
In this section, we propose a method to blindly recover the multipath propagation delays and angles of departure and arrival. The proposed technique assumes prior (approximative) knowledge of the channel coefficients (previously estimated). Our approach consists in first estimating the channel signa-tures, which are structured matrices containing all the spatial
1This is equivalent to having spatially distinguishable incoming signals.
and temporal information of the channel. The ALS algorithm will be used to estimate the tensor channel Parafac com-ponents. Afterwards, we use subspace techniques to extract the physical parameters from the estimated channel signature matrices.
A. The ALS algorithm
Let us consider the 3rd-order tensor H ∈ CQ×M×(L+1),
with scalar representation given by (4) and Parafac compo-nentsAT,ARandF, defined in (5) and (6). Takingq∈[1, Q],
m ∈ [1, M] and ℓ ∈ [0, L], we define three unfolded representations of H, as follows:
⎧ ⎪ ⎨ ⎪ ⎩ H[1]
ℓM+m, q =hmq(ℓ),
H
[2] (m−1)Q+q, ℓ+1 =hmq(ℓ),
H[3]
(q−1)(L+1)+ℓ+1, m =hmq(ℓ),
(9)
where H[1] ∈CM(L+1)×Q
, H[2] ∈ CQM×(L+1) andH [3] ∈
CQ(L+1)×M
are given by [8]:
H[1]=
F⋄AR
AT
T, H[2]=
AR⋄AT
FT,
H[3]=
AT⋄F
AT R,
(10)
with⋄ denoting the Khatri-Rao product [16]. From (10), we can define the following conditional LS cost functions:
ψ1(AT,Fˆ(
r−1),ˆ
A(Rr−1)) =
H[1]−
ˆ
F(r−1)⋄A(Rr−1)
ATT
2 F ,
ψ2(F,Aˆ(Rr−1),Aˆ
(r)
T ) =
H[2]−
ˆ
A(Rr−1)⋄Aˆ
(r)
T FT 2 F ,
ψ3(AR,Aˆ
(r)
T ,Fˆ
(r)) =
H[3]−
ˆ
A(Tr)⋄Fˆ
(r) ATR
2 F ,
where·F denotes the Frobenius norm andris the iteration
number. The LS solutions are given by:
ˆ
A(Tr)T =
ˆ
F(r−1)⋄A(Rr−1)
#
H[1], (11)
ˆ
F(r)T = Aˆ(Rr−1)⋄Aˆ
(r)
T
#
H[2], (12)
ˆ
A(Rr)T =
ˆ
A(Tr)⋄Fˆ
(r)#
H[3], (13)
where (·)# denotes the matrix pseudoinverse operation.
MatricesFˆ(0)andA(0)R can be initialized as Gaussian random
matrices or using some a priori knowledge about the multipath parameters, if available. The algorithm is stopped when2
|e(r)−e(r−1)|2≤ε, whereεis an arbitrary small positive
constant and the estimation error e(r) for the iteration r≥1 is given by e(r) =e1(r) +e2(r) +e3(r), where
e1(r) = Aˆ(Tr)−Aˆ
(r−1)
T
2
F/Aˆ
(r)
T
2
F,
e2(r) = Aˆ(
r)
R −Aˆ
(r−1)
R
2
F/Aˆ
(r)
R
2
F,
e3(r) = Fˆ(r)−Fˆ(r−1)2F/Fˆ( r)2
F.
B. Subspace algorithms for multipath parameter extraction
We now aim at extracting the DOAs, DODs, propagation delays and path attenuations using the estimated spatial and temporal channel signature matrices, obtained after the con-vergence of the ALS algorithm, denoted as AˆR, AˆT and Fˆ.
Exploiting the knowledge of the transmit and receive array manifolds as well as that of the pulse shape filter, we build orthogonal projectors and define localization functions based on the signal and noise subspace structure.
Let us first consider the estimation of DOAs and treat the case of the receive antenna array with M > K. Denote by
ˆ
Un∈CM×(M−K) the matrix formed from the left singular
vectors of AˆR associated with its M −K smallest singular
values. Define wm(θ) =ej π(m−1) cosθ and build a
column-vectorw(θ)∈CM×1. For each given value ofθ, we take the
orthogonal projection ofw(θ)over the noise subspace ofAˆR,
thus defining the following MUSIC localization function:
P2(θ) =
w(θ)
HUˆn
−2
. (14)
Due to the orthogonality between the signal and noise sub-spaces, we haveUˆT
nAˆR =0(M−K)×K, and hence, the DOA
anglesθk,k∈[1, K], are obtained as the argumentsθyielding
theK local maxima of (14).
For the case M ≤ K, an extended localization function P2κ(θ)can be defined as [17]:
P2κ(θ) =
wκ(θ)
HU n
−2
, (15)
with
wκ(θ) =w(θ)⊗ℓ⊗w∗(θ)⊗κ−ℓ,
(16)
where x⊗n=x⊗ · · · ⊗x, the Kronecker product symbol ⊗
appearingn−1 times. In (16), the indexℓ has been omitted on the left-hand side because we take, by convention,ℓ=κ/2 whenκis even andℓ= (κ+ 1)/2whenκis odd. In (15), ma-trixUn∈CMκ×(Mκ−K)
is obtained by concatenating the left singular vectors associated with theMκ−K
smallest singular values of theκth-order virtual arrayAˆ(Rκ)= ˆA⋄ℓ
R ⋄Aˆ
∗⋄κ−ℓ
R .
This technique allows us for estimating up to κ(M −1) DOA angles, in the case of ULA arrays [17]. With κ = 2, for instance, we get Aˆ(2)R = ˆAR ⋄ Aˆ∗
R ∈ C
M2×K
, the rank of which equalsrAˆ(2)
R = min(2M−1, K), meaning that
up to 2M −2 DOA angles can be estimated, provided that M ≤K≤2M −2. Finally, note that the DOD angles ϑk,
k ∈ [1, K] can also be estimated using the above described technique, withAˆTreplacingAˆR, andQinstead ofM [8].
Similarly, path delays can also be extracted from the esti-mated temporal channel signature matrixFˆ. Using the
knowl-edge of the real-valued pulse shape filter g(ℓ), we construct orthogonal projectorsw(τ)∈R(L+1)×1,L+ 1> K, so that wℓ(τ) = g(τ −ℓ+ 1), ℓ ∈[1, L+ 1], for all τ ∈[0, τmax],
whereτmaxis a known upper bound of the path delays. Taking
the SVD of Fˆ, we form Uˆn∈C(L+1)×(L+1−K) with the
left singular vectors associated with the L+ 1−K smallest singular values and find the path delays τk, k ∈ [1, K], by
looking for the values of τ that yield the K local maxima of P2(τ) = w(τ)HUˆn−2. A straightforward extension of
the technique is possible when L+ 1 ≤ K, using the cor-responding localization function P2κ(τ) = wκ(τ)HUn−2,
with the orthogonal projector wκ(τ) =w(τ)⊗κ
. In this case, since g(ℓ) is real-valued, we define the augmented matrix as
ˆ
F(κ)= ˆF⋄κ andUˆ
n is obtained from its SVD. With κ= 2,
we get Fˆ(2) = ˆF⋄Fˆ with rank rFˆ(2) = min(I, K), where
I= (L+ 1)(L+ 2)/2, meaning that up to I−1 path delays can be estimated, L+ 1≤K≤I−1.
Finally note that column scaling and permutation ambigui-ties due to the ALS algorithm are not relevant in the present context since the subspace algorithms allow us to completely characterize the multipath channel, including the correspon-dences between the estimated parameters θˆk1, ϑˆk2 and τˆk3,
k1, k2, k3∈[1, K], and the propagation pathsk∈[1, K][8].
IV. SIMULATION RESULTS
We simulated a MIMO multipath channel with transmit and receive ULA arrays using Q and M antennas, respectively. The multipath specular radio signal model is given by (3), with transmit and receive arrays located far apart each other, andKremote scatterers yielding a set of physical parameters (θk, ϑk, τk, βk). Starting from an estimated channel model,
we recover the spatial and temporal signatures of the MIMO channel using the ALS algorithm and then the multipath parameters (DOAs, DODs and path delays) are extracted using subspace methods, as described in section III.
In which follows, the channel model has been estimated by means of the SS-LS algorithm [7], [8] using synthesized 4th-order output cumulants. The curves shown in the sequel have been obtained with a cumulant error variance of σe2 = 0.01
and a SNR of 20dB. Two sets of channel parameters have been considered and are detailed in Table I.
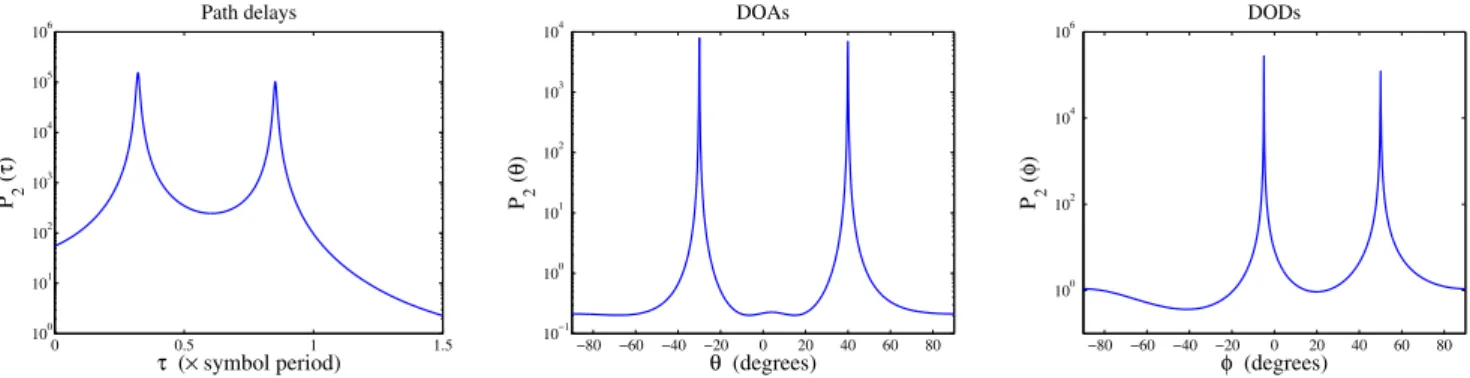
In fig. 2 we show P2(·) as a function of τ, θ and φ,
re-spectively, for one realization of the experiment using channel configuration A (K= 2) withQ= 3,M = 5andL= 2. In fig. 3 we show the results for channel configuration B (K= 3) with the same parameters (Q = 3, M = 5, L = 2). Notice that, in this latter case,Q=L+ 1 =K so thatATandGdo
not have free dimensions in their respective noise subspaces. Hence, in order to estimate the DODs and path delays, we used the 4th-order localization functionsP4(·)with arguments τ andφ. For the DOAs, we usedP2(θ), sinceM > K. From
fig. 2 and 3, we conclude that the proposed method yields good estimation results under given channel configurations, although a deeper performance evaluation is needed.
TABLE I
CHANNEL CONFIGURATION PARAMETERS.
Config. A Config. B
Multipaths K= 2 K= 3
0 0.5 1 1.5 100
101 102 103 104 105 106
τ (× symbol period)
Path delays
P2
(
τ
)
−80 −60 −40 −20 0 20 40 60 80
10−1 100 101 102 103 104
θ (degrees)
DOAs
P2
(
θ
)
−80 −60 −40 −20 0 20 40 60 80
100 102 104
106
φ (degrees)
DODs
P2
(
φ
)
Fig. 2. Multipath parameter extraction using ALS-MUSIC method for channel configuration A withQ= 3,M= 5andL= 2.
0 0.5 1 1.5 2
100 102 104 106
τ (× symbol period)
Path delays
P4
(
τ
)
−80 −60 −40 −20 0 20 40 60 80
10−1 100 101 102 103
104 105
θ (degrees)
DOAs
P2
(
θ
)
−80 −60 −40 −20 0 20 40 60 80
10−1 100 101 102 103
104 105
φ (degrees)
DODs
P4
(
φ
)
Fig. 3. Multipath parameter extraction using ALS-MUSIC method for channel configuration B withQ= 3,M= 5andL= 2.
V. CONCLUSION
In this paper, a new method has been proposed to estimate the physical parameters of a multipath MIMO communication channel characterized by specular reflections due to remote scatterers. We have taken the structure of the multipath MIMO channel into account and introduced a new tensor channel model that admits a Parafac decomposition with rank equal to the number of multipaths. The problem has been treated with a two-stage approach. The ALS algorithm has been used to estimate the channel spatial and temporal signatures and the multipath parameters have been extracted by means of subspace algorithms, enabling us to fully estimate the MIMO channel without ambiguities. Simulation results have been shown demonstrating the applicability of the proposed method, but further investigation must be done in order to assess its performance under a more realistic channel scenario.
REFERENCES
[1] Proakis, J. G.,Digital Communications, 4th ed. McGraw Hill, 2000. [2] Tong, L., Xu, G., and Kailath, T., “Blind identication based on
second-order statistics: A time domain approaches,”IEEE Information Theory, vol. 40, no. 2, pp. 340–349, 1994.
[3] Moulines, E., Duhamel, P., Cardoso, J.-F., and Mayrargue, S., “Subspace methods for the blind identification of multichannel FIR filters,”IEEE Trans. on Signal Process., vol. 43, no. 2, pp. 516–525, feb. 1995. [4] Albera, L., Ferr´eol, A., Comon, P., and Chevalier, P., “Blind
identifi-cation of overcomplete mixtures of sources (BIOME),”Linear Algebra Applications, vol. 391C, pp. 3–30, nov 2004.
[5] De Lathauwer, L., Castaing, J., and Cardoso, J.-F., “Fourth-order cumulant-based blind identification of underdetermined mixtures,”IEEE Trans. on Signal Process., vol. 55, no. 6, pp. 2965–2973, jun. 2007.
[6] Fernandes, C. E. R., Favier, G., and Mota, J. C. M., “Blind channel identification algorithms based on the Parafac decomposition of cumu-lant tensors: the single and multiuser cases,”Signal Processing, Elsevier, vol. 88, no. 6, pp. 1382–1401, jun. 2008.
[7] Fernandes, C. E. R., Favier, G., and Mota, J. C. M., “Parafac-based blind identification of convolutive MIMO systems,” InProc. of the 15th IFAC Symposium on System Identification, Saint-Malo, France, 2009. [8] Fernandes, C. E. R., “High-order stat. methods for blind channel
identif. and source detection with applic. to wireless communic.” PhD Thesis (cotutelle), Univ. of Nice Sophia Antipolis and Federal Univ. of Cear´a (Brazil), Sophia Antipolis, France, May 2008.
[9] Acar, T., Yu, Y., and Petropulu, A. P., “Blind MIMO system estimation based on PARAFAC decomp. of higher order output tensors,” IEEE Trans. on Sig. Process., vol. 54, no. 11, pp. 4156–4168, nov. 2006. [10] Yu, Y., and Petropulu, A. P., “PARAFAC based blind estimation of
possibly under-determined convolutive MIMO systems,”IEEE Trans. on Signal Process., vol. 56, no. 1, pp. 111–124, jan. 2008.
[11] Yu, Y., and Petropulu, A. P., “PARAFAC-based blind estimation of possibly underdtermined convolutive MIMO systems,”IEEE Trans. on Signal Processing, vol. 56, no. 1, pp. 111–124, jan. 2008.
[12] De Almeida, A. L. F., Favier, G., and Mota, J. C. M., “Estimation of frequency-selective block-fading MIMO channels using PARAFAC modeling and Alternating Least Squares,” inProc. of ASILOMAR’06, Pacific Grove, CA, USA, 2006.
[13] Bro, R., “Multi-way analysis in the food industry, models algorithms, and applications,” Ph.D. dissertation, Department of Dairy and Food Science, Royal Veterinary and Agricultural University, Denmark, 1998. [14] Kruskal, J. B., “Three way arrays: rank and uniqueness of trilinear de-compositions with applications to arithmetic complexity and statistics,”
Linear Algebra and Its Applications, vol. 18, pp. 95–138, 1977. [15] Sidiropoulos, N. D., and Liu, X., “Identifiability results for blind
beamforming in incoherent multipath with small delay spread,”IEEE Trans. on Signal Process., vol. 49, no. 1, pp. 228–236, jan. 2001. [16] Brewer, J., “Kronecker products and matrix calculus in system theory,”