The Vortex Lattie in Conventional and
High-T
Superondutors
Ernst Helmut Brandt
Max-Plank-Institutf urMetallforshung,D-70506 Stuttgart,Germany
Reeivedon28February,2002
Someproperties oftheux-linelattie inonventionalandhigh-T
superondutorsarereviewed,
withpartiularstressonphenomenologialtheories,nonloalelastiity,irreversible magnetization
urves,andinueneofthespeimenshapeontheeletromagnetiresponse.
I. Introdution
Afterthedisoveryofsuperondutivityin1912by
Heike Kamerlingh-Onnesin Leiden,it took almost 50
yearsuntilthisfasinatingphenomenonwasunderstood
mirosopially, when in 1957 Bardeen, Cooper and
ShrieerestablishedtheBCStheory. Butlongbefore
this, there were powerful phenomenologial theories,
whih were able to explain most eletromagneti and
thermodynami observations on superondutors,and
whihareveryusefulalsotoday[1,2,3℄. TheLondon
theoryof1935ispartiularlyusefulforthedesription
of thehigh-T
superondutors,whih were disovered
in1987byBednorzandMuller. TheGinzburg-Landau
(GL) theoryof 1951 isquite universal; it ontainsthe
Londontheoryaspartiularlimitandpreditsthat
su-perondutorsanbeoftype-I(withpositiveenergyof
thewallbetweennormalondutingand
superondut-ing domains) orof type-II (with negativewall energy,
pointingto aninstability).
The penetration of vorties into type-II
superon-dutors was predited rst by A. A. Abrikosov when
he disovered a two-dimensional periodi solution of
the Ginzburg-Landau (GL)equations. Abrikosov
or-retly interpreted this solution as a periodi
arrange-ment of ux lines, the ux-line lattie (FLL). Eah
ux line (or uxon, vortex line) arries onequantum
of magnetiux
0
=h=2e=2:0710 15
Tm 2
, whih
is aused by the superurrentsirulating in this
vor-tex. Themagneti eld peaks at thevortexpositions.
The vortex ore is a tube in whih the
superondu-tivity is weakened; the position of the vortex is
de-ned by the line at whih the superonduting order
parametervanishes. Forwellseparatedorisolated
vor-ties, the radius of the tube of magneti ux equals
diusis somewhat largerthan the superonduting
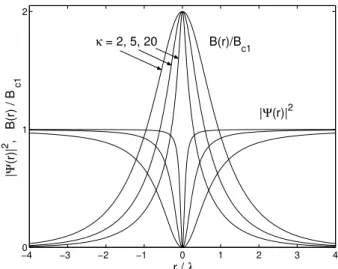
o-herenelength [1, 2, 3℄, see Fig. 1. With inreasing
applied magneti eld, the spaing a
0
of the vorties
dereasesandtheaverageuxdensity
B inreases,one
has
B=2
0 =(
p
3a 2
0
)forthetriangularFLL,seeFig.2.
Theux tubesthen overlapsuh thatthe periodi
in-dution B(x;y) is nearly onstant, with only a small
relativevariationaboutitsaverage
B. Withfurther
in-reaseof
B alsothevortexoresbegintooverlapsuh
that the amplitude of the order parameter dereases
untilitvanisheswhen
B reahestheupperritialeld
B
2 =
0 H
2 =
0 =(2
2
), where the
superondutiv-itydisappears. Fig. 3showsprolesoftheindution
B(x;y) and of the order parameter j (x;y)j 2
for two
valuesof
B orrespondingtoux-linespaingsa
0 =4
anda
0 =2.
−4
0
−3
−2
−1
0
1
2
3
4
1
2
r /
λ
|
Ψ
(r)|
2
, B(r) / B
c1
B(r)/B
c1
|
Ψ
(r)|
2
κ
= 2, 5, 20
Figure1. Magneti eldB(r)andorderparameterj (r)j 2
unit cell area =
Φ
0
/B
flux−line spacing
Figure2. Thetriangularux-linelattie.
−2
−1
0
1
2
3
4
5
6
0
1
2
x /
λ
B(x,0)/B
c1
|
Ψ
(x,0)|
2
κ
= 5
Figure3. TwoprolesofthemagnetieldB(x;y)and
or-derparameterj (x;y)j 2
alongthexaxis(anearestneighbor
diretion)for ux-linelattieswithlattie spaingsa=4
(solidlines)anda=2(thinlines). Thedashedlineshows
themagnetieldofanisolateduxlinefromFig.1.
Cal-ulationsfromGinzburg-Landautheoryfor=5.
Theperiodi solutionwhih desribestheFLL
ex-ists when the GL parameter = = exeeds the
value1= p
2(thisonditiondenestype-II
superondu-tors)and whenthe appliedmagneti eld B
a =
0 H
a
rangesbetweenthe lowerritialeld B
1 =
0 H
1
0 ln(
p
2)=(4 2
) (where
B = 0) and B
2
(where
B = B
a = B
2
). For jB
a j < B
1
the
superondu-tor isin theMeissner state,whihexpelsallmagneti
ux, foring B 0 inside the superondutor. More
preisely, for B
a < B
1
[and in type-I
superondu-tors with<1= p
2forB
a <B
=
0 =(
p
8)℄,the
applied magneti eld penetrates into a surfae layer
of thikness . For a superonduting half spae at
x > 0 one has B(x) = B
a
exp( x=). For a long
strip with retangular ross setion (jxj a = 40,
jyjb=0:4a)andwithB
a
alongy,Fig.4showsthat
inthissurfaelayerbothB(x;y)andthesreening
ur-rentdensity J(x;y) = 1
0
rB(x;y) (owing along
z)are sharply peaked in theorners, favoringthe
nu-leationandpenetrationofvortiesinform ofquarter
loopsatthefourornersof thestrip[4,5℄.
0
0.2
0.4
0.6
0.8
1
0
0.1
0.2
0.3
0.4
0
50
100
150
200
y / a
j(x,y) a / H
a
x / a
y
b
0
0
x
a
Figure4. Astripwithaspetratiob=a=0:4 inthe
Meiss-nerstate withLondonpenetrationdepth=0:025a0 ina
perpendiularmagnetieldHa.Shownistheurrent
den-sityinaquarteroftherosssetionandthemagnetield
lines(inset).
In long slabs or ylinders, with inreasing
paral-lel eld H
a > H
1
, vorties penetrate and the inner
indution
B inreases monotonially. The
magnetiza-tion in this longitudinal geometry is dened as M =
B=
0 H
a
, Fig.5. The negativemagnetization M
initially inreases linearly, M = H
a (H
a = B
a =
0 )
for H
a H
1
(Meissnerstate);at H
a =H
1
, M
de-reases sharplysineux lines start topenetrate; and
when H
a
is inreased further, M dereases
approxi-matelylinearlyuntilitvanishesatH
2
. Theareaunder
themagnetizationurve M(H
a )is
0 H
2
,whereB
=
0 H
=
0 =(
p
8) = B
2 =(
p
2) is the
thermody-namiritialeld. Insuperondutorswith=1= p
2
(this ase is almost exatlyrealized in pure Niobium)
thethreeritialeldsoinide,H
1 =H
=H
2 .
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
H / H
c2
− M / H
c2
2
1.5
1.2
1
0.85
κ
= 3
Ginzburg−Landau magnetization
of type−II superconductors
κ
= 0.75
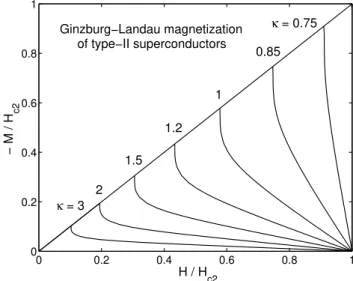
Figure 5. Magnetization urvesM(H) oflong type-II
su-perondutorsinparallelmagnetieldH(demagnetization
fatorN=0)alulatedfromGinzburg-Landautheoryfor
various Ginzburg-Landau parameters = 0.75 ::: 3. For
=1= p
2, M jumpsvertiallyfrom M =Hto M =0
The GL theory originally was derived for
temper-atures T lose to the superonduting transition
tem-perature T
, where / / (1 T=T
)
1=2
diverges.
But pratially the GL piture is a good
approxima-tion at all temperatures 0 < T < T
, in partiular
in impure superondutors with short eletron mean
free path. One usually assumes the temperature
de-pendenes (T) (0)(1 t 4
) 1=2
(with t = T=T
)
and H
(T)H
(0)(1 t 2
),yielding (T)(0)[(1+
t 2
)=(1 t 2
)℄ 1=2
.
At low indutions
B B
2
and large 1, the
propertiesofthevortexlattiemaybealulatedfrom
London theory, to whih theGL theoryredues when
themagnitude j j oftheGL funtion isnearly
on-stant. IntheLondonlimit,B(x;y)isthelinear
super-position of the elds of isolated vorties; the London
expressions for B(x;y) and for the energy apply thus
alsotononperiodiarrangementsofvorties. The
Lon-dontheorywasfurtherextendedtourvedvortiesand
to anisotropisuperondutors. Atlarger
B>0:25B
2
or smaller< 2,the GL theory hasto be used.
An-alyti GL solutions are available only forthe periodi
FLL nearB
2
,butnotforadistortedFLL orat lower
B.
Expanding the energy of the superondutor with
respettosmalldisplaementsofthevortiesfromtheir
ideallattiepositions,oneobtainstheelastimoduliof
the vortex lattie. As opposed to the loal elastiity
of atomilatties,theelastiityofthevortexlattieis
nonloal [3℄, i.e., the energy of ompressional and tilt
deformationsisstronglyreduedwhenthewavevetor
k ofthestraineldislarge,k> 1
,seeSt.4.
II. Results fromLondon Theory
TheLondontheorymaybeformulatedby
minimiz-ing thesumF of thepotentialenergyof themagneti
eld B(r) and the kineti energy of the superurrent
densityJ(r)= 1
0
rB(r) ,
F = 1
2
0 Z
V [B
2
+ 2
(rB) 2
℄d 3
r; (1)
with respet to B=rA. This yields the
homo-geneous London equation B 2
r 2
B = 0 or J =
1
0
2
A where the Maxwell equations rB = 0
and rB =
0
Jwereused and the vetorpotential
Awashoseninthe\Londongauge"rA=0.
A. Parallel vorties
Inthepreseneofvortiesonehastoadd
singulari-tieswhihdesribethevortexore. Forstraightparallel
vortexlinesalong^zonethusgetsthemodiedLondon
equation
B(r) 2
r 2
B(r)=^z
0 X
Æ
2 (r r
): (2)
Here r
=(x
;y
) are the two-dimensional (2D)
vor-tex positions and Æ
2
(r) = Æ(x)Æ(y) is the 2D delta
funtion. This linear equation may be solved by
Fouriertransformusing R
exp(ikr )d 2
k=4 2
Æ
2 (r)and
R
exp(ikr )(k 2
+ 2
) 1
d 2
k=2K
0
(jrj=). HereK
0 (x)
is amodied Bessel funtion with thelimits K
0 (x)
ln(x) forx 1and K
0
(x)(=2x) 1=2
exp( x) for
x 1. The resulting magneti eld of any
arrange-mentofparallelvortiesisthesumofindividualvortex
eldsenteredatthepositionsr
,
B(r)=^z
0
2 2
X
K
0
jr r
j
; (3)
see Fig. 1. The energy F
2D
of this 2D arrangement
of vortex lines with length L is obtainedby inserting
Eq. (2) into (1). Integrating over the delta funtion
onendsthattheLondon energyisdeterminedbythe
magnetield valuesat thevortexpositions,
F
2D
= L
0
2
0 X
B(r
)
= L
2
0
4
0
2 X
X
K
0
jr
r
j
: (4)
Thisexpression showsthat the energyis omposed of
the self-energy of the vorties (terms = ) and a
pairwise interation energy (terms 6= ). To avoid
thedivergene oftheself-energyonehasto utothe
logarithmi innity of B at the vortex enters r
by
introduing anite radius of the vortex oreof order
, the oherene lengthof the GL theory. This uto
may be ahieved by replaing in Eq. (4) the distane
r
=jr
r
jbyr~
=(r
2
+2
2
) 1=2
and
multiply-ingbyanormalizationfator 1to onservetheux
0
of thevortex. Thisanalytialexpressionsuggested
byClem[6℄forasinglevortexandlatergeneralizedto
thevortexlattie[7℄,isanexellentapproximation,as
wasshownnumerially[8℄by solvingtheGL equation
fortheperiodiFLLintheentirerangeof
Band,for
0
BB
2
and1= p
2.
B.Curved vorties
Arbitrary3Darrangementsofurvedvortiesat
po-sitionsr
(z) =[x
(z);y
(z);z℄ satisfy the 3D London
equation[3℄
B(r) 2
r 2
B(r)=
0 X
Z
dr
Æ
3 (r r
): (5)
Heretheintegralis alongthevortexlines andÆ
3 (r)=
Æ(x)Æ(y)Æ(z). Theresulting magnetield and energy
are,with~r
=[jr
(z) r
(z)j
2
+2 2
℄ 1=2
,
B(r) =
0
4 2
X Z
dr
exp[ ~r
(r
=r)=℄
~ r
(r
=r)
F
3D =
0
2
0 X
Z
dr
B(r
)
=
2
0
8
0
2 X
X
Z
dr
Z
dr
exp( r~
=)
~ r
:
This meansallthevortexsegmentsinteratwith eah
othersimilarasmagnetidipolesortinyurrentloops,
but the magneti long-range interation / 1=r is
sreenedbyafatorexp( r~
=). The3Dinteration
betweenurvedvortiesisvisualizedin Fig.6.
Interaction between curved flux lines
Figure6. Visualization ofthepairwiseinterationbetween
alllineelements(arrows)ofurveduxlineswithinLondon
theory,Eqs.(6)and(7).
C. Vorties neara surfae
The solutions (6) apply to vorties in the bulk.
Near the surfae of the superondutor these
expres-sions have to be modied. In simple geometries, e.g.
for superondutors with one or two planar surfaes
surrounded byvauum, themagneti eld andenergy
of a given vortex arrangement is obtained by adding
theeld ofappropriate images(in order tosatisfythe
boundaryonditionthatnourrentrossesthesurfae)
andamagnetistrayeldwhihisausedbyatitious
surfaelayerofmagneti monopoles and whih makes
the total magneti eld ontinuous aross the surfae
[9℄. Themagnetieldandinteration ofstraight
vor-ties orientedperpendiularto asuperondutinglm
ofarbitrarythiknessisalulatedin Ref.[10,11℄.
D. ThinFilms and Layered Superondutors
Near the surfae of a superondutor the self and
interation energies are modied. In lms of
thik-ness d the short 2D vorties interat mainly
viatheirmagnetistrayeld outsidethe
superondu-tor over an eetive penetration depth = 2 2
=d.
At short distanes r this interation is
loga-rithmi as in the bulk ase, and at large r it
dereases as exp( r=). With dereasing thikness
V(r)= R
(d 2
k=4 2
) ~
V(k)exp(ikr)hangesfrom ~
V(k)=
E
0 (k
2
+ 2
) 1
(d ) to ~
V(k)=E
0 (k
2
+k 1
) 1
(d ) whereE
0 =d
2
0 =(
0
2
). A similar (but 3D)
magneti interation exists between the 2D panake
vorties[12℄inthesuperondutingCuOlayersof
high-T
superondutors, ~
V(k)=E
0 dk
2
3 k
2
2 (
2
+k 2
3 )
1
,
where nowd is the distane between the layers, k 2
2 =
k 2
x +k
2
y , k
2
3 =k
2
2 +k
2
z
, and =
ab
is thepenetration
depthforurrentsowingin theselayers[12,3℄.
E. Anisotropi Superondutors
Formanypurposeshigh-T
superondutorsmaybe
onsidered as uniaxially anisotropi materials, whih
within London theory are haraterized by two
pen-etration depths
a
b
ab
(for urrents in the
ab plane)and
(forurrentsalong the axis). The
anisotropy ratio =
=
ab =
ab =
1 desribes
also the anisotropy of the GL oherene lengths,
ab
and
,whihareneededasinner utolengthsin the
anisotropiLondontheory. Thegeneralsolutionfor
ar-bitrarilyarrangedstraightorurvedvortexlinesis[3℄
B
(r) =
0 X
Z
dr
f
(r r
) (7)
F
3D =
2
0
2
0 X
X
Z
dr
Z
dr
f
(r
r
)
withthetensorialinteration(;=x;y;z)
f
(r) =
Z
d 3
k
8 3
exp(ikr)f
(k) (8)
f
(k) =
exp[ 2g(k;q)℄
1+
1 k
2
Æ
q
q
2
1+
1 k
2
+
2 q
2
:
Hereg(k;q)= 2
ab q
2
+ 2
(k
2
q 2
)=(
1 k
2
+
2 q
2
) 2
=
2
ab
enters the uto fator exp( 2g); q=k^ , ^ is the
unitvetoralongthe-axis,
1 =
2
ab ,
2 =
2
2
ab
0,andthesumsandintegralsareoverthethandth
vortexline. Duetothetensorialharateroff
(r)the
ontributionofthesegmentdr
toB(r)nowingeneral
isnotparalleltodr
.
III. Ginzburg-Landau, Pippard, and BCS
The-ories
The London theory was extended in two ways,
whihbothintrodueaseondlength: The
Ginzburg-Landau(GL)theoryisnonlinearin andthePippard
theory is nonloal in A. All three theories later were
shown to follow from the mirosopi BCS theory in
limitingases.
A. Ginzburg-Landau Theory
or-B(r) = rA(r). The GL funtion (r) is
propor-tional to the BCS energy-gap funtion (r), and its
square j (r)j 2
to thedensityofCooperpairs. The
su-peronduting oherene length gives the sale over
whih (r)an vary, while governsthe variationof
the magnetield as in London theory. Both and
divergeat thesuperondutingtransitiontemperature
T
aording to / / (T
T)
1=2
, but their
ra-tio, theGL parameter==,is nearlyindependent
of the temperatureT. The GL theory redues to the
London theory (whih is valid down to T =0) in the
limit,whihmeansonstantmagnitudej (r)j=
onst,exeptinthevortexores,where vanishes. The
GLequationsareobtainedbyminimizingafreeenergy
funtional Ff ;Ag with respet to the GL funtion
(r) and the vetorpotential A(r) . With the length
unit andmagnetieldunit p
2B
theGLfuntional
reads
Ff ;Ag= B
2
0 Z
h
j j 2
+ 1
2 j j
4
+j( ir
A) j 2
+(rA) 2
i
d 3
r: (9)
This funtional and the resulting GL equations may
beexpressed in terms ofthe real funtion j j and the
gauge-invariantsuperveloityr'= Awhere'(r)is
thephaseof =j jexp(i'). Thesuperurrentdensity
is J= 1
0
2
(r'= A)j j 2
. Inanexternaleld H
a
onehastominimizenotthefreeenergyFbuttheGibbs
freeenergyG=F
BH
a
. TheonditionG=
Byields
the equilibrium eld H
a
= F=
B. The reversible
magnetization urves
B(H
a
) of pin-free
superondu-tors, Fig.5,werealulatedinthiswayfromGLtheory
[8℄,togetherwiththeprolesof Fig.3.
TheGLtheorymodiestheLondoninteration
be-tweenvortiesin twoways: (a)Therangeofthe
mag-neti repulsion at large indutions
B beomes larger,
0
==(1
B=B
2 )
1=2
. (b)Aweakattrationofrange
0
= =(2 2
B=B
2 )
1=2
is added, aused by the
on-densation energy that is gained by the overlap of the
vortexores. Parallel vortexlines theninteratby an
eetive potential V(r) / K
0 (r=
0
) K
0 (r=
0
) whih
nolongerdivergesatzerodistane r[13℄.
B. Pippard Theory
Inspired by Chamber's nonloal generalization of
Ohm's law,Pippard1953introduedasuperondutor
oherenelengthbygeneralizingtheLondonequation
0
J= 2
L
Ato anonloalrelationship[2℄
0
J(r)= 2
P 3
4 2
Z
r 0
(r 0
A(r r 0
))
r 03
e r
0
=
d 3
r 0
:(10)
In the presene of eletron sattering with mean
free path l, the Pippard penetration depth
P =
( 2
L
0 =)
1=2
exeedstheLondon penetrationdepth
L
of a pure material with oherene length , sine
the eetive oherene length is redued by
sat-tering, 1
1
0 +l
1
[2℄. In the limit of small
P
,Eq.(10)reduestotheloalrelation
0 J(r)=
2
P
A(r) . In Fourierspae Pippard'sEq. (10) reads
0
J(k)= Q
P
(k)A(k) with
Q
P
(k)= 2
P h(k);
h(x)= 3
2x 3
h
(1+x 2
)atanx x i
; h(0)=1: (11)
ThisPippardtheoryis usefulmainlyfor
superondu-torswithsmallGLparameter.
BCSTheory
The mirosopi BCS theory (in the Green
fun-tion formulationof Gor'kov)for weak magneti elds
yieldsasimilarnonloalrelation
0
J(k)= Q(k)A(k)
assuggestedbyPippard,replaing thePippardkernel
Q
P
(k)bytheBCSkernel[14,3℄
Q
BCS (k)=
2
(T) 1
X
n=1 h[k
K
=(2n+1)℄
1:0518(2n+1) 3
: (12)
Hereh(x)isdenedinEq.(11),(T)=Q
BCS (0)
1=2
(0)(1 T 4
=T 4
)
1=2
isthetemperaturedependent
mag-neti penetration depth, and
K = ~v
F =(2k
B T)
0:844(T)T
=(T)(v
F
= Fermi veloity, = GL
pa-rameter). The range of the BCS Gorkov kernel is of
theorderoftheBCSoherenelength
0 =~v
F =(
0 )
where
0
istheBCSenergygapat T =0.
With the nonloal relation
0
J(k) = Q(k)A(k)
the Eq. (2) for a vortex line at r
= 0 now beomes
[1 +Q(k) 1
k 2
℄ ~
B(k)=
0
withthesolution
~
B(k)=
0 Q(k)
Q(k)+k 2
;
B(r)=
0
2 Z
1
0
Q(k)
Q(k)+k 2
J
0
(kr)kdk; (13)
where J
0
(x) is a Bessel funtion. The Pippard or
BCS eld B(r) (13) of an isolated vortex line is no
longermonotoni asompared with the London eld,
f. Eq. (3), but it exhibitsaeld reversal witha
neg-ative minimum at large distanes r
P
from the
vortexore. Thiseet should beobservableif ,
i.e., forlean superondutorswithsmall GL
parame-teratlowtemperatures. Seealsoreentworkonthis
nonloaleletrodynamis[15℄.
Theeldreversalofthevortexeldispartly
respon-siblefortheattrativeinterationbetweenuxlinesat
largedistanes, whih wasobserved in lean Niobium
attemperaturesnottooloseto T
andwhih follows
from BCStheory at T <T
for pure superondutors
with GL parameter lose to 1= p
2. This attration
leadstoabrupt jumps in themagnetizationurveand
toan agglomerationofux lines that anbeobserved
asFLLislandssurroundedbyMeissnerstate,or
Meiss-nerislandssurrounded byFLL[16℄. For thedenition
ofN seeSe.5.
Another BCS eet whih diers from the GL
re-sult is that in lean superondutors at low
tempera-tures the periodi magneti eld B(x;y) of the FLL
nearB
2
isnotasmoothspatialfuntionasinGL
the-ory, but has sharp onial maxima and minima suh
that the prole B(x;0) along a nearest neighbor
di-retion has zig-zag shape [3℄. The reason for this is
that theeletronmeanfreepathin pure
superondu-tors at T ! 0 beomes larger than the vortex
spa-ing a
0
. This leads to a slow derease of the Fourier
oeÆients B
K
/ ( 1)
m+mn+n
K 3
mn
of B(x;y), while
at T T
the GL theory near B
2
yields arapid
de-rease,B
K
/ ( 1)
m+mn+n
exp( K 2
mn x
1 y
2
=8). Here
K = K
mn
= (2=x
1 y
2 )(my
2 ; mx
2 +nx
1
) (m;n =
1;2;3;:::)arethereiproallattievetorsoftheideal
vortexlattiewithpositionsR
mn =(mx
1 +nx
2 ;ny
2 ),
andx
1 y
2 =
0 =
Bistheareaoftheunitell,see Fig.2.
IV. Elastiity of the Vortex Lattie
Theux-linedisplaementsausedbypinningfores
and by thermal utuations may be alulated
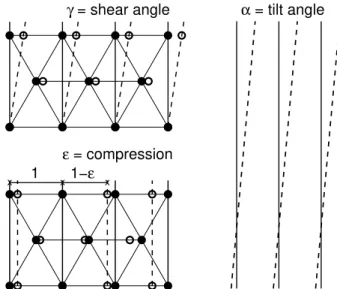
us-ing the elastiity theory of the FLL. Fig. 7
visual-izes the three basi distortions of the triangular FLL:
shear,uniaxial ompression,and tilt. The linear
elas-ti energyF
elast
of the FLL is obtained byexpanding
its free energy F with respet to small displaements
u
(z)=r
(z) R
=(u
x ;u
y
)of theux linesfrom
theiridealparallellattiepositionsR
andkeepingonly
thequadratiterms. Thisyields[3℄
F
elast =
1
2 Z
BZ d
3
k
8 3
u
(k)
(k)u
(k) (14)
whereu(k)istheFouriertransformofthedisplaement
eld u
(z), now (;) = (x;y), and k = (k
x ;k
y ;k
z ).
Thek-integralinEq.(14)isovertherstBrillouinzone
(BZ) of the FLL sine the \elasti matrix"
(k) is
periodiinthek
x ;k
y
plane;thenitevortexoreradius
restritsthek
z
integration to jk
z j
1
. Foran
elas-timedium withuniaxialsymmetrytheelasti matrix
reads
(k)=(
11
66 )k
k
+Æ
[(k
2
x +k
2
y )
66 +k
2
z
44
℄: (15)
The oeÆients
11 ,
66 , and
44
are the elasti
mod-uliofuniaxialompression,shear,andtilt,respetively.
FortheFLL,
(k)wasalulatedfromGLand
Lon-don theories [3℄. The result, a sum over reiproal
lattievetors,should oinidewith expression(15)in
the ontinuum limit, i.e., for small jkj k
BZ , where
k
BZ = (4
B=
0 )
1=2
is the radius of the irularized
FLLwithareak 2
BZ
. IntheLondonlimitonendsfor
isotropisuperondutorstheelastimoduli
11 (k)
B 2
=
0
1+k 2
2
;
66
B
0 =
0
16 2
;
44 (k)
11
(k)+2
66 ln
2
1+k 2
z
2
: (16)
TheGLtheoryyieldsanadditionalfator(1
B=B
2 )
2
in
66
, i.e.,
66 /
B(
B B
2 )
2
, and replaes in
11
(k) by 0
[17, 8℄. The k dependene (dispersion)
of the ompression and tilt moduli
11
(k) and
44 (k)
means that the elastiity of the vortex lattieis
non-loal, i.e., strainswithshort wavelengths2=k 2
haveamuh lowerelastienergy thanahomogeneous
ompression or tilt (orresponding to k ! 0). This
elasti nonloality omes from the fat that the
mag-neti interation between the ux lines typially has
a range muh longer than the ux-line spaing a
0 ,
therefore,eahuxlineinteratswithmanyotherux
lines. Note that large ausesa small shear stiness
sine
66 /
2
,Eq. (16),andasmaller
11 (k>
1
),
but theuniformompressibility
11
(k=0) is
indepen-dentof.
γ
= shear angle
α
= tilt angle
ε
= compression
1
1−
ε
x
x
x
Figure 7. Thethreebasi homogeneouselasti distortions
of the triangular ux-line lattie. Thefull dots and solid
linesmarktheideallattieandthehollowdotsanddashed
linesthedistortedlattie.
The ompressional modulus
11
and the typially
muhsmallershear modulus
66
11
44
originate
from theux-lineinteration, but thelast termin the
tiltmodulus
44
(16)originatesfromthelinetensionof
isolated ux lines, dened by P =lim
B!0 (
44
0 =
B).
In isotropi (or ubi) superondutors like Nb and
its alloys, the line tension P oinides with the self
energy F
s
of a ux line, P = F
s , F
s
=
0 H
1
( 2
0 =4
0
2
)(ln+0:5) for 1. In anisotropi
materials theline tensionand line energyof ux lines
P()=F
s ()+
2
F
s =
2
. UsingF
s ()=F
s (0)(os
2
+
2
sin 2
) 1=2
with =
=
ab
1,oneobtainsP(0)=
F
s (0)=
2
and P(=2)=F
s (=2)
2
=P(0)= 3
(fortilt
out of the ab-plane) [3℄. In isotropisuperondutors
the uniaxial symmetryof the idealvortexlattie, i.e.,
the appearane of a preferred axis, is indued by the
applied magnetield. This indued anisotropyleads
toasmalldierenebetweentheompressionalandtilt
moduli
11 and
44
,butnottoadierenebetweenline
energyandline tension.
As a onsequene of nonloal elastiity, the
ux-linedisplaementsu
(z)ausedbyloalpinningfores,
and also the spae and time averagedthermal
utu-ations hu
(z)
2
i, are muh larger than they would be
if
44
(k) had no dispersion, i.e., if it were replaed
by
44 (0) =
BH
a
B 2
=
0
. The maximum vortex
displaement u(0) / f aused at r = 0 by a point
fore of density fÆ
3
(r), and the thermal utuations
hu 2
i/k
B
T,aregivenbysimilarexpressions[3℄,
2u(0)
f
hu 2
i
k
B T
Z
BZ d
3
k
8 3
1
(k 2
x +k
2
y )
66 +k
2
z
44 (k)
k
2
BZ
8[
66
44 (0)℄
1=2 : (17)
In this result a large fator [
44 (0)=
44 (k
BZ )℄
1=2
k
BZ
=a 1 originates from the elasti
non-loality. InanisotropisuperondutorswithBk, the
thermalutuations(17)areenhanedbyanadditional
fator =
=
ab
[3℄. Foranexatanalytievaluation
oftheintegral(17)forhu 2
isee[18℄.
V. High-T
Superondutors
The nonloal elasti response of the vortex lattie
is partiularly important for understanding the
ther-modynamiandeletrodynamipropertiesofthe
high-T
superondutors,whihweredisoveredin1987and
the following years. These oxideswith high
superon-dutingtransitiontemperatureT
(e.g. YBa
2 Cu
3 O
7 Æ
with T
=92:5K, Bi
2 Sr
2 Ca
2 Cu
3 O
10+Æ
withT
=120
K, and some Hg and Tl ompounds with even higher
T
) arelayeredstrutures withmoreorlessdeoupled
superonduting Cu-O layers. Theythus exhibit high
anisotropyoftheirsuperondutingproperties. For
ex-ample, YBCO has an anisotropy = 5 and BSCCO
has 100. This means in BSCCO the layers are
almostdeoupledandthepenetrationdepth
for
ur-rentsowingalong the axisis marosopiallylarge,
=
a with
ab
140nmatT =0. Therefore,the
magneti eld omponent parallel to the layers
pene-trateseasily.
This large
also auses very pronouned elasti
nonloality,whihmeansaverysoftvortexlattie. The
vortiesare thusstronglypinnedolletively,sinethe
vortexlattieadjuststothepins,butathigher
temper-sinetheelementarypinningenergyofveryexible
vor-tiesissmall. Bythesametoken,thermalutuations
ofthevortiesarelargeandmayevenausemeltingof
thevortexlattieintoavortexliquid.
Theeetsoftheelastinonloalityandanisotropy
on the thermal utuation, melting, and pinning of
the FLL are treated in detail in the review [19℄,
wherealso phasediagramsin theH
a
-T plane are
pre-sentedfor3Dandlayeredsuperondutors. Phase
dia-grams obtained by applying simple Lindemann
rite-ria (hu 2
i = 2
L a
2
0 ,
L
0:25) to both thermal and
pinning-aused utuations in 3D superondutors at
not too low elds (
B > B
1
) are alulated in [20℄,
namely, thelineH
m
(T)where theFLLmelts, theline
H
sv
(T) whih separates the regimes of
single-vortex-pinning and of vortex-bundle-pinning, and the order{
disorderlineH
dis
(T)abovewhihpinningauses
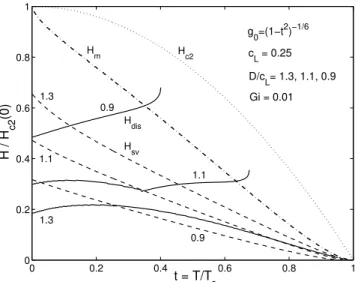
plas-ti deformation of the FLL, see Fig. 8. In this ase
(B =
0
H, no deoupling of layers) the phase
dia-gram in redued units H
a =H
2
(0) and t = T=T
,
de-pendsonlyontheGinzburgnumberGiandonthe
pin-ningstrengthD=[J
(0)=J
0 (0)℄
1=2
(ritialurrentfor
B!0overthedepairingurrent,bothatT =0), see
[20℄.
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
g
0
=(1−t
2
)
−1/6
c
L
= 0.25
D/c
L
= 1.3, 1.1, 0.9
Gi = 0.01
H
c2
1.3
t = T/T
c
H / H
c2
(0)
H
m
1.3
1.1
1.1
0.9
0.9
H
sv
H
dis
Figure8. Theorder{disorderlinesH
dis
(t)(solidlines) and
single-vortex pinning boundaries Hsv(t)(dashed lines) for
threepinningstrengths D=
L
=1:3, 1.1,0.9andGinzburg
numberGi =0:01. Assumedwas ÆT
pinning. The
dash-dotted line is the melting line Hm(t) and the dotted line
showsH
2 (t)=H
2
(0)(1 t 2
).
VI. ContinuumDesription ofthe Vortex State
Ifoneisinterestedonlyin lengthsaleslargerthan
thevortexspainga
0
,onemayuseaontinuum
desrip-tionofthevortexstatetoalulatethedistributionsof
arbi-[21, 22℄ whih in priniple allow to ompute the
ele-tromagneti behavior of superondutors of arbitrary
shapewithandwithoutvortexpinning. Theextension
tonite Londondepthisgivenin[5℄.
ApartfromtheMaxwellequations,aontinuum
de-sriptionrequirestheonstitutivelawsofthe
superon-dutor. These maybeobtained,e.g.,fromtheLondon
theory,St.II,bytakingthelimitsa
0
!0and !0
(or keeping nite [5℄), and from appropriate
mod-els of vortex dynamis. One onstitutive law is the
reversible magnetization urve of a pin-free
superon-dutor, M(H) or
B(H) =
0 H+
0
M(H), where H
is aneetive applied eld whih wouldbe in
equilib-riumwith the loal indution
B. Inthe simplestase
this lawmayread M =0or
B =
0
H, validif
every-where
B islargerthan several timesthe lowerritial
eld B
1
. But in general the reversible M(H)
om-puted from London or GLtheories should be used, as
disussedin[21,22,23,24℄.
WhenthenitelowerritialeldH
1
isaounted
for, themagnetizationurveM(H
a
)in generalis
irre-versible(i.e. a loop) even in omplete absene of
vor-texpinning. This pin-freeirreversibilityisausedbya
geometribarrier forthepenetrationofmagneti ux,
whihisabsentonlyifthesuperondutorhastheshape
ofanellipsoidorifithasasharpedgeorusp,atwhih
theappliedeldH
a
isstronglyenhanedsuhthatux
lines anpenetrate easily. For example, in
superon-duting ylinders orstrips with retangular ross
se-tion 2a2b (2a = diameter or width, 2b = height)
ininreasingH
a
,themagnetiux penetrates rst
re-versiblyat the four orners in form of nearly straight
uxlines,seeFigs.4,9. Whentheeldofrstux
en-tryB
en
isreahed, theseuxlines joinat theequator,
ontrat,andjumptothespeimenenter,fromwhere
theygraduallylltheentiresuperondutor. WhenH
a
isdereased again,someux exits rstreversibly, but
below areversibility eld H
rev > H
en
the
magnetiza-tion loopopens, see Fig.10, sinethe barrier for ux
exitisabsentorweakerthanthebarrierforuxentry.
Forarbitraryaspetratiob=atheentryeldis[22,24℄
H
en H
1 tanh
p
b=a; (18)
where=0:36forstripsand=0:67fordisksor
ylin-ders. This geometri barrier should not be onfused
with the Bean-Livingstonebarrier for the penetration
ofastraightvortexlineintotheplanarsurfaeofa
su-perondutor,whihwould leadto asimilar
asymmet-rimagnetizationloop. Thegeometribarrierisaused
bythelinetensionofthevortiespenetratingatsharp
[21,22,24℄orrounded[25℄orners. ThislinetensionP
(seeSt.IV)isbalanedbytheLorentzforeexertedon
the vortex ends bythe surfaesreening urrentsand
diretedtowardsthespeimenenter. Theirreversible
magneti behaviorof thin strips with an edge barrier
(and without or with bulk pinning) in perpendiular
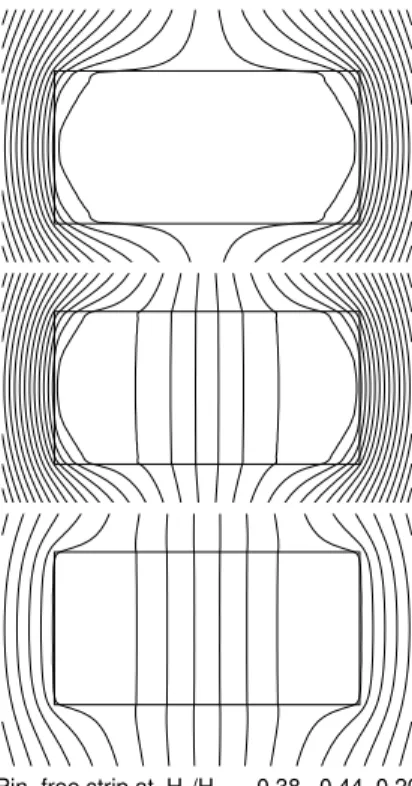
H wasalulatedanalytiallybyZeldovet al.[26℄.
Pin−free strip at H
a
/H
c1
= 0.38, 0.44, 0.20
Figure 9. The magneti eld lines inand near a pin-free
strip of aspet ratio b=a = 0:5 in an inreasing applied
perpendiular eld H
a
at twoeld values H
a =H
1 = 0:38
(top)and0.44(middle)justbelowandabovetheentryeld
H
en
=0:40H
1
, and indereasing eldat H
a =H
1 =0:20
(bottom).
0
0.2
0.4
0.6
0.8
1
1.2
0
0.2
0.4
0.6
0.8
1
1.2
H
a
/ H
c1
−
M / H
c1
Pin−Free cylinders
∞
0.25
b/a = 0.08
1
5
Figure 10. Irreversible magnetization of pin-freeylinders
withvariousaspetratiosb=a=0.08(thindisk)to1(long
ylinder) in ayled axial magnetield Ha (solid lines).
Thedashedlinesshowthereversiblemagnetization urves
of ellipsoids hosen suh that they have the same initial
slope1=(1 N)astheorrespondingylinder.
The omputed irreversible magnetization loops of
pin-free superondutor ylinders with various aspet
ratiosb=a=0:08(thindisk)tob=a=1(longylinder)
withtheorrespondingreversiblemagnetizationurves
of ellipsoids whih have thesame initial slope
(Meiss-ner state)astheylinders. Thesemagnetization loops
of ylinders (like those of other non-ellipsoids) havea
maximumatH
a H
en
,andatH
a >H
rev
theyare
re-versibleandoinidewiththemagnetizationofthe
or-responding ellipsoid. All pin-free magnetization loops
are symmetri, M( H
a
) = M(H
a
) with M(0)= 0,
i.e., noremanentux anremainatH
a
=0sinebulk
pinning is absent and there is no barrier for ux exit
when H
a
=0. Fig. 11 showsmagnetization urvesof
ashortylinderwithniteH
1
forvariousstrengthsof
bulkpinning.
0
0.5
1
1.5
2
−1
−0.5
0
0.5
1
1.5
H
a
/ H
c1
− M / H
c1
Pinning: J
c
a/H
c1
= 0, 0.25, 0.5, 1, 1.5, 2, 3, 4
Disk with b/a = 0.25
H
c1
= const
Figure 11. Magnetization loops of a thik disk with
as-petratiob=a=0:25andonstantH1butvariouspinning
strengths J
=0.25, 0.5,1,1.5, 2,3,4inunitsH
1 =aand
for varioussweepamplitudesoftheappliedeldHa. Bean
model, i.e., the ritial urrent density J
is independent
of theindutionB. Theinnerloopbelongsto thepin-free
diskandtheouterlooptostrongestpinning(J=4). The
bold dashedlineshowsthe reversible magnetizationofthe
orrespondingellipsoid.
The reversible magnetization urves of pin-free
el-lipsoidsM(H
a
;N)followfromthemagnetizationurve
M(H
a
;N=0)=
B=
0 H
a
oflongylindersin
paral-leleld H
a
bytheoneptofademagnetizationfator
N. Onehas0N 1, N =0for parallelgeometry,
N = 1=2 for innite ylinders in perpendiular eld,
N =1=3for spheres,and N =1forthin lmsin
per-pendiulareld. Forellipsoidswith N 6=0onehasto
solvetheimpliitequationforaneetiveinternaleld
H
i [24℄,
H
i =H
a
NM(H
i
;N =0); (19)
to obtain the reversible magnetization M(H
a ;N) =
M(H
i
;N = 0) (dashed lines in Fig. 10) from the
M(H
a
;N=0) oflongitudinalgeometry. Inpartiular,
intheMeissnerstate(
B0)onehasM(H
a
;0)= H
a
and M(H
a
;N) = H
i
= H
a
=(1 N) for jH
a j
(1 N)H
1 .
As a seond onstitutive law one may use the
lo-al eletri eld E=E (J;B) whih is generated by
moving vortiesand whih in a ompat way an
de-sribe free ux ow and Hall eet, but also vortex
pinning and thermally ativated depinning or reep.
A simple but still quite general isotropi model is
E
v
= (J;B)Jwith = onstB (J=J
)
n 1
, where
J
istheritialurrentdensityandnthereep
expo-nent [5, 27℄. This realistimodelmeans anativation
energyU(J)=U
0 ln(J
=J)fordepinningthatentersin
E=E
exp[ U(J)=kT℄=E
(J=J
)
n
withn=U
0 =kT.
Within this model, ux ow is desribed by n = 1,
ux reep (relaxation with approximately logarithmi
timelaw)byn1,andBean's ritialstatemodelof
vortex pinningby the limitn ! 1. In general,both
J
and n may depend on the loal indution
B and
onthe temperature T. Fig. 12 shows some
magneti-zation loops of a short ylinder alulated in [27℄ for
two dierent J
(B) models and two reep exponents.
Fortheeletrodynamisofthin strips,disks,andrings
in a perpendiular eld see [28, 29, 30℄, and for thin
retanglesandlms ofothershapessee[31, 32℄. Thin
strips in perpendiular d and a magneti elds and
withtransporturrentareonsidered in[33℄. Analyti
andnumerialsolutionswerealsoobtainedforux
ex-pulsion and penetration into thin strips with a bend
alongthemiddle line[34℄and forthin shells (or hats)
ofonialshape[35℄.
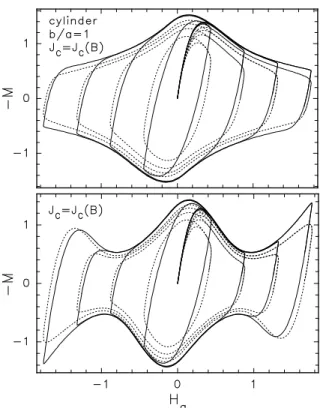
Figure 12. Magnetization loops of ylinders with aspet
ratio b=a = 1, reep exponents n = 51 (bold lines) and
n=5(dashed lines), withB1 =0,insinusoidally yled
appliedeld Ha for two indutiondependent ritial
ur-rent densities J(B)=J0=(1+3)(top,Kim model) and
J
(B) =J
0
(1 3+3 2
) (bottom, a \sh-tail" model),
where =jBj=Bp, Bp =0:880J0a. The magnetization
M is inunits J
0
a=(2) and H
a
inunits J
0
a, where a, b
In all these alulations the London depth was
assumed to be negligibly small. Finite may be
a-ounted forby modifying theurrent{voltagelaw,
us-ingE=E
v
(J;B)+
0
2
j=t[5℄. Here therstterm
is generated by moving vorties and the seond term
desribestheMeissner surfaeurrents[4,5℄.
Referenes
1. P.G. DeGennes, Superondutivity of Metals
andAlloys,NewYork,Benjamin,1966.
2. M. Tinkham, Introdution to
Superondutiv-ity, NewYork,MGraw-Hill,1975.
3. E.H. Brandt, Rep. Progr. Phys. 58 (1995)
1465-1594.
4. E.H.BrandtandG.P.Mikitik,Phys.Rev.Lett.
85(2000)4164.
5. E.H. Brandt,Phys.Rev. B64 (2001)024505,
1-15.
6. J.R.Clem,J.LowTemp.Phys. 18(1975)427.
7. Z.Hao,J.R.Clem,M.W.MElfresh,L.Civale,
A.P. Malozemov, F. Holtzberg, Phys. Rev. B
43(1991)2844.
8. E.H.Brandt,Phys.Rev.Lett. 78(1997)2208.
9. E.H. Brandt, J. Low Temp. Phys. 42 (1981)
557.
10. Jung-ChunWei,Tzong-YerYang,Jpn.J.Appl.
Phys. 35(1996)5696.
11. G. Carneiro, E.H. Brandt, Phys. Rev. B 61
(2000)6370.
12. J.R.Clem,Phys.Rev.B43 (1991)7837.
13. E.H.Brandt,Phys.Rev.B34(1986)6514.
14. A.A.Abrikosov,L.P.Gorkov,I.E.
Dzyaloshin-ski, Methods of Quantum Field Theory in
Statistial Physis, EnglewoodClis, Prentie
Hall,1963.
15. V.G. Kogan et al., Phys. Rev. B 54 (1996)
12386.
16. E.H. Brandt,U. Essmann, phys. stat. sol.(b)
144(1987)13.
17. E.H.Brandt,Phys.Stat.Sol.b,77(1976)709.
18. I.M. Babih, Yu.V. Sharlai,G.P. Mikitik, Fiz.
Nizk. Temp.20(1994) 227[Low Temp. Phys.
20 (1994)220℄.
19. G. Blatter, M.V. Feigel'man, V.B.
Geshken-bein, A.I. Larkin, V.M. Vinokur, Rev. Mod.
Phys. 66(1994)1125.
20. G.P. Mikitik, E.H. Brandt, Phys. Rev. B 64
184514(2001),1-14.
21. R.Labush,T.B.Doyle,PhysiaC290(1997)
143.
22. E.H.Brandt,Phys.Rev.B59(1999)3369.
23. T. Hoquet, P. Mathieu and Y. Simon,
Phys.Rev.B46 (1992)1061.
24. E.H.Brandt,Phys.Rev.B60(1999)11939.
25. M. Benkraouda, J.R. Clem, Phys. Rev. B 58
(1998)15103.
26. E. Zeldov, A.I. Larkin, V.B. Geshkenbein, M.
Konzykowski,D.Majer,B.Khaykovih,V.M.
Vinokur, H. Strikhman, Phys. Rev. Lett. 73
(1994)1428.
27. E.H.Brandt,Phys.Rev.B58(1998)6506.
28. E.H.Brandt,Phys.Rev.B50(1994)4034.
29. D.V.Shantsev,Y.M.Galperin,T.H. Johansen,
Phys.Rev.B60 (1999)13112.
30. E.H.Brandt,Phys.Rev.B55(1997)14513.
31. L. Prigozhin, J. Comput. Phys. 144 (1998)
180.
32. E.H.Brandt,Phys.Rev.B52(1995)15442.
33. G.M. Mikitik and E.H.Brandt, Phys. Rev. B
64 (2001)092502,1-4.
34. Leonardo R.E. Cabral and J. Albino Aguilar,
PhysiaC341-348,1049(2000).
35. Leonardo R.E. Cabral, Thesis, Universidade