Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761
Integral transform of MHD flow with heat and mass transfer of a biofluid
in a parallel plate channel
Transformação integral do escoamento MHD com transferência de calor e
massa de um biofluido em um canal de placa paralela
DOI:10.34117/bjdv5n10-052
Recebimento dos originais: 10/09/2019 Aceitação para publicação: 04/10/2019
Helder Kiyoshi Miyagawa Mestre em Eng. Química pela UFPA
Instituição: Universidade Federal do Pará, Programa de Pós-Graduação em Engenharia de Recursos Naturais da Amazônia.
Endereço: Universidade Federal do Pará, 66075-110 Belém, PA, Brasil E-mail: helderkm@ufpa.br
Fábio de Andrade Pontes Mestre em Eng. Química pela UFPA
Instituição: Universidade Federal do Pará, Programa de Pós-Graduação em Engenharia de Recursos Naturais da Amazônia.
Endereço: Universidade Federal do Pará, 66075-110 Belém, PA, Brasil E-mail: fabioapbelem@hotmail.com
Ingrid Vasconcelos Curcino Bacharel em Eng. Química pela UFPA
Instituição: Universidade Federal do Pará, Programa de Pós-Graduação em Engenharia de Recursos Naturais da Amazônia.
Endereço: Universidade Federal do Pará, 66075-110 Belém, PA, Brasil E-mail: ingrid.curcino@hotmail.com
Jackline Rodrigues Ferreira Mestre em Eng. Química pela UFPA
Instituição: Universidade Federal do Pará, Programa de Pós-Graduação em Engenharia de Recursos Naturais da Amazônia.
Endereço: Universidade Federal do Pará, 66075-110 Belém, PA, Brasil E-mail: jackroguis@hotmail.com
Péricles Crisiron Pontes
Mestre em Engenharia Mecânica pelo Instituto Alberto Luiz Coimbra de Pós Graduação e Pesquisa em Engenharia, COPPE/UFRJ
Instituição: IEA/UNIFESSPA, Universidade do Sul e Sudeste do Pará, Campus Santana do Araguaia
Endereço: IEA/UNIFESSPA, Bel Recanto, Rua Albino Malzoni, 68560-000 Santana do Araguaia, PA, Brasil
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 Emanuel Negrão Macedo
Doutor em Engenharia Mecânica pelo Instituto Alberto Luiz Coimbra de Pós Graduação e Pesquisa em Engenharia, COPPE/UFRJ
Instituição: Universidade Federal do Pará, Faculdade de Engenharia Química Endereço: Universidade Federal do Pará, Faculdade de Engenharia Química, 66075-110
Belém, PA, Brasil E-mail: enegrao@ufpa.br
João Nazareno Nonato Quaresma
Doutor em Engenharia Mecânica pelo Instituto Alberto Luiz Coimbra de Pós Graduação e Pesquisa em Engenharia, COPPE/UFRJ
Instituição: Universidade Federal do Pará, Faculdade de Engenharia Química Endereço: Universidade Federal do Pará, Faculdade de Engenharia Química, 66075-110
Belém, PA, Brasil E-mail: quaresma@ufpa.br
RESUMO
Foi estudado o escoamento transiente pulsátil através de um canal poroso do tipo Darcy-Forchheimer de um biofluido influenciado por um campo magnético externo aplicado transversalmente ao canal com reação química. Na formulação matemática foi considerado o escoamento laminar, bidimensional, incompressível de um fluido eletricamente condutor, através de um meio poroso, dentro de um canal formado entre placas planas paralelas com transpiração da parede. Os campos de velocidade, concentração e temperatura foram solucionados utilizando a Técnica da Transformada Integral Generalizada (GITT) e foi realizada uma análise de convergência das expansões em série, obtendo convergências satisfatórias com poucos termos nos somatórios. As soluções obtidas foram comparadas com as da literatura obtendo-se uma boa concordância em todos os campos e situações estudadas. Foi avaliada ainda a influência do número de Reynolds, do número de Prandtl, do número de Schmidt e do parâmetro magnético nos perfis de velocidade, temperatura e concentração, observando-se que o escoamento é fortemente sensível aos efeitos do número de Reynolds e do parâmetro magnético. Uma análise transiente também foi realizada observando que devido ao fluido estar em repouso no início, ele não é imediatamente acelerado, gerando um retardo no perfil de velocidade para tempos pequenos.
Palavras-chave: Biofluido, GITT, MHD, transferência de massa, transferência de calor.
ABSTRACT
The pulsed transient flow through a Darcy-Forchheimer porous channel of a biofluid influenced by an external magnetic field applied transversely to the channel with chemical reaction was studied. In the formulation, the two-dimensional, incompressible, electrically conductive laminar flow through a porous medium into a channel formed between parallel flat plates with wall transpiration was considered. The velocity, concentration, and temperature fields were solved using the Generalized Integral Transform Technique (GITT) and convergence analysis of the series expansions was performed, obtaining satisfactory convergences with few terms in the summation. The obtained solutions were compared with
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 those of the literature obtaining a good agreement in all the studied fields and situations. The influence of Reynolds number, Prandtl number, Schmidt number and magnetic parameter on the velocity, temperature and concentration profiles was also evaluated. magnetic. A transient analysis was also performed noting that because the fluid is at rest at the beginning, it is not immediately accelerated, causing a delay in the velocity profile for short times.
Keywords: Biofluid, GITT, MHD, Mass Transfer, Heat Transfer
1
INTRODUCTION
The fluid dynamics of biological fluids (biofluidodynamics), i.e., blood, subjected to influence of an external magnetic field (commonly generated by the application of magnetic dipoles) is known as BFD (Biomagnetic Fluid Dynamics) and is an emerging branch of fluid mechanics. The magnetic properties of blood arise from interactions of hemoglobin, cell membrane and intercellular protein (Higashi et al., 1993). Moreover, blood exhibits viscoelastic behavior under certain conditions as a function of the internal structures and viscoelastic properties of individual erythrocytes (Fukada and Kaibara, 1980; Stoltz and Lucius, 1981).
Jang and Lee (2000) mentioned some advantages of using magnetic fields as a way to manipulate fluids (Magnetohydrodynamics, MHD) in microscales such as the simplicity in the fabrication process and bidirectional pumping ability what is useful in some chemical, medical, and biological applications.
Several experimental and theoretical studies have been conducted in recent years in biofluidodynamics, which have important potential applications in biomedical sciences, including drug transport using magnetic particles as carriers, reduction of bleeding during surgery and development of magnetic devices for cell separation (Andra and Nowak, 1998).
As mentioned by Ritman and Lerman (2007) in some diseases a porous structure is formed within the arteries by fatty substances (cholesterol and blood clots), which in excess can lead to problems such as myocardial infarction or stroke. Therefore, it demands special attention to the development of strategies that allow a better understanding and, consequently, to develop remediation measures of such diseases.
The modeling and simulation of physicochemical and biological phenomena allow a theoretical rigorous analysis of the process, so that, from a mathematical model with a reasonable amount of information, the optimal operating conditions can be investigated. It is a complicated task. After all, generally, the larger the information load inserted in a
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 mathematical model, the more complex it tends to be, which implies a great challenge to obtain its solution.
As an alternative to classical numerical methods, the hybrid technique called GITT (Generalized Integral Transform Technique) is capable of treating a wide variety of nonlinear problems (Cotta and Mikhailov, 1997). It is based on the use of orthogonal eigenfunction expansions to express unknown dependent variables (Sphaier et al., 2011).
Pontes et al. (2019) evaluated the oscillating magnetohydrodynamic flow of an electrically conducting micropolar fluid in a porous medium with chemical reaction via GITT, studying the effects of a magnetic field and first-order chemical reaction with constant coefficients, obtaining results in excellent agreement with literature data.
In their work, Ferreira et al. (2019) performed the parameter estimation of a MHD pulsatile blood flow through a porous blood vessel, under the action of a magnetic field, pressure gradient and subjected to an externally imposed periodic acceleration field applying Method of Lines (MOL). The results show the efficiency of ABC algorithm to estimate the parameters of mathematical models of this nature.
In this context, the aim of the present work is the solution by the application of GITT of the pulsatile transient flow (modeling the heart pumping phenomenon) with heat and mass transfer of blood in a parallel plate channel (representing the geometry of the arteries) through a Darcy-Forchhmeir type porous medium (condition of some heart diseases) and in the presence of an homogeneous and irreversible reaction of the first order and to a constant transverse magnetic field. The convergence analysis of the series expansions, the numerical verification of the velocity (U), temperature (θ) and concentration (ϕ) profiles in comparison with the results of Ali et al. (2015), as well as the evaluation of the effects of some physical parameters on these fields are presented.
2 MATHEMATICAL FORMULATION
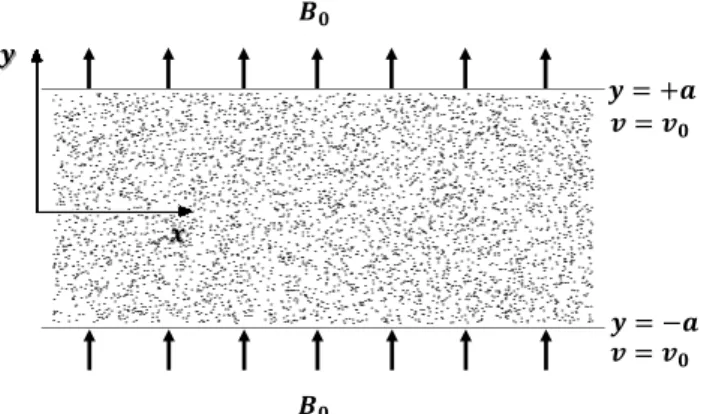
This research considers the transient two-dimensional pulsatile incompressible laminar flow of an electrically conductive biological fluid through a porous medium within a parallel plates channel with wall transpiration subjected to the action of a transverse magnetic field under isothermal conditions and chemical reaction. The flow is driven by a pressure gradient with steady and oscillatory components, whereas the wall transpiration is modeled considering the injection at the lower plate and suction at the upper one. The biofluid has been treated as the Casson fluid in order to model blood flow behavior.
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 No wall transpiration effects (suction/injection) are assumed at the channel walls in initial conditions. Consequently, a linear variation of temperature across the channel is considered. The modification in temperature profile, after this, it due to the imposition of suction or injection.
The mass transfer of blood (homogeneous mixture) is considered since it contains some chemically reactive species, where a 1st order homogeneous and irreversible reaction is supposed to occur in the fluid. Here, the species are assumed to have constant concentrations
C1 and C2 at the lower and upper channel walls, respectively (mol/m3) (Sharma and Borgohain 2014).
The geometry of the problem is Cartesian with the channel plates being located at y = ±a, as illustrated in the flow scheme (Figure 1).
Figure 1 – Conceptual physical model of MHD blood flow through a porous blood channel.
The motion equation is a combination of the Navier-Stokes equation and the Forchheimer law. Temperature and concentration equations are results of the energy and mass balance, respectively. Consequently, velocity, temperature, and concentration field models with their initial and boundary conditions were obtained from Ali et al. (2015) and are presented below: 2 2 2 0 0 2 1 1 1 B B p B u u p u u u bu y x y k + = − + + − − − (1a) 2 0 2 T T T y y + = (1b)
(
)
2 0 2 m C C C D k C C y y + = − − (1c) 0, y , y in 0 u T C a a = = = = (2a-c) 1 1 0, , in u= T =T C=C y= −a (2d-f) 2 2 0, , in u= T =T C =C y= +a (2g-i)Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 Where τ is the dimensional time, u is the horizontal velocity component, υ0 is the wall transpiration velocity, ρ is the density, p is the pressure, υB is the kinematic viscosity, σ is the
electrical conductivity, B0 is the magnetic field intensity, kp is the permeability of the porous
medium, b is the inertial drag coefficient and β is the rheological parameter (calculating the rheological properties of the non Newtonian fluid). It is worthy to mention that the rheological properties are a combination of viscous, elastic and plastic properties that often change nonlinearly.
The factor (1 + 1/β) is present because of the Casson blood-rheology model, which represents a difference in Eq. (1a) from typical Navier-Stokes equation (Boyd et al. 2007). As
β approaches zero, Eq. (1a) reduces to the governing equation for the ordinary Newtonian fluid
(Navier-Stokes Equation).
In Eq. (1b), α is the thermal diffusivity and T is the fluid temperature. The thermal convection and diffusion are represented by the first and second derivative terms in Eq. (1b), respectively. The diffusion has been taken into account since the two channels walls are at different temperature.
Further, in Eq. (1c), C is the species concentration, D is the mass diffusivity and k is the reaction rate constant (reaction velocity measurement). The negative term on the chemical reaction term indicates that the reaction is consuming the species. Additionally, Cm =
(C1+C2)/2 is the average concentration (reference concentration).
The pressure gradient, as well as the main dimensionless groups that were employed in this formulation, is described below:
0 0 2 0 0 0 0 0 2 2 0 2 0 cos( ); ; ; ; ; ; ; ; Re ; ; ; ; ; ; Pr ; s p m m f m m m B B B B P u x y p P P t U t P a a a k T T C C a B a N ab N T T C C a a ka Sc D − = + = = = = = − − = = = = = = − − = = = (3a-h)
Where Re is the Reynolds number, λ is the Darcy parameter, Nf is the Forchheimer
quadratic drag parameter, Nm is the magnetic parameter, Sc is the Schmidt number, γ is a
reaction-related parameter, Pr is the Prandtl number and Ps and P0 are the static and oscillatory
components (with frequency ω) of the pressure gradient. So the following dimensionless models with their initial and boundary conditions can be obtained:
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 2 2 2 1 1 1 1 Re + = − + + − + − m f U U P U N U N U t (4a) 2 2 1 Re Pr + = t (4b) 2 2 1 Re + = − t Sc (4c) 0, , in 0 U = = = t= (5a-c) 0, 1, 1 in 1 U = = − = − = − (5d-f) 0, 1, 1 in 1 U = = = = (5g-i)
In order to improve the convergence of the direct problem solution, the following filters solution are proposed: θ (η, t) = θH (η, t) + η and ϕ (η, t) = ϕH (η, t) + η were used to homogenize
the boundary conditions for the temperature and concentration fields (Eq 5e,f, and 5h,i). The dimensionless filtered models in –1 < η < 1, t ≥ 0 domain with their initial and boundary conditions for the velocity, temperature, and concentration fields are shown below:
2 2 2 1 1 1 1 Re + = − + + − + − m f U U P U N U N U t (6a) 2 2 1 1 Re Pr + + = H H H t (6b) 2 2 1 1 Re Re + + = − − H H H H t Sc (6c) 0, H 0, H 0 in 0 U = = = t = (7a-c) 0, H 0, H 0 in 1 U = = = = − (7d-f) 0, H 0, H 0 in 1 U = = = = (7g-i) 3 SOLUTION METHODOLOGY
The solution methodology to be employed in the filtered models (Eq. 6a-c and 7a-i) consists of eliminating the dependence on the spatial variable via Generalized Integral Transform Technique (GITT). Özisik (1993) presents the appropriate eigenvalue problem to support the construction of potential as an expansion in orthogonal-based eigenfunctions, according to Eq. 8a-c, whose solution for the eigenfunction in the standard version is presented in Eq. 8d-g.
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 2 2 2 ; ( 1) 0; (1) 0 i i i i i d d = − − = = (8a-c) 1 2 1 ( ) ( ) i [ ( 1)]; ( ) d ; / 2, 1, 2, 3,... i i i i i i sen N i i N − = = + =
= = (8d-g)Based on the orthogonality property of the eigenfunctions, it is possible to define the following inverse-transform pairs for the filtered potentials:
Transform Inverse 1 1 1 ( ) ( ) ( , ) ; ( , t) ( ) ( ) i i i i i U t U t d U U t − = =
=
(9a,b) 1 , , 1 1 ( ) ( ) ( , ) ; ( , t) ( ) ( ) H i i H H i H i i t t d t − = =
=
(9c,d) 1 , 1 , 1 ( ) ( ) ( , ) ; ( , t) ( ) ( ) H i i H H i H i i t t d t − = =
=
(9e,f)The integral transform of the original problem is performed by operating with 1
1 i( ) __d −
in the Equations 6a-c, taking into account the definition of the proposed transformed formula in Equations 9c and 9e, boundary conditions and making use of the orthogonality property whenever possible, so that the following system is obtained:,
( )
2 , , 1 1 1 1 1 Re NT NT NT i i j j i i m i f i j k j k j j k dU A U D t N U N F U U dt = + = − + − − −
(10a) 2 , , , , 1 Re Pr NT H i i i j H i i H i j d A G dt = +
+ = − (10b) 2 , , , , , 1 Re Re NT H i i i j H i i H i H i i j d A G H dt Sc = +
+ = − − − (10c) Ui =0, H i, =0, H i, =0 in t = 0 (10d-f)Where the coefficients are defined by:
( )
1 1 1 ' 0 1 1 1 1 1 1 1 ; cos( ) ; ; ij i j i i s ijk i j k i i i i A d D t P P t d F d G d H d − − − − − = = + = = =
(11a-e)Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 The Eq. 10a-11e are valid in –1 < η < 1, t ≥ 0 domain and define a system of ordinary differential equations (ODEs) to be numerically solved for each of the investigated potentials (velocity, temperature, and concentration) as shown below.
4 RESULTS AND DISCUSSION
The numerical solution of the system defined in Eq. 10a-c was implemented on the numerical-symbolic computing platform Mathematica 9.0 (Wolfram, 2005) using the NDSOLVE function at default mode for a number of terms (NT) sufficiently large to provide a satisfactory approximation of series expansion.
4.1 CONVERGENCE ANALYSIS
Table 1 – Convergence analysis for results obtained by GITT for t = 0.3 in different positions in the channel with Pr = 5, Sc = 0,7, Re = 1, Nm = 0,3, Nf = 0,002, ω = 8, Ps = 10, P0 = 7, λ = 5, β = 4 e γ = 4. NT η U (η,t) -1 -0.8 -0.4 0 0.4 0.8 1 20 0.0000 0.7145 18.427 23.892 22.056 10.470 0.0000 25 0.0000 0.7147 18.427 23.894 22.058 10.477 0.0000 30 0.0000 0.7147 18.428 23.894 22.059 10.480 0.0000 35 0.0000 0.7146 18.428 23.893 22.058 10.477 0.0000 40 0.0000 0.7146 18.428 23.893 22.058 10.476 0.0000 NT η θ (η,t) -1 -0.8 -0.4 0 0.4 0.8 1 20 -10.00 -0.9373 -0.6730 -0.2980 0.1019 0.5611 10.000 25 -10.00 -0.9376 -0.6731 -0.2984 0.1015 0.5598 10.000 30 -10.00 -0.9375 -0.6733 -0.2984 0.1012 0.5593 10.000 NT η ϕ (η,t) -1 -0.8 -0.4 0 0.4 0.8 1 20 -10.00 -0.7465 -0.3822 -0.1129 0.1705 0.6245 10.000 25 -10.00 -0.7464 -0.3821 -0.1130 0.1704 0.6242 10.000 30 -10.00 -0.7463 -0.3821 -0.1130 0.1704 0.6241 10.000
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 The convergence analysis of the series expansions of the integral transform solution was calculated at some positions along η for t = 0.3. Table 1 shows that the velocity field has four digits fully converged with 40 terms while 30 terms are required to ensure a numerical solution with four digits fully converged for the temperature and concentration fields. This behavior for velocity can be explained due to the nonlinear character of the momentum balance equation. As for the other fields, the behavior is justified because the mathematical models of these fields do not present coupling, resulting that the convergence of one does not directly influence the number of terms necessary for the solution recovery of the others.
4.2 NUMERICAL VERIFICATION
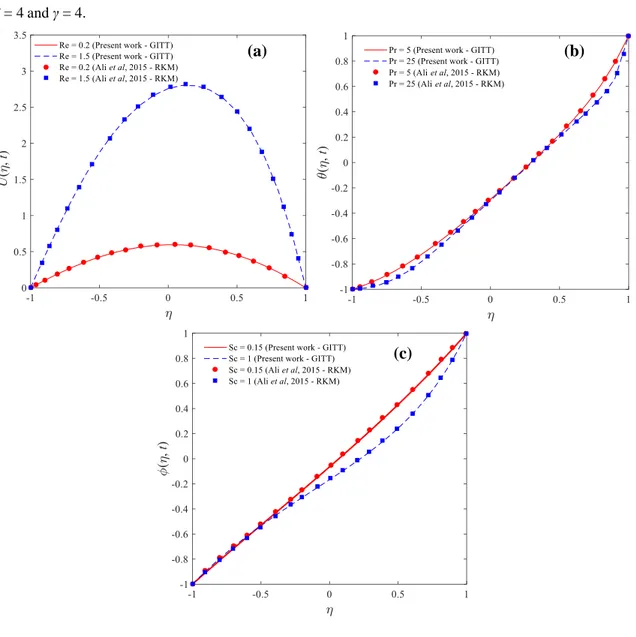
Figure 2 – Numerical verification of the GITT results with Ali et al. (2015) results for (a) velocity field, (b) temperature field and (c) concentration field for t = 0,3 with Nm = 0,3, Nf = 0,002, ω = 8, Ps = 10, P0 = 7, λ =
5, β = 4 and γ = 4.
(a) (b)
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 The results of the present work (GITT) obtained for the velocity, temperature, and concentration fields were numerically compared with those obtained by Ali et al. (2015) (RKM - three step explicit Runge-Kutta Method). In the series expansion were employed 50 terms to ensure that the results are already converged.
The results, in Figure 2, show good agreement between the GITT results and those from Ali et al. (2015), which curves coinciding for all conditions studied. Figure 2 also illustrates the influence of some parameters (Re, Pr, and Sc) on velocity, temperature and concentration fields, but this effect will be explored in more detail in the following section.
4.3 EFFECT OF PARAMETERS VARIATION
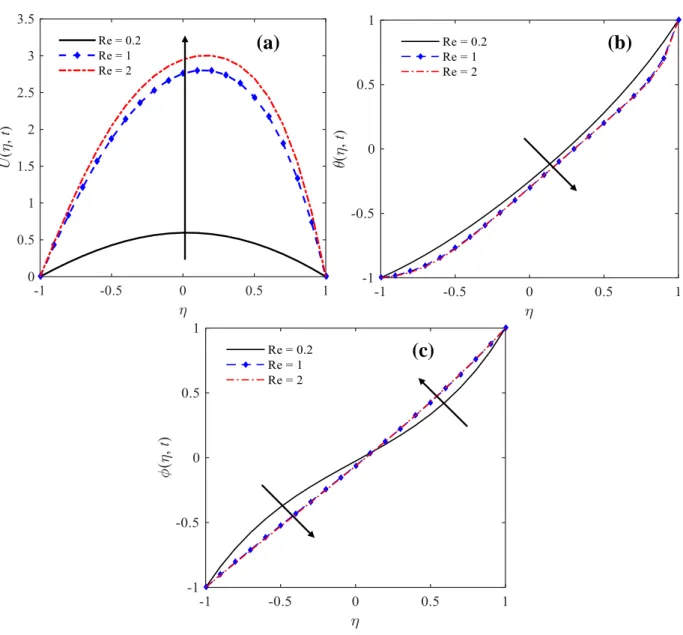
Figures 3a-c presents the influence of Reynolds number (Re = 0.2, 1.0 and 2.0) on velocity, temperature and concentration fields. The Reynolds number establishes the relationship between inertial forces (v0) and viscous forces (νB/a). As can be seen in Figure 3a,
if the other parameters are kept constant, the effect of increasing Re is to accelerate fluid through the channel, since for Re = 2.0, inertial forces are greater than viscous forces when compared to Re = 0.2. However, due to the nonuniform properties of the fluid, there is an increase in suction velocity in the upper plate (set at η = 1) so that the profiles are moved to the upper channel wall. It is possible to observe from the Figure 3b that the Reynolds number disturbs the thermal distribution in the small regions nearby the walls, consequently, the temperature profile holds nearly linear in the middle of the channel. Figure 3c shows that increasing Re it tends to straighten the concentration distribution.
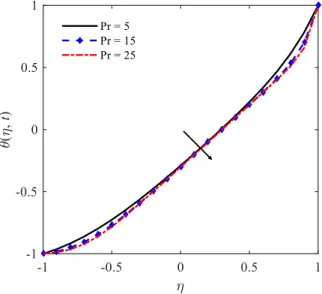
Temperature profiles for three Prandtl number values (Pr = 5.0, 15 and 25) are shown in Figure 4. The Prandtl number is defined as the ratio of viscous diffusion rate (νB) and the
thermal diffusion rate (α). Figure 4b shows that the increase in Pr influences the temperature profile more significantly near the channel walls. It is worthy to mention that for Pr = 5 the viscous diffusion rate is a little greater than the thermal diffusion rate while for Pr = 25 the viscous diffusion rate is a much greater than the thermal diffusion rate. From Figure 4 it is shown that the Reynolds number shifts the temperature profile in the small regions near the walls, especially for high Prandtl numbers. For that reason, the temperature field remains an almost linear function of η, near the middle of the channel.
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 Figure 3 – Influence of the Reynolds number on the velocity, temperature and concentration profiles for t = 0.3 and Re = 0.2, 1.0 and 2.0 with Pr = 5, Sc = 0.15, ω = 8, β = 4, Ps = 10, P0 = 7, λ = 5, γ = 4, Nf = 0.002 and Nm =
0.3.
Figure 5 shows the effect of Schmidt number (Sc = 0.15, 0.5 and 1.0) on the concentration field. The Schmidt number is the relationship between the viscous diffusion rate (ν0) and the mass diffusion rate (D/a). It may be observed from this figure that the Schmidt number influence the concentration profiles. For the cases where the mass diffusion rate is larger than the viscous diffusion rate (Sc = 0.15 and 0.5), the profiles present an oscillatory behavior. On the other hand for the case where Sc = 1, where the mass diffusion rate equals to the viscous diffusion rate, the profile becomes almost linear along the whole channel width.
(a)
(b)
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 Figure 4 – Influence of the Prandtl number on the temperature profile for t = 0.3 and Pr = 5, 15 and 25 with Re = 0.5, Sc = 0.15, ω = 8, β = 4, Ps = 10, P0 = 7, λ = 5, γ = 4, Nf = 0.002 and Nm = 0.3.
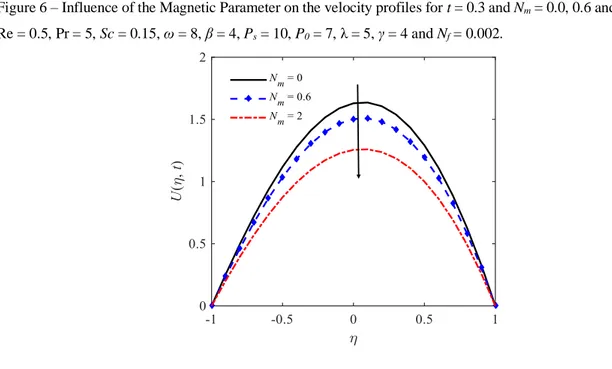
The influence of magnetic parameter (Nm = 0.0, 0.6 and 2.0) on the velocity field can be noticed in Figure 6. This parameter relates the magnetic forces (σB0) and the viscous diffusion rate (ρν0/a). In Figure 6 is exposed that the effect of increasing Nm is to deaccelerate
fluid through the channel, since for Nm = 0.6, magnetic forces are smaller than viscous forces,
in comparison with the case where Nm = 2.0. The application of a magnetic field (B0) to an electrically conductive fluid (σ) produces a resistive force to flow (Lorentz force), slowing the movement of the fluid.
Figure 5 – Influence of the Schmidt number on the concentration profiles for t = 0.3 and Sc = 0.15, 0.5 and 1.0 with Re = 0.5, Pr = 5, ω = 8, β = 4, Ps = 10, P0 = 7, λ = 5, γ = 4, Nf = 0.002 and Nm = 0.3.
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 Figure 6 – Influence of the Magnetic Parameter on the velocity profiles for t = 0.3 and Nm = 0.0, 0.6 and 2.0 with
Re = 0.5, Pr = 5, Sc = 0.15, ω = 8, β = 4, Ps = 10, P0 = 7, λ = 5, γ = 4 and Nf = 0.002.
4.4 TRANSIENT ANALYSIS
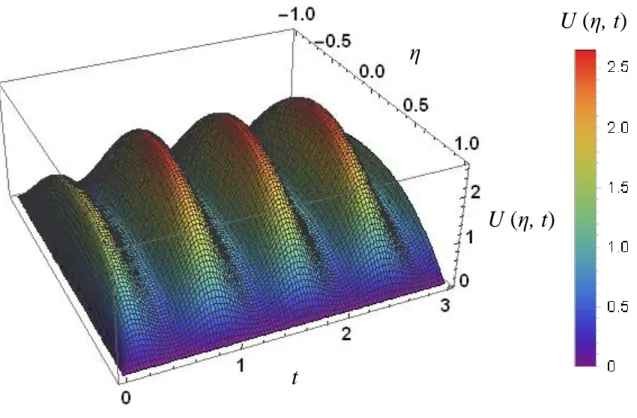
In Figure 7 and Figure 8 are shown the time variation of velocity distribution across the position in the channel and the contour plot (equi-velocity lines), respectively. It is observed that the parameter ω control the number of cycles and, in Figure 7, it is noted that the value of the velocity peak in the first cycle is expressively lower than the other cycles, what is due to inertia, i.e., the fluid initially is stationary. In the first peak, the pressure gradient is not as effective as in the next cycles when the fluid is already in the established motion. Initially (t = 0), high velocity gradient are noticed in Figure 8 because of the application of pressure gradient to the fluid at rest. Another observation is that the cycles are stretched out across the channel width and nearly periodic in the forthcoming.
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 Figure 7 ‒ Transient behavior of velocity along channel width for Re = 0.5, Pr = 5, Sc = 0.15, ω = 8, β = 4, Ps =
10, P0 = 7, λ = 5, γ = 4, Nf = 0.002 and Nm = 0.3.
Figure 8 ‒ Contour plot of velocity field for Re = 0.5, Pr = 5, Sc = 0.15, ω = 8, β = 4, Ps = 10, P0 = 7, λ = 5, γ =
4, Nf = 0.002 and Nm = 0.3. U ,t
η
t
U (η, t)
U (η, t)
η
t
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 5 CONCLUSION
A nonlinear model for BFD blood flow through a porous medium within a channel of parallel plates with wall transpiration under the action of a transverse magnetic field has been solved using GITT. The convergence of the solutions was performed and the GITT results were satisfactorily compared with the literature.
The technique was presented as a robust and versatile method for solving this class of problems involving electromagnetic phenomena with chemical reaction, allowing to obtain results in excellent agreement with literature data and enabling the development of more complex problem solutions.
Increasing the Reynolds number can accelerate channel flow while increasing the Prandtl number causes pronounced effects on the temperature field near the channel walls. An increment in the Schmidt number, however, tends to straighten the profile along the channel. The increase in magnetic parameter decreases the fluid velocity since the application of a magnetic field produces a resistive force to flow slowing the deaccelerating the fluid.
In the initial times, the pressure gradient is not completely effective as observed in the next cycles, producing a smaller velocity peak and generating high velocity gradients due to the fluid being at rest. The cycles are extended along the channel width and almost periodic in the next.
REFERENCES
ALI, K.; AHMAD, S.; ASHRAF, M. Numerical simulation of MHD pulsatile flow of a biofluid in a channel. AIP Advances, v.5, p. 087130, 2015.
ANDRA, W; NOWAK, H. Magnetism in Medicine. Wiley VCH, Berlin, 1998. BOYD, J.; BUICK, J. M.; GREEN, S. Phys. Fluids 19, 93, 2007.
COTTA, R. M.; MIKHAILOV, M.D. Heat conduction: lumped analysis, Integral transforms,
Symbolic Computation. John Wiley & Sons, 1997.
FERREIRA, J. R.; PONTES, F. A.; MIYAGAWA, H. K.; MACÊDO, E. N.; QUARESMA, J. N. N.; ESTUMANO, D. C.; RIBEIRO, N. F. P. Parameters Estimation Using ABC
Technique of MHD Pulsatile Flow of a Non-Newtonian Fluid in Porous Blood Vessels.
CILAMCE, 2019.
FUKADA, E.; KAIBARA, M. Biorheology, v.17, p.177, 1980.
HIGASHI, T.; YAMAGISHI, A.; TAKEUCHI, T.; KAWAGUCHI, N.; SAGAWA, S.; ONISHI, S.; DATE, M. Blood, v.82, p.1328, 1993.
Braz. J. of Develop., Curitiba, v. 5, n. 10, p. 17851-17868 oct. 2019 ISSN 2525-8761 JANG, J.; LEE, S. S. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sensors and Actuators. v.80. p. 84-89, 2000.
ÖZISIK, M. N. Heat Conduction, John Wiley & Sons, New York, 1993.
PONTES, F. A; MIYAGAWA, H. K.; PONTES, P. C.; MACÊDO, E. N.; QUARESMA, J. N. N.; Integral Transform Solution of Micropolar Magnetohydrodynamic Oscillatory Flow
with Heat and Mass Transfer over a Plate in a Porous Medium Subjected to Chemical Reactions. Journal of King Saud University – Science. v. 31, p. 114-126, 2019.
RITMAN, E.L. LERMAN, A. Current Cardiology Reviews. 3, 43, 2007.
SHARMA, B.R. BORGOHAIN, D. International Journal of Innovative Research in Science,
Engineering and Technology. 7, 14867, 2014.
SPHAIER, L. A.; COTTA, R. M.; NAVEIRA-COTTA, C. P.; QUARESMA, J. N. N. The
UNIT algorithm for solving one-dimensional convection-diffusion problems via integral transforms. I. C. Heat and Mass Transfer. v. 38, p. 565-571, 2011.
STOLTZ, J. F.; LUCIUS, M. Biorheology, v.18, p.453, 1981.
WOLFRAM, S. MATHEMATICA – a system for doing mathematics by computer, in: The Advanced Book Program. Addison Wesley, Reading, MA, 2005.