Gráficos Radiais com Curvatura Média Constante no Espaço Hiperbólico

(1)

Instituto de Matem´

atica

Curso de Pós–Graduação em Matemática

Dissertac¸˜ao de Mestrado

Gr´

aficos Radiais com Curvatura M´

edia

Constante no Espac

¸o Hiperb´

olico

Adriano Pedreira Cattai

Salvador —Bahia

(2)

Gr´

aficos Radiais com Curvatura M´

edia Constante

no Espac

¸o Hiperb´

olico

Disserta¸cão apresentada ao colegiado do curso de Pós-Gradua¸cão em Matemática da Universidade Federal da Bahia, como requisito parcial para

obten¸c˜ao do Grau de Mestre em Matem´atica.

Aprovada pela Banca Examinadora abaixo assinada.

Prof. Dr. Jos´e Nelson Bastos Barbosa (Orientador) UFBA

Prof. Dr. Jorge Herbert Soares de Lira UFC

Prof. Dr. Pedro Antonio Hinojosa Vera UFPB

(3)

Gráficos Radias com Curvatura Média Constante no Espa¸co Hiperbólico/ Adriano Pedreira Cattai; orientador: José Nelson Bastos Barbosa. — Salva-dor: UFBA, 2006.

79 p.

1. Disserta¸c˜ao (mestrado) – Universidade Federal da Bahia, Departamento de Matem´atica.

Inclui referˆencias bilbiogr´aficas.

1. Matem´atica - Teses. 2. Geometria Riemanniana. I. Cattai, Adriano Pedreira. II. Barbosa, Jos´e Nelson Bastos. III. T´ıtulo.

(4)

(5)

intrigou a maior parte do ano e achar seu conte´udo mais excitante, mais perfeito, mais maravilhoso do que vocˆe sempre sonhou.

O bebê é a desculpa perfeita para fazer todas aquelas coisas as quais a vida adulta exigiu que você renunciasse.

Não há por do sol mais bonito, não há maravilha maior do que um bebê!”.

(6)

Agradecimentos

Sempre `a Deus!

`

A minha amada fam´ılia: meu pai Ailton Teles Cattai, minha mãe Maria do Carmo Pedreira Cattai e meu irmão Alessandro Pedreira Cattai, por sempre acreditar em mim e pela for¸ca ao longo de todos estes anos (acredito, que todo agradecimento nunca seria suficiente para recompensá–los).

Aos meus amigos e parceiros de surf Bruno Melo, Diogo Rodrigues, Joney Santana e Thiago Melo (e seus familiares), por tornarem a minha vida mais gostosa pelo carinho que dedicam.

`

A minha grande companheira, amiga, namorada e esposa,Tharita Veirapor tudo que fez por mim nesse per´ıodo, profissionalmente e moralmente. Sua presen¸ca em minha vida com nossa filha Gabriela foi mais um presente de Deus.

Aos meus orientadores em tempos de inicia¸cão cient´ıfica: Afonso Henriques por todo seu apoio, incentivo, ensinamentos e amizade; eHumberto José Bortolossi que muito nos ensina com sua amizade, dedica¸cão, disposi¸cão e aten¸cão. Aos professores de gradua¸cão. Aos colegas de gradua¸cão: Antônio Oliveira Simão, Eduardo Palmeira, Fab´ıolo Moraes Amaral, Rosane Funatoe Vin´ıcius Modesto Sertório.

Aos colegas de turma: Ab´ılio Souza, Gabriela Goes, Gilclécio Dantas, Josaphat Ri-cardo, Maur´ıcio Porto, Roberto Pastor, Rolando Restany, Rosane Funato, Silvia Costa e Tailson Jeferson, pela companhia e cumplicidade no dia a dia em cada matéria e nos intermináveis domingos de UFBA. Aos demais mestrandos deste programa que não citei.

(7)

A todos os professores da Pós-Gradua¸cão em Matemática desta universidade, em especial ao coordenador Professor Enaldo Silva Vergasta, pela eterna simpatia, sabedoria e exemplo. Aos funcionários do Instituto de Matemática; às secretárias Tânia Esp´ınola e Dona Zezé sempre atentas aos nossos pedidos.

Um agradecimento especial ao Professor José Nelson Bastos Barbosa pela orienta¸cão no desenvolvimento deste trabalho e escolha do tema; pela amizade e toda sua dedica¸cão. Gostaria de agradecer também aos professores Jorge Herbert S. de Lira ePedro Antonio Hinojosa Vera, os quais compuseram a banca examinadora e verificaram com tanto zelo esta disserta¸cão.

Na tentativa de n˜ao omitir nenhum nome: a todos os amigos de Canavieiras, da EMARC-UR, da UESC, da UFBA; aos colegas de surf, e aos de fora, pelo apoio, compre-ens˜ao e carinho, pelas piadas e pela for¸ca.

Finalmente, `a CAPES pelo apoio financeiro.

(8)

Resumo

Provamos a existência de gráficos radiais com curvatura média constante no espa¸co hiperbólico Hn+1 _{definido sobre dom´ınios em esferas geodésicas do} Hn+1 _{em que a}

cur-vatura média no bordo é positiva com respeito a orienta¸cão interna; descrito no artigo Radial Graphs with Constant Mean Curvature in the Hyperbolic Space, do professor da Universidade Federal do Ceará, Jorge Herbert S. de Lira.

(9)

Abstract

The existence is proved of radial graphs with constant mean curvature in the hyper-bolic space Hn+1 _{defined over domains in geodesic spheres of} Hn+1 _{whose boundary has}

positive mean curvature with respect to the inward orientation; described in the article Radial Graphs with Constant Mean Curvature in the Hyperbolic Space, of the teacher of the Federal University of Cear´a, Jorge Herbert S. de Lira.

(10)

Sum´

ario

Apresenta¸c˜ao 1

Introdu¸c˜ao 2

1 Preliminares de Geometria Riemanniana 5

1.1 Variedades Diferenci´aveis . . . 5

1.2 Espa¸co Tangente . . . 6

1.2.1 Campo de Vetores . . . 8

1.3 M´etricas Riemannianas . . . 9

1.3.1 A Inversa da M´etrica . . . 10

1.4 Variedades Imersas . . . 10

1.5 Conex˜ao Afim . . . 11

1.6 Geod´esicas e a Aplica¸c˜ao Exponencial . . . 12

1.7 Segunda Forma Fundamental . . . 15

1.7.1 Segunda Forma Fundamental de Hipersuperf´ıcies . . . 16

1.8 Gradiente, Divergente, Laplaciano e Hessiano . . . 18

1.9 O Espa¸co Hiperb´olico . . . 27

1.9.1 Isometrias e o Modelo da Bola . . . 28

1.9.2 Superf´ıcies Umb´ılicas do Hn+1 _{. . . .} ₃₀

2 Equa¸cões Diferencias Parciais e o Princ´ıpio do Máximo 32 2.1 Continuidade Hölder . . . 32

2.2 Equa¸c˜oes Diferenciais Parciais El´ıpticas . . . 34

(11)

2.3 O Princ´ıpio do M´aximo . . . 37

2.3.1 O Princ´ıpio do M´aximo para Operadores Lineares . . . 37

2.3.2 O Princ´ıpio do M´aximo para Operadores Quasilineares . . . 46

2.4 Diferencial de Fr´echet . . . 47

2.5 O M´etodo da Continuidade . . . 50

3 Gr´aficos Radiais em Rn+1 _e Hn+1 ₅₃ 3.1 Gr´aficos Radiais emRn+1 _{. . . .} ₅₃

3.2 Gr´aficos Radiais emHn+1 _{. . . .} ₆₅

4 Prova do Teorema 3.3 69 4.1 Preliminares . . . 69

4.2 A Prova . . . 73

(12)

Apresenta¸

c˜

ao

Este trabalho é fruto da orienta¸cão do professor José Nelson Bastos Barbosa, do De-partamento de Matemática desta universidade, para disserta¸cão de mestrado. Estudamos a tese de doutorado Existência e Unicidade de Hipersuperf´ıcie com Bordo e Curvatura Média Constante em Formas Espaciais ([13]), e o artigo Radial Graphs with Constante Mean Curvature in the Hyperbolic Space Hn+1 _{([12]), ambos do professor Jorge Herbert} Soares de Lira do Departamento de Matemática da Universidade Federal do Ceará.

Para uma boa compreensão deste trabalho, o leitor deve ter um n´ıvel de conhecimento semelhante ao aluno que cursa o segundo ano de mestrado em matemática, especialmente com bons conhecimentos de Geometria Riemanniana e de Análise em Espa¸cos Euclidianos. Para este propósito, sugerimos respectivamente, [17] e [8]. Seria desejável ainda, que o leitor tivesse bons conhecimentos de Equa¸cões Diferenciais Parciais (EDP’s) e o Princ´ıpio do Máximo. Sugerimos para este propósito [7]. No entanto, exibimos os resultados mais relevantes para a nossa necessidade no Cap´ıtulo 2.

(13)

Introdu¸

c˜

ao

As calotas esferas, são exemplos clássicos de hipersuperf´ıcies com curvatura médica constante e com bordo conhecido.

A busca por exemplos não-esféricos de hipersuperf´ıcies mergulhadas com curvatura média constante em espa¸cos de curvatura seccional constante é um problema muito co-nhecido. Um jeito corrente de se fazer isto é através da constru¸cão de vários tipos de gráficos. Neste caso as hipersuperf´ıcies são descritas não-parametricamente por fun¸cões definidas sobre um dom´ınio numa hipersuperf´ıcie umb´ılica do ambiente. A condi¸cão que a superf´ıcie tenha curvatura média constante implica que a fun¸cão que descreve o gráfico seja solu¸cão de uma EDP quasilinear.

Gr´aficos com proje¸c˜ao central injetiva sobre uma Esfera Euclidiana em Rn+1 _foram

constru´ıdas por Serrin [16]. Em [3], Treibergs e Wei provam a existência de gráficos radiais definidos sobre toda esfera, cuja curvatura média é prescrita por uma fun¸cão satisfazendo certas condi¸cões de crescimento.

Recentemente, demonstrou-se vários teoremas de existência para gráficos com curva-tura média constante no espa¸co hiperbólico Hn+1 _{com proje¸cão injetiva sobre dom´ınios}

em hipersuperf´ıcies umb´ılicas com curvatura menor ou igual a 1. Por exemplo, J. L. Bar-bosa e R. S. Earp [15] obtiveram gráficos com curvatura média constante sobre dom´ınios em hiperplanos geodésicos. Gráficos sobre horoesfera foram constru´ıdos independente-mente por B. Nelli e J. Spruck em [6] e por R. López e S. Montiel em [18]. Também, López anunciou em [19] a existência de solu¸cões para equa¸cões da curvatura média sobre hipersuperf´ıcies eqüidistastes emHn+1_.

(14)

auto-Introdu¸c˜ao

interseçcões. O gráfico radial de uma fun¸cão χ definida sobre o fecho de um dom´ınio Ω em uma esfera geodésica S em Hn+1 _{é o conjunto Σ dado por}

Σ ={αx(χ(x));x∈Ω},

onde αx é a geodésica minimizante ligando o centro geodésico de S ao ponto x ∈ Ω.

Suponhamos que Γ =∂Ω ´e uma hipersuperf´ıcie de classeC2,α_de_{S, para algum}_α _∈_(0,_1),

denotemos por HΓ a curvatura m´edia de Γ com respeito ao vetor normal apontando para o interior de Ω, demonstramos o seguinte teorema, provado por Jorge Herbert S. de Lira, em Radial Graphs with Constant Mean Curvature in the Hyperbolic Space. Geometriae Dedicata, 93 (2002), 11–23.

Teorema 3.3(Teorema Principal). Sejam S uma esfera geod´esica de raioρem Hn+1 _e _Ω

um dom´ınio em S com fecho contido num hemisfério aberto de S. Se ₋infHΓ < H _≤0, então existe um único gráfico radial Σ sobre Ω com curvatura média H e bordo Γ.

A prova deste teorema utilizamos um teorema devido a Serrin (Teorema 3.1) para garantir a existˆencia de um gr´afico radial m´ınimo emHn+1 _{com bordo Γ. Combinamos as}

estimativasa priori para o gradiente (cf. [13], § 2.3) com o Teorema da Fun¸cão Impl´ıcita (Teorema 2.16) e obteremos o resultado acima recorrendo à teoria clássica de Schauder, assim como está exposta por D. Gilbarg e N. Trudinger em [7].

O trabalho trata da questão de encontrarmos solu¸cões únicas para o seguinte pro-blema: uma hipersuperf´ıcie deve ser o gráfico de uma fun¸cão u _∈ C2,α_{(Ω), onde Ω é}

um dom´ınio em uma esfera geod´esica S de raio ρ em Hn+1 _{cujo fecho est´a contido num}

hemisfério aberto de S, tendo a curvatura média hiperbólica prescrita por uma fun¸cão, sujeita à condi¸cão de u se anular na fronteira Γ = ∂Ω, ou seja, equivale a assegurar a existência de uma solu¸cão u_∈C2,α(Ω), u <0, para o seguinte problema de Dirichlet:

(

QH(u) = 0 em Ω

u= 0 em Γ ,

em que QH(u) ´e definido em (3.31), p´agina 68.

(15)

problemas de Dirichlet. Esta parte foi baseada em [7] e em [20]. Apresentamos ainda a continuidade Hölder e o Método da Continuidade, baseado em [7]. Já no terceiro cap´ıtulo, apresentamos o problema de constru¸cão de gráficos com curvatura média constante em termos da existência de solu¸cões de uma classe espec´ıfica de equa¸cões diferenciais parciais. A partir da no¸cão de gráfico radial no espa¸co EuclidianoRn+1_{, deduzimos equa¸cões para} gráficos radiais sobre esferas geodésicas no espa¸co hiperbólico Hn+1_{. No quarto e ´}_ultimo

(16)

Cap´ıtulo 1

Preliminares de Geometria Riemanniana

Este cap´ıtulo visa dar uma no¸cão de alguns dos principais conceitos e resultados de Geometria Riemanniana, necessários para compreensão dos resultados que pretendemos demonstrar.

1.1 Variedades Diferenci´

aveis

Uma variedade diferenciável de dimensão n é um conjunto M e uma fam´ılia de aplica¸cões biun´ıvocasxα :Uα ⊂Rn →M de abertos Uα deRn em M tais que:

(1) [

α

³

xα(Uα)

´

=M;

(2) Para todo parα,β, comxα(Uα)∩xβ(Uβ) =W 6=∅,os conjuntosx−α1(W) ex−β1(W)

s˜ao abertos em Rn _{e as aplica¸c˜oes} _x−1

β ◦xα s˜ao diferenci´aveis;

(3) A fam´ılia _{(_Uα,xα)}é máxima relativamente às condi¸cões (1) e (2).

O par (_Uα,xα) (ou a aplica¸cão xα) com p ∈xα(Uα) é chamado uma parametriza¸cão

(ou sistema de coordenadas) deM em p ;xα(Uα) ´e chamada umavizinhan¸ca coordenada

emp. Uma fam´ılia{(Uα,xα)}satisfazendo (1) e (2) ´e chamada umaestrutura diferenci´avel

em M.

(17)

Sejam Mm eNnvariedades diferenciáveis. Uma aplica¸cãoϕ :M →N édiferenciável em p _∈ M se dada uma parametriza¸cão y : _{V ⊂} Rn _→ _N _em _{ϕ(p) existe uma}

parame-triza¸c˜aox:_{U ⊂}Rm _→_M _em _p_{tal que} _ϕ(x(_U₎₎_⊂_y(_V_{) e a aplica¸c˜ao}

y−1_◦ϕ_◦x:_{U ⊂}Rm _→Rn

é diferenciável emx−1_(p). _ϕ_{é diferenciável em um aberto de}_M _{se é diferenciável em todos} os pontos deste aberto. Decorre da condi¸cão (2) da defini¸cão de variedades diferenciáveis que a defini¸cão dada independe da escolha das parametriza¸cões.

Em seguida, estenderemos às variedades diferenciáveis a no¸cão de vetor tangente.

1.2 Espa¸

co Tangente

Seja Mn uma Variedade Diferenciável de dimensão n. Uma aplica¸cão diferenciável α: (₋ε, ε)_→M é chamada uma curva diferenciável em M.

Suponha que α(0) =p_∈M e seja D(M) ={f :M →R _;_f _{´e diferenci´avel em} _p_}_{. O}

vetor tangente à curva α em t= 0 é a fun¸cão

α′(0) : _D(M) _→ R

f _7→ (f _◦α)′₍₀₎

ou seja, o vetor tangente `a variedade M em p ´e o vetor tangente em t = 0 de alguma curva α : (−ε, ε)→M com α(0) =p. Indicaremos por TPM o conjuntos desses vetores.

Sejam os seguintes caminhos no Rn_,_λi _{: (}₋_{ε, ε)}_{→ U ⊂}Rn _{tais que}_λi_{(t) =}_q₊_t_·_e_i_,

i= 1, . . . , n, e seja x:_{U ⊂}Rn_→_Mn _{uma paramtriza¸c˜ao em} _p₌_x(q), _q_{∈ U}_{. As curvas}

αi =x_◦λi s˜ao chamadas de curvas coordenadas passando em p.

Com base nas defini¸c˜oes acima, temos

(αi)′(0)_·f = (f_◦αi)′(0) = ((f _◦x)_◦λi)′(0)

= X

j

∂(f_◦x) ∂xj

(q)_·(λi_j)′(0)

= ∂(f◦x) ∂xi

(q)

e poremos a seguinte nota¸c˜ao:

∂ ∂xi

(18)

1.2. Espa¸co Tangente

ou seja,

∂ ∂xi

(p) :D(M)→R _, ∂

∂xi

(p)·f = ∂(f ◦x) ∂xi

(q) , q=x−1_(p)

Queremos escrever o vetor tangenteα′(0) em termos do sistema de coordenadas deM. Sejam x: _{U ⊂}Rn _→_M _{um sistema de coordenadas locais de} _M _em _p, _α _{: (}₋_{ε, ε)}_→ _M

uma curva diferenciável comα((₋ε, ε))_⊂x(_U) e f :M _→R _{uma aplica¸cão diferenciável}

em p. Fa¸camos o seguinte:

α′(0)_·f = (f _◦α)′(0) =¡(f _◦x)_◦(x−1_◦α)¢′(0) =

n

X

i=1

∂(f ◦x) ∂xi

¡

x−1◦α(0)¢·α′_i(0)

=

n

X

i=1

∂(f _◦x) ∂xi

¡

x−1(p)¢·α′_i(0)

=

n

X

i=1

α′_i(0)_·

µ

∂ ∂xi

(p)_·f

¶

=

Ã _n

X

i=1

α′_i(0)_· ∂ ∂xi

(p)

! ·f

portanto, α′(0) =

n

X

i=1

α′_i(0) _· ∂ ∂xi

(p), ou seja, o vetor v = α′(0) pode ser expresso na parametriza¸cão x, e mostra que um vetor tangente a uma curva α em p depende apenas das derivadas de α em um sistema de coordenadas. Decorre também que o conjunto TpM, com as opera¸cões usuais de fun¸cões, forma um Espa¸co Vetorial de dimensão n e

que a escolha de uma parametriza¸c˜ao x : U _⊂ Rn _→ _M _{determina uma base associada}

½

∂ ∂x1

(p), . . . , ∂ ∂xn

(p)

¾

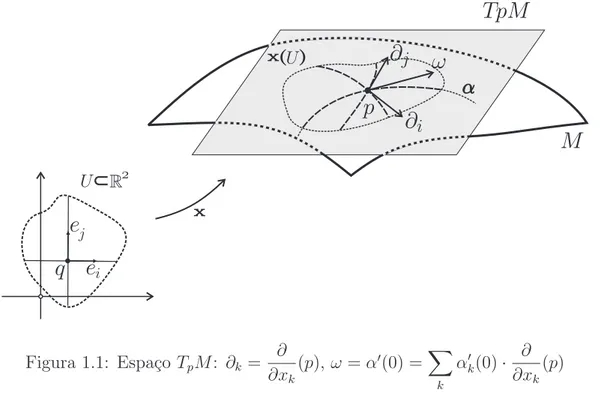
em TpM. Conforme ilustra figura 1.1.

Da no¸cão de espa¸co tangente podemos estender às variedades diferenciáveis a no¸cão de diferencial de uma aplica¸cão diferenciável.

Proposi¸c˜ao 1.1. Sejam Mm _e _Nn _{variedades diferenci´aveis e seja} _ϕ _: _M _→ _N _uma

aplica¸c˜ao diferenci´avel. Para cada p _∈ M e cada v _∈ TpM, escolha uma curva

dife-renci´avel α : (−ε, ε) → M com α(0) = p, α′_{(0) =} _{v. Fa¸ca} _β ₌ _ϕ _◦_{α. A aplica¸c˜ao}

dϕp(v) =β′(0) é uma aplica¸cão linear que não depende da escolha de α.

A aplica¸cão linear dϕp dada pela Proposi¸cão 1.1 é chamada a diferencial deϕ em p.

(19)

Figura 1.1: Espa¸co TpM: ∂k = ∂ ∂xk

(p), ω =α′(0) =X

k

α′_k(0)· ∂ ∂xk

(p)

Seja Mn uma variedade diferenciável. Diz–se que M éorientável se M admite uma estrutura diferenciável (_Uα,xα) tal que, para todo par α, β, com xα(Uα) ∩xβ(Uβ) =

W 6=∅_{, a diferencial da mudan¸ca de coordenadas} _x−1

β ◦xα tem determinante da matriz

Jacobiana positivo em cada ponto do seu dom´ınio. Caso contrário, diz-se que M é não– orientável. Se M é orientável, a escolha de uma estrutura diferenciável é chamada uma orienta¸cão deM eM é, então, ditaorientada. Verifica–se que, seM é orientável e conexa, então existem exatamente duas orienta¸cões distintas em M.

1.2.1 Campo de Vetores

Umcampo de vetores Xe sobre uma variedade diferenciável M é uma correspondência que a cada ponto p ∈ M associa um vetor X(p)∈ TpM, onde TpM é o espa¸co tangente

deM em p. Em termos de aplica¸cão, Xe é uma aplica¸cão deM em T M,

e

X : M _→ T M

p 7→ ³(p),X(p)e ´

onde T M ´e o Fibrado Tangente de M.

Em termos de um sistema local de coordenadas x1, x2, . . . , xn, um campo vetorial

pode ser expresso porX(p) =e Pai(p)_∂x∂_i(p), ondeai s˜ao fun¸c˜oes definidas na vizinhan¸ca

coordenada, chamadas componentesdeXe com respeito ax1, x2, . . . , xn. Nessas condi¸c˜oes

e

(20)

1.3. M´etricas Riemannianas

Outra forma de expressar um campo de vetores, ´e considerando a seguinte aplica¸c˜ao

X : _D(M) _{→ F}

f _7→ X_·f : M _→ R

p _7→ X(p)·f

onde _D(M) é o conjunto das fun¸cões diferenciáveis emM e_F o conjunto das fun¸cões em M, ou seja, todo campo de vetores “leva”o conjunto de fun¸cões diferenciáveis com valores em M no conjunto das fun¸cões em M, definido por (Xf)(p) =X(p)·f.

Seja X_(M_{) o conjunto de todos os campos vetoriais diferenciáveis sobre} _M_{. Então,} X_(M_{) é um espa¸co vetorial real com as opera¸cões naturais de adi¸cão e multiplica¸cão por} escalar. Note que se f é uma fun¸cão sobre M e X _∈X_(M_{), então} _{f X} _∈X_(M_).

1.3 M´

etricas Riemannianas

UmaMétrica Riemanniana numa Variedade Diferenciável M é uma correspondência que associa a cada ponto p de M um produto interno h , _ip (i.é., uma forma bilinear

sim´etrica, positiva definida) no espa¸co tangente TpM, que varia diferenciavelmente no

seguinte sentido: Se x:_{U ⊂}R_→ _M _{´e um sistema de coordenadas locais em torno de} _p,

com x(x1, . . . , xn) = p∈x(U) e

∂ ∂xi

(p) =dxp(0, . . . ,1, . . . ,0), ent˜ao

¿

∂ ∂xi

(p), ∂ ∂xj

(p)

À

p

=gij(x1, . . . , xn)

é uma fun¸cão diferenciável em_U.

´

E claro que esta defini¸c˜ao n˜ao depende da escolha do sistema de coordenadas.

Outra maneira de exprimir a diferenciabilidade da Métrica Riemanniana é dizer que para todo par X e Y de campos de vetores diferenciáveis em uma coordenada em M, a aplica¸cão

hX, Y_i: M _→ R

p _{7→ h}X(p), Y(p)ip

´e diferenci´avel nessa vizinhan¸ca.

As fun¸cões gij :x(U)→R são chamadas asExpressões da Métrica Riemanniana (ou

“os gij da m´etrica”) no sistema de coordenadas x : U ⊂ Rn → M. Uma variedade

(21)

Estabeleceremos uma no¸c˜ao de equivalˆencias entre estruturas.

SejamMmeNnvariedades Riemannianas. Um difeomorfismoϕ:M _→N ´e chamado uma isometria se:

hu, v_iM_p =_hdϕp(u), dϕp(v)iN_ϕ₍_p₎ (1.1)

para todop_∈M; u, v _∈TpM.

Se, al´em disso para um aberto _{U ⊂} M, um difeomorfismo ϕ : _{U →} ϕ(_U) _⊂ N satisfazendo (1.1) chama-se uma isometria local.

´

E usual dizer que a variedade Riemanniana M é localmente isométrica à variedade N se para todo p _∈ M existe uma vizinhan¸ca _V em M e uma isometria local ϕ : _{V →} ϕ(_V)_⊂N.

1.3.1 A Inversa da M´

etrica

Exibiremos a inversa da m´etrica gij =

¿

∂ ∂xi

, ∂ ∂xj

À

, a qual indicaremos por gij.

Sejam os vetores ei =

X

k

aki

∂ ∂xk

e ej =

X

l

alj

∂ ∂xl

, com o seguinte resultado

δij =hei, eji=

X

k,l

akialjh

∂ ∂xk

, ∂ ∂xli

=X

k,l

(aik)⊤·gkl·alj

e do fato que δij =

(

1 se i=j

0 se i₆=j , obtemos a seguinte rela¸c˜ao I = A

⊤ _·_G_·_A _{e logo}

G−1 ₌_A_·_A⊤_{, e portanto a expressão da inversa da métrica em coordenadas é}

gij =X

k

aik(akj)⊤=

X

k

aikaij. (1.2)

1.4 Variedades Imersas

Sejam Mm _e _Nn _{variedades diferenciáveis. Uma aplica¸cão diferenciável} _ϕ _:_M _→_N

é uma imersão se dϕp : TpM → Tϕ(p) é injetiva ∀p ∈ M. Se, além disso, ϕ é um

(22)

1.5. Conex˜ao Afim

Observe que se ϕ : Mm → Nn é uma imersão, então m ≤ n. A diferen¸ca n−m é chamada a codimensão da imersãoϕ. E se, a codimensão for igual a 1,ϕ(M) é chamada dehipersuperf´ıcie.

Suponha ϕ : Mn _→ _Nn+k _{uma imers˜ao,} _Nn+k _{uma variedade Riemanniana e} _Mn

uma variedade diderenci´avel. Defina

hu, v_iM_p :=_hdϕp(u), dϕp(v)iN_ϕ₍_p₎

como sendo a métrica em M. Essa métrica é chamada de métrica induzida por ϕ, e ϕ é uma imersão isométrica.

1.5 Conex˜

ao Afim

Uma conexão afim ∇em uma variedade diferenciável M é uma aplica¸cão:

∇:X_(M₎_×X_(M₎_→X_(M₎

que satisfaz as seguintes propriedades, onde X, Y, Z ∈X_(M₎_{e f, g} _{∈ D}_(M_):

(1) _∇f X+gYZ =f∇XZ+g∇YZ;

(2) ∇X(Y +Z) = ∇XY +∇XZ;

(3) ∇X(f Y) = f∇XY +Xf Y.

Seja M uma variedade diferenciável com uma conexão afim _∇ e uma métrica Rie-manniana h ,_ip. A conexão∇ é dita compat´ıvel com a métrica h ,ip se

X_hY, Z_i=_h∇XY, Zi+hY,∇XZi, X, Y, Z ∈X(M)

Uma conexão afim ∇em uma variedade diferenciável M é dita simétrica se

∇XY − ∇YX = [X, Y] X, Y ∈X(M)

(23)

1.6 Geod´

esicas e a Aplica¸

c˜

ao Exponencial

Nesta se¸cão introduziremos a no¸cão de geodésica como uma curva cuja acelera¸cão é nula. Geodésica é um dos conceitos fundamentais da Geometria Riemanniana, pelo fato de minimizarem comprimento de arco para pontos “suficientemente próximo”, e além disso, se uma curva minimiza o comprimento de arco entre dois quaisquer de seus pontos, ela é uma geodésica.

Uma curva parametrizadaγ :I _→M ´e umageod´esica emt0 _∈I se D dt

dγ

dt = 0 no ponto

t0. Se γ é geodésica em t, para todot ∈I, dizemos que γ é uma geodésica. Se [a, b]⊂I e γ :I _→ M é uma geodésica, a restri¸cão de γ a [a, b] é chamada (segmento de)geodésica ligando γ(a) a γ(b).

´

E comum, por abuso de linguagem, dizermos que geodésica é a imagem γ(I) de uma geodésica γ. Se γ é uma geodésica, então

d dt

¿

dγ dt,

dγ dt

À

= 2

¿

D dt

dγ dt,

dγ dt

À

= 0,

isto é, o comprimento do vetor dγ_dt é constante. Supondo que¯¯dγ_dt¯¯=c₆= 0, o comprimento de arcos deγ, a partir de uma origem fixa, digamos t=t0, é então dado por

s(t) =

Z t

t0

¯ ¯ ¯ ¯

dγ dt

¯ ¯ ¯

¯dt=c(t−t0).

Portanto, o parâmetro de uma geodésica é proporcional ao comprimento de arco. Quando o parâmetro é o próprio comprimento de arco, isto é, c = 1, diremos que a geodésica γ está normalizada.

´

E poss´ıvel determinar as equa¸cões locais satisfeitas por uma geodésica γ em um sistema de coordenadas (_U,x) em torno de γ(t0), conforme exposto em [17], e prova-se que para cada ponto p _∈ M e um vetor v _∈ TpM em p, existe uma única geodésica

passando em pcom dire¸c˜ao v. Temos assim o seguinte lema.

Lema 1.2 (Lema 2.3, p. 63, [17]). Existe um ´unico campo G em T M = {(q, v);q _∈

M, v _∈TpM} cujas trajetórias são da format→(γ(t), γ′(t)), onde γ é uma geodésica em

M.

(24)

1.6. Geod´esicas e a Aplica¸c˜ao Exponencial

Proposi¸c˜ao 1.3 (Proposi¸c˜ao 2.5, p. 63, [17]). Dado p ∈ M, existem um aberto

V _⊂ M, p _∈ V, n´umeros δ > 0 e ε1 > 0 e uma aplica¸c˜ao C∞ γ : (−δ, δ)× U → M,

U = {(q, v);q ∈ V, v ∈ TqM,|v| < ε1}, tais que a curva t → γ(t, q, v), t ∈ (−δ, δ), ´e a

´

unica geod´esica de M que nos instante t = 0 passa por q com velocidade v, para cada

q∈V e cada v ∈TpM com |v|< ε1.

Esta última proposi¸cão afirma que se |v_| < ε1, a geodésica γ(t, q, v) existe em um intervalo (−δ, δ) e é única. Em verdade, é poss´ıvel aumentar a velocidade deuma geodésica diminuindo o seu intervalo de defini¸cão, ou vice-versa. Isto decorre do seguinte lema.

Lema 1.4 (Lema 2.6, p. 64, [17]). Se a geod´esica γ(t, q, v) est´a definida no intervalo

(₋δ, δ), então a geodésica γ(t, q, av), _∈ R_, _{a >} _{0, está definida no intervalo} ¡₋δ

a, δ a

¢

e

γ(t, q, av) =γ(at, q, v).

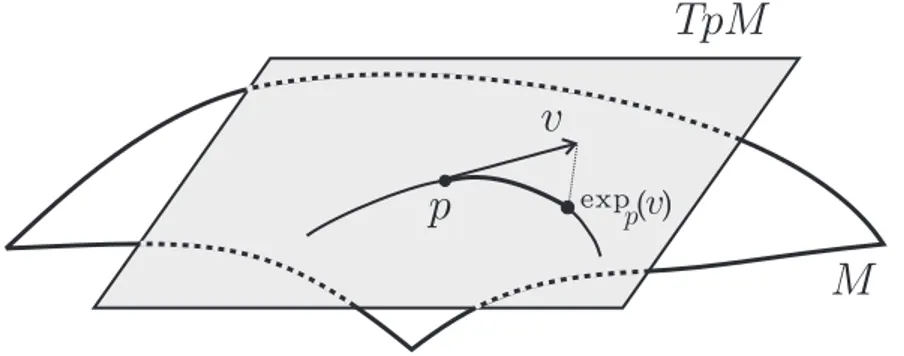
Uma aplica¸cão muito útil para nossos propósitos, é a aplica¸cão exponencial, que definiremos agora. Seja V uma vizinhan¸ca de p _∈ M e U = {(q, w) ∈ T M, q _∈ V, w _∈ TqM,|w|< ε} um aberto. Então a aplica¸cão exp :U →M dada por

exp(q, v) = γ(1, q, v) =γ

µ

|v_|, q, v

|v_|

¶

, (q, v)_{∈ U},

´e chamadaaplica¸c˜ao exponencial em U.

Geometricamente, exp_q(v) ´e o ponto de M obtido percorrendo um comprimento igual a _|v_|, a partir deq, sobre a geod´esica que passa porq com velocidade igual a v

|v|.

Figura 1.2: Aplica¸c˜ao Exponencial expp

Proposi¸c˜ao 1.5 (Proposi¸c˜ao 2.9, p. 65, [17]). Dado q _∈ M, existe um ε > 0 tal que

(25)

Se a aplica¸cão exponencial exp_p é um difeomorfismo em uma vizinhan¸ca V da origem em TpM, exppV = U é chamada uma vizinhan¸ca normal de p. Se Bε(0) é tal que

Bε(0)⊂V, chamamos exppBε(0) =Bε(p) a bola normal (ou geod´esica) de centrope raio

ε. A fronteira de uma bola normal é um hipersuperf´ıcie em M ortogonal às geodésicas que partem de p, denotamos porSε(p) e denominamos por esfera normal(ou geodésica).

As geodésicas em Bε(p) que partem de psão chamadas geodésicas radiais.

Figura 1.3: Esfera geod´esica: exp_pBε(0) =Bε(p)

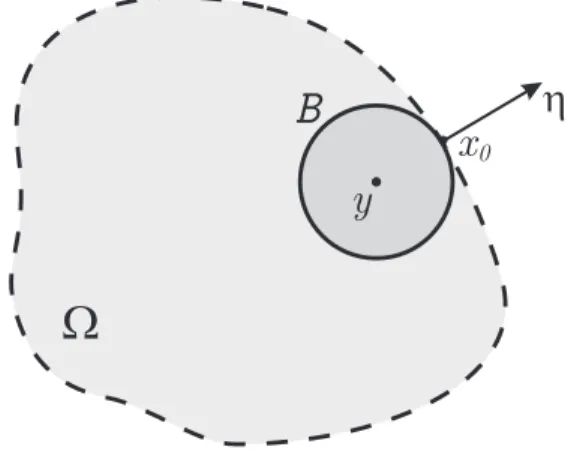
Um segmento geodésico γ : [a, b] → M é chamado minimizante se ℓ(γ) ≤ ℓ(c), em que ℓ(.) indica o comprimento de uma curva e c é qualquer curva diferenciável por partes ligandoγ(a) aγ(b). A seguinte proposi¸cão assegura que as geodésicas minimizam, localmente, o comprimento de arco.

Proposi¸c˜ao 1.6 (Proposi¸c˜ao 3.6, p. 71, [17]). Sejam p_∈M, U uma vizinhan¸ca normal

de p, B _⊂U uma bola normal de centro p. Seja γ : [0,1]_→B um segmento de geod´esica

com γ(0) = p. Se c: [0,1]→M ´e qualquer curva diferenci´avel por partes ligando γ(0) a

γ(1) ent˜ao ℓ(γ)_≤ℓ(c) e se a igualdade vale ent˜ao γ([0,1]) =c([0,1]).

Cabe observar que a proposi¸cão acima não é global, pois se considerarmos as geodésicas de uma esfera que partem de um ponto p não são minizantes depois que passam pelo ant´ıpoda de p. Por outro lado, se uma curva c diferenciável por partes é minimizante, então cé uma geodésica. Como afirma o seguinte corolário.

Corolário 1.7 (Corolário 3.9, p.73, [17]). Se uma curva diferenciável por partes γ :

[a, b] _→M, com parˆametro proporcional ao comprimento de arco, tem comprimento

me-nor ou igual ao comprimento de qualquer outra curva diferenci´avel por partes ligandoγ(a)

(26)

1.7. Segunda Forma Fundamental

1.7 Segunda Forma Fundamental

Seja ϕ : Mn _→ Mn+k uma imersão isométrica. Para simplificar a nota¸cão, identifi-caremos, para cada p_∈ M, cada vetor v _∈ T pM com dϕp(v) ∈ Tϕ(p)M e ϕ(W) com W,

onde _{W ⊂} M é uma vizinhan¸ca de p. Então a métrica de M decompõe TpM na soma

direta:

TpM =TpM ⊕(TpM)⊥,

onde (TpM)⊥ ´e o complemento ortogonal de TpM em TpM.

Se X, Y são campos locais de vetores em M, e X, Y são suas extensões locais a M , então a conexão Riemanniana de M é dada por ∇XY = (∇XY)T, onde ∇ é a conexão

Riemanniana de M.

Queremos definir a segunda forma fundamental da imers˜aoϕ. Para tanto, definiremos B(X, Y) = _∇_XY _{− ∇}XY como um campo local em M normal a M , onde X e Y

são campos locais em M. Segue que B(X, Y) não depende das extensões de X, Y, e a aplica¸cãoB :X₍_W₎_×X₍_W₎_→X₍_W₎⊥_{é bilinear e simétrica, onde}X₍_W₎⊥_{são os campos} diferenciáveis em M de vetores normais a M.

Estamos aptos a definir a segunda forma fundamental. Sejap_∈M eη_∈(TpM)⊥. A

aplica¸c˜ao Hη :TpM ×TpM →R dada por

Hη(u, v) =hB(u, v), ηi, ∀u, v ∈TpM

é uma forma bilinear simétrica. E portanto temos a seguinte defini¸cão.

A forma quadr´atica IIη definida emTpM por IIη(v) =Hη(v, v) ´e chamada a segunda

forma fundamental de ϕ em p segundo o vetor normalη.

Denotaremos por Sη : TpM → TpM a aplica¸c˜ao linear auto–adjunta associada `a

segunda forma fundamental de ϕ, isto ´e,

hSη(u), vi=Hη(u, v) =hB(u, v), ηi, ∀ u, v ∈TpM.

E essa aplica¸c˜ao linear, em termos da derivada covariante, pode ser expressa como

Sη(v) =−(∇vN)T,

onde N ´e uma extens˜ao local de η normal a M.

(27)

K(u, v) e K(u, v) as curvaturas seccionais de M e M, respectivamente, no plano gerado por u ev.

Teorema 1.8 (Gauss). Sejam p_∈M e u, v vetores ortonormais de TpM. Ent˜ao

K(u, v)−K(u, v) =hB(u, u), B(v, v)i − |B(u, v)|2.

Uma imersãoϕ :M _→M égeodésica em p_∈M se para todoη _∈(TpM)⊥ a segunda

forma fundamental Hη é identicamente nula emp. A imersãoϕ étotalmente geodésica se

ela ´e geod´esica para todo p_∈M.

Uma imers˜ao ϕ:M _→M ´em´ınima se para todo p_∈M e todo η _∈(TpM)⊥ tem–se

que o tra¸co de Sη = 0.

Escolhendo um referencial ortonormal ξ1, . . . , ξk de vetores em (TpM)⊥, ovetor

cur-vatura m´edia deϕ em p´e definido por

H = 1 n

X

k

(trSξk)ξk

que não depende do referencial ξk escolhido. E, é claro que ϕ é m´ınima se, e somente se,

H(p) = 0, para todop_∈M.

1.7.1 Segunda Forma Fundamental de Hipersuperf´

ıcies

Consideremos o caso particular em que a imersão é uma hipersuperf´ıcie, isto é, ϕ : Mn _→ Mn+1. Seja p _∈M e η _∈(TpM)⊥, |η| = 1. Como Sη : TpM → TpM é simétrica,

existe uma base ortonormal de vetores pr´oprios_{ξ1, . . . , ξn}deTpM com valores pr´oprios

λi, . . . , λn, i.é., Sη(ξ1) = λiξi, 1 ≤ i ≤ n. Se M e M são orientáveis e estão orientas,

ent˜ao o vetor η fica univocamente determinado se exigirmos que sendo {ξ1, . . . , ξn} uma

base na orienta¸c˜ao de M e _{ξ1, . . . , ξn, η} seja uma base na orienta¸c˜ao de M. Neste caso,

denominamos, osξi dire¸c˜oes principais e osλi =ki curvaturas principais deϕ e portanto,

a curvatura de Gauss–Kronecker de ϕ é det(Sη) = λ1. . . λn, e a curvatura média de ϕ é

1

ntr(Sη) =

1

n(λ1+. . .+λn).

Um caso importante ocorre quando M = Rn+1_{. Neste caso, podemos expressar a} curvatura média em coordenadas. Inicialmente, seja N uma extensão local deη, unitária e normal a M. Sejam α(t) = (a1(t), . . . , an(t)) e β(t) = (b1(t), . . . , bn(t)) duas curvas

(28)

1.7. Segunda Forma Fundamental

Escrevendo u=X

i

a′_i∂X ∂xi

e v =X

j

b′_j∂X ∂xj

temos que

hB(u, v), N_i = _hSη·u, vi

= _{− h}dN_·u, v_i

= − *

dN_·X

i

a′_i∂X ∂xi

,X

j

b′_j∂X ∂xj + = ₋ * X i

a′_i dN_·∂X ∂xi

,X

j

b′_j∂X ∂xj

+

= −X

i,j

a′_ib′_j

¿

dN·∂X

∂xi ,∂X ∂xj À = X i,j

a′_ib′_j

¿

N, ∂ 2_X ∂xi∂xj

À

onde a ´ultima igualdade vem do fato que

∂ ∂xi ¿ N,∂X ∂xj À = ¿

dN_·∂X ∂xi ,∂X ∂xj À + ¿ N, ∂ 2_X ∂xi∂xj

À

= 0.

Portanto,

bkl:=

¿ B µ ∂X ∂xk ,∂X ∂xl ¶ , N À = ¿ N, ∂ 2_X ∂xk∂xl

À

,

e ent˜ao a curvatura m´edia pode ser escrita

H = 1 n

X

i,j

gijbij (1.3)

onde gij ´e a inversa da m´etrica gij =

¿ ∂ ∂xi , ∂ ∂xj À

(29)

1.8 Gradiente, Divergente, Laplaciano e Hessiano

Definiremos nesta se¸cão, o gradiente, a divergência, o laplaciano e o hessiano em uma variedade Riemanniana, determinando para cada um destes suas expressões em rela¸cão a um referencial ortonormal e a um sistema de coordenadas. Destacaremos alguns resultados básicos que utilizaremos ao longo do nosso trabalho, também veremos a rela¸cão que existe entre os laplacianos de duas variedades conformes.

Dada uma fun¸c˜ao f _{∈ D}(M), o gradiente def ´e o campo de vetores

gradf :M _→ T M

p _7→ (p,gradf(p)),

definido por

hgradf, X_i=X(f) = df _·X, _∀X _∈X_(M_).

Dado X _∈X_{(M), o} _divergente_de _X _{´e a fun¸c˜ao divX} _:_M _→R_,_{definida por}

divX(p) = tr¡Y(p)7→(∇YX)(p)

¢

,

onde tr representa o tra¸co da aplica¸c˜ao linear Y(p)_7→(_∇YX)(p).

O operador linear ∆ : D(M)→ D(M) definido por:

∆f = div(gradf), _∀ f _{∈ D}(M)

´e chamado o operador Laplaciano de M.

Calcularemos, primeiramente, as express˜oes de gradf, divX e ∆f em rela¸c˜ao a um referencial ortogonal (ξ1, . . . , ξn) definido em um aberto de M. Observemos no entanto

que as expressões do gradiente, da divergência e do laplaciano independem do referencial escolhido, pois o gradiente em cara ponto p _∈ M é o vetor que representa o funcional linear dfp e a divergência é o tra¸co de uma aplica¸cão linear.

Como, por defini¸c˜ao,

hgradf, ξii=ξif, i= 1, . . . , m,

a express˜ao de gradf ´e

gradf =

m

X

i=1

¡

ξif

¢

(30)

1.8. Gradiente, Divergente, Laplaciano e Hessiano

De acordo com a defini¸c˜ao da divergˆencia de um campo X, temos

divX =

m

X

i=1

D

∇ξiX, ξi

E

,

e escrevendo X =

m

X

j=1

Xjξj segue que

h∇ξiX, ξii =

* ∇ξi

Ã _m

X

j=1 Xjξj

!

, ξi

+ = m X j=1 D ∇ξi

¡

Xjξj

¢

, ξi

E = m X j=1 D¡

ξiXj

¢

ξj +Xj∇ξiξj, ξi

E

= ξiXi+ m

X

j=1 Xj

D

∇ξiξj, ξi

E

= ξiXi− m

X

j=1 Xj

D

∇ξiξi, ξj

E

= ξiXi−

D

∇ξiξi, X

E

.

Conclu´ımos ent˜ao que

divX =

m

X

i=1

n

ξiXi −

∇ξiξi, X

®o

. (1.5)

Para o c´alculo do laplaciano, combinando (1.4) e (1.5) para obter

δf = div(gradf) =

m X i=1 n ξi ¡

ξif

¢

−∇ξiξi,gradf

®o , isto ´e, δf = m X i=1 n ξi ¡

ξif

¢

−¡∇ξiξi

¢

fo. (1.6)

Em particular, de {ξ1, . . . , ξm} é um referencial geodésico em p, ou seja, se além da

ortogonalidade temos ¡∇ξiξj

¢

(p) = 0, i, j = 1, . . . , m,então as expressões da divergência e do laplaciano no ponto p são

divX(p) =

m

X

i=1

¡

ξiXi

¢

(p) e ∆f(p) =

m

X

i=1 ξi

¡

ξif

¢

(p).

Seja x :_{U →} M um sistema de coordenadas locais, vamos calcular as express˜oes de gradf, divX e δf nesse sistema de coordenadas. Denotando ∂i =

∂ ∂xi

, seja {∂1, . . . , ∂m}

a base associada a esse sistema e considere a matrizG=¡gij

¢

definida por gij =

∂i, ∂j

®

(31)

i, j = 1, . . . , m. Denotemos por g = detG, G−1 = ¡gij¢ o determinante e a inversa de G, respectivamente.

Para o gradiente, escrevendo

gradf =

m

X

i=1 αi∂i,

temos que

∂f ∂xi

=_hαi∂i∂ji= m

X

i=1 αigij,

e pondo A =¡αi

¢

m×1 e F =

µ

∂f ∂xi

¶

m×1

, obtemos GA = F, ou seja, A = G−1_F_{. Segue} que

αi = m

X

j=1 gij ∂f

∂xi

e conseq¨uentemente,

gradf =

m

X

i=1

( _m

X

j=1 gij ∂f

∂xi

)

∂i. (1.7)

Calculemos a expressão da divergência. Se _{ξ1, . . . , ξm} é um referencial ortogonal

definido em x(U), escrevendo

ξi = m

X

k=1

eki∂k, i= 1, . . . , m,

temos

δij =

ξi, ξj

®

=

m

X

k,l=1

ekleljgkl, i= 1, . . . , m.

Pondo E = (eij), segue que ETGE =I. Portanto, podemos tamb´em escrever

δij = m

X

i,j=1

gikeklejl, i, j = 1, . . . , m. (1.8)

Para um campo X _∈X_(M_{) dado por}

X =

m

X

(32)

tem-se que

divX = X

k

∇ξkX, ξk

® =X k * ∇X i

eik∂i

X

j

aj∂j,

X

l

elk∂i

+

= X

i,j,k,l

elkeikh∇∂iaj∂j, ∂li

= X

i,j,k,l

elkeik

½¿

∂aj

∂xi

∂j, ∂i

À

+aj

∇∂i∂j, ∂l

®¾

= X

i,j,k,l

(

gjlelkeik

∂aj

∂xi

+X

r

³

grlelkeikajΓrij

´)

,

em que Γr

ij, i, j, r= 1, . . . , m, s˜ao os. utilizando s´ımbolos de Christoffel da conex˜ao ∇ no

sistema de coordenadas x. Utilizando (1.8), obtemos

divX =X

i ( ∂ai ∂xi +X j

ajΓiij

)

, (1.9)

e como

Γk_ij = 1 2 X l glk ½ ∂gjl ∂xi

+∂gli ∂xj −

∂ij ∂xl ¾ , segue que X i,j

Γiij =

1 2

X

i,j,l

ajgli

½

∂gjl

∂xi

+ ∂gli ∂xj −

∂gij ∂xl ¾ = 1 2 X i,j,l ½

ajgli

∂gjl

∂xi

+aiglj

∂glj

∂xi −

ajgil

∂glj ∂xi ¾ = 1 2 X i,j,l

ajgjl

∂glj

∂xi

.

Conseq¨uentemente,

divX = X

i

(

∂ai

∂xi

+ 1 2ai

X

j,l

gjl glj ∂xi ) =X i ½ ∂ai ∂aj +1 2aitr

µ

G−1∂G ∂xi ¶¾ = X i ½ ∂ai ∂xi + 1 2ai

1 g ∂g ∂xi ¾ =X i ½ ∂ai ∂xi

+ _√1 g

∂ ∂xi

(√g)

¾

,

em que ∂G ∂xi

denota a matriz obtida deGderivando-se cada elemento em rela¸cão à i-ésima

coordenada, e onde usamos o fato que ∂g ∂xi

=gtr

µ

G−1∂G ∂xi

¶

(veja [So], p. 56). Logo, a

expressão da divergência de X é

divX = _√1 g

X

i

∂i

¡

ai√g

¢

(33)

Finalmente, a partir de (1.7) e (1.10) obtemos o laplaciano como

∆f = _√1 g

X

i,j

∂i

µ

gij√g ∂f ∂xj

¶

. (1.11)

Convém mencionar agora algumas propriedades, que usando as defini¸cões de gradi-ente, divergente e laplaciano, por um cálculo direto podemos mostrar que

grad(f g) = fgradh+hgradf

div(f X) = fdivX+_hgradf, X_i (1.12)

∆(f g) = f∆h+h∆f+ 2_hgradf,gradh_i, (1.13)

para quaisquer f, g _{∈ D}(M). Se M ´e compacta e orient´avel, com bordo ∂M, para X _∈X_{(M) tem-se que}

Z

M

(divX)dV =

Z

∂Mh

X, ν_idA,

em que dV e dA são os elementos de volume deM e do bordo ∂M, respectivamente, e ν é o campo unitário normal exterior em∂M Este resultado é conhecido como Teorema da Divergência ([Sp], p. 192). Decorrem deste teorema e de (1.12) as chamadas Fórmulas

de Green _Z

M

©

f∆g+hgradf,gradgiªdV =

Z

∂M

f_hgradg, νidA (1.14)

e _Z

M

©

f∆g₋g∆fªdV =

Z

∂M

©

f_hgradg, ν_{i −}g_hgradf, ν_iªdA, (1.15)

para f, g_{∈ D}(M).

Introduziremos o conceito de variedades conformes. Seja ϕ : M _→ N um difeomor-fismo, em que N é uma variedade Riemanniana. Denotaremos por_h ,_i, _∇e ∆ a métrica em N, a conexão Riemanniana e o laplaciano relativos a esta métrica, respectivamente. Suponha que existe uma fun¸cão µ_{∈ D}(M) que satisfa¸ca, para todo p_∈M e todo par de vetores v, w_∈TpM, µ(p)6= 0 e

hdϕp·v, dϕp·wi=µ2(p)hv, wi.

(34)

Observemos que dados X ∈ X_(M_{) e} _f _{∈ D}_(M_{), pondo} _g ₌ _f _◦_ϕ−1_{, temos para} q=ϕ(p),

¡

(dϕ_·X)g¢(q) = dgq·

¡

dϕp·X(p)

¢

=¡dfp◦dϕ−1◦dϕq

¢¡

X(p)¢

= dfp·

¡

X(p)¢=¡Xf¢(p)

= ¡Xf _◦ϕ−1¢(q),

isto ´e,

¡

dϕ_·X¢g =Xf _◦ϕ−1. (1.16)

O lema a seguir nos mostra como se relacionam as conex˜oes de duas variedades conformes, neste caso as deM e N.

Lema 1.9. Se X, Y _∈X_(M_{), ent˜ao}

∇dϕ·X(dϕ·Y) =dϕ·

½

∇XY +

1 2µ

−2³_X¡_µ2¢_Y ₊_Y ¡_µ2¢_X

− hX, Y_igrad¡µ2¢ ´

¾

(1.17)

Demonstra¸c˜ao. Seja S(X, Y) o campo que satisfaz

∇dϕ·X(dϕ·Y) = dϕ·

³

∇XY +S(X, Y)

´

, (1.18)

para quaisquer X, Y, Z _∈X_(M_{). Utilizando (1.16) obtemos}

¡

dϕ_·X¢_hdϕ_·Y, dϕ_·Z_i = ¡dϕ_·X¢ ¡µ2_hY, Z_{i ◦}ϕ−1¢ = X¡µ2_hY, Z_i¢_◦ϕ−1,

ou seja,

¡

dϕ·X¢hdϕ·Y, dϕ·Zi=nX(µ2)hY, Zi+µ2XhY, Zio◦ϕ−1. (1.19)

Temos tamb´em que

h∇dϕ·X(dϕ·Y), dϕ·Zi = hdϕ·

¡

∇XY +S(X, Y)

¢

, dϕ_·Z_i

= µ2_h∇XY +S(X, Y), Zi ◦ϕ−1

= nµ2_h∇XY, Zi+µ2hS(X, Y), Zi

o

◦ϕ−1. (1.20)

Permutando-se Y eZ em (1.20) obtemos

hdϕ_·Y,_∇dϕ·X(dϕ·Z)i=

n

µ2_hY,_∇XZi+µ2hY, S(X, Z)i

o

(35)

Como

¡

dϕ_·X¢_hdϕ_·Y, dϕ_·Z_i=h∇dϕ·X(dϕ·Y), dϕ·Zi+hdϕ·Y,∇dϕ·X(dϕ·Z)i,

decorre de (1.19), (1.20) e (1.21) que (1.18) equivale a

Por outro lado, S(X, Y) dado por

S(X, Y) = 1 2µ

−2n_X¡_µ2¢_Y ₊_Y ¡_µ2¢_X_{− h}_{X, Y}_i_grad¡_µ2¢ o

obviamente verifica

hS(X, Y), Z_i= 1 2µ

−2n_X¡_µ2¢

hY, Z_i+Y ¡µ2¢_hX, Z_{i −}Z¡µ2¢_hX, Y_io

e, conseqüentemente, satisfaz a equa¸cão (1.22), o que conclui a demonstra¸cão do lema. ¤

A proposi¸c˜ao seguinte nos mostra a rela¸c˜ao que existe entre os laplacianos das varie-dades conformesM e N.

Proposi¸c˜ao 1.10. Sejam f _{∈ D}(M) e g _{∈ D}(N) tais que g =f _◦ϕ−1. Ent˜ao

∆g(q) =

½

1 µ2∆f+

m−2

2µ4 grad(µ 2_)f

¾

(p), (1.23)

em que q=ϕ(p), p_∈M.

Demonstra¸c˜ao. Seja {ξ1, . . . , ξm} um referencial ortogonal definido num aberto

V _⊂ M. Temos que que {ηζ1, . . . , ηζm} ´e um referencial ortogonal definido no aberto

W =ϕ(V), em que η = 1 µ ◦ϕ

−1 _e _ζ

i = dϕ·ξi, i = 1, . . . , m. Assim, de acordo com 1.6,

em W, temos

∆g = m X i=1 n ηζi ¡

ηζig

¢

−¡∆ηζi(ηζ1)g

¢ o

. (1.24)

Utilizando (1.16), vem que

ζig =

¡

dϕ_·ξi

¢

g =¡ξif

¢

◦ϕ−1, ζi

¡

ζig

¢

= (dϕ·ξi)

³

(ξif)◦ϕ−1

´

,

ζiξ = (dϕ·ξi)η =

½ ξi µ 1 µ ¶¾ ◦ϕ−1.

Calculemos cada parcela da soma em (1.24). Temos que

ηζi(ηζig) = η(ζiη)(ζig) +η2ζi(ζig) =

½ 1 µ µ ξi µ 1 µ ¶¶

(ηif) +

1 µ2ηi(ηi)

(36)

e

³

∆ηζi(ηζi)

´

g =η(ζiη)(ζig) +η2

³

(∆ζiζi)g

´

.

Para desenvolvermos esta ´ultima igualdade, vamos determinar a express˜ao de∇ζiζi. Pelo Lema 1.9 tem-se que

∇ζiζi =dϕ·

½

∇ξiξi+ 1 2µ2

³

2ξi

¡

µ2¢ξi −grad

¡

µ2¢ ´

¾

,

e decorre de (1.16) que

³ ∇ζiζi

´

g =½³∇ξiξi

´

f + 1 2µ2

³

2ξi

¡

µ2¢ξi−grad

¡

µ2¢ ´f

¾

◦ϕ−1.

Portanto,

³ ∇ηζi

¡ ηζi ¢´ g = ½ 1 µ µ ξi µ 1 µ ¶¶ ³

ξif

´

+ 1 µ2

·³ ∇xiiξi

´

f + 1 2µ2

³

2ξi

¡

µ2¢ξi−grad

¡

µ2¢ ´f

¸¾ ◦ϕ−1.

Conseqüentemente, o termo do somatório em (1.24) é

ηζi

¡

ηζig

¢

− ∇ηζi(ηζi) =

½

1 µ2

³

ξi(ξif)−(∇ξiξi)f

´ − 1 2µ4 ³ 2ξi ¡

µ2¢ξi−grad

¡

µ2¢ ´f

¾

◦ϕ−1. Logo, ∆g = ( 1 µ2 m X i=1 ³

ξi(ξif)−(∇ξiξi)f

´ + 1 2µ4 Ã _m X i=1

grad¡µ2¢₋2

m

X

i=1 ξi

¡

µ2¢ξi

!

f

) ◦ϕ−1

=

½

1 µ2∆f +

1 2µ4grad

¡

µ2¢f

¾

◦ϕ−1,

e em q=ϕ(p) temos (1.23). ¤

Para finalizarmos a se¸c˜ao, definiremos o Hessiano de uma fun¸c˜ao f _∈X_(M_).

Sejam f _∈ X_{(M) e} _p _∈ _M_{. Defina o} _hessiano _de _f _{no ponto} _p _{como a aplica¸c˜ao} bilinear, Hessf :TpM ×TpM →R dada por:

Hessf(X, Y) =_∇X(gradf), Y

®

(37)

Observando que

[X, Y](f) = XY(f)₋Y X(f) = (_∇XY − ∇YX)(f),

temos que Hessf(X, Y) = Hessf(Y, X), em queX, Y _∈X_(M_{), isto ´e, Hessf} _{´e uma forma}

bilinear sim´etrica. Se (x1, . . . , xn) ´e um sistema de coordenadas locais em M e ∂i =

∂ ∂xi

ent˜ao:

Hessf(∂i, ∂j) =∂i∂jf−(∇∂i∂j)(f).

Como ∇∂i∂j =

X

k

Γk_ij∂k podemos escrever a express˜ao acima da seguinte maneira:

Hessf(∂i, ∂j) =

³

∂i∂j−

X

k

Γk_ij∂k

´

(f).

Denotaremos tamb´em por Hessf o operador linear auto–adjunto associado ao hessiano de f.

As igualdades abaixo decorrem das propriedades do gradiente e divergente j´a vistas anteriormente:

∆(f g) = f∆g+g∆f+ 2h∇f,_∇g_i); 1

2∆(f

2_{) =} _f_∆f₊

(38)

1.9. O Espa¸co Hiperb´olico

1.9 O Espa¸

co Hiperb´

olico

Os espa¸cos de curvatura seccional constante podem ser agrupadas em três tipos: os de curvaturas seccional positiva, os de negativa e os que possuem curvatura seccional nula. Se multiplicarmos uma métrica Riemanniana por uma constante positiva c, então a sua curvatura seccional é multiplicada pelo inverso dec. Portanto, podemos supor que a curvatura seccional constante de uma variedade é 1, 0 ou −1.

O espa¸co euclidiano Rn+1 _{tem curvatura seccional nula, na esfera} Sn _{esse valor ´e 1;}

portanto para estudarmos as variedades com curvatura seccional constante devemos obter uma com curvatura ₋1. E esse ´e o caso do espa¸co hiperb´olico.

Definimos como Espa¸co Hiperb´olico de dimens˜ao n+ 1, o semi-espa¸co do Rn+1 _dado

por

Hn+1 _:=_{_{(x0, . . . , x}_n₎_∈Rn+1_;_x_n _>₀_}

munido da m´etrica

ds2 = dx 2

0+· · ·+dx2n

x2

n

= 1 x2

n n

X

i=0

dx2_i. (1.25)

Este espa¸co ´e simplesmente conexo e ´e completo. Antes de justificarmos estes fatos, vejamos o seguinte exerc´ıcio.

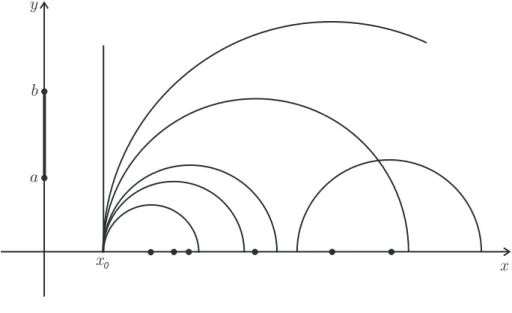
Consideremos H2 _{o plano hiperb´olico, ou seja,} H2 ₌_{_{(x, y)}_∈ R2_;_{y >}₀_}_.

Mostrare-mos que o segmento γ : [a, b] _→H2_, _{a >} _{0, do eixo dos} _{y, dado} _{γ(t) = (0, t) ´e a imagem}

de uma geod´esica. De fato, para qualquer arco c: [a, b]_→H2 _{dado por} _{c(t) = (x(t), y(t))}

com c(a) = (0, a) e c(b) = (0, b), temos que

ℓ(c) =

Z b

a k

c′(t)_kdt =

Z b

a

1 y

q£

x′_(t)¤2₊£_y′_(t)¤2_dt

≥ Z b

a

1 y

q£

y′_(t)¤2_dt_≥

Z b

a

|y′(t)_| y dt

≥ Z b

a

dy

y =ℓ(γ),

ou seja, γ minimiza arcos diferenciáveis por partes, e então pelo Corolário 1.7, a imagem deγ é uma geodésica. A aplica¸cão

z _7→ az+b

cz+d, z =x+iy, ad−bc= 1,

que ´e uma isometria emH2_{, transforma o eixo}_y_{em semi-c´ırculos superiores ou semi-retas}

(39)

as geod´esicas de H2_{, pois por cada ponto} _p _∈ H2 _{e cada dire¸c˜ao em} _T_pH2 _{passa um tal}

c´ırculo com centro no eixo x.

Figura 1.4: Geod´esicas em H2

O espa¸co Hn+1 _{´e completo pois as restas perpendiculares ao hiperplano} _x_n _{= 0, e os}

c´ırculos de Hn+1 _{cujos planos s˜ao perpendiculares ao hiperplano} _x

n = 0 e cujos centros

estão neste hiperplano são geodésicas de Hn+1_{. De fato, observe que uma isometria do} Rn+1 _{que só envolver as variáveis} _{x0, . . . , x}_n _{não altera a métrica dada em (1.25) e é,}

portanto, uma isometria em Hn+1_{. Ent˜ao basta considerar retas e c´ırculos no plano}_x0x_n

e o exerc´ıcio que fizemos acima. Na verdade, essas s˜ao todas as geod´esicas de Hn+1_.

1.9.1 Isometrias e o Modelo da Bola

Uma aplica¸c˜ao f : U _⊂ Rn+1 _→ _Rn+1 _{de um aberto} _U _⊂ _Rn+1 _´e _conforme _{se para} todop_∈U e todo par de vetoresv1 ev2 em p tivermos

hdfp(v1), dfp(v2)i=λ2(p)hv1, v2i, λ2 6= 0.

A fun¸c˜ao positiva λ:U _→R _{´e chamada o}_{coeficiente de conformalidade} _de_f

As isometrias do espa¸co hiperbólico no modelo do semi-espa¸co são as restri¸cões a

Hn+1 _⊂ _Rn+1 _{das transforma¸c˜oes conformes de} _Rn+1 _{que levam} _Hn+1 _{sobre si mesmo.} Uma demonstra¸c˜ao deste resultado, encontra-se em [17].

Identificaremos algumas hipersuperf´ıcies importantes do espa¸co hiperb´olicoHn+1_{. As}

(40)

deRn+1 _{ortogonais a}_∂Hn+1_{, e as interse¸c˜oes de} Hn+1 _{com as esferas de} Rn+1 _{com centro}

em ∂Hn+1_.

O espa¸co hiperbólico possui outros modelos além do semi-espa¸co. Um deles veremos agora, que é o modelo da bola. Considere a bola Bn+1 _⊂ _Rn+1 _{de raio 2 e centro na} origem,

Bn+1 ₌_{_p_∈Rn+1_;_|_p_|_{= 2}_}

e introduza a m´etrica

hij(p) =

δij

¡

1₋ 1₄_|p_|2¢2.

Considere a aplica¸c˜ao f :Bn+1 _→_Hn+1 _{dada por} f(p) = 4 p−p0

|p−p0|2 −(0, . . . ,0,1), em que p0 = (0, . . . ,0,−2).

Mostraremos que f é uma isometria, e portanto, Bn+1 _{é isométrico a}Hn+1_.

Com efeito, sev ´e um vetor empe_h,_iindica o produto interno na m´etrica euclidiana,

hdfp(v), dfp(v)i=

16hv, v_i

|p₋p0_|4. Por outro lado, indicando f(p) = (f1(p), . . . , fn(p)), obteremos

fn(p) =

4(xn+ 2)

|p₋p0_|2 −1 =

4− |p_|2

|p₋p0_|2. Portanto,

hdfp(v), dfp(v)i

¡

fn(p)

¢2 =

16_|p₋p0_|4_hv, v_i

¡

4− |p_|2¢2_|_p₋_p 0|4

= _¡ hv, vi 1−1

4|p|2

¢2.

Da injetividade de f, conclui-se que f ´e uma isometria de Bn+1 _em Hn+1_{. Observe que} _f

leva ∂Bn+1_{− {}_p_} _em _∂Hn+1_.

Note que uma aplica¸cão g : Bn+1 _→ _Bn+1 _{é uma isometria de} _Bn+1 _{na métrica} _h

ij,

se e somente se, g é a restri¸cão de uma transforma¸cão conforme do Rn+1 _{que leva} Bn+1

sobre Bn+1_.

Observe f leva∂Bn+1_{− {}_p₀_} _em _∂Hn+1_{. O ponto}_p₀ _{seria ent˜ao levado no “infinito”,}

pois nesse ponto o denominador da fra¸cão na fórmula de f se anularia uma potência a mais do que o numerador.

(41)

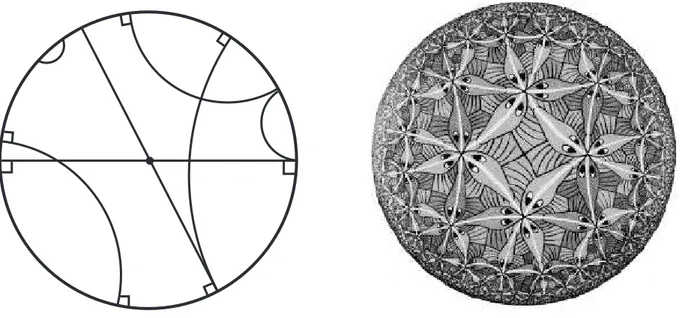
Figura 1.5: Modelo da bola, Bn+1

do plano hiperbólico mapeado no disco. A gravura mostra como nós, euclidianos natos, vemos o mundo hiperbólico desses chatóides. Quando um chatóide se afasta do centro do disco, vemos seu tamanho encolher ficando cada vez menor à medida que se aproxima do c´ırculo limite. O chatóide, é claro, não concorda com essa nossa descri¸cão do que acontece em seu mundo. Para ele, nada muda de tamanho quando se desloca pelo disco. Isso se justifica já que suas réguas e trenas são modificadas na mesma propor¸cão que seus corpos.

1.9.2 Superf´

ıcies Umb´

ılicas do

H

n+1

As superf´ıcies Umb´ılicas no espa¸co hiperbólico são as esferas, horoesferas e as su-perf´ıcies eqüidistantes (ou hiperesferas), como descreveremos a seguir.

As esferas s˜ao as esferas euclidianas que est˜ao totalmente contidas em Hn+1_{. Se o}

modelo do espa¸co hiperbólico for o da bola Bn+1_{, então essas superf´ıcies serão esferas}

contidas na bola aberta de raio 2, centradas na origem.

Consideremos, a seguir, uma n-esfera euclidiana S tangente a ∂Hn+1 _{em um ponto} _p,

tal que S_{− {}p_{} ⊂}Hn+1_{. Por uma invers˜ao do} Rn+1 _em _p_{(que ´e uma isometria do} Hn+1₎

S é levada em um hiperplano P paralelo a ∂Hn+1_{. Como a métrica induzida em} _P _por Hn+1 _{é um m´}_{ultiplo da métrica euclidiana, e} _P _{tem curvatura constante zero, o mesmo}

acontece com S _{− {}p_}. Essas subvariedades s˜ao chamadas de horoesfera. No modelo

(42)

limite de uma fam´ılia de esferas que passam por um pontoppr´e-fixado e cujos centros se deslocam ao longo de uma reta fixa.

Figura 1.6: Horoesfera

Quando q_{→ ∞} em L, as esferas se aproxima a uma superf´ıcie. Esta superf´ıcie ´e um plano passando emp no caso do Rn+1_{. No}Hn+1_{, esta superf´ıcie ´e a horoesfera.}

Considere finalmente uma esfera euclidiana S que corta∂Hn+1 _{segundo um ˆangulo} _θ,

e sua interse¸c˜ao S_∩Hn+1 _{= Σ com}Hn+1_{. Por uma invers˜ao de}Rn+1 _{em um ponto de}_S_∩

∂Hn+1_{, Σ ´e levada isometricamente na interse¸c˜ao com}Hn+1 _{de um hiperplano}_P _{que corta}

∂Hn+1 _{segundo o mesmo ângulo} _{θ. Considere o hiperplano} _Q _{que é ortogonal a} _∂_Hn+1 _e contémP _∩∂Hn+1_{. Vejamos, que}_P _{é uma hipersuperf´ıcie eq¨}_{uidistante da hipersuperf´ıcie}

totalmente geod´esicaQ. Para isto, sejaγr uma geod´esica, ,representada em Hn+1 por um

semi-c´ırculo de raior, com centro 0 emP _∩∂Hn+1 _{e no plano perpendicular a} _P_∩_∂Hn+1_.

Como existe uma homotetia de centro 0 (isometria hiperb´olica) levando o c´ırculo de raio r em um c´ırculo de raio qualquer, o comprimento de γr entre os pontos de interse¸c˜ao

de γr com P e Q não depende de r. Conclui-se que P, ou sua imagem isométrica Γ, é

obtida tomando geodésicas perpendiculares a uma hipersuperf´ıcie totalmente geodésicaQ e marcando sobre elas uma distância fixa. tais hipersuperf´ıcies são chamadas superf´ıcies eqüidistantes (ou hiperesferas).

As superf´ıcies umb´ılicas em Hn+1_{, possuem curvatura m´edia constante, mais}

(43)

Cap´ıtulo 2

Equa¸

c˜

oes Diferencias Parciais e o

Princ´ıpio do M´

aximo

Apresentaremos neste cap´ıtulo ferramentas necessárias de Equa¸cões Diferenciais Par-ciais (EDPs) que nos serão úteis para obten¸cão dos próximos resultados, que podem ser encontrados no livro de Gilbarg & Trundiger [7]. Estamos interessados no Princ´ıpio do Máximo e o Método da Continuidade para Equa¸cões Quasilineares El´ıpticas de 2a _ordem.

2.1 Continuidade H¨

older

Sejax0um ponto emRn_e_f _{uma fun¸c˜ao definida em um conjunto}_D_{limitado contendo}

x0. Se 0< α <1, dizemos quef ´eH¨older cont´ınuacom expoenteαemx0 se a quantidade

[f]α,x0 = sup D x6=x0

|f(x)−f(x0)|

|x₋x0_|α (2.1)

é finita. Chamamos [f]α,x0 o α-Coeficiente de Hölder de f no ponto x0 com respeito a D. Claramente, se f é Hölder cont´ınua em x0, então f é cont´ınua em x0. Quando (2.1) é finita para α= 1, f é dita ser lipschitziana em x0.

(44)

2.1. Continuidade H¨older

expoente α em Dse a quantidade

[f]α,D = sup

x,y∈D x6=y

|f(x)₋f(y)_|

|x₋y_|α , 0< α≤1 (2.2)

é finita; elocalmente Hölder cont´ınuacom expoenteαemD sef é uniformemente Hölder cont´ınua com expoente α em todo subconjunto compacto de D. Obviamente que esses dois conceitos coincidem quandoDé compacto. Além disso note que continuidade local de Hölder é uma propriedade mais forte do que Hölder continuidade pontual em subconjuntos compactos.

Continuidade de Hölder mede a continuidade que especialmente é bem adaptada ao estudo de EDPs. Num certo sentido, pode ser visto também como uma diferenciabilidade fracionária. Isto sugere uma extensão natural dos espa¸cos bem conhecidos de fun¸cões diferenciáveis.

Seja Ω um conjunto aberto de Rn _e_k _{um inteiro n˜ao negativo. Os} _{espa¸cos de H¨older}

Ck,α(Ω) (Ck,α_{(Ω)) s˜ao definidos como os subespa¸cos de} _Ck_{(Ω) (C}k_{(Ω)) consistindo de}

fun¸cões cujas derivadas parciais de ordem k são uniformemente Hölder cont´ınuas (local-mente Hölder cont´ınuas) com expoenteα em Ω. Por simplicidade escrevemos

C0,α(Ω) =Cα(Ω), C0,α(Ω) =Cα(Ω),

com a compreensão que 0< α < 1 sempre que esta nota¸cão é usada, a menos que, caso contrário seja declarado.

Tamb´em, fixando

Ck,0(Ω) =Ck(Ω), Ck,0(Ω) =Ck(Ω),

podemos incluir os espa¸cos Ck_{(Ω) (C}k_{(Ω)) entre os espa¸cos} _Ck,α_{(Ω) (C}k,α_{(Ω)) para}

0 < α < 1. Designamos por C₀k,α(Ω) o espa¸co de fun¸c˜oes em Ck,α(Ω) que tem suporte compacto em Ω.

Estabelecemos as seguintes defini¸c˜oes:

[u]k,0;Ω = |Dku|0;Ω = sup

|β|=k

sup Ω |

Dβ_|u, k= 0,1,2, . . .

a[u]k,α;Ω = [Dku]α;Ω = sup

|β|=k

[Dβu]α;Ω,

onde que, para todo β = (β1, . . . , βn), onde βi ´e um inteiro positivo e |β| =Piβi, temos

Dβu= ∂

|β|_u

∂xβ1 1 · · ·∂x

βn

n

(45)

Com estas “semi-normas”, n´os podemos definir as normas relacionadas

ku_k_Ck_(Ω) = |u|k;Ω =|u|k,0;Ω =

k

X

j=0

[u]j,0;Ω=

k

X

j=0

|Dju_|0;Ω,

ku_k_Ck,α_(Ω) = |u|_k,α_;Ω =|u|_k_;Ω+ [u]_k,α_;Ω =|u|_k_;Ω+ [Dku]_α_;Ω,

nos espa¸cos Ck(Ω) e Ck,α(Ω), respectivamente. Às vezes é útil introduzir normas não-dimensionais em Ck(Ω), Ck,α(Ω). Se Ω é limitado, temos

ku_k′_Ck_(Ω) = |u|

′

k;Ω=

k

X

j=0

dj[u]j,0;Ω=

k

X

j=0

dj_|Dju_|0;Ω,

ku_k′_Ck,α_(Ω) = |u|

′

k,α;Ω =|u|′k;Ω+dk+α[u]k,α;Ω =|u|′k;Ω+dk+α[Dku]α;Ω.

onde d= diam Ω = sup x,y∈Ω

x6=y

|x₋y_|.

Os espa¸cos Ck(Ω), Ck,α(Ω), munidos com essas respectivas normas, s˜ao espa¸cos de Banach.

2.2 Equa¸

c˜

oes Diferenciais Parciais El´

ıpticas

Apresentaremos, nesta se¸cão, a solu¸cão do clássico problema de Dirichlet para certos tipos de equa¸cões el´ıpticas totalmente não-lineares; isto é, equa¸cões el´ıpticas que não são quasilinear.

Uma equa¸cão diferencial parcial de segunda ordem pra fun¸cões reais em um dom´ınio Ω⊂Rn_{é uma expressão da forma}

F[u] =F(x, u,∇u,Hess u) = 0, (2.3)

onde F : Γ → R _{´e uma fun¸c˜ao definida no conjunto Γ = Ω} _×R_×Rn_{× A}m_{, em que}

Am ₌_Rn(n−1)/2 _{´e o espa¸co vetorial das formas bilineares sim´etricas. Denotaremos pontos} em Γ porγ = (x, z, p, r), em quex_∈Ω,z _∈R_,_p_{= (p}_i₎₁_≤_i_≤_n_∈Rn_e_r_{= (r}_ij₎₁_≤_i,j_≤_n_{∈ A}m_.

Se F é linear nas variáveis z, p e r então a equa¸cão (2.3) é dita linear. Se é linear nas variáveis r= (r)ij, então a equa¸cão (2.3) é dita quase-linear.

O operador F ´eel´ıptico num subconjunto U de Γ se a matriz ¡Fij(γ)

¢

, dada por

Fij(γ) =

∂F ∂rij