Superfícies de curvatura média constante

(1)

Invariantes por Subgrupos a 1-Parˆ

ametro de Isometrias

Gil F. de Souza

1

Susana C. Fornari

2

1

Aluno de pós-gradua¸cão em Matemática UFMG, e-mail: gil@mat.ufmg.br

2

(2)

Sum´

ario

1 Isometrias e Grupos a um parˆametro 4

1.1 Um pouco sobre transforma¸c˜oes lineares ortogonais. . . 4

1.2 Isometrias . . . 5

1.3 O Grupo de Isometrias deR3. . . 6

2 Curvas e Superf´ıcies 11 2.1 Curvas . . . 11

2.2 Superf´ıcies . . . 12

2.3 Superf´ıcies e Isometrias . . . 14

2.4 A Imagem da a¸c˜ao dos grupos Gα,β em pontos deR3. . . 15

3 Superf´ıcies Translacionais 17 4 Superf´ıcies Rotacionais 19 4.1 As Roulettes das cˆonicas. . . 19

4.1.1 A Roulette da Par´abola. . . 20

4.1.2 Roulettes em rela¸c˜ao a uma reta . . . 23

4.1.3 A Ondul´oide . . . 25

4.1.4 A Nod´aria . . . 28

4.2 As Curvaturas Médias do Catenóide, Ondulóide e Nodóide. . . 30

4.3 Superf´ıcies Rotacionais de Curvatura M´edia Constante. . . 31

5 Superf´ıcies Helicoidais 34 5.1 Parametriza¸c˜ao Natural e o Lema de Bour. . . 34

(3)

Agradecimentos

Agrade¸co à minha orientadora Susana pela paciência e tempo empreendido não somente no desenvolvimento deste trabalho como, também, durante a minha Inicia¸cão cient´ıfica sempre me apresentando belos temas. Agrade¸co aos professores do Dmat-Icex e amigos dos demais cursos. Em especial à Sônia pelas dicas valiosas que tanto me ajudaram na corre¸cão deste trabalho e o enriqueceram. Agrade¸co ao professor Alberto Sarmiento pelas sugestões e cr´ıticas, ao Michel pelas belas figuras em Cabri e ao meu amigo Agnaldo pela confeçcão da figura 5.1.

(4)

SUM ´ARIO ₃

Introdu¸

c˜

ao

Neste trabalho estudamos as superf´ıcies em R3 de curvatura m´edia constante invariantes por subgrupos a 1-parˆametro de isometrias.

No cap´ıtulo 1, revisamos alguns conceitos de ´Algebra Linear e Teoria de Grupos. Identificamos ainda o grupo ISO(R3) das isometrias de R3 com o subgrupoG(4) de matrizes 4×4 da forma:

G(4) =

T a

0 1

, T ∈O(3), a∈M3×1(R),0∈M1×3(R)

e mostramos que subgrupos a 1-parâmetro deG(4) são, a menos de conjuga¸cão, da forma

Gα,β =

  

  

 

cos(αt) sen(αt) 0 0

−sen(αt) cos(αt) 0 0

0 0 1 βt

0 0 0 1



 ;t∈R

  

  ,

sendoαeβ n´umeros reais.

No cap´ıtulo 2, revisamos alguns conceitos da Geometria das curvas e superf´ıcies. Al´em de estudarmos a a¸c˜ao dos gruposGα,β sob pontos deR3. Grande parte dos cap´ıtulos 1 e 2 foi baseada em [8].

Seα= 0, o grupoG0,β contém as transla¸cões e é denominadogrupo de transla¸cão; no caso em que β = 0,Gα,0

contém as rota¸cões e é ditogrupo de rota¸cão; seαeβ são ambos não nulos, Gα,β é chamadogrupo de movimentos

helicoidais. Uma superf´ıcieS tal queg(S) =Spara todog∈Gα,β´e ditaGα,β-invariante. As superf´ıcies invariantes

pelos gruposG0,β, Gα,0eGα,β s˜ao chamadas superf´ıcies translacionais, rotacionais e helicoidais, respectivamente.

No cap´ıtulo 3, estudamos as superf´ıcies translacionais, concluindo que as únicas superf´ıcies translacionais de curvatura média constante são o cilindro circular e o plano.

No cap´ıtulo 4, estudamos as superf´ıcies rotacionais e mostramos um resultado devido a Ch, Delaunay: “Su-perf´ıcies rotacionais de curvatura média constante são obtidas pela rota¸cão das roulettes das cônicas.” Sendo roulette a trajetória descrita por um dos focos de uma cônica enquanto ela (a cônica) rola sobre uma reta sem deslizar. O conteúdo deste cap´ıtulo foi baseado no artigo [5] de J. Eells.

Seja:

ΣH={superf´ıcies helicoidais emR3 de curvatura m´ediaH =cte6= 0}

e S1 _{o c´ırculo unit´ario parametrizado por (cos}_θ,_sen_θ_{) (}_θ _∈ _[0_,₂_π_{)). No cap´ıtulo 5, mostramos que existe uma}

aplica¸cão diferenciável, 2π-periódica e sobrejetiva

φ(θ, B0) : S1×[0,∞)→ΣH,

tal queφ(0,[0,∞)) s˜ao as superf´ıcies rotacionais em ΣH. Para a superf´ıcie rotacional S(B0) =φ(0, B0) (B0 fixo),

φ(θ, B0) (θ∈[0,2π)) ´e uma fam´ılia de superf´ıcies helicoidais associada a S(B0) (no sentido de que cada superf´ıcie

dessa fam´ılia é isométrica aS(B0)). O conteúdo deste cap´ıtulo foi baseado no trabalho de Manfredo P. do Carmo e

(5)

Isometrias e Grupos a um parˆ

ametro

Para dar in´ıcio ao estudo dassuperf´ıcies invariantes por subgrupos a 1-parâmetro de isometriasR3, faremos uma breve exposi¸cão sobre isometrias, grupos de isometrias e subgrupos a um parâmetro de isometrias.

1.1 Um pouco sobre transforma¸

c˜

oes lineares ortogonais.

Defini¸cão 1.1 Uma transforma¸cão ortogonal, é uma transforma¸cão linearC:R3→R3 tal que

hCv, Cwi=hv, wi,

para todo par de vetoresv e w∈R3.

Defini¸cão 1.2 Para cada transforma¸cão linearT :R3→R3, a adjunta de T é a transforma¸cão T∗ _:_R3 _→_R3 _tal

que

hT u, vi=hu, T∗_v_i_,

para todo paru, v∈R3.

Segue naturalmente de [7] que seCé uma transforma¸cão ortogonal, então:

(a)CC∗₌_C∗_C₌_I_{, onde}_I _{´e a identidade de}_R3_.

(b)C∗_{´e uma transforma¸c˜}_{ao ortogonal.}

(c) detC=±1.

(d)C preserva a norma euclideana.

Defini¸c˜ao 1.3 O(3) ={C:R3→R3; CC∗₌_I_}_{´e o conjunto das transforma¸c˜}_{oes ortogonais de}_R3_.

Proposi¸cão 1.1 O conjuntoO(3), em rela¸cão à opera¸cão de multiplica¸cão de matrizes (ou composi¸cão de fun¸cões), é um grupo.

Demonstra¸c˜ao:

(1) Vejamos queO(3) é fechado em rela¸cão à opera¸cão. SejamC eC′_∈_O_{(3), então}

hCC′u, CC′vi=hC′u, C′vi=hu, vi. LogoCC′ _∈_O_(3).

(2) Sabemos que a opera¸c˜ao ´e associativa.

(3) O elemento neutro ´e dado pela identidadeIdeR3.

(6)

CAP´ITULO 1. ISOMETRIAS E GRUPOS A UM PAR ˆAMETRO ₅

(4) Pela defini¸cão deO(3), o inverso deC∈O(3) éC∗ _logo_O_{(3) é um grupo.}

Defini¸cão 1.4 Um subespa¸co V ⊂R3 é dito invariante por uma transforma¸cão linearT :R3→R3 se T(V) =V.

Proposi¸c˜ao 1.2 Sejam C ∈O(3) e V um subespa¸co invariante por C. Ent˜ao o complemento ortogonal, V⊥_{, de V}

´e invariante por C.

Demonstra¸c˜ao:

C´e bijetora, pois detC=±16= 0. Sejam x∈V ey∈V⊥. ComoV ´e invariante porC,Cx∈V e logo

hCx, yi= 0. ComoC´e bijetora, existe y′ _∈_R3_{tal que} _y₌_Cy′_{. Portanto}

0 =hCx, yi=hCx, Cy′_i₌_h_{x, y}′_i

e logoy′_∈_V⊥_{, ou seja,}_V⊥ _{´e invariante por}_C_.

Proposi¸cão 1.3 DadaC∈O(3), existe uma base ortonormal em que a representa¸cão de C é

Cα=





cosα −senα 0 senα cosα 0

0 0 ±1



, α∈R.

Demonstra¸c˜ao:

O polinômio caracter´ıstico deC p(λ) =det(C−λI) é um polinômio de coeficientes reais e grau três. Portanto p(λ) possui pelo menos uma raiz realλ0. EntãoCv=λ0v. Desde queCé transforma¸cão ortogonal o valor deλ0é 1

ou -1, poiskCvk=kvk=|λ0| kvk. Suponhamos queC possua apenas um autovalor real e que esse autovalor ´e 1.

Consideremos a base ortonormal{v1, v2, v3}tal quev3´e autovetor associado aλ0 = 1 e os vetoresv1 ev2 formam

uma base (ortonormal) de{v: Cv=v}⊥_{. Como}_C _{´e transforma¸c˜}_{ao ortogonal e}_v

1⊥v2, resultaCv1⊥Cv2. Al´em

disso,Cv1 eCv2 são unitários e ,por hipótese,{v: Cv=v}⊥ não possui nenhum subespa¸co de dimensão 1 deixado

invariante por C. Portanto existeα∈Rtal que Cv1= cosαv1−senαv2 eCv2 = senαv1+ cosαv2 . Assim na base

{v1, v2, v3} a representa¸c˜ao deC´eCα.

No caso em que todas as ra´ızes dep(λ) são reais,R3pode ser escrito comoR3={v: Cv=v} ⊕ {v: Cv=−v}. Nesse último caso, com a escolha de uma base ortonormal para esses dois subespa¸cos, a representa¸cão matricial de CéCα, comα= 0 ouα=π, o que conclui a proposi¸cão.

1.2 Isometrias

Defini¸cão 1.5 Uma fun¸cão g : R3 →R3 tal que k g(u)−g(v) k=ku−v k para todo paru, v em R3 é dita uma isometria.

Exemplo 1.1 Um exemplo trivial de isometria ´e a transla¸c˜ao por um vetora∈R3,Ta(v) =a+v , pois

kTa(u)−Ta(v)k = ka+u−(a+v)k

= ku−vk.

Exemplo 1.2 Um outro exemplo de isometria ´e uma transforma¸c˜ao linear ortogonalC∈O(3), pois

kCv−Cwk2 ₌ _h_{Cv, Cv}_i₊_h_{Cw, Cw}_{i −}₂_h_{Cv, Cw}_i

= hv, vi+hw, wi −2hv, wi

(7)

Exemplo 1.3 Uma fun¸cão definida porg(v) =a+Cv,a∈R3eC∈O(3)é uma isometria pelos exemplos anteriores. Na próxima proposi¸cão mostraremos que toda isometriagé da formag(v) =a+Cv,a∈R3eC∈O(3). Proposi¸cão 1.4 Seja g:R3→R3 uma isometria. Então existema∈R3 eC∈O(3) tais que

g(v) =a+Cv,

para todov∈R3.

Demonstra¸c˜ao:

Come¸camos definindoa=g(0) eC(v) =g(v)−a. Mostraremos: (a)C preserva a norma,

(b)C preserva o produto interno,

(c)C ´e linear.

Prova de (a). kC(v)k=kg(v)−ak=kg(v)−g(0)k=kv−0k=kvk. LogoC preserva a norma. Prova de (b).

hC(v), C(w)i = kC(v)−C(w)k2_{− k}_C₍_v₎_k2_{− k}_C₍_w₎_k2

= kg(v)−g(w)k2_{− k}_C₍_v₎_k2_{− k}_C₍_w₎_k2

= kv−wk2_{− k}_v_k2_{− k}_w_k2

= hv, wi. PortantoC preserva o produto interno.

Prova de (c). Da defini¸c˜ao deC temosC(0) = 0. Al´em disso, dos itens (a) e (b) obtemos

kC(v+w)−C(v)−C(w)k2 ₌ _h_C₍_v₊_w₎₋_C₍_v₎₋_C₍_w₎_{, C}₍_v₊_w₎₋_C₍_v₎₋_C₍_w₎_i

= kC(v+w)k2₊_k_C₍_v_{) +}_C₍_w₎_k2₋₂_h_C₍_v₊_w₎_{, C}₍_v₎_i

−2hC(v+w), C(w)i

= kC(v+w)k2₊_k_C₍_v₎_k2₊_k_C₍_w₎_k2₊₂_h_C₍_v₎_{, C}₍_w₎_i

−2hC(v+w), C(v)i −2hC(v+w), C(w)i

= kv+wk2₊_k_v_k2₊_k_w_k2₊₂_h_{v, w}_i

−2hv+w, vi −2hv+w, wi

= kv+wk2₊_k_v₊_w_k2₋₂_h_v₊_{w, v}₊_w_i

= 0.

Logo,C(v+w) =C(v) +C(w) para todo parv, w∈R3. Juntando ao fato de queC(0) = 0, obtemos queCé linear. Como C é linear e preserva produto interno, resulta que C é uma transforma¸cão ortogonal. O que conclui a proposi¸cão.

1.3 O Grupo de Isometrias de

_R

3

.

Proposi¸cão 1.5 ISO(R3)={isometrias deR3} é um grupo com a opera¸cão de composi¸cão de fun¸cões.

Demonstra¸c˜ao:

Se g, hek ∈ ISO(R3), pela Proposi¸c˜ao 1.4 existem a, b, c ∈ R3 e T, S, R ∈ O(3) tais que, g(u) =a+T u, h(u) =b+Suek(u) =c+Ru. Temos ent˜ao que

(8)

CAP´ITULO 1. ISOMETRIAS E GRUPOS A UM PAR ˆAMETRO ₇

• g(hk) = (gh)k, pois

g(hk)(u) =g((b+Sc) +SRu) = (a+T(b+Sc)) +T SRu= (a+T b+T Sc) +T SRu

e

(gh)k(u) = (a+T b) +T S(c+Ru) = (a+T b+T Sc) +T SRu;

• o elemento neutro deISO(R3) ´ee(u) =u,∀u∈R3;

• o inverso de g´e g−1₍_u_{) =}₋_T−1_a₊_T−1_u_{, pois}_gg−1₍_u_{) =}_a₊_T₍₋_T−1_a₊_T−1_u_{) =}_u_e_g−1_g₍_u_{) =}₋_T−1_a₊

T−1₍_a₊_{T u}_{) =}_u_.

PortantoISO(R3) ´e um grupo.

Defini¸c˜ao 1.6 Definimos por G(4), o subgrupo de matrizes 4×4 com a forma

G(4) =

T a

0 1

, T ∈O(3), a∈M3×1(R), 0 = (0,0,0)∈M1×3(R)

. (1.1)

Proposi¸c˜ao 1.6 ISO(R3)´e isomorfo aG(4).

Demonstra¸c˜ao:

Recordemos que dois gruposG1 eG2, s˜ao isomorfos quando existe uma fun¸c˜ao bijetora ψ : G1 → G2 tal que

ψ(g.g′_{) =}_ψ₍_g₎_.ψ₍_g′_{), para todo}_g _e_g′_∈_G

1. Seja

φ: ISO(R3) −→ G(4)

g(u) =a+T u 7→

T a

0 1

.

Parag(u) =a+T u, h(u) =b+Sutemosg.h= (a+T b) +T Su eφ(g) =

T a

0 1

eφ(h) =

S b

0 1

. Ent˜ao

φ(g).φ(h) = T a 0 1 . S b 0 1 =

T S T b+a

0 1

=φ(gh).

Agora devemos mostrar queφé um isomorfismo, i.e, uma aplica¸cão bijetora. Oraφé injetora, pois seφ(g) =φ(h) entãoT =S ea=b, portantog=h. Para mostrar a sobrejetividade, seja

T a

0 1

∈G(4),

ent˜ao

T a

0 1

=φ(g),

comg(u) =a+T u.

Defini¸cão 1.7 Dizemos que um subgrupo H de G é subgrupo a 1-parâmetro se existe uma aplica¸cão cont´ınua e sobrejetoraψ: (R,+)→Gtal queψ(r+s) =ψ(r).ψ(s)para todo r e s ∈R.

Lema 1.0.1 SejamH ⊂G(4) um subgrupo a 1-parâmetro eh∈H. Então deth= 1. Demonstra¸cão:

Com efeito, sejah=

C a

0 1

∈G(4). O determinante dehé dado por deth= detC=±1. ComoH é subgrupo a 1-parâmetro, existe um homomorfismo sobrejetivoψ : (R,+) →H tal que ψ(1) = h. Mas ψ(1) = ψ(1

2).ψ( 1 2) =

ψ(1₂)2. Assim

deth= detψ(1) = det ψ 1 2 2 = detψ 1 2 2

>0.

(9)

Defini¸c˜ao 1.8 g1 e g2∈Gs˜ao conjugados, se existeg∈Gtal queg2=gg1g−1, analogamente dois subgruposH1 e

H2 deGs˜ao conjugados, se existeg∈Gtal queH2=gH1g−1.

Exemplo 1.4 SeC∈O(3), da Proposi¸c˜ao 1.3, existe uma base ortonormalB={u1, u2, u3}tal que a representa¸c˜ao

deC ´eCα. Denotemos por Aa matriz de passagem da base ortonormal fixa para a base B. Ent˜ao Cα =A−1CA.

AssimC eCα s˜ao conjugadas.

Lema 1.0.2 Seja H ⊂G(4) um subgrupo a 1-parˆametro Ent˜ao todo

h= C a 0 1 ∈H

´e conjugado, por elemento deG(4), a uma matriz da forma

φα,β =



 

cosα senα 0 0

−senα cosα 0 0

0 0 1 β

0 0 0 1

  =    

C

α 0 0 β

0 0 0 1



  

ondeα, β∈R.

Demonstra¸c˜ao:

Sejah=

C a

0 1

∈H e suponhamos que exista g=

S b

0 1

∈G(4) tal queh=gφα,βg−1, i.e,hg=gφα,β, ou

seja C a 0 1 S b 0 1 = S b 0 1    

C

_α 00 β

0 0 0 1



 

. (1.2)

O que faremos ´e determinarS, beβ satisfazendo a equa¸c˜ao (1.2). Por igualdade de matrizes em (1.2), obtemos

CS=SCα, (1.3)

Cb+a=S(0,0, β) +b. (1.4)

De (1.3) vemos que,Sé a matriz de passagem da base canônica para a base formada por vetores ortonormais tal que a matriz deC tem a representa¸cãoCα. Portanto S∈O(3). ConsideremosS = [v1v2 v3], sendov1,v2 ev3 vetores

coluna deS. Além disto, de (1.3) temos que v3é base do subespa¸co de dimensão 1 invariante porC. Temos então

que

(C−I)b=βv3−a,

Assim, perguntamos: Para qualβ o vetorβv3−a∈Im(C−I)? Respondendo a esta pergunta encontraremosbeβ

e, finalmente, determinaremosg.

Pelo Lema 1.0.1, deth= 1, poishé um elemento de um subgrupo a 1-parâmetro. Logo o número de subespa¸cos de dimensão 1 da forma{v: Cv=v} deixados invariantes porC é 1 ou 3. Além disso, o número de subespa¸cos de dimensão 1 da forma{v: Cv=−v} é 0 ou 2, pois senão ter´ıamos detC=−1. Assim dividimos a pergunta acima em dois casos:

1o _{Caso) dim}_Im₍_C ₋_I_{) = 2: Nesse caso dim}_{N uc}₍_C ₋_I_{) = 1 e} _v

3 ´e base de N uc(C−I), pois v3 ´e base de

{v: Cv=v}=N uc(C−I). Comov1,v2 ev3 formam uma base ortonormal deR3 temos que

Cv1= (cosα)v1+ (senα)v2

e

(10)

CAP´ITULO 1. ISOMETRIAS E GRUPOS A UM PAR ˆAMETRO ₉

para algumα∈R. Temos ent˜ao que

(C−I)v1= (cosα−1)v1+ (senα)v2

e

(C−I)v2=−(senα)v1+ (cosα−1)v2.

Logoh(C−I)v1,(C−I)v2i= (cosα−1)senα−senα(cosα−1) = 0 e{(C−I)v1,(C−I)v2}´e um conjunto linearmente

independente que geraIm(C−I), ou seja, {(C−I)v1,(C−I)v2}´e base para Im(C−I). Desde que (C−I)v1 e

(C−I)v2 são escritos como combina¸cão linear dev1ev2, então podemos tomar{v1, v2} base paraIm(C−I). Além

dissoR3=Im(C−I)⊕N uc(C−I). Ent˜ao todo vetor dev∈R3 pode ser escrito na forma v= ˜v+ ˜βv3, com ˜v∈Im(C−I),v3∈N uc(C−I) e ˜β ∈R.

Assim, escrevemos

a=ha, v1iv1+ha, v2iv2

| {z }

∈Im(C−I)

+ ha, v3iv3

| {z }

∈N uc(C−I)

.

Tomamosβ =ha, v3ie escolhemos b na imagem inversa do vetorha, v1iv1+ha, v2iv2 por (C−I). O que conclui a

primeira parte.

2o _{Caso) dim}_Im₍_C₋_I_{) = 0: Escolhemos uma nova base ortonormal de} _R3 _{tal que a matriz de passagem para}

esta base seja dada porS = [v1 v2 v3], com o vetor v3 que forma a terceira coluna de S sendov3 = _ka_a_k (a6= 0),

β=kak eb= 0, o que conclui o Lema.

Teorema 1.1 Todo subgrupo a 1-parˆametro deG(4)´e conjugado (por elemento de G(4)) a um subgrupo da forma

Gα,β=

   

   

  

C

αt

0 0 βt

0 0 0 1



  ;t∈R

   

  

, α eβ∈Rfixos.

Demonstra¸c˜ao do Teorema 1.1:

Sejam eH grupo a 1-parˆametro deG(4) eh∈H. Suponhamos quehtenha a representa¸c˜ao abaixo,

h=



 

cosα senα 0 0

−senα cosα 0 0

0 0 1 β

0 0 0 1





, (1.5)

comα, β∈R. Ent˜ao existe um homomorfismo cont´ınuoψ: (R,+)→H tal queψ(1) =h. Temos

ψ(n) =ψn_{(1) =}_hn₌



 

cos(nα) sen(nα) 0 0

−sen(nα) cos(nα) 0 0

0 0 1 nβ

0 0 0 1



 .

Analogamenteψ(1) =ψm₍₁_/m_{) sendo}

ψ(1/m) = 

 

cos(α/m) sen(α/m) 0 0

−sen(α/m) cos(α/m) 0 0

0 0 1 β/m

0 0 0 1



(11)

comn, m6= 0∈Z. Ent˜ao

ψ(n/m) = 

 

cos(n

mα) sen( n

mα) 0 0

−sen(n

mα) cos( n

mα) 0 0

0 0 1 n

mβ

0 0 0 1



 .

Comoψ´e cont´ınua, parat∈Rresulta

ψ(t) = 

 

0 0 1 βt

0 0 0 1



 ,

e esta ´e a express˜ao do homomorfismoψ.

Agora seja ˜H ⊂ G(4) um subgrupo a 1-parˆametro qualquer. Ent˜ao existe um homomorfismo cont´ınuo ˜ψ : (R,+)→H˜ tal que

˜ ψ(1) =

T a

0 1

=g



 

cosα senα 0 0

−senα cosα 0 0

0 0 1 β

0 0 0 1



 g

−1_,

comg dado peloLema 1.0.2. Repetindo o racioc´ınio anterior

˜ ψ(t) =g



 

0 0 1 βt

0 0 0 1



 g

−1_,

portanto, um subgrupoH a 1-parˆametro deG(4) ´e conjugado a umGα,β.

O Teorema 1.1 afirma que podemos considerar apenas os grupos Gα,β como subgrupos a 1-parˆametro de G(4),

(12)

Cap´ıtulo 2

Curvas e Superf´ıcies

2.1 Curvas

Defini¸cão 2.1 Uma curva parametrizada diferenciável de Rn é uma aplica¸cão α, de classe C∞_{, de um intervalo}

abertoI⊂Rem Rn. O conjunto dos pontos de Rn formado pelos pontosα(t),t ∈I, é o tra¸co de α. A curvaαé regular se seu vetor tangente é não nulo para todot∈I, ou seja,α′₍_t₎₆_{= 0}_{para todo} _t_∈_I_.

Neste trabalho estamos interessados apenas nos casos em quen= 2 ou 3.

Exemplo 2.1 α(t) = (x0+at, y0+bt, z0+ct),t ∈R, ´e uma parametriza¸c˜ao da reta de R3 que passa pelo ponto

(x0, y0, z0) na dire¸c˜ao do vetor (a, b, c).

Exemplo 2.2 β(t) = (x0+rcost, y0+rsent, z0),t∈R, ´e uma parametriza¸c˜ao de um c´ırculo de centro (x0, y0, z0)

e raior >0.

Exemplo 2.3 γ(t) = (rcost, rsent, δt),t∈R, é uma parametriza¸cão da hélice circular de passoδe eixoz. Defini¸cão 2.2 Uma curva α está parametrizada pelo comprimento de arco s se k α′₍_s₎ _k_{= 1} _{para todo valor do}

parâmetro s. Ou seja, se α: J ⊂→Rn, entãoαé parametrizada pelo comprimento de arco seα′₍_s₎_{é unit´}_{ario para}

todos∈J.

Exemplo 2.4 A curvaα(s) = (rcos _rs, rsen s_r) coms∈[0,2π) e r >0 ´e parametrizada pelo comprimento de arco, pois

kα′₍_s₎_k₌_k₍₋_sens

r

,coss r

)k= r

sen2s

r

+ cos2s

r

= 1.

Defini¸c˜ao 2.3 A curvatura k(t) de uma curvaα(t) = (x(t), y(t))deR2 ´e dada por

k(t) = x

′₍_t₎_y_”(_t₎₋_y′₍_t₎_x_”(_t₎

(x′₍_t₎2₊_y′₍_t₎2₎3/2 (2.1)

ou

k(s) =x′(s)y”(s)−y′(s)x”(s) (2.2) seαest´a parametrizada pelo comprimento de arcos.

Exemplo 2.5 A curva α(t) = (acost, bsent), t ∈Ré a curva cujo tra¸co é a elipse de equa¸cão x_a22 +

y2

b2 = 1 e sua curvatura ´e

k(t) = ab

(a2_sen2_t₊_b2_cos2_t₎3/2.

Observamos que a curvatura da elipse n˜ao se anula.

(13)

Exemplo 2.6 A curvaα(t) = (acosht, bsenht),t∈Ré a curva cujo tra¸co é a hipérbole de equa¸cão x_a22 −

y2

b2 = 1 e sua curvatura ´e

k(t) = −ab

a2_senh2_t₊_b2_cosh2_t3/2.

Observamos que a curvatura da hipérbole é não nula para todot∈R.

Defini¸c˜ao 2.4 Sejaαuma curva parametrizada pelo comprimento de arco emR2e sejan(s)o vetor normal unit´ario `

aαno pontoα(s). As F´ormulas de Frenet s˜ao:

α”(s) = k(s)n(s)

n′₍_s₎ ₌ ₋_k₍_s₎_α′₍_s₎ (2.3)

2.2 Superf´ıcies

Defini¸cão 2.5 Uma superf´ıcie parametrizada regular é uma aplica¸cão X : U ⊂R2 →R3, onde U é um aberto, tal que

(a)X´e diferenci´avel de classeC∞_;

(b) para todo par(u, v)∈U, temos Xu(u, v)∧Xv(u, v)6= 0, onde Xu(u, v)∧Xv(u, v) denota o produto vetorial de

Xu(u, v)eXv(u, v).

O subconjunto S deR3 formado pelos pontos X(u, v)´e o tra¸co da aplica¸c˜ao X.

Exemplo 2.7 O tra¸co de X(u, v) = (rcosu, rsenu, v), com (u, v)∈R2er >0, ´e o cilindro de equa¸c˜aox2₊_y2₌_r2_.

Exemplo 2.8 O tra¸co de X(u, v) = (cosusenv,senusenv,cosv), com (u, v)∈(0,2π)×(0, π) ´e a esferaS2_{de centro}

na origem e raio 1 menos um meridiano.

Exemplo 2.9 Sejaα(u) = (f(u),0, g(u)),u∈I ⊂Ruma curva regular tal queg′₍_u₎₆_{= 0 para todo}_u_{do intervalo}

I. Então a superf´ıcie obtida pela rota¸cão de α(u) em torno do eixo z é uma superf´ıcie regular parametrizada por X(u, v) = (f(u) cosv, f(u)senv, g(u)),v∈[0,2π].

Exemplo 2.10 O tra¸co deX(u, v) = (ucosv, usenv, v), com (u, v)∈R2, ´e chamado helic´oide.

(14)

CAP´ITULO 2. CURVAS E SUPERF´ICIES ₁₃

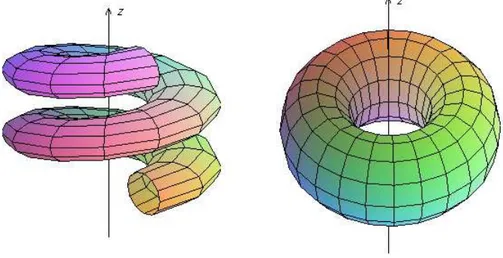
Exemplo 2.11 Consideramos superf´ıcie obtida pela rota¸cão de ângulo v em torno do eixo z seguida da eleva¸cão de δv da curva (2 + cosu,0,senu). Uma parametriza¸cão para tal superf´ıcie é X(u, v) = ((2 + cosu) cosv,(2 + cosu)senv,senu+δv), (u, v)∈R2, ondeδ é um número real e seu caso particularδ= 0. Observamos que seδ= 0, a parametriza¸cãoX(u, v) descreve o toro obtido pela rota¸cão do c´ırculo no planoxOz de raio 1 e centro(0,2,0).

Figura 2.2: O tra¸co das superf´ıcies do exemplo 2.11

Defini¸cão 2.6 A aplica¸cão de GaussN :U →S2 _{de uma superf´ıcie}_{X :} _U _→_R3 _{é definida por}

N(u, v) = Xu(u, v)∧Xv(u, v)

kXu(u, v)∧Xv(u, v)k =

Xu∧Xv

kXu∧Xv k,

onde Xu=

∂X

∂u e Xv=

∂X ∂v.

Defini¸cão 2.7 A curvatura média H de uma superf´ıcie S, parametrizada por X(u, v) e a curvatura Gaussianna K são dadas respectivamente por

H= gE−2f F+eG

2 (EG−F2₎ (2.4)

e

K= eg−f

2

EG−F2, (2.5)

onde

 



E=hXs,Xsi

F =hXs,Xti

G=hXt,Xti

, (2.6)

s˜ao os coeficientes da Primeira Forma Fundamental e  



e=hXss, Ni

f =hXst, Ni

g=hXtt, Ni

, (2.7)

(15)

Exemplo 2.12 As curvaturas m´edia e gaussiana do cilindro circular reto do exemplo 2.7, com parametriza¸c˜ao dada

porX(u, v) = (rcosu, rsenu, v)s˜ao H=−₂1_r e K= 0.

Exemplo 2.13 SejaS a superf´ıcie obtida pela rota¸c˜ao da curva (x(u), y(u),0),u∈I⊂R, em torno do eixo x. S ´e parametrizada por

X(u, v) = (x(u), y(u) cosv, y(u)senv), v∈R. Temos

     

    

Xu= (x′(u), y′(u) cosv, y′(u)senv) Xv= (0, y(u)senv, y(u) cosv)

N(u, v) =₍_x′(u)2+y1′(u)2)1/2(−y

′₍_u₎_{, x}′₍_u_{) cos}_{u, x}′₍_u_)sen_v₎ _X

uu= (x”(u), y”(u) cosv, y”(u)senv)

Xuv= (0,−y′(u)senv, y′(u) cosv) Xvv= (0,−y(u) cosv,−y(u)senv)

.

Assim  



E=x′₍_u₎2₊_y′₍_u₎2 _F _{= 0} _G₌_y₍_u₎2

e= x”(u)y

′₍_u₎

−x′(u)y”(u)

(x′₍_u₎2₊_y′₍_u₎2₎3/2 f = 0 g=−

y(u)x′(u) (x′₍_u₎2₊_y′₍_u₎2₎1/2

.

Portanto,

H =x”(u)y

′₍_u₎₋_x′₍_u₎_y_”(_u₎

(x′₍_u₎2₊_y′₍_u₎2₎3/2 −

x′₍_u₎

y(u)(x′₍_u₎2₊_y′₍_u₎2₎1/2. (2.8)

Observemos que a primeira parcela deH em (2.8) ´e a curvatura da curva (x(u), y(u),0) (dacurva geratrizdeS).

2.3 Superf´ıcies e Isometrias

Veremos que a curvatura médiaH de uma superf´ıcieS e a curvatura média ˜H da superf´ıcieh(S), onde hpertence a um subgrupo a 1-parâmetro deISO(R3), são iguais (i.e,H = ˜H).

Proposi¸cão 2.1 Sejamh∈G, G subgrupo a 1-parâmetro deISO(R3), S parametrizada porX(u, v)eh(S) parame-trizada porh(X(u, v)). Então as curvaturas médias H e ˜H, respectivamente, são iguais.

Demonstra¸c˜ao: Mostraremos:

(a) Os coeficientesE,F eGdeS s˜ao iguais aos coeficientes ˜E, ˜F e ˜Gdeh(S) s˜ao iguais.

(b) Os coeficientese,f eg deS s˜ao iguais aos coeficientes ˜e, ˜f e ˜gdeh(S) s˜ao iguais.

Do cap´ıtulo 1, temos que seh∈ISO(R3), ent˜ao h(u) =a+T u, a∈R3, T ∈O(3). Logo: z(u, v) =h(X(u, v)) = a+T(X(u, v)). Portanto

zu = TXu

zv = TXv .

Ent˜ao

˜

E=hzu, zvi=hXu,Xvi=E.

Analogamente temos que ˜F=F e ˜G=G. Temos ainda;

 



zuu = TXuu

zuv = TXuv

zvv = TXvv

.

No vetor normal ˜N(u, v) = zu×zv

kzu×zv k

= TXu×TXv

kTXu×TXv k

, podemos escreverkTXu×TXvk=kXu×Xv k, pois

pelaidentidade de Lagrange

(16)

CAP´ITULO 2. CURVAS E SUPERF´ICIES ₁₅

Assim

˜

N(u, v) = TXu×TXv

kXu×Xv k

.

Calculando o coeficiente ˜eda Segunda Forma Fundamental.

˜

e = hTXuu,N˜(u, v)i=

TXuu,

TXu×TXv

kXu×Xv k

=

det 

 TXuu

TXu

TXv





kXu×Xvk

= det(h)

kXu×Xv k

det   Xuu Xu Xv 

 = det(h)hXuu, N(u, v)i

= det(h).e.

SendoN(u, v) o vetor normal de X(u, v). Pelo Lema 1.0.1, det(h) = 1. Logoe= ˜e. Analogamente, ˜f =f e ˜g=g. Juntando (a) e (b) com a express˜ao (2.4), obtemosH = ˜H.

Defini¸c˜ao 2.8 Dizemos que uma superf´ıcie S ´e invariante por um subgrupo G⊂ISO(R3)(G-invariante) seh(S) =S

para todoh∈G.

Unindo a Proposi¸cão 2.1 com o Teorema 1.1, vemos que para estudar as superf´ıcies em R3 de curvatura média constante invariantes por subgrupos a 1-parâmetro de ISO(R3), basta estudar as superf´ıcies de curvatura média constante invariantes pelos grupos Gα,β. A nossa próxima se¸cão se dedicará a descrever as formas que os grupos

Gα,β podem assumir e estudar a imagem da a¸c˜ao desses grupos.

2.4 A Imagem da a¸

c˜

ao dos grupos

G

_α,β

em pontos de

_R

3

No cap´ıtulo 1, vimos que o grupoISO(R3) é isomorfo ao grupoG(4). Além disso, todo subgrupo a 1-parâmetro de ISO(R3) é identificado, a menos de conjuga¸cão, com um subgrupo de G(4) da forma

Gα,β =

       

0 0 1 βt

0 0 0 1

        ,

ondeαeβ∈R.

Primeiramente, veremos comoGα,β age sobre pontos deR3. Recordemos que uma isometriahdeR3´e da forma

h(u) =a+T u, a∈R3 eT ∈O(3). Ap´os a identifica¸c˜ao com G(4), temos ˜h=

T a

0 1

. Observamos que ˜hage

sobre u 1 =     u1 u2 u3 1   

do mesmo modo quehage sobre o vetor u= (u1, u2, u3)∈R

3_{, pois}

˜ h u 1 = T a 0 1 u 1 =

T u+a 1

.

Portanto, ˜h∈G(4) age sobre vetores (u1, u2, u3,1)∈R4 da mesma forma queh∈ISO(R3) age sobre (u1, u2, u3)∈

R3.

Agora, estudaremos as formas deGα,βe sua a¸c˜ao em vetores (u1, u2, u3) (estamos identificando (u1, u2, u3,1)∈R4

com o vetor (u1, u2, u3)∈R3).

(17)

(a)α= 0 eG0,β contém transla¸cões na dire¸cão do eixo z. A imagem da a¸cão deG0,β sobre (x0, y0, z0) é uma reta

na dire¸c˜ao do eixoz, pois 

  

I

00 βt

0 0 0 1

        x0 y0 z0 1    =     x0 y0

z0+βt

1 

  .

(b)β= 0 eGα,0 contém as rota¸cões em torno do eixoz. A imagem da a¸cão deGα,0sobre (x0, y0, z0) é um c´ırculo

de centro (0,0, z0) e raio

p x2

0+y02.



 

0 0 1 0

0 0 0 1

       x0 y0 z0 1    =    

x0cos(αt)−y0sen(αt)

x0sen(αt) +y0cos(αt)

z0 1    .

(c) No casoα6= 0 eβ6= 0, temosGα,β=G1,δ, ondeδ=α/β, pois, seja

φ

αt,βt=



 

0 0 1 βt

0 0 0 1





∈Gα,β.

Ent˜ao

φ

_αt,βt

=

φ

₁_.αt,β.δt∈G1,δ. Reciprocamente, temos

φ

_t,δt

=

φ

_α.t α,β.

t

α∈Gα,β, logoGα,β=G1,δ.

Quanto `a a¸c˜ao deG1,δ sobre um ponto (x0, y0, z0), temos



 

cost sent 0 0

−sent cost 0 0

0 0 1 δt

0 0 0 1

       x0 y0 z0 1    =    

x0cost−y0sent

x0sent+y0cost

z0+δt

1



  ,

(18)

Cap´ıtulo 3

Superf´ıcies Translacionais

Superf´ıcies Translacionaissão aquelas invariantes por transla¸cões em uma dada dire¸cão deR3.

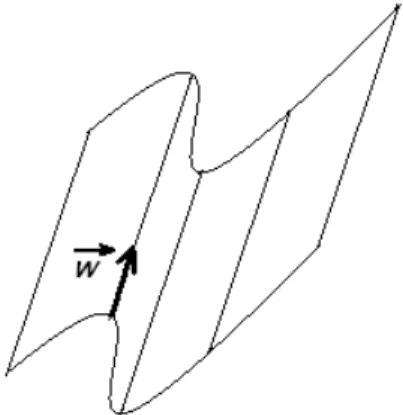
Exemplo 3.1 O cilindro α(t) +rw, sendo α(t) = (x(t), y(t),0), t definida no intervalo I⊂ R, r ∈ R e

w= (w1, w2, w3), é invariante pela transla¸cão de qualquer múltiplo de w.

Figura 3.1: Um cilindro.

Proposi¸cão 3.1 Seja S uma superf´ıcie translacional de curvatura média constante, então ou S é um plano, ou S é um cilindro.

Demonstra¸c˜ao:

Pelo Teorema 1.1, o subgrupo a 1-parâmetro das transla¸cões em uma dada dire¸cão é identificado, via mudan¸ca de coordenadas, com o subgrupo a um parâmetroG0,β. As superf´ıcies translacionais são então superf´ıcies invariantes

porG0,β. Observamos que uma superf´ıcieG0,β-invariante possui um ponto da forma (x, y,0), pois se (x, y, z)∈S,

comoS´eG0,β-invariante e a transla¸c˜aogdada por (0,0,−z) pertence aG0,β, resultag(x, y, z) = (x, y,0)∈S.

SeS uma superf´ıcieG0,β-invariante parametrizada por X(u, v), (u, v)∈U ⊂R2. Como para todo p∈S existe

uma reta na dire¸cão de (0,0,1), consideramos a parametriza¸cão de uma destas retas dada por X(u(t), v(t)), t∈R, então

dX dt = Xu

du dt + Xv

dv dt

(19)

é um vetor na dire¸cão de (0,0,1), portanto (0,0,1) pertence a todo plano tangente de S. Logo seu vetor normal em cada ponto é linearmente independente com o vetor (0,0,1) o que faz da interseçcão de S com o planoxOy uma curva regular plana, denotemos esta curva porγ(s) = (x(s), y(s),0), já tomando-a com o parâmetro comprimento de arcos, então uma parametriza¸cão paraS é X(s, t) = (x(s), y(s), t).

Ent˜ao calculamos os vetores Xse Xt, tangentes aS.

Xs= (x′(s), y′(s),0), (3.1)

e

Xt= (0,0,1). (3.2)

Seu vetor normal ´e dado por,

Xs∧Xt=β(y′(s),−x′(s),0).

Então a aplica¸cão normal deS éN(s, t) = (y′₍_s₎_,₋_x′₍_s₎_,_{0), pois}_k_X

s∧Xtk= 1.

Temos

     

    

xss = (x”(s), y”(s),0)

xst = (0,0,0)

xtt = (0,0,0)

,

e

     

    

e = x”(s)y′₍_s₎₋_x′₍_s₎_y_”(_s₎

f = 0

g = 0

,

a expressão da curvatura média de Sé,

2H =x”(s)y′₍_s₎₋_x′₍_s₎_y_”(_s₎_. _(3.3)

A expressão obtida em (3.3) é a expressão da curvatura deγa menos de sinal, portantoγ(s) é uma reta ou uma

circunferência. Reciprocamente, seS é um cilindro circular reto de raioa >0, sua curvatura média éH = 1 2a ([2], pg 147); se S é um plano entãoH = 0 ([2], pg 147). Portanto se S é uma superf´ıcie G0,β-invariante de curvatura

(20)

Cap´ıtulo 4

Superf´ıcies Rotacionais

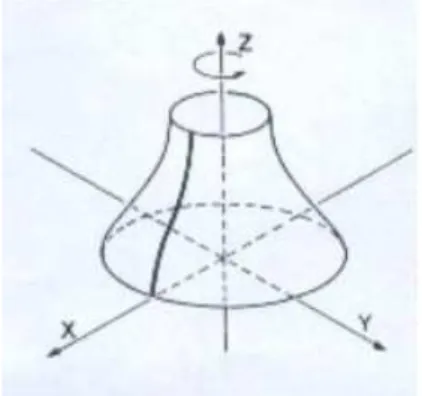
Superf´ıcies rotacionais são as superf´ıcies que são invariantes por rota¸cões emR3, ou seja, por rota¸cões em rela¸cão a uma dada reta. Seu estudo se reduz ao estudo da curva geratriz, isto é, a curva descrita pela interseçcão da superf´ıcie com um plano que contenha o eixo de rota¸cão.

Figura 4.1: Uma superf´ıcie de rota¸c˜ao de eixoz.

Pelo Teorema 1.1, o subgrupo das rota¸cões em rela¸cão a um determinado eixo é identificado, via mudan¸ca de coordenadas, com o subgrupo a um parâmetroGα,0. As superf´ıcies rotacionais, são, então, superf´ıcies invariantes

porGα,0.

Neste cap´ıtulo mostraremos os seguinte resultado provado por C. Delaunay em 1841 [4]:

Teorema 4.1 (Delaunay) Uma superf´ıcie rotacional de curvatura média constante é obtida pela rota¸cão da roulette de uma cônica.

A demonstra¸c˜ao apresentada se baseia no artigo de Eells [5] e segue as seguintes etapas: 1o_{) descreveremos as roulettes das cˆ}_onicas;

2o_{) iremos calcular as curvaturas m´edias das superf´ıcies obtidas pela rota¸c˜}_{ao destas curvas;}

3o_{) via express˜}_{ao da curvatura m´edia, demonstraremos que a curva geratriz de uma superf´ıcie de rota¸c˜}_{ao de curvatura}

média constante não-nula satisfaz às equa¸cões das roulettes da elipse ou da hipérbole.

4.1 As Roulettes das cˆ

onicas.

Descreveremos as roulettes das cˆonicas.

(21)

4.1.1 A Roulette da Par´

abola.

Como ilustra¸cão, determinaremos , primeiro a roulette da parábola. Uma parábolade focoF e retadiretrizré o conjunto {K ∈R2 : dist(K, F) =dist(K, r)}. O ponto V da parábola com a menor distância a ré denominado vértice da parábola. V está na reta perpendicular arque contém o focoF da parábola, pois a reta que é perpendicular are passa porF é a que dá a menor distância entreF e a diretriz, portanto a menor distância entre a parábola e a diretriz.

Figura 4.2: Par´abola com foco F=(0,c).

Tomando o sistema de coordenadas cartesianas (x, y) em queV=(0,0) e o eixo xé paralelo à reta diretriz, sejamF= (0, c) o foco ey=−c a reta diretriz. A equa¸cão da parábola é

y= x

2

4c. (4.1)

Defini¸cão 4.1 A roulette do foco F em rela¸cão a uma reta tangente à parábola é a trajetória que F descreve enquanto a parábola rola sobre esta reta sem deslizar.

O objetivo desta se¸cão é mostrar que esta roulette é uma catenária. Para tal vamos mostrar os seguintes lemas:

Lema 4.1.1 Sejam t a reta tangente `a par´abolay= x

2

4c em um pontoK= (x0, x2

0

4c)e P o ponto de intersec¸c˜ao de t

com o eixo x. Ent˜ao P =x0 2 ,0

.

Demonstra¸c˜ao:

A equa¸c˜ao det´ey= x0 2cx−+

x0

2cx− x2

0

4c. Logo, paray= 0 temos P = _x₀

2 ,0

. Para determinar

a coordenaday da roulette, encontraremos um pontoP′ _de_t _{tal que}_P′_F _{seja perpendicular a}_t_{. O pr´}_{oximo lema}

determinar´aP′_.

Lema 4.1.2 Com a nota¸cão do Lema 4.1.1, FP é perpendicular à reta t.

Demonstra¸c˜ao:

Sejam m := coeficiente angular da reta F P e m′ _{:= coeficiente angular de} _t_{. Basta mostrar que}_m.m′ ₌₋₁_.

Comom= −c x0/2

=−2c

x0

em′₌ x0

2c e portanto,m.m

′ ₌₋2c

x0

.x0

2c =−1. LogoF P ⊥t.

A figura 4.3 representa dois instantes diferentes em que a parábola rola sem deslizar sobre o eixox, que é a reta tangente do vértice.

.

o primeiro instante (em linha cheia) representa o momento inicial do movimento em que a parábola é tangente ao eixoxemV = (0,0) e o foco está emF = (0, c) e está representada também a reta tangentetemK;

(22)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₂₁

Figura 4.3: Par´abola rolando.

Lema 4.1.3 Uma parametriza¸cão em coordenadas cartesianas da roulette da parábola de equa¸cão y= x

2

4c ´e

β(x) = Z x

0

r 1 + r

2

4c2dr−

x 2

r 1 + x

2

4c2 , c

r 1 + x

2

4c2

!

(4.2)

Demonstra¸c˜ao:

A par´abola de equa¸c˜aoy = x

2

4c pode ser parametrizada porα(x) =

x,x

2

4c

. Pelo Lema 4.1.1, P =x 2,0

e logo|P F|=

c2₊x2

4 1/2

=c

1 + x

2

4c2

1/2

. Analisando o instante em que o pontoK =

x,x

2

4c

´e tangente ao

eixox, as coordenadas do foco (agora representado por F˜) s˜ao dadas por (|VP˜|,|P˜F˜|) = (|VP˜|,|P F|). Ora

|VP˜|=|VK˜| − |P ˜˜K|, onde|VK˜|é o comprimento do arco da parábola de 0 atéx,ou seja

|VK˜|= Z x

0

1 + r

2

4c2

1/2

dr.

Por outro lado,

|P K|=x−x₂2+

x2

4c 1/2

= x 2

1 + x

2

4c2

1/2

.

Logo

|VP˜|= Z x

0

1 + r

2

4c2

1/2

dr−x₂

1 + x

2

4c2

1/2

.

Lema 4.1.4 Seja α(s) = (x(s), y(s))a reparametriza¸c˜ao por comprimento de arco da roulette da par´abola dada por

β(x) = (x(x), y(x))do Lema 4.1.3. Ent˜ao

dx

ds =

c

(23)

Demonstra¸c˜ao: Ora

e

x(x) = Z x

0

1 + r

2

4c2

1/2

dr−x₂

1 + x

2

4c2

1/2

y(x) = c

1 + x

2

4c2

1/2

. Calculando a derivada dex(x), temos

x′(x) =

1 + x

2

4c2

1/2

−1₂

1 + x

2

4c2

1/2

−x₂₍₄(2_cx2)₎

1 2

1 + x

2

4c2

−1/2

= 1 2

1 + u

2

4c2

1/2

.

Calculando a derivada dey(x), temos

y′(x) =c2x 4c2

1 2

1 + x

2

4c2

−1/2

= x 4c

1 + x

2

4c2

−1/2

.

Logo

x′(x)2+y′(x)2=1 4

1 + x

2

4c2

−1

+ x

2

16c2

1 + x

2

4c2

−1

=1 4.

Como o parˆametro comprimento de arco sdeβ ´e dado pors(x) =R₀x|β′₍_r₎_|_dr₌Ru

0

p

x′₍_r₎2₊_y′₍_r₎2_dr_{, temos}

ds

dx =

q

x′₍_x₎2₊_y′₍_x₎2_{. Logo} dx

ds =

1 p

x′(x(s))2₊_y′₍_x₍_s₎₎2 = 2. Assim, pela regra da cadeia,

dx ds = dx dx. dx ds = 1 2

1 + x(s)

2

4c2

1/2

.2 = c

y(x(s))= c y(s).

Proposi¸cão 4.1 A roulette da parábola de equa¸cão y= x

2

4c é a catenária de equa¸cão y=ccosh( x c)

Demonstra¸c˜ao:

Pela equa¸c˜ao (4.3) dx

ds =

c

y(s). Comoβ(x(s)) =β(s) é regular, temos que a roulette da parábola é (localmente)

o gráfico de uma fun¸cão (x, y(x)). Além disso, ds

dx = 1 +

dy dx

2!1/2

6

= 0,portanto,

dx

ds = 1 +

dy dx

2!−1/2

.

Ent˜ao reescrevemos (4.3) como,

1 + _dy

dx

2!−1/2

= c

y. (4.4)

Logo, 1 + dy dx 2 = y 2 c2 dy

dx = ±

_y

c 2

−1 1/2

(24)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₂₃

Observando quez/c≥1 (cé a menor distância do foco a parábola) e resolvendo a equa¸cão diferencial acima por separa¸cão de variáveis obtemos

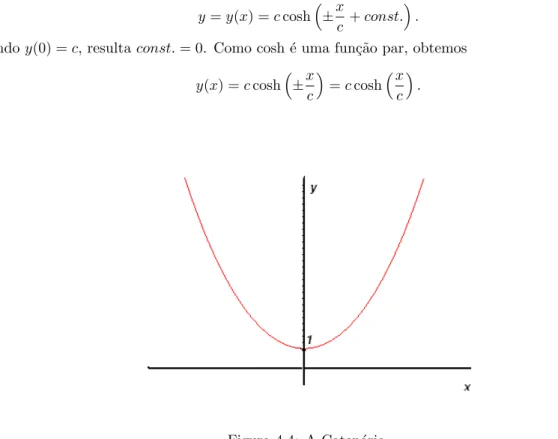
y=y(x) =ccosh±x_c +const.. Considerandoy(0) =c, resultaconst.= 0. Como cosh ´e uma fun¸c˜ao par, obtemos

y(x) =ccosh±x_c=ccoshx c

.

Figura 4.4: A Caten´aria.

4.1.2 Roulettes em rela¸

c˜

ao a uma reta

A subse¸cão anterior é a motiva¸cão desta subse¸cão. Determinaremos propriedades úteis das roulettes em rela¸cão a uma reta.

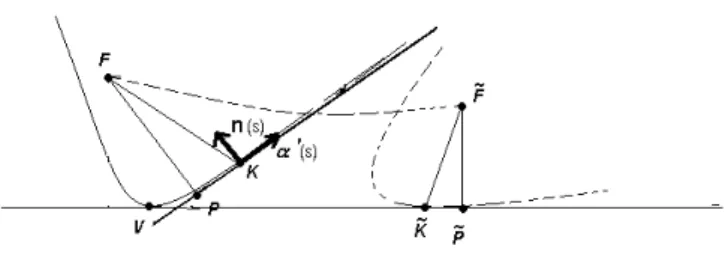
Defini¸cão 4.2 A roulette de um ponto F associado a curva C em rela¸cão a uma reta tangente à C é a trajetória descrita por F enquanto C rola sobre esta reta tangente sem deslizar.

Proposi¸cão 4.2 SejamC uma curva regular com curvatura que não se anula eF um ponto que não pertence aC. Seja β a roulette de F associado a C em rela¸cão a uma retra tangente à C. Sejam F˜ um ponto de β e K˜ o ponto de contato de C com o eixo x (nesse instante). Então a roulette de F em rela¸cão à reta tangente de C é uma curva regular, além disso a reta normal a roulette em ˜F passa por ˜K, ou seja o segmento ˜F ˜K é perpendicular à reta tangente `

a roulette em ˜F.

Demonstra¸c˜ao:

Consideramos a roulette deF = (x0, y0) associada à curvaC parametrizada porα(s), ondesé o parâmetro

comprimento de arco da curvaC.

A figura 4.5 representa dois instantes diferentes:

• No primeiro instante, antes deCcome¸car a rolar, est˜ao indicados o pontoF = (x0, y0), a retat, tangente aC

emK=α(s), o pontoP ∈ttal queF P ⊥te os vetores tangente e normal `a C (α′₍_s_{) =}_α′ _{e n(}_s_{) = n);}

• o segundo momento representa o instante em queC rolou sobre o eixox, sem deslizar, at´e o pontoK (agora representado por ˜K) ser tangente ao eixo x.

(25)

Figura 4.5: Uma roulette.

1. determinamos o vetor−−→F K;

2. determinamos uma parametriza¸c˜aoβ(s) para a roulette;

3. calculamosh−−→F˜K, α˜ ′₍_s₎_i_{, concluindo a proposi¸c˜}_ao.

SuponhamosCorientada de tal modo que o vetor normal unit´ario n(s) emK=α(s) aponte para “dentro”(fig. 4.5).

Temos−−→F K =h−−→F K, α′_i_α′₊_h−−→_{F K,}_n_i_{n = (}_|_PK_|₎_α′₋₍_|_PF_|_)n.

No segundo instante,C rolou atéKser tangente ao eixox(Kagora é representado por ˜K). Nesse instante os vetores (1,0) e (0,1) desempenham o papel de vetores tangente e normal, respectivamente, àC em ˜K e

−−→_˜

FK˜ = (h−−→F K, α′_i_, _h_{F K,}−−→ _n′_i_{) = (}_|_{P K}_|_,_−|_{P F}_|_).

As coordenadas de ˜F = (˜x,y˜) s˜ao dadas por

˜

x=|VK˜| − |P˜K˜|=|VK˜| − |P K|

˜

y=|P˜F˜|=|P F| . (4.5)

|VK˜|é igual ao comprimento de arco deC entreV =α(0) eK=α(s). Logo|VK˜|=s, pois sé o parâmetro comprimento de arco deC. Como|P K|=h−−→F K, α′_i_e_|_{P F}_|₌_−h−−→_{F K,}_n_i_{, uma parametriza¸c˜}_{ao da roulette de}

F ´e

β(s) = (s− h−−→F K, α′_i_, _−h−−→_{F K,}_n_i₎_. _(4.6)

O vetor−−→F K=−−→F K =α(s)−F e logo d ds

−−→

(26)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₂₅

β′₍_s₎ ₌ ₍₁₋ d

dsh

−−→

F K, α′i, d dsh

−−→

F K,ni) =

1−

d ds

−−→

F K, α′

+h−−→F K, α”i

,

d ds

−−→

F K,n′

+h−−→F K,n′_i

= 1−hα′, α′i+h−−→F K, α”i , hα′,ni+h−−→F K,n′i

= −h−−→F K, α”i, h−−→F K,n′_i

= k−h−−→F K,ni, −h−−→F K, α′_i

= k(−|P F|,−|P K|),

pois pelas f´ormulas de Frenet,α” =kn e n′₌₋_kα′ _{, onde}_k_{a curvatura de}_C _em_α₍_s_{). Portanto}

h−−→F˜K, F˜ ′(s)i=k(−|P K|.|P F|+ (−|P F|)(−|P K|)) = 0,

o que conclui a demonstra¸cão. A afirma¸cão de que a roulette é uma curva regular é resultado imediato da equa¸cãoβ′₍_s_{) =}_k₍_−|_{P F}_|_,_−|_{P K}_|_{), pois}_k₆_{= 0.}

Observa¸cão 4.1 Na demonstra¸cão da Proposi¸cão 4.2, para a deduzir uma equa¸cão para β(s) utilizamos a hipótese de que a retat, tangente àC, tem inclina¸cão positiva (figura 4.5). No entanto, settivesse inclina¸cão negativa, com a mesma escolha de orienta¸cão em C, obter´ıamos a mesma parametriza¸cãoβ(s) para a roulette.

Observa¸cão 4.2 A Proposi¸cão 4.2 foi demonstrada sob a hipótese de que a curvatura deC não se anula, o que garante que a trajetória deF é uma curva regular.

Corolário 4.2.1 Seja γ(s) = (x(s), y(s))a reparametriza¸cão de β(s)pelo parâmetro comprimento de arco s. Então, com a mesma nota¸cão da Proposi¸cão 4.2,

|F˜K˜|=±|P˜F˜|

dx ds

−1

=±y(s)

dx ds

−1

, (4.7)

onde ˜K ´e o ponto de contato de C com o eixo x.

Demonstra¸c˜ao: Com efeito, como visto na proposi¸c˜ao anterior ,β′₍_s_{) =}_k₍_−|_{P F}_|_,_−|_{P K}_|_{) =}₋_k₍_|_{P F}_|_,_|_{P K}_|_),

logo

kβ′(s)k=|k|p(|P F|)2_{+ (}_|_{P K}_|₎2₌_|_k_|_._|_{F K}_|_.

Por hip´otesek6= 0, da´ı

β′₍_s₎

kβ′₍_s₎_k =±

|P F| |F K| ,

|P K| |F K|

.

Comoγ(s) = (x(s), y(s)) é a reparametriza¸cão pelo comprimento, então

dx

ds =±

|P F| |F K| =±

y(s)

|F K|.

4.1.3 A Ondul´

oide

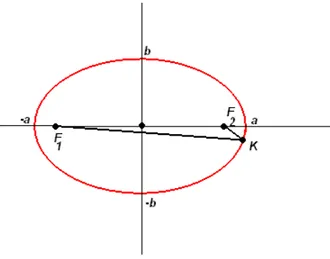
A elipse de focosF1= (−c,0) eF2= (c,0) ´e o conjunto dos pontosK∈R2 tais que a soma dos comprimentos

dos raios focais ´e constante, ou seja|F1K|+|F2K|= 2a >0, onde a > c´e o comprimento do semi-eixo maior

eb=√a2₋_c2_{o comprimento do semi-eixo menor.}

(27)

Figura 4.6: A Elipse.

Proposi¸cão 4.3 A roulette de um dos focos de uma elipse(ondulária) em ela¸cão a uma reta tangente é uma curva regular.

Analogamente ao caso da parábola, faremos uso de propriedades da tangentet, para deduzir uma equa¸cão para a ondulóide.

Proposi¸cão 4.4 Seja β(s) = (x(s), y(s))a parametriza¸cão da ondulária pelo comprimento de arco. Então a fun¸cão coordenadax(s)satisfaz

dx

ds =±

y(s)2₊_b2

2ay(s) , (4.8)

sendo “a”o semi-eixo maior e “b”o semi-eixo menor da elipse.

Demonstra¸c˜ao:

Vamos considerar a elipse de centroO e semi-eixos maior e menor dados poraeb. Consideramos ainda o c´ırculo de centroO e raioa. Relativamente `a elipse e o c´ırculo, temos:

– O ˆangulo formado pelos raios focais e a tangentets˜ao iguais (figura 4.7).

– Os pontosP1eP2de interseçcão detcom o c´ırculo de centroOe raioa, são tais queP1F1⊥teP2F2⊥t.

– _|P1F1|.|P2F2|=b2.

As duas últimas propriedades são menos conhecidas. Para uma demonstra¸cão das mesmas, ver [9], página 111. Na figura 4.8, consideramos a trajetória do focoF2 da elipse enquanto ela rola sem deslizar sobre o eixox.

Os triˆangulos

F1P1KeF2P2Ks˜ao semelhantes. Logo

|P1F1|

|P2F2|

=|F1K|

|F2K|

. (4.9)

Manipulando (4.9),

|P1F1|

|P2F2|

= |P1F1|.|P2F2| (|P2F2|)2

= b

2

(|P2F2|)2

(28)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₂₇

Figura 4.7: Segmentos ortogonais na elipse.

Figura 4.8: Elipse rolando.

Al´em disso

|F1K|

|F2K|

= |F1K|+|F2K|

|F2K| −

|F2K|

= 2a

|F2K|−

1

e portanto

b2

(|P2F2|)2

= 2a

|F2K|−

1. (4.10)

Pela Proposi¸cão 4.3 a roulette de uma elipse é uma curva regular e portanto admite parametriza¸cão pelo comprimento de arco. O segmento |P2F2| é a coordenada y da roulette da elipse e pelo Corolário 4.2.1,

|F2K|=±y(s)

dx ds

−1

que ao ser substitu´ıda em (4.10) d´a

b2

y(s)2 =±

2a y(s)

dx

ds −1 (4.11)

sendoso parˆametro comprimento de arco da roulette. Ent˜ao

dx

ds =±

y(s)2+b2 2ay(s) ,

o que demonstra a Proposi¸c˜ao.

(29)

el´ıpticas ( ver [4]).

Observa¸cão 4.3 Considera¸cões sobre a equa¸cão dx ds =±

y(s)2₊_b2

2ay(s) :

a) No caso em quea=b a elipse ´e um c´ırculo de raioade “focos”F1=F2 e a roulette se reduz a uma reta da

formay=a;

b) no caso limiteb= 0 (i.e,limb→0dx_ds) a elipse degenera-se em um segmento de reta de comprimento 2aeF2

em um dos extremos do segmento. Nesse caso, a roulette ´e constituida por semi-c´ırculos de raio 2a.

4.1.4 A Nod´

aria

AHip´erboledefocosF1 eF2´e o conjunto dos pontosK do plano tais que

|F1K| − |F2K|=±2a; (4.12)

em que a < c. Sendo o semi-eixo tranverso o valor a e b =√c2₋_a2 _o _{semi-eixo conjugado}_{. Os segmentos}

|F1K|e|F2K|s˜ao denominados porraios focais(fig. 3.12).

Figura 4.9: Hip´erbole.

Segue daProposi¸c˜ao 4.3 que

Proposi¸cão 4.5 A roulette de um dos focos de uma hipérbole (nodária) em rela¸cão a uma reta tangente é uma curva regular.

Analogamente aos casos da parábola e da elipse, faremos uso de propriedades da tangentet, para de deduzir uma equa¸cão para a nodária.

Proposi¸cão 4.6 Seja β(s) = (x(s), y(s))a parametriza¸cão da nodária pelo comprimento de arco. Então

dx

ds =±

y(s)2₋_b2

2ay(s) , (4.13)

sendo a e b os semi-eixos transverso e conjugado da hip´erbole.

Demonstra¸c˜ao:

Relativamente `a hip´erbole de semi-eixosaeb, centroO e focosF1eF2. Temos;

(30)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₂₉

Figura 4.10: Segmentos ortogonais na hip´erbole

Figura 4.11: Hip´erbole rolando.

– tintercepta o c´ırculo de raioae centro O, em pontosP1 eP2 tais queP1F1⊥teP2F2⊥t.

item|P1F1|.|P2F2|=b2.

Na figura 4.11, consideramos a trajet´oria do focoF2 enquanto a hip´erbole rola sobre o eixox.

Como P2KPˆ 1 = P1KFˆ 2 e F1Pˆ1K = KPˆ2F2 =

π

2, observamos que os triângulos F1KP1 e F2KP2 são semelhantes (três ângulos iguais), logo

|P1F1|

|P2F2|

= |F1K|

|F2K|

. (4.14)

Manipulando (4.14),

|P1F1|

|P2F2|

=|P1F1|.|P2F2| (|P2F2|)2

= b

2

(|P2F2|)2

,

al´em disso,

|F1K|

|F2K|

=|F1K| − |F2K|

|F2K|

+|F2K|

|F2K|

=± 2a |F2K|

+ 1,

portanto

b2

(|P2F2|)2

=± 2a |F2K|

+ 1. (4.15)

(31)

´e uma curva regular. Pelo Corol´ario 4.2.1 |F2K| = ±y(s)

_dx

ds −1

que ao ser substitu´ıda em (4.15),

mostra que a equa¸c˜ao da roulette deF2 satisfaz

b2

y(s)2 =±

2a y(s)

dx

ds+ 1, (4.16)

sendoso parˆametro comprimento de arco da roulette, ent˜ao

dx

ds =±

y(s)2₋_b2

2ay(s) ,

o que demonstra a Proposi¸c˜ao.

Novamente, a equa¸cão anterior possui solu¸cão em termos de fun¸cões el´ıpticas (veja [4]).

Figura 4.12: A Nod´aria.

4.2 As Curvaturas M´

edias do Caten´

oide, Ondul´

oide e Nod´

oide.

Nesta se¸cão realizaremos o cálculo das curvaturas médias das superf´ıcies obtidas pela rota¸cão das roulettes, acatenária, aondulária e anodáriaque originam ocatenóide, oondulóidee onodóide, respec-tivamente.

No Cap´ıtulo 2, observamos que uma superf´ıcie de rota¸cão pode ser parametrizada por X(u, v) = (x(x), y(x) cosv, y(x)senv) e que a expressão de sua curvatura média é dada por

H =x”(x)y

′₍_x₎₋_x′₍_x₎_y_”(_x₎

(x′₍_x₎2₊_y′₍_x₎2₎3/2 −

x′₍_x₎

y(x)(x′₍_x₎2₊_y′₍_x₎2₎1/2

ou

H =x”(s)y′(s)−x′(s)y”(s)−x

′₍_s₎

y(s) (4.17)

se a curva geratriz da superf´ıcie est´a parametrizada pelo parˆametro comprimento de arco.

Lema 4.1.5 Se a curva geratriz de uma superf´ıcie de rota¸cão com eixo de rota¸cão x está parametrizada ex′₍_s_{) =}_f₍_y₍_s₎₎_{, ent˜}_ao

H=−1₂

f′(y) +f(y) y

(32)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₃₁

Demonstra¸c˜ao:

Sex′₍_s_{) ´e como acima, ent˜ao}

y′₍_s_{) =}_±₍₁₋_f2₍_y₎₎1/2_⇒_y_{” =}_∓₍₁₋_f2₍_z₎₎−1/2_{f f}′_y′ ₌₋_f₍_y₎_f′₍_y₎_,

enquanto

x” =f′(y)y′⇒x”y′ =f′(y)(y′)2=f′(y)(1−f2(y)). Ent˜ao pela equa¸c˜ao (4.17),

H =−1

2

f2₍_y₎_f′₍_y_{) +}_f′₍_y₎₍₁₋_f2₍_y_{)) +}f(y)

y

=−1

2

f′₍_y_{) +}f(y)

y

.

Pela equa¸c˜ao (4.3) dx

ds =

c

y, por (4.8) dx

ds = ±

y2₊_b2

2ay , de (4.13) dx

ds = ±

y2₋_b2

2ay e por (4.18) calculamosH das superf´ıcies obtidas pela rota¸c˜ao das roulettes das cˆonicas:

∗ Caten´oide; f(y) = c y

H =−1

2

− c

y2 +

c y2

= 0.

Pelos cálculos acima, a curvatura média do catenóide éH = 0, portanto o catenóide é uma superf´ıcie m´ınima, a única superf´ıcie m´ınima de revolu¸cão (ver [2]).

∗ Ondul´oide, Cilindro e Esfera ; f(y) =±y

2₊_b2

2ay

H = −1

2

±4ay

2₋₍_y2₊_b2₎₂_a

4a2_y2 ±

y2₊_b2

2ay2

= ∓ 1

2a.

∗ Nod´oide;f(y) =±y

2₋_b2

2ay

H = −1

2

±4ay

2₋₍_y2₋_b2₎₂_a

4a2_y2 ±

y2₋_b2

2ay2

= ∓ 1

2a.

4.3 Superf´ıcies Rotacionais de Curvatura M´

edia Constante.

Pelo que vimos anteriormente, se uma superf´ıcie rotacionalS com curva geratriz parametrizada pelo comprimento de arco (x(s), y(s),0) satisfaz

dx

ds =±

y(s)2_±_b2

2ay(s) ,

para constantesaeb, então a curvatura média deS é não nula.

Proposi¸cão 4.7 Uma superf´ıcie rotacional S possui curvatura média constante H6= 0 se, e só se, a curva geratriz de S satizfaz

y2±2aydx ds±b

2_{= 0}_{, a}_e_b_constantes_. _(4.19)

Demonstra¸c˜ao:

ComoS é uma superf´ıcie parametrizada regular podemos supor que localmente a sua curva geratriz é o gráfico de uma fun¸cão, i.e, sua curva geratriz pode ser parametrizada por (x,y˜(x),0). Logo,

H =1

2

˜ y”(x) (1 + ˜y′₍_x₎2₎3/2 −

1 ˜

y(x)(1 + ˜y′₍_x₎2₎1/2

(33)

ComoS ´e de

curvartura m´edia constante, escrevemosH =₂1_a >0. Logo _y_˜_”(_x₎

(1 + ˜y′₍_x₎2₎3/2 −

1 ˜

y(x)(1 + ˜y′₍_x₎2₎1/2

=1

a

ay˜”(x)−(1 + ˜y

′₍_x₎2₎

˜

y(x)(1 + ˜y′₍_x₎2₎3/2 = 1,

ay˜”(x)−(1 + ˜y

′₍_x₎2₎

(1 + ˜y′₍_x₎2₎3/2 −y˜(x) = 0.

Multiplicando ambos os membros desta ´ultima express˜ao por 2˜y′₍_x_{), obtemos}

2ay˜′(x)y˜”(x)−(1 + ˜y

′₍_x₎2₎

(1 + ˜y′₍_x₎2₎3/2 −2˜y(x)˜y

′₍_x_{) = 0}_. _(4.21)

A express˜ao (4.21), pode ser integrada emx. E assim,

− 2ay˜(x)

(1 + ˜y′₍_x₎2₎1/2 −y˜(x) 2₌

±b2, (4.22)

sendob2_{uma constante. Agora, reparametrizando pelo parˆametro comprimento de arco}_s₌Rx 0

p

1 + ˜y′₍_t₎2_dt_,

obtemos

−2ay(s)dx ds −y(s)

2₌

±b2, (4.23)

pois dx

ds = (1 + ˜y

′₍_x₎2₎−1/2_{. Isolando} dx

ds em (4.23), resulta

dx

ds =

y(s)2_±_b2

2ay(s) .

Considerando tamb´em o casoa <0, obtemos

dx

ds =±

y(s)2_±_b2

2ay(s) .

Considerando, tamb´em, o caso em queH = 0 e j´a tomando da curva geratriz da superf´ıcie parame-trizada pelo comprimento de arco, obtemos

H =1

2

˜ y”(x) (1 + ˜y′₍_x₎2₎3/2 −

1 ˜

y(x)(1 + ˜y′₍_x₎2₎1/2

.

FazendoH = 0 em (2.8) obtemos

˜ y”(x) 1 + ˜y′₍_x₎2 =

1 ˜ y(x).

Definindo u(x) = ˜y′₍_x_{), obtemos ˜}_y_”(_x_{) =} du

dx =

du dy˜y˜

′₍_x_{) =} du

dy˜u. Substituindo este resultado na ´

ultima equa¸c˜ao, obtemos

du d˜yu

1 + ˜u2 =

1 ˜ y,

que possui y = c(1 +u2_{)como solu¸c˜}_{ao, onde} _c ₆_{= 0 ´e uma constante. Da´ı ˜}_y′ ₌

r _y

c 2

−1, cuja solu¸c˜ao ´e y = ccoshx

c + ˜c

, ou seja, a catenária. Reciprocamente, se a curva geratriz de uma superf´ıcie rotacionalS satisfaz (4.19) ou é uma catenária, pelos cálculos da se¸cão anterior conclu´ımos queS possui curvatura média constante.

Juntando as Proposi¸c˜oes 4.1, 4.4, 4.6 e 4.7 conclu´ımos oTeorema4.1de Delaunay.

(34)

CAP´ITULO 4. SUPERF´ICIES ROTACIONAIS ₃₃

0

Figura 4.13: As roulettes de Delaunay.

(35)

Superf´ıcies Helicoidais

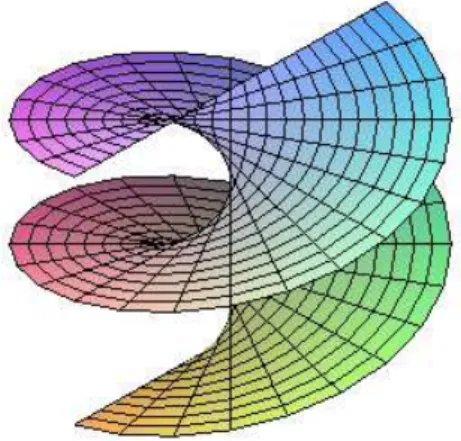
Superf´ıcies Helicoidais são aquelas invariantes por movimentos helicoidais em R3, ou seja, por movimentos helicoidais em rela¸cão a uma dada reta. Pelo que vimos no cap´ıtulo 2, um exem-plo de superf´ıcie helicoidal é dado pela superf´ıcie parametrizada por X(u, v) = (x(u) cos(αv) + y(u)sen(αv),−x(u)sen(αv) +y(u) cos(αv), z(u) +βv).

Como vimos, pelo Teorema 1.1, o subgrupo a 1-parâmetro de movimentos helicoidais em rela¸cão a um determinado eixo é identificado, via mudan¸ca de coordenadas, com o subgrupo a 1-parâmetro G1,δ. Assuperf´ıcies helicoidais de passo δsão então superf´ıcies invariantes porG1,δ.

Nos exemplos 2.10 e 2.11 s˜ao descritas duas superf´ıcies helicoidais.

O objetivo deste cap´ıtulo é encontrar uma representa¸cão para as superf´ıcies helicoidais de Cur-vatura Média constante não nula. Esta representa¸cão é uma generaliza¸cão do resultado obtido por K. Kenmotsu no artigo [6]. O Lema de Bour e O Teorema de Lawson são pe¸cas chaves para a obten¸cão dessa representa¸cão.

5.1 Parametriza¸

c˜

ao Natural e o Lema de Bour.

Seja W ⊂ R2 um aberto e X: W → R3 uma parametriza¸cão tal que X(W) é o tra¸co de uma superf´ıcie helicoidal de passoδ. Suponhamos que para um abertoV ⊂W, a interseçcão de X(V) com um plano Π⊃ {eixoz}, seja localmente o gráfico de uma fun¸cãoλ(ρ) comρ∈Π∩ {z= 0}.

Renomeando eixos podemos supor Π∩ {z= 0}= eixox. Então uma parametriza¸cão para X(V)∩Π é β(ρ) = (ρ,0, λ(ρ)). Rodando β(ρ) em torno do eixoz de um ângulo ϕ∈R simultaneamente com uma eleva¸cão deδ0ϕ(δ0=cte) obtemos a seguinte parametriza¸cão para X(V)

X(ρ, ϕ) = (ρcosϕ, ρsenϕ, λ(ρ) +δ0ϕ), ρ∈Π∩ {z= 0}, ϕ∈R. (5.1)

SejaImm(W,R3) ={parametriza¸c˜oes deW emR3}. Dado H ∈Rconsideremos

ΣH ={X∈Imm(W,R3) : X ´e superf´ıcie helicoidal de

curvatura m´edia constante H6= 0}.

Defini¸cão 5.1 Seja X(s, t) : W → R3 ∈Imm(W,R3) uma superf´ıcie helicoidal parametrizada por parâmetros (s, t) tais que as s-curvas (t = cte) são parametrizadas pelo comprimento de arco e as

t-curvas (s=cte) são hélices ortogonais àss-curvas, então os parâmetros(s, t)são ditos parâmetros naturais.

Observa¸cão 5.1 Pela defini¸cão, a Primeira Forma Fundamental de uma superf´ıcie helicoidal para-metrizada por parâmetros naturais (s, t) é dada por

dσ2=ds2+U2(s)dt2. (5.2)