YN) sucessoes cronol6gicas conjuntamente es-

Estudos de Economia, vol. xt, n.' 3, Abr .. Jun .. 1991

ANALISE DE SUCESSOES CRONOLOGICAS:

MODELOS DE FUN<;AO TRANSFERENCIA.

TEORIA E PRATICA

Daniel Muller ("')

1 - lntrodu~ao

Os modelos Box-Jenkins univariados permitem fazer a analise - descrigao e previsao - de uma sucessao cronol6gica atraves do conhecimento exclusivo dos seus valores. Contrariamente aos modelos econometricos, sao modelos nao causais, no sentido em que uma sucessao cronol6gica em cada instante e apenas explicada por valores anteriores a esse instante.

A existencia de fen6meos aleat6rios relacionados entre si conduz-nos ao tratamento simulta.neo das correspondentes sucessoes cronol6gicas, de forma que a informagao contida em cada uma delas possa beneficiar desse rela-cionamento e, deste modo, melhorar e enriquecer o estudo desses fen6menos.

Assim, a extensao da analise univariada a uma abordagem conjunta de diversas sucess6es cronol6gicas correlacionadas representa o desenvolvimento 16gico do estudo das sucessoes temporais e constitui o objecto deste trabalho, no qual iremos expor os aspectos te6ricos e praticos dos modelos multivariados de fungao transferencia introduzidos por Box e Jenkins (1970).

Como iremos constatar, estes modelos combinam algumas das caracterfsticas dos modelos Box-Jenkins univariados (modelos ARIMA) com a analise da regressao linear multipla, representando uma «mistura .. das metodologias nao causais e causais para a analise das sucess6es cronol6gicas. ·

Os modelos de fungao transferencia permitem descrever uma sucessao cronol6gica, designada output, como fungao de uma ou mais sucessoes, input, e representam um modelo de resposta dinamica, uma vez que uma mudanga num dos input em determinado instante produz uma resposta retardada, sem efeito imediato, no output. Tais modelos tem uma importancia particular em economia, pois permitem definir as variaveis input como indicadores avangados

do output.

Neste trabalho para facilidade de exposigao iremos desenvolver a teoria para os modelos bivariados de fungao transferencia, isto e, modelos em que apenas existe uma sucessao input. No paragrafo 6 faremos uma referencia breve aos modelos multivariados mais gerais.

Os modelos bivariados sao estabelecidos para sucessoes conjuntamente estacionarias; por esta razao, o problema da estacionariedade entre sucessoes merece um estudo proprio. Este assunto sera tratado no paragrafo 2. No para-grato 3 iremos definir rigorosamente os modelos de fungao transferencia,

explicitando as suas hip6teses de validade. Em seguida, no paragrafo 4 apresentaremos o estudo detalhado de alguns desses modelos, salientando as suas caracteristicas especificas. No paragrafo 5 iremos tratar da metodologia de analise, constituida pelas tradicionais etapas: identificac;ao, estimac;ao, avaliac;ao do diagn6stico e previsao. Finalmente, no paragrafo

7

apresentaremos alguns exemplos praticos, onde iremos utilizar como meio informatico de calculo

o

software BOXX.

Como nota previa

a

leitura deste texto, iremos admitir que os aspectos Msicos da metodologia Box-Jenkins para o tratamento de sucessoes cronol6gicas univariadas sao conhecidos.

2 - Estacionariedade

Dois processos estocasticos {X1 ; t= 0,1, ... } e {Y1 ; t= 0,1, ... } dizem-se conjuntamente estacionarios de 2.9 _{ordem se:}

a) Gada urn deles e, individualmente, urn processo estocastico esta-cionario de 2.9 _ordem:

E(X21) < + oo

e

E( )121) < + oo, V

t

E(Xt)

=

J..Lx

e

E(Yt)

=

J..l.y, V

t

cov(Xt-k.Xt)

=

y x(k)

e

cov( Yt-k. Y1)

=

y y(k), V

t,

k

=

0,1, ...

b) A co-varifmcia cruzada, cov (X1, Y5 ), existe e e apenas fungao da diferenc;a entre os instantes

s

e t:

E(X1• Y5 ) < + oo, V

s,t

cov(Xt-k.Yt)

=

Yxy(k), V t, k

=

0,1, ...

Para estes processos podemos definir a correspondente func;ao de correlac;ao cruzada:

Yxv(k)

pxy(k) = --(yx(-0-).-y.,f.-0-)'i-,- (2.1)

Tendo em conta a sua definic;ao, facilmente se pode verificar que esta func;ao satisfaz as seguintes propriedades:

P1 -

I

pxy(k)

I

:5: 1, V k;

P2-pxy(k)

=

pyx(-k), V k;

P3- max

I

pxy(k)

I

:5: 1;

k

P4-pxy(k) nao e em geral uma func;ao simetrica.

Assim, admitindo que foram observadas as duas seguintes sucessoes cronol6gicas (X,, ... ,XN) e (Y,, ... , YN) a funao de co-variancia cruzada pode ser estimada pela forma habitual:

Oeste modo obtem-se como estimador da func;ao de correlac;ao cruzada:

Cxv(k)

rxy{k) =

-(cx_.(O).cyy(O)) 112

2 2

em que cxx(O)

=

s x e cvy{O)

=

s y.

As propriedades estatfsticas da correlac;ao cruzada rxy{k) sao, de uma forma geral, diffceis de estabelecer. No entanto, em alguns casas particulares conse-guern-se obter resultados interessantes e de grande aplicac;ao pratica, como iremos ver adiante. Assim, pode provar-se [teorema 11.2.2(2)] que se {Xr} e { Yr} representarem dais rufdos brancos independentes, entao rxv(k) e assintoticamente normal de esperanc;a matematica nula e de desvio padrao n·1

/2. Bartlett estendeu este resultado ao caso em que as duas sucessoes sao nao correlacionadas, sendo uma delas urn rufdo branco, e demonstrou que

rxy{k) tem assintoticamente esperan<;:a matematica nula e desvio padrao (n-k}-112.

0

resultado de Bartlett permite-nos estabelecer a seguinte regra de teste ao nfvel de 5%:

se

I

rxy{k)

I

> 1.96 (n-k)-1/2;

rejeita-se a hip6tese de nao correlac;ao entre as variaveis Xr-k e Y r ({Xr} rufdo branco), ou seja, a correlac;ao cruzada te6rica no lag k e diferente de zero,

Pxv(k)

*

0. Do ponto de vista pratico esta regra de teste traduz que se podem

estabelecer valores fora dos quais rxy{k) e significativamente diferente de zero, permitindo assim definir barras de significancia a 5% no grafico da fungao de correlac;ao cruzada, dentro das quais rxy{k) e considerada estatisticamente nula.

3 - 0 modelo de fun<;:ao transferencia

Sejam (X1, ... XN) e (Y1, ... , YN) sucessoes cronol6gicas conjuntamente es-tacionarias, de valor media nulo

E(Xr) = E(Yr) = 0, Vt

sendo a primeira delas considerada como a sucessao input.

0

modelo de func;ao transferencia

e

entao definido por:

Yt

=

i.l1 Y t-1 + ... + i.lr Yr-r + c.ooXr-b - c.u1 Xr-b-1 - ... - c.usXt-b-s + Nt (3.1) onde {Nr;t

=

0,1 , ... } representa a sucessao residual, que se admite ser:

a) De esperanc;a matematica nula:

b) Nao correlacionada com {Xt}: cov(N1,X5 )

=

0, Vs,t

c) Urn processo ARMA(p,q) invertfvel e estacionario (1):

cflp(B)Nr = 9q(B)Er

2

em que {Ed representa urn ruido branco estacionario (E(Ed

=

0, V t e var(Ed

=

0£, V t). 0 modelo (3.1) pode ser escrito de uma forma compactada, utilizando o operador atraso:

o(B) Yr = w(B)Xr.b + Nr

(3.2)

em que:

o(B) = 1 -

a

1 B - ... -

a,ar

Como hip6tese suplementar do modelo de funcao transferencia, iremos admitir que os parametros (a1, ... ,a,) e (mo, ... ,m5 ) sao tais que as raizes dos correspondentes polin6mios, o(B) e w(B), se encontram estritamente fora do circulo unitario.

Esta ultima hip6tese permite-nos escrever (3.2) na forma:

onde:

Observar;oes:

Yr

=I,

vjXr-j

+

N;

=

v(B)Xr

+N;

j=O

-v(B)

=

I,

vjBj

=

c5-

1 _(B)ro(B)Bb

j=O

N'r = 8-1(8)Nr

1 - Como se pode reparar, o modelo de funcao transferencia descreve a sucessao cronol6gica

output

{

Y1}, como funcao do seu passado, da sucessao

input

{X1) e de uma serie residual {Nr}, que combina os efeitos de outros factores que eventualmente possam influenciar { Yr}.

2 - 0

modelo de funcao transferencia fica completamente caracterizado

em termos dos inteiros (r,s,b) e (p,q).

3 -Estamos perante urn modelo de resposta dinamica; com efeito, urn valor assumido pela variavel

input

no instante

t

tera apenas efeito no

output

no

instante

t

+ b (b > 0), comportando-se desta forma a variavel Xr como urn indicador avan<;ado de Yr.

4 -Em (3.3) a serie residual {N'r} continua a ter esperan<;a matematica nula e a ser nao correlacionada com {Xr}. Eventualmente, {N'r} podera ser modelizada por urn ARMA.

5 -

Ao operador v(B) em (3.3) chamamos fum;ao transferencia, sendo os respectivos parametros (vo,v_{1, ... )} designados pesos da func;ao transferencia.

4 -

Estudos de alguns modelos

Neste paragrafo iremos estudar alguns modelos particulares, numa tentativa de os caracterizar em termos da respectiva fun<;ao de correla<;ao cruzada. Esta caracteriza<;ao sera feita no caso particular em que a sucessao input representa urn rufdo branco, uma vez que as fun<;oes de correla<;ao cruzada para tais modelos resultam bastante mais simples, facilitando, deste modo, a tarefa de identifica<;ao. Assim, como se vera no proximo paragrafo, sera nesta forma que iremos utilizar os modelos de fun<;ao transferencia na fase de identifica<;ao. Suponhamos, entao, que a variavel input e urn rufdo branco, que designaremos por {ar}, e que representamos o output por {~r}. Nestas condi<;Oes o modelo (3.1) vira:

~~

=

d1~t-1 + ... + drf3t-r + UlQUt-b- ffi1Ut-b-1 - ... - ffisUt-b-s + T\t (4.1)

onde {T\1}, sera de esperan<;a matematica nula e nao correlacionada com {ar}:

4.1- Modelo (O,O,b)

E(T\r) = 0, Vt cov(T\r,as) = 0, Vs,t

Este modelo assume a forma:

~~ = UlQUt-b + T\t

Multiplicando ambos os membros desta igualdade por ar-k. k

=

0, ± 1, ... e tomando valores medios, obtemos, tendo em conta (4.2), a fun<;ao de co-va-riancia cruzada:

E(ar-k-~t) = ffioE(ar-k-Ut-b) + E(ar-k-T\r)

Ya~(k) = ffiOYa(k-b) E uma vez que {ar} e urn rufdo branco, vern:

{

ffi

₀

cr~. k=b

Ya~(k) =

Donde, atendendo a (2), obtem-se como func;ao de correlac;ao cruzada deste modelo:

4.2 - Modelo (O,s,b)

Este modelo e uma generalizac;ao do modelo anterior:

~t

=

WOClt-b - Ol1Clt-b-1 - ... - Olsflt-b-s + llt

Por urn raciocfnio analogo ao anteriormente efectuado, tem-se:

'Yafl(k)

=

E(Clt-k·~t)

=

WO'Ya.(k-b) - OlHa.(k-b-1) - ... - Ols'Ya.(k-b-s)

resultando:

2

Olo<Ja, k = b

'Yap(k) =

- m

1

cr~, k = b+1

- Ol

5

0"~, k = b+s

0, k < b

e

k > b

+

s

o que implica que a func;ao de correlac;ao cruzada vira: -1

mocr a. cr~, k = b

-1

- Ol1 O"a.O"~, k = b + 1

'Yap(k) =

-

Ols<J"a.0"~-.

1 k = b +

s

0, k < b

e

k > b +

s

4.3- Modelo (1,0,b)

Tomemos o modelo:

e ponhamo-lo na forma:

~t = mo(1 - a1 B)-1_{ar-b + ll't}

Como por hip6tese

lo1l

< 1, este modelo assumira a forma:

~

Entao, multiplicando ambos os membros desta expressao por ar-k,

k = 0, ± 1, ... e tomando valores medios, vira, tendo em conta a observa<_;:ao 4 do paragrafo anterior:

ou seja:

Resultando:

00

Ya~(k)

= E (O.t-k

~t)

=roo

L

a:Ya. (k-b-j) J=O

{

0, k < b

Ya~(k}

=

₂

rooa~cr

a k

=

b + i,i

=

0,1,2, ...

{

0, k < b

Pa~(k} =

rooa~cra..cr·;. k= b+ i,i= 0,1,2, ...

Como se pode notar, para k > b a fun<_;:ao de correla<_;:ao cruzada verifica a rela<.;:ao:

4.4 - Modelo (r,O,b)

Para este tipo de modelos a dedu<_;:ao da fun<_;:ao de correla<_;:ao cruzada envolve urn tipo de calculos mais fastidioso, podendo, contudo, provar-se que tern a seguinte forma:

Pa~(k} = (J)QO"a.CJ\ k = b

{

0, k < b

a1Pa.~('k-1)

+ ... +

a,pa.~(k-1},

k > b

4.5- Modelo (1,1,b)

Este modelo: _

pode ser escrito na forma, atendendo as hip6teses enunciadas:

~ ~

f3t = Wo

La{

at·b-j- W1

La{

at·b·j·1 +

1];

Oeste facto resulta, ap6s alguns calculos:

4.6- Modelo (r,s,b)

roocrao.-~. k = b {

0, k < b

Pa13(k) = (rooS1 -

ro1)cracr~

k = b

+

1 01Paj3(k-1), k > b + 1

A deduc;ao da func;ao de correlac;ao cruzada para estes modelos segue urn tipo de raciocfnio semelhante ao que foi feito anteriormente, sendo os respectivos calculos bastante mais pesados e resultando numa forma explfcita de grau de complexidade elevado. Todavia, a tftulo de exemplos, diremos que para o modelo (1,2,b) se tern:

para o modelo (2,1,b):

e para o modelo (2,2,b):

4.7- Caracterizac;Bo dos modelos

A pratica tern demonstrado, tal como sucedia na modelizac;ao Box-Jenkins univariada, que a utilizac;ao de modelos com urn numero reduzido de parametres

resultados. Assim, no quadro 1 apresentamos, de forma reduzida e esquematica, a caracteriza<;ao dos modelos mais frequentemente utilizados, em termos das respectivas fun<;oes de correla<;ao cruzada.

A identifica<;ao de urn modelo particular de fun<;ao de transferencia far-se--a por compara<;ao da fun<;ao de correla<;ao cruzada estimada, relativa as sucessoes em analise, com os diferentes figurinos te6ricos anteriormente estabelecidos. Pode dizer-se que a tarefa de ident~ica<;ao deste tipo de modelos nao

e

facil, sendo constitufda por urn certo grau de subjectividade. No entanto, uma analise atenta as fun<;oes de correla<;ao dos diferentes modelos, em particular dos modelos expressos no quadro 1, permite salientar urn conjunto

de aspectos que podem auxiliar o analista no processo de identifica<;ao:

a) Em qualquer dos modelos constatamos que a fun<;ao de correla<;ao cruzada

e

sempre nula para valores inferiores a b, isto

e:

Pa~(k) = 0, k < b

Este facto permite na pratica, sem grande dificuldade, a identifica<;ao do inteiro b apenas por observa<;ao directa da fun<;ao de correla<;ao estimada.

b) Como consequencia da constata<;ao anterior, conclui-se de imediato que os modelos de fungao transferencia podem apenas ser aplicados a variaveis cuja fungao de correlagao cruzada estimada tenha urn comportamento daquele tipo, ou seja, tome valores sempre nulos abaixo de urn certo lag k. Esta observagao tern urn significado pratico extremamente importante; com efeito, pode-se dizer que nem todas as sucessoes cronol6gicas correlacionadas admitem uma modelizagao atraves das fungoes de transferencia.

c) 0 quadro 1 permite constatar, para os modelos com N 0 e s-F 0, a existencia de duas estruturas distintas nos graficos das fungoes de correlagao cruzada. Uma prime ira sem figurino fixo, correspondente aos slags b+ 1 , ... , b+s, e uma segunda com figurino amortecido, de tipo exponencial ou de tipo alternado, a partir do lag b+S+1. Esta configuragao dos graficos das fungoes de correlagao cruzada permite ccadiantar, na fase de identificagao urn valor aproximado para o inteiros. Note-se contudo, que o estabelecimento correcto do valor de

s

nem sempre e evidente, uma vez que a percepgao onde acaba o figurino fixo e comega o figurino amortecido nao

e

facilmente identificavel. Quanto a identificagao do valor do inteiro r, a questao torna-se bastante mais problematica: como podemos observar no quadro 1 os modelos

(1 ,O,b) e (2,0,b), por exemplo, apresentam graficos das fungoes de

QUADROI

(r,s,b) ParAmetres Fun9ao de correl~ao cruzada

(O,O,b) 000 > 0

I

b

(0,1,b) 000 > 0

I

I

oo, < 0

b

000 > 0

Ill

(0,2,b) oo, < 0

002 < 0

b

(1 ,O,b) 000 > 0

IIIII

o,

> 0

b

(2,0,b) 000 > 0

I

IIIII

o,

> 0 02 < 0

b

(1 '1,b) 000 > 0 oo, < 0

•lll11

o,

> 0

b

(1,2,b) 000 > 0 oo, < 0

IIIII.

002 < 0

o,

> 0

b

(2,1,b) 000

_o,

> 0 _{> 0} oo, < 0

Ill

02 < 0

I

I

I

b

(2,2,b) 000 > 0 _{002 < 0} oo, < 0

111

I

o,

> 0 02 < 0

5 - Metodologia de analise

Como se referiu anteriormente a metodologia de analise compreende as seguintes fases: identificac;:ao, estimac;:ao, avaliac;:ao do diagn6stico e previsao. Cada uma destas fases sera constitufda por diversas subfases.

A fase de identificac;:ao tern por objectives a especificac;:ao dos inteiros

(r,s~b) definidores da func;:ao de transferencia e dos inteiros (p,q) referentes

a

modelizac;:ao da sucessao residual. 0 primeiro conjunto de inteiros sera especificado com auxilio da func;:ao de correlac;:ao cruzada, de acordo com as regras estabelecidas no paragrafo anterior, sendo o segundo especificado atraves da metodologia habitual de Box-Jenkins. Esta fase e constitufda pelas seguintes subfases:

a) Estacionarizac;:ao das sucessoes input e output; b) Branqueamento da sucessao input;

c) «Branqueamento, da sucessao output;

d) Calculo das correlac;:oes cruzadas; ~ Especificac;:ao de (r,s,b);

g) Estimac;:ao dos pesos da func;:ao transferencia; h) Estimac;:ao da sucessao residual;

t) Especificac;:ao de (p,q).

0 faseamento acabado de descrever sera efectuado com auxflio de meios informaticos (iremos utilizar como foi referido o software BOXX), sendo a intervenc;:ao e experiencia do analista estatistico urn factor de especial relevancia. ldentificado urn modelo de func;:ao transferencia, passa-se em seguida

a

estimac;:ao dos seus parametres. Esta fase do processo de analise e composta pelas seguintes subfases:

a) Estimac;:ao preliminar dos parametres; b) Estimac;:ao final dos parametres.

De uma forma geral pode dizer-se que esta fase tera uma intervenc;:ao reduzida do analista; com efeito, como se vera mais adiante nos exemplos, o

software que utilizaremos resolve automaticamente esta questao.

Completada esta fase, estamos em condic;:oes de proceder

a

avaliac;:ao do diagn6stico relativo ao modelo ja identificado e estimado. Esta avaliac;:ao sera efectuada atraves da aplicac;:ao de diferentes criterios, destacando-se em particular os baseados nas fungoes de autocorrelac;:ao (FAC) e de autocorrelac;:ao parcial (FACP) dos resfduos e da func;:ao de correlac;:ao cruzada entre os resfduos e a sucessao branqueada, sendo constitufda pelas subfases:

a) Avaliac;:ao da qualidade estatistica do modelo; b) Avaliac;:ao da qualidade do ajustamento; c) Comparac;:ao entre diferentes modelos.

Conclulda a fase de avalia<;ao do diagn6stico passa-se a fase da previsao, se o modelo tiver sido aceite pela generalidade dos testes a que foi sujeito. Caso contrario, isto e, concluindo-se pela rejei<;ao do modelo, tera de se retomar o processo de identifica<;ao ate se conseguir urn modelo satisfat6rio.

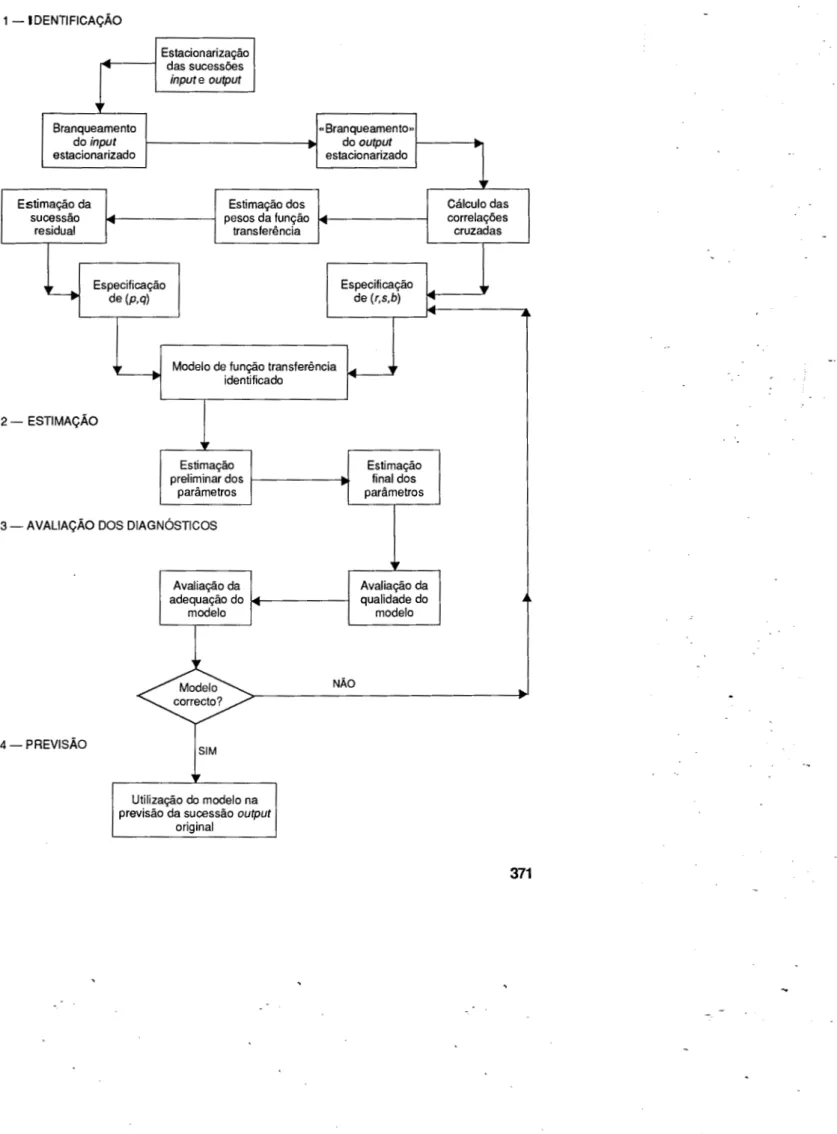
A metodologia de analise exposta anteriormente pode ser esquematizada pelo diagrama da fig 1 .

5.1 -ldentificac;io

5.1.1 - Estacionarizac;:ao das sucessoes input e output

Esta primeira fase do processo de identifica<;ao tern por finalidade a prepara<;ao das sucessoes cronol6gicas em analise, de forma que possam ser modelizaveis por uma fun<;ao transferE'mcia.

Como foi visto no paragrafo 2, os modelos de fun<;ao transferemcia dizem respeito a sucessoes estacionarias. Sendo assim, a aplica<;ao destes modelos tera de passar por uma analise previa das sucessoes em estudo com vista a torna-las estacionarias, eliminando-lhes a tendencia e a sazonalidade e esta-bilizando-as relativamente as respectivas variancias.

A estacionariza<;ao das sucessoes input e output, {X_1} e {Y_1}, respectiva-mente, sera feita pelos processes habituais: diferencia<;ao simples e sazonal e transforma<;ao de Box-Cox, dando Iugar as sucessoes estacionarias {x_1} e {y_1}. Sera para estas sucessoes que o modelo de fun<;ao transferencia e aplicado, tanto na forma (3.2) como na forma (3.3).

5.1.2 - Branqueamento da sucessao input

Nesta segunda subfase procede-se ao branqueamento da sucessao input,

isto e, transforma-se a sucessao {xt} num ruldo branco, que designaremos por {at}, por aplica<;ao de operadores auto-regressivos (AR) e de medios m6veis (MA). Esta transforma<;ao e obtida procurando o melhor modelo ARMA que se ajuste a {x_1}:

representando <J>x(B) e ex(B) os operadores autoregressivos e de medias m6veis respectivamente.

A sucessao input branqueada sera entao:

(5.1)

e corresponde a sucessao dos reslduos relatives a modeliza<;ao Box-Jenkins de {xt}.

FIGURA 1 1 -IDENTIFICA<;AO

Estacionarizagao r<l"'l----i das sucessoes

input e output

Branqueamento

do input

estacionarizado

Estimagao da sucessao

residual

"Branqueamento»

r---~~ doou~ut

estacionarizado

Estimagao dos pesos da fungao

transferencia I"

Calculo das correlagoes cruzadas

Especificagao

de(p,q)

Especificagao

de (r,s,b) ,... .... r----..J' ~

Modele de fungao transferencia 1..11 ~

-,. identificado

2- ESTIMA<;Ao

Estimagao

preliminar dos r---1111

parametres

3 - AVALIAQAO DOS DIAGNOSTICOS

4-PREVISAO

Avaliagao da adequagao do ~<~~~r---J

modele

Modele correcto?

SIM

Utilizagao do modele na previsao da sucessao output

original

NAO

Estimagao final dos parametres

Avaliagao da qualidade do

modele "'

5. 1.3 - "Branqueamento» da sucessao output

A sucessao output {Yt} sera «branqueada, por aplica9ao dos mesmos operadores auto-regressivos e de medias m6veis que foram aplicados

a

sucessao {xt} e que a transformaram no rufdo branco {at}. Obtem-se deste modo a sucessao «branqueada»:

Pt

=e)

(B)<!>xYt

(5.2)

Note-se que, de uma maneira geral, a sucessao {Pt} nao e um rufdo branco; daf poder dizer-se que se procedeu ao «branqueamento, (entre aspas) da su-cessao output.

Como se pode reparar, este procedimento vai manter entre as duas su-cessoes branqueadas o mesmo relacionamento funcional, traduzido pela mesma fun9ao transferencia que existia entre as sucessoes {xr} e {yt}. Com efeno, a partir do modelo (3.3):

Yt= v(BJXt+ N't

obtem-se por aplica9ao dos operadores <j>x(B) e EJ1(8) a ambos os membros desta igualdade:

Pt = v(B)at + nt (5.3)

onde nt =

e~

(B)<j>x(B)N't representa, como facilmente se pode verificar, uma su-cessao crono16gica de esperanc;:a matematica nula e nao correlacionada com {ad.

5. 1.4 - Cidculo das correla¢es cruzadas e especificac;:ao de (r, s, b)

Obtidas as sucessoes branqueadas {at} e {Pt}, ira proceder-se em seguida

a

estima9ao da correspondente fun<;ao de correla9ao cruzada rt;tJ3 (k), por aplica9ao da formula (2.1 ). 0 estabelecimento desta fun9ao estimada ira permnir especificar, de acordo com as regras expostas no paragrafo 3.7, o conjunto dos inteiros (r, s, b), identificando-se deste modo o tipo de modelo de fun9ao transferencia.

5. 1.5 - Estimagao des pesos da fungao transferencia

A partir do modelo formulado para as series input e output branqueadas pode proceder-se

a

estimagao dos pesos da fungao transferencia.

Considere-se o modelo na forma:

multiplicando ambos os termos desta equagao por O.t-k· K=0,1 ... , e tomando esperangas matematicas vern, uma vez que {o.r} e urn rufdo branco nao correlacionado com {nr}:

donde resulta:

r~(k)

=

vkra.(o)

=

Vk<Ja

o que implica:

vk = y~(k)cr;, k=0,1, ...

Tendo em conta a expressao anterior, obtem-se uma estimativa para os pesos da fungao transferencia, fazendo:

II -2 -1

Vk = c~(k)sa = r~(k)s~s a

5.1.6- Estimac;;ao da sucessao residual

(5.4)

Estimados os pesos da fungao transferencia, iremos proceder em seguida

a

estimagao preliminar da sucessao residual {N'r}, a tim de que possa ser modelizada por urn ARMA na etapa seguinte.

Assim, tendo em conta (2.3) podemos escrever:

N'r= Yr-v(B)xr=

yt

-

voxr- v1xr-1 - v2xr-2 - ...

e admitido que a partir do lag k=g ra~ (k) esta dentro das barras de significancia, obtem-se a estimagao preliminar da sucessao residual fazendo:

II II II II

N'k=

Yr-voxr- v1Xt-1 - Y2Xt-2 - ... - VgXt-g

II

5.1.7-Especifica~o de (p,q)

Utilizando a metodologia Box-Jenkins univariada, procede-se a

modeliza-11

~o da serie residual estimada no passo anterior, { N'1}:

(5.5)

onde p e q representam respectivamente os graus dos polin6mios auto-regres-sivos e de medias m6veis <j>p(B) e 9cf..B).

Estabelecido o modele ARMA (p,q) definido em (5.5) fica, deste modo, completado o processo de identifica9ao do modele de fun9ao transferencia:

(5.6)

onde {er} representa urn rufdo branco.

5.2-Estima~o dos parametres

Do ponto de vista das aplica96es a fase da estima9ao e pouco interessante. Na realidade e de uma forma geral, o analista tern pouca interven9ao pessoal nesta fase de analise, nao podendo escolher a metodologia de estima9ao a utilizar, sujeitando-se, portanto, as caracterfsticas do software que tern a sua disposi9ao, Contudo, neste paragrafo, iremos descrever, esquematicamente e sem grande profundidade, as principais questoes que se colocam na fase de estima9ao dos parametres.

Esta fase e constitufda, como foi referido, por duas subfases: na primeira procede-se a estima9ao preliminar dos parametres, os quais irao permitir, em seguida, inicializar o algoritmo que estabelece a estima9ao final dos parametres do modele.

5.2.1- Estimac;ao preliminar

se se desenvolver os polin6mios em ambos os termos desta expressao e igualar os respectivos coeficientes relativos a mesma potencia em B, somos conduzi-dos as seguintes rela<;6es entre os parametros:

Vj= 0, j< b

vi

= a1

vi_,

+ ... +

al'li-n

+ roo. j = b

Vj = a1Vj-1 + ... + a,vj·r - (J)j-b• j= b+ 1, ... ,b+ S Vj

=

a1Vj-1 + ... +arV(r• j > b + S

Estas rela<;6es permitem estabelecer estimativas preliminares para os parametros

a

_{1 •...}

,a,

e c.oo •...

,ro

5 , substituindo Uj pelas estimativas dos pesos da func;:ao transferencia obtidas anteriormente e calculadas pela expressao (5.4).

A estima<;ao preliminar dos parametros auto-regressivos e de medias m6-veis, correpondentes a modeliza<;ao da sucessao residual

{N'd,

e realizada pelos processos habituais da teoria Box-Jenkins univariada.

5.2.2-Estimac;:ao final

0 algoritmo de Marquardt (3) pode ser usado iterativamente para estimar os valores dos parametros do modelo. Este processo de estima<;ao iterativa sera inicializado os valores fornecidos pela fase anterior.

Em cada itera<;ao, novos valores dos parametros sao encontrados e novas estimativas dos resfduos {f1} do modelo (5.6) serao calculadas. A soma dos quadrados deste resfduos indicara quantas itera¢es deverao ser efectuadas de forma a torna-la minima.

No paragrafo referente aos exemplos iremos ver que o software BOXX resolve o problema da estima<;ao sem grande interven<;ao pessoal do analista estatfstico.

5.3- Avalia~o do diagn6stico

ldentificado urn modelo e estimados os seus parametros, passa-se a fase de avalia<;ao do diagn6stico, onde se ira proceder ao estudo da qualidade esta-tfstica desse modelo estimado e a verifica<;ao do seu grau de adequa<;ao as sucessoes cronol6gicas em analise.

Existem diversos criterios de decisao que permitem avaliar esse diagn6s-tico e podem ser agrupados em duas classes. Na primeira, dizendo respeito a qualidade estatfstica do modelo, destacamos os criterios referentes a qualidade da estima<;ao propriamente dita e a observancia de uma hip6tese fundamental;

a segunda classe refere-se

a

qualidade do ajustamento efectuado, sendo cons-tituida por criterios incidindo sobre a analise dos residuos.

Finalmente e para concluir esta fase de analise, devera ser tratado o problema da comparagao entre os dijerentes modelos que eventualmente tenham sido selecionados

a

luz dos criterios anteriores, de modo que se possa obter, tanto quanto possivel, urn modelo que seja nitidamente melhor que qualquer outro.

5.3.1 - Qualidade da estimagao

A qualidade de urn modelo estimado pode ser comprovada estatisticamente a partir da aplicagao dos seguintes criterios:

a) Signiticancia estatfstica dos parametros estimados. - Este criterio e

baseado no principio estatistico da parcim6nia, o qual estabelece que se devera procurar modelos sem parametres desnecessarios. Com efeito, tanto melhor sera urn modelo quanto menor for o seu numero de parametres, pois a pratica tern demonstrado que a utilizagao de modelos parcimoniosos conduz em geral a melhores previs6es.

Nesse sentido, tern interesse verijicar se urn determinado parametro e es-tatisticamente significative, uma vez que, se nao o for, devera ser eliminado no modelo e proceder-se a nova estimagao.

Considere-se entao urn parametro qualquer <1>. representemos por

$

a sua estimativa e por s(~) o respective desvio padrao. Nestas condigoes, o teste so-bre a hip6tese de nulidade deste parametro, ao nivel de 5%, pode ser obtido atraves da seguinte regiao critica:

I

~

I> 1,96 s($)

0 software BOXX na fase de estimagao fornece como output o ratio

t

=

<j>.s-1 (~) para cada parametro do modelo, permitindo a realizagao da sua analise estatistica.

b) Corre/a(_(ao entre os parametros estimados.-Pode dizer-se que a

existencia de estimativas de parametres altamente correlacionadas conduz a modelos de rna qualidade. Com efeito, uma variagao, por pequena que seja, numa das estimativas podera reproduzir uma correspondente variagao nas outras estimativas que lhe estao correlacionadas, contribuindo assim para uma certa instabilidade do modelo.

Oeste modo e como regra pratica, dever-se-a recusar urn modelo sempre que qualquer correlagao entre estimativas seja superior a 0,7, procurando-se modelos alternatives para as sucessoes em estudo. Tambem, como iremos ver

o output do BOXX fornece a matriz de correlagao entre as estimativas obtidas,

5.3.2 - Observancia de uma hip6tese fundamental

Uma das hip6teses introduzidas na defini<_;:ao do modelo de fu~o transferencia estabelecida que as sucessoes

input

e residual eram nao correlacionadas, isto e:

cov(N'1,x5) = 0, V

s,

t

(5.7)

Ora, uma vez que {N't} foi modelizada pelo processo ARMA invertfvel e estacionario:

cj>p( B) N'1

=

9q(B)er

resu~a que se pode escrever, pela invertibilidade:

er =

I_

8jN't-j

)=0

Por outro lado, vimos que se tinha por (5.1):

resu~ando, tambem pela invertibilidade:

(5.8)

(5.9)

Assim, tendo em conta a hip6tese formulada em (5.7), tem-se por (5.8)

e

(5.9):

cov(a1,e5)

=

f

f

bi 8j cov(Xt-i, N's-j)

=

0, Vs,t

I =0 } =0

Ou seja, a hip6tese fundamental traduzida pela relac;ao (5.7) implica que a sucessao

input

branqueada {at} tera de ser nao correlacionada com a suces-sao residual rufdo branco {q}. lsto significa, do ponto de vista pratico, que o modelo de func;ao transferencia e considerado estatisticamente de qualidade se os correspondentes resfduos estimados {tt} forem nao correlacionados com a sucessao branqueada estimada {&t}:

Estas duas sucessoes estimadas podem ser obtidas pela forma habitual: {&.1} representa os resfduos referentes

a

modelizac;ao Box-Jenkins da variavel

e tendo e conta (5.6) pode escrever-se:

8(8)1/Jp(B)yt = 1/lp(B)ro(B)Xt-b + 8(B)9q(B)er

donde resulta que os resfduos estimados {tt} serao definidos por:

onde os operadores com "".. representam os correspondent as polin6mios em

B, em que os parametres foram substitufdos pelas respectivas estimativas. Assim e resumindo, podemos dizer que a qualidade estatfstica de um mo-delo sera testada a partir da analise da func;:ao de correlac;:ao cruzada entre as duas sucess6es {&.t} e {l'r}, concluindo-se pela sua qualidade se esta correlac;:ao cruzada for significantemente nula.

De acordo com o resultado de Bartlett referido no paragrafo 2, este teste pode ser efectuado para cada lag k atraves da seguinte regiao crftica:

No entanto, pode obter-se um teste geral global relativamente ao conjunto de todos os N* lags analisados, utilizando uma generalizac;:ao do teste de Box-Peirce para series univariadas: prova-se [Makridakis (4)] que a estatfstica:

N'

0 = ( N-c{)

2.

f2~(k)

k=1

onde d= max {s + b + P,Px} com Px o numero de parametres auto-regressivos do polin6mio ¢Jx(B), tem sob a hip6tese de nao correlac;:ao entre {tit} e {tt} uma distribuic;:ao assint6tica de um

x2

com (N*-r-s) graus de liberdade. Oeste modo se o valor da estatfstica Q foi inferior ao quantil desta distribuic;:ao:

aceita-se a hip6tese de que os resfduos do modelo e a sucessao branqueada sao nao correlacionados.

5.3.3 -Analise dos residuos

A analise dos resfduos {er} vai permitir verificar se modelo estimado explica suficientemente bem a relac;:ao funcional existente entre as variaveis input e

output. Com efeito, se o modelo for adequado para explicar aquela relac;:ao

Ora como e sabido, urn rufdo branco e caracterizado por ter as fun<;oes de autocorrela<;ao e de autocorrela<;ao parcial sempre nulas

a

excep<;ao do lag zero. Oeste modo, nesta fase de avalia<;ao do diagn6stico, dever-se-a proceder

a

analise daquelas fun¢es de forma analoga

a

realizada na metodologia Box-Jenkins univariada.

Assim e resumindo podemos estabelecer a seguinte bateria de testes:

a) Teste de Bartlett. - Este teste e definido pela regiao crftica:

l~k) 1>1 ,96s(r~k)]

com:

k·1 1

s[,f(k)] =

[~

1

(1

+

L.

r2:tk)] 12

i= 1

onde se rejeita ao nfvel de 5 % a hip6tese de o modelo ser adequado.

b) Teste de Ljung-Box.-

E

uma generaliza<;ao do teste de Box-Pierce,

definido pela estatrstica:

N'

0= n (n + 2~~ (N- kt1_t2£lk)

com n = N- r- s- b e que permite testar conjuntamente N*tags da fun<;ao de

autocorrela<;ao. Sob a hip6tese de o modelo se encontrar bern ajustado, a regiao crftica de nfvel 5% e:

0

> x2(N'-p·q)(1-a)

onde >(2(N*-p-q)(1-a.) representa o quantil (1 -a) da distribui<;ao do

x2

com (N*-~q) graus de liberdade.

c) Teste de Jenkis e Daniels. - Este teste e realizado sobre fun<;ao de

autocorrela<;ao parcial ~(k) e estabelece a seguinte regiao de rejei<;ao ao nfvel de 5%, referente

a

adequagao do modelo:

5.3.4 - Compara<fao entre modelos

A selec<;ao entre dijerentes modelos que foram aceites pelos criterios an-teriormente definidos podera ser feita por varies criterios nomeadamente os uti-lizados na teoria Box-Jenkins univariada: AIC, BIG, SC, etc.

0 software BOXX permite utilizar o criterio AIC; por esta razao apenas iremos

referir resumidamente este criteria. Defina-se a grandeza:

onde

m

representa o numero de parametres estimados no modelo e tf2 a

va-. £

riancia estimada dos residuos:

fJ

2

= N-SSR

£

em que SSR designa a soma dos quadrados dos residuos.

0 modelo selecionado sera, entao, o que minimiza a grandeza AIC relativamente aos outros modelos alternatives.

5.4- Previsio

Qualquer que seja a metodologia utilizada, urn processo de previsao permHe estabelecer antecipadamente os valores futuros de determinada variavel, de-sempenhando por este facto urn papel crucial no planeamento e na tomada de decis6es.

No caso presente, a previsao da sucessao output {y1}, constituindo a fase final da analise que tern vindo a ser exposta em paragrafos anteriores, e com frequencia consideravelmente melhorada, relativamente a outras metodologias de previsao, com a introduc;:ao da informac;:ao adicional resultante do conhe-cimento da sucessao {xt}. Alem disso, os modelos de func;:ao transferencia podem permHir o conhecimento antecipado de modifica<;:6es operadas na variavel output, . a partir das correspondentes modificac;:6es operadas na variavel input, comportando-se esta variavel como urn indicador avanc;:ado de {y1}.

0 desenvolvimento da metodologia de previsao com base num modelo de func;:ao transferencia sup6e o conhecimento previo desse modelo, ap6s uma correcta identificac;:ao e estimac;:ao dos respectivos parametros. Nestas condi-<;:6es iremos assumir que se tern:

Yt =

o-

1(B)w(B)Xt-b + <!>; (B)8q(B)Et =

0

·1 _{(B)w(B)<j>~(B)8x(B)ar.b + <!> ·;(B)8q(B)Et}

(5.10)

em que as ordens e os valores dos parametros dos polin6minos constituintes deste modelo sao conhecidas. As sucessoes {a1} e {Et} representam, como e sabido, rufdos brancos, sendo a primeira referente ao branqueamento da su-cessao input e a segunda

a

sucessao redidual.

lremos admitir que as sucessoes input e output foram observadas ate ao instante t e que se pretende prever, com base nessas observa<;:6es, o valor do

output no instante t+m, o qual sera designado por i,{m). Ao instante t chamamos

origem da previsao

e

m perfodo de previsao.

Tomando:

a te<>ria geral da previsao estabelece que esta esperan~a matematica condicio-nal define urn preditor que minimiza o respectivo erro quadratico medio:

Apliquemos, entao, o result ado (5.11) aos mode los de fun~ao transfe-rencia.

Considere-se o modelo na forma:

o qual pode ser escrito como:

(5.12)

em que os polin6mios

s·

(B), rr/(B) e e*(B) tern graus (p + (), (p + s) e (q + (),

respectivamente.

Atendendo a (5.12), o

output

no instante

t +

m vira:

Yt+m

=a

;Yt+m-1

+ ... +

a

p:r Yt+m-p-r

+

(I)~

Xt+m-b-

(l);

Xt+m-b-1- ...

- (l)

p:₅Xt+m-b-p-s + Et+m-8; Et+m-1- · · · - 8 q:rEt+m-q-r (5.13)

Entao, tomando esperan~as condicionais em (5.13) e fazendo, para facili-dade de nota~ao:

obtem-se a previsao do

output

no instante

t +

m:

* * *

- ro1 E"[xt+m-b-1]- · .. - ro p+s E [Xt+m-b-p-sl

+

1 *

+

E"(Et+m]-8 E"(Et+m-1]- . ·· - 8q+r E'(Et+m-q-rl (5.14)

sendo os resfduos {tr} calculados pela forma hab~ual como foi vista anteriormente e as previs6es

Xi<J)

obtidas pela teoria Box-Jenkins univariada a partir do modelo (5.1).

Como se pode notar, a previsao com origem em t e perfodo

m

expressa par (5.14) e uma func;:ao dos valores obseNados das sucess6es cronol6gicas input e output, das previs6es destas variaveis para perfodos inferiores a m e finalmente dos resfduos do modelo.

Par uttimo pode provar-se [(1), pp. 404 e 405] que a variancia do erro da previsao assim obtida e dada par:

m·1 m-1

v( m) = cr2

.2.

f:

+ cr2

.2.

'¥?

a 1=b 1 a 1=0 1

(5.16)

a

£

sendo os coeficientes 'Yj e 'l'j calculados respectivamente pelas relac;:6es:

00

8(B)<jlx(B) 't(B) = oo(B)9x(B)Bb <l>p(B)'P(B) = 9q(B)

00

onde r(B) =I. 'Yiai e '¥(8) =I. 'Viai

j=O i=O

Exemplo:

Considere-se o modelo (1,1,2) (1,1):

tal que:

(1-<Px1B) Xt=(1-9x1B)ar

onde os parametros

roo.

001, a1, e1, <1>1. <Px1 e ex1 sao todos conhecidos.

(5.17)

Vamos admitir que as sucess6es input e output foram obseNadas ate ao instante t e que se pretende calcular a previsao do output no instante t+3. Esta previsao pode ser obtida recursivamente pela expressao (5.14), com os respectivos parametros a*, oo* e e* calculados do modo seguinte:

Escreva-se o modelo anterior na forma:

por (5.12) tem-se:

o*(B) = (1-<!>18) (1-018) = 1-(<!>1 +o1)B+cJ>1o1B2

resuttando:

o1

=

-(<!>1 + 01)

Nestas condi<;Oes, recorrendo a (5.14)

e

(5.15), obtem-se sucessivamente as previs6es:

y~1)

=

-(<!>1 + 01)Yt+ cJ>101Yt-1 + COOXt-1 + (<!>1COO + W1)Xr-2-<!>1W1Xt-3+ + (o1 + e1)rr-o181er-1

Estabelecida a previsao Yr(3) podemos calcular a variancia do correspondente erro de previsao. Assim a partir das equagoes (5.17) obtem-se as igualdades:

resuttando, ap6s alguns calculos:

'1'0

= 1

concluindo-se, assim, por (5.16), que a variancia do erro de previsao toma a forma:

6 - Modelos multivariados

Neste paragrafo iremos fazer uma referencia aos modelos multivariados de funGaO transferencia, ou seja, modelos que descrevem uma sucessao output {yt} como fun~o do seu proprio passado e dos valores de uma ou mais suces-soes input independentes. Estes modelos sao definidos pela seguinte equaGao:

em que:

a) As u sucessoes input {Xkt}, k= 1, ... ,u, sao independentes;

b) {yt} e conjuntamente estacionaria com cada uma das sucessoes input,

c) {N't} tern esperanGa matematica nula, e nao correlacionada com qualquer das u sucessoes input e e modelizavel por urn processo ARMA (p,q):

E(N't) = O,'tlt

cov(N'r, Xks)

=

0, V s,t e k= 1 , ... ,u

$p(B)N't= 9q(B)Et

0

modelo (6.1) pode ser escrito na forma:

Yt = U1 (B)x1t + U2(8JX2t + ... + Uu(B)Xut + N't (6.2)

onde uk(B), k = 1 , ... , u, representa a funGao transferencia entre a sucessao output e a correspondente sucessao input {xkt}:

(6.3)

A metodologia de analise relativa a estes modelos multivariados e semelhante

a

dos modelos bivariados, sendo constitufda pelas mesmas fases. No que diz respeito

a

fase de identificagao, em particular, fazemos notar os seguintes aspectos:

a) As sucessoes output e input deverao ser previamente estacionarizadas pelos processos habituais, a fim de se poder aplicar o modelo muHivariado tanto na forma (6.1) como na (6.2).

b) As sucessoes input deverao ser individualmente branqueadas por aplicagao dos correspondentes operadores auto-regressivos e de medias m6veis:

<Pk)B)xkt

=

ekx(B)akt. k

=

1 , ... ,u

c) A sucessa.o

outupt

e «branqueada, uma vez para cada sucessa.o

input,

procedendo-se em seguida

a

especificac;:a.o da correspondente func;:a.o transferencia:

Tome-se o modelo na forma (6.2):

Yt

=

U1 (8)X1t + U2(B)X2t + ... + Uu(B)Xut + N 't

por branqueamento, por exemplo, da sucessa.o {x1 1} obtem-se:

91;

(B)G>1x(B)y1=

u1(B)e~;(B)G>1x(8)x1t+

u;(B)X2t+ ... +uJB)Xut+ nt (6.4)

com:

e:

resultando a expressa.o:

(6.5)

em que {~1 1} representa a sucessao

output

«branqueada» relativamente ao

input

{x1t}:

Multiplicando ambos os membros de (6.5) por a1t-k. k = 0,1 , ... e tomando esperanc;:as matematicas, vira, atendendo a (6.3):

E(a1r-!<-~1t)

=I.

u11E(a1t-1<-a1t-j)

i= 0

(6.6)

uma vez que as sucessoes

input

sao independentes e alem disso as sucessoes {n1} e {a1 r} sao na.o correlacionadas.

A expressao (6.6) permite concluir, dado que {a1 1} e urn rufdo branco:

u1k= (Ya:1(0))- 1Ya:1~1(k) = Pa:1~1(k)cr~1~~· k= 0,1, ...

A partir desta expressao obtem-se as estimativas dos pesos da func;:ao transferencia referentes ao

input

{x1 1}, fazendo:

-G1k= fa;1~1(k)S~1%~· k

=

0,1 , ...

Procedendo-se de forma analoga

a

acabada de descrever para cada uma das sucessoes input, obtem-se as especifica~oes de todas as fun~oes

transferencias do modelo e as respectivas estimativas dos pesos.

d) Conhecidas as estimativas dos pesos das fun¢es transferencia, estarnos em condi¢es de estimar a sucessao residual {N'_1}:

II II II

N't = Yt-U1(B)xw ... - u,J.B)Xut

a qual podera ser modelizada por um processo ARMA, concluindo-se desta forma

a identifica~ao do modelo multivariado.

7-Exemplo

0 exemplo que iremos tratar foi retirado do livro de Makridakis (4) e sera apresentado neste paragrafo de uma forma mais desenvolvida, utilizando o

software

BOXX.

A sucessao input {Xt} representa as despesas mensais efectuadas na publicidade de um determinado artigo (milhares de d61ares) e a sucessao output { Yt} diz respeito ao numero total de artigos vendidos em cada mes (milhares). No quadro 11 encontramos os valores de cada uma destas sucessoes cronol6gicas.

7.1 - ldentificac;iio

7.1.1 - Estacionariza(fiio do input e do output

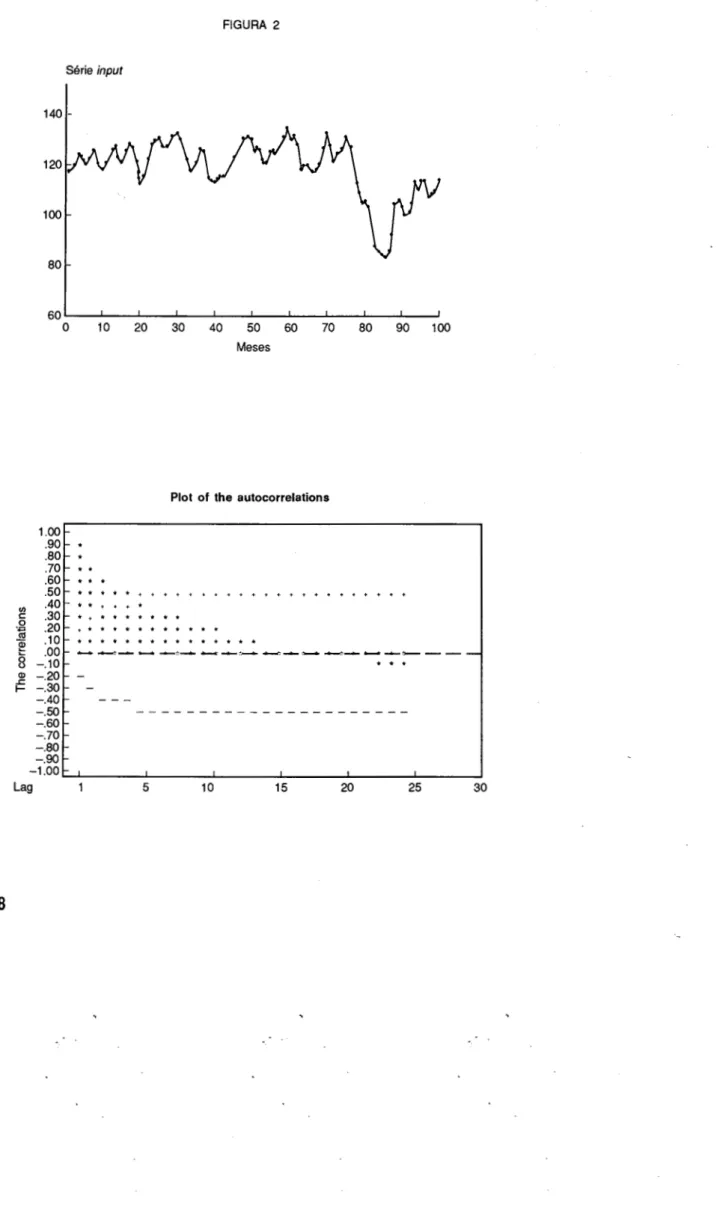
Os graficos das figuras 2 e 3 representam, respectivamente, o cronograma e a fun~ao de autocorrela~ao das sucessoes input e output. Como se pode obseNar, qualquer destas sucessoes nao se encontra estacionarizada. Com efeito, as respectivas fun~oes de autocorrelac;:ao tendem muito lentamente para zero, indicando a necessidade de se proceder a uma estacionarizac;:ao em media atraves da aplicac;:ao do operador diferenciac;:ao.

As sucessoes input e output estacionarizadas por este processo passarao a ser designadas por {xt} e {Yt}. respectivamente, de acordo com a nota~ao

utilizada anteriormente.

7.1.2- Branqueamento das sucessoes input e output

A figura 4 mostra os graficos das fun~6es de autocorrelac;:ao e de auto-correlac;:ao parcial da sucessao input estacionarizada {x₁}. A sua obseNac;:ao

indica-nos que esta sucessao pode ser modelizada porum processo ARMA(1 ,1 ):

QUADRO II

x,

Y, X, Y,

1 ... 116.44 202.66 51 _··· 123.90 266.69 2 _··· 119.58 232.91 52 ... 122.45 253.07 3 ... ,.. ... 125.74 272.07 53 _··· 122.85 249.12

4 ... -··· ... 124.55 290.97 54 _··· 129.28 253.59 5 ... 122.35 299.09 55 _··· 129.n 262.13 6 ... 120.44 296.95 56 _··· 127.78 279.66 7 _{···-···} 123.24 279.49 _{57··· 134.29 302.92} 8 ... 127.99 255.75 58 . ... 140.61 310.77 9 ... 121.19 242.78 59 ... 133.64 307.83 10 ... 1 18.00 255.34 60 ... 135.45 313.19 1 1 _{. •···} 121.81 271.58 61 ... 130.93 312.80 12 _{. ···} 126.54 268.27 62 ... 118.65 301.23 13 ... 129.85 260.51 63 .. ... 120.34 286.64 14 ... 122.65 266.34 64 .. ... 120.35 257.17 15 ... 121.64 281.24 65 .. ... 1 17.09 229.60 16 ... 127.24 286.19 66 ... 117.56 227.62 17 ... 132.35 271.97 _{67 ··· 121.69 238.21} 18 . . . 0. 130.86 265.01 68 .. ... 128.19 252.07

19 . . . 0 . . . 122.90 274.44 69 . • • . . . . • . • • . . • • • . . . • • • • . • • • • • • 0 • • • • . 134.79 269.86

20 ... 1 17.15 291.81 70 . . • • • . • • . . • . • • • • . . • • • . . 0 • . • • • • • • • • • . • • 128.93 291.62

21 ... 109.47 290.91 71 .. ... 121.63 314.06 22 ... 114.34 264.95 72 .. ... 125.43 318.56 23 ... 123.72 228.40 73 .. ... 126.80 289.11 24 ... 130.33 209.33 74 . ... 131.56 255.88

25 ... o ... 133.17 231.69 75 . ... 126.43 249.81

26 ... 134.25 281.56 76 . ... 1 16.19 268.82 27 ... 129.75 327.16 77 ... 112.72 288.24 28 ... 130.05 344.24 78 . ... 109.53 281.26 29 ... 133.42 324.74 79 . . • • • . . . • . . • • • . . • • • • . • • • • • . • • • • • • • • • • 0 110.38 250.92

30 ... 135.16 289.36 80 .. ... 107.31 222.26 31 ... 130.89 262.92 81 .. ... 93.59 209.94 32 ... 123.48 263.65 82 . ... 89.80 213.30 33 ... 1 18.46 276.38 83 .. ... 88.70 207.19 34 ... 122.11 276.34 84 . . . . • • • • . • • . • . . . • • • • • • • . . . . • • • • • • • • • . 0 86.64 186.13

35 ... 128.75 258.27 85 .. ... o ... o. 89.26 171.20

36 ... 127.09 242.89 86 .. ... 96.51 170.33 37 ... 1 14.55 255.98 87 .. ... 107.35 183.69 38 ... 1 13.26 278.53 88 . ... 1 10.35 211.30 39 ... 1 11.51 273.21 89 .. ... 102.66 252.66 40 ... 1 11.73 246.37 90 . ... 97.56 286.20

41 ... o·•··· 1 14.08 221.10 91 ... 98.06 279.45

42 ... oo••··· 1 14.32 210.41 92 ... o ... 103.91 237.06

43 . . . 0 " 0 " ' ' " ' ' " ' " " ' ' ' ' ' ' ' ' " ' " ' 115.03 222.19 93 • • • • . . • • . . . • • • • • • . • • • • . • • • • • • • • • 0 . • • . • 1 15.66 193.40

44 . . . 0 " ' 124.28 245.27 94 ... ··· ... 112.91 180.79

FIGURA 2

Serie input

140

-80

60~--~--~--~--~--~----~--~--~--~--~

1.00 .90 .80 .70 .60 .50 (/) .40

§ .30 . .., .20 ~ .10

~ .00

8 -.10

CD -.20 ~ -.30 -.40 -.50 -.60 -.70 -.80 -.90

0 1 0 20 30 40 50 60 70 80 90 1 00

Meses

Plot of the autocorrelations

+ • •

+ • •

-.... ...._,.,_ .__.

-:.':"--

.._,. -~-- ~--- ,..__,. ~--- ...

. .

-~--­

.

-1.00 L...J'---~---L---L.---~---~---~

Serie output 400

350-300

250

200

150

1.00 .90 .80 .70 .60 .50

rJl .40

c .30 .g .20

C\1 .10

0 10

• + +

+ *

FIGURA 3

20 30 40 50 60 70 80 90 100

Meses

Plot of the autocorrelations

~

.00 -...

...

~...- ...-.

...

~.-

---

-.';"---.. ...

~---8

-.10

Q) -.20

~ -.30 -.40 -.50 -.60 -.70 -.80 -.90

-1.00 ...._..__ _ _ ___.. _ _ _ __._ _ _ _ _,_ _ _ _ ~ _ _ _ ..._ _ _ ____.

1.00 .90 .80 .70 .60 .50 "' .40

<: .30

-~ .20

a; .10

t:: .00

8

-.10

Q) -.20

~ -.30 -.40 -.50 -.60 -.70 -.80 -.90

FIGURA 4

Plot of the autocorrelations

-1.00 L . . . J ' - - - ' - - - l . . . - - - L . . . - - - - ' - - - ' - - - ' Lag

1.00 .90 .80 .70 .60 .50 "' .40

<: .30

0

"iii .20

a; .10

t:::: .00

8 -.10

Q) -.20 ~ -.30 -.40 -.50 -.60 -.70 -.80 -.90

5 10 15 20 25 30

Plot of the partial autocorrelations

-1.00 ..._.__ _ _ _ _ _ . J ' - - - ' - - - ' - - - ' - - - -... - - - - 1

A aplicac;ao da metolodogia Box-Jenkins univariada, ap6s a conclusao das fases de estimac;ao e avaliac;ao do diagn6stico, permite estabeler como mais adequado o modelo anterior com:

<~>x

= -

0,26495 ex

= -

0,75352

Os valores destes dois parametres serao fornecidos ao computador, o qual, utilizando o software BOXX, ira proceder ao branqueamento das sucessoes input

e output, conforme o estabelecido em 5.1.2 e 5.1.3.

7.1.3 - Especificacilo de (r,s,b) e (p,q)

Estabelecidos os operadores auto-regressivos e de medias m6veis que branqueiam as duas sucessoes, obtem-se como output do software BOXX os resultados que constam do quadro Ill, que permitem proceder

a

identificac;ao do modelo de func;ao transferencia.

As figuras 5 e 6 representam a func;ao de correlac;ao cruzada entre as sucessoes branqueadas {a,} e {~,} para os lag posigtivos e negatives, respectivamente. Na figura 7 encontra!;l1-Se as func;oes de autocorrelac;ao e de autocorrelac;ao parcial dos resfduos

{N;}.

A analise do quadro Ill e dos graficos das figuras 5, 6 e 7 permite-nos propor o modelo de func;ao transferencia (2,2,2) (1 ,2):

7.2- Estimagao e avaliac;io do diagn6stico

ldentificado o modelo (7.1) e fornecida a correspondente informac;ao ao computador obtem-se o output relativo

a

fase de estimac;ao (quadro IV).

A figura 8 da-nos os graficos das func;oes de autocorrelac;ao e de auto-correlac;ao parcial da sucessao residual do modelo {e,} e a figura 9 e repre-senta o g~afico da correlac;ao cruzada entre a sucessao branqueada {a,} e os resfduos {e,}, para os lag positives e negatives.

A analise do output do computador e dos graficos anteriormente referidos permite concluir:

a)

0

modelo (7.1) tern como para metros estimados:

6}0

=

1 ,3022

01,

= -

0,59326 &')2

=

0,81834

S,

= 1,2094

g2

= - 0,70298

~,

=

0,27176

QUADROIII

Time series identification

STEP 1 OF TRANSFER FUNCTION IDENTIFICATION- THE ANALYSIS BETWEEN

INPUT SERIES 1 : MX1 MAKR.DAT OUTPUT SERIES: MY1 MAKR.DAT

THE PREWHITENING MODEL

...

DATA: MX1 MAKR. DAT 100 OBSERVATIONS

DIFFERENCING FACTORS (ORDER, DEGREE) : 1, 1

BACKCASTING :OFF

...

PREWHITENING MODEL PARAMETERS

*************************************************************************************************** TYPE LAG COEFFICIENT

*******************************************************************•***************************** 1 AUTOREGRESSIVE 1

2 MOVING AVERAGE 1

1 -.26495E+00 1 -. 75352E+00

**************************************************************************************************

THE PREWHITENING MODEL

...

DATA: MX1MAKR. DAT 100 OBSERVATIONS

DIFFERENCING FACTORS (ORDER, DEGREE) : 1, 1

BACKCASTING : OFF

************************************************************************************************* PREWHITENING MODEL PARAMETERS

*************************************************************************************************** TYPE LAG COEFFICIENT

************************************************************************************************* 1 AUTOREGRESSIVE 1

2 MOVING AVERAGE 1

1 -.26495E+00 1 -. 75352E+00

OUADRO Ill (continu~qao)

CROSS-CORRELATIONS ANAL VSIS

MEAN OF THE INPUT SERIES STANDARD DEVIATION

MEAN OF THE OUTPUT SERIES STANDARD DEVIATION

NUMBER OF OBSERVATIONS

-4 7901E-04

-4 7510E-01

-.3 0505E-03 .1 6841E-OO

98

THE CROSS-CORRELATIONS

LAGS 0- 7 -.084 -.133 .344 .601 .286 -.189

STANDARD ERROR (.102) (.103) (.103) (.104) (.104) (.105)

LAGS 8- 15 -.031 -.123 .106 .051 .009 -.006

STANDARD ERROR (.107) (.107) (.108) (.108) (.109) (.110)

LAGS 16-- 23 -.014 -.013 .037 -.054 -.067 .073 STANDARD ERROR (.112) (.113) (.113) (.114) (.115) (.115)

LAGS 24- -.017

STANDARD ERROR (.118)

-T-TEST FOR SIGNIFICANCE AT EACH LAG:

-.440 -.390 (.105) (.106)

-.008 -.014 (.110) (.111)

.172 .078 (.116) (.117)

-BOXX IDENTIFIES 6 CROSS CORRELATIONS OUTSIDE 1.500 SIGMA.

LAGS: 2, 3, 4, 6, 7.

CROSS-CORRELATION FEEDBACK ANAL VSIS

(PRELIMINARY TEST OF UNIDERECTIONAL CAUSALITY) (I. E. LACK OF FEEDBACK)

THE CROSS-CORRELATIONS

LAGS 0- 7 -.084 -.087 .114 .048 .065 -.098

STANDARD ERROR (.102) (.103) (.103) (.104) (.104) (.105)

LAGS 8- 15 .028 .007 .067 .028 .010 -.053

STANDARD ERROR (.107) (.107) (.108) (.108) (.109) (.110)

LAGS 16-- 23 .004 .038 -.042 .103 .055 -.034

STANDARD ERROR (.112) (.113) (.113) (.114) (.115) (.115)

LAGS 24 -.003

STANDARD ERROR (.118)

T-TEST FOR SIGNIFICANCE AT EACH LAG:

-.074 -.041 (.105) (.106)

-.055 -.025 (.110) (.111)

-.123 -.026 (.116) (.117)

QUADRO Ill (continuat;ao)

THE AUTOCORRELATION AND PARTIAL AUTOCORRELATION ANALYSES OF THE NOISE SERIES

MEAN OF THE RESIDUAL SERIES -.20149E-02

STANDARD DEVIATION .98054E-01

NUMBER OF OBSRRVATIONS 75

MEAN DIVIDED BY THE STANDARD

ERROR OF THE MEAN -.17795E+OO

---

-THE AUTOCORRELATIONS

LAGS 1- 8 .451 -.405 -.601 -.127 .346 .248 -.147 -.241

STANDARD ERROR (.115) (.137) (.152) (.181) (.182) (.191) (.195) (.196)

QSTATISTIC 16. 29. 58. 59. 69. 74. 76. 81.

P-VALUE .000 .000 .000 .000 .000 .000 .000 .000

LAGS 9- 16 -.059 .037 -.004 -.011 .123 .228 .048 -.201

STANDARD ERROR (.200) (.201) (.201) (.201) (.201) (.202) (.205) (.205)

QSTATISTIC 81. 81. 81. 81. 83. 88. 88. 92.

P-VALUE .000 .000 .000 .000 .000 .000 .000 .000

LAGS 17- 24 -.164 .069 .160 -.033 -.256 -.161 .118 .078

STANDARD ERROR (.208) (.210) (.210) (.212) (.212) (.216) (.217) (.218)

QSTATISTIC 95. 95. 98. 98. 105. 108. 109. 113.

P-VALUE .000 .000 .000 .000 .000 .000 .000 .000

- - - -

-T-TEST FOR SIGNIFICANCE AT EACH LAG:

BOXX IDENTIFIES 3 AUTOCORRELA TIONS OUTSIDE 1.960 SIGMA.

LAGS: 1, 2, 3.

THE PARTIAL AUTOCORRELATION

LAGS 1- 8 .451 -.764 .200 -.067 .041 -.288 .132 -.025

STANDARD ERROR (.115) (.115) (.115) (.115) (.115) (.115) (.115) (.115)

LAGS 9- 16 -.258 -.156 .123 -.006 .082 -.084 -.063 -.097

STANDARD ERROR (.115) (.115) (.115) (.115) (.115) (.115) (.115) (.115)

LAGS 17- 24 .037 -.036 -.122 -.062 -.058 .008 -.096 -.054

STANDARD ERROR (.115) (.115) (.115) (.115) (.115) (.115) (.115) (.115)

BOXX IDENTIFIES 4 PARTIAL AUTOCORRELATIONS OUTSIDE 1.960 SIGMA.

1.00 .90 .80 .70 .60 .50

Cll .40

g .30 . ., .20

<11 .10

~

.00

8

-.10

CD -.20

F

-.3o -.40 -.50 -.60 -.70 -.80 -.90

FIGURA 5

Plot of the cross-correlations

-1.00 ..._..__ _ _ ___.. _ _ _ -.J... _ _ _ _._ _ _ _ _._ _ _ _ _._ _ _ _ _ .

Lag

1.00 .90 .80 .70 .60 .50 "' .40

g

.30

"iii

.20

(ii .10

t::: .00

8 -.10

Q) -.20 ~ -.30 -.40 -.50 -.60 -.70 -.80 -.90

0 4 9 14 19 24 29

FIGURA 6

Plot of the cross-correlations

-1.00 ..._..__ _ _ __. _ _ _ ... _ _ _ __._ _ _ _ __._ _ _ _ ... _ _ ___.

1.00 .90 .80 .70 .60 .50 .40

~ .30

.g .20

111 _.10

~ .00

8

-.10

Q) -.20

~ -.30 -.40 -.50 -.60 -.70 -.80 -.90

FIGURA 7

Plot of the autocorrelations

...

. .

-..::_,._

.

...._

.

-~

..

... -....,.. -~

-.';-

...

~

.__----

--1.00 .__,_ _ _ ___. _ _ _ __,_ _ _ _ _._ _ _ _ _._ _ _ _ ..._ _ _ ----J

Lag

"'

c: 0 -~

~

8

Q) .c I-1.00 .90 .80 .70 .60 .50 .40 .30 .20 .10 .00 -.10 -.20 -.30 -.40 -.50 -.60 -.70 -.80 -.90

5 10 15 20 25 30

Plot of the partial autocorrelations

-1.00 ...._....__ _ _ ___. _ _ _ ---~. _ _ _ __,_ _ _ _ _._ _ _ _ _._ _ _ __,

QUADROIV

The estimated model

···***************************************************************

DATA: Y

=

MY1MAKR.DAT 100 OBSERVATIONS

DIFERENCING FACTORS (ORDER, DEGREE) : 1, 1

BACKCASTING :OFF

···•*************************'**

...•..•...•...•...•...••...

NOISES SERIES

DIFERENCING FACTORS ON NOISE : NONE

•••••••••••••••••• ** * * •••••• * * •••• * *. ** ... * * ** ** ••••• * * ** •• ** ••••••••• * ••••• ** •••••••••••••••••••• NOISE MODEL PARAMETERS

...

FACTOR LAG COEFICIENT T RATIO

...

1 AUTOREGRESSIVE 1 2 MOVING AVERAGE 1 3 MOVING AVERAGE 1

1 1 2 .57958E+00 .27176E+00 .59139E+00 4.69 2.37 6.66 ************************************************************************************************** INPUT SERIES 1

DATA-X1

=

MX1MAKR. DAT

DIFERENCING FACTORS (ORDER, DEGREE): 1, 1

VALUE OF LAG PARAMETER IS 2

...

TRANSFER FUNCTION PARAMETERS

FACTOR LAG COEFICIENT T RATIO

* •• ** ** **** * * ** •• *** •• *. ** ... ** * *. * * ** **** ** * * ** •• * •• * ••• ** •••• ** ** •• * ** •••• **** •••••••••••••••• 4 OUTPUT LAG

50UTPUT LAG 61NPUT LAG ?INPUT LAG 81NPUT LAG 1 1 1 1 1

1 .12094E+01 2 -.70298E+00 0 .13022E+01 1 -.59326E+00 2 .81834E+00

159.23 -105.02 38.57 -10.86 18.97 ···••*****************************************

CORRELATION MATRIX OF THE PARAMETERS

2 3 4 5 6 7 8