MATLAB PARA SISTEMAS DE CONTROLE

INTRODUÇÃO AO MATLAB

O

MATLAB®

O software surgiu em meados da década de 1970, e fundamentalmente fora criado para operações com matrizes, como o próprio nome do software sugere: MATLAB® é o acrônimo do inglês Matrix Laboratory (Laboratório de Matrizes).

Naturalmente, no MATLAB® operações com matrizes (que normalmente são extremamente complexas de serem realizadas em outras linguagens) são simples e diretas, como o cálculo de uma matriz inversa, e.g.

Com o tempo, porém, o software evoluiu muito, e hoje pode ser utilizado nos mais diversos tipos de aplicações, como operações em tempo real, processamento de imagens dentre outras aplicações.

Este material apresenta funções e scripts desenvolvidos em MATLAB especificamente criados para analisar sistemas lineares, com enfoque em sistemas de controle clássicos.

M

ANIPULANDO

V

ARIÁVEIS

Por se tratar de uma linguagem em mais alto nível, no MATLAB® (ou M-Código) não é necessário que variáveis sejam declaradas, e tampouco um tipo é necessário para a variável. Isso é um pouco complicado de processar em um primeiro momento, mas com o tempo essa flexibilidade apresenta-se como uma vantagem. O comando whos apresenta a que tipo (classe no MATLAB®) a variável pertence, bem como outras características da variável. Para visualizar tais diferenças, execute na janela de comando os seguintes comandos:

clc clear all

close all

a = 10;

b = 'Agora é no MATLAB!!'; c = 5 - 3j;

d = int16(452); whos

Perceba que não é necessário declarar a variável, nem especificar o tipo ao qual ela pertence.

O comando clc limpa a janela de comandos, o comando clear all limpa a área de trabalho (deletando

as variáveis criadas até então), o comando close all fecha qualquer janela aberta por algum comando (como

gráficos). O comando whos, como já mencionado, apresenta detalhes das variáveis da área de trabalho.

No MATLAB®, o tipo padrão para números é ponto flutuante de dupla precisão (double), porém é possível trabalhar com números inteiros, necessitando-se para tanto converter o número utilizando uma função, como em int16(452);

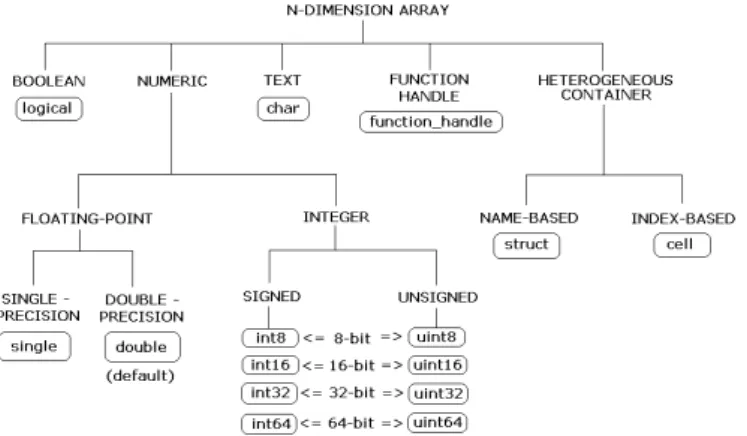
A Figura 1 (na próxima página) apresenta os tipos de dados básicos do MATLAB, separado em suas respectivas classes. Os nomes dentro das caixas equivalem ao nome da classe de dado. Percebe-se que todos os tipos podem ser organizados em matrizes de dados com qualquer dimensão.

O ponto-e-vígurla no MATLAB® tem função diferente do que em C. Quando se executa um comando terminado em ponto-e-vírgula, o valor das variáveis envolvidas não é apresentado. Execute os comandos abaixo para perceber essa diferença:

Figura 1 - Classes de dados no MATLAB.

Uma variável, depois de criada, pode receber qualquer tipo de dado. Observe a saída após executar os comandos:

clc clear all

close all

a = 10; whos a = '!?'; whos

a = [1 2 3 4 5]; whos

Nos exemplos até aqui apresentados é possível constatar que o desenvolvimento de códigos no

MATLAB® se dá de maneira mais intuitiva e em mais alto nível. Por exemplo, não foi necessário criar nenhuma

estrutura para representar um número complexo, simplesmente foi escrito: c = 5 - 3j; bem como o comando do último exemplo a = [1 2 3 4 5]; criou um vetor com cinco números double. Isso torna a linguagem muito versátil quando se busca uma solução numérica para problemas, e é por essa razão que o MATLAB® é muito utilizado, principalmente no meio acadêmico. Como dito, o MATLAB® é uma ferramenta feita para manipulação de matrizes, portanto, suporta naturalmente operações envolvendo matrizes. Então é fundamental saber como criar matrizes e como a indexação de elementos é realizada nessa ferramenta.

I

NTRODUÇÃO ÀS

M

ATRIZES

A manipulação de matrizes é direta no MATLAB®, bastando criar a matriz na atribuição, como nos exemplos abaixo:

clear all

close all

A = [1 2 3 4 5];

B = int16([ 1, 3 ; 2 , 5 ]); C = [-1 5 2; 6 -2 1];

whos

Perceba que para criar uma matriz basta utilizar colchetes []. Os elementos da linha são separados por espaços ou vírgulas (formando colunas), e as linhas são separadas por ponto-e-vírgula.

A indexação de matrizes no MATLAB® se dá de forma diferente do que se fazia em C, utilizando parênteses ao invés de colchetes. Execute o código:

A = [1 2 3; 2 -4 5; 9 4 2]; B = [-1 5 2; 6 -2 1];

B(1,3)

O que se pode concluir a respeito da indexação de matrizes no MATLAB®?

O processo de indexação inicia em 1, e não em 0 (como se fazia em C). Essa é uma diferença crucial e que gera muitos problemas se não observada desde o início da utilização do software.

É possível ainda criar matrizes diretamente com a manipulação de índices, e não necessariamente atribuindo toda uma matriz no comando. O MATLAB® entenderá o comando e completará a matriz, preenchendo os termos restantes com zeros. Verifique a saída dos comandos:

vet(6) = 10 imagem(3,2) = 3 vid(3,3,5) = -10

A manipulação algébrica de matrizes pode ser realizada de forma direta no MATLAB®. Observe o exemplo abaixo:

A = [2 5 2; -4 2 1; 5 3 1]; B = [1 2 3; 3 3 4; 4 5 7]; C = [3 2];

A * B C' inv(B)

É fundamental compreender como manipular matrizes no MATLAB®, pois muitas funções fazem uso de matrizes como argumentos de entrada e saída.

Além da sintaxe apresentada até agora para criar matrizes, é possível utilizar o operador dois-pontos ( : ). É mais fácil entender a utilidade deste operador executando os comandos abaixo:

clc clear all

close all

vet = 1 : 10 vet2 = 1 : 2 : 10

vet3 = -0.5 : 0.2 : 0.6

Com o operador dois-pontos fica fácil criar vetores com muitos elementos que serão utilizados em cálculos numéricos e em gráficos. Por exemplo, execute e observe a saída dos comandos.

clear all

close all

t = 0 : 0.25 : 2; t = t*pi

v = sin(t)

Aumente a quantidade de pontos substituindo a linha t=0:0.25:2; por t=0:0.025:2;

Perceba que a função seno (sin) já retornou um vetor contendo o seno de cada um dos elementos do vetor t. Note que em códigos como esse a utilização do ponto-e-virgula torna-se interessante para suprimir respostas intermediárias desnecessárias.

É possível criar vetores e matrizes utilizando funções. Algumas das funções que podem ser utilizadas para criar vetores e matrizes serão apresentadas agora.

zeros()

retorna uma matriz 2x5 contendo somente zeros. Se mais dimensões são necessárias, basta adicioná-las separando-as com vírgulas na função zeros(). Execute comandos semelhantes aos abaixo apresentados.

mat = zeros(5) vet = zeros(1,5) zeros(4,1)

zeros(2,2,3)

ones()

Esta função é análoga a função zeros(), porém retorna matrizes onde todos os elementos são uns (1). Repita os mesmos comandos executados anteriormente mudando a função utilizada de zeros() para ones().

linspace()

Cria um vetor linearmente espaçado, i.e., cuja diferença entre dois elementos subseqüentes sempre é igual. Muito utilizado quando é desejável um número conhecido de pontos em um vetor. Por exemplo, desejando-se um vetor de 0 até 100 contendo exatamente 10 pontos, basta escrever:

vet = linspace(1,100,10);

Interessante notar que o vetor criado com o comando abaixo gera um resultado diferente. vet = 0:10:100

O vetor criado apresenta 11 pontos, e não 10.

logspace()

Semelhante à linspace. Esta função, porém, gera um vetor cujos elementos são espaçados logaritmicamente. É extensivamente utilizado quando a resposta em freqüência de sistemas é calculada, uma vez que tais gráficos utilizam esta escala. Em um vetor espaçado logaritmicamente, a 'distância' entre dois elementos subseqüentes varia conforme uma função logarítmica (de base dez). Notório também que os argumentos de valor inicial e final do vetor são potências de 10. Por exemplo, para criar um vetor de 0.1 até 100, com 8 pontos, deve-se utilizar a potência de 10 que origina 0.1 e 100, deve-sendo respectivamente -1 e 2, pois 10-1=0.1 e 102=100. O código para gerar o vetor citado é:

vet = logspace(-1,2,8)

Avalie a distância entre os elementos. Após, execute a linha: log10(vet)

Perceba que esta operação retorna um vetor linearmente espaçado!

I

NDEXAÇÃO DE

M

ATRIZES

O processo de indexação de matrizes no MATLAB pode ser realizado utilizando-se vários índices de uma só vez. Isso permite que mais de um elemento seja acessado em uma única operação. Os índices utilizados no processo de indexação, no MATLAB, podem assumir mais de uma dimensão (podem ser vetores ou até mesmo matrizes). Isto é um pouco complexo em um primeiro momento e é melhor compreendido estudando-se exemplos.

A = 1 : 0.2 : 2; A(1)

Outro exemplo desse tipo de indexação pode ser observado na seqüência: A = [0:4;5:9;10:14;15:19;20:24];

A(2,5)

A([1:2],[1:3]) A([2 3 4],[3 5])

É possível ainda acessar todos os elementos de uma dada dimensão. Para realizar tal tarefa basta utilizar o operador dois-pontos (:) na dimensão que se deseja obter todos os elementos. Observe os exemplos.

A = [0:4;5:9;10:14;15:19;20:24];

A(:,2) %retorna todos os elementos da segunda coluna

A(4,:) %retorna todos os elementos da quarta linha

Para obter os elementos de uma matriz de um dado índice até o último índice da dimensão, basta utilizar a palavra reservada end.

A = [0:4;5:9;10:14;15:19;20:24]; k = 3;

A(k:end,2) %retrona os elementos a partir de k da segunda coluna

A(k:end,k:end)

Perceba que é possível utilizar variáveis no processo de indexação de matrizes.

O

PERAÇÕES COM

M

ATRIZES

O MATLAB suporta operações diretas com matrizes, utilizando os mesmos operadores utilizados para manipulação de escalares. Porém, deve-se atentar às regras básicas de álgebra linear. Além de permitir operações algébricas com matrizes, o MATLAB possui alguns operadores com função específica para matrizes, como o operador divisão (/) e barra-invertida (\), bem como funções padrão como a função inv(), que computa a inversa de uma matriz.

As operações básicas (soma, subtração e multiplicação) são análogas àquelas vistas no curso de álgebra linear, portanto não serão explicadas em demasia. Para avaliar essas operações execute os comandos abaixo.

clear all

A = [1 2; 4 -1]; B = [-1 0; 1 1]; C = [1 2 3]; D = [3; 1; 4];

disp( B * A ); disp( A + B ); disp( A - 3 ); disp( C * D ); disp( D * C ); disp( D + C * D );

O operador divisão (/) e barra-invertida (\) implementam operações diferentes daquelas imaginadas (a operação de divisão não é definida matematicamente para matrizes). A expressão A\B implementa a operação matemática _𝐴𝐴−1_{∙ 𝐵𝐵 enquanto a operação A/B implementa a operação matemática𝐴𝐴 ∙ 𝐵𝐵}−1_{. A primeira das} expressões é usada amplamente para a solução de um sistema de equações lineares da forma _{𝐴𝐴 ∙ 𝑥𝑥}=𝐵𝐵, uma vez que multiplicando ambos os lados da equação por A-1 se obtém:_𝑥𝑥=𝐴𝐴−1∙ 𝐵𝐵. Logicamente, deve-se relembrar dos conceitos e conhecimentos angariados nos cursos de álgebra. O operador divisão ainda mantém sua função original quando manipulado com escalares.

É possível ainda (e é muito comum) a operação de matrizes "elemento por elemento". Imaginemos agora um vetor de tempo definido no MATLAB: t = 0 : 0.1 : 10;

Matematicamente, para calcular os valores de _𝑓𝑓(𝑡𝑡) para uma função dada por _𝑓𝑓(𝑡𝑡) =𝑡𝑡2 por exemplo, deve-se, para cada instante _𝑡𝑡 calcular _𝑡𝑡·𝑡𝑡, ou seja, para _𝑡𝑡= 0, _𝑓𝑓(0) = 0 · 0, para _𝑡𝑡= 1, _𝑓𝑓(1) = 1 · 1 = 1, para

mesmo para calcular f(t). É natural, matematicamente, que se tente escrever no MATLAB, então, o comando: f =

t*t; ao se deparar com esta situação. Tente então executar os comandos sugeridos e observe o que ocorre.

t = 0 : 0.1 : 10; f = t*t;

Logicamente, o comando resultou em erro, pois não é possível, matematicamente, multiplicar duas matrizes-linha. Porém o problema em se computar _𝑡𝑡2 _{persiste. Portanto, o MATLAB permite a operação elemento} por elemento entre matrizes. Essas operações são realizadas adicionando-se um ponto (.) antes da operação a ser executada. Estude atentamente a saída gerada pelos comandos abaixo.

A = [1 2; 3 4]; B = [2 3; 4 5];

A*B %multiplica as matrizes

A.*B %multiplicação elemento por elemento

A/B %realiza a operação A*B^(-1)

A./B %divisão elemento por elemento

A.^B

Portanto, para computar os valores de _𝑓𝑓(𝑡𝑡) utilizando o MATLAB deve-se utilizar os comandos abaixo.

t = 0 : 0.1 : 10; f = t.*t;

f2 = t.^2; %também funciona

Finalmente, existem muitas funções para a manipulação ou processamento de matrizes no MATLAB, algumas são apresentadas no código de exemplo na seqüencia deste material.

A = [1 2; 3 4];

t = linspace(-5,5,100); %cria um vetor de -5 a 5 com 100 pontos

vet = [5 5 3 -2 3 -1];

mean(vet) %calcula média de vetor

max(vet) % valor máximo (e pode retornar o índice: ver "help")

min(vet) % valor mínimo (e pode retornar o índice: ver "help")

sort(vet) %ordena vetor

det(A) %calcula o determinante

inv(A) %calcula a inversa se existir

D

ELETANDO

E

LEMENTOS DE

M

ATRIZES

No MATLAB ainda é possível deletar elementos, utilizando a abertura e fechamento de colchetes []. Observe o exemplo.

A = rand(4); %cria uma matriz randômica com elementos de zero a um

V = rand(1,5); A

A(:,1) = [] V

V([1 3]) = []

V

ERIFICANDO

T

AMANHO E

D

IMENSÕES

O MATLAB possui duas funções básicas para verificar tamanho de matrizes: length e size.

A primeira retorna o tamanho da maior dimensão, enquanto a segunda retorna o tamanho de todas as dimensões da matriz. Crie matrizes e verifique o que length e size retornam.

A = rand(randi(5),randi(5)) length(A)

size(A)

M

ATRIZES DE

C

ÉLULAS

(

CELL ARRAYS

)

No MATLAB, é possível agrupar matricialmente tipos diferentes de dados em cada "elemento" da matriz. Em uma matriz desse tipo, cada elemento é chamado de célula, e pode conter qualquer tipo de dado em seu interior.

O processo de manipulação de matrizes de células é muito semelhante à de matrizes comuns. Deve-se atentar que o processo de criação de matrizes de células utiliza chaves ({}) ao invés de colchetes ([]). Observe o exemplo abaixo, principalmente lendo cuidadosamente a saída do comando whos.

clc clear all

close all

A = [1 2 3;4 5 6;7 8 9]; B = {1 2 3;4 5 6;7 8 9}; whos

Note que a classe de A é double, enquanto a de B é cell. No exemplo supracitado, a matriz de células B contém dados homogêneos, ou seja, todas as células possuem o mesmo tipo de dado. Porém, matrizes de células são utilizadas, na grande maioria dos casos, quando dados heterogêneos devem ser manipulados. Observe e estude o próximo exemplo.

clc clear all

close all

notas = {'Cid',[9.6 8.4 7.4];'Vincent',[10 9 5.5];'Tifa',[8.8 9 7.5]}; disp(notas)

Note que, neste caso, foram agrupados dados distintos (heterogêneos) em uma mesma matriz. Daí a definição observada no organograma da Figura 1.

O processo de indexação de matrizes de células não é tão simples quanto se imagina. É possível utilizar parênteses () ou chaves {} no processo de indexação de matrizes celulares.

 notas(ind) - Retorna as células da matriz de células notas especificadas pelo índice ind.  notas{ind} - Retorna conteúdo das células de notas especificadas pelo índice ind.

E

STRUTURAS

Estruturas são um conjunto de dados que são agrupados e referenciados como uma entidade única. Estruturas contém, na maioria das vezes, dados heterogêneos, isto é, de tipos distintos (daí, novamente, a definição apresentada na Figura 1 para esse tipo de dado). A diferença básica de matrizes celulares e estruturas é que nas estruturas os campos são nomeados, enquanto nas matrizes celulares o mesmo processo é feito com a utilização de índices (e não de nomes).

Para criar uma estrutura, basta utilizar o ponto, concatenando o nome da estrutura com o nome do campo.

clc clear all

close all

Como todos os tipos de dados do MATLAB, é possível criar uma matriz de estruturas com grande facilidade:

clc clear all

close all

aux(1,10) = struct('Campo1',[],'Campo2',[]);

%Criando struct com campos vazios

aux2(1:3,1:3) = struct('C1',10,'C2',20,'C3',30);

%Inicializando os campos com valores não-nulos

whos

disp( aux(1) ) disp( aux2(1,1) ) disp( aux2(:,1) ) C = aux2(:,1); disp( C(2).C2 )

O

COMANDO

HELP

APLICAÇÕES PARA SISTEMAS LINEARES E SISTEMAS DE CONTROLE

C

RIANDO

F

UNÇÕES DE

T

RANSFERÊNCIA

O MATLAB dispõe de duas classes de dados básicas para representar funções de transferência. São elas: a classe tf e a classe zpk. Além disso, o MATLAB dispõe de outras classes para representar modelos lineares (cita-se especialmente o modelo em espaço de estados: ss), mas que não (cita-serão abordados neste material, pois este material visa operar com funções de transferência, abordagem clássica de sistemas controle. Para saber mais, execute help ltimodels na janela de comandos.

tf

Esta classe de dados, homônima da função tf() que instancia o objeto (criando a variável), é utilizada para criar funções de transferência de acordo com os coeficientes dos polinômios do numerador e do denominador da função. A sintaxe básica é

G = tf(NUM,DEN)

Onde NUM e DEN são vetores que contém os coeficientes do numerador e do denominados da função de transferência.

𝐺𝐺(𝑠𝑠) = 𝑠𝑠+ 2

𝑠𝑠3_{+ 5}𝑠𝑠2₊𝑠𝑠_{+ 6}

Basta escrever:

G = tf([1 2],[1 5 1 6])

É possível criar modelos MIMO, i.e., que contenham múltiplas entradas e múltiplas saídas. Para tanto, deve-se utilizar matrizes celulares para indicar as funções referentes a cada entrada e saída. Porém, novamente, tal funcionalidade foge ao escopo deste material, mas pode ser explorada nas disciplinas avançadas do currículo. Mesmo assim, o procedimento para criar tais sistemas é muito fácil. Para mais informação leia o help da função tf.

A função tf pode ser utilizada de uma maneira diferente para criar funções de transferência. Essa segunda forma se aproxima sensivelmente da forma analítica que funções de transferência são tratadas nos cursos de controle, pois evita o uso da representação de polinômios como vetores. O código abaixo cria a mesma função de transferência apresentada acima.

s = tf('s'); % Cria uma ft simples que é utilizada na construção de

G = (s+2)/(s^3+5*s^2+1*s+6) % Funções mais complexas...

Funções de transferência discretas podem ser criadas com a função tf. Para tanto, o número de argumentos de entrada deve ser acrescido. O argumento extra automaticamente é entendido como a taxa de amostragem utilizada no sistema. Por exemplo, para criar o sistema:

𝐻𝐻[𝑧𝑧] = 𝑧𝑧

2

𝑧𝑧2_+𝑧𝑧+1 2

𝑇𝑇𝑠𝑠= 0.01

no MATLAB, basta escrever:

H = tf([1 0 0],[1 1 1/2],1/100)

Ou, alternativamente

zpk

A função (e classe homônima) zpk se assemelha muito com a classe tf. Porém, enquanto tf trabalha com os coeficientes do numerador e do denominador, a função zpk recebe, em ordem, a localização dos zeros (zpk), dos polos (zpk) e o ganho da função (zpk), trabalhando com a função de transferência fatorada, na forma:

𝐺𝐺(𝑠𝑠) =𝑘𝑘∏ (𝑠𝑠 − 𝑧𝑧𝑖𝑖) 𝑀𝑀

𝑖𝑖=1

∏ �𝑠𝑠 − 𝑝𝑝𝑁𝑁𝑗𝑗=1 𝑗𝑗�

Onde _{𝑧𝑧𝑖𝑖} e _{𝑝𝑝𝑗𝑗} são as localizações dos M zeros e N polos do sistema.

As localizações dos polos e zeros são passadas como vetores para a função zpk, seguindo a sintaxe básica: G = zpk(polos,zeros,ganho)

Por exemplo, a função

𝐺𝐺(𝑠𝑠) = 𝑠𝑠+ 1

𝑠𝑠2_{+ 5𝑠𝑠+ 6}

Possui um zero em -1, e polos em -3 e -2 (facilmente verificável utilizando a função roots()), assim, tal função poderia ser escrita no MATLAB utilizando zpk:

G = zpk([-1],[-2 -3],1)

Ou ainda:

s = zpk('s');

G2 = 1/((s+2)*(s+3))

Obviamente, a função zpk é usada preferencialmente quando as localizações das raízes são dadas ou quando a forma apresentada já é a fatorada. Atenção, o ganho utilizado na função não é o ganho DC. O ganho DC da função será:

𝐺𝐺(0) =𝑘𝑘∏ 𝑧𝑧𝑖𝑖 𝑀𝑀 𝑖𝑖=1

∏𝑁𝑁𝑗𝑗=1𝑝𝑝𝑗𝑗

No exemplo acima, o ganho DC é 1/6. Aliás, o ganho DC de qualquer sistema pode ser obtido mediante a função dcgain. Execute:

G = zpk([-1],[-2 -3],1) dcgain(G)

A função zpk também pode ser utilizada para sistemas MIMO e para sistemas discretos. As regras são as mesmas que para a função tf. Neste material, apenas um exemplo de sistema discreto será apresentado. A linha abaixo:

H = zpk([0 0 0],[-1/2 1/3 1/4],1,0.2)

Implementa no MATLAB o sistema discreto com _{𝑇𝑇𝑠𝑠} = 0.2 𝑠𝑠 cuja função de transferência é:

𝐻𝐻[𝑧𝑧] = 𝑧𝑧

3

�𝑧𝑧+1

2� �𝑧𝑧 − 1 3� �𝑧𝑧 −

1 4�

O mesmo procedimento, utilizando z = zpk('z',0.2) pode ser utilizado aqui também.

G1 = tf([1 5],[1 3 2]);

G2 = zpk([-3 -1],[-1 -2 -6],10); G1a = tf(G2)

G2a = zpk(G1)

É possível obter a localização dos polos e dos zeros de qualquer função de transferência no MATLAB utilizando as funções pole() e zero(). Rode as linhas abaixo para descobrir as singularidades do primeiro sistema apresentado no material.

G = tf([1 2],[1 5 1 6]); pole(G)

zero(G)

O código abaixo apresenta o diagrama de polos e zeros do sistema. close all

clear all

clc

G = tf([1 2],[1 5 1 6]); p = pole(G);

z = zero(G);

hc = plot(real(p),imag(p),'x',real(z),imag(z),'or',[0 0],[-1/eps 1/eps],'k'); set(gca,'YLim',[-3/2 3/2]);

set(hc(1:2),'MarkerSize',13,'LineWidth',3); grid on

xlabel('Eixo Real'); ylabel('Eixo Imaginário');

Alternativamente, pzmap automaticamente retorna o diagrama de polos e zeros de qualquer sistema. O MATLAB ainda oferece uma interessante função que, além de apresentar os polos, apresenta a freqüência natural e o fator de amortecimento dos mesmos. Trata-se da função damp. Execute:

G = tf([1],[1 1 200]); damp(G)

O

BTENDO A

R

ESPOSTA

N

UMÉRICA DE

F

UNÇÕES DE

T

RANSFERÊNCIA

O MATLAB possui uma interface dedicada para apresentar a resposta de sistemas lineares, desde a resposta do sistemas a sinais até a resposta em freqüência e gráficos polares. Trata-se do LTI Viewer. Tal ferramenta gera gráficos interativos, diferentes de um plot normal que simplesmente grafica pontos em uma curva. São três as funções básicas para obter a resposta de sistemas lineares: impulse(), step() e lsim().

As duas primeiras irão apresentar a resposta impulsiva e ao degrau de sistemas, respectivamente, enquanto a última, lsim, realiza a simulação de sistemas frente a qualquer entrada. As funções impulse e step devem ser utilizadas com cuidado, pois permitem a simulação de sistemas sem indicar qualquer parâmetro (nem mesmo quantidade de pontos), e o número de pontos e tempo de simulação do modelo são escolhidos automaticamente pelo algoritmo, o que muitas vezes gera resultados não satisfatórios.

As linhas abaixo irão apresentar na tela a resposta impulsiva e ao degrau de um sistema de segunda ordem com fator de amortecimento de 0,1 e ganho DC unitário.

wn = 1; csi = 0.1;

G = tf(wn^2,[1 2*csi*wn wn^2]); figure(1)

Perceba que a qualidade do gráfico deixa a desejar, pois um número pequeno de pontos foi utilizado. As funções permitem, no entanto, que o vetor de valores de tempo desejado seja enviado para a função. Isso faz com que melhores resultados sejam obtidos. Rode o exemplo abaixo, onde o vetor de tempo é enviado para step.

wn = 1; csi = 0.1; t = 0:0.001:60;

G = tf(wn^2,[1 2*csi*wn wn^2]); figure(1)

step(G,t)

É possível obter os pontos calculados pela função, porém, nesse caso a função não irá utilizar o LTI Viewer para apresentar o gráfico, portanto, o gráfico deve ser traçado. Observe o exemplo abaixo:

G = tf(1,[1 1]); figure(1)

[y,t] = step(G);

plot(t,y,'LineWidth',3); grid on

Note que o vetor de tempo utilizado também é retornado pela função.

O programa abaixo foi feito para se estudar o efeito de zeros em sistemas lineares. Perceba como a função é utilizada no laço para recalcular a saída do sistema de acordo com a nova localização do zero. O sistema é recriado de maneira que o ganho DC permaneça unitário. Atente para o comportamento derivativo quando o zero se aproxima da origem do plano. Lembre que a entrada é um degrau, e com um zero na origem teríamos um efeito impulsivo devido a presença da derivada, motivo pelo qual não se utiliza derivadores puros, e se evita a presença de zeros em malha fechada nas proximidades da origem. Todavia, o efeito de zeros em malha fechada no SPE é facilmente compensada com um controlador em série com a planta que opera em malha fechada, alocando-se polos nesse compensador para cancelar o efeito indesejado dos zeros.

clear all

close all

clc

t = 0:0.001:1;

hpz = subplot(2,1,1); hgr = subplot(2,1,2);

set(hpz,'Position',[0.05 0.8 0.92 0.17]); set(hgr,'Position',[0.05 0.05 0.92 0.67]); G1 = zpk([-11],[-5 -10],5*10/11);

y = lsim(G1,ones(1,length(t)),t); hp = plot(hgr,t,y);

hz = plot(hpz,[-10 -5],[0 0],'xb',[-11],[0],'or','Linewidth',3,'MarkerSize',14); set(hpz,'XLim',[-11 0]);

set(hgr,'YLim',[0 3],'XLim',[0 1],'XGrid','on','YGrid','on'); for k = -11:0.1:-1

G1 = zpk([k],[-5 -10],5*10/abs(k)); y = step(G1,t);

set(hp,'YData',y);

set(hz(2),'XData',k); drawnow

tic

while toc < 0.1 end

end

A sintaxe básica é:

lsim(sistema,vetor_entrada,vetor_tempo)

Para obter a resposta do sistema 1

𝑠𝑠+1 a uma entrada senoidal com freqüência angular de 1𝑟𝑟𝑟𝑟𝑟𝑟/𝑠𝑠, por exemplo, basta escrever:

clc clear all

close all

G = zpk([],[-1],1);

wc = 1; fc = wc/(2*pi); T = 1/fc; t = 0:T/1000:5*T;

u = sin(wc*t); lsim(G,u,t)

O código abaixo pode ser utilizado para estudar a resposta do sistema a várias freqüências. clc

clear all

close all

G = zpk([],[-1],1); wc = 1;

fc = wc/(2*pi); T = 1/fc;

t = 0:T/1000:5*T;

y = zeros(1,length(t)); hc = plot(t,y,t,y); set(gca,'XLim',[0 5*T]);

wv = logspace(log10(0.2),log10(5),1000); for wc = wv

u = sin(wc*t);

y = lsim(G,u,t); %aqui o MATLAB não plota, mas calcula...

set(hc(1),'YData',u); set(hc(2),'YData',y); drawnow;

tic

while toc < 0.001 end

end

Perceba que, da mesma maneira que impulse e step, lsim não apresenta o gráfico se os pontos forem solicitados.

O

PERAÇÕES COM

F

UNÇÕES DE

T

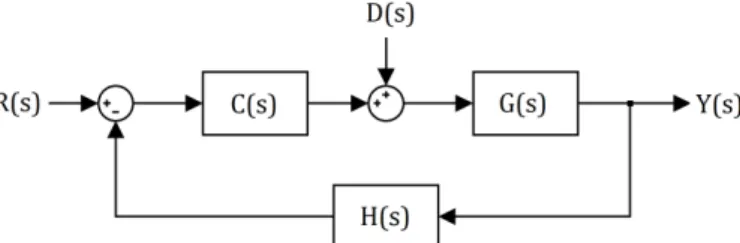
RANSFERÊNCIA

O MATLAB suporta operações algébricas com funções de transferência, portanto, supondo o sistema de controle da figura abaixo, onde R(s) é o sinal de referência, D(s) um sinal de distúrbio e Y(s) o sinal de saída:

Figura 2 - Sistema de Controle Clássico.

𝐺𝐺𝑌𝑌𝑌𝑌(𝑠𝑠) =𝑌𝑌

(𝑠𝑠)

𝑌𝑌(𝑠𝑠)=

𝐶𝐶(𝑠𝑠)𝐺𝐺(𝑠𝑠) 1 +𝐶𝐶(𝑠𝑠)𝐺𝐺(𝑠𝑠)𝐻𝐻(𝑠𝑠)

𝐺𝐺𝑌𝑌𝑌𝑌(𝑠𝑠) =𝑌𝑌

(𝑠𝑠)

𝑌𝑌(𝑠𝑠)=

𝐺𝐺(𝑠𝑠) 1 +𝐶𝐶(𝑠𝑠)𝐺𝐺(𝑠𝑠)𝐻𝐻(𝑠𝑠)

A primeira é comumente chamada de equação de malha fechada, que indica o quão bem o sistema segue uma referência. A segunda é utilizada para estudar a rejeição de distúrbio do sistema, i.e., o desempenho do controlador C(s) frente a distúrbios. Em ambos os casos, é necessário operações algébricas com funções de transferência. O código abaixo apresenta tais equações supondo 𝐺𝐺(𝑠𝑠) = 1/(𝑠𝑠+ 2), 𝐶𝐶(𝑠𝑠) = 1/𝑠𝑠 e 𝐻𝐻(𝑠𝑠) = 1, apresentando a resposta ao degrau de ambas as funções de transferência.

clc close all

clear all

G = tf(1,[1 2]); C = tf(1,[1 0]); H = 1;

Gyr = C*G/(1+C*G*H); Gyd = G/(1+C*G*H); figure(1); step(Gyr); figure(2); step(Gyd);

Perceba que a saída do sistema em malha fechada tende para 1, indicando que o erro é nulo em regime permanente (a saída tende para o valor da referência). Na equação de rejeição de distúrbio, no entanto, a saída tende a zero, indicando que o efeito do distúrbio é transitório na saída (devido a ação do integrador).

Interessante notar que tais equacionamentos não promovem cancelamentos. Para realizar associação de sistemas, é aconselhado o uso de funções. Cita-se aqui, para emprego rápido em sistemas SISO: parallel, series e feedback. Tais funções são simples quando operam com sistemas SISO, porém podem ser utilizadas em construções com sistemas MIMO. Para tais aplicações consulte o help destas funções. De maneira a entender a diferença entre as saídas das funções, observe que o código abaixo, mesmo sendo equivalente analiticamente falando, gera funções de transferência distintas.

G = tf(1,[1 2]); C = tf(1,[1 0]); H = 1;

Gyr1 = C*G/(1+C*G*H) Gyr2 = feedback(C*G,H)

A saída do programa é:

Transfer function: s^2 + 2 s

---s^4 + 4 s^3 + 5 s^2 + 2 s

Transfer function: 1

---s^2 + 2 s + 1

Note que as equações são matematicamente equivalentes, devido a cancelamento de polos e zeros (verifique utilizando zeros e poles).

close all

clear all

t = 0:0.001:10; G = tf(1,[1 2]);

C = tf(1,[1 0]); %controlador será um ganho, neste caso

H = 1;

Gyr = feedback(C*G,H); yr = step(Gyr,t); Gyd = feedback(G,C*H); yd = step(Gyd,t); figure(1)

subplot(2,1,1);

hr = plot(t,yr,'LineWidth',3); grid on

subplot(2,1,2);

hd = plot(t,yd,'LineWidth',3); grid on

set(gca,'YLim',[-0.1 0.45],'XLim',[0 10]);

for k = 1:0.1:10 %será o ganho do controlador

yr = step(feedback(k*C*G,H),t); yd = step(feedback(G,k*C*H),t);

set(hr,'YData',yr); set(hd,'YData',yd); drawnow

end

O MATLAB disponibiliza uma função que testa se o sistema é estável, que pode ser utilizada nas investigações de estabilidade sem necessitar a simulação do sistema utilizando step ou impulse: verifique isstable.

A

NÁLISE DE

E

STABILIDADE E

T

RANSITÓRIO COM

LGR

Como visto na disciplina de Análise de sistemas de Controle, o Lugar Geométrico das Raízes é uma poderosa ferramenta para a análise de sistemas de controle, pois permite inferir facilmente o comportamento em malha fechada do sistema em função de um parâmetro variante, normalmente o ganho do controlador no ramo direto ou no ramo de realimentação. No MATLAB, a análise de sistemas utilizando o LGR pode ser realizada mediante a uma função (rlocus) ou através da ferramenta rltool ou alternativamente sisotool, toolboxes especificamente projetado para estudar sistemas de controle.

Lembre-se que para traçar o LGR de sistemas é necessário obter _𝐿𝐿(𝑠𝑠), que na maioria dos casos, coincide com a função de malha aberta do sistema (sem o ganho _𝐾𝐾). Assim, o traçado do LGR é função da malha aberta do sistema, fazendo o parâmetro _𝐾𝐾 variar. Dessa maneira, para traçar o LGR de qualquer sistema a partir de _𝐿𝐿(𝑠𝑠), basta criar _𝐿𝐿(𝑠𝑠) e chamar rlocus utilizando a função criada. Por exemplo, para o sistema apresentado na Figura 2, considerando as seguintes funções:

𝐺𝐺(𝑠𝑠) = 1

(𝑠𝑠+ 2)(𝑠𝑠+ 4) 𝐶𝐶(𝑠𝑠) =

𝑘𝑘

𝑠𝑠 𝑒𝑒 𝐻𝐻(𝑠𝑠) = 1

A equação de malha fechada é:

𝐺𝐺𝑚𝑚𝑓𝑓(𝑠𝑠) = 𝑘𝑘 𝑠𝑠

1 (𝑠𝑠+2)(𝑠𝑠+4)

1 +𝑘𝑘 𝑠𝑠

1 (𝑠𝑠+2)(𝑠𝑠+4)

∴ 𝐿𝐿(𝑠𝑠) = 1

𝑠𝑠(𝑠𝑠+ 2)(𝑠𝑠+ 4)

Para traçar o LGR desse sistema, basta digitar as linhas abaixo. L = zpk([],[0 -2 -4],1);

rlocus(L)

Perceba que o algoritmo escolhe automaticamente o número de pontos e os limites de ganho que são utilizados para a construção do LGR do sistema. Porém, a função rlocus permite que um vetor com os ganhos seja enviado como argumento, o que ajuda muito na obtenção e verificação de faixas de estabilidade.

Para o sistema anterior, por exemplo, não é possível obter com precisão o ganho que instabiliza o sistema, porém, caso isso seja necessário, basta criar um vetor com valores mais precisos, assim a função apresentará apenas os valores de ganho desejados:

K = 20:0.01:80;

L = zpk([],[0 -2 -4],1); rlocus(L,K)

É possível, assim, estudar com detalhes áreas valores de ganho específicos. Novamente, a função rlocus retorna a localização caso for utilizada com argumentos à esquerda. Nesta sintaxe, a função retorna a localização dos polos como primeiro argumento de saída e o ganho como segundo argumento de saída. Novamente, se argumentos de saída forem utilizados, a função não retorna nenhum resultado gráfico.

L = zpk([],[0 -2 -4],1); [P,K] = rlocus(L);

O MATLAB dispõe ainda do rltool, ferramenta muito poderosa, que será apresentada brevemente aqui. Para iniciar a ferramenta, basta digitar rltool na janela de comando.

ferramenta possibilita o projeto de compensadores tanto no LGR quanto na freqüência, sendo, portanto, de grande auxílio no projeto e na análise de sistemas de controle. Outra ferramenta amplamente difundida é a sisotool.

D

IAGRAMAS DE

B

ODE

,

D

IAGRAMAS DE

N

YQUIST E

M

ARGENS DE

E

STABILIDADE

No MATLAB, tais gráficos são feitos com funções com o mesmo nome. A resposta em frequência

de sistemas é obtida com a função bode, enquanto a função nyquist traça o gráfico polar ou diagrama

de nyquist da função. Já a função margin apresenta o diagrama de bode e as margens de ganho e de

fase para o sistema.

Dada a função abaixo:

𝐺𝐺(𝑠𝑠) = 80000(𝑠𝑠+ 20)

(𝑠𝑠+ 2)2₍𝑠𝑠_{+ 400)}2

Para obter o nyquist e o bode, pode-se escrever no MATLAB:

G = zpk([-20],[-2 -2 -400 -400],80e3); figure(1)

bode(G) grid on

figure(2) nyquist(G) figure(3) margin(G)

Vale lembrar que estas funções trabalham com pontos escolhidos automaticamente, assim como

a maioria das funções vistas aqui. Porém, é possível enviar o vetor de freqüências ou ainda estipular

limites inferiores e superiores. Observe os diagramas de bode gerados pelo código abaixo:

G = zpk([-20],[-2 -2 -400 -400],80e3); w = logspace(0,2,10000);

figure(1); bode(G); grid on

figure(2); bode(G,{0.1,10}); grid on

figure(3); bode(G,w); grid on

Essas funções também possuem sintaxes alternativas que retornam os pontos dos gráficos (ou as

margens de estabilidade) sem graficar os diagramas.

Vale lembrar que as funções vistas aqui apresentam resultados inclusive para objetos que

contenham sistemas MIMO.

E

XTRA

entanto, um sistema de primeira ordem, caso apresente atraso de transporte, pode instabilizar com

certos valores de ganho.

Para adicionar o atraso de transporte ao sistema, basta alterar a propriedade

'ioDelay'

.

Observe a saída do programa abaixo, comparando a resposta de um sistema com o mesmo sistema

apresentando um atraso de transporte.

clc clear all

close all

G = zpk([],[-1-3*j -1+3*j],10); Gca = G;

set(Gca,'ioDelay',0.3); [y,t] = step(G);

[yca] = step(Gca,t);

plot(t,[y yca],'LineWidth',3); set(gca,'XLim',[0 max(t)]); grid on

Muito embora as funções consigam trabalhar com atraso de transporte, não é possível

interconectar sistemas com esta característica (apenas com objetos da classe ss é possível). Para

terminar, observe a diferença do diagrama de Nyquist dos sistemas apresentados anteriormente e tente

verificar que o sistema com atraso de transporte pode se tornar instável em malha fechada.

w = logspace(-1,100,10000); G = zpk([],[-1-3*j -1+3*j],10); Gca = G;

set(Gca,'ioDelay',0.3); nyquist(G,w);

hold on

nyquist(Gca,w);

Como o atraso de transporte é modelado apenas como um atraso no sinal de entrada em relação

ao sistema, a função de transferência com atraso de transporte sofre uma multiplicação por

_𝑒𝑒

𝑠𝑠𝑡𝑡0

, onde

𝑡𝑡

0

é o atraso (devido à propriedade do deslocamento de Laplace). Isto explica o formato do Nyquist

verificado. Assim, Gca é, matematicamente:

𝐺𝐺

𝑐𝑐𝑟𝑟

(

𝑠𝑠

) =

10

𝑠𝑠

2

_{+ 2}

_𝑠𝑠

_{+ 10}

𝑒𝑒

−