Directeur de recherche SeassalChristian INL CNRS/ECL SouteyrandEliane directeur de recherche INL CNRS/ECL TardyJacques directeur de recherche INL CNRS/ECL ViktorovitchPierre directeur de recherche INL CNRS/ECL. KapsaPhilippe directeur de recherche LTDS CNRS/ECL Le BotAlain directeur de recherche LTDS CNRS/ECL LoubetJean-Luc directeur de recherche LTDS CNRS/ECL.

Les différents systèmes de freinage sur TGV
Nous proposons dans ce chapitre une description des systèmes de freinage des TGV et des différents composants qui les caractérisent. a) Essieu porteur (b) Garniture de frein.
Caractéristiques du système
Caractéristiques mécaniques
C'est ainsi qu'apparaissent sur la flotte des TGV des disques en acier forgé, permettant de dissiper 2,5 fois plus d'énergie que des disques en fonte, à poids égal. Le disque de frein utilisé dans cette étude est donc un disque plein non ventilé en acier forgé.
Les garnitures
Le facteur de friction des garnitures couramment utilisées sur les freins à disque des matériels ferroviaires est considérablement réduit en présence d’humidité. A noter que parmi les équipements actuellement utilisés sur les TGV, aucun ne respecte ce gabarit. a) Evolution du facteur de frottement sec moyen.

Principe de fonctionnement du frein à disque sur TGV
Problématique du crissement des freins ferroviaires
Parmi les premiers mécanismes avancés on retrouve ceux d'origine purement tribologique qui sont le stick slip et la déstabilisation du système par amortissement négatif induit par la loi du frottement ; ces mécanismes sont capables d'expliquer les vibrations des systèmes quel que soit leur nombre de degrés de liberté, mais avec des variations de frottement. Dans un premier temps, nous montrerons sur un système mécanique à un degré de liberté comment on étudie la possibilité de l'existence de vibrations auto-entretenues, puis nous verrons les deux mécanismes tribologiques et enfin les deux mécanismes structurels.
Mécanismes d’origine tribologique
Cas du stick-slip
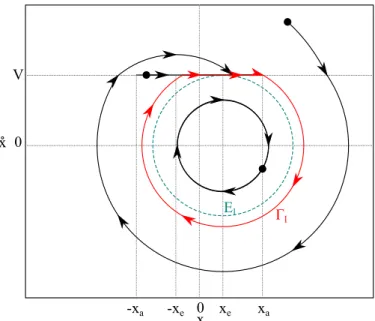
Si les conditions initiales sont dans l'ellipse frontière El de centre (xe, 0) et tangente au segment d'adhésion ([−xa, xa], V), le système est stable et est décrit par une ellipse incluse dans El. Dans tous les autres cas, le système décrira des parties de l’ellipse jusqu’à ce qu’elle croise le segment d’adhésion et revienne au comportement précédent.
Cas de l’amortissement négatif
En effet, dans le système linéarisé, la force de frottement avec un coefficient décroissant en fonction de la vitesse se traduit par un amortissement négatif équivalent µV1. Dans le cas où le système est instable, le point d'équilibre S= (xe, 0) est un équilibre instable : si le système commence à s'en écarter, alors sa trajectoire est dans l'espace.
Sprag-slip et couplage de modes
Cas du sprag-slip
Étant donné que nous avons un plongement O', la force tangentielle en fonction de l'angle θ s'exprime comme suit. Lorsque la force devient suffisamment importante, on ne peut plus considérer la liaison en O' comme un encastrement, il est plus juste de considérer un pivot parfait en O' et une tige rigide PO'.
Cas du couplage de modes
Les mécanismes de couplage de modes Desprag-slipet ont montré un excellent accord avec des expériences telles que celles de Jarvis et Mills [65] sur un système faisceau sur disque. Kx, qui combine l'effet d'un coefficient de frottement décroissant avec la vitesse de glissement du stick-slip et celui du renforcement du sprag-slip.
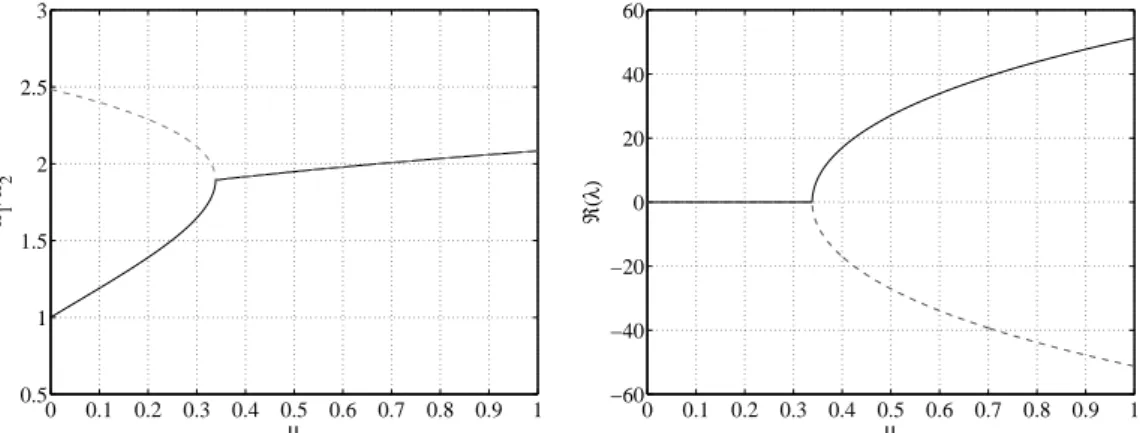
Effet de l’amortissement dans le couplage de modes
On peut observer que la répartition de l'atténuation a un effet très sensible tant sur les fréquences que sur les parties réelles. Figure 2.11 – Influence de l'amortissement et sa répartition sur les parties réelles des valeurs propres.

Notions sur la stabilité des systèmes non-linéaires
Stabilité d’un point d’équilibre pour des systèmes linéaires
Si toutes les valeurs propres d'une matrice n×n A ont une partie réelle non nulle, le flux associé à x˙ = f(x) est dit hyperbolique. Ici, définit pour i6s les vecteurs propres associés à des valeurs propres à parties réelles strictement négatives, pour s < i6s+ucose associés à des valeurs à parties réelles strictement positives, et pour s+u < iles vecteurs propres associés à des parties réelles nulles.
Stabilité d’un point d’équilibre pour des systèmes non-linéaires
Si tous les exposants caractéristiques de x ont une partie réelle strictement négative, alors x est un point asymptotiquement stable au sens de Lyapunov. Un point hyperbolique dont les exposants caractéristiques ont tous des parties réelles négatives est un point attractif.
Bifurcations de Hopf, section de Poincaré et cycle limite
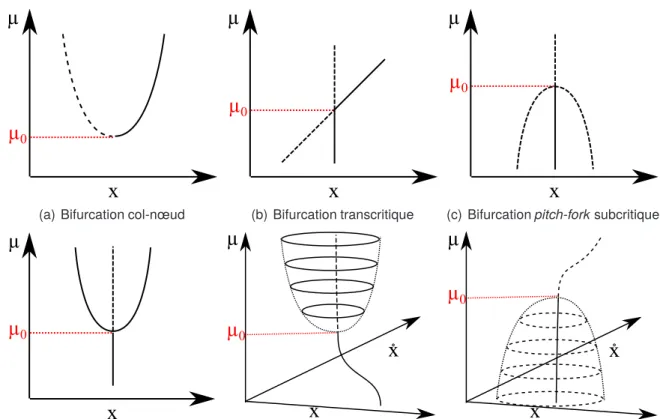
La bifurcation de Hopf se caractérise donc par le changement de nature d'un point singulier hyperbolique vers un point non hyperbolique avec évolution du paramètre µ autour de la valeur critique µ0. Le troisième point qu'une bifurcation de Hopf doit vérifier est une condition de traversalité de l'axe imaginaire : pour µ, µ0 nous avons un point hyperbolique.
Synthèse
Figure 3.2 – Test de Bergman et al.[7] – Détermination d'un coefficient de frottement critique sur deux séries d'essais (a) et (b). Ils ont établi l'existence expérimentale d'un coefficient de frottement critique µc en dessous duquel le crissement apparaît inexistant.

Définition du protocole d’essais
- Sélection des garnitures prioritaires
- Présentation du banc d’essais de freinage de l’Agence d’Éssais Ferroviaire
- Instrumentation
- Caractérisation vibratoire du système couplé
- Description des essais
Le point d'excitation sur le porte-joint du FRF est le point repéré Pt74 (figure 3.7). Tableau 3.2 – Conditions opératoires des essais stationnaires sur garniture GP1 3.2.5.2 Frein de maintien – Essais stationnaires.
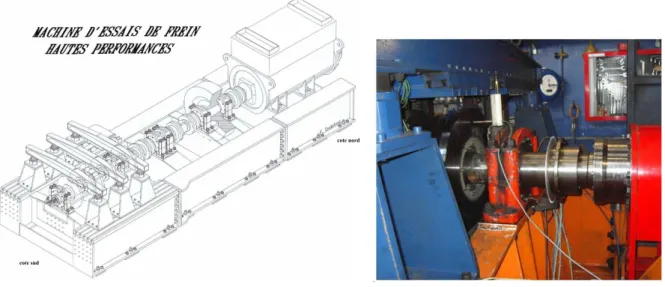
Analyse des résultats d’essais
Analyse des essais de freinage d’arrêt
On observe que lors de cet essai le facteur de frottement évolue en fonction de la vitesse. Comme précédemment, une évolution du coefficient de frottement en fonction de la vitesse de rotation du disque à.
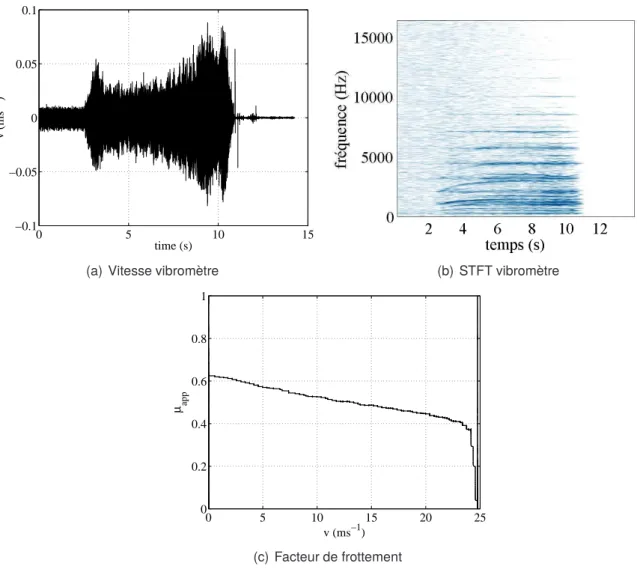
Analyse des essais de freinage de maintien
On observe une seule instabilité qui persiste tout au long de l'essai, qui est également différente de ce que l'on observe dans les essais de freinage au décrochage (c.f. Il est intéressant de noter que l'on retrouve les fréquences apparaissant dans l'essai non stationnaire à 8 kN montrées sur vu dans figures 3.12.
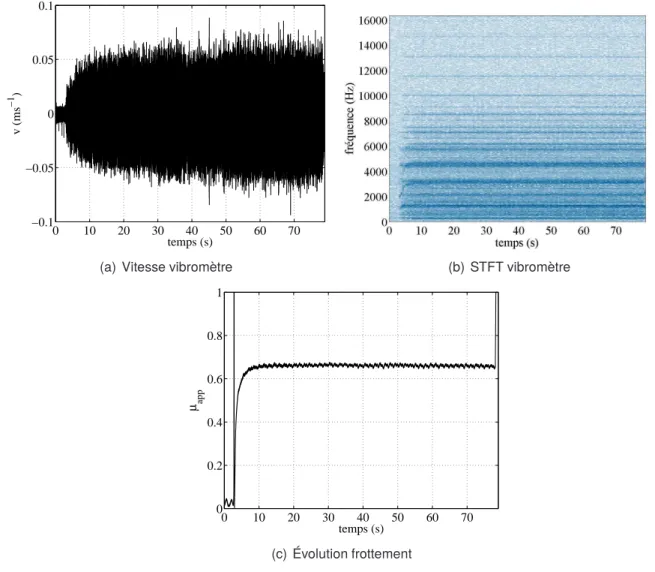
Synthèse sur les essais de freinages d’arrêt et de maintien
Conclusions sur l’étude expérimentale du crissement
Modélisation du contact unilatéral
Il s'agit d'un modèle idéalisé de contact dans lequel tout jeu entre deux corps en contact est interdit et tout effort exercé entre les deux corps est de type répulsif. En pratique, les lois de contact hertziennes sont souvent appliquées globalement à l'ensemble de la zone de contact [32], ou avec une méthode dite semi-hertzienne, qui consiste à diviser la zone de contact en sous-zones, dans lesquelles la raideur hertzienne est recalculée. 104].
Modélisation du frottement
La loi de frottement de Coulomb peut être exprimée sous la forme de l'équation (4.3), où w˙ désigne la vitesse de glissement relative. Le formalisme de la loi de Coulomb permet de prendre en compte de nombreux effets si l'on permet au coefficient de frottement d'être fonction de plusieurs variables.

Méthodes numériques pour traiter le contact frottant en transitoire
Simulations en dynamique non-linéaire transitoire
D’une part, pour rester au plus près de la physique, il est souhaitable de ne pas introduire d’amortissement. Une méthode élégante pour surmonter ces problèmes consiste à introduire une discontinuité dans le schéma d’intégration temporelle.
Traitement numérique du contact frottant
La figure 6.15 montre la projection sur les neuf modes instables de la solution transitoire obtenue. La première consiste à choisir les conditions initiales et à échantillonner la solution simulée.
Les choix retenus pour la dynamique transitoire
Utilisation du lagrangien augmenté incrémental
Dans le cas de systèmes non linéaires, on peut faire face à une évolution des modes en fonction de l'évolution de la solution. Utiliser la projection sur les modes complexes permet d'identifier les contributions des modes linéaires à la solution non linéaire.

Analyse de stabilité avec contact de Signorini-Coulomb
Calcul de l’équilibre quasi-statique
Une première étape essentielle pour caractériser la stabilité d'un équilibre est le calcul de cet équilibre. Du fait de la recherche d'une solution de glissement stationnaire, le frottement est automatiquement pris en compte dans la matrice de rigidité non symétrique.
Calcul des modes et valeurs propres complexes du système
Des moyens d'optimiser cette méthode peuvent être de condenser statiquement le problème sur l'interface de contact, ce qui réduit la taille du système mais le rend plein, d'effectuer une réduction de l'interface de contact, ou de sauvegarder une partie de factorisation de la matrice en utilisant le nœud approprié. numérotation, c'est-à-dire avec les nœuds de contact à la fin. En particulier, le choix de la matrice pour l'orthonormalisation de la base peut avoir un impact significatif sur la convergence de cette méthode.
Méthodes de réduction modales et approximations non-linéaires
- Méthode de Ritz
- Réduction sur les variétés centrales
- Méthodes d’appoximation
- Choix d’une méthode de réduction
- Description du modèle étudié
- Validation des procédures développées
La méthode Ritz peut être appliquée à un problème déjà discrétisé par la méthode des éléments finis. Toute la difficulté de la méthode Ritz est donc le choix d'une base adaptée au calcul de la solution.
Outils d’analyse des solutions
- Transformée de Fourier à court terme (STFT)
- Transformée en ondelettes continue (CWT)
- M-MAC pic à pic et pic à modes
- Projection sur les modes complexes
La deuxième façon d'utiliser ce critère est de prendre pour B plusieurs modes complexes issus de l'analyse de stabilité. Nous recherchons donc la décomposition du vecteur d'état α en solutions modes complexesΦ0 du problème des valeurs propres généralisées (GEP) de l'analyse de stabilité (voir section 4.4.2).
Étude de stabilité du système
La croix × indique le type d'analyse décrite dans ce chapitre pour le cas correspondant : "Comportement non linéaire" pour l'analyse transitoire, "Réduction".
Comportement du système de référence
Système comportant un unique mode instable
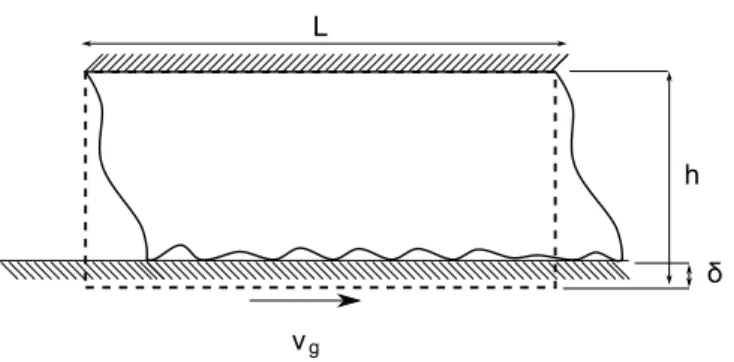
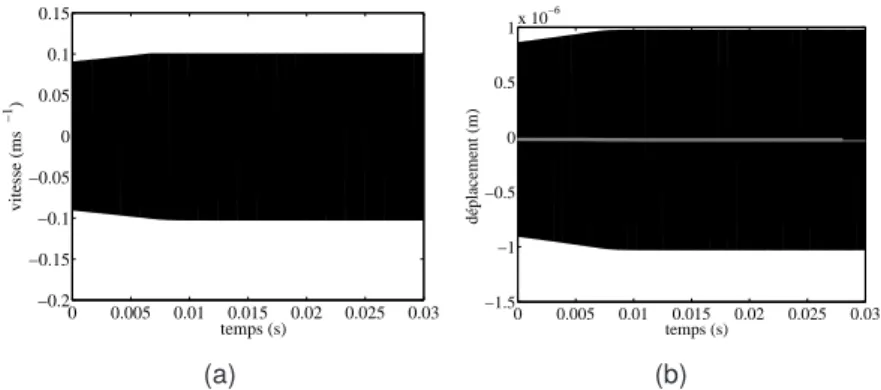
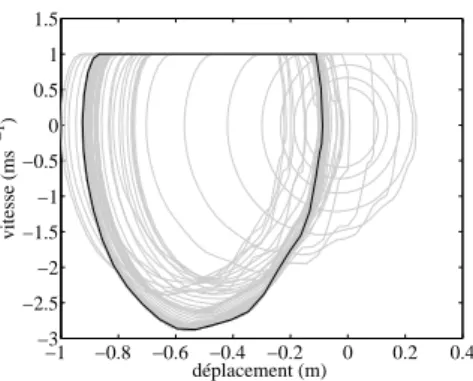
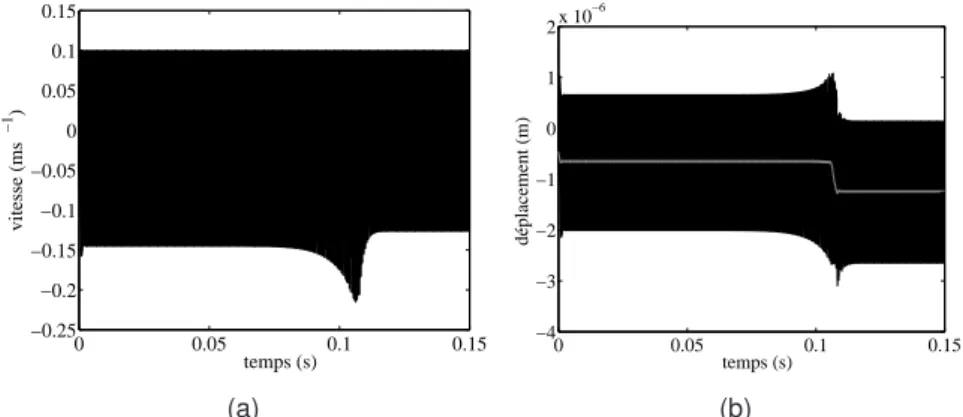
La saturation de la solution obtenue par adhésion peut être constatée dans la mesure où la vitesse est limitée par la vitesse de glissement vg. Dans ce cas - ce qui favorise dans la plupart des cas l'adhésion - la composante normale de la vitesse n'est pas représentée car elle est négligeable par rapport à la composante tangentielle.
Système comportant plusieurs modes instables
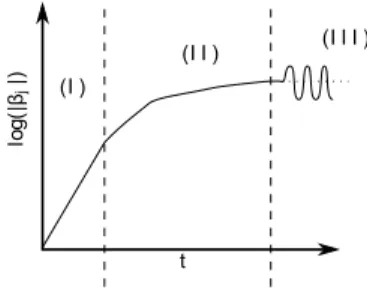
En projetant la solution sur les modes complexes – figure 5.22(a) – il est possible d'obtenir une représentation claire de l'évolution de la solution transitoire et stationnaire. L'étude de la projection de la solution sur les modes complexes (figure 5.28(a)) montre une compétition assez compliquée lors de la phase (II) : le mode 6 atteint sa saturation alors que le mode 9 est déjà saturé depuis quelques millisecondes.

Cas avec 9 modes instables
Figure 5.39 - Cas9_33S - Déplacement au nœud de contact (en gris : valeur moyenne) - (a) Composante tangentielle, (b) Composante normale. Figure 5.44 - Exemple 9_3×33S - Déplacement au nœud de contact (en gris : valeur moyenne) - (a) Composante tangentielle, (b) Composante normale.
Conclusion sur le comportement du système
Mise en œuvre d’une réduction efficace
Définition de deux types de base de réduite
Un autre principe est que la construction de la base réduite sera réalisée selon des méthodes complexes issues de l'étude de stabilité. Il est possible de transférer la trace des modes statiques aux degrés de liberté physiques en incluant partS.

Performances des bases réduites
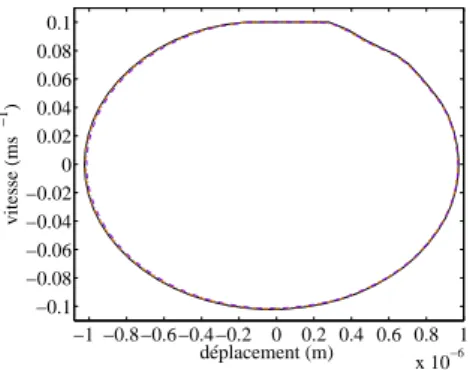
Le FCs100 de base a des performances similaires dans les deux cas, tandis que le FC100 voit la séparation dégrader la qualité de la solution. Cela confirme que la plupart des bases donnent des résultats proches de la solution de référence.
Conclusion
Dans ce chapitre, l'application des méthodes développées à un modèle plus représentatif d'un frein de TGV industriel est mise en œuvre. Cette application nécessite, d'une part, de vérifier que le passage d'un modèle 2D à nombre de degrés de liberté réduit à un modèle 3D à nombre de degrés de liberté plus élevé n'entraîne pas de problèmes numériques et, d'autre part , pour rendre cette étude la plus pertinente possible, pour obtenir un modèle éléments finis du frein TGV suffisamment proche du système réel tout en conservant une taille permettant d'effectuer certains calculs de référence sans réduction.
Description du système réel
Dans le chapitre précédent, nous avons étudié le comportement d'un système simple déstabilisé par frottement pour différentes configurations de fonctionnement et conditions initiales. Dans la section suivante, nous tenterons d'établir un modèle par éléments finis de ce système qui sera représentatif tout en restant de taille modeste : l'un des objectifs restants est de pouvoir décider de l'impact de la réduction comme suggéré dans le chapitre précédent sur un cas plus industriel.
Choix du modèle aux éléments finis de frein TGV
Modélisation du disque et de la cloche
De plus, les éléments choisis sont de type quadratique, pour mieux représenter le comportement modal du disque, sauf dans la zone de contact, où l'on applique une linéarisation de ces éléments pour pouvoir traiter le contact sur les efforts généralisés et les déplacements à les nœuds plutôt que de subir des pressions locales.
Modélisation de la garniture, du porte-garniture et de la timonerie
Deux zones sont prises en compte : d'une part le disque et la cloche, d'autre part l'équipage et les supports de trim. Le modèle éléments finis global ainsi obtenu présente un total de 72685 degrés de liberté, dont 49473 pour l'ensemble disque/cloche et 23212 pour les joints et porte-joints.

Recalage des paramètres sur FRF
On voit que la solution S1 reste assez proche des valeurs estimées à partir des plans, tandis que la solution S2 s'en écarte sensiblement pour certains paramètres. C'est le cas de la solution S2 en raison du fort contraste présent dans la matrice d'amortissement entre le disque et la gaine.
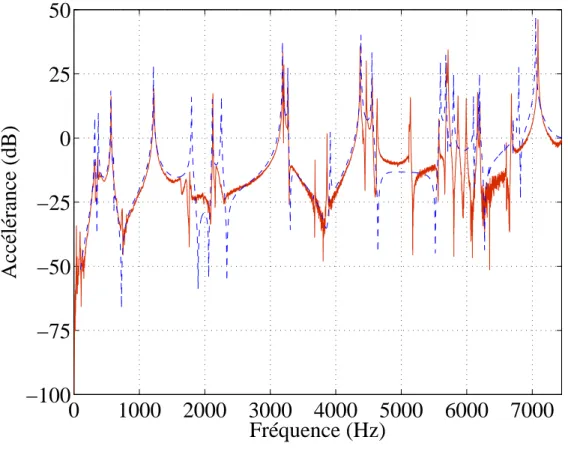
Simulations temporelles sur le modèle simplifié de frein TGV
Caractérisation de la stabilité du système
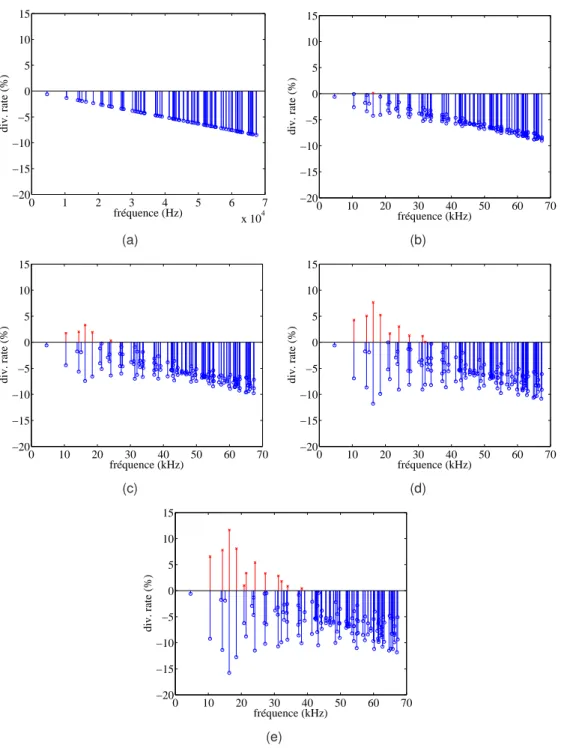
Nous comparerons ensuite la simulation réduite basée sur le type FCs1000 pour évaluer la capacité à réaliser des calculs réduits en utilisant la méthode Ritz pour simuler un système de grincement représentatif des freins des TGV. Ainsi, l'architecture même du système de freinage des TGV semble favoriser l'apparition de modes à très faible degré de divergence, ce qui rend difficile l'exploitation de l'analyse de stabilité et pose la question du comportement de ces modes dans les simulations temporelles.

Simulation temporelle sur le modèle de référence
Nous pouvons voir dans la section précédente 6.2.3 que la stabilité de la solution S2 montre également des modes stables avec une vitesse presque nulle. La figure 6.12 montre l'évolution de la vitesse normale sur le disque en un point correspondant au point de mesure vibrométrique lors des essais.
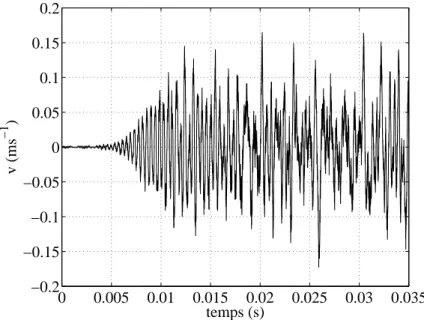
Accord entre simulation non-linéaire et analyse de stabilité
Les modes adjoints sont nécessaires pour obtenir la projection sur les modes complexes et correspondent aux modes propres du système avec les vecteurs à gauche des matrices. Malgré les limites mentionnées, la projection sur les états instables présentée dans la figure 6.15 peut être divisée en quatre phases.
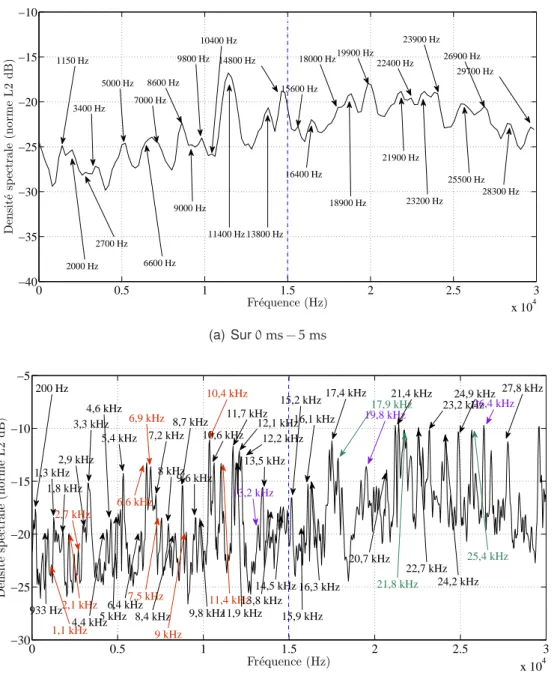
Choix des quantités observées
Comparaison avec l’expérience
Calcul sur base réduite pour le modèle de frein simplifié
Conclusions sur l’application au cas d’un frein simplifié
Perspectives
Objectifs à court terme
Objectifs à plus long terme
Problème de référence
Principe de l’algorithme
Stratégies d’utilisation
Matrices de ressemblances
Exemple d’utilisation
Cadre global
Optimisation des paramètres d’augmentation
Paramètres constants
Alternatives à ce choix de paramètres d’augmentation
Notations


![Figure 3.2 – Essais de Bergman et al. [7] – Mise en évidence d’un coefficient de frottement critique sur deux séries d’essais (a) et (b).](https://thumb-eu.123doks.com/thumbv2/1bibliocom/463510.69264/53.892.172.727.515.768/figure-essais-bergman-évidence-coefficient-frottement-critique-séries.webp)
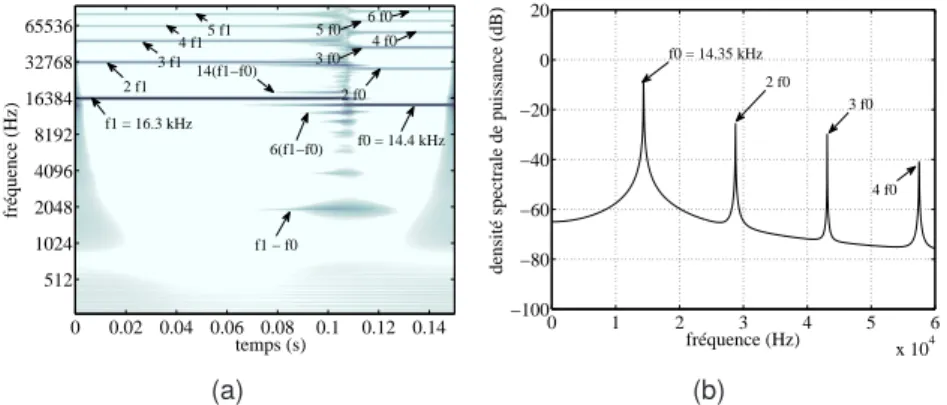
![Figure 5.27 – Cas 5_9S – CWT de la vitesse normale sur des sous intervalles – (a) t ∈ [0; 0, 02], (b) t ∈ [0, 02; 0, 06], (c) t ∈ [0, 06; 0, 14]](https://thumb-eu.123doks.com/thumbv2/1bibliocom/463510.69264/143.892.205.688.217.637/figure-27-cas-9s-cwt-vitesse-normale-intervalles.webp)