finis de Galerkin continus

Dans le deuxième chapitre, nous décrivons en détail le problème quasi-électrostatique et présentons quatre méthodes de résolution par éléments finis nodales. Pour le problème statique, détaillé au chapitre huit, nous étudions cinq méthodes de résolution par éléments finis nodales.

Introduction

L’´electrodynamique classique

Les ´equations de Maxwell

Champs et sources
Lois de comportement
Energie ´electromagn´etique
Conditions de transmission entre deux milieux mat´eriels
Condition aux limites en domaine born´e
Condition de radiation en domaine non-born´e
Effet de pointe

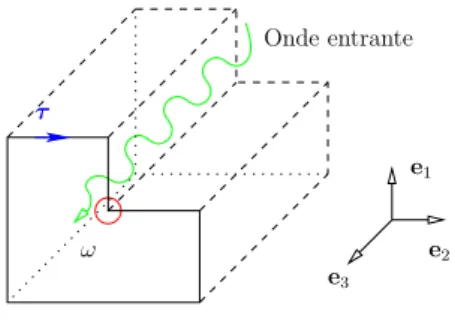
Dans le cas particulier, lorsque le milieu 2 est un conducteur parfait (on note alors Γ = ΓC), le champ. Le champ électromagnétique diffusé doit alors satisfaire à la condition de rayonnement Silver-Müller suivante [85].

Hypothèses mathématiques sur les données

Nous observons que le champ est plus grand à la surface de la plus petite sphère. A noter que la régularité du champ dépend entre autres de la présence de singularités.

Diff´erents mod`eles

Le mod`ele de Darwin
Les modèles quasi-électrostatique et quasi-magnétostatique
Les ´equations harmoniques
Contrˆolabilit´e
Equations instationnaires

Enfin, une analyse de la convergence des éléments finis pour ce modèle a été faite par P. Zou prouvant des estimations d'erreur pour la discrétisation en temps et en espace de (1.36) avec des éléments finis N´ed´elec.

M´ethodes de r´esolution

Diff´erences finies
Eléments finis de Nédélec
El´ements finis discontinus
El´ements finis ´ hp
M´ethodes spectrales
Obtention d’un domaine born´e

Dans [81] des estimations d'erreur sont prouvées pour la discrétisation spatiale de (1.36) avec des éléments finis N´ed´elec. Demkowicz décrit comment programmer cette méthode pour les éléments de frontière finis (voir aussi [60]).

La ligne microruban

Le filtre `a stubs

Notations relatives au domaine d’´etude

On appellera γi = A0i∪AΘi ∪Oi : les arêtes de l'angle de rentrée Oi et l'angle de rentrée Oi lui-même.

Op´erateurs bidimensionnels

Notations

Relations entre op´erateurs bidimensionnels

Espaces de Hilbert usuels et leurs normes associ´ees

Espaces des champs scalaires

L'équivalence entre la norme du graphe et la semi-norme dans H01(ω) due à l'inégalité de Poincaré. ΦN et ΦD sont les espaces solutions du Laplacien : ΦN =. l'inégalité de Poincaré-Friedrich pour ΦD ; Inégalité de Poincar´e-Wirtinger et théorème de Lax-Milgram pour ΦN).

Espaces de champs vectoriels

XE et XH sont les espaces de solutions des équations de Maxwell quasi-statiques : XE.

Espaces des traces

Espaces de Sobolev `a poids

Espaces de Sobolev classiques

Espaces duaux

Formules d’int´egration par parties classiques dans un ouvert

Formules de Green

G´en´eralisation des formules de Green

Cette méthode sera décrite en détail dans la section 2.3 pour le problème fédéré et dans la section 4.6 pour le problème discrétisé. C'est l'objet de la section 2.5 pour le problème fédéral et de la section 4.10 pour le problème discret.

Champ ´electrique 2D : d´ecomposition de Helmholtz

CL non-homog`enes
CL homog`enes
Le probl`eme aux potentiels, ` a la Grisvard
Le probl`eme aux potentiels, ` a la Nazarov-Plamenevsky

Proposition 2.13 ϕD , i et ϕN , sont décomposés en partie H2-régulière et partie singulière comme suit. Une décomposition partielle-singulière régulière est également possible pour les potentiels φD et φN, c'est-à-dire avec une condition aux limites inhomogène pour le problème de Neumann.

Champ ´electrique 2D : CL naturelles

Champ ´electrique 2D : le compl´ement singulier

Introduction
La λ-approche
Simplification du calcul de λ
Le compl´ement singulier orthogonal
Autres d´ecompositions conformes
R´egularit´e dans les espaces singuliers conformes
Conclusions sur la m´ethode du compl´ement singulier

Nous allons montrer que l'on peut simplifier le calcul de λ grâce à l'hypothèse que e disparaît près de l'angle réentrant. Il existe un lift régulier de ee ∈ H1(ω), tel que nous avons la formule d’intégration suivante.

Champ électrique 2D : la régularisation à poids

Condition pour obtenir la coercivit´e
Condition pour obtenir la densité des éléments finis
Choix du poids
Cas o` u il existe plusieurs coins rentrants

Théorème 2.56 Lorsque l'injection de X dans L2(ω) est compacte, la norme du graphe dans X est équivalente à la semi-norme. D'après la proposition 2.58, l'injection compacte de V dans H−1(ω) permet d'obtenir l'injection compacte de W dans L2(ω), et donc, d'après la proposition 2.56, AX est impératif.

Milieux inhomog`enes

Supposons que ε soit constant par morceaux : ω est composé de J sous-domaines ω1, .., ωJ tels que ε(x) =εj >0 dans ωj. Si les interfaces présentent des angles réentrants, le champ électromagnétique est singulier au voisinage de ces points singuliers.

Conclusion

Lorsque nous voulons résoudre le problème dépendant du temps, nous devons garder la relation ∂tρ + divJ = 0. Dans la perspective de traiter le problème dépendant du temps, nous introduirons un typificateur mul-Lagrange sur la divergence de E en variation de la formulation du problème.

Formulation mixte 2D : CL naturelles

Nous allons montrer que la propriété 3.1 est vérifiée pour les espaces considérés, puis que la formulation mixte est équivalente à la formulation variation, c'est-à-dire p = 0 dans l'espace Q.

Formulation mixte 2D : MCSO

Formulation mixte 2D : r´egularisation `a poids

Discrétisation par les éléments finis de Galerkin continus

L’approximation de Galerkin

En général, V est un espace de Sobolev dans lequel les fonctions régulières sont condensées.

Les ´el´ements finis de Lagrange continus d’ordre k

Discr´etisation du domaine d’´etude

Il y a donc trois degrés de liberté par triangle. euh est entièrement déterminé par ses valeurs aux sommets des triangles Tl. Les points de discrétisation du maillage sont les sommets des triangles et le milieu des arêtes des triangles.

D´ecomposition de Helmholtz : discr´etisation

Le Laplacien avec CL de Dirichlet

Dans la suite de cette partie nous nous intéressons uniquement à la discrétisation du problème quasi-électrostatique. Pour le problème quasi-magnétostatique, tout se passe de manière similaire, en remplaçant τ par ν pour les conditions aux limites.

Le Laplacien avec CL de Neumann

Considérons la matrice MD ∈RN×N appelée matrice de masse interne, la matrice des éléments : Mi , j. Enfin, considérons BN ∈ RN×N, appelée matrice de masse limite la matrice des éléments : Bi , j.

D´erivation du champ ´electrique

Calcul des singularit´es du Laplacien

Singularit´es duales : CL de Dirichlet
Singularit´es duales : CL de Neumann
Coefficients des singularit´es duales
Coefficients des singularit´es primales

L'intégrale sur ω\ωR est approchée par un schéma d'intégration numérique (voir section 15.2.1). Cette approximation sera calculée au moyen d'un schéma d'intégration numérique en sept points (Section 15.2.1).

Calcul des singularités électromagnétiques

Singularit´es primales : CL de Dirichlet

Singularit´es primales : CL de Neumann

M´ethode avec CL naturelles : discr´etisation

Matrice de raideur interne

Matrice de masse du bord

Second membre

Elimination des CL essentielles

Discr´etisation de l’espace avec CL essentielles

Matrice de raideur interne

Ces sous-blocs agissent sur les vecteurs de R2 décomposés en base locale (τj, νj) : Eh(Mj). Nous ne décrirons pas en détail les calculs des éléments de Aa , a etc., car ils sont similaires aux calculs de.

Second membre

Champ électrique : partie régulière

Une fois Ee calculé, l’approximation calculée aux arêtes dans la base canonique (e1,e2) peut être écrite. Pour rendre la matrice inversible, on impose que (COT . l )2,2 = 1, puis on multiplie à droite par Ol pour revenir à la base canonique.

Rel`evement de la CL

Compl´ement singulier orthogonal : discr´etisation

Champ électrique : partie régulière

Pour calculer xSl, h par la méthode λ, il suffit de procéder comme expliqué ci-dessus en prenant simplement : fh = sN, l, h et sD, l, h.

Champ ´electrique : partie singuli`ere

Conclusion

Régularisation à poids : discrétisation

Analyse d’erreur

M´ethode avec CL naturelles : convergence
M´ethode du compl´ement singulier : convergence
R´egularisation `a poids : convergence
Conclusion

Pour prouver le théorème 4.17 ci-dessous, obtenu par l'astuce d'Aubin-Nitsche, nous avons besoin du lemme suivant, prouvé dans la section 14.4 de la partie IV. Définition 5.1 On parle d'élément fini de Taylor-Hood P2-P1 lorsque le multiplicateur de Lagrange et le champ électrique sont évalués sur la même grille, où le multiplicateur de Lagrange est approché par éléments finis de Lagrange continus sur P1 et le champ électrique est approché en composantes- sous-composante par éléments finis de Lagrange continus sur P2.

Condition inf-sup discr`ete

M´ethode avec CL naturelles

M´ethode avec CL essentielles

R´egularisation `a poids

M´ethode avec CL naturelles mixte : discr´etisation

Matrice mixte

Pour chaque triangle Tl il faut donc calculer les fonctions de base P1, notées ui1 et les fonctions de base P2, notées vj.

Second membre

Compl´ement singulier orthogonal mixte : discr´etisation

Matrices mixtes

Second membre

Régularisation à poids mixte : discrétisation

Matrices mixtes

Second membre

Analyse d’erreur

Optimalit´e de l’algorithme d’Uzawa

Eφ, approximation du champ électrique calculée à partir des potentiels φD et φN, -Enat, approximation du champ électrique calculée en XE,. Eλ, une approximation du champ électrique calculé par l'approche λ, et λh, une approximation de λ, -E⊥, une approximation du champ électrique calculé dans X0E, R,.

Tab. 6.1 – Caract´eristiques des maillages.

Calcul direct

Cas r´egulier

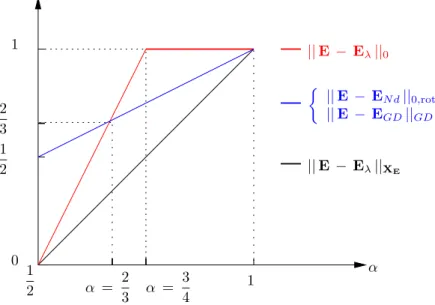
Dans le tableau 6.2 nous avons représenté à gauche les erreurs en norme L2(Ω) et à droite les taux de convergence pour ces erreurs. Dans le tableau 6.3 nous avons représenté à gauche les erreurs dans normX et à droite les taux de convergence pour ces erreurs.

Premier cas singulier

Tab. 6.5 – Cas singulier 1 : Erreurs L 2 (ω) et taux de convergence.

Second cas singulier

Utilisation du multiplicateur de Lagrange

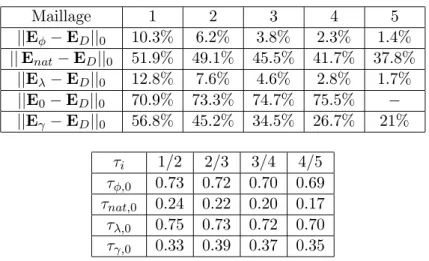
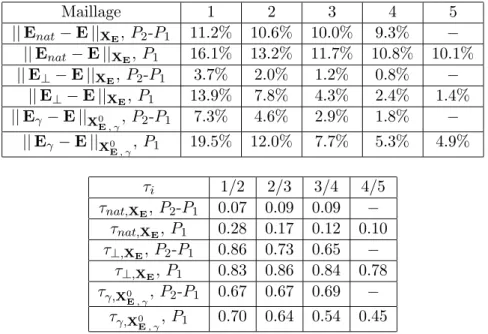
Dans le tableau 6.13 nous donnons le nombre d'itérations et le nombre de conditionnement de M−1CA−1CT, où M est la matrice de masse exacte. Dans le tableau 6.14 nous donnons le nombre d'itérations et le nombre de conditionnement de e.

Tab. 6.11 – Probl`eme mixte : Erreurs X et taux de convergence.

Allure du champ quasi-´electrostatique

Conclusions

Op´erateurs tridimensionnels

Espaces de Hilbert usuels et leurs normes associ´ees

Espaces de champs scalaires

L'équivalence entre la norme du graphe et la semi-norme dans H01(Ω) est due à l'inégalité de Poincaré. ΦN et ΦD sont les espaces solutions du Laplace : . Inégalité de Poincar'e-Friedrichs pour ΦD et inégalité de Poincar'e-Wirtinger et théorème de Lax-Milgram pour ΦN).

Espaces de champs vectoriels

Espaces des traces

Espaces `a poids

Formules d’int´egration par parties classiques dans un ouvert

Formules de Green

G´en´eralisation des formules de Green

Espaces fonctionnels du probl`eme en temps

D'autre part, on a la relation de compatibilité suivante entre e et f (propriété Définitions 8.2. On appelle norme du graphe (ou norme naturelle) de XE la grandeur suivante. Comme l'injection de XE dans L2 (Ω) est compacte, il existe une sous-suite de (vn)n∈N∗, que l’on assimile à (vn)n∈N∗, qui converge fortement dans L2(Ω) vers v.

Champ ´electrostatique 3D

Cette méthode sera décrite en détail dans les sections 8.3 (problème continu) et 10.3 (problème discret). E0 peut également être calculé avec les éléments finis lagrangiens continus Pk dans XE0 si Ω est convexe : voir sections 8.4 (Problème continu) et 10.4 (Problème discret).

Champ ´electrique 3D : CL naturelles

D'autre part, le problème peut être résolu numériquement en utilisant les éléments finis de Lagrange Pk continu, en calculant E directement dans XE. Lorsque Ω n’est pas convexe, le calcul de E0 par les éléments finis de Lagrange continus dans XE0 ne converge pas car on ne capte pas les parties singulières du champ électrique.

Champ ´electrique 3D : CL essentielles

Champ électrique 3D : régularisation à poids

Le choix optimal de γ pour lequel on a l'injection compacte de L2(Ω) dans XE0, γ et la densité de fonctions H1-régulières dans XE0, γ est donc. XE0, γ∩ H1(Ω) est alors dense dans XE0, γ, on peut donc approximer la solution de (8.17) par les éléments finis de Lagrange continus Pk.

Introduction

De même, les données du problème sont décomposées en séries de Fourier. Comme f.ν|Γz = 0, nous décomposons la série f.zen de sinus le long de la direction z, et f en série de cosinus dans le plan (ex, ey).

Cas prismatique : CL essentielles

Champ électrique 2D12 : le complément singulier 175 On obtient ainsi des systèmes d'équations découplées en ( (Eb0, k,ck), E0z, k), qui facilitent la résolution. On peut choisir d'écrire un système linéaire en dimension trois ou deux systèmes linéaires, l'un en dimension deux (voir le calcul discret du champ électrique bidimensionnel au paragraphe 10.6.1), et l'autre en dimension un (voir le calcul discret du champ électrique scalaire Ez au paragraphe 10.6.3).

Cas prismatique : CL presque essentielles

Pour k = 0, le système d'équations (Eb0, k, ck) est également déconnecté car la décomposition choisie de X0E est orthogonale. Pour k = 0, le système d'équations (Eb0, k, ck) n'est pas déconnecté car la décomposition choisie de XAE n'est pas orthogonale.

Formulation mixte 3D : CL naturelles

Les preuves de la condition inf-sup sont les mêmes que dans le cas bidimensionnel. La condition inf-sup est remplie, le problème est donc bien posé et permet une solution unique.

Formulation mixte 3D : CL essentielles

La condition inf-sup sur ce multiplicateur de Lagrange supplémentaire est satisfaite pour l'induction magnétique mais pas pour le champ électrique [36].

Formulation mixte 3D : r´egularisation `a poids

Le Laplacien avec CL de Dirichlet

Elle est résolue en pratique dans RN : on procède à une pseudo-élimination des degrés de liberté associés à la frontière ∂Ω, en modifiant ensuite le système linéaire (10.3) du fa ¸con. Considérons la matrice M0 ∈RN×N, appelée matrice de masse interne, la matrice des éléments : Mi , j.

D´erivation du champ ´electrique

M´ethode avec CL naturelles : discr´etisation

Matrice de raideur interne

Matrice de masse du bord

Second membre

M´ethode avec CL essentielles : discr´etisation

Champ ´electrique

Tout se passe comme dans le cas bidimensionnel (voir section 4.7 et paragraphe 4.7.1), on se contente donc de donner les éléments de la matrice, sans détailler la discrétisation. Nous montrons de la même manière qu'à la section 4.7.1 que les équations (10.13) peuvent être réécrites sous la forme du système matriciel suivant.

Rel`evement de la CL

Régularisation à poids : discrétisation

31, 32], le champ électrique est moins singulier dans la direction des bords rentrants que perpendiculairement à ces directions. Dans [32] les auteurs étudient la convergence d'éléments limites finis sur un maillage anisotrope pour un problème harmonique.

Cas prismatique : discr´etisation

Champ ´electrique transverse : CL essentielles

Ainsi, on peut imaginer utiliser des éléments finis anisotropes, c'est-à-dire qu'en dehors d'un voisinage d'angles réentrants, les arêtes des tétraèdres parallèles aux arêtes de Ω sont plus longues que les autres. Pour le calcul des coefficients diagonaux, le calcul de (xSl , h, xSl , h)0,ω se décompose de la même manière que pour le calcul de βl , l, expliqué dans la section 4.4.3.

Champ ´electrique transverse : CL presque essentielles

Nous limitons l’ensemble d’index Ic à Ic0 = Ic\IAC, puis complétons l’ensemble d’index Ia à Ia∪IAC. Ensuite, nous complétons l'ensemble des indices Iω, à Io= Iω∪IA, et limitons l'ensemble des indices Ia∪IAC à Ia0 := (Ia\IA)∪IAC.

Champ ´electrique longitudinal

M´ethode avec CL naturelles mixte : discr´etisation

M´ethode avec CL essentielles mixte : discr´etisation

Régularisation à poids mixte : discrétisation

Cas prismatique mixte : discr´etisation

CL essentielles

CL presque essentielles

Champ ´electrique : formulations variationnelles

Introduction

Formulation variationnelle classique

Formulation variationnelle augment´ee

Formulation variationnelle augment´ee mixte

Existence d’une fronti`ere artificielle

Champ magn´etique : formulation variationnelle

Semi-discr´etisation en temps

Discr´etisation compl`ete

Formation des second-membres

Champ ´electromagn´etique

Pr´esentation du code de calcul

Méthode de régularisation à poids

Introduction

Conclusions sur les m´ethodes utilis´es

Cas d’un unique coin rentrant

Cas de plusieurs coins rentrants

Simplification du calcul de λ

Preuve du lemme 2.37

Int´egration num´erique 2D

Schémas d’intégration numérique intérieure

Schémas d’intégration numérique sur la frontière

Schémas d’intégration numérique 3D

Algorithme du gradient conjugu´e

Gradient conjugué non-préconditionné

Gradient conjugué préconditionné

R´eduction de la matrice de masse

Cas g´en´eral

Triangulation ou tétraèdrisation régulière et quasi-uniforme

Réduction de la matrice de masse pondérée en 2D

Triangles int´erieurs

Triangles touchant le coin rentrant

Matrice ´equivalente

Introduction

Le probl`eme direct

Le probl`eme quasi-magn´etostatique 3D

Introduction

Le probl`eme direct

Champ quasi-magn´etostatique : discr´etisation 3D

M´ethode avec CL naturelles

M´ethode avec CL essentielles

Rappel des espaces fonctionnels et des formes bilin´eaires 3D