De nombreux outils utilisés dans ce domaine font partie du contrôle géométrique. Il ne s'agit donc que d'une étude préliminaire avant l'application d'outils de gestion optimaux.
Introduction
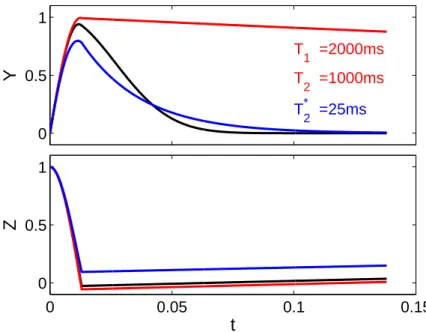
En résumé, selon la valeur de la fonction de commutation, la commande prend la forme Le champ de contrôle devient trop grand vers la fin pour s'approcher de la cible. 6.1 : (Haut) Evolution du coût terminal Φt en fonction de la durée de contrôle tf.
Ce type de contrôle n’est pas réalisable en considérant uniquement la dérivée première. L’utilisation de la dérivée seconde explique la qualification de contrôle local généralisé. Notez que ces lignes correspondent aux lignes singulières du problème de contrôle optimal de la section (3.3).

Outils de contrˆ ole optimal
Introduction
Contrˆ olabilit´e des syst`emes quantiques
En l’absence d’effets dissipatifs, l’évolution du système est uniforme et l’opérateur densité contrôle. 2.4) Cette notion de contrôlabilité peut être liée au groupe et à l'algèbre de Lie du système.
D´efinition d’un probl`eme de contrˆ ole optimal
Enfin, la fonction f0(x(t), u(t)) est un coût dépendant du chemin qui peut, par exemple, décrire l'énergie utilisée pour contrôler le système. Notons que cette définition du problème de contrôle optimal est très générale et ne dépend pas de la forme du coût considéré ni de la dynamique du système.
Contrˆ ole g´eom´etrique
- Introduction au Principe du maximum de Pontryagin
- Contrˆ ole en temps optimal d’un syst`eme sur R 2
- M´ethode de tir
- M´ethode d’homotopie
Dans ce cas, le contrôle u ne peut pas être déterminé directement à partir de la fonction Φ. Le lieu de colinéarité correspond donc à l'ensemble des points fixes de la dynamique, tel que m∈R.
M´ethodes num´eriques
- Algorithme monotone
- Algorithme GRAPE
Lorsque le paramètre λ est petit, la précision de l'algorithme est privilégiée et des intensités de champ de contrôle significatives peuvent être obtenues car l'énergie est peu pénalisée. Il suffit alors de choisir la meilleure valeur de α pour accélérer la convergence de l'algorithme.
Comparaison des algorithmes de type monotones et de type gradient
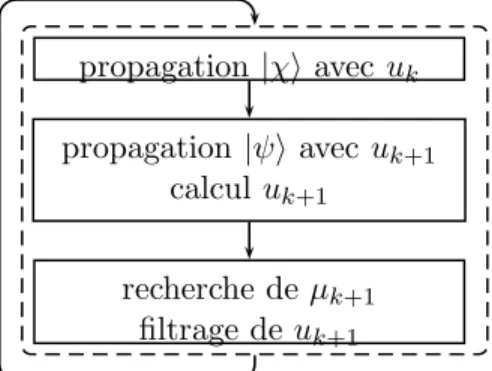
Une fois l’algorithme initialisé par un champ de test, l’état conjoint et l’état du système sont propagés respectivement vers l’arrière et vers l’avant. A chaque étape, nous recalculons les propagations aller et retour de l'état du système |ψ(t)ie et de l'état d'agrégation |χ(t)i avec le nouveau contrôle.
Diff´erence qualitative entre le tir et les m´ethodes it´eratives
Les résultats théoriques de la stratégie de contrôle bi-impulsion sont très encourageants. Dans la figure (5.9) la forme du champ de contrôle, le développement de la projection et les informations de Fisher sont présentés.

Contrˆ ole optimal en R´ esonance Magn´ etique Nucl´ eaire
Introduction
Dans ce chapitre, nous présenterons une application de contrôle optimal de la dynamique de spin en résonance magnétique nucléaire (RMN) et en imagerie par résonance magnétique nucléaire (IRM). Nous utiliserons à la fois des techniques de contrôle géométrique optimal pour les systèmes dimensionnels plus petits et des algorithmes numériques tels que Grapevine pour les systèmes plus complexes.
Dynamique des spins en r´esonance magn´etique nucl´eaire
- Construction du Mod`ele
- Effet de la temp´erature
- Principe de la RMN
- Principe de l’IRM
- Normalisation de l’´equation de Bloch
- Effet de l’inhomog´en´eit´e des champs magn´etiques
- Effet du radiation damping
Le problème le plus important réside dans la mesure libre de la magnétisation. L'aimantation microscopique M~(x, y) de l'échantillon (bleu) induira un champ magnétique et le flux de ce champ magnétique à travers les spires de la bobine de mesure (rouge) induira un courant électrique mesurable.

Contrˆ ole en temps minimum
- Introduction
- Contrˆ ole optimal g´eom´etrique
- Construction de la synth`ese optimale
- Saturation d’un spin 1/2
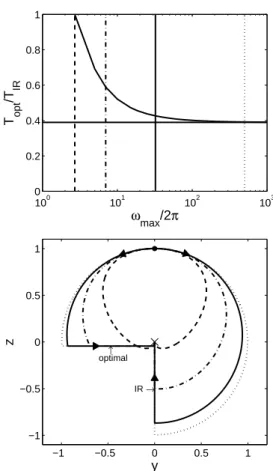
En effet, la singularité est localement optimale, elle ne doit donc pas être exclue de la synthèse. Le premier cas est celui où un seul point de l’unité horizontale appartient à la communauté.

Rˆ ole de l’effet de radiation damping
- Cas k > 0 et point fixe simple
- Cas k < 0 et point fixe triple
Regardons maintenant l'influence de la non-linéarité sur la position des points fixes. Il est à noter que dans cette synthèse l’usage du singulier est obligatoire.

Optimisation du contraste en IRM
- Introduction
- Contrˆ ole g´eom´etrique du contraste
- R´esultat num´erique du probl`eme de contraste
- Construction de la solution BSBS
- Impl´ementation exp´erimentale
- Conclusion
La position de la molécule est décrite uniquement par les données de l'axe Z. La figure ci-dessous représente l'évolution de la projection sur l'état cible au cours de la séquence de contrôle.
Contrˆ ole optimal de la rotation mol´ eculaire par champ laser
Introduction
Le chapitre débutera par un rappel du modèle qui décrit la rotation moléculaire ainsi que l'interaction avec le laser. La stratégie de contrôle obtenue pour délocaliser les molécules a été utilisée expérimentalement à Dijon par le groupe d'O.
Contexte du contrˆ ole mol´eculaire
La première vérification expérimentale de l'alignement post-impulsion a été réalisée par Vrakking [54]. On en déduit que c'est l'enveloppe de l'impulsion qui permet de contrôler la rotation.
Mod`ele physique
- Dynamique libre de la rotation des mol´ecules
- Interaction du rotateur rigide avec un champ ´electrique
La répartition des charges électroniques autour de la molécule sera alors inhomogène et anisotrope. L’interaction avec le champ s’écrit alors : avec −→µ le moment dipolaire électrique de la molécule.

Algorithme monotone avec contraintes spectrales
- Description de l’algorithme
- Application ` a temp´erature nulle
- Application au cas du pulse-shaping
L'avant-dernière ligne représente l'évolution de la projection au carré de l'état du système sur l'état cible. On peut voir que le transfert de l’état de base vers l’état cible s’effectue par mise à l’échelle.
D´elocalisation planaire
- Construction de l’´etat d’alignement planaire
- Contrˆ ole optimal de l’alignement planaire
- D´elocalisation planaire : Exp´erience
Le troisième exemple est dessiné juste après l'action de la deuxième impulsion le long de y. En partie basse, on voit que la délocalisation de la molécule se produit réellement pour τ > Tper.

Roues dent´ees quantiques
- Construction de l’´etat roue dent´ee
- Strat´egies de contrˆ ole
- Extension au cas des mol´ecules sym´etriques et asym´etriques
Le nombre de lobes est alors égal à (2j-n) et le signe permet encore de contrôler le sens de rotation de la roue. En revanche, la figure (4.15)(en bas) représente l'évolution de la densité de probabilité angulaire d'un état de roue.

Conclusion
Ce chapitre vise à appliquer les techniques de contrôle optimal (géométrique et numérique). 5.9:(Haut) Evolution du champ de contrôle ω obtenu à l'aide d'un algorithme monotone initialisé par la solution géométrique.
Contrˆ ole optimal des condensats de Bose-Einstein
Introduction
Après un bref rappel du modèle utilisé, nous utiliserons le contrôle géométrique dans un modèle semi-classique s'appliquant à un grand nombre de particules, puis des algorithmes monotones au début d'un système quantique. L'objectif des deux contrôles sera de créer ce que l'on appelle l'état du chat de Schrödinger en un temps minimum pour le contrôle géométrique ou en un temps fixe et en énergie minimale pour le contrôle avec des algorithmes numériques.
Introduction du mod`ele
- Mod`ele quantique
- Mod`ele semi-classique
- Information de Fisher
L'état du système à l'équilibre correspond généralement à une superposition des états propres de la base de Fock. Du point de vue semi-classique, l'état du système est assimilé à ces coordonnées en un point.

Contrˆ ole optimal d’une superposition quantique macroscopique
- Contrˆ ole optimal g´eom´etrique
- Contrˆ ole optimal par algorithme num´erique
La forme du champ de contrôle obtenu est visible sur la figure (5.8) ainsi que les voies associées. Le paramètre représente le rapport entre la durée du contrôle et le temps minimum Tc.
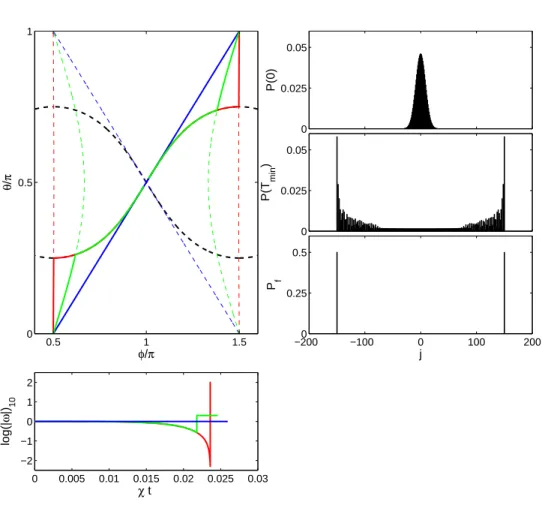
Discussion
En bas à droite) Evolution de l'énergie de commande en fonction de la durée en traits pleins et évolution du produit énergie temps de commande. A l’inverse lorsque le temps de contrôle diminue et tend vers la valeur de temps minimum alors

Comparaison du contrˆ ole optimal g´ eom´ etrique avec d’autres m´ ethodes de contrˆ ole
Comparaison des m´ethodes de contrˆ ole optimal g´eom´etrique et num´erique
- Cas du temps minimum
- Cas de l’´energie minimum
- Conclusion
Sur la figure (6.2), on voit que lorsque le temps de contrôle augmente, l'énergie diminue et tend vers une valeur fixe. L'énergie unitaire verticale est nulle car la commande unitaire associée est également nulle.

Comparaison avec le contrˆ ole local
- Introduction au contrˆ ole local
- Comparaison des m´ethodes de contrˆ ole optimal et local
- Conclusion
Le contrôle local utilise la dérivée temporelle d'un observateur correctement choisi pour l'entrée. Mais le contrôle local essaie d'augmenter V le plus rapidement possible (car il s'ensuit qu'il essaie d'augmenter la courbure de ¨V). Une autre comparaison est faite entre la méthode de guidage local généralisé et le guidage géométrique.
Une évolution dans ce sens serait très bénéfique dans le contexte du contrôle quantique.

Conclusion
Annexe
D´etermination des points fixes de l’´equation de Bloch non-lin´eaire
Nous étudions dans cette section les points fixes de l'équation de Bloch non linéaire (voir section 3.4). Notez que si = pm alors les deux points fixes supplémentaires sont dégénérés, et si υ = 0 alors il n'y a qu'un seul point fixe.
Construction de la synth`ese optimale dans le cas non-lin´eaire
Rechercher la ligne de liaison (trajectoire BB(t01, t02), c'est à dire trajectoires de type AGH). On choisit t03 comme paramètre de continuation (variation de t3 à 0) et on utilise la fonction de prise de vue suivante.

Fonction de tir du probl`eme du contraste
- L´egende
- Fonction de tir en temps libre
- Fonction de tir en temps fixe
On choisit t4 comme paramètre de continuation (début de t2) et on utilise la fonction de tir suivante paramétrée part4. Le but de cette fonction d'enregistrement est de résoudre le problème du chapitre (3).
Split-Operator
Approximation de Galerkin
La dynamique du système peut alors simplement se séparer en deux équations différentielles couplées. L'approximation de Galerkin consiste à négliger le terme |ψQi dans la dynamique du système tronqué.
On peut aussi exprimer le terme croisé cosθxcosθy : cosθxcosθy = 1. Les carrés des opérateurs cosinus directeurs ne relient pas les espaces symétriques pairs et impairs. Il est important de noter que dans l’espace de Hilbert complet, les opérateurs cosθx et cosθy.
En revanche, dans une base de dimension finie (en projetant l'espace de Hilbert sur un sous-espace délimité par une valeur j=jm), ils ne commutent plus. Remarque : Notez ici que nous avons les relations entre passages pour diviser l'espace {j, m} en huit sous-espaces.
Dans la formule ci-dessus, la somme sur ν est faite pour toutes les valeurs de ν de sorte que chaque factorielle soit fonction d'un entier strictement positif. A partir de la formule (8.36) on peut évaluer l'expression des matrices de Wigner dans la base |J, K, Mi.
Expression des op´erateurs de moment angulaire dans la base de Wigner
Monotonically convergent optimal control theory of quantum systems under a nonlinear interaction with the control field. Monotonically convergent optimal control theory of quantum systems with spectral constraints on the control field.
Expression de quelques matrices D m,k 1
Expression des carr´es des cosinus directeurs
Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. Sub-Riemannian geometry and time optimal control of three spin systems: Quantum gates and coherence transfer.