Je lui suis particulièrement reconnaissant de m'avoir confié un sujet de recherche qui, de par son originalité, m'a passionné à la frontière entre mécanique, acoustique et instruments de musique, et par sa portée, à la fois théorique et expérimentale. Je remercie également sincèrement François Ollivier pour son temps et son intérêt pour le Gong.
Les cymbales et les gongs
G´eom´etrie, utilisation
La première famille comprend des timbres très épais par rapport à leur diamètre (environ 4 mm pour un diamètre extérieur de 600 mm par exemple). Ces timbres, de même diamètre, présentent une rigidité moindre que celle des timbres de la première famille.
Fabrication
Cadre de la pr´esente ´etude
- Acoustique instrumentale et mod`eles physiques
- Vibrations non-lin´eaires de cymbales et de gongs
- Mod´elisation
- Organisation du manuscrit
Les phénomènes d'origine non linéaire impliqués dans ces instruments se manifestent sous différentes formes. Cela permet notamment d'identifier des interprétations physiques des phénomènes non linéaires observés dans les structures continues.
Analyse modale exp´erimentale
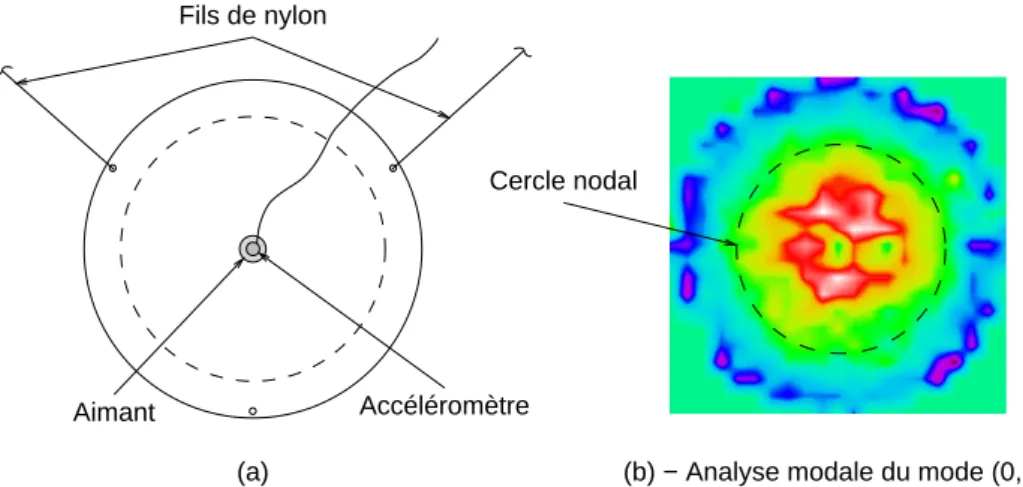
Les propriétés de symétrie produisent des valeurs propres de multiple 2, qui correspondent aux fréquences des modes asymétriques [67]. Dans le cas d'une structure présentant des défauts de symétrie, comme un timbre, les fréquences des configurations privilégiées sont doublées et les formes modales ne sont plus les mêmes, rendues identiques par rotation.
Analyse en r´egime libre
Analyse en r´egime forc´e
- D´etails exp´erimentaux
- Vibrations unimodale
- Route vers le chaos
- Examen de quelques couplages
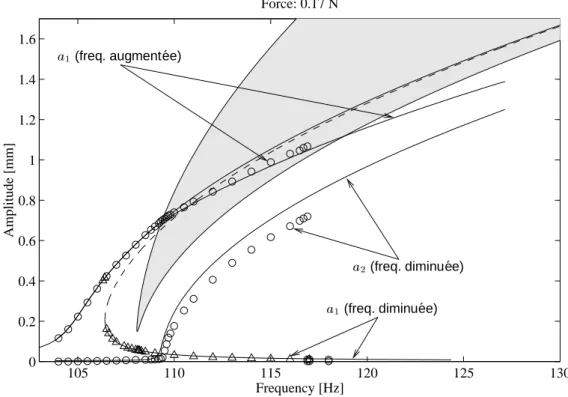
Dans le cas d'un oscillateur linéaire, la fréquence d'oscillation du système à l'état libre ne dépend pas de l'amplitude des oscillations. Fréquence d'excitation [Hz] Fréquences en combinaisons Les fréquences propres de résonance mesurées [Hz] correspondent à [Hz].
Conclusion
Premièrement, même si les hypothèses nécessaires à l'établissement des équations sont précisées dans les travaux d'Hermann, le domaine de validité de la théorie ne semble pas clair. Les développements mathématiques sont effectués sur la base des équations de la mécanique des milieux continus en grandes transformations.
Etablissement des ´equations non-lin´eaires de plaque
- Notations
- La transformation
- Les d´eformations
- Les contraintes
Nous supposons que le déplacement transversal est de l’ordre de grandeur de l’épaisseur de la plaque. Ces équations étant linéaires, l’évolution des contraintes planes le long de l’épaisseur de la plaque est la même que celle des déformations planes (Eq.
Formulation non-lin´eaire du probl`eme de vibration de plaque
- R´ecapitulatif : formulation en efforts
- Formulation en d´eplacement
- Fonction de force et conditions de compatibilit´e
- Formulation mixte
- Conditions aux limites
L'expression de ces conditions aux limites dans les cas simples classiques est résumée dans le tableau 3.1. D’autres conditions préalables sont théoriquement envisageables, mais ne se vérifient pas dans la pratique13.
Discussion
- Non-lin´earit´es et domaine de validit´e
- Validation math´ematique des hypoth`eses
- Mod`eles d’ordre sup´erieur
- Projection sur les modes propres lin´eaires
- Modes normaux non-lin´eaires
Le problème spatial peut être résolu en développant la solution sur les modes propres du système. Ces approximations dépassent le cadre de cette étude, car les amplitudes de vibration de la plaque que nous étudions restent de l'ordre de grandeur de son épaisseur.
Formulation du probl`eme
Amortissement
Formulation adimensionn´ee des ´equations
Dans le cas de conditions aux limites libres, les forces sont fixées à zéro au bord, qui est ici une courbe sans points de coin, donc les conditions aux limites sont (Eq.
Modes de vibration
Fr´equences et d´eform´ees
Les valeurs e>calculées à partir d'une solution numérique de l'équation précédente avec MATLAB5 et les formes modales correspondantes sont spécifiées dans la Figure 4.1, For. Les valeurs calculées avec la résolution numérique de l'équation précédente avec MATLAB6, similaires à celles présentées dans [58], et les formes modales correspondantes, sont présentées dans la figure 4.2.
Orthogonalit´e
Cette dernière proposition montre que si le problème des valeurs propres est auto-adjoint, alors les valeurs propres distinctes ont leurs fonctions propres orthogonales correspondantes pour les formes bilinéaires F A et F A. Lorsque les valeurs propres sont multiples, les fonctions Les états corrects correspondants sont orthogonaux par rapport aux autres États, mais en général ils ne sont pas orthogonaux les uns aux autres.
Projection modale
- Fonction de force
- D´eplacement transversal
- Discussion
- Relations de r´esonances
- Cadre de notre ´etude
On peut noter que les équations décrivant les vibrations transversales de la plaque n'ont qu'une non-linéarité cubique. Le nombre de modes en combinaison avec la résonance est donc limité par l'ordre des non-linéarités : dans le cas de la plaque au maximum 3 modes (et donc au maximum 4 avec résonance interne, avec = ) [74] .
Vibrations de flexion axisym´etriques
Solution perturbative en r´egime forc´e
C'est l'origine des phénomènes de saut associés au comportement d'hystérésis lorsque l'on change lentement la fréquence d'excitation à amplitude d'excitation constante. D'un point de vue physique, pour une carte donnée, seule la figure 5.3 à gauche a une signification, puisque c'est le seul paramètre modifiable # et chargé pour chaque mod.
Solution perturbative en r´egime libre conservatif
5.4 – « Courbes de squelette » pour les deux premiers modes axisymétriques de la dalle, avec ou sans effets du second ordre. Les remarques précédentes sont valables, à condition que l'amortissement soit très faible, car le calcul de la solution en régime libre a été effectué à partir de l'équation (5.22), qui est conservatrice.
Vibrations de flexion asym´etriques
- Influence de l´eg`eres imperfections de la plaque
- Couplage non-lin´eaire entre les deux configurations pr´ef´erentielles
- Influence des param`etres
- Solution g´en´erale - Ondes progressives
Et en fonction de 4, est décrite par la courbe de résonance de la figure 5.2, également représentée sur la figure 5.6. Les deux configurations sont toujours très proches de la quadrature du fait du très faible amortissement (5.3.2)).
Effets non-lin´eaires de membrane
Mode axisym´etrique
Dans notre cas, l'importance des non-linéarités dépend de la valeur de l'amplitude du mouvement, que l'on note. Si le système est celui de la figure de droite, le comportement n'est plus symétrique.
Mode asym´etrique
Vibrations de membrane en r´egime coupl´e
Lorsque, cette fois et est non nul, on montre que parmi les coefficients qui interviennent, seuls ceux où +.
Conclusion
Le signal d'excitation est choisi sinusoïdal, de fréquence proche d'une fréquence propre de la plaque. Les vibrations sont mesurées avec des accéléromètres, qui donnent l'accélération locale de la plaque, à l'endroit où elle est bloquée.

Mode axisym´etrique
6.3 – Adaptation du modèle aux expériences pour deux amplitudes d'excitation différentes ; LE.
Couplage non-lin´eaire entre les deux configurations pr´ef´erentielles
Configurations pr´ef´erentielles
Les variations de position des rayons nodaux et les fréquences propres des configurations préférées ont fait l'objet d'une étude minutieuse dans [121]. La configuration de la plaque est celle de la figure 6.4(a), avec les fréquences propres de la dernière ligne du tableau 6.3.
Mod`ele th´eorique avec ¾ non nul
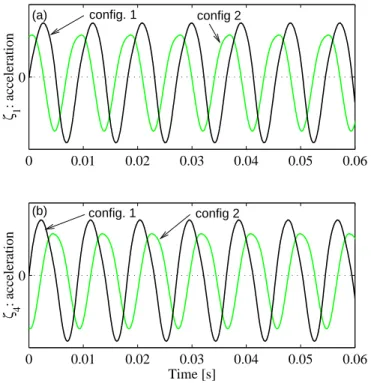
La réponse en oscillations libres du système de la figure 7.8 est constituée d'un terme qui oscille à la fréquence fondamentale !, fonction et proche de !, des harmoniques de fréquence !, ! et d'un terme constant. Si le système est celui de la figure de gauche, il a un comportement symétrique par rapport à
Recalage du mod`ele
Cas d’un d´esaccord n´egatif entre les pulsations propres
Un peu de th´eorie
La figure 6.13, à comparer avec la figure 6.5, montre en outre qu'il existe des valeurs de 4 pour lesquelles la solution 1DOF quitte la région d'instabilité et redevient stable. Des simulations numériques avec DSTOOL montrent que dans le cas étudié ici, l'amplitude de la configuration 1, non directement excitée ici, atteint des valeurs supérieures à l'amplitude e.
Observations exp´erimentales
Discussion
Sym´etrie du syst`eme
La présence d'harmoniques paires peut provenir soit de l'excitation électromagnétique, soit de la structure. Premièrement, lorsque l’excitation est parfaitement transversale, la présence d’une composante continue en plus de la sinusoïde fondamentale crée des harmoniques douces dans la réponse.
Ordre de grandeur du d´eplacement
Benamar et al ont également rapporté dans [9] et étudié dans [6] la présence d'harmoniques paires dans leurs signaux de mesure, mais n'ont donné aucune explication. Dans notre cas, il est difficile de déterminer la(les) raison(s) de la présence de ces harmoniques d’ordre égal.
Effet du second ordre
Le champ magnétique n'étant pas uniforme sur l'axe de la bobine et donc sur le trajet de l'aimant, même si l'intensité du signal est parfaitement sinusoïdale, en grande amplitude, la force appliquée sur l'aimant peut présenter des harmoniques paires (voir Annexe UN). Deuxièmement, lorsque l'excitation n'est pas purement transversale, la réponse de la plaque est constituée, en plus des harmoniques impaires, d'une composante continue et d'harmoniques paires.
Conclusion
Effort normal
Du fait de l'articulation en un point, la tige qui est en équilibre sous l'action de la force appliquée n'est chargée que selon son axe longitudinal courant. Après intégration sur la partie de la tige on montre (??) que la force normale est égale.
Domaine de validit´e
Un échantillon est soumis à une tension et la contrainte normale (rapport de section initiale ¼) est tracée en fonction de la déformation CC¼. Lors du fonctionnement normal des gongs et des cymbales, le matériau ne dépasse pas la limite d'élasticité, car cela entraînerait des dommages à la structure, qui se manifesteraient notamment par une modification de la géométrie de l'étrier et de la tonalité de l'instrument. ".
Syst`eme “plat”
Force de rappel
Lorsque les effets non linéaires mentionnés dans la section précédente (Ü7.1.1) sont négligés, l'effort normal dans la barre est proportionnel à la déformation linéarisée ee, et s'écrit. Ainsi, les effets des non-linéarités géométriques sur une tige isolée ne sont perceptibles que lorsque les contraintes dans la tige ont dépassé la limite élastique du matériau.
Force de rappel avec comportement lin´eaire des barres
Comme dans la section précédente 7.1, nous utilisons le tenseur symétrique de Piola-Kirchhoff pour calculer la force normale dans les barres, de sorte que. La force de rappel (#, de direction verticale, est obtenue en sommant les projections verticales des forces normales dans les barres, d'où.
Discussion
Cet effet est communément appelé effet câble [41], typique des non-linéarités de type géométrique. Examinons maintenant plus précisément les causes de ces non-linéarités géométriques.
Syst`eme avec inclinaison initiale
Force de rappel
La détermination de l'effort normal dans les barres est moins immédiate et nécessite d'effectuer un développement CC limité, c'est-à-dire On peut noter que l’on retrouve les expressions de(# et calculées dans le cas du système planaire au paragraphe 7.2 ci-dessus (Eq.
Influence de la courbure
Syst`emes avec raideur en flexion
Equations d’´equilibre
Les relations de comportement de chacune des barres (Eq. 7.5) permettent alors de calculer les forces de rappel. Les forces normales dans les barres dépendent des longueurs actuelles de chacune des barres, qui, à l'aide de la Fig.
Cas des extr´emit´es fixes : influence de l’´epaisseur
En ajoutant "épaisseur" et le système donne une rigidité linéaire de valeur &C dans le système plat au repos (avec. Lorsque le système est chargé transversalement selon, les fibres situées au-dessus du plan médian sont chargées en traction, tandis que les fibres inférieures sont en compression .
Cas des extr´emit´es mobiles : retour sur les ´equations de Von K`arm`an
Une expression non-linéaire cubique inC est également ajoutée, analogue à la non-linéarité cubique des plaques (Cf. Chapitre 5). Nous constatons que les grands déplacements transversaux créent un étirement du plan carré moyen (Eq.
Conclusion
8.3 – Evolution temporelle de la pente8, de la vitesse angulaire8', de l'accélération angulaire (et de la fréquence instantanée du pendule amorti. L'amortissement est choisi non nul pour montrer l'évolution du profil de la solution en fonction de l'amplitude de les oscillations.
Effet raidissant ou assouplissant
- Solution analytique perturbative de l’´equation du mouvement
- Influence de l’inclinaison et de l’´epaisseur
- Les gongs d’op´era chinois
- Les modes du tam-tam
En fait, on voit qu'il s'agit d'une échelle rapide, qui prend en compte les variations de réponse du système aux fréquences de l'ordre de !, et ainsi de suite. D’après l’équation (8.25b), la pulsation des oscillations libres est une fonction croissante (dans un système raidisseur) ou décroissante (dans un système adoucissant) de l’amplitude, selon le signe de !¾.

Distortion dissym´etrique des oscillations
Effets de la courbure
Pour chaque système on retrouve : les profils temporels du déplacement, de la vitesse et de l'accélération(, et le spectre de cette dernière ; la force de rappel( et l'énergie potentielle en fonction du déplacement. Cette dernière propriété étend le résultat de l'équation ( 8.25a), valable pour les oscillations de.
Interpr´etation g´eom´etrique des effets raidissant et assouplissant
Dans cette étude, seules les simulations numériques de ces petits systèmes en vibration de forte amplitude seront présentées, au paragraphe 8.4. On peut encore faire un parallèle entre ces deux systèmes de barres et de plaques et de coques.
Vibrations de grande amplitude
Syst`eme sans raideur en flexion
Le comportement du système est flexible, car la fréquence augmente à mesure que l'amplitude diminue. Le deuxième régime, noté (II), est obtenu de ` à s pour les oscillations de grande amplitude du système, lorsque son énergie mécanique est suffisamment grande pour que les oscillations franchissent le point d'équilibre instable %.
Influence de l’´epaisseur
Les conditions aux limites longitudinales influencent l'importance des non-linéarités. En fait, c'est cette dernière qui crée la déformation de la surface moyenne qui est responsable des effets non linéaires.
Vers un mod`ele continu de cymbales et de gongs
En régime forcé, la dynamique de la structure est gouvernée uniquement par les modes directement excités, c'est-à-dire ceux en combinaison avec des résonances. Ensuite, des équations analogues aux équations de Von-K`ar`an seront obtenues, qu'il faudra ensuite concevoir à partir des modes propres de la structure, dans le but d'obtenir le système 9.2.
Description
Mod´elisation du comportement magn´eto-dynamique
Champ magn´etique cr´e´e par la bobine
Force exerc´ee sur l’aimant
Mesures de la force exerc´ee sur la structure
Montage exp´erimental
Etude m´ecanique du syst`eme tˆete d’imp´edance-aimant
Force en fonction de la position
Force en fonction de l’intensit´e du courant
Conclusions
Analyses modales par la m´ethode des ´ El´ements Finis
Travail virtuel des efforts ext´erieurs
Travail virtuel des quantit´es d’acc´el´eration
Cas des vibrations axisym´etriques
Cas des vibrations asym´etriques
Coefficients
Cas d’un mode axisym´etrique
Cas d’un mode asym´etrique