Desenvolvimento de uma T´
ecnica N˜
ao Intrusiva
de Medi¸c˜
ao do Coeficiente de Convec¸c˜
ao
-Solu¸c˜
ao do Problema T´
ermico Inverso
Tese apresentada `a Escola de Engenharia de S˜ao Carlos, da Universidade de S˜ao Paulo, como parte dos requisitos para obten¸c˜ao do t´ıtulo de Doutor em Engenharia Mecˆanica.
´
Area de Concentra¸c˜ao: T´ermica e Fluidos Orientador: Prof. Tit. Paulo Seleghim J´unior
`
A Deus, por estar presente em todos os momentos da minha vida. `
A minha m˜ae, Ivete, pelo amor incondicional em todos os momentos, pelo apoio, dedica¸c˜ao, carinho e principalmente, pela confian¸ca durante todos esses anos. “Agrade¸co a minha m˜ae, cuja f´e em mim me ensinou a ter f´e em mim mesma e em Deus”. (David Samuel)
Aos meus irm˜aos, Alberto e Andr´eia, pelo amor, paciˆencia e incentivo em toda minha vida. “Ainda que eu falasse a l´ıngua dos homens, e falasse a l´ıngua dos anjos, sem vocˆes, eu nada seria...”
Ao Prof. Paulo Seleghim J´unior, pelo apoio, dedica¸c˜ao e orienta¸c˜ao durante este trabalho. “O s´abio n˜ao ´e o homem que fornece as verdadeiras respostas; ´e o que formula as verdadeiras perguntas”. (Claude L´evi-Strauss)
A todos os meus amigos que contribu´ıram para a realiza¸c˜ao desta conquista. “Depois de algum tempo vocˆe aprende que verdadeiras amizades continuam a crescer mesmo a longas distˆancias, e o que importa n˜ao ´e o que vocˆe tem na vida, mas quem vocˆe tem na vida”. (William Shakespeare)
Aos funcion´arios e professores da EESC. `
A FAPESP, processo no
“O segredo ´e n˜ao correr atr´as das borboletas... ´
BRANDI, A. C.Desenvolvimento de uma t´ecnica n˜ao intrusiva de medi¸c˜ao
do coeficiente de convec¸c˜ao - solu¸c˜ao do problema t´ermico inverso. 2010.
145 f. Tese (Doutorado) - Escola de Engenharia de S˜ao Carlos, Universidade de S˜ao Paulo, S˜ao Carlos, 2010.
platˆos, etc. Desse modo, uma t´ecnica bastante sofisticada, capaz de convergir para a solu¸c˜ao correta mesmo na presen¸ca dessas patologias ´e necess´aria para obten¸c˜ao da solu¸c˜ao. Neste trabalho optou-se pelo m´etodo de Newton para a mi-nimiza¸c˜ao deste funcional em que a inversa da matriz Hessiana ´e substitu´ıda por uma pseudo-inversa constru´ıda a partir da t´ecnica de Decomposi¸c˜ao em Valores Singulares Truncados. Os resultados mostram que a t´ecnica proposta foi capaz de superar os problemas de convergˆencia associados `a natureza intr´ınseca mal con-dicionada do problema inverso e o coeficiente de convec¸c˜ao foi reconstru´ıdo com precis˜ao razo´avel.
BRANDI, A. C.Development of a non-intrusive technique for measuring
of the convection coefficient - solution of the inverse thermal problem.
2010. 145 f. Tese (Doutorado) - Escola de Engenharia de S˜ao Carlos, Universi-dade de S˜ao Paulo, S˜ao Carlos, 2010.
is necessary to obtain the solution. In this thesis the Newton’s method was used for the minimization of this functional in which the inverse Hessian matrix was re-placed by a pseudo-inverse built from the truncated singular value decomposition technique. Results show that the proposed technique was capable of overcoming the convergence problems associated with the intrinsic ill-conditioned nature of the inverse problem and the convection coefficient was reconstructed within rea-sonable precision.
3.1 (a) Exemplo de um dom´ınio discreto contendo o subdom´ınio dos elementos e seus respectivos n´os; (b) elemento triangular adotado para os c´alculos. . . 49
3.2 Fun¸c˜ao de pondera¸c˜ao. . . 49
4.1 Algoritmo de solu¸c˜ao do problema inverso. . . 62
4.2 Varia¸c˜ao dos autovalores w1 ew2 em rela¸c˜ao ax1 para x2 = 0. . . 69
4.3 Fun¸c˜ao de erro (vermelho), suas derivadas primeira (azul) e segunda (roxo). (Destaque para os dom´ınios de influˆencia do m´ınimo local
|x1|<√2/2 e do m´ınimo difuso|x1|>√2/2). . . 69
4.4 Gr´afico da fun¸c˜ao de erro (4.35). . . 70
4.5 Trajet´orias de convergˆencia para diferentes estimativas iniciais: 0,35 (linha cont´ınua), 0,47 (linha pontilhada) e 2,5 (linha tracejada). . 71
4.6 Trajet´orias de convergˆencia para diferentes estimativas iniciais: 0,45 (linha cont´ınua) e 0,44 (linha pontilhada). . . 72
4.7 Corre¸c˜oes da vari´avel de otimiza¸c˜ao conforme a equa¸c˜ao (4.12). . 72
4.8 Trajet´orias de convergˆencia para diferentes estimativas iniciais: 0,35 (linha cont´ınua), 0,47 (linha pontilhada) e 2,5 (linha tracejada). . 72
5.1 Geometria do problema de condu¸c˜ao bidimensional em uma placa. 74
5.2 Compara¸c˜ao na malha grossa (25 n´os) entre as solu¸c˜oes: (a) num´erica e (b) anal´ıtica. . . 75
5.3 Compara¸c˜ao na malha intermedi´aria (81 n´os) entre as solu¸c˜oes: (a) num´erica e (b) anal´ıtica. . . 75
5.5 Geometria do problema de condu¸c˜ao bidimensional com condi¸c˜ao de Dirichlet. . . 77
5.6 Geometria do problema de condu¸c˜ao bidimensional com condi¸c˜ao de Neumann. . . 78
5.7 Geometria do problema de condu¸c˜ao bidimensional com condi¸c˜ao de Dirichlet e mista. . . 80
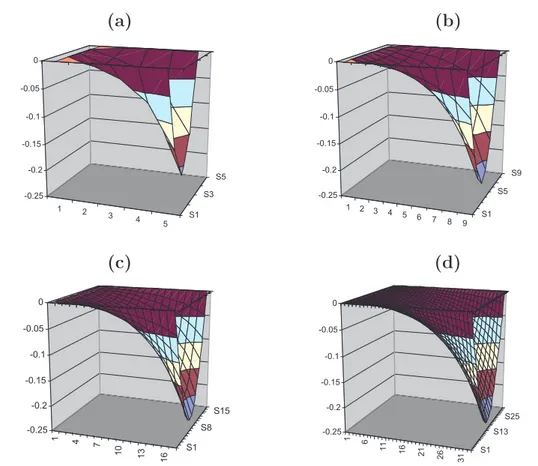
5.8 Solu¸c˜ao num´erica para quatro malhas: (a) 25 n´os, (b) 81 n´os, (c) 289 n´os e (d) 1089 n´os. . . 81
5.9 Solu¸c˜ao anal´ıtica calculada nas quatro malhas da Figura 5.8: (a) 25 n´os, (b) 81 n´os, (c) 289 n´os e (d) 1089 n´os. . . 82
5.10 Geometria do problema simulado numericamente. . . 82
5.11 Superf´ıcies de erro: (a) caso 1, (b) caso 2, (c) caso 3 e (d) caso 4. 85
5.12 Sequˆencia de convergˆencia de uma estimativa inicial n˜ao centrada n˜ao aleat´oria (azul) em rela¸c˜ao a solu¸c˜ao real (vermelho). . . 87
5.13 Sequˆencia de convergˆencia de uma estimativa inicial centrada n˜ao aleat´oria (azul) em rela¸c˜ao a solu¸c˜ao real (vermelho). . . 88
5.14 Sequˆencia de convergˆencia de uma estimativa inicial centrada aleat´oria (azul) em rela¸c˜ao a solu¸c˜ao real (vermelho). . . 88
5.15 Estimativas iniciais e solu¸c˜ao real do coeficiente de convec¸c˜ao, con-forme a equa¸c˜ao (5.9). . . 89
5.16 Estimativas iniciais e solu¸c˜ao real do coeficiente de convec¸c˜ao, con-forme a equa¸c˜ao (5.10). . . 90
5.17 Estimativas iniciais e solu¸c˜ao real do coeficiente de convec¸c˜ao, con-forme a equa¸c˜ao (5.11). . . 90
5.18 Representa¸c˜ao esquem´atica da trajet´oria de otimiza¸c˜ao associada ao aumento da norma do erro. . . 91
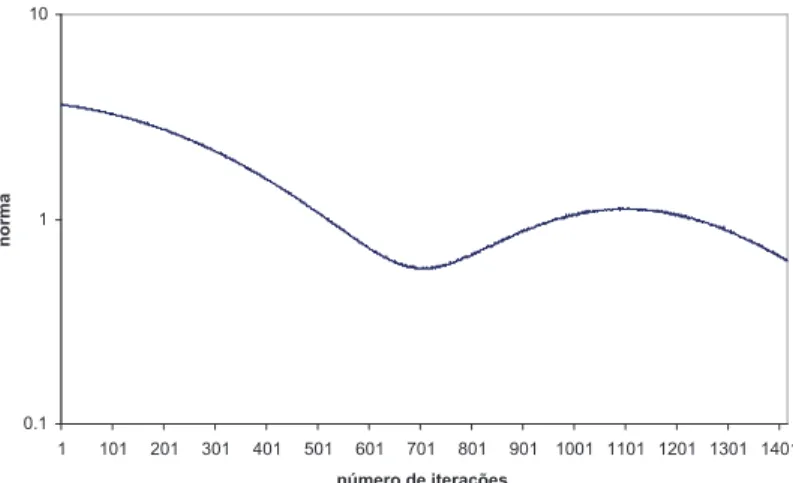
5.19 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.1 e λ= 0,02. . . 92
5.20 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.1 e λ= 0,01. . . 93
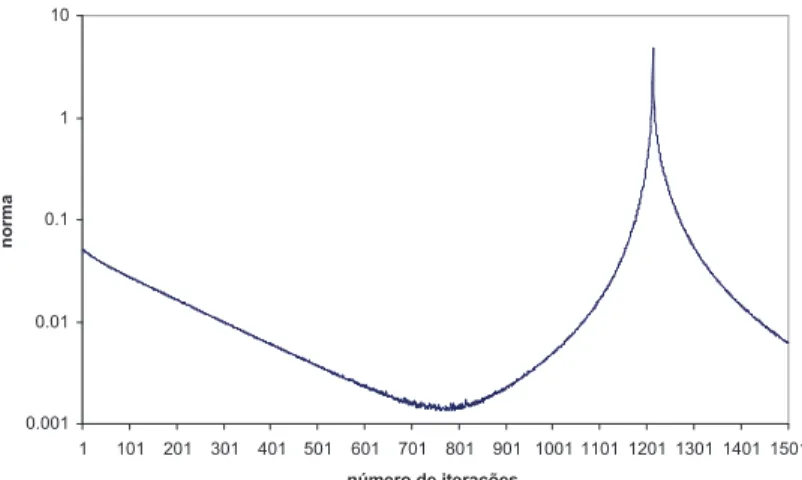
5.23 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.2 e λ= 0,01. . . 94
5.24 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.2 e λ= 0,005. . . 94
5.25 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.3 e λ= 0,02. . . 95
5.26 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.3 e λ= 0,01. . . 95
5.27 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 1.3 e λ= 0,005. . . 96
5.28 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.1 e λ= 0,02. . . 96
5.29 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.1 e λ= 0,01. . . 97
5.30 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.1 e λ= 0,005. . . 97
5.31 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.2 e λ= 0,02. . . 98
5.32 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.2 e λ= 0,01. . . 98
5.33 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.2 e λ= 0,005. . . 98
5.34 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.3 e λ= 0,02. . . 99
5.35 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.3 e λ= 0,01. . . 99
5.36 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 2.3 e λ= 0,005. . . 100
5.38 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.1 e λ= 0,01. . . 101
5.39 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.1 e λ= 0,005. . . 101
5.40 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.2 e λ= 0,02. . . 101
5.41 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.2 e λ= 0,01. . . 102
5.42 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.2 e λ= 0,005. . . 102
5.43 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.3 e λ= 0,02. . . 102
5.44 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.3 e λ= 0,01. . . 103
5.45 Trajet´oria de convergˆencia usando o m´etodo de Newton para o caso 3.3 e λ= 0,005. . . 103
5.46 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.1 eλ = 0,02. . . 105
5.47 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.1 eλ = 0,01. . . 105
5.48 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.1 eλ = 0,005. . . 105
5.49 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.2 eλ = 0,02. . . 106
5.50 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.2 eλ = 0,01. . . 106
5.51 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.2 eλ = 0,005. . . 106
5.52 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 1.3 eλ = 0,02. . . 107
5.55 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.1 e λ= 0,02. . . 108
5.56 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.1 e λ= 0,01. . . 108
5.57 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.1 e λ= 0,005. . . 108
5.58 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.2 e λ= 0,02. . . 109
5.59 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.2 e λ= 0,01. . . 109
5.60 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.2 e λ= 0,005. . . 109
5.61 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.3 e λ= 0,02. . . 110
5.62 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.3 e λ= 0,01. . . 110
5.63 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 2.3 e λ= 0,005. . . 110
5.64 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.1 e λ= 0,02. . . 111
5.65 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.1 e λ= 0,01. . . 111
5.66 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.1 e λ= 0,005. . . 111
5.67 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.2 e λ= 0,02. . . 112
5.68 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.2 e λ= 0,01. . . 112
5.70 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.3 eλ = 0,02. . . 113
5.71 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.3 eλ = 0,01. . . 113
5.72 Trajet´oria de convergˆencia usando o m´etodo de Newton com In´ercia para o caso 3.3 eλ = 0,005. . . 113
5.73 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.1 eλ = 0,02. . . 115
5.74 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.1 eλ = 0,01. . . 115
5.75 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.1 eλ = 0,005. . . 116
5.76 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.2 eλ = 0,02. . . 116
5.77 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.2 eλ = 0,01. . . 116
5.78 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.2 eλ = 0,005. . . 117
5.79 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.3 eλ = 0,02. . . 117
5.80 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.3 eλ = 0,01. . . 117
5.81 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 1.3 eλ = 0,005. . . 118
5.82 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.1 eλ = 0,02. . . 118
5.83 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.1 eλ = 0,01. . . 118
5.84 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.1 eλ = 0,005. . . 119
5.87 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.2 e λ= 0,005. . . 120
5.88 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.3 e λ= 0,02. . . 120
5.89 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.3 e λ= 0,01. . . 120
5.90 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 2.3 e λ= 0,005. . . 121
5.91 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.1 e λ= 0,02. . . 121
5.92 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.1 e λ= 0,01. . . 121
5.93 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.1 e λ= 0,005. . . 122
5.94 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.2 e λ= 0,02. . . 122
5.95 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.2 e λ= 0,01. . . 122
5.96 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.2 e λ= 0,005. . . 123
5.97 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.3 e λ= 0,02. . . 123
5.98 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.3 e λ= 0,01. . . 123
5.99 Trajet´oria de convergˆencia usando o m´etodo da Descida M´axima para o caso 3.3 e λ= 0,005. . . 124
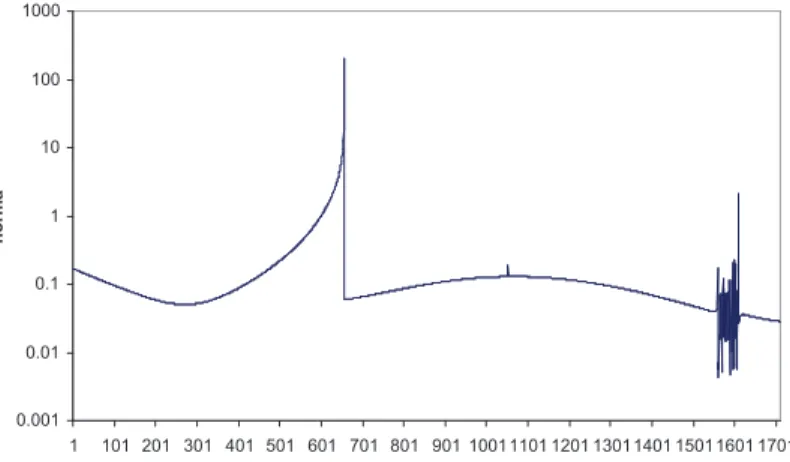
5.100Espectro dos autovalores da matriz Hessiana para as itera¸c˜oes 350 (laranja) e 450 (azul) da Figura 5.41. . . 125
5.102Histogramas de autovalores para as itera¸c˜oes 1 a 200 (azul) e de 400 a 700 (vermelho) da Figura 5.23. . . 127
5.103Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 1.1. . . 129
5.104Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 1.2. . . 129
5.105Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 1.3. . . 129
5.106Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 2.1. . . 130
5.107Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 2.2. . . 130
5.108Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 2.3. . . 130
5.109Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 3.1. . . 131
5.110Trajet´oria de convergˆencia usando o m´etodo de Newton com TSVD para o caso 3.2. . . 131
5.1 Erros para o problema de condu¸c˜ao de calor definido na Figura 5.1. 76
5.2 Distribui¸c˜ao final de temperatura com condi¸c˜ao de contorno de Di-richlet (Figura 5.5) conforme obtidos por (FORTUNA, 2000). . . 77
5.3 Distribui¸c˜ao final de temperatura com condi¸c˜ao de contorno de Di-richlet (Figura 5.5) obtidos neste trabalho. . . 78
5.4 Distribui¸c˜ao final de temperatura com condi¸c˜ao de contorno de Neumann (Figura 5.6) conforme obtidos por (FORTUNA, 2000). . 79
5.5 Distribui¸c˜ao final de temperatura com condi¸c˜ao de contorno de Neumann (Figura 5.6) obtidos neste trabalho. . . 79
S´ımbolo Descri¸c˜ao
a Extremidade esquerda do intervalo de busca (a, b) b Extremidade direita do intervalo de busca (a, b) ou a
extremidade esquerda do intervalo de busca (b, c) c Extremidade direita do intervalo de busca (b, c)
d Dire¸c˜ao de refinamento
diag Matriz diagonal
e Funcional de erro ou fun¸c˜ao objetivo
h Coeficiente de convec¸c˜ao ou coeficiente de transferˆencia de calor
hinicial Coeficiente de convec¸c˜ao inicial referente a estimativa
inicial
hnum Coeficiente de convec¸c˜ao num´erico resultante do modelo
prospectivo
hreal Coeficiente de convec¸c˜ao real resultante do modelo de
referˆencia
H Matriz Hessiana
k Condutividade t´ermica
n Vetor normal
q Fluxo de calor
R Res´ıduo
T Temperatura
T∞ Temperatura ambiente
U Matriz ortogonal
v Fun¸c˜ao de pondera¸c˜ao
V Matriz ortogonal
w Elementos da matriz W
W Matriz diagonal
x Eixo horizontal
y Eixo vertical
S´ımbolo Descri¸c˜ao
δ Vetor de perturba¸c˜ao aleat´oria uniforme δx Espa¸camento da malha na dire¸c˜ao x δy Espa¸camento da malha na dire¸c˜ao y
λ Passo de refinamento
θ Potencial t´ermico ou temperatura θ0 Temperatura inicial conhecida
θnum Temperatura num´erica resultante do modelo
prospectivo
θreal Temperatura real resultante do modelo de referˆencia
θ∞ Temperatura ambiente
Ω Dom´ınio do problema
1 Introdu¸c˜ao 25
1.1 Motiva¸c˜ao para o Trabalho . . . 27
1.2 Objetivos . . . 28
1.3 Organiza¸c˜ao do Texto . . . 29
2 Revis˜ao Bibliogr´afica 31
2.1 Tomografia T´ermica . . . 32
2.2 Problemas Direto e Inverso . . . 33
2.3 Mau Condicionamento . . . 35
2.4 M´etodos de Solu¸c˜ao de Problemas Inversos . . . 36
2.5 T´ecnicas de Regulariza¸c˜ao . . . 40
3 Modelagem do Problema de Transferˆencia de Calor 45
3.1 Formula¸c˜ao Matem´atica . . . 45
3.2 Formula¸c˜ao Num´erica . . . 46
3.2.1 M´etodo dos Elementos Finitos . . . 47
4 Medi¸c˜ao n˜ao Intrusiva do Coeficiente de Convec¸c˜ao como um PI 57
4.1 Formula¸c˜ao da Medida como um Problema Inverso . . . 57
4.2 Caracter´ısticas do Problema de Minimiza¸c˜ao . . . 59
4.3 M´etodos de Otimiza¸c˜ao . . . 60
4.4 Fatora¸c˜ao Matricial: Decomposi¸c˜ao em Valores Singulares . . . . 64
4.5 Condicionamento da Matriz Hessiana . . . 69
5 Testes Num´ericos e Resultados 73
5.2 Estudo de Caso . . . 80
5.3 Caracteriza¸c˜ao das Superf´ıcies de Erro . . . 83
5.4 Estudo Preliminar da Convergˆencia . . . 86
5.5 Patologias das Trajet´orias de Convergˆencia . . . 87
5.5.1 Testes Num´ericos . . . 90
5.5.2 M´etodo de Newton . . . 91
5.5.3 M´etodo de Newton com In´ercia . . . 103
5.5.4 M´etodo da Descida M´axima . . . 114
5.6 Estabilidade da Trajet´oria e Espectro de Autovalores . . . 124
5.7 Aplica¸c˜ao da TSVD na Regulariza¸c˜ao das Trajet´orias . . . 127
6 Conclus˜oes e Perspectivas 133
1
Introdu¸c˜
ao
A tomografia de processos industriais ´e uma t´ecnica para mapear a estru-tura espacial interna de um objeto atrav´es de medidas externas n˜ao intrusivas, a partir da determina¸c˜ao de uma propriedade f´ısica. Por exemplo, um escoa-mento ´oleo-´agua em um po¸co de petr´oleo pode ter sua fra¸c˜ao de fase monitorada atrav´es da tomografia ac´ustica (ultra-som). Mais especificamente, o mapeamento consiste em aplicar um est´ımulo sobre a fronteira externa da regi˜ao (est´ımulo) e medir a resposta sobre esta mesma superf´ıcie externa (resposta). A rela¸c˜ao est´ımulo/resposta cont´em informa¸c˜oes sobre o interior do objeto e ´e usada na reconstru¸c˜ao tomogr´afica.
Um exemplo ´e a tomografia t´ermica em que a id´eia b´asica ´e aquecer o ma-terial ou aproveitar seu calor e estudar as mudan¸cas de temperatura no inte-rior dele aprendendo sobre sua composi¸c˜ao. A t´ecnica ´e r´apida, econˆomica e o mais importante, tem uma ´otima resposta com medidas experimentais simples (CAMPOS, 2004).
Processos industriais envolvendo transferˆencia de calor s˜ao extremamente co-muns em aplica¸c˜oes de ´areas t˜ao diversas quanto o setor petroqu´ımico e a seca-gem de gr˜aos na agroind´ustria. Em particular, a convec¸c˜ao for¸cada ou natural ´e provavelmente o processo mais difundido dentre as diversas modalidades de trans-ferˆencia de calor. Desta forma, uma ampla compreens˜ao e dom´ınio de seus meca-nismos fenomenol´ogicos ´e condi¸c˜ao imprescind´ıvel para uma engenharia t´ermica de alto n´ıvel e, consequentemente, para a utiliza¸c˜ao racional e otimizada de nossos insumos energ´eticos.
Os trocadores de calor constituem um exemplo bastante eloquente desta
26
tua¸c˜ao, sobretudo devido a sua aplica¸c˜ao quase que universal em m´aquinas fri-gor´ıficas, geradores de vapor, radiadores automotivos, pasteurizadores industriais e outros. Nestes casos a transferˆencia de calor se d´a por interm´edio das paredes que separam os fluidos quente e frio e ´e governada basicamente pelos coeficientes de convec¸c˜ao em ambas as interfaces. Em outras palavras, as resistˆencias t´ermicas as-sociadas `as trocas convectivas geralmente predominam sobre a resistˆencia t´ermica associada `a condu¸c˜ao de calor. Portanto, a pedra angular do projeto termo-hidr´aulico de um trocador de calor ´e representada pelos processos convectivos e sua engenharia requer conhecimento espec´ıfico sobre o c´alculo dos coeficientes de convec¸c˜ao.
Historicamente o conceito de coeficiente de convec¸c˜ao foi introduzido por Isaac Newton em 1701 como forma de quantificar a rela¸c˜ao entre o fluxo de calor e a diferen¸ca de temperatura na interface e longe dela. Trata-se portanto de uma lei emp´ırica que, para ser utilizada com sucesso em aplica¸c˜oes pr´aticas requer a determina¸c˜ao experimental pr´evia do coeficiente de convec¸c˜ao em fun¸c˜ao de diversas vari´aveis como, por exemplo, geometrias, propriedades f´ısicas do fluido, condi¸c˜oes de escoamento, etc. De fato pode-se encontrar na literatura t´ecnica um n´umero bastante expressivo de correla¸c˜oes emp´ıricas constru´ıdas para as mais diversificadas situa¸c˜oes.
Entretanto, a otimiza¸c˜ao de processos tradicionais assim como o desenvolvi-mento de novos equipadesenvolvi-mentos frequentemente recai em situa¸c˜oes novas para as quais n˜ao existem dados quantitativos ou mesmo um conhecimento superficial so-bre o problema. Assim, a determina¸c˜ao experimental do coeficiente de convec¸c˜ao ´e base para o desenvolvimento de novas tecnologias aplic´aveis aos processos que envolvem transferˆencias convectivas de calor.
desenvolvi-mento de uma nova t´ecnica de reconstru¸c˜ao num´erica adaptada `a fenomenologia do sensoriamento t´ermico.
A id´eia b´asica para a determina¸c˜ao do coeficiente de convec¸c˜ao interno pode ser feita atrav´es da aplica¸c˜ao de um fluxo de calor na superf´ıcie externa do dom´ınio e na medi¸c˜ao de temperaturas resultantes nessa mesma superf´ıcie ( ¨OZISIK; OR-LANDE, 2000). Estas temperaturas resultantes s˜ao comparadas `as temperaturas de um modelo prospectivo por meio de um funcional de erro, cuja minimiza¸c˜ao resulta na distribui¸c˜ao correta do coeficiente de convec¸c˜ao.
Trabalhos anteriores (ROLNIK, 2003; BRANDI; SELEGHIM JR., 2008) per-mitiram conhecer em detalhes as principais caracter´ısticas topol´ogicas dos fun-cionais de erro, sobretudo aquelas associadas ao mau condicionamento intr´ınseco do problema. Essas caracter´ısticas, ditas patol´ogicas, s˜ao determinantes no de-senvolvimento de m´etodos de otimiza¸c˜ao capazes de convergir para a solu¸c˜ao do problema em tempo adequado para as aplica¸c˜oes em vista.
Simula¸c˜oes num´ericas extensivas realizadas por Brandi e Seleghim Jr. (2008) mostraram que as principais patologias do funcional de erro consistem numa regi˜ao plana (platˆo) envolvendo o m´ınimo global associado `a solu¸c˜ao, muitas vezes cer-cado de m´ultiplos m´ınimos locais, pontos de sela, vales estreitos e at´e mesmo vale com eixo curvil´ıneo. Nessas condi¸c˜oes, as patologias das superf´ıcies de erro permi-tem antecipar grandes dificuldades na aplica¸c˜ao de um algoritmo de minimiza¸c˜ao convencional, tornando-se necess´ario ent˜ao desenvolver algoritmos capazes de con-vergir para a solu¸c˜ao correta mesmo na ocorrˆencia dessas patologias t´ıpicas do problema estudado.
1.1
Motiva¸c˜
ao para o Trabalho
De acordo com a teoria de problemas inversos, a reconstru¸c˜ao num´erica da tomografia t´ermica ´e tratada como um problema de minimiza¸c˜ao global, cuja fun¸c˜ao objetivo ´e um funcional de erro que representa a diferen¸ca entre medidas (temperatura) de referˆencia e medidas aproximadas, obtidas numericamente por meio de uma distribui¸c˜ao prospectiva do coeficiente de convec¸c˜ao. O m´ınimo global do funcional de erro corresponde a solu¸c˜ao procurada.
pro-28 1.2 Objetivos
curada em tempo vi´avel. Isso deve-se `a n˜ao linearidade e ao mau condicionamento do problema tomogr´afico que impedem a convergˆencia do algoritmo para a solu¸c˜ao correta, na presen¸ca de patologias.
Desse modo, uma t´ecnica aprimorada ´e necess´aria para obten¸c˜ao da solu¸c˜ao. Uma t´ecnica interessante ´e o m´etodo de Newton que, al´em das derivadas de pri-meira ordem do funcional de erro, conforme utilizadas no m´etodo da Descida M´axima e dos Gradientes Conjugados, faz uso tamb´em da derivada de segunda ordem para acelerar a convergˆencia. O funcional de erro n˜ao ´e regularizado atrav´es de t´ecnicas espec´ıficas, como o m´etodo de Tikhonov por exemplo. A t´ecnica de regulariza¸c˜ao proposta neste trabalho ´e baseada na constru¸c˜ao de uma pseudo-inversa da matriz Hessiana do m´etodo de Newton a partir da truncagem de sua Decomposi¸c˜ao em Valores Singulares (TSVD), que tem por efeito a atenua¸c˜ao do mau condicionamento intr´ınseco do problema inverso.
1.2
Objetivos
Neste trabalho prop˜oe-se o desenvolvimento de uma t´ecnica n˜ao intrusiva para a determina¸c˜ao do coeficiente de convec¸c˜ao a partir de medidas externas de tempe-ratura e fluxo de calor baseada na solu¸c˜ao do problema t´ermico inverso. Para tanto ´e necess´ario resolver um problema de condu¸c˜ao acoplado a um problema de con-vec¸c˜ao de calor. Este acoplamento ocorre atrav´es do coeficiente de concon-vec¸c˜ao no interior do dom´ınio do problema, ao passo que as medidas de temperatura e fluxo de calor s˜ao feitas na superf´ıcie externa sujeita a condu¸c˜ao. Assim, tratando-se de um problema inverso, e portanto intrinsecamente mal condicionado, a formula¸c˜ao tradicional do problema deve ser alterada de forma a torn´a-lo menos suscept´ıvel `a presen¸ca de ru´ıdos experimentais e erros de truncamento.
O objetivo fundamental deste trabalho ´e desenvolver uma nova estrat´egia de regulariza¸c˜ao baseada na constru¸c˜ao de uma pseudo-inversa da matriz Hessiana a partir da truncagem de sua Decomposi¸c˜ao em Valores Singulares. Desse modo, as seguintes metas intermedi´arias s˜ao apresentadas:
• Implementa¸c˜ao num´erica do problema t´ermico e testes extensivos com dife-rentes t´ecnicas de otimiza¸c˜ao;
• Implementa¸c˜ao num´erica de t´ecnicas de regulariza¸c˜ao e testes extensivos para determina¸c˜ao do n´ıvel de corte da TSVD;
• Valida¸c˜ao da metodologia desenvolvida confrontando-se resultados num´ericos com valores de referˆencia, obtidos da solu¸c˜ao num´erica do modelo do pro-blema de referˆencia.
A solu¸c˜ao desse problema de otimiza¸c˜ao ´e obtida combinando-se um m´etodo de discretiza¸c˜ao, em geral o m´etodo dos elementos finitos, e um algoritmo de otimiza¸c˜ao como o m´etodo de Newton, com aux´ılio da t´ecnica de regulariza¸c˜ao TSVD. O m´etodo adotado neste trabalho para a reconstru¸c˜ao da solu¸c˜ao dever´a ser capaz de estimar distribui¸c˜oes do coeficiente de convec¸c˜ao, de forma que seja poss´ıvel diagnosticar caracter´ısticas do escoamento.
1.3
Organiza¸c˜
ao do Texto
O presente texto est´a organizado da seguinte forma:
• No Cap´ıtulo 2 ´e apresentada a revis˜ao bibliogr´afica dos temas envolvidos neste trabalho, tais como: tomografia t´ermica, problemas inversos, m´etodos de solu¸c˜ao de problemas inversos e t´ecnicas de regulariza¸c˜ao.
• No Cap´ıtulo 3 s˜ao apresentadas a formula¸c˜ao matem´atica e a formula¸c˜ao num´erica do problema de transferˆencia de calor utilizando o m´etodo dos elementos finitos.
• No Cap´ıtulo 4 s˜ao apresentadas a formula¸c˜ao da medida como um problema t´ermico inverso, as caracter´ısticas do problema de otimiza¸c˜ao, os m´etodos de otimiza¸c˜ao, em particular os m´etodos de Newton e Decomposi¸c˜ao em Valores Singulares e um estudo do condicionamento da matriz Hessiana.
30 1.3 Organiza¸c˜ao do Texto
um estudo preliminar da convergˆencia dos diferentes tipos de estimativa inicial, as patologias das trajet´orias de convergˆencia para diferentes m´etodos de otimiza¸c˜ao e os resultados dos testes num´ericos da aplica¸c˜ao da TSVD na regulariza¸c˜ao das trajet´orias de convergˆencia.
2
Revis˜
ao Bibliogr´
afica
A primeira modalidade de transferˆencia de calor a ser tratada na literatura de problemas inversos foi a condu¸c˜ao de calor. Isto ´e provavelmente devido ao interesse de pesquisadores envolvidos com o programa espacial na d´ecada de 50 e 60, visando a estimativa precisa das propriedades t´ermicas e o fluxo de calor na blindagem externa por ocasi˜ao da reentrada de artefatos e ve´ıculos aeroespa-ciais. Alguns m´etodos heur´ısticos de solu¸c˜ao para problemas inversos, que foram mais baseados na pura intui¸c˜ao do que no formalismo matem´atico, foram desen-volvidos nos anos 50. Mais tarde, na d´ecada de 60 e 70, a maioria dos m´etodos, que s˜ao de uso comum nos dias de hoje, foram formalizados em termos de suas capacidades para tratar problemas mal postos inst´aveis (TIKHONOV, 1963a,b; TIKHONOV; ARSENIN, 1977; ALIFANOV, 1974, 1994; BECK; ARNOLD, 1977; BECK; BLACKWELL; CLAIR, 1985). A base de tais m´etodos formais reside na id´eia de reformula¸c˜ao do problema inverso em termos de uma aproxima¸c˜ao do problema bem posto, utilizando algum tipo de t´ecnica de regulariza¸c˜ao (estabi-liza¸c˜ao).
O interesse na solu¸c˜ao dos problemas inversos de convec¸c˜ao de calor ´e mais recente que a solu¸c˜ao dos problemas inversos de condu¸c˜ao de calor. O primeiro artigo que trata de um problema inverso de convec¸c˜ao de calor ´e de Moutsoglou (1989). Posteriormente, v´arios outros artigos que envolvem convec¸c˜ao inversa apa-receram na literatura (MOUTSOGLOU, 1990; HUANG; ¨OZISIK, 1992; BOKAR;
¨
OZISIK, 1995; LIU; ¨OZISIK, 1996a,b; ZABARAS; YANG, 1997; PARK; CHUNG, 1999, 2000; HUANG; CHEN, 2000). Em sua maioria, esses artigos tratam de con-vec¸c˜ao for¸cada no interior de tubos ou canais, com fluxo de calor desconhecido
32 2.1 Tomografia T´ermica
na parede (MOUTSOGLOU, 1990; HUANG; ¨OZISIK, 1992; LIU; ¨OZISIK, 1996a; HUANG; CHEN, 2000) ou condi¸c˜ao de entrada desconhecida (BOKAR; ¨OZISIK, 1995; LIU; ¨OZISIK, 1996b). No entanto, problemas inversos de convec¸c˜ao natu-ral tamb´em foram abordados (MOUTSOGLOU, 1989; ZABARAS; YANG, 1997; PARK; CHUNG, 1999, 2000). Em todos esses trabalhos que tratam de convec¸c˜ao de calor inversa, uma ´unica fun¸c˜ao desconhecida foi considerada na an´alise.
A solu¸c˜ao de problemas inversos ´e normalmente problem´atica devido ao mau condicionamento das equa¸c˜oes, que se manifesta atrav´es da sensibilidade de solu-¸c˜oes aos erros nos dados de entrada ou truncamento num´erico. Isso significa que uma pequena imprecis˜ao de dados (usualmente medidos) pode resultar em gran-des imprecis˜oes dos resultados. Estes problemas resultaram em um atraso no desenvolvimento das t´ecnicas de solu¸c˜ao de problemas inversos que, com a neces-sidade de satisfazer normas de qualidades mais rigorosas, otimiza¸c˜ao de custos e do uso de insumos energ´eticos, vˆem recebendo aten¸c˜ao de um grande n´umero de pesquisadores.
Este cap´ıtulo apresenta a revis˜ao bibliogr´afica dos temas envolvidos neste tra-balho, tais como: a tomografia t´ermica, os problemas inversos, os m´etodos de solu¸c˜ao de problemas inversos e as t´ecnicas de regulariza¸c˜ao.
2.1
Tomografia T´
ermica
A tomografia de processos industriais ´e uma t´ecnica de determina¸c˜ao de vari´aveis operacionais atrav´es de medidas externas n˜ao intrusivas. Por exem-plo, um escoamento ´oleo-´agua em um po¸co de petr´oleo pode ter sua fra¸c˜ao de fase monitorada atrav´es da tomografia ac´ustica (ultra-som).
quais a velocidade do escoamento ´e determinada atrav´es da medida do coeficiente de convec¸c˜ao. O princ´ıpio de funcionamento da tomografia t´ermica geralmente se baseia na aplica¸c˜ao de um fluxo de calor na superf´ıcie externa do processo e na medi¸c˜ao das temperaturas resultantes nessa mesma superf´ıcie.
Dentre as principais vantagens da tomografia t´ermica est˜ao o seu baixo custo e robusteza, o que a torna extremamente interessante para aplica¸c˜oes industriais. Uma desvantagem significativa, no atual n´ıvel de conhecimento tecnol´ogico, refere-se a baixa precis˜ao dos resultados assim obtidos. Mais especificamente, atualmente a tomografia t´ermica ´e capaz de produzir apenas imagens qualitativas do processo industrial estudado.
Estas dificuldades surgem da n˜ao linearidade das vari´aveis e do mau condicio-namento intr´ınseco, apresentando-se extremamente sens´ıvel `a presen¸ca de erros, tanto de origem experimental nos dados de entrada quanto de truncamento nas opera¸c˜oes num´ericas do procedimento computacional.
A t´ecnica tomogr´afica de princ´ıpio t´ermico possui ainda uma limita¸c˜ao impor-tante, quando comparada com raios-X ou outras t´ecnicas de transmiss˜ao/emiss˜ao: o campo t´ermico ´e deform´avel (soft) no sentido de que depende do meio sensoriado. O efeito soft field explica os grandes erros nos resultados obtidos nos primeiros trabalhos de tomografia t´ermica devido ao emprego de t´ecnicas de reconstru¸c˜ao num´erica originalmente desenvolvidas para campos indeform´aveis, como o m´etodo deback projection (BARBER; BROWN; FREESTON, 1983) por exemplo.
Genericamente, mapear o interior de um objeto a partir de sinais perif´ericos com aux´ılio de t´ecnicas tomogr´aficas envolve resolver um problema inverso. Pro-blemas inversos s˜ao caracter´ısticos de um grande n´umero de problemas matema-ticamente mal condicionados das ciˆencias f´ısicas, m´edicas e outras. Este mau condicionamento intr´ınseco pode, sob certas condi¸c˜oes, afetar a qualidade das solu¸c˜oes, principalmente com rela¸c˜ao `a visualiza¸c˜ao tomogr´afica de escoamentos multif´asicos (SELEGHIM JR.; MILIOLI, 2001).
2.2
Problemas Direto e Inverso
34 2.2 Problemas Direto e Inverso
resposta (por exemplo, uma fun¸c˜ao), como sendo trˆes objetos de um dado pro-blema, ´e poss´ıvel caracterizar um problema como direto, inverso ou de identi-fica¸c˜ao de acordo com o conhecimento desses parˆametros. Silva Neto e Moura Neto (2005) esclarecem que se est´ımulo e mecanismo transformador s˜ao conhe-cidos e o objetivo ´e calcular a resposta ent˜ao o problema ´e direto. Entretanto, se resposta e mecanismo transformador s˜ao conhecidos, diz-se que o problema ´e inverso. Finalmente, quando a inc´ognita ´e o mecanismo transformador e est´ımulo e resposta s˜ao conhecidos ent˜ao o problema ´e dito inverso tomogr´afico ou de iden-tifica¸c˜ao.
Observe que no problema inverso tomogr´afico a determina¸c˜ao de inc´ognitas tridimensionais ´e feita a partir de medidas bidimensionais, consequentemente, o n´umero de inc´ognitas ´e superior ao n´umero de equa¸c˜oes conhecidas (ROLNIK, 2003). Contudo, a formula¸c˜ao do problema como um problema inverso tem a vantagem de unir a an´alise matem´atica aos dados experimentais, ou seja, a id´eia ´e associar um modelo f´ısico (experimental) a um matem´atico e fazer previs˜oes obtidas a partir do confronto entre os dois modelos na determina¸c˜ao do mecanismo de transforma¸c˜ao.
Problemas inversos s˜ao intrinsecamente mal condicionados, significando que o processo ser´a extremamente sens´ıvel a erros experimentais e num´ericos a ponto de comprometer completamente os resultados obtidos. Por causa desta instabilidade, a solu¸c˜ao dos problemas inversos deixa de ser simples e passa a ser complexa, motivo este de constantes estudos na ´area.
Os problemas inversos constituem uma ´area de pesquisa que tem crescido consideravelmente nos ´ultimos anos, por ser uma ´area multidisciplinar que une a an´alise matem´atica dos problemas aos dados experimentais. As aplica¸c˜oes dos problemas inversos est˜ao em v´arias ´areas como engenharia, medicina, geof´ısica, astrof´ısica e outros ramos da ciˆencia (SILVA NETO; MOURA NETO, 2000).
DANTAS; ORLANDE, 1996); a estimativa da condi¸c˜ao inicial de problemas tran-sientes em transferˆencia de calor por condu¸c˜ao (SILVA NETO; ¨OZISIK, 1994b); a identifica¸c˜ao de fontes poluentes em rios (ALVIM, 2004) e a estimativa das formas de fronteiras de corpos (HUANG; CHIANG; CHEN, 1998).
2.3
Mau Condicionamento
Apesar da abordagem em termos de est´ımulos e respostas ser simples, pro-blemas inversos, matematicamente, pertencem `a classe de propro-blemas mal postos. Segundo Hadamard (1902) um problema ´e dito bem posto se as trˆes condi¸c˜oes forem satisfeitas:
• Existˆencia - o problema dever´a apresentar solu¸c˜ao;
• Unicidade - a solu¸c˜ao dever´a ser ´unica;
• Estabilidade - a solu¸c˜ao dever´a exibir dependˆencia cont´ınua e suave em rela¸c˜ao aos dados de entrada.
A quest˜ao da existˆencia se coloca no sentido de ser poss´ıvel determinar a solu¸c˜ao de um problema em que partes das condi¸c˜oes de contorno s˜ao desconheci-das atrav´es da medi¸c˜ao de condi¸c˜oes de contorno redundantes na regi˜ao acess´ıvel da fronteira do problema.
Quanto `a unicidade, um resultado significativo at´e o momento para dimens˜oes maiores ou iguais a trˆes ´e para condutividades satisfazendo a condi¸c˜ao de Lipschitz (P ¨AIV ¨ARINTA; PANCHENCKO; UHLMANN, 2003). Ainda que a unicidade encontra-se garantida, Borcea (2002) concluiu que, geralmente, n˜ao ´e poss´ıvel a existˆencia de uma f´ormula expl´ıcita de reconstru¸c˜ao do interior do dom´ınio . Se um problema exibe m´ultiplas solu¸c˜oes, as informa¸c˜oes que definem o operador s˜ao insuficientes para descrevˆe-lo corretamente. Assim, crit´erios adicionais baseados em informa¸c˜oes realistas da modelagem devem ser adotados.
36 2.4 M´etodos de Solu¸c˜ao de Problemas Inversos
Assim, os problemas inversos violam a terceira condi¸c˜ao de Hadamard por serem intrinsecamente mal condicionados. Ser bem ou mal condicionado ´e uma propriedade intr´ınseca do problema inverso que se pretende avaliar. A avalia¸c˜ao ´e dita bem condicionada quando um pequeno erro no ponto de avalia¸c˜ao n˜ao afeta fortemente o valor da fun¸c˜ao. J´a, quando esta ´e mal condicionada o valor da fun¸c˜ao ´e afetado significativamente. Um erro introduzido em um c´alculo, por meio de um dado experimental ou de um arredondamento, pode produzir diversos efeitos no resultado final como redu¸c˜ao, permanecer pequeno ou, ainda, amplia¸c˜ao (SILVA NETO; MOURA NETO, 2005).
Portanto, o problema de tomografia t´ermica ´e intrinsecamente mal condicio-nado e, desse modo, extremamente sens´ıvel na presen¸ca de erros, tanto de natureza experimental nas medidas quanto de arredondamento/truncamento nos dados do procedimento computacional. Esta sensibilidade ´e comprovada por Seleghim e Milioli (2001) na determina¸c˜ao de histogramas de diˆametros a partir do histo-grama de cordas obtido de uma sonda de detec¸c˜ao de fase imersa em escoamento a bolhas. Neste trabalho foi comprovado que erros da ordem de 0,01% em am-plitude nos dados de entrada (cordas) produziram desvios de mais de 100% na solu¸c˜ao reconstru´ıda numericamente (diˆametros).
Devido o mau condicionamento, as t´ecnicas de reconstru¸c˜ao tradicionais s˜ao inadequadas, podendo destacar, resolu¸c˜ao pobre, baixa distinguibilidade e pro-du¸c˜ao de artefatos que, em geral, violam grandezas f´ısicas como fra¸c˜oes de vazio menores do que 0 ou maiores do que 1 (L ´ANYI, 1998).
2.4
M´
etodos de Solu¸c˜
ao de Problemas Inversos
experi-mentais de fluxo de calor ou de temperatura em determinadas posi¸c˜oes do meio estudado e em diferentes instantes ao longo de um intervalo de tempo determinado para o experimento.
A resolu¸c˜ao do problema inverso pode ser formulada como um problema de otimiza¸c˜ao em que a fun¸c˜ao inc´ognita, por exemplo, a distribui¸c˜ao do coeficiente de convec¸c˜ao, ´e refinada at´e que o funcional de erro atinja seu m´ınimo global. Por´em, ´e extremamente importante ressaltar que, relativamente `a constru¸c˜ao da solu¸c˜ao num´erica, n˜ao existem algoritmos de uso geral capazes de lidar com as particularidades de cada problema. Ao contr´ario, a escolha de uma rotina deve se basear no tipo de otimiza¸c˜ao (condicionada ou n˜ao), na disponibilidade de express˜oes anal´ıticas para as derivadas, na quantidade de informa¸c˜oes a priori (valor inicial), esfor¸co computacional, mem´oria e assim por diante.
Os m´etodos de solu¸c˜ao de um problema inverso tˆem sido motivo de intensas pesquisas cient´ıficas encontrando espa¸co nas mais diversas ´areas do conhecimento (entre elas, geof´ısica, meteorologia, oceanografia e transferˆencia de calor). No-vas metodologias surgem continuamente como resposta `a dificuldade na solu¸c˜ao do problema inverso. Entre as mais conhecidas podemos citar os m´etodos de otimiza¸c˜ao, decomposi¸c˜ao em valores singulares, m´etodos variacionais, m´etodos de regulariza¸c˜ao, molifica¸c˜ao, m´etodos bayesianos, filtros digitais, redes neurais e outras novas metodologias (ZABARAS; YANG, 1997; CAMPOS VELHO, 2001; VOGEL, 2002; OLIVEIRA, 2006). Alguns m´etodos s˜ao apresentados com exem-plos de aplica¸c˜ao:
1. M´etodo da Descida M´axima: determina o m´ınimo local iterativamente cons-truindo uma sequˆencia que minimiza a fun¸c˜ao que converge para a solu¸c˜ao do problema. Huang, Yuan e Ay (2003) resolveram um problema inverso tridimensional de condu¸c˜ao de calor para especificar a superf´ıcie do fluxo de calor de uma chapa com tubos para estabilizar a troca de calor. O m´etodo da Descida M´axima combinado com o c´odigo comercial CFX4.4 determinaram os coeficientes de transferˆencia de calor baseado na temperatura simulada por um m´etodo tomogr´afico infravermelho.
38 2.4 M´etodos de Solu¸c˜ao de Problemas Inversos
usou o m´etodo de Newton para resolver um problema inverso com um sis-tema de duas equa¸c˜oes n˜ao lineares, proveniente do estudo da propaga¸c˜ao de uma onda tridimensional em um meio anisotr´opico.
3. M´etodo de Levenberg-Marquardt: consiste em uma variante do m´etodo de Newton para a solu¸c˜ao de sistemas de equa¸c˜oes n˜ao-lineares. Em etapa inter-medi´aria, este m´etodo inclui uma regulariza¸c˜ao que apresenta equivalˆencia com a regulariza¸c˜ao de Tikhonov. O problema inverso ´e resolvido como um problema de otimiza¸c˜ao, de dimens˜ao finita, onde se busca minimizar o fun-cional dos res´ıduos quadrados. Silva Neto e ¨Ozisik (1995) usaram o m´etodo de Levenberg-Marquard de minimiza¸c˜ao para resolver o sistema de equa¸c˜oes n˜ao-lineares do problema inverso de estimar simultaneamente os coeficientes de uma fun¸c˜ao de fase, albedo de espalhamento simples e a espessura ´optica de um meio paralelo plano de escala anisotr´opica.
4. M´etodo dos Gradientes Conjugados: considera diretamente o problema de minimiza¸c˜ao do funcional construindo uma sequˆencia minimizante. O m´etodo tem sido usado com sucesso na solu¸c˜ao de problemas inversos de estimativa de fun¸c˜oes, pois possui duas qualidades muito importantes, uma ´e que a regulariza¸c˜ao est´a embutida na sua constru¸c˜ao e outra ´e que o m´etodo pos-sui boa eficiˆencia computacional. Bokar e ¨Ozisik (1995) usaram o m´etodo dos Gradientes Conjugados de minimiza¸c˜ao com problema adjunto para re-solver um problema inverso de estimar a temperatura de entrada de um escoamento laminar dentro de um duto de placas paralelas usando tempe-raturas transientes medidas por um termopar simples localizado na jusante de entrada.
como cruzamento e muta¸c˜ao (corresponde `as perturba¸c˜oes) a fim de criar uma nova popula¸c˜ao. Rolnik (2003) desenvolveu uma nova t´ecnica de re-constru¸c˜ao num´erica do problema de tomografia por impedˆancia el´etrica. O m´ınimo global do funcional de erro definido est´a relacionado com a imagem do escoamento sensoriado. O mau condicionamento do funcional de erro prejudica os m´etodos de otimiza¸c˜ao na obten¸c˜ao do m´ınimo. Ent˜ao para contornar os problemas encontrados, algoritmos gen´eticos foram utilizados uma vez que eles escapam de m´ınimos locais e n˜ao dependem da solu¸c˜ao inicial.
6. M´etodo de Decomposi¸c˜ao em Valores Singulares: usado quando um sistema de equa¸c˜oes ou matrizes s˜ao singulares ou numericamente perto de ser singu-lar. A matriz original passa a ser representada pelo produto de trˆes matrizes, duas ortogonais (possuem seus vetores ortogonais entre si e com m´odulos unit´arios) e uma diagonal (possui os vetores singulares da matriz original). Lagier, Lemonnier e Coutris (2004) usaram o m´etodo de decomposi¸c˜ao em valores singulares para resolver o sistema linear mal condicionado do pro-blema inverso de condu¸c˜ao de calor vari´avel. O propro-blema f´ısico consiste em identificar o fluxo de calor de uma chapa exposta a um fluido quente com temperaturas coletadas por termopares do lado oposto da chapa.
7. M´etodos Variacionais: minimiza um funcional de res´ıduo formado entre a solu¸c˜ao exata e a solu¸c˜ao aproximada do problema. Tessler e Sprangler (2005) formularam um princ´ıpio variacional para resolver um problema in-verso de reconstru¸c˜ao das deforma¸c˜oes de uma placa tridimensional sujeita a um carregamento transversal a partir de medidas experimentais. A formu-la¸c˜ao ´e baseada sob a minimiza¸c˜ao de um funcional dos m´ınimos quadrados.
40 2.5 T´ecnicas de Regulariza¸c˜ao
9. M´etodos Bayesianos: s˜ao procedimentos estat´ısticos para estimar parˆame-tros de uma informa¸c˜ao obtida anteriormente. Wang e Zabaras (2004) usa-ram a inferˆencia bayesiana aproximada para solucionar o problema inverso de condu¸c˜ao de calor, a fun¸c˜ao densidade de probabilidade posterior da su-perf´ıcie do fluxo de calor ´e calculada utilizando a medida da temperatura dentro de um s´olido condutor e o problema inverso ´e regularizado estatisti-camente atrav´es do modelo de distribui¸c˜ao obtidoa priori.
10. Redes Neurais: baseia-se no c´erebro humano, assim os elementos de pro-cessamento (neurˆonios) realizam tarefas de maneira paralelas e s˜ao aptos para aprender e tomar decis˜oes baseadas na aprendizagem. Utilizando esta t´ecnica, Dolenko et al. (2003) resolveu o problema inverso de determina¸c˜ao de temperatura de um espectro de emiss˜ao ´optica, em que os resultados do modelo de espectro em diferentes temperaturas, pr´e-processadas por outra rede neural trabalhando como uma mem´oria auto-associativa, foram usados para treinar a rede principal.
Muitos m´etodos surgem a cada dia, mas na sua maioria s˜ao t´ecnicas que tratam os dados a posteriori. Outras trabalham com os sinais em tempo real, mas tˆem longos c´odigos computacionais impossibilitando a implementa¸c˜ao em hardware dedicado.
2.5
T´
ecnicas de Regulariza¸c˜
ao
Independentemente da t´ecnica de resolu¸c˜ao do problema inverso ou da abor-dagem variacional ou funcional para a reconstru¸c˜ao da distribui¸c˜ao do coeficiente de convec¸c˜ao no objeto em estudo, as dificuldades s˜ao intr´ınsecas uma vez que o problema ´e mal posto e, provavelmente, sem solu¸c˜ao na ausˆencia de uma estrat´egia de regulariza¸c˜ao.
bif´asicos industriais em que as dificuldades de medi¸c˜ao se somam `as exigˆencias ligadas ao ambiente em que a medida deve ser realizada.
Uma primeira id´eia sugerida para trabalhar com o mau condicionamento de um problema foi dada por Tikhonov e Arsenin (1977), chamada de regulariza¸c˜ao. Os m´etodos de regulariza¸c˜ao, em geral, consistem na determina¸c˜ao da solu¸c˜ao aproximada mais suave compat´ıvel com os dados observados, para certo n´ıvel de ru´ıdo. O objetivo ´e limitar o efeito do aumento do erro proveniente dos dados atrav´es de alguma restri¸c˜ao imposta `a solu¸c˜ao.
Ent˜ao, ao inv´es de resolver o problema inverso diretamente, resolve-se um pro-blema levemente alterado por um parˆametro de regulariza¸c˜ao, perturbando os dados de tal forma que o problema mantenha tanto quanto poss´ıvel o comporta-mento do problema original. Diz-se que este novo problema levemente alterado ´e uma regulariza¸c˜ao do problema original. Entretanto, existe o problema de es-colher o melhor parˆametro de regulariza¸c˜ao, sabendo que para resolver problemas mal condicionados, informa¸c˜oes adicionais e de boa qualidade contribuem para uma melhor determina¸c˜ao da solu¸c˜ao.
Uma forma de avaliar se o parˆametro de regulariza¸c˜ao ´e ´otimo ´e calcular um funcional de erro entre o problema original e o problema regularizado. Quando este funcional se aproximar de zero ´e que a solu¸c˜ao do problema regularizado se aproxima da solu¸c˜ao do problema original. Nem sempre ´e aconselh´avel a obten¸c˜ao do funcional de erro igual a zero, uma vez que, na presen¸ca inevit´avel de erros, os erros na solu¸c˜ao do problema inverso podem ser minimizados por uma escolha criteriosa do valor de regulariza¸c˜ao. Deve-se, portanto, buscar o parˆametro de regulariza¸c˜ao ´otimo, de forma a se obter `a m´ınima altera¸c˜ao do problema original, mas com a desejada estabilidade da solu¸c˜ao.
42 2.5 T´ecnicas de Regulariza¸c˜ao
podem ser dispostos em um mesmo funcional.
De acordo com a teoria de problemas inversos, a reconstru¸c˜ao num´erica deste problema ´e tratada como um problema de minimiza¸c˜ao global. Assim, a t´ecnica de regulariza¸c˜ao proposta neste trabalho, baseia-se na constru¸c˜ao de uma pseudo-inversa da matriz Hessiana, do m´etodo de Newton, a partir da truncagem de sua Decomposi¸c˜ao em Valores Singulares, para a determina¸c˜ao do coeficiente de convec¸c˜ao, a partir de medidas n˜ao intrusivas.
Uma variedade de m´etodos tˆem sido propostos para resolver os problemas in-versos. No entanto, um m´etodo amplamente aceito para resolver problemas que envolvam matrizes mal condicionadas ´e a Decomposi¸c˜ao em Valores Singulares (SVD) para calcular sua pseudo-inversa. Esta t´ecnica, que ´e bem compreendida, facilmente implementada e direta, tem sido utilizada para resolver problemas in-versos de transferˆencia de calor na matriz de discretiza¸c˜ao do problema direto, e n˜ao na matriz Hessiana do problema de otimiza¸c˜ao como ´e proposto neste tra-balho.
onde as solu¸c˜oes anal´ıticas estavam dispon´ıveis.
Shen (1999) estudou a aplica¸c˜ao de dois m´etodos de elementos de contorno, o m´etodo da coloca¸c˜ao e o m´etodo dos res´ıduos ponderados, para a solu¸c˜ao do problema inverso de condu¸c˜ao de calor unidimensional. Quando os m´etodos num´ericos s˜ao diretamente aplicados sobre um problema inverso de condu¸c˜ao de calor, sistemas lineares mal condicionados s˜ao inevit´aveis. Assim, mostrou-se que os n´umeros de condi¸c˜ao das matrizes que representam estes sistemas aumentam exponencialmente em fun¸c˜ao do n´umero de passos de tempo, se o intervalo de tempo ´e fixo. Por causa do mau condicionamento do sistema linear, um trata-mento especial nesse sistema ´e necess´ario e foi usado o m´etodo de decomposi¸c˜ao em valores singulares truncados (TSVD) e dois m´etodos de regulariza¸c˜ao de Tikho-nov para estabilizar esse sistema linear. Consideravelmente um grande n´umero de passos de tempo foram usados para testar a confiabilidade desses m´etodos. Neste trabalho foi testado o m´etodo da coloca¸c˜ao com o m´etodo TSVD e o m´etodo dos res´ıduos ponderados com a regulariza¸c˜ao de Tikhonov e Tikhonov generalizada. O m´etodo TSVD ignora as partes oscilat´orias da solu¸c˜ao para evitar grandes erros num´ericos. Um m´etodo de regulariza¸c˜ao tamb´em sacrifica a precis˜ao para alcan¸car um sistema linear bem condicionado. Os resultados apresentados mostram que os m´etodos diretos n˜ao s˜ao aplic´aveis at´e mesmo para um n´umero pequeno de ele-mentos. O m´etodo de decomposi¸c˜ao em valores singulares truncado requer muito mais c´alculos do que os m´etodos de regulariza¸c˜ao tradicional, mas os resultados para a regulariza¸c˜ao s˜ao melhores que os do m´etodo de decomposi¸c˜ao em valores singulares.
ma-44 2.5 T´ecnicas de Regulariza¸c˜ao
trizes de decomposi¸c˜ao que est˜ao associadas com pequenos valores singulares que foram mostrados estar associados com as frequˆencias onde a rela¸c˜ao sinal/ru´ıdo ´e pequena. As vantagens do m´etodo s˜ao que as matrizes de ordem reduzida per-mitem estimar o fluxo de calor a ser obtido a partir de dados de temperatura contendo grande quantidade de ru´ıdo e n˜ao h´a parˆametrosad hoc para especificar o processo de filtragem a fim de obter resultados razo´aveis.
3
Modelagem do Problema de
Transferˆencia de Calor
A solu¸c˜ao do problema de tomografia t´ermica requer a solu¸c˜ao de uma equa¸c˜ao diferencial parcial que rege a temperatura dentro do dom´ınio. Para isso, s˜ao ne-cess´arias condi¸c˜oes de contorno adequadas que simulem o processo de est´ımulo e resposta (ou excita¸c˜ao e medi¸c˜ao). Por´em, algumas destas condi¸c˜oes de contorno, bem como propriedades termof´ısicas internas, podem ser desconhecidas e, por-tanto, a equa¸c˜ao diferencial n˜ao pode ser resolvida. Faz-se necess´ario introduzir informa¸c˜oes adicionais para suprir esta deficiˆencia, o que pode ser feito atrav´es da imposi¸c˜ao de condi¸c˜oes de contorno redundantes nas fronteiras acess´ıveis do dom´ınio. Assim, dados experimentais s˜ao confrontados com a formula¸c˜ao ma-tem´atica, constituindo um funcional de erro cuja minimiza¸c˜ao corresponde a solu¸c˜ao procurada. Este cap´ıtulo apresenta a formula¸c˜ao do problema direto cuja solu¸c˜ao requer um m´etodo de discretiza¸c˜ao como, por exemplo, o m´etodo dos elementos finitos.
3.1
Formula¸c˜
ao Matem´
atica
Na tomografia t´ermica a rela¸c˜ao entre a distribui¸c˜ao espacial da condutivi-dade t´ermica k e a temperatura θ podem ser derivadas a partir do princ´ıpio de conserva¸c˜ao de energia. Ap´os algumas simplifica¸c˜oes, a equa¸c˜ao que governa a condu¸c˜ao de calor bidimensional pelo potencial t´ermico θ no dom´ınio ´e dada por
− →
∇ ·(−k−→∇θ) = 0 em Ω, (3.1)
46 3.2 Formula¸c˜ao Num´erica
em que Ω denota o dom´ınio do problema.
A intera¸c˜ao entre Ω e o ambiente externo ocorre por meio de seu contorno ∂Ω e ´e definida pelas rela¸c˜oes entre excita¸c˜ao e resposta t´ermicas. Em termos pr´aticos isso pode ser realizado aplicando-se um fluxo de calor sobre o contorno e medindo a distribui¸c˜ao de temperaturas resultantes. Neste trabalho considera-se as seguintes condi¸c˜oes de contorno
θ =θ0 em ∂Ω1, (3.2)
−k∂θ
∂n =hθ+q em ∂Ω2, (3.3)
em que n ´e o vetor normal, h ´e o coeficiente de convec¸c˜ao e q ´e o fluxo de calor imposto no contorno. As equa¸c˜oes (3.1)–(3.3) se possu´ırem parˆametros total-mente conhecidos formam um problema matematicatotal-mente bem posto, podendo ser resolvido por t´ecnicas num´ericas convencionais (BORCEA, 2002). No caso da tomografia t´ermica isso n˜ao ocorre: al´em da vari´avelθum ou mais parˆametros, por exemplo h, podem ser desconhecidos em partes do contorno. Assim, a estrat´egia para a solu¸c˜ao consiste em suprir esta deficiˆencia de informa¸c˜ao atrav´es da medi¸c˜ao de condi¸c˜oes de contorno redundantes nas partes acess´ıveis do contorno ou do dom´ınio.
A equa¸c˜ao (3.2) imp˜oe a condi¸c˜ao de Dirichlet, ou seja, temperaturas prescri-tas no contorno. A equa¸c˜ao (3.3) imp˜oe a condi¸c˜ao de contorno mista, ou seja, o acoplamento entre a condu¸c˜ao e a convec¸c˜ao de calor.
3.2
Formula¸c˜
ao Num´
erica
3.2.1
M´
etodo dos Elementos Finitos
A aplica¸c˜ao do m´etodo dos elementos finitos (MEF) (ASSAN, 1999; BECKER; CAREY; ODEN, 1981; CAREY; ODEN, 1984; HUNTER; PULLAN, 2002; MEN-DONC¸ A, 2005) foi escolhida para discretizar as equa¸c˜oes do problema por mos-trar vantagens expressivas em rela¸c˜ao ao m´etodo das diferen¸cas finitas (MDF) (CUNHA, 2000; FORTUNA, 2000). Algumas dessas vantagens s˜ao:
• Dom´ınio particionado em c´elulas (elementos), as quais podem assumir di-versas formas como, por exemplo, triangulares ou quadril´ateras e retil´ıneas ou curvil´ıneas. Uma vez que a malha pode ser n˜ao estruturada, geometrias complexas podem ser tratadas com facilidade (HUNTER; PULLAN, 2002).
• A solu¸c˜ao de interesse ´e a solu¸c˜ao de alguma forma integral da equa¸c˜ao dife-rencial parcial. A formula¸c˜ao integral ´e, em geral, obtida de uma formula¸c˜ao residual ponderada, a qual permite que o m´etodo incorpore, de maneira na-tural, diversos tipos de condi¸c˜ao de contorno (ZIENKIEWICZ; TAYLOR, 2000).
• A matriz do sistema alg´ebrico gerada pelo m´etodo ´e sim´etrica, positiva-definida, esparsa e dependendo da numera¸c˜ao dos n´os e elementos pode ser banda. A simetria da matriz (aij = aji, ∀i, j), a positividade (xT.A.x≥ 0,
∀x6= 0) e a esparsidade podem ser confirmadas adiante atrav´es da equa¸c˜ao resultante da discretiza¸c˜ao.
Os passos para obten¸c˜ao do sistema linear mediante o uso do MEF est˜ao descritos a seguir.
De acordo com a equa¸c˜ao governante (3.1), o res´ıduo R de uma solu¸c˜ao apro-ximada θ(x, y), ´e definido por
R(x, y) = −−→∇ ·[k(x, y)−→∇θ(x, y)]. (3.4)
48 3.2 Formula¸c˜ao Num´erica
m´edia ponderada resultante de R igual a zero, ou seja, Z
Ω
[−−→∇ ·(k−→∇θ)]v dx dy = 0. (3.5)
A maior vantagem da equa¸c˜ao integral ´e que a ordem das derivadas dentro da integral pode ser reduzida de 2 para 1 pela integra¸c˜ao por partes. Usando a regra da diferencia¸c˜ao do produto (BECKER; CAREY; ODEN, 1981), tem-se que
v[−→∇ ·(k−→∇θ)] =−→∇ ·[vk→−∇θ]−k−→∇θ·−→∇v. (3.6)
Substituindo (3.6) em (3.5) tem-se Z
Ω n−→
∇ ·[vk−→∇θ]−k−→∇θ·−→∇vodx dy = 0. (3.7)
A integral (3.7) pode ser transformada numa integral de contorno usando o teorema do divergente. Assim,
Z
Ω
− →
∇ ·[vk−→∇θ]dx dy= Z
∂Ω k∂θ
∂nv ds, (3.8)
em que ∂θ/∂n=−→∇θ· −→n.
Reescrevendo a equa¸c˜ao (3.8) tem-se Z
Ω
k−→∇θ·−→∇v dx dy− Z
∂Ω k∂θ
∂nv ds= 0. (3.9)
Como ∂Ω = ∂Ω1∪∂Ω2 ent˜ao a equa¸c˜ao (3.9) torna-se Z
Ω
k−→∇θ·−→∇v dx dy− Z
∂Ω1 k∂θ
∂nv ds− Z
∂Ω2 k∂θ
∂nv ds = 0. (3.10) Como a ´unica restri¸c˜ao sobre v ´e que seja suave, pode-se arbitrar v = 0 em ∂Ω1. Substituindo a condi¸c˜ao de contorno (3.3) na integral de contorno em (3.10),
assume-se Z
Ω
k−→∇θ·−→∇v dx dy+ Z
∂Ω2
E
a b
c
1 2 3 4
6 7 8 9
1 3 1 4 1 5 1 6
1 8 1 9 2 0 2 1
1 0 1 1 1 2
1 7 5 1 2 3 4 5 6 7 8 1 0 9 1 1 1 2 1 4 1 3 1 5 1 6 1 8 1 7 1 9 2 0 2 1 2 2 2 4 2 3 2 5 2 6 2 7 2 8
( b )
( a )
D
Figura 3.1: (a) Exemplo de um dom´ınio discreto contendo o subdom´ınio dos elementos e seus respectivos n´os; (b) elemento triangular adotado para os c´alculos.
apenas valores nodais em seus v´ertices. Para uma varia¸c˜ao quadr´atica ou de or-dem superior s˜ao necess´arios n´os adicionais que poor-dem ser definidos nos pontos m´edios de suas arestas, baricentros, etc.
A equa¸c˜ao (3.11) ser´a aplicada tantas vezes quantos forem os n´os cujas tem-peraturas forem desconhecidas gerando assim um n´umero suficiente de equa¸c˜oes para que sejam determinadas. Em particular, no m´etodo dos elementos finitos a fun¸c˜ao de pondera¸c˜ao v tem uma forma especial assumindo valor unit´ario no n´o cuja temperatura ´e desconhecida e zero nos demais n´os que o circundam. A Figura 3.2 ilustra melhor a fun¸c˜ao de pondera¸c˜ao.
1 0 0 0 0 0
50 3.2 Formula¸c˜ao Num´erica
Assim, o res´ıduo correspondente ao n-´esimo n´o, denotado por Rn, se escreve
como
Rn=
X
E
∆RE,n+
X
D
∆RD,n, (3.12)
ou seja, a soma dos res´ıduos dos elementos que tˆem o n´onem um de seus v´ertices, sendo RE,n o res´ıduo do E-´esimo elemento interno e RD,n o res´ıduo do D-´esimo
elemento de contorno. O res´ıduo dos elementos internos podem ser calculados por
∆RE,n =
Z
Ω
k−→∇θ·−→∇v dx dy= Z
Ω
k(x, y)−→∇θ(x, y)·−→∇φn(x, y)dx dy= 0. (3.13)
Para que as integrais dos res´ıduos associados a cada elemento n˜ao precisassem ser calculadas numericamente, express˜oes anal´ıticas extremamente complexas fo-ram deduzidas e implementadas computacionalmente. Esta escolha proporcionou um ganho de tempo crucial nos testes realizados, tendo em vista que o custo computacional revelou-se um fator importante neste trabalho.
Sejaφuma fun¸c˜ao triangular que depende apenas das coordenadas dos v´ertices do elemento triangular, definida por
φi =
1
Area(αi+βix+γiy), i={a, b, c} com Area= 1 2 ¯ ¯ ¯ ¯ ¯ ¯
1 xa ya
1 xb yb
1 xc yc
¯ ¯ ¯ ¯ ¯
¯, (3.14) em que
αi =xjyk−xkyj,
βi =yj −yk, i, j, k={a, b, c},
γi =xk−xj.
(3.15)
e{a, b, c}denotam os n´umeros dos n´os que definem oE-´esimo elemento, conforme mostrado na Figura 3.1(b).
As vari´aveis θ ek s˜ao aproximadas por
θelemento(x, y) = θaφa(x, y) +θbφb(x, y) +θcφc(x, y), (3.16)
kelemento(x, y) = kaφa(x, y) +kbφb(x, y) +kcφc(x, y). (3.17)
Substituindo (3.16) e (3.17) em (3.13) tem-se que
∆RE,n =
Z
Ω
Reescrevendo a equa¸c˜ao (3.18), tem-se
∆RE,n = θa
Z
Ω
[kaφa+kbφb+kcφc]−→∇φa·−→∇φndx dy+
+θb
Z
Ω
[kaφa+kbφb+kcφc]−→∇φb·−→∇φndx dy+
+θc
Z
Ω
[kaφa+kbφb+kcφc]−→∇φc·−→∇φndx dy. (3.19)
Simplificando a equa¸c˜ao anterior, tem-se
∆RE,n =θaAa,n+θbAb,n+θcAc,n, (3.20)
em que
Aa,n =
Z
Ω
[kaφa+kbφb+kcφc]−→∇φa·−→∇φndx dy =
= Z
Ω
[kaφa+kbφb+kcφc]
·
βa
2Areaˆi+
γa
2Areaˆj
¸ ·
·
βn
2Areaˆi+
γn
2Areaˆj
¸
dx dy=
= βaβn+γaγn
(2Area)2
·
ka
Z
Ω
φadx dy+kb
Z
Ω
φbdx dy+kc
Z
Ω
φcdx dy
¸
, (3.21)
Ab,n =
Z
Ω
[kaφa+kbφb+kcφc]−→∇φb·−→∇φndx dy =
= Z
Ω
[kaφa+kbφb+kcφc]
·
βb
2Areaˆi+
γb
2Areaˆj
¸ ·
·
βn
2Areaˆi+
γn
2Areaˆj
¸
dx dy =
= βbβn+γbγn
(2Area)2
·
ka
Z
Ω
φadx dy+kb
Z
Ω
φbdx dy+kc
Z
Ω
φcdx dy
¸
, (3.22)
Ac,n =
Z
Ω
[kaφa+kbφb+kcφc]−→∇φc·−→∇φndx dy=
= Z
Ω
[kaφa+kbφb+kcφc]
·
βc
2Areaˆi+
γc
2Areaˆj
¸ ·
·
βn
2Areaˆi+
γn
2Areaˆj
¸
dx dy =
= βcβn+γcγn
(2Area)2
·
ka
Z
Ω
φadx dy+kb
Z
Ω
φbdx dy+kc
Z
Ω
φcdx dy
¸
, (3.23)
e αn, βn e γn s˜ao calculados pela equa¸c˜ao (3.15) quando um dos ´ındices {a, b, c}
corresponde ao n´o pivˆo n. Considerando
Ia =
Z
E
φadx dy, Ib =
Z
E
φbdx dy, e Ic =
Z
E
52 3.2 Formula¸c˜ao Num´erica
As equa¸c˜oes (3.21), (3.22) e (3.23) tornam-se
Aa,n =
βaβn+γaγn
(2Area)2 h
kaIa+kbIb+kcIc
i
, (3.25)
Ab,n =
βbβn+γbγn
(2Area)2 h
kaIa+kbIb+kcIc
i
, (3.26)
Ac,n =
βcβn+γcγn
(2Area)2 h
kaIa+kbIb+kcIc
i
. (3.27)
Empregando a mudan¸ca de vari´aveis abaixo:
x=rxξ+sxη+tx,
y=ryξ+syη+ty,
em que
rx = xb −xa ry =yb−ya
sx = xc−xb e sy =yc−yb
tx = xa ty =ya
e tomandopum ponto qualquer, as integrais da equa¸c˜ao (3.24) podem ser escritas como uma integral geral Ip, em quep assume um dos valores{a, b, c}. Assim,
Ip =
Z
E
φp(x, y)dx dy,=
Z
E
φp(x(ξ, η), y(ξ, η))
¯ ¯ ¯ ¯ ¯ ∂x ∂ξ ∂x ∂η ∂y ∂ξ ∂y ∂η ¯ ¯ ¯ ¯
¯ dξ dη = =
Z
E
φp(x(ξ, η), y(ξ, η))
¯ ¯ ¯
¯ rrxy ssxy
¯ ¯ ¯
¯ dξ dη = = rxsy −rysx
2Area Z
E
h
αp+βp(rxξ+sxη+tx) +γp(rxξ+sxη+tx)
i
dξ dη =
= rxsy −rysx 2Area
½ 1 2αp+
βp
6(2rx+sx+ 3tx) + γp
6(2ry+sy + 3ty) ¾
. (3.28)
Substituindo (3.28) em (3.24), tem-se
Ia=
xa(yb−yc) +xb(yc−ya) +xc(ya−yb)
2Area
½ 1
2αa+
βa
6 (xa+xb+xc)+
γa
6 (ya+yb+yc)
¾ ,
(3.29)
Ib =
xa(yb−yc) +xb(yc−ya) +xc(ya−yb)
2Area
½ 1
2αb+
βb
6 (xa+xb+xc)+
γb
6(ya+yb+yc)
¾ ,
Ic=
xa(yb−yc) +xb(yc−ya) +xc(ya−yb)
2Area
½ 1
2αc+
βc
6 (xa+xb+xc)+
γc
6 (ya+yb+yc)
¾ .
(3.31)
Considerando a possibilidade de realizar uma valida¸c˜ao dos resultados num´eri-cos com dados experimentais, ´e conveniente reescrever essas express˜oes em fun¸c˜ao da temperatura T, em que T = θ+T∞ e T∞ ´e a temperatura ambiente. Desse
modo, reescrevendo a equa¸c˜ao (3.20) tem-se
∆RE,n =
X
i=a,b,c
θiAi,n =
X
i=a,b,c
(Ti−T∞)Ai,n=
X
i=a,b,c
TiAi,n−
X
i=a,b,c
T∞Ai,n. (3.32)
Substituindo os valores deIa,Ib eIcnas equa¸c˜oes (3.25), (3.26) e (3.27), e estas
equa¸c˜oes em (3.32), termina-se o c´alculo dos ∆RE,n. Desse modo, s˜ao obtidos os
valores da temperatura T no dom´ınio.
O pr´oximo passo ´e tratar a condi¸c˜ao de contorno mista, ou seja, a integral de contorno da equa¸c˜ao (3.11), ou os termos do segundo somat´orio da equa¸c˜ao (3.12). Desse modo, o c´alculo ´e feito da seguinte maneira
∆RD,n=
Z
∂Ω2
[hθ+q]·v ds = Z
∂Ω2
[hθ+q]·φndu, (3.33)
e considerando u=s[(xd−xe)2+ (yd−ye)2]1/2, du=ds[(xd−xe)2+ (yd−ye)2]1/2,
a integral (3.33) torna-se
∆RD,n =
Z 1 0
[h(s)θ(s) +q(s)]φn(s)ds[(xd−xe)2+ (yd−ye)2]1/2. (3.34)
Substituindox(s) =xe+s(xd−xe),y(s) =ye+s(yd−ye),h(s) = he+s(hd−he)
e q(s) = qe+s(qd−qe) na equa¸c˜ao (3.34), tem-se que
∆RD,n =
Z 1
0 {
[he+s(hd−he)]
X
i=a,b,c
θi
1 2Area
³
αi+βi[xe+s(xd−xe)] +
+γi[ye+s(yd−ye)]
´
+ [qe+s(qd−qe)]
1 2Area
³
αn+βn[xe+s(xd−xe)] +
+γn[ye+s(yd−ye)]
´
ds[(xd−xe)2+ (yd−ye)2]1/2,