Journal of Applied Fluid Mechanics, Vol. 9, No. 3, pp. 1265-1272, 2016. Available online at www.jafmonline.net, ISSN 1735-3572, EISSN 1735-3645.
Effect of Rotation on Natural Convection in Differentially
Heated Rotating Enclosure by Numerical Simulation
M. Narendra Kumar
1G. Pundarika
2K. Rama Narasimha
3†and K. N. Seetharamu
41,3
Centre for Emerging Technologies, Jain University, Bangalore, Karnataka, 562112, India 2
Government Engineering College, Ramanagara, Karnataka, 571511, India 4
PES University, Bangalore,Karnataka, 560085, India
†Corresponding Author Email:k.ramanarasimha@gmail.com
(Received May 6, 2014; accepted June 24, 2015)
ABSTRACT
Natural convection heat transfer in a two dimensional unsteady rotating differentially heated enclosure is studied numerically in this paper. The enclosure is filled with air and executes a steady counterclockwise rotation about the centre of the enclosure. A finite volume code on a staggered grid arrangement with TDMA algorithm is developed and employed to solve the governing equations subject to Boussinesq approximation. The numerical investigation is carried out for fixed Prandtl number equal to . , Rayleigh number equal to . while Taylors number vary from . . and Rotational Rayleigh number from
. . .Results reveal that there are considerable change in heat transfer rates beyond 15 rpm. The effect of rotation on the Nusselt number for a given Rayleigh number is shown in the present work which is not normally indicated and discussed in the available literature
Key words: Rotating enclosure; Natural convection; Coriolis force; Heat transfer.
NOMENCLATURE
k thermal conductivity (W/m-K) L length of the enclosure (m) Nu local Nusselt number P dimensionless pressure
p,Pm pressure and motion pressure (N/m2) Pr Prandtl number
Ra Rayleigh Number Raw rotational Rayleigh number
system
T temperature (K) t time (s) Ta taylor number
u, v dimensional velocity components (m/s) U, V dimensionless velocity components X, Y dimensionless Cartesian coordinate x,y dimensional Cartesian coordinate system
Ω magnitude of angular rotation rate (rpm, rad/s)
α thermal diffusivity (m2/s)
τ dimensionless time
θ dimensionless temperature angular position of enclosure (o)
ρ density (kg/m3)
μ dynamic viscosity (Pas)
Subscript
c cold h hot f fluid
Superscript
- space average = Time average
1.
INTRODUCTION
The fluid flow and heat transfer characteristics of a rotating enclosure were treated in detail according to its functional and practical importance in the thermal management. The unsteady rotating
M. Na temper failure rotatin turbine experi in a w layer
increa trend i numbe mercu therma box fi roll ce numbe of a experi (1994) arising influen rotatin differe Signifi the rot Raylei in heat reporte al.(200 rectang They betwee circula oscilla reduce effects therma on a di al.(200 Howev natura heated natura convec flow import neglec state o to refl fluid, (Boub A det differe especi Coriol same f challen reporte In the effects enclos walls. charac rate ar
arendra Kumar e
rature and vibr es. There had b ng ducts, for ins e blades by Lin mentally obser water layer for
for
,the Nuss se with the T is the case for er, oscillatory ury. Buhler an
al cellular conv illed with a vis ells changed ori
er. The flow an rotating squ mentally and n ). They conclu g from rotatio nce on heat tra ng results. Ker a ential heated ficant flow mo
tational Raylei igh number. A t transfer could ed by Baig 05)carried ou gular enclosur found that rot en clockwis ations, increase ations of Nuss es the average p s of Coriolis al buoyancy fo
ifferentially hea 07)
ver, there are al convection d sources in al convection i ction because
where as the tant role and th cted. In a sense, on earth, since ect the effect o is about unity nov and Golitsy
tailed 3-D num entially heated
ally with the in lis force and c frame. When th nging and use ed by Jin et al.
e present work s of rotation on sure, with differ The effect cteristics of flu re considered.
et al. /JAFM, V
ration amounts been many stu stance in relatio n et al. (2001) rved the subcr r
. In addition elt number w Taylor number
air. Besides, a convection i nd Oertel (198 vection in a rota scous fluid and entation with in nd heat transfe uare enclosur numerically by uded that the on may have ansfer when co and Lin (1996, rotating cu difications are igh number is
significant incr d be achieved d et al.(2001, ut numerical
re with discre tation results in se and co es heat transfer selt number. performance in force, centrifu rce are segrega ated square enc
limited studie cooling from rotation. The is very differe
the latter is e centrifugal f he thermal buo , there is no abs Taylor number of Coriolis forc y at the equat
yn 1995).
merical compu source conditio nfluence of the entrifugal forc he enclosure is r
ful to study a (2005).
k, it is intende n natural convec rentially heated of rotational uid flow as we
Vol. 9, No. 3, p
s to 75% of a udies on flow i on to cooling o . Rossby (1969 ritical instabilit
and in an ai n, for water a was found t r. The opposit at a large Taylo is preferred i 82) studied th ating rectangula d found that th ncreasing Taylo er characteristic e are studie y Hamady et a Coriolis forc e a remarkabl ompared to no 1997) studied ubic enclosure obtained whe greater than th rease or decreas due to rotation a 2006). Jin e studies on te heat source n an imbalanc ounter-clockwis and reduces th It improves o each cycle. Th fugal force an ated numericall closure by Tso e
es on unstead m differentiall situation wit ent from force pressure-drive force plays a oyancy effect i solute stationar r, normally use e in the rotatin torial sea leve
utation for thi on is formidable buoyancy force e all within th rotated, it is sti a 2-D model a
ed to study th ction in a squar d top and bottom
speeds on th ell heat transfe
pp. 1265-1272, all in of 9) ty ir at to te or in he ar he or cs ed al. ce le on a e. en he se as et a e. ce se he or he nd ly et dy ly th ed en an is ry ed ng el. is e, e, he ll as he re m he er
2.
The sch under in time stationar enclosur clockwis surface temperat subjecte walls a surround position the enc rotation the Bou 1982; K density both the terms r buoyanc equal to and developmFig. 1. The con are u v x y 2 u u t g ( v u t g y 2016.
MATHEMA
FORMULA
hematic diagra nvestigation is d, the enclosu ry and isoth re executes a se rotation ab at ⁄ is ture and d to uniform are thermally dings. The in
of the enclosu closure is sim and the therm ussinesq approx Ker and Lee 199 variation with
body force and representing th cies and Corio
ment can be de
Schematic rep s ntinuity, mome 0 1 ( )sin(
2 ( )
o c c u u v x y
T T t
v T T
1 ( )cos(
) 2 2 (
o c v v v x y T T
y u T
ATICAL
ATION
am of the phy depicted in Fig ure and inside hermal at . A a steady unif bout a horizon subjected the surface temperature well insulate n Fig. 1 define ure. Thus the a multaneously d mal buoyancies ximation, (Buhl
96 and Jin et al temperature is d centrifugal fo he thermal a olis force are,
,
. The scribed as follo
presentation of system.
entum and ene
2 2 ) c p u x xt T T
v
2 2 ) ( ) o c c p v y xt T T
T T u
ysical system g.1. Initially at e air are both
At ,the form counter ntal axis. The
to uniform at ⁄ ,
. The lateral ed from the es the angular air flow inside driven by the
. By adopting ler and Oertel l. 2005) linear considered in rce terms. The and rotational
respectively,
Ω Ω
resulting flow ows:
f the physical
2 2
2 2 (4)
T T T T T
u v
t x y x y
Boundary Conditions are
0 0
2
0 0
2
(5) 0
2
0 2
c
h
L T
At x , u v , x
L T
At x , u v , x L
At y , u v , T T
L
At y , u v , , T T
With the motion pressure defined as
2 2 2 2
1 1
sin( ) cos( )
2 2
m
P x y gx t gy t
(6) As mentioned by Vanyo (1993) in a rotating Eulerian coordinate system the centrifugal term can be included in the pressure term and disappears from the typical rotating fluid computation. With Boussinesq approximation, the main part of the centrifugal force term is combined with the pressure term and others are caused by density change and centrifugal buoyancy. The governing equations can be converted to non-dimensional forms using the non-dimensional parameters as indicated in (7).
2
2 2
3
2 4 2 4
2
Pr
4
m
h c
c
h c
h c
w
x y uL vL tα P L
X Y U V τ P
L L α α L ρα
g T T L
T - T
θ Ra
T - T
T T L L
Ra Ta
(7) The Coriolis buoyancy force is neglected as
| | in the present study [Jin et al. (2005)]. The dimensionless governing equations and boundary conditions are written as
follows:-Continuity equation:
0 (8)
U V
X Y
Momentum equations:
2 2
2 2
0.5
0.5
Pr
sin 0.5 (9)
w
U U U P U U
U V Pr
X Y X X Y
Ta V Ra Pr X
RaPr Ta Pr
2 2
2 2
0.5
0.5
Pr
cos 0.5 (10)
w
V V V P V V
U V Pr
X Y Y X Y
Ta U Ra Pr X
RaPr Ta Pr
Energy equation:
2 2
2 2 (11)
U V
X Y X Y
Boundary Conditions:
0.5 0 0
0.5 0 0 (12)
0.5 0 0.5
0.5 0 0.5 θ
At X , U V ,
X θ At X , U V ,
X At Y , U V , At Y , U V ,
The above formulation clearly shows that the flow to be examined is governed by dimensionless parameters, namely Prandtl number, Rayleigh number and Taylor number and rotational Rayleigh number. The rotational Rayleigh number reflects the effect of the rotational buoyancy force which depends on the other non-dimensional parameters. The rotational buoyancy becomes important when the rotational speed is high or the enclosure dimensions are too large, viz is whenΩ L is much larger than g (Lin et al. 1996).
The fluid motion is displayed using the stream function obtained from the velocity components and and the temperature fields using the isotherms. In addition to the time evaluation of velocity and temperature fields, results for the local, spaced averaged and time space averaged Nusselt number on the heated or cooled wall are important in thermal design and can be evaluated from
0 5 0.5
0.5 2
0
(13)
1 2
Y .
n
Nu Y
Nu NudX
Nu Nud
n
3. SOLUTION
METHODOLOGY
line-by-M. Na
line enforc at eac proced equati the pr conver the su variab been e the obtain chosen Code develo convec
4.
The an is perf
.
explici indepe as
4.1 G
Unifor enclos examin density from indepe consid Consid compu chosen
Fig. 2 size
As a v the iso Hamad shown
arendra Kumar e
application o cing under-rela
ch time step dure, the m ons are used to revious calcul rgence of the m of the absol bles between t evaluated. Whe
convergence ned. The conv
n as in th based on oped indigeno ction problem
. RESULTS
nalysis in the p formed in the fo
. , . , a
is not disc itly. This is d endent paramet well as on
Grid Testing
rm grid distrib sure. The eff
ned in order t y. Appropriate
endence. After derable change dering the a utational time n for the presen
2. Grid indepen
for .
validation, the otherms compa dy et al. (1994 n in Fig. 3.
et al. /JAFM, V
of the TDM axation to ensu
considered. I motion pressu o derive the new
ated velocity. sequential ite lute differences two successive en this summat criterion, co vergence crite his study. A de Finite Volum ously to solv in enclosure w
S AND DISC
present numeric ollowing dimen
. ,
and .
cussed except due to the
ter but depend Ta. Other pa
and Code Va
bution is used fect of grid to select the a grid densities are consider r grid in the average N accuracy requ
involved, a nt study as exhib
ndency study
, .
.
present results are well with t 4) and with. Jin
Vol. 9, No. 3, p
MA algorithm ure convergenc In the iteratio ure correctio w velocity from
To check th erative solution s of the solutio e iterations ha tion falls below onvergence i erion has bee edicated Fortra me Method i ve the natura with rotation.
CUSSION
cal investigatio nsionless groups
.
.
t to specify not being a ding on an arameter isΩ
alidation
d for the whol resolution wa appropriate gri among a rang red to study gri ds, there is n Nusselt number uired and th grid i bited in Fig. 2.
Nuversus grid
of the code fo that obtained b n et al.(2005) a
pp. 1265-1272,
m, ce on on m he n, on as w is en an is al
on s:
it an nd
le as id ge id no r. he is
d
or by as
Fig. 3. pres (left) (b)
Fig. 4. isotherm the expe the two with present experim
Fig. 4. prese
(b)
Fig. 5 a dimensio length o different compare figures s with th (1994).
Fig. 5. temp
2016.
. Comprasion sent work (mid
) and with Jin °,
(a) and (b) ms of the presen
erimental work angular position
° and case very clos mental work.
. Comprasion ent work with
) °,
and 6 show the onless temper of the enclosure
t positions edwith that of H
show good agr e experimenta
Comprasion o erature along
. , .
of computed I ddle) with Ham
et al. (right) (a . ,
shows the h nt work matche of Hamady et n of the enclosu ° . The iso sely match wit
of computed I Hamady et al.
. ,
e variation of t rature along e of the present
of the Hamady et al. reement of the al work of H
of computed d dimensiomless
sotherms of mady et al.
a) ° , . .
half sectioned ed with that of
al. (1994) for ure considered otherms of the th that of the
Isotherms of
.(a) °
. .
the computed dimensionless t work at two enclosureand (1994). These present work amady et al.
imensionless s length for
Fig .6. Com tempera for
Close agreem results of Ham governing eq the present sim
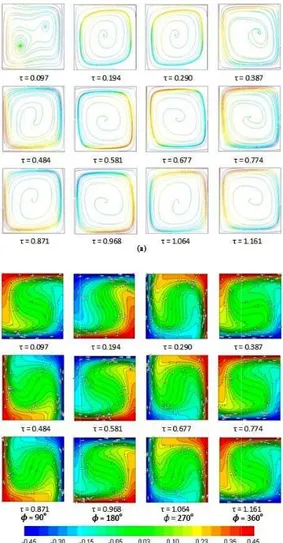
4.2 Effect
Temperatu
Fig. 7 (a) to F Fig. 7 (b) to F different rota figures repres where the hot left vertical p positionwhere relatively the column for wall occupy t the last colu isothermal wa position of th
For a fixed
Ω ,
dominating fo Coriolis force the Taylor nu magnitude of a function o buoyancy is 7(a) shows m function. The near isotherm the core as
, the s formation of magnitude c isotherms in F stratification convective m Coriolis force their magnitu thermal buoy disruption tak thermal and decrease of h Taylor numb order. Further
Ω
change in the rolls as evid
mprasion of com ature along dim
. ,
ment is obtaine mady et al. (19 quations and th
mulation result
of Rotati
re Fields
Fig 10(a) repre Fig. 10 (b) show
tional speed. T sents the po t isothermal wa position, the se e the hot iso e bottom horizo position w the relatively ri umn for
all occupy relat he enclosure.
. , the thermal orce compared es due to the fa umber is smalle f Rayleigh numb
of Taylor num a function of multi cellular e isotherms sho mal walls with
s evident fro stream function f multiple ro ompared to th Fig. 8 (b) depic in the core motion in the co
es are stronger ude is quite s yancy. Stable s kes place by o d Coriolis for
heat transfer, a ber and Raylei r increase in ro
andΩ e pattern format dent in Fig. 9
mputed dimen mensiomless len
. .
ed when compa 994), who used his gives confi ts.
ion on Flo
sents the stream ws isotherm cou The first column osition of the e all occupy relat econd column othermal wall ontal position, where the hot is ght vertical pos positionwhere tively the top h
.
buoyancy to smaller mag act that the mag er when compar ber. As Corioli mber and the
Rayleigh num roll pattern o ow thin bound stable stratific om Fig. 7(b). n [Fig. 8(a)] aga olls of slightl he previous c ct beginning of signifying inc re of the enclos near the walls small compare tratification of opposing intera rces which re as the magnitud igh number is otation correspo
, itresults in tion of stream
(a) and 10 (a
nsionless ngth
ared with the same idence to
ow and
mline and unters for n in these enclosure, tively the for occupy
the third sothermal sition and e the hot horizontal
and at is the gnitude of gnitude of red to the is force is thermal mber, Fig.
of stream ary layer cation of . AtΩ ain shows ly larger ase. The f unstable crease in
sure. The s but still ed to the f the core
action of esults in de of the
of same onding to n drastic functions a). These
f t r C t t c I o e s d c s
4
F
Ω
l c a s s e s
figures show f towards the iso rolls are prima Coriolis forces the streamline the magnitude compared to th Isotherms in Fi of spiral shap enclosure wh stratification of dominant force cold wall whic shaped isotherm
Fig. 7. (a) Stre contours for
4.3 Effect of
For low rota
Ω , th
local peaks in N circulation. Th and tends to co seen that with suppressed by evident from F speed to Ω
formation of c othermal wall o
arily formed d on the fluid wh from the centr of the Taylor n he magnitude ig. 9 (a) and10 ped structure hich leads t f the core. Cor e from centre of ch leads to the ms.
eamline contou . ,
f Rotations to
ation cases w hermal buoyan Nu and the flow he clockwise ci over the other h low rotation,
the thermal Fig. 11. With th
and
counter rotatin f the enclosure due to the act hich offsets the re of the enclos number is large of Rayleigh n (b) shows gen in the core to strong u riolis forces ar f hot wall towa e formation of
urs and (b) Iso . .
o Heat Trans
with Ω ncy force cau w consists of clo irculation is en
circulation. It the swing of buoyancy wh he increase in r
Ω ,t
ng rolls . These tion of e eye of
sure, as er when number. neration of the unstable
re more ards the f spiral
otherm
sfer
and uses no ockwise
M. Na
buoyan Nu an counte betwee rise an therma Corres three i points and al minim therma corresp the do summa
Fig .8 cont
4.4 E
Avera
The t compu Fig. 1 time a progre numbe is dom
arendra Kumar e
ncy force caus nd the flow con er clockwise ci en them. The p nd fall of Nu is al buoyancy sponding to th inflexion points
are shown in T lmost cyclic h ma correspond
al buoyancy is pond to the du minating force. arized in Table
8. (a) Streamlin ours for
Effects of Rot
aged Heat Tr
transient behav uted as a funct
2. Initially, th and varies per esses this behav er attains steadi minated by the
, there is disr
et al. /JAFM, V
ses two or mor nsists of clockw irculation and t possible source due to alternat y and Co e three local p s and the angle Table 1.Fig. 11 heat transfer at
to the time s dominant wh uration when C . The effects du 1.
ne contours an . ,
tations to Tim
ransfer
vior of the N tion of rotation he heat transfer riodically with vior disappears iness. At Ω
e thermal buo ruption of he
Vol. 9, No. 3, p
e local peaks i wise circulation transition stage
of almost cycli te domination o oriolis forces peaks, there ar e at the inflexio shows unstead the walls. Th interval whe hile the maxim Coriolis force i ue to rotation ar
nd (b) Isotherm .
me and Spac
Nusselt numbe n is exhibited i r is sensitive t time. As tim and the Nusse
, the flow oyancy. At Ω
eat transfer b
pp. 1265-1272,
in n, es ic of s. re on dy he en ma is re
m
ce
er in to me lt w
by
opposing which
by Cori boundar and henc heat tran range an ranges a
Fig. 9. ( contou
5.
The foll present s
1. For dom sup tran 2. For tran rota of h 3. For loca hea
2016.
g interaction o results in de and , th iolis force and ry layers but by ce there is rise nsfer performan nd increases it as shown in Fig
(a) Streamline
urs for .
CONCLUS
lowing conclus studies
rΩ an
minated by th presses the nsfer is by therm
rΩ ,
nsfer by opposin ational buoyanc heat transfer.
r Ω a
ation of the loc at transfer are s
f thermal and ecrease of N
he heat transfe d occurs not y the spiral sh
of Nu. Thus ro nce in the low in the relative . 13.
contours and
. , .
.
SION
sions can be dr
nd Ω
he thermal b oscillation in mal buoyancy e there is disrup ng interaction o cy which resul
and Ω cal maximum sensitive to rota
Coriolis force
Nu. For Ω
er is governed through the aped structure otation reduces rotation speed ely high speed
(b) Isotherm
rawn from the
,the flow is buoyancy and nNuand heat
effect.
ption of heat of thermal and lts in decrease
4. The loca to move rotated a 5. At high
Ω
dominati forces an of Nuss correspo buoyancy correspo is the dom 6. At high
Ω
Nusselt dominati buoyancy
Fig. 10. (a) S contours fo
Tab
al maximum and to higher angle at higher rotatio h rotational sp
and Ω ion of Coriolis nd results in al elt number w nd to the time y is dominan nd to the durat minating force. h rotational sp ), there is number which ion of Coriolis
y effect.
Streamline cont
r . ,
ble 1 Effect of r
d minimum poi es when the enc onal speed.
peed correspon
,there is s and thermal b lmost periodic with time. The e interval when nt while the tion when Corio
. peeds (Ω
significant in h is primarily s forces and r
tours and (b) I . .
.
rotation (
ints tends closure is
nding to alternate buoyancy variation e minima
n thermal maxima olis force
and crease in y due to
rotational
Isotherm
B
B
. ,
Fig. 11. Va angular p
Fig. 12. Var number
Fig. 13. Var number
REFERE
Baig, M. F. convection heated squ Numerical
Baig, M. F. a simulation
. )
ariation of Nus position of enc
. , .
riation of time with rotation f
.
riation of time r with rotation
.
ENCES
and A. Mas n in a two-dime
uare enclosure l Heat Transfer
and M. Zunai n of liquid me
sselt number w losure for
.
e averaged Nus
for .
.
e averaged Nus
n ( . ,
).
ood (2001). N ensional differe
undergoing ro Part A 40, 181
id (2006). Num etals in differe
with
sselt ,
sselt
Natural entially otation. 1–202.
M. Narendra Kumar et al. /JAFM, Vol. 9, No. 3, pp. 1265-1272, 2016.
heated enclosure undergoing orthogonal rotation. International Journal of Heat and Mass Transfer 49, 3500–3513.
Bobco, R. P. (1981). Free convection in enclosures exposed to compressive heating, Heat Transfer Therm. Control: Progr. Astronaut. Aeronaut. 78, 487–515.
BoubnovB.M., G.S. Golitsyn,( 1995), Convection in Rotating Fluids. Kluwer Academic Publishers.
Buhler. K. and H. Oertel (1982). Thermal cellular convection in rotating rectangular boxes. J. Fluid Mech. 114, 261– 282.
Hamady, F. J., J. R. Lloyd, K. T. Yang and H. Q. Yang (1994). A study of natural convection in a rotating enclosure. J. Heat Transfer 116, 136–143.
Jin, L. F., S. K. W. Tou and C. P. Tso (2005). Effects of rotation on natural convection cooling from three rows of heat sources in a rectangular cavity. International Journal of Heat and Mass Transfer 48, 3982–3994.
Ker, Y. T. and T. F. Lin (1996). A combined numerical and experimental study of air convection in a differentially heated rotating cubic cavity. International Journal of Heat and Mass Transfer 39, 3193–3210.
Ker, Y. T. and T. F. Lin (1997). Time-averaged and reverse transition in oscillatory air convection in a differentially heated rotating cubic cavity.
International Journal of Heat and Mass Transfer 40, 3335–3349
Lee, T. L. and T. F. Lin (1996). Transient three-dimensional convection of air in a differentially heated rotating cubic cavity. International Journal of Heat and Mass Transfer 39, 1243–1255.
Lin, Y. L., T. I. P. Shih, M. A. Stephens and M. K. Chyu (2001). A numerical study of flow and heat transfer in a smooth and ribbed U-Duct with and without rotation. J. Heat Transfer 123, 219–232.
Patankar, S. V. ( 1980). Numerical heat transfer and fluid flow. Hemisphere Publishing Corporation.
Rossby, H. T. (1969). A study of Benard convection with and without rotation. J. Fluid Mech. 36, 309-335
.
Tso, C. P., L. F. Jin and S. K. W. Tou (2007). Numerical segregation of the effects of body forces in a rotating, differentially heated enclosure. Numerical Heat Transfer PartA 51, 85–107.
Vanyo, J. P. (1993). Rotating Fluids in Engineering and Science. Butterworth-Heinemann Press.