Efeito nernst anômalo em Materiais com anisotropia magnetocristalina (110)

(1)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE F´ISICA TE ´

ORICA E EXPERIMENTAL

Disserta¸c˜ao de Mestrado

Efeito Nernst Anˆ

omalo em Materiais

com Anisotropia Magnetocristalina

(110)

Por

Jos´

e Crisanto da Costa Neto

(2)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE F´ISICA TE ´

ORICA E EXPERIMENTAL

Efeito Nernst Anˆ

omalo em Materiais

com Anisotropia Magnetocristalina

(110)

Jos´e Crisanto da Costa Neto

Orientador: Prof. Carlos Chesman de Ara´ujo Feitosa

Disserta¸cão apresentada ao Departamento de F´ısica Teórica e Experimental da Universidade Fe-deral do Rio Grande do Norte como parte do re-quisito para obten¸cão do grau de Mestre em F´ısica.

(3)

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

CENTRO DE CIˆ

ENCIAS EXATAS E DA TERRA

DEPARTAMENTO DE F´ISICA TE ´

ORICA E EXPERIMENTAL

A Comiss˜ao Examinadora, abaixo assinada, aprova a disserta¸c˜ao:

Efeito Nernst Anˆ

omalo em Materiais

com Anisotropia Magnetocristalina

(110)

Elaborada por:

Jos´

e Crisanto da Costa Neto

Como requisito parcial para obten¸c˜ao do t´ıtulo de

MESTRE EM F´ISICA

Comiss˜

ao Examinadora

———————————————————————

Prof. Dr. Carlos Chesman de Ara´ujo Feitosa - Presidente (Orientador), UFRN

———————————————————————

Prof. Dr. Claudionor Gomes Bezerra - Examinador Interno, UFRN

———————————————————————

Prof. Dr. Edson Passamani Caetano - Examinador Externo, UFES

(4)

Agradecimentos

Agrade¸co primeiramente `a for¸ca maior que criou todo este universo que tentamos entender.

Agrade¸co aos meus pais, Evaniel Medeiros da Costa e Geizer Estevam do Amaral, ao meu irmão Isaac Medeiros do Amaral Costa e ao meu avô José Crisanto da Costa, por tudo.

Agrade¸co `a Jonir Oaiana Crisanto da Cunha, pelo companheirismo, paciˆencia e carinho a todo momento.

Agrade¸co ao professor Carlos Chesman, pela orienta¸cão e paciência na produ¸cão deste trabalho.

Agrade¸co ao professor Claudionor Bezerra e ao professor Edson Passamani, por aceitarem participar da banca e pelas orienta¸c˜oes para melhorar ainda mais este trabalho.

Agrade¸co aos meus amigos, Tibério Alves, Pierre Niau, Zayra Sátiro e Ricardo Borges, pelas discussões e diversões proporcionadas nestes dois anos de mestrado.

Agrade¸co aos professores Luciano Rodrigues, Madras Gandhi, Dory Hélio e Brady, pela forma¸cão acadêmica no mestrado.

Agrade¸co a todos que formam o DFTE, em especial à nossa secretária Celina por toda paciência e informa¸cões dadas em todo processo burocrático e ao coordenador professor José Renan, por seu trabalho em manter o alto n´ıvel da pós-gradua¸cão em F´ısica.

Agrade¸co aos meus familiares.

(5)

Resumo

Quando um material ferromagnético é submetido a um gradiente de temperatura e a um campo magnético surge o chamado efeito Nernst-Anômalo, medido através da voltagem que surge na amostra magnética. Este efeito atualmente vem sendo investigado em materiais para aplica¸cão em spintrônica e caloritrônica [1]. Atualmente, os materiais chamados de Heusler são os mais promissores para essa nova área de pesquisa. Neste trabalho, investigamos as curvas de voltagem associadas ao efeito Nernst-Anômalo com anisotropia magneto-cristalina, em termos da voltagem versus campo magnético aplicado e da voltagem versus ângulo planar. Analisamos três tipos de anisotropias: cúbica (100), que apresenta simetria C4, uniaxial que é do tipo C2 e a cúbica (110), que também é do tipo C2. O objetivo foi comprovar que o uso da anisotropia cúbica (110) é equivalente a anisotropia (100) adicionada de uma uniaxial. Especificamente, quando a constante de anisotropia uniaxial é considerada grande, cerca de 40% da constante de anisotropia cúbica (110), e o seu eixo fácil está a 90◦ _{do eixo fácil da}

(6)

Abstract

When a ferromagnetic material is exposed to a temperature gradient and a magnetic field, the anomalous Nernst effect (ANE) appears, which is measured by a voltage on the magnetic sample. This effect has presently been investigated in materials for application in spintronic and caloritronics [1]. Currently, called Heusler materials are the most promising for the new area of research. In this study, we investigated the voltage curves associated to the (ANE) with magneto-crystalline anisotropy, in terms of voltage versus magnetic field and voltage versus angle planar. We investigated three kind of anisotropy, the cubic anisotropy (100) which has C4 (four-fold) symmetry, uniaxial anisotropy and cubic (110) anisotropy where both exhibit C2 symmetry. The goal is to prove that the use of anisotropy (110) is equivalent to the (100) anisotropy plus uniaxial, specifically when the constant of uniaxial anisotropy is considered large, almost 40% of the constant of cubic (110) anisotropy, and the easy axis it’s at 90◦ _{the easy axis of (100). The results demonstrate that full equivalence and produces}

(7)

Sum´

ario

Introdu¸c˜ao 1

1 Energia Magn´etica 3

1.1 Materiais Ferromagn´eticos . . . 3

1.2 Energia de Troca . . . 8

1.3 Energia Zeeman . . . 9

1.4 Energia de Anisotropia Magnetocristalina . . . 11

1.4.1 Simetria C´ubica . . . 13

1.4.2 Simetria Tetragonal e Simetria Hexagonal . . . 14

1.4.3 Comportamento da Anisotropia Magnetocristalina para cristais c´ubicos 16 1.4.4 Anisotropia Uniaxial . . . 25

1.5 Energia de Anisotropia de Forma . . . 26

1.6 Energia de Anisotropia Magnetoel´astica . . . 30

1.7 Dom´ınios e Paredes de Dom´ınios Magn´eticos . . . 32

1.7.1 Dom´ınios Magn´eticos . . . 32

1.7.2 Paredes de Dom´ınio . . . 34

2 Modelo Teórico para a Magnetiza¸cão e o Processo de Minimiza¸cão da Energia 36 2.1 Processo de Magnetiza¸cão . . . 36

2.2 M´etodo de Minimiza¸c˜ao . . . 38

2.3 Curvas de magnetiza¸c˜ao . . . 43

2.3.1 Curvas de Magnetiza¸c˜ao da Anisotropia Uniaxial . . . 43

2.3.2 Curvas de Magnetiza¸c˜ao da Anisotropia C´ubica (100) . . . 47

2.3.3 Curvas de Magnetiza¸c˜ao da Anisotropia C´ubica (110) . . . 52

3 Resultados e Discuss˜oes 55 3.1 Efeitos Termoel´etricos . . . 55

3.2 Curvas de magnetiza¸c˜ao para oCo2F eAl e o Efeito Nernst Anˆomalo . . . 59

3.2.1 Materiais Heusler . . . 59

3.2.2 O efeito Nernst anˆomalo e o material Heusler Co2F eAl . . . 60

(8)

(9)

Lista de Figuras

1.1 Ilustra¸cão do campo molecular [21]. . . 4 1.2 Gráfico da magnetiza¸cão de satura¸cão para o ferro, n´ıquel e o cobalto em

fun¸cão da temperatura [7]. . . 6 1.3 Representa¸cão dos dom´ınios magnéticos; a) material com um único dom´ınio

ou monodom´ınio; b) material com dois dom´ınios magnéticos, sendo sua mag-netiza¸cão externa nula; c) uma estrutura com mais dom´ınios e de intensidades distintas [8]. . . 7 1.4 a) Representa¸cão do comportamento ferromagnético devido aJ(_|~ri−~rj|)>0.

b) Representa¸c˜ao do caso antiferromagn´etico devido a J(_|~ri−~rj|)<0. . . . 9

1.5 Representa¸cão dos vetores magnetiza¸cão e campo magnético em coordenadas esféricas. . . 10 1.6 Representa¸cão dos cossenos diretores e da dire¸cão da magnetiza¸cão[13]. . . . 12 1.7 S . . . 15 1.8 A esquerda é mostrada a superf´ıcie de energia representando os eixos de fácil

e de dif´ıcil magnetiza¸cão para simetria cúbica com K1 > 0, este é o caso do bcc-Fe. A direita é mostrado a mesma representa¸cão mas para K1 < 0, é o caso do fcc-Ni [13]. . . 17 1.9 Dependência da magnetiza¸cão com o campo externo aplicado H~ ao longo de

diferentes eixos dos cristais de Fe(figura a)) e Ni(figura b)) [15]. . . 18 1.10 Esquema mostrando o crescimento de um filme de um material com simetria

c´ubica na dire¸c˜ao [100]. . . 19 1.11 Esquema mostrando o crescimento de um filme de um material com simetria

c´ubica na dire¸c˜ao [110]. . . 19 1.12 Esquema mostrando o crescimento de um filme de um material com simetria

cúbica na dire¸cão [111]. . . 19 1.13 Esquema mostrando o filme localizado no plano x₋z. . . 20 1.14 Comportamento angular da energia magnetocristalina para a dire¸cão de

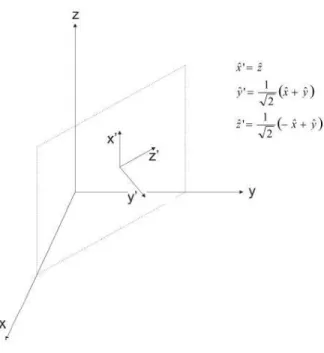
cres-cimento (010). . . 21 1.15 Representa¸c˜ao do plano (110) e os dois sistemas com linha e sem linha, ligados

aos eixos do filme e do cristal respectivamente. . . 22 1.16 Comportamento angular da energia magnetocristalina (110). . . 24 1.17 Representa¸c˜ao do plano (111) e os dois sistemas com linha e sem linha, ligados

(10)

1.18 Gráfico da energia de anisotropia uniaxial com o ângulo θ para K positivo. . 26 1.19 Representa¸cão dos dipolos magnéticos que surgem no material e o campo

desmagnetizante [12]. . . 27 1.20 Valores da magnetostriçcão de satura¸cão de alguns materiais [7]. . . 31 1.21 Gráfico da magnetiza¸cão de satura¸cão em fun¸cão da temperatura, o ponto

onde a curva toca o eixo T corresponde a temperatura de Curie. . . 33 1.22 Exemplo de estruturas de dom´ınios magn´eticos cuja resultante ´e uma

magne-tiza¸cão nula [2]. . . 33 1.23 Classifica¸cão das paredes de dom´ınio com rela¸cão ao ângulo de orienta¸cão

entre a magnetiza¸c˜ao dos dom´ınios adjacentes. a) Paredes de dom´ınio de 180◦ e b) Paredes de dom´ınio de 90◦ _{[12]. . . .} ₃₄

1.24 Representa¸cão da estrutura interna da parede de Bloch, onde o padrão de rota¸cão dos dom´ınios magnéticos ocorre para fora do plano dos dom´ınios ad-jacentes [19]. . . 35 1.25 Representa¸cão da estrutura interna da parede de Néel, onde o padrão de

rota¸c˜ao dos dom´ınios magn´eticos ocorre dentro do plano dos dom´ınios adja-centes [19]. . . 35

2.1 O esquema acima mostra como a magnetiza¸cão de um material magnético varia em fun¸cão da intensidade do campo ferromagnético aplicado sobre ele [20]. . . 37 2.2 Curvas de histereses magnéticas t´ıpicas: a) de um material magnético duro e

b) de um material magnético macio. . . 38 2.3 Esquema do conceito da teoria de campo médio,: a Figura a) é um sistema

com N part´ıculas e a Figura b) represemta a troca da intera¸cão de todas as part´ıculas pelo potencial médio representado por um única part´ıcula [22]. . . 39 2.4 Gráfico da densidade de energia em fun¸cão do ângulo para um valor de campo

magn´etico aplicado. . . 40 2.5 Esquema para descrever o comportamento da evolu¸c˜ao do m´ınimo de energia

para alguns valores de campo (a-g) e a curva de histerese com os pontos de cada m´ınimo representada em (h) . . . 41 2.6 Curvas de magnetiza¸c˜ao de um material que possui uma anisotropia

mag-netocristalina uniaxial para os valores de θH = 0◦, θH = 45◦, θH = 60◦ e

θH = 90◦. . . 45

2.7 Curvas de magnetiza¸c˜ao da anisotropia magnetocristalina uniaxial variando o campo de anisotropia para os ˆangulos a) θH = 90◦ e b) θH = 0◦. . . 46

2.8 Comportamento da magnetiza¸cão remanente com rela¸cão ao ângulo de aplica¸cão do campo magnético para a anisotropia uniaxial. . . 47 2.9 Curvas de magnetiza¸cão da anisotropia magnetocristalina (100) para os

valo-res de θH = 0◦, θH = 30◦,θH = 45◦ eθH = 90◦. . . 48

(11)

2.11 Comportamento da magnetiza¸cão remanente em fun¸cão do ângulo de aplica¸cão do campo magnético para um material com anisotropia (100). O gráfico inse-rido sugere que a magnetiza¸cão remanente possui a mesma simetria C4 que a anisotropia. . . 52 2.12 Comportamento das curvas de magnetiza¸cão para um material com

anisotro-pia magnetocristalina c´ubica (110) paraθH = 0◦, θH = 35◦ e θH = 90◦. . . . 53

2.13 Comportamento das curvas de magnetiza¸c˜ao para um material com aniso-tropia magnetocristalina c´ubica (110), para θH = 0◦, variando o campo de

anisotropia. . . 54 2.14 Comportamento da magnetiza¸cão remanente com rela¸cão ao ângulo de aplica¸cão

do campo magn´etico para a anisotropia (110). . . 54

3.1 Ilustra¸cão de um metal A colocado entre os metais B, para observar o efeito Seebeck. . . 56 3.2 Ilustra¸cão de um circuito elétrico formado por uma fonte de diferen¸ca de

potencial e um termopar. . . 57 3.3 Ilustra¸cão de um material submetido a um campo magnético na dire¸cão z e

um gradiente de temperatura na dire¸cão y produzindo uma corrente elétrica na dire¸cão x, mostrando o efeito Nernst. . . 58 3.4 Disposi¸cão dos elementos X, Y e Z que constituem os materiais Heusler na

tabela peri´odida [29]. . . 60 3.5 a) Estrutura cristalina de umfull-Heusler; b) Estrutura cristalina de um half

-Heusler [30]. . . 60 3.6 a)O laser de d´ıodo produz um gradiente de temperatura local perpendicular ao

plano do filme nanom´etrico de Co2F eAl(CFA). A voltagem VEN A, que surge

devido ao efeito Nernst anômalo, depende da magnetiza¸cão M~ na posi¸cão (x,y); b) Voltagem determinada entre os contatos 2 e 4 da placa Hall como fun¸cão da posi¸cão do laser (x, y) e do campo magnético externo [1]. . . 62 3.7 a) Valor médio da voltagem VEN A no Co2F eAl na região delimitada pelos

contatos da placa Hall mostrado no centro da figura como fun¸cão do campo magnético paraα= 0◦_,_α_{= 45}◦_e_α_{= 90}◦_{(triângulos, quadrados, circulos); b)}

VEN Aem fun¸cão do ânguloαparaµ0H = 100mT (quadrados) eµ0H = 20mT (circulos) [1]. . . 63 3.8 Curvas de magnetiza¸cão do filme nanométrico Co2F eAl para 0◦, 45◦ e 90◦.

Note que as curvas para 0◦ _{e 90}◦ _{s˜ao diferentes, o que indica que a simetria}

do material não é C4 [33]. . . 64 3.9 a) Comportamento da densidade de energia para a anisotropia cúbica 100

mais uma uniaxial paraH110 = 0.2kOe. b) Comportamento da densidade de energia para a anisotropia cúbica (110) para H110= 0.2kOe. . . 66 3.10 Simula¸cão da voltagem VEN A para a anisotropia cúbica (100) mais uniaxial

(12)

3.11 Simula¸c˜ao da voltagem VEN A para a anisotropia c´ubica (110) para comparar

com os resultados do efeito Nernst anômalo para oCo2F eAl. . . 67 3.12 Simula¸cão da voltagem VEN A para a anisotropia cúbica (100) mais uniaxial,

considerandoH100 = 7₈H110 e Hu = 1₈H110. . . 68 3.13 Simula¸c˜ao da voltagemVEN A para: a) a anisotropia c´ubica (110) para 0◦, 35◦,

45◦ _{e 90}◦_{. b) a anisotropia c´}_{ubica (100) mais uniaxial para 0}◦_{, 35}◦_{, 45}◦ _{e 90}◦_. ₆₈

3.14 Simula¸cão da curva de magnetiza¸cão para: a) Anisotropia cúbica (100) mais uniaxial para compara¸cão com os resultados experimentais obtidos na figura acima para o CFA. b) Anisotropia cúbica (110) para compara¸cão com os resultados experimentais obtidos na figura acima para o CFA . . . 69 3.15 Simula¸cão da curva de magnetiza¸cão para anisotropia cúbica (100) mais

(13)

Introdu¸c˜

ao

O estudo sobre filmes magnéticos vem gerado interesse na comunidade cient´ıfica há pouco mais de 60 anos devido à sua alta aplica¸cão na tecnologia. A forma como estes materiais agem frente a um campo magnético, temperatura, e a varia¸cão de tantas propriedades, abre espa¸cos nunca antes vistos para nossa sociedade moderna. Do ponto de vista da F´ısica, o in´ıcio de toda esta jornada se dar no entendimento da magnetiza¸cão destes materiais. O fato da magnetiza¸cão estar inicialmente nula em alguns materiais e rapidamente chegar a um estado de satura¸cão magnética pela simples aplica¸cão de um pequeno campo magnético externo vem gerando fasc´ınio. Devido a isso muitas teorias para compreender este tipo de comportamento foram criadas [2] [3].

O conhecimento dos fenômenos magnéticos remonta a Grécia antiga [4]. Os primeiros rela-tos a esse respeito, mas sem nenhum caráter cient´ıfico, datam do ano de 800 AC, onde gregos tinha o conhecimento de um material conhecido como magnetita (proveniente da prov´ıncia da magnésia), capaz de atrair outras rochas. Com advento do método cient´ıfico no fim da idade média, o magnetismo passou a ser tratado do ponto de vista mais experimental. O ano de 1600 é considerado o in´ıcio do magnetismo com a publica¸cão do tratadoDe magnete, escrito por William Gilbert (1544₋1603), onde analisa os fenômenos do magnetismo e da eletricidade. No ano de 1820 o f´ısico Hans Christian Oersted (1777₋1851) descobre, por meio de uma experiência, a produ¸cão de um campo magnético a partir de uma corrente elétrica. A descri¸cão do magnetismo por meio de equa¸cões matemáticas foi constru´ıda prin-cipalmente por André Marie Ampére (1775₋1836). Ampére também propõe o modelo de ´ımãs permanentes em termos de correntes elétricas moleculares e sua formula¸cão permitiu o estudo da eletrodinâmica independente da eletrostática. Em 1831 Michael Faraday descobre a produ¸cão de uma for¸ca eletromotriz por meio da varia¸cão temporal do fluxo magnético, que é descrita através da lei de indu¸cão eletromagnética. Todas as leis que envolvem a eletricidade e o magnetismo são escritas na forma de equa¸cões no tratado publicado por Ja-mes Clerck Maxwell (1831₋1879) no ano de 1873, chamado deA treatise on Eletricity and Magnetism. Neste trabalho J.C. Maxwell unifica também o eletromagnetismo aos fenômenos ópticos, descrevendo a radia¸cão como uma onda eletromagnética.

(14)

os fatos experimentais relacionados ao magnetismo da mat´eria remonta ao in´ıcio do s´eculo

XIX, cuja proposta é de que a estrutura dos materiais magnéticos consistia de pequenos ´ımãs elementares, de forma semelhante a sua composi¸cão formada por átomos e moléculas. O modelo dos ´ımãs elementares explicava bem alguns fatos experimentais. Por exemplo, o fenômeno de satura¸cão magnética poderia ser entendido como o estado em que todos os ´ımãs elementares estão orientados na mesma dire¸cão. Porém, este conceito ainda era muito simples para grande variedade de comportamentos que os materiais apresentavam, tais como a mudan¸ca da magnetiza¸cão de satura¸cão com a temperatura ou mesmo o fato de alguns materiais a temperatura ambiente estarem magnetizados e outros não, sem a presen¸ca de um campo magnético externo. No fim, os fenômenos do magnetismo só puderam ser compreendidos com o advento da Mecânica Quântica [4].

Esta disserta¸cão está dividida em quatro cap´ıtulos. No primeiro cap´ıtulo é feita uma revisão sobre o modelo proposto por Weiss a partir do paramagnetismo de Langevin, para explicar o ferromagnetismo. Também é feita uma descri¸cão sobre os termos que compõem a energia magnética total, com maior enfoque na energia de anisotropia magnetocristalina. No segundo cap´ıtulo há uma breve revisão sobre o processo da histerese e é apresentada a forma de como foi constru´ıda a simula¸cão computacional, para obten¸cão das curvas de magnetiza¸cão a partir da minimiza¸cão da energia, além de mostrar algumas propriedades através das equa¸cões. São simuladas as curvas de magnetiza¸cão para as anisotropias cúbicas (100), (110) e a anisotropia uniaxial e é analisado como as curvas se comportam frente a mudan¸ca de alguns parâmetros, tais como, o campo de anisotropia. O objetivo principal está descrito no terceiro cap´ıtulo, onde será analisado o efeito Nernst anômalo para o filme nanométrico

(15)

Cap´ıtulo 1

Energia Magn´

etica

1.1 Materiais Ferromagn´

eticos

A resposta da matéria à presen¸ca de um campo magnético excitante ou mesmo o fato desta possuir ou não uma magnetiza¸cão permanente encontra-se diretamente relacionada às propriedades particulares de cada material a se considerar. Desta forma, os materiais magnéticos podem ser dividos em três grandes classes, são elas:

- Materiais diamagnéticos estão relacionados ao fato de surgir um campo no interior da amostra no sentido contrário ao do campo externo. Alguns deles são o cobre, a prata e o chumbo.

- Materiaisparamagnéticosestão associados ao fato de surgir um campo no interior da amos-tra, no mesmo sentido do campo externo e são caracterizados por possu´ırem uma pequena magnetiza¸cão quando colocados na presen¸ca de um campo magnético externo. Materiais deste tipo são fracamente atra´ıdos por ´ımãs, alguns deles são o alum´ınio, o sulfato de cobre e o magnésio.

- Materiaisferromagnéticostambém estão associados ao fato de surgir um campo no interior do material no mesmo sentido que o campo externo e são caracterizados por possu´ırem uma alta magnetiza¸cão e podem estar magnetizados sem a presen¸ca de um campo magnético. Materiais deste tipo são altamente atra´ıdos por ´ımãs. São eles, o ferro, o cobalto e o n´ıquel.

(16)

Para explicar o caso de materiais ferromagnéticos, no ano de 1907 Pierre Weiss (1865₋1940) sugeriu que a desordem provocada pela agita¸cão térmica poderia ser minimizada devido a existência de um campo molecular. O campo molecular foi postulado como uma intera¸cão mútua entre os elétrons que tenderia a alinhar os seus ´ımãs elementares (ver Figura 1.1), ou seja, além do campo magnético, surge outro campo no interior do material devido a conexão entre os ´ımãs elementares do material. A temperatura de Curie corresponde ao ponto onde um material ferromagnético perde toda sua capacidade de magnetiza¸cão e se torna paramagnético. Com isso, abaixo desta temperatura, o campo molecular proposto por Weiss é superior à flutua¸cão térmica da amostra e o material se comporta como um ferromagneto. Já na situa¸cão de temperaturas superiores à temperatura de Curie, o efeito da flutua¸cão térmica é superior ao efeito do campo molecular e desta forma, o material se comporta como um paramagneto. A equa¸cão abaixo mostra este ponto de transi¸cão entre as fases ferromagnética e paramagnética,

kTC =µBHCM, (1.1)

onde o lado esquerdo da Equa¸cão 1.1 representa a energia associada à agita¸cão térmica e o lado direto a energia associada ao campo molecular, sendo k a constante de Boltzman,

TC a temperatura de Curie,µB o magn´eton de Bohr e HCM o campo molecular.

Figura 1.1: Ilustra¸c˜ao do campo molecular [21].

A teoria de Weiss funciona como uma extensão da teoria clássica do paramagnetismo de Langevin. Weiss investigou matematicamente como se comportava um conjunto de átomos, cada um possuindo um momento magnéticoµA, sobre a influência de uma campo magnético

(17)

representa a rela¸cão entre cada momento magnético e o campo é

H=₋X

i

µAi Hcosθ, (1.2)

onde θ é o ângulo entre cada momento magnético µA e o campo H. Como o sistema

está sujeito à agita¸cão térmica, os métodos da mecânica estat´ıstica sugerem que em uma temperatura T, a distribui¸cão dos momentos magnéticos está associada a seguinte fun¸cão de parti¸cão [17]

Z =Xe−_kTH ₌X

eµAHkTcosθ. (1.3)

Na primeira formula¸cão de Langevin são feitas duas considera¸cões: (1) os momentos magnéticos estão sujeitos à agita¸cão térmica e podem se orientar em qualquer dire¸cão com rela¸cão ao campo, (2) estes momentos estão distanciados de modo a nenhum sofrer a in-fluência um dos outros. Com o advento da teoria quântica, a primeira considera¸cão é al-terada, pois as dire¸cões se tornam limitadas devido ao principio de exclusão de Pauli. No caso mais simples só pode haver duas orienta¸cões, sendo uma paralela e outra antiparalela a dire¸cão do campo. Com isso, a equa¸cão de Langevin fica [17]

M M0

= tanhµAH

kT . (1.4)

Pode-se observar que esta formula¸cão implica que mesmo para o campo mais alto atingido em um laboratório, mas ainda sobre a influência da temperatura ambiente, a magnetiza¸cão atingirá apenas uma fra¸cão do valor finalM0. Neste intervalo a magnetiza¸cão é proporcional ao campo. O problema é que se o campo magnético externo for nulo, magnetiza¸cão se torna nula, por isso o nome paramagnetismo de Langevin, pois ele não explica o caso dos materiais ferromagnéticos que podem possuir magnetiza¸cão diferente de zero abaixo da temperatura de Curie sem estarem na presen¸ca de um campo magnético externo.

A solu¸c˜ao deste problema surge quando Weiss substitui na equa¸c˜ao de Langevin o campo

H, por um novo campo H+N M, onde a quantidade N M representa o campo molecular e N é a constante de campo molecular. Com esta ideia, os momentos magnéticos dos ´ımãs elementares sofrem influência um dos outros, indo de encontro com a teoria de Langevin. Substituindo o novo campo H+N M na equa¸cão 1.4, a equa¸cão de Langevin se torna

M M0

= tanhµA(H+N M)

kT . (1.5)

Fazendo H= 0 e Θ = µAN M0

k se chega a seguinte equa¸c˜ao:

(18)

Agora, pode-se observar que quando o campo magnético externo é nulo, um material ferro-magnético permanece magnetizado. A equa¸cão 1.6 leva a conclusão de que quando o campo é igual a zero, a magnetiza¸cão se comporta igualmente para todos os materiais, já que temos uma fun¸cão de M

M0 e

T

Θ.

Com isso, os materiais ferromagnéticos são caracterizados por terem a sua magnetiza¸cão de satura¸cão dependente da temperatura MS(T). Um material ferromagnético torna-se

espontaneamente magnetizado abaixo de uma temperatura cr´ıtica chamada de temperatura de Curie e devido a este comportamento tem-se que para qualquer temperatura abaixo de Θ =TC, a magnetiza¸c˜ao de satura¸c˜ao apresenta um valor bem definido mesmo sem a presen¸ca

de um campo magnético externo aplicado. A figura 1.1 mostra a varia¸cão da magnetiza¸cão de satura¸cão MS(T) com rela¸cão a temperatura, para o ferro, o n´ıquel e o cobalto. Para

temperaturas acima da temperatura de Curie, que ´e uma constante de cada material, todos os materiais apresentam um comportamento paramagn´etico.

Figura 1.2: Gráfico da magnetiza¸cão de satura¸cão para o ferro, n´ıquel e o cobalto em fun¸cão da temperatura [7].

(19)

De acordo com o modelo de Weiss, um peda¸co de ferro não poderia de forma alguma estar desmagnetizado à temperatura ambiente, mas ainda sim observamos este fenômeno na natureza. Para contornar este impasse, Weiss considerou que as amostras reais dos materiais ferromagnéticos, quando estão abaixo da temperatura de Curie, são compostas por peque-nas regiões magnetizadas em alguma dire¸cão, mas de alguma forma a soma destas pequepeque-nas regiões no final resulta em uma magnetiza¸cão externa nula. Este é um conceito muito im-portante no entendimento da estrutura dos materiais magnéticos, conhecido como dom´ınios magnéticos [5]. A figura 1.22 mostra uma representa¸cão destes dom´ınios magnéticos.

Figura 1.3: Representa¸cão dos dom´ınios magnéticos; a) material com um único dom´ınio ou monodom´ınio; b) material com dois dom´ınios magnéticos, sendo sua magnetiza¸cão externa nula; c) uma estrutura com mais dom´ınios e de intensidades distintas [8].

Weiss conseguiu explicar grande parte dos fenômenos relacionados ao ferromagnetismo com o conceito de campo molecular e da estrutura de dom´ınios, porém ele não conseguiu explicar a origem f´ısica destes termos por meio de for¸cas atômicas. A explica¸cão do campo molecular foi dada por Werner Heisenberg (1901₋1976) no ano de 1926 através do conceito de energia de troca e a explica¸cão da origem dos dom´ınios só foi dada por Lev Davidovich Landau (1908₋1968) e Evgeny Mikhailovich Lifshitz (1915₋1985) no ano de 1935, por meio do entendimento dos vários termos que compõem a energia total de um sistema magnético.

(20)

forma [2][5][7] [9]

ET =

Z

V

(etroca+eZ+eani+ema+eme)dV, (1.7)

o próximo passo será dar continuidade a cada energia citada para entender como o pro-cesso da minimiza¸cão da energia afeta a magnetiza¸cão de um material ferromagnético, com uma maior ênfase na energia de anisotropia magnetocristalina que é o foco deste trabalho.

1.2 Energia de Troca

Umas das mais importantes intera¸cões que surgem nos materiais magnéticos é conhecida por energia de troca, pois é ela a responsável pelo ordenamento ferromagnético do material, ou seja, ela quem comanda o ferromagnetismo e é a origem do campo molecular proposto por Weiss [9][10]. Este tipo de energia também é conhecida como energia de exchange e surge a partir de diferentes causas, tais como, a intera¸cão eletrostática, a intera¸cão dos spins dos elétrons através do princ´ıpio de exclusão de Pauli e a anti-simetria da fun¸cão de onda, já que se trata de férmions. Para um conjunto de átomos numa dada rede que compõem o material, considerando as fun¸cões de onda dos elétrons localizados em s´ıtios vizinhos representados pelos vetores posi¸cão ~ri, e~rj e seus respectivos momentos angulares de spin S~(~ri), e S~(~rj)

medidos em m´ultiplos de ~_{, a densidade de energia de troca pode ser escrita na seguinte}

forma

etroca=−

X

J(_|~ri−~rj|)S~(~ri)·S~(~rj) (1.8)

onde J(_|~ri−~rj|) ´e a integral de troca e ´e dada por

J(_|~ri−~rj|) =

Z

ψ∗_a(~r1)ψ_b∗(~r2)_Hψa(~r1)ψb(~r2)dV1dV2, (1.9) onde ψa(~r1) e ψb(~r2) representam as fun¸cões de onda dos elétrons vizinhos e H é o

hamilto-niano do sistema. A integral de troca decai rapidamente (na forma _r12 devido ao potencial

coulombiano) para altos valores de _|~ri −~rj|, por isso est´a intera¸c˜ao afeta mais fortemente

os primeiros vizinhos e corresponde a uma soma em todos os átomos da rede [13]. O sinal da integral de troca é quem vai ser o determinante se um dado material tem um ordena-mento magnético do tipo ferromagnético, ou antiferromagnético, para o caso ferromagnético

J(_|~ri −~rj|) >0 e antiferromagn´etico J(|~ri −~rj|) < 0. De todo modo, o estado m´ınimo de

energia acontece quando os momentos angulares de spin dos elétrons adjacentes são paralelos no caso ferromagnético e antiparalelos no caso antiferromagnético.

(21)

Figura 1.4: a) Representa¸c˜ao do comportamento ferromagn´etico devido a J(_|~ri−~rj|) > 0.

b) Representa¸c˜ao do caso antiferromagn´etico devido a J(_|~ri−~rj|)<0.

~

S(~ri) seja substitu´ıdo pela vari´avel cont´ınua de magnetiza¸c˜ao M~, desta forma a densidade

de energia de troca pode ser dada na seguinte forma [5]

etroca =A

3

X

i=1

(_∇Mi(~r))2, (1.10)

onde A é a constante de troca obtida a partir da deriva¸cão de J(_|~ri −~rj|) e Mi são as

componentes da magnetiza¸c˜ao M~ [5].

1.3 Energia Zeeman

Como já foi visto, os materiais estudados neste trabalho são filmes nanométricos cuja estru-tura magnética consiste de dom´ınios magnéticos com diferentes orienta¸cões de magnetiza¸cão, a soma de todos estes termos geram no final um vetor que vai identificar o comportamento da magnetiza¸cão do material na presen¸ca de um campo magnético externo. Quando é apli-cado um campo magnético externo, surge uma intera¸cão entre o vetor magnetiza¸cão M~ e o campoH~ semelhante à intera¸cão do campo magnético com um dipolo [21], que faz com que a magnetiza¸cão tenda a se alinhar com o campo. A energia associada a este tipo de intera¸cão é conhecida como energia Zeeman e pode ser descrita através da integral envolvendo o produto escalar [7][11]

Ez =−

Z

V

~

M _·HdV.~ (1.11)

Neste trabalho o que terá maior importância é a densidade de energia Zeeman, ou seja, nos cálculos de minimiza¸cão estaremos dividindo pelas dimensões da amostra, com isso a densidade de energia Zeeman é dada por

(22)

o sinal negativo na equa¸cão 1.12 indica que o m´ınimo de energia se da quando os vetores magnetiza¸cão e campo magnético estão paralelos, ou seja, isto indica o fato da magnetiza¸cão tentar se alinhar com o campo.

Expressando a magnetiza¸cão e o campo magnético em coordenadas esféricas, pois no estudo das anisotropias que será feito mais adiante essas expressões serão úteis:

~

M =MS(sinθcosφxˆ+ sinθsinφyˆ+ cosθzˆ) (1.13)

e

~

H =H(sinθHcosφHxˆ+ sinθHsinφHyˆ+ cosθHzˆ), (1.14)

Figura 1.5: Representa¸cão dos vetores magnetiza¸cão e campo magnético em coordenadas esféricas.

ondeMS representa a magnetiza¸cão de satura¸cão do material eH é a intensidade do campo

magnético externo aplicado. Substituindo estes vetores na densidade de energia Zeeman (equa¸cão 1.12) obtém-se

(23)

como o termo da energia de anisotropia de forma que será tratada na próxima se¸cão faz com que a magnetiza¸cão fique no plano do filme caso o campo seja aplicado neste plano e supondo que o filme esteja localizado no planox₋z, então isto implicará em φH = 0, como

consequência do que foi afirmado acima, φ = 0. Desta forma obtém-se nesta situa¸cão a seguinte expressão para densidade de energia Zeeman:

ez =−MSHcos(θ−θH). (1.16)

1.4 Energia de Anisotropia Magnetocristalina

No estudo teórico de materiais magnéticos uma das formas de energia que tem maior relevância está associada a rede cristalina do material. O termo anisotropia está relacionado ao quanto uma propriedade f´ısica depende da dire¸cão espacial que esta é analisada. No caso de filmes nanométricos, a magnetiza¸cão na, maioria das vezes, vai se comporta de forma distinta dependendo da dire¸cão do espa¸co em que se aplica o campo magnético. Todos os materiais magnéticos possuem uma estrutura cristalina bem definida e quando a energia interna do sistema, associada à magnetiza¸cão do material, depende do eixo cristalográfico tem-se uma anisotropia magneto-cristalina.

Este tipo de energia está relacionada à intera¸cão spin-órbita dos elétrons ligados aos átomos que formam a estrutura cristalina. Por isso, a dependência com a rede, onde no processo de magnetiza¸cão há o surgimento de eixos fáceis de magnetiza¸cão e eixos duros de magnetiza¸cão, cujos nomes já indicam o fato do material ferromagnético se magnetizar facilmente ou não, simplesmente com a mudan¸ca da dire¸cão do campo magnético externo aplicado.

Devido a dependência deste termo de energia estar associado a rede do cristal, surgem comportamentos distintos para cada estrutura, seja ela cúbica, hexagonal, tetragonal. Há algumas formas distintas na literatura para se encontrar a expressão matemática que repre-sente esta energia de anisotropia, algumas delas se baseiam nas opera¸cões de simetria do grupo ligado a cada rede cristalina. Isto acontece devido ao fato de algumas exigências que a magnetiza¸cão tem que satisfazer, tais como, ser invariante através de uma transforma¸cão que leve eixos cristalográficos aos seus equivalentes [por exemplo os eixos (100) e (100)], porém todas as formas no final estarão ligadas a expansão da energia em potências das componentes da magnetiza¸cão M~. Estas componentes que também indicam a dire¸cão da magnetiza¸cão

~

m= _|M_M~_~_| ´e dada em termos dos cossenos diretores αi m~ = (α1, α2, α3)(ver Figura 1.6): Escrevendo em termos de coordenadas esf´ericas tem-se

α1 = sinθcosφ

α2 = sinθsinφ

(24)

Figura 1.6: Representa¸cão dos cossenos diretores e da dire¸cão da magnetiza¸cão[13].

onde satisfazem a seguinte rela¸c˜ao:

α2₁ +α2₂ +α2₃ = 1. (1.18)

Com isso, pode-se escrever a energia de anisotropia magnetocristalina com a seguinte ex-pans˜ao [13]

Eani=E0+

X

i

biαi+

X

ij

bijαiαj +

X

ijk

bijkαiαjαk (1.19)

+X

ijkl

bijklαiαjαkαl+O(α5),

os termos de quinta ordem _O(α5_{) tem uma dependˆencia muito pequena em} _α_{. Por isto,} a s´erie pode ser truncada a partir deste termo.

Como já citado no presente texto, umas das opera¸cões de simetria que esta expressão deve ter é que não existe diferen¸ca nos valores de energia entre eixos equivalentes, ou visto de outra forma não há diferen¸ca entre sistemas que simplesmente possuem magnetiza¸cões opostas. Isto pode ser descrito como segue abaixo[13]

Eani(M~) =Eani(−M~), (1.20)

o que implica em

(25)

Com esta condi¸cão se faz necessário fazer uma análise na paridade da fun¸cão, que não pode apresentar comportamento de uma fun¸cão ´ımpar. Seguindo este passo, todos os termos de ordem ´ımpar da expansão em série devem ser desconsiderados. Com isto, pode-se escrever a seguinte expressão geral para representar a energia magnetocristalina

Eani=E0+

X

ij

bijαiαj +

X

ijkl

bijklαiαjαkαl, (1.22)

Com esta expressão, pode-se analisar cada rede cristalina poss´ıvel e o tipo de anisotropia. Por exemplo, no caso da rede cúbica pode haver vários tipos de anisotropia, identificados a partir de qual seja o eixo fácil: é o caso das anisotropias (100) e (110), que serão estudadas neste trabalho. O próximo passo será a partir da Equa¸cão 1.22, escrever sua forma para a uma estrutura que possua simetria cúbica, tetragonal e hexagonal e por fim falar de um tipo espec´ıfico, que é a uniaxial.

1.4.1 Simetria C´

ubica

No caso da simetria c´ubica e usando a condi¸c˜aoE(αi) = E(−αi), os termos cruzadosαiαj

que aparecem na Equa¸c˜ao 1.22 devem desaparecer, ou seja, bij = 0. Os valores do ´ındice

para i = 1,2,3 são indistingu´ıveis para simetria cúbica. Ou seja, b11 = b22 = b33. Sendo assim, usando a rela¸cão dada por 1.18, o termo de segunda ordem fica

X

ij

bijαiαj =b11(α21+α22+α23) = b11. (1.23) Para o termo de quarta ordem a indistinguibilidade parai, implicar´a emb1111 =b2222 =b3333, e b1122 = b1133 = b2233, mas pra cada termo neste caso tem-se uma repeti¸c˜ao, por exemplo para b1122

b1122 =b2211 =b1212 =b1221 =b2112 =b2121, ligado a cada termo deste tem-se α2

1α22, o que implica que este está aparecendo 6 vezes na expansão, o mesmo racioc´ınio serve para b1133 e b2233, que pode ser calculado como uma combina¸cão simples de 4 elementos agrupados 2 a 2. Com isso, o termo de quarta ordem é dado por

X

ijkl

bijklαiαjαkαl=b1111(α41+α42+α43) + 6b1122(α21α22+α21α23 +α22α23), (1.24) usando a rela¸c˜ao dos cossenos diretores abaixo

(26)

e calculando o segundo lado da equa¸c˜ao

1 = α4₁+α4₂+α4₃+ 2(α2₁α₂2+α2₁α2₃ +α2₂α2₃), (1.26) obt´em-se

α₁4 +α₂4+α₃4 = 1₋2(α2₁α2₂+α2₁α₃2+α₂2α2₃), (1.27) substituindo em (1.24), tem-se que

X

ijkl

bijklαiαjαkαl =b1111+ (6b1122−2b1111)(α21α22 +α21α32+α22α23), (1.28) finalmente adicionando os dois termos, pode-se escrever a expressão para energia magne-tocristalina de uma rede cúbica, que terá a seguinte forma

Ecubic

ani =E0+b11+b1111+ (6b1122−2b1111)(α21α22+α21α23+α22α23), (1.29) escrevendo K0 =E0+b11+b1111 e K1 = 6b1122−2b1111, tem-se que

Eanicubic =K1+K2(α21α22+α12α23+α22α23), (1.30) que é a forma mais usada na literatura para representar a energia magnetocristalina de uma rede cristalina com simetria cúbica, onde os coeficientes K0 e K1 são as constantes de anisotropia magnetocristalina. Esta expressão foi obtida pela primeira vez pelo f´ısico russo Akulov no ano de 1929 [7].

1.4.2 Simetria Tetragonal e Simetria Hexagonal

Para o caso em que o sistema possui uma rede cristalina tetragonal, a diferen¸ca entre ele e o sistema cúbico está apenas no caso de que a indistinguibilidade que antes era nos ´ındices 1,2 e 3, se reduz para os ´ındices 1 e 2. Então, seguindo estas condi¸cões, pode-se encontrar (serão omitidas as contas, por esse tipo de sistema não ser o foco deste trabalho, caso queria saber mais sobre este tipo de simetria olhar na referência [13]) a partir da expressão (1.22) o seguinte resultado:

Etetra

ani =K0+K1α

2

(27)

Caso o sistema possua uma rede cristalina hexagonal, realizando cálculos análogos aos dos dois sistemas anteriores, obtém-se a seguinte expressão [13]

Ehex

ani =K0 +K1(α21+α22) +K2(α21+α22)2 (1.32) +K3(α21+α22)3+K4(α21−α22)(α41−14α12α22+α42),

´

E interessante notar que os sistemas tetragonal e hexagonal apresentam alguns termos com simetria cil´ındrica, ou seja, a dependência da energia se dar somente através do ângulo θ

entre a magnetiza¸cão e a dire¸cão do eixo z [14]. Isto é propriedade da anisotropia magneto-cristalina conhecida como anisotropia uniaxial que será analisada posteriormente.

Figura 1.7: S

(28)

De modo geral, pode-se ver que todas as express˜oes possuem coeficientes K′_s _que

repre-sentam as constantes de anisotropia do material. Alguns resultados bastantes aceitos na literatura ´e que [13]:

• Estas constantes dependem do material e da temperatura em que o mesmo se encontra.

• As experiências demonstram que algumas dessas constantes, por exemplo (K1 e K2), já produzem uma boa concordância entre o teórico e o experimental.

• O sinal e a razão entre as constantes determinam os eixos de fácil magnetiza¸cão ou preferenciais, ou seja, as dire¸cões da rede cristalina onde a magnetiza¸cão se alinha facilmente com o campo magnético externo. Será mostrado neste trabalho que estes eixos podem ser identificados através do processo de minimiza¸cão da energia.

Na tabela abaixo s˜ao mostradas as constantes de anisotropia magnetocristalinaK1 eK2 para o Ferro, N´ıquel, e o Cobalto h´a uma temperatura de 4.2 Kelvin [13].

1.4.3 Comportamento da Anisotropia Magnetocristalina para

cris-tais c´

ubicos

(29)

Figura 1.8: A esquerda é mostrada a superf´ıcie de energia representando os eixos de fácil e de dif´ıcil magnetiza¸cão para simetria cúbica com K1 >0, este é o caso do bcc-Fe. A direita é mostrado a mesma representa¸cão mas paraK1 <0, é o caso do fcc-Ni [13].

(30)

Figura 1.9: Dependˆencia da magnetiza¸c˜ao com o campo externo aplicado H~ ao longo de diferentes eixos dos cristais de Fe(figura a)) e Ni(figura b)) [15].

Dire¸c˜ao de crescimento

Antes de analisar o comportamento de cada anisotropia se faz necessário definir o que é a dire¸cão de crescimento para um filme nanométrico ferromagnético. Todo filme nanométrico ferromagnético é crescido em um substrato sobre um plano cristalino, a dire¸cão de cresci-mento é a dire¸cão perpendicular ao plano cristalino que este material é crescido. Por exemplo, a dire¸cão [100] é perpendicular ao plano cristalino (100) e a dire¸cão [110] é perpendicular ao plano cristalino (110). Quando um material é crescido, os seus átomos são lan¸cados de ma-neira igual e organizada sobre algum plano cristalino do substrato, isto irá definir a dire¸cão de crescimento.

(31)

Figura 1.10: Esquema mostrando o crescimento de um filme de um material com simetria c´ubica na dire¸c˜ao [100].

Figura 1.11: Esquema mostrando o crescimento de um filme de um material com simetria c´ubica na dire¸c˜ao [110].

(32)

Os três gráficos ilustram teoricamente está ideia para as dire¸cões de crescimento [100],[110] e [111].

Anisotropia (100)

Agora pode-se escrever a Equa¸cão (1.30) para cada dire¸cão de crescimento espec´ıfica da simetria cúbica. Como já foi, visto a energia foi dada em fun¸cão dos cossenos diretores, ou seja, esta expressão está no final das contas em fun¸cão dos eixos do cristal. Devido a isso, quando se calcula o caso (100) os eixos do filme estão na mesma dire¸cão dos eixos do cristal, mas no caso (110) e (111) o sistema muda e a expressão precisa passar por uma transforma¸cão para o novo sistema de eixos. No caso da dire¸cão de crescimento (100), pode-se escrever

α1 = sinθcosφ α2 = sinθsinφ α3 = cosθ (1.33) substituindo em (1.30) obtém-se (o termo K0 será omitido, já que não possui dependência angular e a energia é medida através de varia¸cões.)

Eanicubic =K1(sin4θcos2φsin2φ+ sin2θcos2θcos2φ+ sin2θcos2θsin φ

). (1.34)

Nos casos que serão analisados, devido ao termo de anisotropia de forma, quando um campo magnético externo é aplicado no plano do filme, a magnetiza¸cão tende a ficar no plano do filme. Na Figura 1.13 tem-se a representa¸cão de um filme localizado no plano x₋z

(33)

No caso da Figura 1.13, pode-se ver que o ânguloφ= 0 eθé o ângulo entre a magnetiza¸cão e o eixo z. Usando estas condi¸cões e algumas identidades trigonométricas, a expressão final, que representa o comportamento da energia magnetocristalina para um filme nanométrico com simetria cúbica (100) situado no plano x₋z(dire¸cão de crescimento [010])[16], é dada por:

Eanicubic =

K1 4 sin

2₍₂_θ₎_. _(1.35)

O gráfico 1.14 representa com comportamento desta energia em fun¸cão do ângulo θ.

Figura 1.14: Comportamento angular da energia magnetocristalina para a dire¸c˜ao de cres-cimento (010).

A partir da Figura 1.14, pode-se ver quem são os eixos fáceis e duros a partir dos pontos cr´ıticos. Se para um dado ângulo a energia possui um m´ınimo, isto indica um eixo fácil e no caso de máximo tem-se um eixo duro. Assim pode-se ver que os eixos fáceis correspondem aos ângulos θ = 0◦_, _θ _{= 90}◦_, _θ _{= 180}◦ _e _θ _{= 270}◦_{, enquanto os eixos duros correspondem a}

θ = 45◦_, _θ_{= 135}◦_, _θ _{= 225}◦ _e_θ _{= 315}◦_.

Anisotropia (110)

(34)

Figura 1.15: Representa¸c˜ao do plano (110) e os dois sistemas com linha e sem linha, ligados aos eixos do filme e do cristal respectivamente.

O objetivo principal aqui é escrever a Equa¸cão 1.30 no sistema sem linha e reescrever no sistema com linha. Para isso, se faz necessário escrever a rela¸cão entres os dois sistemas usando as componentes da magnetiza¸cão M~ escritas com rela¸cão aos eixos do cristal e aos eixos do filme.

Primeiramente escrevendo o vetor unitário ˆM que representa a dire¸cão da magnetiza¸cão como ˆM =α1xˆ+α2yˆ+α3zê também como ˆM =α1′xˆ′+α2′yˆ′+α′3zˆ′. Tanto o conjunto ˆx,ˆye ˆ

z, quanto o conjunto ˆx′_{, ˆ}_y′ _{e ˆ}_z′_{, s˜ao ambos bases ortogonais. Escrevendo o vetor ˆ}_M _{na base}

do sistema sem linha e utilizando a defini¸cão de cosseno diretor e as transforma¸cões dadas na Figura 1.15, pode-se encontrar as seguintes rela¸cões:

α₁′ = ˆx′ _·Mˆ = ˆz_·(α1xˆ+α2yˆ+α3zˆ) =α3 (1.36)

α′₂ = ˆy_·Mˆ = _√1

2(α1+α2)

α′₃ = ˆz′_·Mˆ = √1

2(−α1+α2).

(35)

α′

3, obt´em-se

α1 = 1

√

2(α

′

2−α′3) (1.37)

α2 = 1

√

2(α

′

2+α′3)

α3 =α′1.

Usando as rela¸cões acima e substituindo na Equa¸cão 1.30, encontra-se a expressão para energia de anisotropia magnetocristalina cúbica (110) em termos do sistema com linha li-gado aos eixos do filme,

Eanicubic =K1

α′ 24 4 + α′ 34 4 +α

′

12α3′2−

α′

22α′32 2

.

(1.38)

Escrevendo os cossenos diretores e colocando o fato de que magnetiza¸cão não sai do plano do filme, com φ = 0 obtém-se, o seguinte resultado:

Eanicubic =

K1 4 (cos

4_θ′_{+ sin}2₍₂_θ′₎₎_. _(1.39)

Na Figura 1.16 mostra-se da dependˆencia angular da anisotropia c´ubica para o caso do

cres-cimento [110].

Assim como no caso anterior, pode-se ver que os eixos f´aceis correspondem a θ′ _{= 90}◦ _e

θ′ _{= 90}◦_{, os eixos intermedi´arios a} _θ′ _{= 0}◦ _e _θ′ _{= 180}◦ _{e os eixos duros em} _θ′ ∼_{= 35}◦ _e

(36)

Figura 1.16: Comportamento angular da energia magnetocristalina (110).

Anisotropia (111)

Neste trabalho não iremos trabalhar com a dire¸cão (111), mas por questão de completeza, daremos uma breve descri¸cão da energia anisotrópica para esta dire¸cão. Na Figura 1.17 mostra-se os vetores unitários que representam o novo sistema de coordenadas (x′_{, y}′_{, z}′_).

Da mesma forma que foi calculado para a dire¸cão (110), encontra-se uma rela¸cão entre os cossenos diretos dos dois sistemas (com linha e sem linha) e em seguida faz-se uma transforma¸cão inversa para achar as seguintes rela¸cões:

α1 =− 1 √ 2α ′ 1 + 1 √ 3α ′ 2+ 1 √ 6α ′ 3 (1.40)

α2 = 1 √ 2α ′ 1 + 1 √ 3α ′ 2+ 1 √

6α′

3

α3 = 1 √ 3α ′ 2− r 2 3α ′ 3,

usando estas rela¸c˜oes e substituindo na Equa¸c˜ao (1.30) tem-se que

Eanicubic =K1

α′ 14 4 + α′ 24 3 + α′ 34 4 + 1 2α ′

12α′32−

√

2α′₁2α′₂α′₃+

√

2 3 α

′

2α′23

!

. (1.41)

Como já foi visto a magnetiza¸cão não sai da região do plano do filme, então φ′ _{= 0,}_α′

1 = sinθ′_,_α′

(37)

Figura 1.17: Representa¸c˜ao do plano (111) e os dois sistemas com linha e sem linha, ligados aos eixos do filme e do cristal respectivamente.

tem-se

Eanicubic=

K1

4 . (1.42)

O plano (111) possui um alta simetria. Com isso, todas as dire¸cões neste plano têm o mesmo valor de energia de anisotropia cúbica. A equa¸cão (1.42) sugere este efeito já que não tem nenhuma dependência angular. Com isso, chega-se a conclusão que um sistema com este tipo de simetria não possui eixos fáceis, intermediários ou duros.

1.4.4 Anisotropia Uniaxial

Para finalizar toda esta discussão sobre anisotropia magnetocristalina, falta falar de um tipo que também será estudado neste trabalho. Nos casos anteriores, pode ser notado que quando foi analisada as anisotropias ligadas a uma simetria tetragonal ou hexagonal, havia o surgimento de um único eixo preferencial e a isto se denomina de comportamento de uma anisotropia dita uniaxial (depende de um único eixo). Nesta se¸cão, se falará diretamente deste tipo de anisotropia.

(38)

portanto só há um único eixo fácil e consequentemente um eixo duro. Como já foi dito, este é o caso mais simples de anisotropia, pois sua dependência está associada somente ao ângulo

θ entre a dire¸cão da magnetiza¸cão e o eixo fácil. A equa¸cão que define está forma de energia é usualmente dada em termos do seno do ânguloθ, como [7]:

Eaniuni =Ksin2θ, (1.43)

onde K ´e a constante de anisotropia efetiva uniaxial.

Algo que deve ser mencionado aqui é que quando foi afirmado queθé o ângulo entre o eixo fácil e a magnetiza¸cão, está impl´ıcito que a constante K sempre é positiva, pois analisando a equa¸cão acima com K positivo vê-se que a energia Euni

ani ´e m´ınima em θ = 0◦, que ´e

comportamento de eixo fácil (a origem está situada no eixo fácil). SeK fosse negativo seria um eixo duro, então no geral o ângulo θ está localizado entre o eixo seja ele duro ou fácil, quem vai indicar qual tipo eixo será é o valor de K. No caso deste trabalho, K sempre é positivo. Com isso tem-se m´ınimo além de θ = 0◦ também em θ = 180◦ e um eixo duro ou de dif´ıcil magnetiza¸cão em θ = 90◦_{(na anisotropia uniaxial sempre o eixo duro e fácil estão}

defasados em 90◦_{) como est´a representado na Figura 1.18:}

Figura 1.18: Gr´afico da energia de anisotropia uniaxial com o ˆangulo θ para K positivo.

1.5 Energia de Anisotropia de Forma

Na se¸cão anterior para poder escrever uma equa¸cão mais simples para a densidade de ener-gia Zeeman, foi mencionado a enerener-gia de anisotropia de forma, cuja contribui¸cão é fazer com que a magnetiza¸cão permane¸ca no plano do filme, quando o campo magnético externo é apli-cado neste plano. Este tipo de intera¸cão tem sua origem na energia magnetostática, através da cria¸cão de uma campo desmagnetizante H~D. Este, por sua vez, é originado a partir da

(39)

´e representada pela seguinte equa¸c˜ao [11]

σ= ˆn_·(M~1−M~2), (1.44)

onde M~1 e M~2 representam as magnetiza¸cões de dois meios distintos, separados por uma interface com vetor normal ˆn e densidade superficial de carga magnética σ. Fisicamente, o que ocorre é o surgimento de dipolos magnéticos, que podem representados por pequenos ´ımãs (como mostrado na Figura 1.5) em todo o material. Dentro do material todo polo norte é compensado por um polo sul adjacente. Porém, quando chegamos à superf´ıcie, não há mais dipolos para compensar. Por exemplo, polos nortes, surgem livres na superf´ıcie. São estes polos induzidos que criam o campo desmagnetizante [7].

(40)

A energia magnetostática é dada através da seguinte rela¸cão entre a magnetiza¸cão e o campo desmagnetizante [11] [21]

Ema=−

1 2

Z

~

M _·H~ddV, (1.45)

está integral é calculada sobre todo o volume da amostra magnética e o 1₂ é um fator que corrige o fato de a integral contar duas vezes o conteúdo energético. Na maioria dos casos as geometrias envolvidas complica a solu¸cão desta integral, mas há casos em que as simetrias envolvidas facilitam. Um destes casos é justamente o do plano infinito que representa o filme nanométrico de interesse para a este trabalho. Há também outros casos como o do elipsoide, o da esfera e o do cilindro infinitamente longo.

O campo desmagnetizante como o próprio nome indica age como um campo que tende a eliminar a magnetiza¸cão do material, e sua equa¸cão é dada na seguinte forma

~ Hd=−

↔

N ·M ,~ (1.46)

onde N↔ é o tensor desmagnetizante cujas componentes vão estar ligadas à geometria e si-metrias do material. Com isso substituindo esta expressão do campo desmagnetizante na equa¸cão da energia magnetostática tem-se que

Ema=

1 2

Z

~

M_·N↔·M dV,~ (1.47) Logo, a densidade de energia magnetost´atica ´e dada por [13]

ema =

1 2M~·

↔

N ·M .~ (1.48)

A partir de agora será analisado o que acontece no caso do elipsoide, da esfera, do cilindro. Por último, o caso de maior interesse que é do plano infinito.

No caso do elipsoide, se os seus eixos coincidirem com os eixos do sistema de coordenadas, o tra¸co da matriz que representa o tensor N↔´e dado por

tr(N↔) = 4π. (1.49)

(41)

que a magnetiza¸c˜ao faz com os semi-eixos do elipsoide. Por fim, o tensor N↔ ´e dado pela seguinte matriz[13] ↔ N=  

N1 0 0

0 N2 0

0 0 N3



,

usando estes resultados na densidade de energia magnetostática (Equa¸cão 1.48), obtém-se o seguinte resultado

ema =

1 2M

2

S(N1α12+N2α22+N3α23). (1.50) Nos demais casos haver´a somente uma mudan¸ca na forma do tensor. Por exemplo, no caso da esfera o tensor N↔´e dado por

↔

N=





4π

3 0 0

0 4₃π 0 0 0 4π

3





e a densidade de energia magnetost´atica se torna

ema =

4 3πM

2

S(α21 +α22 +α23). (1.51) Pela condi¸c˜ao de normaliza¸c˜ao dos cossenos diretores tem-se que α2

1 +α22 +α23 = 1 e como consequˆencia surge a seguinte express˜ao para uma esfera

ema =

4 3πM

2

S. (1.52)

Para um cilindro infinitamente longo, o tensor N↔ ´e dado por

↔

N=





2π 0 0 0 2π 0

0 0 0





e a densidade de energia magnetost´atica ´e dada por

ema =

1 2M

2

S2π(sin2θsin2φ+ sin2θcosφ), (1.53)

colocando sin2θ em evidˆencia, tem-se

(42)

Finalmente para o caso de um plano infinito que se estende por todo planox₋y o tensor desmagnetizante N↔ ´e dado por

↔

N=





0 0 0

0 0 4π



,

o que tem como resultado a seguinte energia magnetost´atica

ema = 2πMS2cos2θ. (1.55)

Com isso se obtém um importante resultado para o caso de filmes nanométricos que serão abordado neste trabalho [13]. Primeiro, pelo fato da densidade de energia magnetostática depender diretamente deM2

S, este termo predomina sobre todos os outros termos de energia.

Outro resultado de grande utilidade para o presente trabalho é com rela¸cão ao m´ınimo da energia magnetostática, que como pode-se ver acontece em θ = π

2, ou seja, a magnetiza¸c˜ao de um filme fino tende a se orientar em alguma dire¸c˜ao no plano do filme.

1.6 Energia de Anisotropia Magnetoel´

astica

A intera¸cão spin-órbita, que gera a anisotropia magnetocristalina e explica grande parte do ferromagnetismo, pode produzir na rede do cristal algumas deforma¸cões. Estas deforma¸cões, por sua vez, geram um novo tipo de anisotropia pelo fato de afetar os eixos do cristal. O efeito magnetoestictivo consiste justamente na deforma¸cão de um material ferromagnético na presen¸ca de campo magnético externo. A magnetostriçcão é quantificada pelo alogamento

λ = ∆l

l , onde o termo ∆l representa a varia¸c˜ao de comprimento em alguma dire¸c˜ao da

amostra e l representa seu comprimento inicial[12].

As deforma¸cões que um dado material pode ser submetido além de serem produzidos pela intera¸cão dos átomos em sua estrutura interna, também podem ser criadas por uma tensão mecânica externa, que no fim irá fazer surgir dire¸cões privilegiadas de magnetiza¸cão, ou seja, eixos que são favoráveis do ponto de vista energético. Resumindo, a energia magnetoelástica expressa a intera¸cão entre a magnetiza¸cão do material ferromagnetico e sua deforma¸cão na rede cristalina. A expressão geral que define a energia magnetoelástica é dada por [7][12]

Eme =

Z X

αβγδ

λαβγδσαβMγdV, Mδ (1.56)

onde os termos σαβ, e λαβγδ representam respectivamente o tensor de tens˜ao mecˆanica e

(43)

Para o caso de um material cuja estrutura cristalina é representada por uma rede cúbica, a densidade de energia magnetoelástica é dada por

eme =−

3 2λ100σ

α₁2β₁2+α2₂β₂2+α2₃β₃2₋ 1

3

(1.57)

−3λ111σ(α1α2β1β2+α2α3β2β3+α3α1β3β1),

onde σ é o módulo da tensão mecânica, αi são os cossenos diretores da magnetiza¸cão, βi

representam os cossenos diretores da tensão e os termosλ100 e λ111 são os valores da magne-tostriçcão quando a magnetiza¸cão está saturada nas dire¸cões (100) e (111) respectivamente. Considerando um caso bem particular onde a magnetostriçcão é isotrópica, ou seja, sua de-forma¸cão não possui um dire¸cão privilegiada, o que siginifica que λ100 =λ111 =λS, onde λS

é o valor da magnetostriçcão no estado saturado. Com estas considera¸cões pode-se escrever a densidade de energia magnetoelástica da seguinte forma

eme =−

3

2λSσ( ˆm·uˆe)

2_, _(1.58)

onde ûerepresenta o vetor na dire¸cão da tensão aplicada e ˆmé o vetor que indica a dire¸cão da

magnetiza¸cão. Na Tabela 3.4 apresentam-se alguns valores da magnetostriçcão de satura¸cão de alguns materiais.

Figura 1.20: Valores da magnetostriçcão de satura¸cão de alguns materiais [7].

(44)

de tensão. Por exemplo, se o produto λσ > 0, a equa¸cão possui um m´ınimo quando o produto escalar entre ûe e ˆmassume seu valor máximo, ou seja, há o surgimento de um eixo

fácil de magnetiza¸cão paralelo ao eixo da tensão. Caso o produtoλσ <0, a Equa¸cão 1.58 se torna positiva, e o m´ınimo agora só acontece quando o produto escalar ûe ˆmé zero, ou seja, há o surgimento de um eixo fácil de magnetiza¸cão na dire¸cão ortogonal ao eixo de tensão.

Para o caso de filmes nanométricos ferromagnéticos, a medida da magnetostriçcão é extre-mamente complicada de ser obtida, devido ao fato do filme se aderir ao substrato impendido que seu comprimento varie livremente. No fim a maior parte da energia magnetoelástica nos filme se dar no momento da produ¸cão da amostra, devido ao surgimento de muitas tensões internas. Este fato serve de base para a maioria das explica¸cões na literatura sobre as medidas observadas nos materiais Heusler.

1.7 Dom´ınios e Paredes de Dom´ınios Magn´

eticos

1.7.1 Dom´ınios Magn´

eticos

Já foi visto no ´ınicio deste cap´ıtulo que devido à intera¸cão de troca os materais ferro-magnéticos são caracterizados por possuirem uma intera¸cão entre os ´ımãs elementares ou momentos magnéticos de sua estrutura, ou seja, apresenta uma magnetiza¸cão espontânea mesmo sem estar na presen¸ca de um campo magnético externo aplicado. Além disso, a sua magnetiza¸cão de satura¸cão depende da temperatura a qual o material é submetido, caindo para zero em um valor de temperatura bem definida para cada material ferromagnético, conhecida como temperatura de Curie. Na Figura 2.8 tem-se o gráfico de MS versus T, a

temperatura de Curie corresponde ao ponto onde um material deixa de ser ferromagn´etico e passa a ser paramagn´etico[2].

Já foi discutido acima, que embora os momentos magnéticos devam estar alinhados na escala microscópica, é poss´ıvel encontrar materiais ferromagnéticos com uma magnetiza¸cão fraca ou até mesmo desmagnetizado. Para solucionar este problema Weiss teve que conside-rar, que através do processo de minimiza¸cão da energia livre magnética, surgia nos materais ferromagnéticos pequenas regiões, distribu´ıdas no material com uma magnetiza¸cão igual a magnetiza¸cão de satura¸cão. Estas pequenas regiões ficaram conhecidas como dom´ınios magnéticos e assim quando um material está desmagnetizado abaixo da temperatura de Cu-rie, era devido a estes dom´ınios estarem dispostos de tal forma que a magnetiza¸cão total é nula[12].

(45)

Figura 1.21: Gráfico da magnetiza¸cão de satura¸cão em fun¸cão da temperatura, o ponto onde a curva toca o eixo T corresponde a temperatura de Curie.

Figura 1.22: Exemplo de estruturas de dom´ınios magnéticos cuja resultante é uma magne-tiza¸cão nula [2].

(46)

1.7.2 Paredes de Dom´ınio

As paredes de dom´ınio representam a zona de transi¸cão da magnetiza¸cão dos dom´ınios magnéticos. Na região da parede, a magnetiza¸cão sai do estado em que se encontra num dado dom´ınio e aproxima-se gradualmente da orienta¸cão da magnetiza¸cão do dom´ınio adjacente. As paredes de dom´ınio são primeiramente classificadas pelo ângulo formado entre os vetores que representam as magnetiza¸cões dos dom´ınios adjacentes [5]. Os caso mais comuns são os das paredes de dom´ınio de 180◦_{, cujas magnetiza¸cão dos dom´ınios adjacentes são}

opos-tas e as paredes de 90◦_{, cujas magnetiza¸c˜ao dos dom´ınios adjacentes s˜ao perpendiculares,}

representadas respectivamente na Figura 2.3.

Figura 1.23: Classifica¸cão das paredes de dom´ınio com rela¸cão ao ângulo de orienta¸cão entre a magnetiza¸cão dos dom´ınios adjacentes. a) Paredes de dom´ınio de 180◦ _{e b) Paredes de}

dom´ınio de 90◦ _[12].

As paredes de dom´ınios magnéticos, além de serem classificadas com rela¸cão ao ângulo de orienta¸cão das magnetiza¸cão de dom´ınios adjacentes, também podem ser classificadas com rela¸cão ao padrão de rota¸cão dos dom´ınios magnéticos dentro da parede de dom´ınio. Dentro deste contexto, temos dois tipos de classifica¸cão: as paredes de Bloch e as paredes de Néel.

As paredes de Bloch [2][5] correspondem as paredes cujo padrão de rota¸cão dos momentos magnéticos ocorre fora do plano dos dom´ınios magnéticos adjacentes. Já as paredes de Néel [18] correspondem as paredes cujo padrão de rota¸cão dos momentos magnéticos ocorre no mesmo plano dos dom´ınios magnéticos adjacentes. As figuras 1.24 1.25 mostram o compor-tamento destes dois tipos de paredes.

(47)

Figura 1.24: Representa¸cão da estrutura interna da parede de Bloch, onde o padrão de rota¸cão dos dom´ınios magnéticos ocorre para fora do plano dos dom´ınios adjacentes [19].

Figura 1.25: Representa¸cão da estrutura interna da parede de Néel, onde o padrão de rota¸cão dos dom´ınios magnéticos ocorre dentro do plano dos dom´ınios adjacentes [19].

(48)

Cap´ıtulo 2

Modelo Te´

orico para a Magnetiza¸c˜

ao

e o Processo de Minimiza¸

c˜

ao da

Energia

A partir de agora será analisado como se dá o processo de magnetiza¸cão através da mi-nimiza¸cão da energia livre magnética. Para isto, será usado métodos anal´ıtico e numérico de minimaza¸cão de energia afim de construir as curvas de histerese para materiais que pos-suam anisotropias magnetocristalinas cúbicas do tipo (100), (110) e uniaxial, no intuito de se testar o método.

2.1 Processo de Magnetiza¸c˜

ao

Antes de descrever o método de calcular as curvas de histerese, se faz necessário entender o processo de magnetiza¸cão, para poder construir um método que solucione o problema.

O processo de magnetiza¸cão de um material ferromagnético consiste na evolu¸cão da mag-netiza¸cão quando este é submetido a presen¸ca de um campo magnético externo. Os dom´ınios magnéticos e as paredes de dom´ınios se rearranjam à medida que o campo tem seu valor mu-dado gradualmente. A cada novo valor, o sistema tende a estar em um estado de equil´ıbrio, que é identificado justamente quando se obtém a minimiza¸cão da energia [24][9].

(49)

o campo magnético é nulo, os dom´ınios ainda estão parcialmente alinhados de tal forma que há uma magnetiza¸cão, mesmo não havendo valor de campo. O ponto que em que a curva toca o eixo das ordenadas é conhecido como magnetiza¸cão remanente. Quando se passa a inverter o sentido do campo, a magnetiza¸cão de cada dom´ınio se desalinham até um ponto em que a magnetiza¸cão total se torna nula mesmo na presen¸ca de um campo externo. A este ponto onde a curva toca o eixo das abscissas, o campo é chamado de campo coercivo. Então a coercividade de um material representa a situa¸cão em que um campo aplicado anula a magnetiza¸cão deste, mesmo depois de magnetizado. À medida que o campo tem seu valor aumentado no sentido oposto, os dom´ınios iram se alinhado até a magnetiza¸cão do material saturar no sentido em que o campo se encontra. Quando o valor do campo é diminu´ıdo até inverter seu sentido, a magnetiza¸cão segue por outro caminho, mas simétrico à curva anterior até saturar novamente. A esta curva se dá o nome de histerese e ela representa um fenômeno termodinâmico irrevers´ıvel [9][11][21][24]. A Figura 2.1 representa a curva de histerese de um material ferromagnético na presen¸ca de campo e com estrutura de dom´ınios esquematizandos para representar os respectivos estados dos pontos acima descritos.

Figura 2.1: O esquema acima mostra como a magnetiza¸cão de um material magnético varia em fun¸cão da intensidade do campo ferromagnético aplicado sobre ele [20].

(50)

A largura da curva de histerese na Figura 2.2 representa a coercividade do material. ela pode ser larga, o que caracteriza um material duro, ou seja, é necessário valores alto de campo magnético para poder saturar o material, já quando essa abertura é mais estreita, o material é dito macio, devido a sua satura¸cão ser atingida para valores bem menores de campo, ou seja, um material dito duro tem um campo coercivo relativamente alto, já um material é dito macio se este tem um campo coercivo relativamente baixo [24].

Figura 2.2: Curvas de histereses magnéticas t´ıpicas: a) de um material magnético duro e b) de um material magnético macio.

2.2 M´

etodo de Minimiza¸c˜

ao

Existem vários métodos anal´ıticos e numéricos para o cálculo das curvas de magnetiza¸cão. A maioria consiste no cálculo do estado de equil´ıbrio do sistema e se baseiam na teoria de campo médio, ou seja, a primeira aproxima¸cão que se pode fazer é substituir todas as flutua¸cões existentes no sistema pelo valor médio. No geral, está formula¸cão apresenta uma solu¸cão, pelo menos, em princ´ıpio [22]. A Figura 2.3 dá uma ideia da teoria de campo médio.