2018
UNIVERSIDADE DE LISBOA
FACULDADE DE CIÊNCIAS
DEPARTAMENTO DE ESTATÍSTICA E INVESTIGAÇÃO OPERACIONAL
Modelos para o Problema do Caixeiro Viajante Periódico
Ana Margarida Garcia Crespo
Mestrado em Estatística e Investigação Operacional
Especialização em Investigação Operacional
Dissertação orientada por:
Professor Doutor Luís Eduardo Neves Gouveia
Professora Doutora Ana Maria Duarte Silva Alves Paias
Em primeiro lugar quero agradecer aos meus orientadores, o Professor Doutor Lu´ıs Eduardo Neves Gouveia e a Professora Doutora Ana Maria Duarte Silva Alves Paias, por toda a sua disponibilidade, apoio demonstrado e partilha de conhecimentos, na elaborac¸˜ao da presente dissertac¸˜ao. Foi uma honra. Em segundo lugar quero agradecer a minha fam´ılia, em especial aos meus pais e irm˜a, a quem lhes devo a pessoa que sou hoje e representam um s´ımbolo de motivac¸˜ao e forc¸a para alcanc¸ar os objetivos propostos.
Por fim, agradec¸o a pessoa que mais me acompanhou durante esta dissertac¸˜ao, o meu namorado. Agradec¸o-lhe por me incentivar e acreditar mais em mim que eu pr´opria.
Esta dissertac¸˜ao foi financiada por fundos nacionais da FCT - Fundac¸˜ao para a Ciˆencia e a Tecnologia, ao abrigo do projecto: PTDC/MAT-NAN/2196/2014”.
Resumo
Dado um per´ıodo de planeamento de alguns dias e um conjunto de clientes que devem ser visitados em um ou mais dias no respetivo per´ıodo, o Problema do Caixeiro Viajante Peri´odico (PTSP) consiste em determinar uma rota para cada dia, com in´ıcio e fim num determinado dep´osito, garantindo que todos os clientes s˜ao visitados o n´umero de vezes requeridas. Conhecendo os custos de deslocac¸˜ao entre cada par de clientes e entre cada cliente e o dep´osito e, sabendo quantas visitas devem ser realizadas a cada cliente, sendo que um cliente s´o pode ser visitado uma vez por dia, pretende-se que as rotas minimizem o custo total.
O PTSP ´e uma variante do cl´assico Problema do Caixeiro Viajante (TSP), onde a este ´e associado o per´ıodo de planeamento. Caso o per´ıodo tenha apenas um dia e todos os clientes tenham que ser visitados uma vez, o PTSP reduz-se ao TSP e, portanto, tamb´em pertence `a classe de problemas NP-dif´ıcil, sendo um problema de resoluc¸˜ao exata dif´ıcil.
No problema considerado todas as combinac¸˜oes de dias poss´ıveis para as visitas dos clientes s˜ao ad-miss´ıveis, mas nesta dissertac¸˜ao ser´a tamb´em considerada uma variante do problema. Esta consiste em que as visitas de alguns clientes sigam uma determinada pol´ıtica de visitas, fazendo com que o n´umero de combinac¸˜oes de visitas aceites para o cliente, diminuam.
Nesta dissertac¸˜ao foram desenvolvidos quatro modelos: trˆes modelos para o PTSP e um modelo para o PTSP relaxado. Destes modelos dois foram baseados no Modelo de Fluxo Agregado (MFA) e os outros dois baseados no Modelo de Fluxo Desagregado (MFD). Pretende-se comparar os modelos em termos de eficiˆencia na obtenc¸˜ao de soluc¸˜oes ´otimas bem como na qualidade da respetiva relaxac¸˜ao linear.
Para comparar os modelos foram utilizadas tanto instˆancias retiradas da literatura como novas instˆancias geradas aleatoriamente, com um n´umero de clientes a variar entre 20 e 47. Na experiˆencia computaci-onal consideraram-se matrizes de custos assim´etricas e sim´etricas e variados padr˜oes de visitas. Foram realizados testes para os per´ıodos de dois, trˆes e quatro dias.
No caso da variante do problema, consideraram-se tamb´em diversas distribuic¸˜oes para as regras de visitas e resolveu-se a mesma, para os per´ıodos de planeamento de trˆes e quatro dias.
Palavras-chave: Probema do Caixeiro Viajante Peri´odico, Modelos Exatos, Relaxac¸˜ao Linear, Matrizes Assim´etricas e Sim´etricas
Abstract
Given a planning period of a several days and a set of clients that should be visited in one or more days in the respective period, knowing the travel costs between each pair of clients and between each client and the deposit, and knowing how many visits must be made to each client, since a customer can only be visited once a day, the Period Traveling Salesman Problem (PTSP) consists of determining a set of routes of minimum total cost, one for each day, and ensuring that all customers are visited the required number of times.
PTSP is a variant of the Traveling Salesman Problem (TSP). If the period has only one day, the PTSP reduces to the TSP and therefore also belongs to the problem class of NP-hard problems.
The PTSP considers all combinations of possible days for the visits of the clients as being admissible, but in this dissertation, a variant where some rules will be imposed that will reduce the number of combinations accepted will be also studied.
In this dissertation four models were developed: three models for PTSP and one model for relaxed PTSP. These two models were based on the Aggregate Flow Model (MFA) and the other two were based on the Disaggregated Flow Model (MFD). The models are compared in terms of efficiency in obtaining the optimal solutions as well as in the quality of their linear relaxations.
To compare the models, instances from the literature and new randomly generated instances are used, with a number of customers ranging from 20 to 47. In the computational experiment were considered matrices of asymmetric and symmetrical costs and varied patterns of visits. Tests were performed for periods of two, three and four days.
In the case of the variant of the problem where some rules are imposed, several distributions for the visiting rules were also considered and resolved for the three and four day planning periods.
Keywords: Period Traveling Salesman Problem, Exact Models, Linear Relaxation, Asymmetric and Symmetric Matrix
´Indice
Lista de Figuras x
Lista de Tabelas xii
1 Introduc¸˜ao 1
2 Revis˜ao Bibliogr´afica 5
2.1 Problema do Caixeiro Viajante (TSP) . . . 5
2.2 Problema do Caixeiro Viajante Peri´odico (PTSP) . . . 7
3 Modelos em PLI 11 3.1 Definic¸˜ao do Problema . . . 11
3.2 Formulac¸˜oes . . . 11
3.2.1 Modelo de Fluxo Agregado Peri´odico (MFAP) . . . 12
3.2.2 Modelo de Fluxo Agregado Peri´odico com Restric¸˜oes de Sub-circuitos (MFAPSC) 13 3.2.3 Modelo de Fluxo Desagregado Peri´odico (MFDP) . . . 14
3.2.4 Modelo de Fluxo Desagregado Relaxado (MFDR) . . . 15
3.3 Variante do Problema . . . 17
3.3.1 Variante de Per´ıodo de 3 dias . . . 18
3.3.2 Variante de Per´ıodo de 4 dias . . . 18
4 Experiˆencia Computacional 19 4.1 Instˆancias de Teste . . . 19
4.1.1 Custos de Deslocac¸˜ao . . . 19
4.1.2 Visitas . . . 20
4.1.3 Regras . . . 21
4.2 Comparac¸˜ao dos Modelos . . . 21
4.2.1 Resultados Computacionais - Instˆancias com 20 Clientes . . . 22
4.2.2 Resultados Computacionais - Instˆancias com 40 Clientes . . . 31
4.2.3 Comparac¸˜oes dos Resultados para V´arias Dimens˜oes de Per´ıodo . . . 34
4.2.4 Comparac¸˜oes dos Resultados para V´arias Dimens˜oes do Conjunto de Clientes . . 40
4.2.5 Considerac¸˜oes Finais . . . 43
4.3 Testes Computacionais das Instˆancias com Matriz de Custos de Testes da Literatura . . . 44
4.4 Testes Computacionais da Variante do Problema . . . 47 vii
4.4.1 Resultados Computacionais - Variante de Per´ıodo de 3 Dias . . . 48 4.4.2 Resultados Computacionais - Variante de Per´ıodo de 4 Dias . . . 51 4.4.3 Comparac¸˜ao da Variante do Problema para os Dois Per´ıodos de Planeamento . . 53
5 Conclus˜oes 57
5.1 Conclus˜oes Principais . . . 57 5.2 Trabalho Futuro . . . 60
Referˆencias 65
A Resultados Completos 67
A.1 Resultados obtidos com vista `a comparac¸˜ao dos modelos - instˆancias com 20 clientes . . 68 A.1.1 Resultados para o per´ıodo de 2 dias . . . 68 A.1.2 Resultados para o per´ıodo de 3 dias . . . 71 A.1.3 Resultados para o per´ıodo de 4 dias . . . 74 A.2 Resultados obtidos com vista `a comparac¸˜ao dos modelos - instˆancias com 40 clientes . . 78 A.3 Resultados obtidos para as instˆancias com matriz de custos de testes da literatura . . . . 81 A.4 Resultados obtidos para a variante do problema . . . 82 A.4.1 Resultados para a variante com per´ıodo de 3 dias . . . 83 A.4.2 Resultados para a variante com per´ıodo de 4 dias . . . 84
Lista de Figuras
1.1 Matriz de Custos de Deslocac¸˜ao . . . 1 1.2 Vetor de Visitas dos Clientes . . . 1 1.3 Representac¸˜ao da soluc¸˜ao ´otima do Exemplo 1 . . . 2 4.1 Comparac¸˜ao dos gaps para as matrizes de custos assim´etricas e sim´etricas em instˆancias
com 20 clientes e per´ıodo de 2 dias . . . 24 4.2 Comparac¸˜ao dos gaps para as matrizes de custos assim´etricas e sim´etricas em instˆancias
com 20 clientes e per´ıodo de 3 dias . . . 27 4.3 Comparac¸˜ao dos gaps para as matrizes de custos assim´etricas e sim´etricas em instˆancias
com 20 clientes e per´ıodo de 4 dias . . . 30 4.4 Comparac¸˜ao dos gaps para as matrizes de custos assim´etricas e sim´etricas em instˆancias
com 40 clientes e per´ıodo de 2 dias . . . 33 4.5 Comparac¸˜ao da percentagem de instˆancias, com matriz de custos assim´etrica e sim´etrica,
resolvidas pelos modelos MFAP, MFAPSC e MFDP nos per´ıodos de dois, trˆes e quatro dias . . . 34 4.6 Comparac¸˜ao dos tempos de execuc¸˜ao, na resoluc¸˜ao do problema inteiro, obtidos por cada
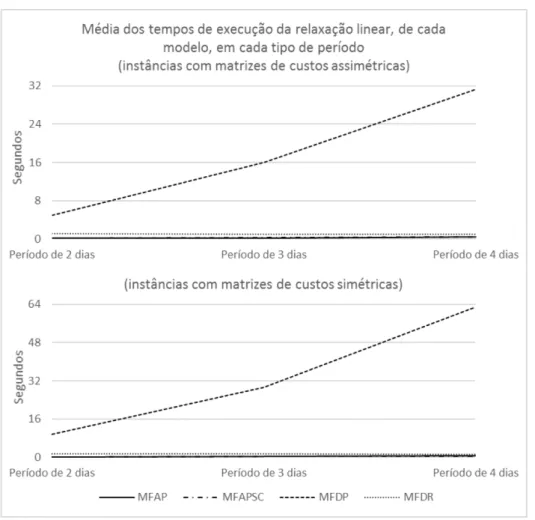
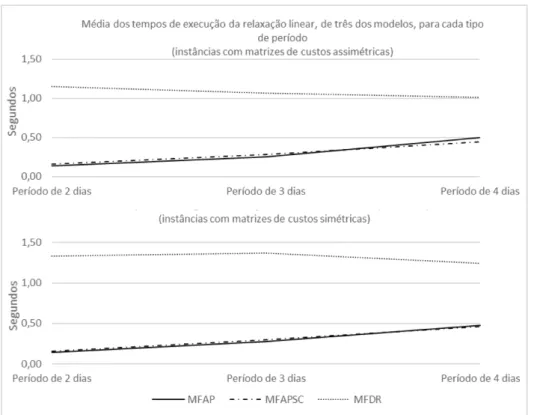
modelo, para cada tipo de per´ıodo e para os dois tipos de matrizes . . . 35 4.7 Comparac¸˜ao dos tempos de execuc¸˜ao, na resoluc¸˜ao da relaxac¸˜ao linear, obtidos por cada
modelo, para cada tipo de per´ıodo e para os dois tipos de matrizes . . . 36 4.8 Comparac¸˜ao dos tempos de execuc¸˜ao, na resoluc¸˜ao da relaxac¸˜ao linear, obtidos pelos
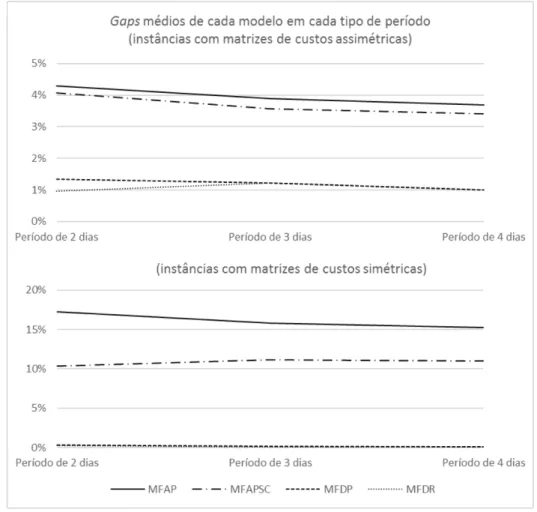
modelos MFAP, MFAPSC e MFDR, para cada tipo de per´ıodo e para os dois tipos de matrizes . . . 37 4.9 Comparac¸˜ao dos gaps obtidos por cada modelo em cada tipo de per´ıodo, para os dois
tipos de matrizes . . . 38 4.10 Comparac¸˜ao dos tempos de execuc¸˜ao, na resoluc¸˜ao do problema inteiro e na resoluc¸˜ao
da relaxac¸˜ao linear do modelo MFDR, para cada tipo de per´ıodo e matriz de custos . . . 39 4.11 Comparac¸˜ao das m´edias dos gaps entre a soluc¸˜ao do problema inteiro e da relaxac¸˜ao
linear do modelo MFDR para cada tipo de per´ıodo e matriz de custos . . . 39 4.12 Comparac¸˜ao do n´umero de soluc¸˜oes ´otimas encontradas pelos modelos MFAP, MFAPSC
e MFDP, nas instˆancias com 20 e 40 clientes, no per´ıodo de dois dias . . . 40 4.13 Comparac¸˜ao dos gaps obtidos, nos v´arios conjuntos de instˆancias, pelos modelos MFAP
e MFAPSC . . . 50 4.14 Comparac¸˜ao dos gaps obtidos, nos v´arios conjuntos de instˆancias, pelo modelo MFAPSC 52
4.15 Comparac¸˜ao da percentagem de instˆancias resolvidas at´e `a otimalidade pelo modelo MFAPSC em cada tipo de per´ıodo para a variante do problema . . . 53 4.16 Comparac¸˜ao dos tempos de execuc¸˜ao obtidos pelo modelo MFAPSC na resoluc¸˜ao do
problema inteiro, para os dois tipos de per´ıodo . . . 54 4.17 Comparac¸˜ao dos tempos de execuc¸˜ao obtidos pelo modelo MFAPSC na resoluc¸˜ao da
relaxac¸˜ao linear, para os dois tipos de per´ıodo . . . 55 4.18 Comparac¸˜ao dos gaps obtidos pelo modelo MFAPSC nos v´arios conjuntos de instˆancias
e para os dois tipos de per´ıodo de planeamento . . . 56
Lista de Tabelas
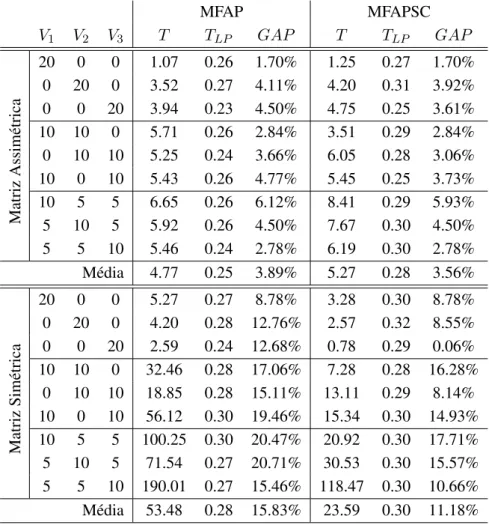
4.1 N´umero de padr˜oes de visitas associado a cada matriz de custos . . . 20 4.2 Comparac¸˜ao dos modelos MFAP e MFAPSC para instˆancias com 20 clientes e per´ıodo
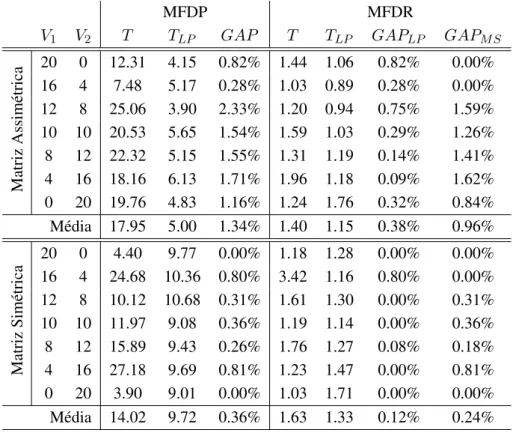
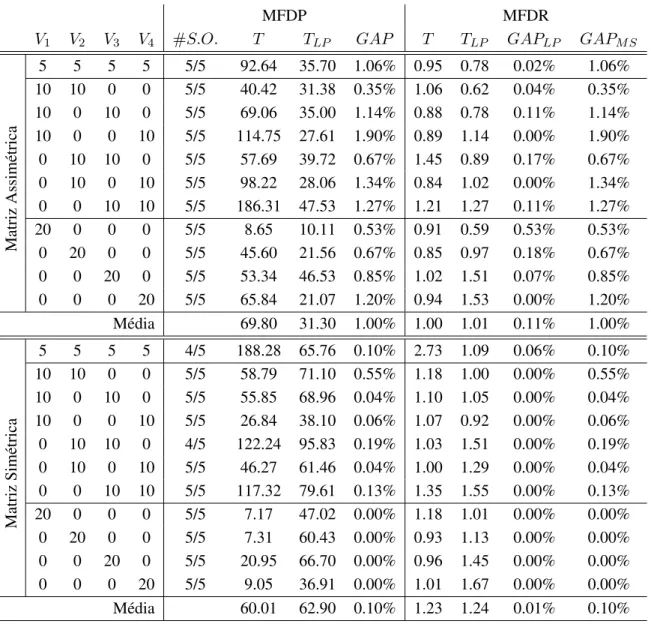
de 2 dias . . . 23 4.3 Comparac¸˜ao dos modelos MFDP e MFDR para instˆancias com 20 clientes e per´ıodo de
2 dias . . . 23 4.4 Comparac¸˜ao dos modelos MFAP e MFAPSC para instˆancias com 20 clientes e per´ıodo
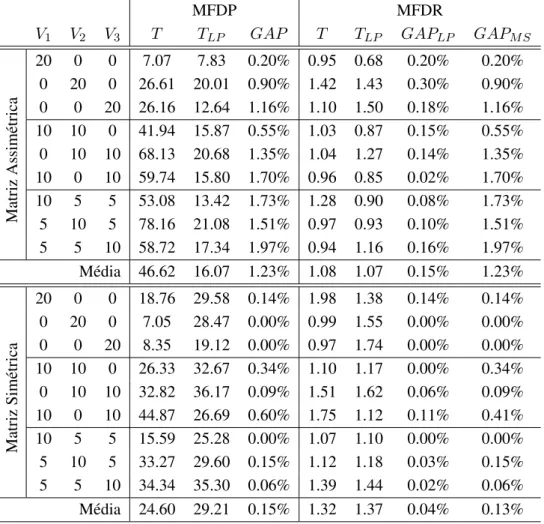
de 3 dias . . . 25 4.5 Comparac¸˜ao dos modelos MFDP e MFDR para instˆancias com 20 clientes e per´ıodo de
3 dias . . . 26 4.6 Comparac¸˜ao dos modelos MFAP e MFAPSC para instˆancias com 20 clientes e per´ıodo
de 4 dias . . . 28 4.7 Comparac¸˜ao dos modelos MFDP e MFDR para instˆancias com 20 clientes e per´ıodo de
4 dias . . . 29 4.8 Comparac¸˜ao dos modelos MFAP e MFAPSC para instˆancias com 40 clientes e per´ıodo
de 2 dias . . . 31 4.9 Comparac¸˜ao dos modelos MFDP e MFDR para instˆancias com 40 clientes e per´ıodo de
2 dias . . . 32 4.10 Comparac¸˜ao dos tempos de execuc¸˜ao dos quatro modelos para instˆancias com 20 e 40
clientes para o per´ıodo de dois dias . . . 41 4.11 Comparac¸˜ao dos gaps dos quatro modelos para instˆancias com 20 e 40 clientes para o
per´ıodo de dois dias . . . 42 4.12 Comparac¸˜ao do GAPLP, do modelo MFDR, para instˆancias com 20 e 40 clientes para o
per´ıodo de dois dias . . . 43 4.13 Comparac¸˜ao dos modelos MFAP e MFAPSC para instˆancias da literatura e per´ıodo de 2
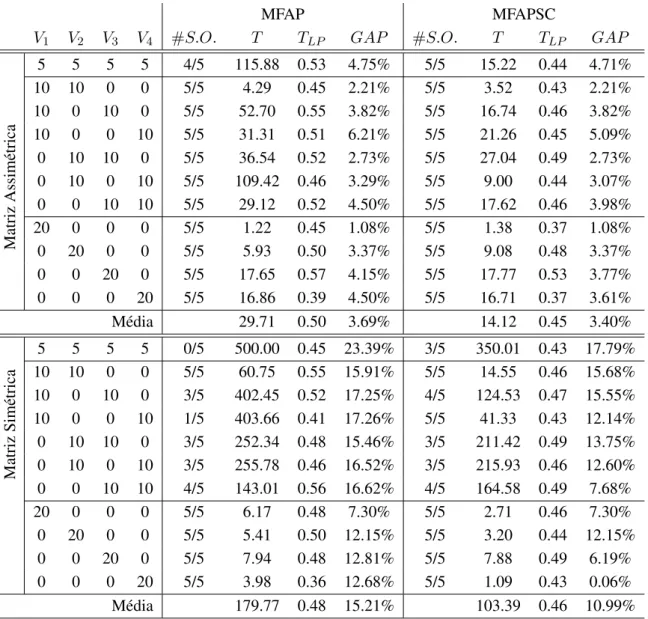
dias . . . 45 4.14 Intervalos de variac¸˜ao dos custos de deslocac¸˜ao de cada um dos testes considerado . . . 46 4.15 Comparac¸˜ao dos modelos MFAP e MFAPSC para instˆancias com 40 clientes e per´ıodo
de 3 dias . . . 49 4.16 Resultados do modelo MFAPSC para instˆancias com 40 clientes e per´ıodo de 4 dias . . . 51 5.1 Pontos positivos e negativos de cada modelo . . . 58 A.1 Resultados obtidos pelos modelos MFAP e MFAPSC para as instˆancias com 20 clientes
e per´ıodo de 2 dias . . . 68 xi
A.2 Resultados obtidos pelos modelos MFDP e MFDR para as instˆancias com 20 clientes e per´ıodo de 2 dias . . . 69 A.3 Resultados obtidos pelos modelos MFAP e MFAPSC para as instˆancias com 20 clientes
e per´ıodo de 3 dias . . . 71 A.4 Resultados obtidos pelos modelos MFDP e MFDR para as instˆancias com 20 clientes e
per´ıodo de 3 dias . . . 72 A.5 Resultados obtidos pelos modelos MFAP e MFAPSC para as instˆancias com 20 clientes
e per´ıodo de 4 dias . . . 74 A.6 Resultados obtidos pelos modelos MFDP e MFDR para as instˆancias com 20 clientes e
per´ıodo de 4 dias . . . 76 A.7 Resultados obtidos pelos modelos MFAP e MFAPSC para as instˆancias com 40 clientes
e per´ıodo de 2 dias . . . 78 A.8 Resultados obtidos pelos modelos MFDP e MFDR para as instˆancias com 40 clientes e
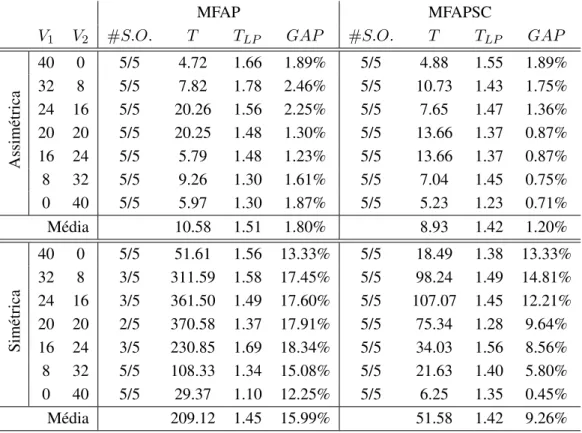
per´ıodo de 2 dias . . . 80 A.9 Resultados obtidos pelos modelos MFAP e MFAPSC para as instˆancias com matriz de
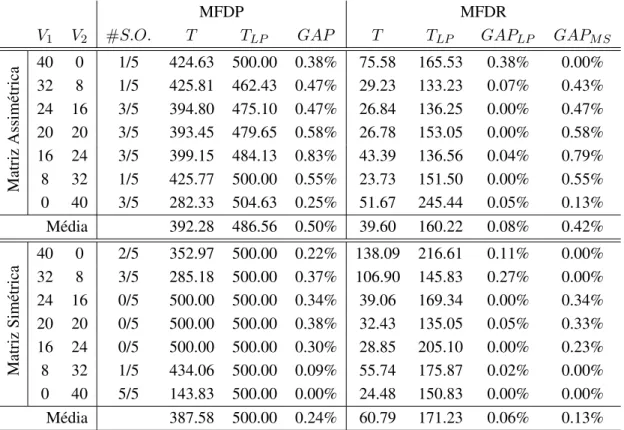
custos de testes da literatura e per´ıodo de 2 dias . . . 81 A.10 Resultados obtidos pelos modelos MFAP e MFAPSC para a variante do problema com
per´ıodo de 3 dias . . . 83 A.11 Resultados obtidos pelo modelo MFAPSC para a variante do problema com per´ıodo de
4 dias . . . 85
Cap´ıtulo 1
Introduc¸˜ao
Hoje em dia existem diversas entidades que disponibilizam enfermeiros ao domicilio, possibilitando que qualquer pessoa usufrua de servic¸os de enfermagem nas suas habitac¸˜oes.
Supondo que um enfermeiro tem de visitar cinco pessoas num per´ıodo de dois dias. Saindo de um determinado local e voltando, ao mesmo, ap´os realizar todas as visitas, este pretende que as suas visitas sejam realizadas de modo a demorar o menor tempo poss´ıvel em viagens.
Designando por dep´osito, o local onde o enfermeiro se encontra, por clientes, o conjunto de pessoas que devem ser visitadas pelo enfermeiro e, por custos de deslocac¸˜ao, o custo da viagem entre dois locais. O exemplo traduz-se em determinar as duas rotas de custo total m´ınimo, com in´ıcio e fim no dep´osito, garantindo que os todos os clientes s˜ao visitados o n´umero de vezes requeridas. Considerem-se as seguintes matrizes representativas do Exemplo 1:
Figura 1.1: Matriz de Custos de Deslocac¸˜ao
Figura 1.2: Vetor de Visitas dos Clientes
Na figura 1.1 est˜ao representados os custos de deslocac¸˜ao entre cada par de locais. A primeira li-nha/coluna ´e correspondente ao dep´osito, e as restantes 5 linhas/colunas correspondentes aos clientes. Esta matriz de custos ´e assim´etrica, mas futuramente tamb´em ser˜ao considerados casos com matriz sim´etrica. Na figura 1.2 ´e indicado quantas visitas devem ser feitas a cada um dos nodos clientes, sendo que cada cliente s´o pode ser visitado no m´aximo uma vez por dia. Os clientes 1, 3 e 5 devem ser visitados uma vez, enquanto que os clientes 2 e 4 devem ser visitados duas vezes. Como o per´ıodo tem dois dias, os clientes 2 e 4 estar˜ao presentes nas duas rotas.
Cap´ıtulo 1. Introduc¸˜ao 2
A soluc¸˜ao ´otima do Exemplo 1 ´e constitu´ıda pelas seguintes rotas: a rota do primeiro dia ´e {0, 2, 4, 5, 0} e a rota do segundo dia ´e {0, 3, 4, 1, 2, 0}, sendo que o nodo 0 representa o dep´osito. Esta soluc¸˜ao tem um custo total de 333 u.m. e est´a representada na figura 1.3.
Figura 1.3: Representac¸˜ao da soluc¸˜ao ´otima do Exemplo 1
O Exemplo 1 ´e resolvido de forma ´otima facilmente, contudo quando se considera um exemplo de maior dimens˜ao, a resoluc¸˜ao deste pode n˜ao ser t˜ao f´acil. A determinac¸˜ao de uma soluc¸˜ao implica definir quais os dias do per´ıodo em que cada pessoa deve ser visitada e definir a ordem pela qual as visitas devem ser feitas. Estas duas fases na determinac¸˜ao de uma soluc¸˜ao fazem com que existam muitas soluc¸˜oes e a procura pela melhor soluc¸˜ao n˜ao seja f´acil.
A ´area de Investigac¸˜ao Operacional tem como objetivo a determinac¸˜ao de soluc¸˜oes ´otimas ou pr´oximas da ´otima, de problemas deste g´enero. Estas soluc¸˜oes s˜ao encontradas atrav´es da resoluc¸˜ao de modelos matem´aticos representativos dos problemas. O exemplo anterior ´e um exemplo representativo do pro-blema, designado em Investigac¸˜ao Operacional, como Problema do Caixeiro Viajante Peri´odico (PTSP).
Dado um determinado per´ıodo de dias, um conjunto limitado de clientes e um dep´osito. Cada cliente requer um determinado n´umero de visitas no per´ıodo, mas s´o pode ser visitado no m´aximo uma vez por dia. Al´em disso, sabe-se os custos de deslocac¸˜ao entre cada par de clientes e entre cada cliente e o dep´osito. O objetivo do PTSP consiste em determinar uma rota para cada dia, tal que:
- O ponto de partida e de chegada de cada rota ´e o dep´osito;
- As visitas realizadas a cada cliente no final do per´ıodo devem corresponder ao n´umero de visitas requeridas por estes;
- O custo total, dado pela soma dos custos de deslocac¸˜ao de cada rota, seja m´ınimo.
Como j´a foi visto, este problema pode ser modelado atrav´es de um grafo orientado, onde o dep´osito e os clientes s˜ao representados atrav´es de nodos e a possibilidade de viagens entre estes ´e representada por arcos. Assumindo esta representac¸˜ao, uma rota corresponde a um circuito no grafo e, portanto, uma soluc¸˜ao do problema ir´a corresponder a um conjunto de circuitos, um por cada dia do planeamento.
Esta dissertac¸˜ao foca-se no estudo de m´etodos exatos quer na variante do PTSP onde, embora se saiba o n´umero de vezes que cada cliente tem de ser visitado, n˜ao s˜ao definidos os dias no per´ıodo em que estas
Cap´ıtulo 1. Introduc¸˜ao 3
visitas devem ocorrer, quer na variante onde ´e considerada uma pol´ıtica de visitas dos clientes, onde nem todos os dias s˜ao admitidos para as visitas de alguns clientes. Para este estudo foram desenvolvidos quatro modelos, dos quais trˆes modelam o problema original e outro modela a relaxac¸˜ao do mesmo. Estes modelos ser˜ao utilizados para resolver variadas instˆancias de teste, de modo a avaliar as respetivas performances.
Ap´os a introduc¸˜ao da dissertac¸˜ao, ´e apresentado o cl´assico Problema do Caixeiro Viajante (TSP), bem como v´arias variantes conhecidas do mesmo. Ainda neste cap´ıtulo, ´e feita uma caracterizac¸˜ao do PTSP, problema em estudo nesta dissertac¸˜ao e, ´e feita uma revis˜ao bibliogr´afica do mesmo. Por fim, neste cap´ıtulo s˜ao tamb´em apresentadas algumas variantes do PTSP.
No cap´ıtulo 3 comec¸a-se por definir o problema e apresenta-se as quatro formulac¸˜oes em programac¸˜ao linear inteira (PLI) desenvolvidas para o mesmo. Ainda neste cap´ıtulo ´e definida uma variante do PTSP, bem como as adaptac¸˜oes necess´arias nos modelos de modo a representarem o novo problema.
No cap´ıtulo seguinte s˜ao apresentados os resultados da experiˆencia computacional efetuada para as instˆancias de referˆencia consideradas, tamb´em apresentadas neste cap´ıtulo. Neste s˜ao tamb´em apre-sentadas algumas comparac¸˜oes retiradas a partir dos destes realizados.
Por fim, no capitulo 5 s˜ao referidas as conclus˜oes retiradas do estudo apresentado e algumas sugest˜oes de trabalho futuro.
Cap´ıtulo 2
Revis˜ao Bibliogr´afica
O corrente cap´ıtulo subdivide-se em duas partes. Na primeira parte introduz-se brevemente o cl´assico Problema do Caixeiro Viajante (Traveling Salesman Problem – TSP) bem como de algumas variantes deste problema. Na segunda parte ´e apresentado o Problema do Caixeiro Viajante Peri´odico (Period Traveling Salesman Problem– PTSP), variante do TSP e problema em estudo nesta dissertac¸˜ao. Neste cap´ıtulo s˜ao tamb´em referidos alguns trabalhos que tˆem sido realizados em relac¸˜ao a este problema e apresentadas algumas variantes do mesmo.
2.1
Problema do Caixeiro Viajante (TSP)
Dado um conjunto de clientes e um dep´osito (e conhecidas as distˆancias entre entre cada par de clientes e entre cada cliente e o dep´osito), o problema do caixeiro viajante consiste em determinar a rota de custo m´ınimo, com in´ıcio e fim no dep´osito, tal que todos os clientes s˜ao visitados uma e uma s´o vez.
Este problema foi introduzido por volta de 1934 por Hassler Whitney num semin´ario, mas s´o em 1954 ´e que foi formalmente apresentado por Dantzig, Fulkerson e Johnson [11], que escrevem a primeira formulac¸˜ao do problema e utilizam a mesma para resolver algumas instˆancias representativas do pro-blema. Desde ent˜ao, o TSP tem sido alvo de imenso estudo, tanto a n´ıvel de resoluc¸˜oes exatas como atrav´es de m´etodos de heur´ısticos e meta-heur´ısticos. Este problema j´a deu origem a muitos outros problemas que tamb´em tˆem sido fortemente estudados.
Alguns grandes grupos de problemas que surgiram a partir do TSP foram os seguintes:
– Problema do Caixeiro Viajante com Janelas Temporais (TSPTW - TSP with Time Windows); – Problema de Roteamento de Ve´ıculos (VRP - Vehicle Routing Problem);
– Problema do Caixeiro Viajante com Dependˆencias Temporais (TDTSP - Time-Dependent TSP); – Problema do Comprador Viajante (TPP - Traveling Purchaser Problem);
– Problema do Caixeiro Viajante Peri´odico (PTSP - Period TSP).
Karp em 1972 [20] provou que o TSP pertence `a classe de problemas NP-dif´ıcil. Desta forma, as varian-tes deste problema, que correspondem a uma generalizac¸˜ao do mesmo e, mais especificamente a variante em estudo nesta dissertac¸˜ao, tamb´em pertencem a esta classe de problemas – a classe NP-dif´ıcil.
Cap´ıtulo 2. Revis˜ao Bibliogr´afica 6
Problema do Caixeiro Viajante com Janelas Temporais (TSPTW)
Como no TSP, pretende-se visitar um conjunto de clientes uma e uma s´o vez, mas neste caso a visita de um determinado cliente deve ser feita dentro da sua janela temporal. Para este problema sabe-se o custo de deslocac¸˜ao entre cada par de clientes e entre cada cliente e o dep´osito, assim como a janela temporal associada a cada cliente. Deseja-se determinar uma rota de custo m´ınimo, com in´ıcio e fim no dep´osito. Este problema resume-se ao TSP quando a amplitude das janelas temporais ´e suficientemente grande deixando de ser restritivas do problema.
Alguns trabalhos realizados sobre o TSPTW s˜ao os desenvolvidos por Dumas, Desrosiers, Gelinas e Solomon [13], por Ascheuer, Fischetti e Gr¨otschel [1] e por Gendreau, Hertz, Laporte, Gilbert e Stan [14].
Problema de Roteamento de Ve´ıculos (VRP)
Neste problema pretende-se satisfazer a procura de um conjunto de clientes a partir de uma frota de ve´ıculos que partem de um ´unico dep´osito, minimizando o custo total das rotas (uma rota corresponde ao percurso realizado por um ve´ıculo).
Este problema reduz-se ao TSP quando a frota de ve´ıculos ´e constitu´ıda apenas por um ve´ıculo, sendo a soluc¸˜ao constitu´ıda apenas por uma rota que passa por todos os clientes e tem custo m´ınimo.
A descric¸˜ao feita do problema corresponde ao problema na sua forma mais simples. A partir deste podem ser formulados outros problemas, como por exemplo:
- Problema de Roteamento de Ve´ıculos com Capacidades: existem capacidades associadas aos ve´ıculos;
- Problema de Roteamento de Ve´ıculos com M´ultiplas Viagens: os ve´ıculos podem fazer mais de uma viagem;
- Problema de Roteamento de Ve´ıculos com Multiplos Dep´ositos: existe um ou mais dep´ositos; - Problema de Roteamento de Ve´ıculos com Entrega e Recolha: permite existir simultaneamente
entrega e recolha no cliente;
- Problema de Roteamento de Ve´ıculos sem Retorno: n˜ao ´e necess´ario que os ve´ıculos retornem ao dep´osito.
Os livros editados em 2008 por Golden, Raghavan e Wasil [16] ou por Toth e Vigo em 2002 [32] apre-sentam uma revis˜ao interessante das diversas variantes deste problema, com m´etodos exatos e heur´ısticos propostos.
Problema do Caixeiro Viajante com Dependˆencias Temporais (TDTSP)
Como acontece com o TSP, este problema consiste em determinar uma rota, com in´ıcio e fim num determinado dep´osito, de custo m´ınimo, garantindo que um conjunto de clientes ´e visitado uma e uma s´o vez. A diferenc¸a para o TSP ´e que os custos associados a cada arco varia consoante a posic¸˜ao em que estes se encontram na rota. Desta forma, a matriz de custo ser´a uma matriz tridimensional, pois cada posic¸˜ao depende de trˆes fatores: do nodo inicial e final do arco e da posic¸˜ao do respetivo arco na rota.
Cap´ıtulo 2. Revis˜ao Bibliogr´afica 7
Dos trabalhos realizados sobre este problema, referencia-se o realizado por Gouveia e Voss, em 1995 [18] e por Godinho, Gouveia e Pesneau, em 2014 [15].
Problema do Comprador Viajante (TPP)
Dado um conjunto de mercados e uma lista dos itens que se pretende adquirir, pretende-se determinar a rota, com in´ıcio e fim num dep´osito, que minimiza o custo total de deslocac¸˜ao e aquisic¸˜ao dos itens. Sabe-se o custo de deslocac¸˜ao entre cada par de mercados e entre o dep´osito e os mercados, bem como os mercados em que cada item est´a dispon´ıvel e o respetivo prec¸o.
Quando em cada mercado apenas se encontra dispon´ıvel um tipo de item, para adquirir todos os itens da lista ´e necess´ario percorrer todos os mercados existentes. Se os custos de deslocac¸˜ao forem transfor-mados de forma a englobarem os custos de aquisic¸˜ao, existindo apenas custos associados `a deslocac¸˜ao, est´a-se perante o TSP.
Deste problema tamb´em existem algumas variantes, como por exemplo, uma variante com capacidades onde a quantidade dispon´ıvel de cada item em cada mercado pode ser inferior `a procura e, portanto, um item pode ter que ser adquirido em mais do que um mercado.
O interesse da comunidade cientifica por este problema tem sido bastante elevado, tendo sido j´a de-senvolvidos v´arios m´etodos de resoluc¸˜ao e estudadas in´umeras variantes do problema, que pretendem alargar o leque de aplicac¸˜oes do TPP.
Algumas referˆencias na literatura deste problema s˜ao o trabalho realizado por Boctor, Laporte e Renaud [4] e por Teeninga e Volgenant [31], onde em ambos os artigos s˜ao desenvolvidos m´etodos heur´ısticos como forma de resoluc¸˜ao. Referˆencia-se tamb´em os artigos [17] por Gouveia, Paias e Voss e [23] por Mansini e Tocchella, onde s˜ao estudadas algumas variantes do TPP.
2.2
Problema do Caixeiro Viajante Peri´odico (PTSP)
Dado um per´ıodo de alguns dias e um conjunto de clientes que devem ser visitados em um ou mais dias no respetivo per´ıodo, o PTSP consiste em determinar uma rota, para cada dia, com in´ıcio e fim num determinado dep´osito, garantindo que todos os clientes s˜ao visitados o n´umero de vezes requeridas. O objetivo consiste em minimizar o custo total das rotas.
Neste problema, sabe-se `a partida o n´umero de vezes que cada cliente tem de ser visitado no respetivo per´ıodo, sendo que cada cliente s´o pode ser visitado uma vez por dia. Embora se saiba o n´umero de vezes que cada cliente tem de ser visitado, n˜ao s˜ao definidos os dias no per´ıodo em que estas visitas devem ocorrer. Para al´em do n´umero de visitas de cada um dos clientes, conhece-se tamb´em os custos de deslocac¸˜ao entre cada par de clientes e entre cada cliente e o dep´osito.
Uma soluc¸˜ao para o PTSP define um conjunto de rotas (uma rota para cada dia do per´ıodo), tal que o conjunto de clientes ´e visitado o n´umero de vezes requeridas no total das rotas definidas. Cada soluc¸˜ao tem um custo associado, resultante da soma dos custos de deslocac¸˜ao totais de cada rota.
Cap´ıtulo 2. Revis˜ao Bibliogr´afica 8
Este problema reduz-se ao TSP quando o per´ıodo em quest˜ao corresponde a apenas um dia. Neste caso, a soluc¸˜ao ´e composta por apenas uma rota de custo m´ınimo que passa por todos os nodos uma e uma s´o vez, ou seja, a rota ir´a corresponder a um circuito hamiltoniano.
Considere-se tamb´em o caso particular em que todos os clientes tˆem de ser visitados em todos os dias do per´ıodo. Como neste caso sabe-se quantos clientes v˜ao ser visitados em cada dia (todos), a sua resoluc¸˜ao consiste em resolver um TSP para cada dia. Como s˜ao sempre os mesmos clientes e os mesmos custos de deslocac¸˜ao entre eles, a soluc¸˜ao ser´a constitu´ıda por um conjunto de rotas iguais. Neste caso, cada rota ir´a tamb´em corresponder a um circuito hamiltoniano e, portanto, a soluc¸˜ao corresponde a um conjunto de circuitos hamiltonianos.
Apesar da primeira referˆencia a este problema j´a contar com mais de 30 anos, existe apenas um pequeno n´umero de trabalhos sobre este. Para al´em disso, os estudos centram-se na resoluc¸˜ao do problema atrav´es de m´etodos heur´ısticos. A resoluc¸˜ao do problema atrav´es de m´etodos exatos foi estudada em apenas dois artigos, onde o per´ıodo considerado era de somente dois dias.
O PTSP foi inicialmente introduzido por Christofides e Beasley [9] em 1984, como forma de encontrar soluc¸˜oes aproximadas para o Problema de Roteamento de Ve´ıculos Peri´odico (Period Vehicle Routing Problem - PVRP). Este problema corresponde ao PTSP quando se considera que existe mais de um ve´ıculo para satisfazer o conjunto de clientes. Desta forma, quando se tem o caso particular do PVRP com apenas um ve´ıculo, est´a-se perante o PTSP.
Christofides e Beasley apresentam o problema de forma an´aloga `a considerada nesta dissertac¸˜ao, consi-derando, `a partida, que cada cliente deve ser visitado num subconjunto de dias especifico. Por exemplo, para um per´ıodo de quatro dias, alguns clientes podem requisitar apenas uma visita, que pode ser feita em qualquer dos quatro dias, enquanto que para clientes que pec¸am duas visitas, estas s´o poder˜ao ser realizadas nos dias 1 e 3 ou 2 e 4, correspondendo apenas a duas das seis combinac¸˜oes poss´ıveis para as visitas do respetivo cliente.
Christofides e Beasley desenvolvem uma heur´ıstica para o problema e utilizam o PTSP como forma de avaliar alterac¸˜oes na soluc¸˜ao quando se procede a trocas nas combinac¸˜oes de dias de visita dos clientes.
Mais tarde, em 1992, Paletta [24] apresenta o problema como um Problema do Caixeiro Viajante de Multi-Per´ıodo (Multiperiod Traveling Salesman Problem - MPTSP), onde um conjunto de cidades deve ser visitado com uma certa periodicidade. Isto ´e, cada cidade deve ser visitada pelo menos uma vez durante um respetivo intervalo de dias. Nesta abordagem s˜ao consideradas as distˆancias (sim´etricas) entre cidades e pretende-se determinar as rotas que minimizam a distˆancia total.
Paletta desenvolveu duas heur´ısticas que utilizam um procedimento de procura do caminho mais curto numa rede em n´ıveis. As duas heur´ısticas diferem apenas num passo de selec¸˜ao.
As heur´ısticas desenvolvidas foram utilizadas para resolver 10 instˆancias, apresentadas em [9]. Os resul-tados obtidos pelas duas heur´ısticas foram comparados com os melhores resulresul-tados obtidos por Christo-fides e Beasley. Uma das novas heur´ısticas obteve melhores resultados num maior n´umero de testes, mas o tempo computacional ´e muito superior ao obtido pela outra heur´ıstica, que n˜ao apresenta resultados muito afastados. Ou seja, a qualidade das soluc¸˜oes obtidas pelas heur´ısticas ´e muito semelhante mas uma
Cap´ıtulo 2. Revis˜ao Bibliogr´afica 9
heur´ıstica apresenta tempos computacionais melhores. De qualquer modo, o melhor resultado entre as duas heur´ısticas ´e melhor que os resultados obtidos por Christofides e Beasley, no total dos 10 testes.
Em 1995, Chao, Golden e Wasil [8] prop˜oem uma nova heur´ıstica para o PTSP. O problema ´e apre-sentado de forma idˆentica a [9], sendo que tamb´em n˜ao s˜ao consideradas todas as combinac¸˜oes de dias poss´ıveis para as visitas dos clientes. Por exemplo, para um per´ıodo de 5 dias e um cliente com 3 visi-tas, as combinac¸˜oes de dias permitidas, isto ´e, os dias em que o cliente pode ser visitado, s˜ao apenas as combinac¸˜oes (dia 1, dia 3, dia 5), ( dia 1, dia 2, dia 4) ou (dia 2, dia 4, dia 5).
Os autores desenvolveram uma heur´ıstica que a partir de uma soluc¸˜ao inicial, onde a cada cliente ´e associada uma combinac¸˜ao de dias das admitidas, ´e realizada uma etapa de melhoramento. Nesta etapa ´e alterada, para cada cliente, a combinac¸˜ao de dias considerada para outra admitida e ´e verificada a alterac¸˜ao provocada por esta troca de dias. Se a alterac¸˜ao provocar uma reduc¸˜ao da distˆancia total ou aumentar a distˆancia total at´e a um valor limite, ´e assumida a alterac¸˜ao na soluc¸˜ao, caso contr´ario ser´a considerada a combinac¸˜ao de dias inicial. Este processo de melhoramento ´e denominado de record-to-recorde foi introduzido por Dueck [12].
A heur´ıstica desenvolvida foi testada em 23 instˆancias, das quais 10 s˜ao as propostas em [9] e, 13 foram desenvolvidas pelos pr´oprios. No total dos testes realizados concluiu-se que a heur´ıstica produz bons resultados num tempo computacional relativamente curto.
Butler, Williams e Yarrow [5] introduzem o PTSP com per´ıodo de dois dias, aplicado `a recolha de leite. Os autores sugerem uma formulac¸˜ao para o problema em programac¸˜ao linear inteira (PLI) para resolver uma instˆancia de 42 nodos, com distˆancias sim´etricas.
Uma meta-heur´ıstica baseada no m´etodo de tabu search foi desenvolvida por Cordeau, Gendreau e La-porte [10], para resolver trˆes problema: o problema de roteamento de ve´ıculos peri´odico (PVRP), o problema do caixeiro viajante peri´odico(PTSP) e o problema de roteamento de ve´ıculos com m´ultiplos dep´ositos(MDVRP).
Os autores comec¸am por apresentar uma formulac¸˜ao em programac¸˜ao linear inteira para o PVRP e mostram como esta se pode adaptar para os outros dois problemas. De seguida, ´e apresentado o algoritmo de tabu search.
A heur´ıstica foi utilizada para resolver instˆancias para os trˆes problemas. Em relac¸˜ao ao PTSP foram resolvidas 23 instˆancias, das quais 10 s˜ao as apresentadas em [9] e 13 em [8]. Os resultados obtidos foram comparados com os resultados obtidos por Christofides and Beasley [9], Paletta [24] e Chao, Golden e Wasil [8], sendo que a meta-heur´ıstica desenvolvida obteve os melhores resultados. Esta obteve, em todas as instˆancias, as soluc¸˜oes de menor valor num tempo computacional reduzido.
Paletta em [25] prop˜oe uma outra heur´ıstica para o PTSP baseada num procedimento de melhoramento incorporado num processo de construc¸˜ao de rotas. Duas heur´ısticas, semelhantes `a desenvolvida em [25], foram propostas por Bertazzi, Paletta e Speranza [3] e Paletta e Triki [26].
Cap´ıtulo 2. Revis˜ao Bibliogr´afica 10
agente tem de visitar um conjunto de clientes periodicamente, sendo que essa periodicidade depende do n´umero e da frequˆencia dos pedidos.
Este problema foi considerado, mais uma vez, para um per´ıodo de dois dias, onde alguns clientes re-querem visitas nos dois dias e, os restantes, apenas num dos dias. ´E tamb´em imposta uma restric¸˜ao que obriga a que a diferenc¸a entre o n´umero de clientes que ´e visitado em cada dia, n˜ao seja maior que um dado valor. No estudo foram considerados apenas os valores zero e um, ou seja, apenas os casos em que as duas rotas tˆem o mesmo n´umero de clientes ou diferem em apenas um cliente.
Bassetto e Mason prop˜oem uma formulac¸˜ao em programac¸˜ao linear inteira para o PTSP e desenvolvem trˆes heur´ısticas. Os autores constru´ıram 70 instˆancias, com distˆancias euclidianas entre cada par de nodos: 10 instˆancias, de 15 nodos que foram resolvidas quer pelo do m´etodo exato quer pelas trˆes heur´ısticas e, 60 instˆancias, de 48 nodos que foram resolvidas apenas usando as heur´ısticas. Tanto a performancedo m´etodo exato, como das trˆes heur´ısticas ´e avaliada apenas em termos da qualidade da soluc¸˜ao encontrada, n˜ao sendo apresentados nem comparados os tempos de execuc¸˜ao.
Algumas variantes do PTSP
Uma variante que tem sido alvo de muito interesse ´e o Problema do Caixeiro Viajante Consistente (CTSP) ou para o grupo de problemas de ve´ıculos, o Problema de Roteamento de Ve´ıculos Consistente (CVRP). Este problema considera um determinado horizonte de planeamento e caracteriza-se por fornecer um servic¸o consistente a um determinado conjunto de clientes. Num per´ıodo de v´arios dias, cada cliente pode requerer servic¸o num ou mais dias, sendo que a exigˆencia de servic¸o consistente aplica-se apenas aos clientes que requerem servic¸o em mais de um dia. Um servic¸o ´e consistente quando se garante que as visitas de um determinado cliente, do conjunto de clientes com mais de uma visita, s˜ao realizadas mais ou menos na mesma altura do dia para todo os seus dias de visita. No CVRP esta consistˆencia pode ainda ser estendida para o condutor do ve´ıculo, onde se pretende garantir que um cliente ´e sempre visitado pelo mesmo condutor.
Algumas referˆencias destes problemas s˜ao os artigos [21] e [22] de Kovacs, Golden, Hartl e Parragh e o artigo [30] de Subramanyam e Gounaris.
Uma outra variante do PTSP que j´a foi mencionada nesta dissertac¸˜ao ´e o Problema de Roteamento de Ve´ıculos Peri´odico (PVRP). Como j´a foi dito, este problema generaliza o PTSP para o caso onde existe mais de um ve´ıculo para visitar os clientes, ou seja, est´a dispon´ıvel uma frota de ve´ıculos, geralmente ilimitada, no dep´osito. Neste problema, ´e tamb´em considerado que os ve´ıculos tˆem certas capacidades e os clientes tˆem uma determinada procura que tem de ser satisfeita.
Esta variante tem sido mais estudada do que a considerada nesta dissertac¸˜ao, pois esta retrata um maior conjunto de problemas reais por considerar uma frota de ve´ıculos. A este problema ´e ainda poss´ıvel adicionar restric¸˜oes de forma a ter mais aplicac¸˜oes pr´aticas. Por exemplo, existˆencia de restric¸˜oes ao limite da dimens˜ao da frota de ve´ıculos; limite da durac¸˜ao das rotas; possibilidade de se considerar um ou mais dep´ositos; entre outras.
Campbell e Wilson, em 2014 [6] apresentam algumas abordagens que foram apresentadas para o PVRP ao longo dos anos, fazendo referˆencia a alguns dos m´etodos de resoluc¸˜ao desenvolvidos e aplicac¸˜oes reais do mesmo.
Cap´ıtulo 3
Modelos em PLI
Neste cap´ıtulo s˜ao apresentados os modelos propostos e estudados para resolver o PTSP. Primeiro ´e definido o problema e, de seguida, s˜ao apresentados os modelos desenvolvidos. Por fim, s˜ao apresentadas algumas adaptac¸˜oes necess´arias para uma variante considerada.
3.1
Definic¸˜ao do Problema
Para um determinado conjunto de clientes e um per´ıodo definido, o PTSP consiste em determinar rotas com custo total m´ınimo, com in´ıcio e fim num dep´osito, que garantam que os clientes s˜ao visitados o n´umero de vezes requeridas no respetivo per´ıodo, mas no m´aximo uma vez por dia.
O problema pode ser modelado atrav´es de um grafo orientado. Seja G = (N, A) um grafo orientado, onde N = {0, 1, ..., n} representa o conjunto de todos os nodos e A = {(i, j) : i, j ∈ N, i 6= j} o conjunto de arcos que ligam os nodos entre si. Considerando o nodo 0 o dep´osito, existem n clientes, que podem ser representados atrav´es do conjunto NC = N \ {0}.
A cada nodo i ∈ NC ´e associado um valor vique representa o n´umero de vezes que cada cliente deve ser
visitado. Assumindo que o per´ıodo tem p dias e P = {1, ..., p} representa o conjunto de dias do per´ıodo, como cada nodo s´o pode ser visitado no m´aximo uma vez por dia tem-se vi ≤ p, ∀i ∈ NC.
A cada arco (i, j) ∈ A est´a associado um custo (n˜ao negativo) cij, que corresponde ao custo de se
deslocar do nodo i para o nodo j. A matriz associada a estes custos ser´a considerada tanto assim´etrica (cij 6= cji) como sim´etrica (cij = cji). Nesta dissertac¸˜ao n˜ao ser´a considerada alterac¸˜ao dos custos de
deslocac¸˜ao ao longo do per´ıodo.
Como j´a foi referido o objetivo do problema ´e determinar um conjunto de circuitos (um circuito para cada dia do per´ıodo), com in´ıcio e fim no dep´osito, de modo que o n´umero de visitas de cada cliente seja satisfeito. Pretende-se que o custo total seja m´ınimo, sendo este a soma dos custos de deslocac¸˜ao dos v´arios circuitos.
3.2
Formulac¸˜oes
Nesta secc¸˜ao ser˜ao apresentadas as formulac¸˜oes, em PLI, dos quatro modelos desenvolvidos. Os modelos desenvolvidos s˜ao os seguintes:
Cap´ıtulo 3. Modelos em PLI 12
– Modelo de Fluxo Agregado Peri´odico (MFAP);
– Modelo de Fluxo Agregado Peri´odico com Restric¸˜oes de Sub-Circuitos (MFAPSC); – Modelo de Fluxo Desagregado Peri´odico (MFDP);
– Modelo de Fluxo Desagregado Relaxado (MFDR).
Note-se que o ´ultimo modelo corresponde ao modelo desenvolvido para o problema relaxado, porque, neste modelo, os dias de cada per´ıodo n˜ao s˜ao diferenciados. Desta forma, o valor das soluc¸˜oes obti-das por este modelo relaxado, tanto na resoluc¸˜ao do problema em programac¸˜ao linear inteira como na resoluc¸˜ao da respetiva relaxac¸˜ao linear, fornecem limites inferiores para o problema original. Isto ser´a explicado de forma mais detalhada na secc¸˜ao 3.2.4.
3.2.1 Modelo de Fluxo Agregado Peri´odico (MFAP)
Para cada par de nodos (i, j) e cada dia k considere-se as vari´aveis bin´arias xkij. Estas vari´aveis tomam o valor 1 caso o arco (i, j) esteja na rota do dia k e o valor 0, caso contr´ario. Assim, estas vari´aveis permitem definir as rotas da soluc¸˜ao e est˜ao definidas para todos os arcos (i, j) e todo o per´ıodo, ou seja, ∀ (i, j) ∈ A e k ∈ P .
De forma a garantir a conexidade das rotas na soluc¸˜ao foram criadas as vari´aveis yijk, ∀ (i, j) ∈ A e k ∈ P , que representam o fluxo que passa no arco (i, j) na rota do dia k. Este fluxo representa o n´umero de clientes que ainda v˜ao ser visitados ap´os o cliente j. Estas vari´aveis est˜ao definidas nos mesmos conjuntos das vari´aveis x e tomam valores inteiros n˜ao negativos.
Recordando que cada rota deve comec¸ar e terminar no dep´osito (nodo 0) e todos os clientes devem ser visitados o n´umero de vezes requeridas, o MFAP pode ser formulado da seguinte forma:
M inimizarX k∈P X (i,j)∈A cijxkij (3.1) Sujeito a : X j∈NC xk0j = 1 ∀k∈P (3.2) X j∈N xkij =X j∈N xkji ∀i∈N,k∈P (3.3) X k∈P X j∈N xkij = vi ∀i∈NC (3.4) X j∈NC y0jk = X (i,j)∈A xkij− 1 ∀k∈P (3.5) X i∈N ykij−X i∈N yjik =X i∈N xkij ∀j∈NC,k∈P (3.6) yijk ≤ nxkij ∀(i,j)∈A,k∈P (3.7) xkij ∈ {0, 1} ∀(i,j)∈A,k∈P (3.8) yijk ≥ 0 ∀(i,j)∈A,k∈P (3.9)
Cap´ıtulo 3. Modelos em PLI 13
As restric¸˜oes 3.2 garantem que todas as rotas comec¸am no dep´osito. As restric¸˜oes 3.3, garantem, para cada rota, que se entra um arco num determinado nodo tamb´em ir´a existir um arco a sair. No conjunto de restric¸˜oes seguintes, 3.4, ´e assegurado que cada cliente ´e visitado, no conjunto das rotas, o n´umero de vezes pedidas.
Os trˆes seguintes conjuntos de restric¸˜oes, 3.5 - 3.7, correspondem `as restric¸˜oes de fluxo garantido que cada rota corresponde a um ´unico circuito conexo. Na primeira garante-se que o fluxo inicial de cada rota ´e igual ao n´umero total de nodos que esta ir´a visitar, excluindo o nodo dep´osito. A segunda certifica-se que o fluxo diminui uma unidade sempre que passa por um nodo que ´e visitado na respetiva rota, com excec¸˜ao do nodo do dep´osito. Por fim, nas restric¸˜oes 3.7 assegura-se, para cada rota, que num arco s´o passa fluxo caso este pertenc¸a `a respetiva rota na soluc¸˜ao. Como a vari´avel x ´e bin´aria e y ´e n˜ao negativa, ´e necess´ario multiplicar as vari´aveis bin´arias por uma constante suficientemente grande. Neste caso, considerou-se o valor n, por corresponder ao valor mais pequeno que pode ser considerado.
Por fim, as restric¸˜oes 3.8 e 3.9 definem o dom´ınio das vari´aveis. Como j´a foi mencionado, as vari´aveis y s˜ao vari´aveis de fluxo e, portanto, tˆem de ser inteiras, mas devido `a formulac¸˜ao considerada, esta restric¸˜ao j´a ´e imposta pelas restantes restric¸˜oes, n˜ao sendo necess´ario consider´a-lo nas restric¸˜oes 3.9.
3.2.2 Modelo de Fluxo Agregado Peri´odico com Restric¸˜oes de Sub-circuitos (MFAPSC)
O objetivo dos modelos em PLI propostos nesta dissertac¸˜ao ´e o de melhoramento das soluc¸˜oes obtidas pelas relaxac¸˜oes lineares, de modo a que estas tenham o valor mais pr´oximo poss´ıvel das soluc¸˜oes ´otimas. Desta forma, decidiu-se melhorar o modelo anterior adicionando desigualdades v´alidas.
Ao se adicionar desigualdades v´alidas ao modelo MFAP ´e poss´ıvel obter um novo modelo, equivalente ao modelo original em termos de obtenc¸˜ao da soluc¸˜ao ´otima inteira, mas com soluc¸˜oes de relaxac¸˜ao linear mais pr´oximas do valor ´otimo e, possivelmente, num tempo de execuc¸˜ao menor. Estas desigual-dades melhoram o modelo na pesquisa de soluc¸˜oes, atrav´es do corte da regi˜ao admiss´ıvel do problema, mantendo todas as soluc¸˜oes inteiras admiss´ıveis. As desigualdades v´alidas que ser˜ao introduzidas ao modelo s˜ao do tipo:
X
i∈S,j∈S
xkij ≤ |S| − 1 ∀S ⊂ {2, ..., n} , |S| ≥ 2, k ∈ P (3.10)
Estas desigualdades foram apresentadas em [11] por Dantzig, Fulkerson, and Johnson e s˜ao conhecidas pelas restric¸˜oes de eliminac¸˜ao de subcircuitos (Eliminate Subtours Constraints). Estas desigualdades podem ser separadas em tempo polinomial por algoritmos sofisticados de fluxo m´aximo.
Das desigualdades v´alidas anteriores ser˜ao consideras, por agora, apenas as que consideram |S| = 2, ou seja, a restric¸˜ao que ´e introduzida na formulac¸˜ao considerada na secc¸˜ao anterior ´e:
xkij + xkji ≤ 1 ∀i ∈ NC, j ∈ NC, k ∈ P (3.11)
Esta restric¸˜ao significa que cada rota k cont´em o arco (i, j), (xkij = 1), ou o arco (j, i), (xkji = 1), ou nenhum dos dois, (xkij = 0 e xkji= 0).
Cap´ıtulo 3. Modelos em PLI 14
3.2.3 Modelo de Fluxo Desagregado Peri´odico (MFDP)
Este modelo ´e constru´ıdo da mesma forma que os modelos anteriores, considerando tamb´em dois con-juntos de vari´aveis: vari´aveis que representam o conjunto de rotas na soluc¸˜ao e vari´aveis de fluxo que garantem que as rotas s˜ao circuitos conexos.
A diferenc¸a entre estes modelos ´e a forma como o fluxo ´e representado. Nos modelos anteriores, para cada rota, o fluxo ´e inicializado com o valor m´aximo que pode tomar e vai diminuindo uma unidade de cada vez at´e se tornar nulo. A cada arco est´a associada apenas uma vari´avel de fluxo. Neste novo modelo, a cada arco pode estar associada mais do que uma vari´avel de fluxo bin´aria, sendo que a soma destas vari´aveis, para cada arco, corresponde ao fluxo dado pelas vari´aveis consideradas nos modelos anteriores.
Para cada par de nodos (i, j) e cada dia k definam-se as vari´aveis bin´arias xkij. Estas tomam o valor 1 caso o arco (i, j) pertenc¸a `a rota do dia k e o valor 0, caso contr´ario. Estas vari´aveis est˜ao definidas para todos os arcos (i, j) e para todos os dias do per´ıodo, ou seja, ∀ (i, j) ∈ A e k ∈ P .
Quanto `as vari´aveis de fluxo, defina-se fijtk, ∀ (i, j) ∈ A, t ∈ NC, k ∈ P , que representa a quantidade
de fluxo que passa no arco (i, j) com destino ao nodo t na rota do dia k. Neste caso, em particular, estas vari´aveis podem ser interpretadas como indicando se (i, j) est´a no caminho para t na rota do dia k, ou n˜ao. Assim, estas vari´aveis ser˜ao tamb´em vari´aveis bin´arias.
Mais uma vez, cada rota deve ter inicio e fim no dep´osito (nodo 0) e todos os clientes devem ser visitados o n´umero de vezes requeridas. Este modelo pode ser formulado da seguinte forma:
M inimizar 3.1 Sujeito a : 3.2 − 3.4 3.8 X t∈NC X j∈NC f0jtk = X (i,j)∈A xkij − 1 ∀k∈P (3.12) X i∈N fijtk−X i∈N fjitk= 0 ∀j,t∈NC, t6=j, k∈P (3.13) X i∈N fijjk−X i∈N fjijk =X i∈N xkij ∀j∈NC, k∈P (3.14) X t∈NC fijtk ≤ nxkij ∀(i,j)∈A, k∈P (3.15a) fijtk ≤ xkij ∀(i,j)∈A, t∈NC, k∈P (3.15b) fijtk≥ 0 ∀(i,j)∈A, t∈NC, k∈P (3.16)
Como se pode ver a parte da formulac¸˜ao referente `as vari´aveis x ´e igual `a dos modelos anteriores, isto isto porque o que difere estes modelos, como j´a foi referido, s˜ao apenas as vari´aveis de fluxo (vari´aveis f ).
Cap´ıtulo 3. Modelos em PLI 15
As restric¸˜oes 3.12 – 3.14 correspondem `as restric¸˜oes de fluxo, garantindo que cada rota constitui um ´unico circuito conexo. A primeira faz com que, para cada rota, saia do dep´osito o mesmo n´umero de vari´aveis de fluxo com valor 1 como o n´umero de clientes que ir˜ao ser visitados na respetiva rota, isto ´e, a soma de todas as vari´aveis f correspondentes aos arcos que saem do dep´osito ser´a igual ao n´umero de nodos que ser˜ao visitados nessa rota. Nas duas seguintes garante-se que o fluxo apenas diminui quando este chega ao nodo a que estava designado. O fluxo total de uma rota diminui uma unidade de cada vez, alterando o valor de uma determinada vari´avel f de 1 para 0. A segunda parcela das restric¸˜oes 3.14 (P
i∈Nfjit) ´e sempre nula, sendo que esta restric¸˜ao pode ser substitu´ıda apenas por:
X
i∈N
fijjk =X
i∈N
xkij , ∀j∈NC, k∈P (3.17)
As restric¸˜oes 3.15 asseguram, para cada rota, que num arco s´o passa fluxo caso este pertenc¸a `a respe-tiva rota na soluc¸˜ao. A restric¸˜ao 3.15a pertence `a formulac¸˜ao fraca do MFD enquanto que a restric¸˜ao 3.15b constitu´ı o modelo forte do MFD. Nesta dissertac¸˜ao ser˜ao consideradas as restric¸˜oes 3.15b que correspondem ao modelo forte, pois embora os dois modelos sejam equivalentes em termos de obtenc¸˜ao da soluc¸˜ao ´otima inteira, o modelo forte geralmente permite obter soluc¸˜oes de relaxac¸˜ao linear mais pr´oximas do valor ´otimo.
Por fim, as restric¸˜oes 3.16 correspondem `a restric¸˜ao de dom´ınio das vari´aveis f . Neste caso n˜ao ´e necess´ario forc¸´a-la a pertencer ao conjunto {0, 1}, pois se prova que em qualquer soluc¸˜ao bin´aria das vari´aveis xkij, as vari´aveis fijtk tomam valores bin´arios.
Deste modelo n˜ao foi considerada uma variante com desigualdades v´alidas como foi considerado para o MFAP (modelo MFAPSC), pois esta formulac¸˜ao j´a implica as restric¸˜oes de subcircuitos consideradas (restric¸˜oes 3.11).
3.2.4 Modelo de Fluxo Desagregado Relaxado (MFDR)
Este modelo resulta do modelo MFDP retirando o ´ındice referente ao dia do per´ıodo de todas as vari´aveis consideradas. Desta forma, as soluc¸˜oes obtidas por este s˜ao representadas de forma diferente.
Nos modelos anteriores uma soluc¸˜ao ´e constitu´ıda por um conjunto de rotas, sendo que a cada dia est´a associada uma e uma s´o rota. Nas soluc¸˜oes desta formulac¸˜ao, as rotas em vez de serem representadas individualmente, s˜ao representadas como um todo. Assim, nas outras formulac¸˜oes, as vari´aveis que representam a utilizac¸˜ao dos arcos indicam, para cada dia, se um determinado arco ´e utilizado ou n˜ao na respetiva rota e, nesta formulac¸˜ao, estas vari´aveis indicam, para cada arco, a quantas rotas no total este pertence.
Devido a esta representac¸˜ao das rotas, para uma dada instˆancia aleat´oria, se o modelo MFDR encontrar uma soluc¸˜ao inteira com valor igual `a soluc¸˜ao ´otima da instˆancia, conhecida a partir da resoluc¸˜ao dos outros modelos, esta poder´a n˜ao corresponder de facto `a soluc¸˜ao ´otima da respetiva instˆancia. Isto acontece porque, n˜ao ´e poss´ıvel ter certeza que as rotas da soluc¸˜ao encontradas por este modelos s˜ao as mesmas da soluc¸˜ao ´otima, uma vez que n˜ao ´e poss´ıvel discriminar as rotas da soluc¸˜ao.
Cap´ıtulo 3. Modelos em PLI 16
per´ıodo n˜ao s˜ao diferenciados. Desta forma, o valor das soluc¸˜oes obtidas por este modelo relaxado, tanto na resoluc¸˜ao do problema em programac¸˜ao linear inteira como na resoluc¸˜ao da respetiva relaxac¸˜ao linear, fornecem limites inferiores para o problema original.
O primeiro conjunto de vari´aveis neste modelo s˜ao as vari´aveis inteiras xij, ∀ (i, j) ∈ A, k ∈ P , que
representam o conjunto de arcos utilizados nas rotas da soluc¸˜ao. Como cada rota est´a associada a um dia do per´ıodo e estas vari´aveis n˜ao tˆem o ´ındice referente ao dia, neste modelo as rotas s˜ao representadas de forma conjunta. Estas vari´aveis est˜ao definidas para todos os arcos, isto ´e, para (i, j) ∈ A e ir˜ao tomar valores entre 0 e p (dimens˜ao do per´ıodo) da seguinte forma:
– Se xij = 0, o arco (i, j) n˜ao pertence a nenhuma rota;
– Se xij = p, o arco (i, j) pertence a p rotas, ou seja, pertence a todas as rotas;
– Se xij = m com 0 < m < p, o arco (i, j) pertence a exatamente m rotas.
Em relac¸˜ao `as vari´aveis de fluxo, seja fijt a quantidade de fluxo que passa no arco (i, j) com destino ao nodo t para todo (i, j) ∈ A e t ∈ NC. Estas vari´aveis tomam valores inteiros n˜ao negativos. A
quantidadeP
t∈NCf
t
ij representa a quantidade de fluxo total que passa no arco (i, j) ∈ A, no conjunto
das rotas.
Sabendo que as rotas devem comec¸ar e terminar no dep´osito e que todos os clientes devem ser visitados o n´umero de vezes requeridas, o MFDR pode ser formulado da seguinte forma:
M inimizar X (i,j)∈A cijxij (3.18) Sujeito a : X j∈NC x0j = p (3.19) X j∈N xij = X j∈N xji ∀i∈N (3.20) X j∈N xij = vi ∀i∈NC (3.21) X t∈NC X j∈NC f0jt = X i∈NC vi (3.22) X i∈N fijt −X i∈N fjit = 0 ∀j,t∈NC, t6=j (3.23) X i∈N fijj −X i∈N fjij =X i∈N xij ∀j∈NC (3.24) X t∈NC fijt ≤ nxij ∀(i,j)∈A (3.25a) fijt ≤ xij ∀(i,j)∈A,t∈NC (3.25b) xij ≥ 0 e inteiros ∀(i,j)∈A (3.26) fijt ≥ 0 ∀(i,j)∈A,t∈N C (3.27)
A func¸˜ao objetivo consiste em minimizar o custo total da soluc¸˜ao, multiplicando o custo de utilizac¸˜ao de um arco pelo o n´umero de vezes que este ´e usado, ou seja, pelo n´umero de rotas `a qual este pertence. Esta
Cap´ıtulo 3. Modelos em PLI 17
func¸˜ao objetivo ´e traduzida em 3.18. Se os custos de utilizac¸˜ao de um determinado arco aumentassem ou diminu´ıssem consoante os dias em que ele seria utilizado, n˜ao seria poss´ıvel formular a func¸˜ao objetivo com estes conjuntos de vari´aveis.
Nas restric¸˜oes 3.19 e 3.20 garante-se que todas as rotas comec¸am no dep´osito e o n´umero de arcos que entram num determinado nodo ´e igual ao n´umero de arcos que saem desse mesmo nodo, ou seja, que sempre que se entra num nodo tem de sair do mesmo. Nas restric¸˜oes 3.21 ´e garantido que todos os nodos s˜ao visitados o n´umero de vezes solicitadas.
O conjunto de restric¸˜oes 3.22 – 3.25 correspondem `as restric¸˜oes de fluxo do modelo. Nas restric¸˜oes 3.22 garante-se que a fluxo total das p rotas ´e igual ao n´umero de visitas totais dos clientes. Nas restric¸˜oes 3.23 e 3.24 restric¸˜oes garante-se que fluxo apenas diminui quando este chega ao seu nodo destino. Para cada arco (i, j) ∈ A, a quantidade de fluxo que diminui quando se chega ao nodo j corresponde ao n´umero de vezes que este arco ´e utilizado no total das p rotas. A segunda parcela das restric¸˜oes 3.24 (P
i∈Nfjit)
´e sempre nula, como no modelo anterior, sendo que esta restric¸˜ao pode ser substitu´ıda apenas por: X
i∈N
fijj =X
i∈N
xij , ∀j∈NC (3.28)
Por fim, as restric¸˜oes 3.25 obrigam a que um determinado arco seja utilizado como passagem de fluxo apenas se este pertencer `a soluc¸˜ao, ou seja, caso este pertenc¸a a alguma rota. As restric¸˜oes 3.25a corres-pondem `as restric¸˜oes do modelo fraco enquanto que a 3.25b correscorres-pondem `as do modelo forte. Nesta dissertac¸˜ao ser˜ao utilizadas apenas as restric¸˜oes 3.25b correspondentes ao modelo forte.
As restric¸˜oes 3.26 e 3.27 correspondem `as restric¸˜oes de dom´ınio dos dois conjuntos de vari´aveis garan-tindo que estas s˜ao inteiras n˜ao negativas. Nas vari´aveis y n˜ao ´e necess´ario dizer que ´e inteira porque a formulac¸˜ao j´a as obriga a isso.
3.3
Variante do Problema
Nas formulac¸˜oes apresentadas anteriormente n˜ao ´e considerada uma pol´ıtica de visitas, isto ´e, as visitas de um determinado cliente podem seguir uma combinac¸˜ao aleat´oria de dias. A variante do problema que ser´a agora estudada consiste em considerar uma determinada pol´ıtica de visitas para os clientes.
A pol´ıtica de visitas que ser´a considerada consiste em os clientes que exigem duas visitas sigam uma de duas regras: as visitas aos clientes tˆem de ocorrer em dias seguidos (regra 1), ou com pelo menos um dia de intervalo (regra 2). Desta forma, por exemplo para um per´ıodo de 3 dias, um cliente que requeira duas visitas, na regra 1 deve ser visitado nos dias 1 e 2 ou 2 e 3, enquanto que pela regra 2 deve ser visitado nos dias 1 e 3. Esta pol´ıtica s´o ´e admiss´ıvel para per´ıodos de planeamento com mais de dois dias.
Esta variante foi considerada apenas para os per´ıodos de planeamento com trˆes e quatro dias, pois estes correspondem aos per´ıodos em an´alise nesta dissertac¸˜ao com mais de dois dias. Esta foi estudada em apenas algumas instˆancias que foram resolvidas atrav´es dos modelos MFAP e MFAPSC. Contudo, a variante pode ser generalizada para outras dimens˜oes de per´ıodos e para clientes com outro n´umero de visitas, que n˜ao apenas duas.
Cap´ıtulo 3. Modelos em PLI 18
De forma a resolver a variante em estudo, foi necess´ario fazer adaptac¸˜oes aos modelos MFAP e MFAPSC para que estes respeitem a pol´ıtica de visitas considerada por esta. As adaptac¸˜oes feitas s˜ao iguais nos dois modelos e consistem na introduc¸˜ao de algumas restric¸˜oes para cada uma das regras. As restric¸˜oes introduzidas nos modelos s˜ao apresentadas para os dois per´ıodos de planeamento separadamente.
3.3.1 Variante de Per´ıodo de 3 dias
Nesta variante, um cliente que solicite duas visitas, pela regra 1 ser´a visitado nos dias 1 e 2 ou 2 e 3 e, pela regra 2 ser´a visitado nos dias 1 e 3.
Assim, pela regra 1 um cliente ´e visitado sempre no segundo dia e num dos outros e, pela segunda regra, um cliente nunca ser´a visitado no segundo dia. Note-se que que na frase anterior, cliente corresponde a um cliente que exige duas visitas, pois, caso contr´ario, a este nem seria aplicada a pol´ıtica de visitas. Desta forma, as restric¸˜oes introduzidas para cada uma das regras s˜ao as seguintes:
X j∈NC x2ij = 1 , ∀ {i ∈ NC : vi = 2 e i segue a regra 1} (3.29) X j∈NC x2ij = 0 , ∀ {i ∈ NC : vi = 2 e i segue a regra 2} (3.30)
Na restric¸˜ao 3.29, para o cliente i ∈ NC tal que vi = 2, obriga-se a que o segundo dia seja um dia de
visita do cliente i, enquanto que na restric¸˜ao 3.30 obriga-se a que o segundo dia n˜ao fac¸a parte dos dias de visita do cliente i.
3.3.2 Variante de Per´ıodo de 4 dias
Nesta variante de quatro dias, j´a existem mais combinac¸˜oes poss´ıveis de dias para cada uma das regras. Para a regra 1 j´a s˜ao poss´ıveis os dias 1 e 2, 2 e 3 ou 3 e 4 e, para a regra 2 s˜ao poss´ıveis os dias 1 e 3, 1 e 4 ou 2 e 4.
Assim, para este caso s˜ao necess´arios os seguintes conjuntos de restric¸˜oes para cada uma das regras: x1ij + x3ij ≤ 1 x1ij + x4ij ≤ 1 , ∀ {i ∈ NC : vi = 2 e i segue a regra 1} x2ij + x4ij ≤ 1 (3.31) x1ij + x2ij ≤ 1 x2ij + x3ij ≤ 1 , ∀ {i ∈ NC : vi = 2 e i segue a regra 2} x3ij + x4ij ≤ 1 (3.32)
Neste caso, as restric¸˜oes que se introduziram para cada uma das regras consiste em garantir que o con-junto de dias que n˜ao satisfazem a respetiva regra correspondem a uma soluc¸˜ao n˜ao admiss´ıvel.
Cap´ıtulo 4
Experiˆencia Computacional
Neste cap´ıtulo comec¸a-se por descrever as instˆancias de testes utilizadas nesta dissertac¸˜ao. De seguida, s˜ao apresentados os resultados da experiˆencia computacional realizada no ˆambito desta dissertac¸˜ao. A par da apresentac¸˜ao dos resultados ser˜ao feitos alguns coment´arios em relac¸˜ao aos mesmos.
Os resultados s˜ao apresentados de forma sintetizada, pelo que todos os resultados obtidos est˜ao dis-pon´ıveis em anexo para consulta.
Para efeitos de comparac¸˜ao e de resoluc¸˜ao dos modelos em estudo, foi considerado um tempo computa-cional m´aximo de 500 segundos de processamento. Todos os resultados apresentados foram obtidos com recurso ao software FICO Xpress IVE 1.24.18 e com um computador com o processador Inter CoreR TM2Duo CPU E7400 @ 2.80 GHz, com 4GB de RAM.
4.1
Instˆancias de Teste
Uma instˆancia de teste do problema em estudo ´e composta por uma matriz quadrada onde ´e indicado, para cada par de nodos, o respetivo custo de deslocac¸˜ao e, por um vetor com o respetivo padr˜ao de visitas, ou seja, onde, para cada cliente, se indica quantas visitas este exige. As instˆancias de teste correspondentes `a variante do problema s˜ao tamb´em compostas por um vetor onde, para cada cliente com duas visitas, ´e indicado que regra da pol´ıtica de vistas (regra 1 ou regra 2) este ir´a seguir.
Os trˆes conjuntos de matrizes considerados na experiˆencia computacional ser˜ao descritos, separada-mente, de seguida.
4.1.1 Custos de Deslocac¸˜ao
A primeira matriz que comp˜oe uma instˆancia de teste corresponde `as matrizes referentes aos custos de deslocac¸˜ao entre cada par de nodos. Para estas considerou-se matrizes geradas aleatoriamente, mas tamb´em algumas matrizes de custos dispon´ıveis na literatura.
O primeiro conjunto de matrizes de custos foi obtido a partir de um gerador desenvolvido no software j´a mencionado. O gerador criado tem como inputs o n´umero de nodos, o intervalo de variac¸˜ao dos custos e a informac¸˜ao se a matriz ser´a assim´etrica ou sim´etrica. Para cada matriz, os custos de deslocac¸˜ao s˜ao gerados de forma aleat´oria, n˜ao verificando a desigualdade triangular.
Cap´ıtulo 4. Experiˆencia Computacional 20
A partir deste gerador criaram-se instˆancias de 20 e 40 clientes, ou seja, 21 e 41 nodos no total e com custos de deslocac¸˜ao entre 0 e 100. Para cada dimens˜ao criaram-se 10 matrizes de custos distintas, das quais 5 s˜ao assim´etricas e as outras 5 s˜ao sim´etricas.
O segundo conjunto de matrizes de custos consideradas nesta dissertac¸˜ao correspondem aos custos de deslocac¸˜ao de instˆancias de referˆencia para o TSP que se encontram dispon´ıveis no site [28]. Do conjunto de instˆancias dispon´ıveis no site mencionado, selecionaram-se apenas 8 matrizes, de ordens entre 39 e 48 nodos. As instˆancias contemplam v´arias caracter´ısticas, das quais se retirou apenas a matriz pretendida. Das 8 matrizes consideradas, 5 s˜ao assim´etricas e 3 sim´etricas.
Assim, o conjunto de matrizes de custos considerado nesta dissertac¸˜ao ´e constitu´ıdo por 28 matrizes: 8 matrizes retiradas da literatura e 20 novas matrizes geradas aleatoriamente.
4.1.2 Visitas
Como j´a foi visto, o n´umero m´aximo de visitas que podem ser feitas a um determinado cliente ´e igual `a dimens˜ao do per´ıodo, ou seja, a dimens˜ao do per´ıodo considerado ir´a influenciar o padr˜ao de visitas. Nesta dissertac¸˜ao foram considerados per´ıodos de planeamento com dois, trˆes e quatro dias, ou seja, p ∈ {2, 3, 4}.
A cada matriz de custos associaram-se diferentes padr˜oes de visitas originando v´arias instˆancias com a mesma matriz de custos.
Os diferentes padr˜oes de visitas diferem na percentagem de clientes associada a cada possibilidade de visita. Por exemplo para as instˆancias com per´ıodo de planeamento com dois dias e matriz de custos gerada aleatoriamente, os padr˜oes de visitas associados variam a percentagem de clientes com duas visitas no conjunto {0%, 20%, 40%, 50%, 60%, 80%, 100%}.
As instˆancias constitu´ıdas por matrizes de custos de testes de referˆencia retirados da literatura foram estudados apenas para o per´ıodo de planeamento com dois dias, associando a cada uma das matrizes de custos, 7 padr˜oes de visitas distintas.
As instˆancias de teste obtidas a partir de matrizes de custos geradas aleatoriamente foram constru´ıdas considerando v´arios padr˜oes de visita para cada matriz de custos. O n´umero de padr˜oes de visitas consi-derados para cada matriz de custos varia de acordo com o n´umero de clientes e a durac¸˜ao do per´ıodo. Na tabela seguinte (tabela 4.1) ´e indicado o n´umero de padr˜oes associado a cada matriz de custos conso-ante o n´umero de clientes da mesma, |NC|, e o tipo de per´ıodo de planeamento, |P |.
|P |
2 3 4
|NC|
20 7 9 11
40 7 3 4
Cap´ıtulo 4. Experiˆencia Computacional 21
4.1.3 Regras
As instˆancias com 40 clientes e per´ıodo com trˆes e quatro dias foram utilizadas para resolver a variante do problema introduzida no cap´ıtulo 3.3. Esta variante considera que as visitas dos clientes, que requerem duas visitas, devem seguir uma de duas regras: as visitas aos clientes tˆem de ocorrer em dias seguidos (regra 1), ou com pelo menos um dia de intervalo (regra 2). O que foi feito neste caso foi considerar v´arias percentagens para o n´umero de clientes que segue uma regra e que segue a outra.
Assim, para cada conjunto de matriz de custos e padr˜ao de visitas distintos considerou-se os seguintes trˆes casos, de distribuic¸˜ao das duas regras:
- 100% dos clientes com duas visitas seguem a regra 1 e 0% segue a regra 2; - 50% dos clientes com duas visitas seguem a regra 1 e, os outros 50%, a regra 2; - 0% dos clientes com duas visitas segue a regra 1 e 100% seguem a regra 2.
4.2
Comparac¸˜ao dos Modelos
De forma a comparar os modelos desenvolvidos, em termos de eficiˆencia na obtenc¸˜ao de soluc¸˜oes ´otimas e na qualidade da respetiva relaxac¸˜ao linear, foram realizados diversos testes computacionais. A comparac¸˜ao dos modelos ´e feita com recurso `a resoluc¸˜ao de um conjunto de instˆancias de teste para os trˆes tipos de per´ıodos de planeamento em an´alise nesta dissertac¸˜ao.
A primeira analise realizada foi para as instˆancias de teste com 20 clientes e 40 clientes, com matriz de custos gerada aleatoriamente. As instˆancias de teste com 20 clientes foram analisadas para os quatro mo-delos desenvolvidos, nos trˆes per´ıodos distintos. As instˆancias de teste com 40 clientes foram analisadas igualmente para os quatro modelos, mas apenas para o per´ıodo de planeamento de dois dias.
Ap´os a apresentac¸˜ao e an´alise dos testes mencionados acima, ser˜ao apresentadas tamb´em comparac¸˜oes de performance dos modelos quando se aumenta a dimens˜ao do per´ıodo de planeamento e, comparac¸˜oes de performance dos modelos quando se aumenta a dimens˜ao do conjunto de clientes.
Os testes computacionais desenvolvidos para cada instˆancia ser˜ao apresentados com recurso a tabelas, de forma sintetizada, atrav´es do c´alculo da m´edia para cada conjunto de 5 instˆancias nas mesmas condic¸˜oes. Todos os resultados obtidos s˜ao apresentados de forma detalhada em anexo.
As primeiras colunas de cada tabela caracterizam o conjunto das 5 instˆancias nessas condic¸˜oes. A pri-meira indica se as correspondentes instˆancias tˆem matriz de custos assim´etrica ou sim´etrica, sendo apre-sentadas primeiro todas as instˆancias com matriz de custos assim´etrica e s´o depois as com matriz de custos sim´etrica, para cada modelo.
As seguintes duas a quatro colunas, dependendo do per´ıodo de planeamento, identificam o padr˜ao de visi-tas considerado, indicando, para cada n´umero de visivisi-tas poss´ıvel, quantos clientes est˜ao nessas condic¸˜oes. Considerando Vk = |i ∈ NC : vi = k| , ∀k ∈ P , para o per´ıodo de dois dias apresenta-se o par V1.V2,
para trˆes dias o terno V1.V2.V3e, por fim, para o per´ıodo de quatro dias, tem-se a quadra V1.V2.V3.V4.