EDM HUMBERTO MESTRADO PROFISSIONAL

(1)

HUMBERTO TODESCO

UM ESTUDO COM OS NÚMEROS INTEIROS NAS

SÉRIES INICIAIS

: Re-aplicação da Pesquisa de Passoni.

MESTRADO PROFISSIONAL EM ENSINO DE

MATEMÁTICA

PUC/SP

São Paulo

(2)

HUMBERTO TODESCO

UM ESTUDO COM OS NÚMEROS INTEIROS NAS

SÉRIES INICIAIS

: Re-aplicação da Pesquisa de Passoni.

Dissertação apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para obtenção do título de

MESTRE PROFISSINAL EM ENSINO DE MATEMÁTICA, sob a orientação da Profª Drª

Sandra Maria Pinto Magina.

PUC/SP

São Paulo

(3)

Banca Examinadora

____________________________________________

(4)

Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total

ou parcial desta Dissertação por processos de fotocopiadoras ou eletrônicos.

(5)

À minha base:

Lucimara, Thiago e André,

Aos meus pais, Ao meu sogro e sogra,

Meu carinho,

(6)

AGRADECIMENTOS

Ao longo desta jornada, muitas pessoas auxiliaram-me com conhecimento,

incentivo, amizade e amor. Foram momentos compartilhados com intensidade e

alegria. Agora que chegamos ao final é tempo de agradecer. A Deus pelo dom

divino da vida, proteção e providência. À minha esposa Lucimara, pelo

constante incentivo, pela paciência em momentos difícies, pela compreensão

em minhas ausências, sempre demonstrando o seu amor. Aos meus filhos peço

desculpa pela ausência em momentos que foram preenchidos pela mãe, avôs e

tios. Ao Governo do Estado de São Paulo, através da Prof.ª Ana Fava da Leste

4, pelo apoio financeiro. À minha orientadora Prof.ª Sandra Maria Pinto Magina

por ser, uma grande pessoa com seu apoio, incentivo, compreensão e paciência

com os iniciantes em pesquisa, acrescentados às suas firmes orientações

transmitindo confiabilidade e respeito. Obrigado pela paciência de sempre em

reorientar o nosso caminho principalmente nos momentos mais difícies da

nossa pesquisa. À Prof.ª Leila Zardo Puga integrante da banca examinadora

pelas suas sugestões que direcionaram e enriqueceram muito este trabalho e

pela sua grande alma que acolheu de modo carinhoso nossas dificuldades. À

Prof.ª Abigail Fregni Lins integrante da banca examinadora pelas sugestões que

muito contribuíram para o enriquecimento deste trabalho. Aos professores do

Programa de Mestrado Profissional em Educação Matemática pelas experiências

e pelo conhecimento compartilhado durante o curso. Aos meus colegas do

Programa de Mestrado Profissional em Educação Matemática pela União e

(7)

e Evanilton pela convivência harmoniosa, pela ajuda mútua e pela compreensão

durante o período de trabalho coletivo. Ao Centro Integrado Ensino Jovens e

Adultos onde lecionei e a Escola Estadual Romeu Montoro onde leciono pela

compreensão de nossas dificuldades através de palavras de incentivo e carinho

de todos os professores e funcionários (principalmente Sra. Luiza e Sra. Laíde)

que muitas vezes por um abraço, um sorriso e até por um lanche nos ajudaram

muito em nosso caminho. À Terbraz Industrial, através de seu Diretor

Alexandre e o Presidente Sr. Nelson Tercero por liberar do horário de trabalho

para as atividades necessárias a nossa pesquisa. À Escola Municipal Rodrigues

de Carvalho por abrir suas portas para realização desta pesquisa, especialmente

à coordenadora Elaine Aparecida Ribeiro Felipe, a Prof.ª Izabel Alves de Oliveira

e principalmente a Prof.ª Célia Regina Fraccaroli que além de ceder as horas de

trabalho com seus alunos a nós, demonstraram um grande carinho com o

nosso trabalho. E principalmente aos alunos da 3ª. série B que com entusiasmo

participaram de nossas atividades e foram os responsáveis por este trabalho:

Adriano Tavares da Silva, Amanda Gabriela Luglio do Melo, Bruna Batatello dos

Santos, Danilo Marcelo Pereira, Edna Ferreira Xavier Pereira, Flavio França da

Silva, Gabriela Soares de Souza, Isabela Cristina Gonçalves Barbosa, Isadora

Fernandes Gama, Jaqueline Oliveira do Nascimento, Jefferson de Souza,

Jhemerson Pereira da Silva, Jhonata Gobato dos Santos, José Everton Gomes

da Silva, Joyce Alves Pereira, Lais Miria Pereira de Abreu, Leonardo Rocha Nieri

Moreno, Lucas Medeiros Bezerra, Marcela Martins dos Santos, Maria Tainá da

Silva, Mariana da Silva, Mayara Aline Damião, Naiane Eduardo dos Santos,

(8)

Shirlene Maria da Silva, Silvania Maria da Silva, Vanessa Ricardo de Freitas,

Vitor Miranda de Alencar, Washington Lima de Souza, Wendell Camargo dos

Santos, Wesley Coelho Farias, Jéssica Mayara Munhoz de Assis, Mikael Henrique

Araújo de Souza, Yasmin Oliveira da Silva, Henrique Eduardo de Oliveira. Enfim

a todos que de uma maneira ou outra participaram de minha jornada, quero

(9)

“O que é preciso é desenvolver o desejo infantil de

reconhecimento e direcionar a criança para campos de

atividades importantes para a sociedade”.

(10)

RESUMO

O objetivo desta dissertação foi investigar a possibilidade e eficiência de se

introduzir o número inteiro negativo na 3ª. série do Ensino Fundamental de

uma escola pública, reaplicando parte do estudo desenvolvido por Passoni

(2002), a fim de responder às seguintes questões de pesquisa: “Partindo de

uma seqüência elaborada que utilize um contexto familiar e significativo, qual a

compreensão que as crianças de 3ª. série passam a ter sobre os números

negativos? Até onde tal seqüência pode ajudar na introdução desse conceito?

E, por último, em que consiste o avanço?” Para tanto, foi desenvolvida uma

pesquisa de caráter intervencionista com alunos de duas classes de 3ª. série

do Ensino Fundamental de uma escola da rede pública municipal de São

Paulo; uma delas constituiu-se em grupo controle (GC) e a outra em grupo

experimental (GE). A pesquisa de campo complementou duas etapas –

aplicação dos instrumentos diagnósticos (pré e pós-testes), tanto no GE como

no GC e aplicação da intervenção de ensino com uso de material manipulativo

apenas no GE. Os resultados obtidos em cada uma dessas etapas foram

analisados considerando a possibilidade da introdução dos números inteiros

negativos na 3ª. série do Ensino Fundamental. Do ponto de vista teórico,

apoiamos-nos nas idéias de Jean Piaget e Raymond Duval relacionados ao

papel que as representações desempenham na compreensão da Matemática.

A meta é de tornar os alunos capazes de transformar tratamentos intencionais

de representações semióticas em tratamentos quase-instantâneos. Os

resultados mostraram um crescimento de quase 50% no desempenho dos

alunos do GE, no pós-teste. Tendo por base tais resultados pode-se concluir

que a associação da intervenção de ensino com o material manipulativo

possibilitou o desenvolvimento de estratégias para resoluções das atividades.

As atividades foram desenvolvidas com 17 crianças do grupo GE e 18 crianças

do grupo GC. Os resultados obtidos foram satisfatórios.

(11)

ABSTRACT

The objective of this dissertation was to investigate the possible performance of

introducing the entire negative number on the 3rd cycle of the fundamental

school in a public organization on replication of part of the Passoni (2002) work

so as to respond the following questions of the investigation: “Starting from a

sequence formed by a familiar and significant context, what is the

comprehension that the 3rd cycle school children will have over negative

numbers? To what extended level this sequence might aid on introducing this

concept? At last, what’s this improvement consisted of?” On this approach, an

interventionist investigation was developed with students of two groups of the

3rd cycle fundamental public school in the city of Sao Paulo; one of them named

as the control group (CG) and the other one being the experimental group (EG).

The field survey had two steps – execution of diagnostic instruments (before

and after tests) on the CG as well as the EG group and carrying out the

teaching intervention with the usage of manipulative material only at the EG.The

results obtained in each of these steps were evaluated considering the possible

introduction of the negative numbers to the students of the 3rd fundamental

cycle. In theory, we lay down on the ideas of Jean Piaget and Raymond Duval

related to the kind of representations that can act upon the Mathematic

conception. The target is to make students able to convert intentional

treatments of semiotic representations in “roughly” instantaneous treatments.

The results show a 50% increase on student’s performance of EG group, at pos

test. Taking into account these results, it can be concluded that the associative

intervention on teaching with manipulative material has developed strategies for

the solution of the activities. The activities were developed with 17 children of

EG and 18 ones of the CG. The results are said to be satisfactory.

(12)

SUMÁRIO

CAPÍTULO 1 – APRESENTAÇÃO...01

1.1 – Introdução...01

1.2 – Justificativa...06

1.3 – Objetivo e Questões de Pesquisa...09

1.4 – Descrição dos Capítulos da Dissertação...10

CAPÍTULO 2 – APORTE TEÓRICO...12

2.1 – Introdução...12

2.2 – A Representação...13

2.2.1 – A Representação Sob Duas Óticas...16

2.2.2 – A Representação do Ponto de Vista de Piaget...16

2.2.3 – A Representação do Ponto de Vista de Duval...23

2.3 – A Revisão de Estudos Científicos Correlatos...33

2.3.1 – O Estudo de Solange dos Santos Nieto...33

2.3.2 – O Estudo de Alciony Regina Hérdérico Souza Silva...43

2.3.3 – O Estudo de Luís Augusto Sbardellini...48

2.3.4 – O Estudo de Regina Flemming Damm...49

2.3.5 – O Estudo de Ana Paula Jahn...53

2.4 – O Estudo de Passoni...57

2.5 – Histórico dos Números Negativos...61

2.6 – Os Números Inteiros Negativos na Escola...69

2.6.1- Parâmetros Curriculares Nacionais ...70

2.6.2- Livro Didático...72

2.6.2.1 – Referente 1ª à 4ª série...72

(13)

CAPÍTULO 3 - METODOLOGIA.....78

3.1 – Universo do Estudo...78

3.2 – Os Sujeitos...78

3.3 – Desenho do Experimento...79

3.4 – Procedimento...80

3.5 – Material Utilizado...81

3.5.1 – Materiais da Etapa 1 – Os Testes...82

3.5.1.1 – Pré-Teste...82

3.5.1.2 – Pós-Teste...88

3.5.2 – Materiais da Etapa 2 – A Intervenção...98

CAPÍTULO 4 – ANÁLISE DOS RESULTADOS....111

4.1 – Análise Quantitativa...112

4.1.1 – Análise Geral: Comparação entre o número de acertos dos grupos GE e GC nos Pré e Pós -testes...113

4.1.1.1 – Análise, por item, dos instrumentos diagnósticos...114

4.1.1.2 – Apresentação dos desempenhos dos alunos dos GE e GC nos pré e pós-testes...116

4.1.2 – Comparação Intra e Inter Grupos uma Síntese...118

4.2 – Análise Qualitativa...118

4.2.1- Análise qualitativa do pré-teste...120

4.2.2 – Intervenção de Ensino...133

4.2.3 – Pós-Teste...159

CAPÍTULO 5 – CONCLUSÃO...176

5.1 – Introdução...176

(14)

5.3 - Respondendo nossa Questão de Pesquisa...179

5.4 - Sugestões para futuras pesquisas...182

REFERÊNCIAS BIBLIOGRÁFICAS....183

(15)

LISTA DAS FIGURAS

FIGURA 1.1: PROMAT, Grasseschi, Andretta, Silva, 2004, p.44...02

FIGURA 1.4: SAEB (2001), p.45...06

FIGURA 1.5: Jahn (1994), p.98...07

FIGURA 3.1: Protocolo de resposta do aluno GC 2 do pré-teste...89

FIGURA 3.4: Protocolo de resposta do aluno GE 6 do pré-teste...93

FIGURA 4.1: Esquema de nossa análise Qualitativa...119

FIGURA 4.3: Protocolo de resposta dos alunos GE15 e GC15 do pré-teste..122

FIGURA 4.8: Protocolo de resposta dos alunos GC 4 e GE 9 do pré-teste....129

FIGURA 4.9: Protocolo de resposta do aluno GC 8 e GE 15 do pré-teste...130

(16)

FIGURA 4.12: Protocolo de resposta do aluno GE 8 da intervenção...134

(17)

FIGURA 4.41: Protocolo de resposta do aluno GE 2 do pós-teste...161

FIGURA 4.42: Protocolo de resposta do aluno GC 2 do pós-teste...161

(18)

LISTA DOS QUADROS

Quadro 2.1: Duval, 2001, p.3.- sistema de tratamento ou conversão...025

Quadro 2.2: Representação e compreensão para o conhecimento matemático (Duval 2000, composição da figura 2, p.59 e da figura 6, p.65) ...027

Quadro 2.3: (Duval, 2000, p.65), registros multifuncionais ou registros monofuncionais. ...028

Quadro 2.4: Várias coordenações entre sistemas produtivos requeridos para compreensões matemática. Fonte: Duval (2000 p. 66). ...030

Quadro 2.5: Sinopse dos 16 conjuntos de atividades desenvolvidas por Passoni (2002, p.25)...059

Quadro 3.1: Desenho do experimento...079

. Quadro 3.2 - Questão 1 do pré - teste. ...082

Quadro 3.3 - Questão 2 do pré-teste. ...083

Quadro 3.11 - Questão 1 do pós-teste. ...089

Quadro 3.13 - Questão 3 do pós-teste...092

(19)

Quadro 3.19 - Questão 9 do pós-teste. . ...097

Quadro 3.20 - Questão 10 do pós-teste. . ...098

Quadro 3.21 - Atividade 1 da seqüência de ensino. . ...099

Quadro 3.23 - Atividade 3 da seqüência de ensino. . . ...101

Quadro 3.28 - Atividade 8 da seqüência de ensino...104

Quadro 3.30 - Atividade 10 e 11 da seqüência de ensino. . . ...105

Quadro 3.31 - Atividade 12 e 13 da seqüência de ensino...106

Quadro 3.34 - Atividade 18 e 19 da seqüência de ensino...107

(20)

(21)

LISTA DE TABELAS

Tabela 2.1 - Registro da língua natural, registro do sistema escrito, registro

figural, registro gráfico...025

Tabela 2.2 - Livro Didático 1ª. à 4ª...073

Tabela 2.3 - Livro Didático 5ª. à 8ª...077

Tabela 3.1 - Correspondência entre pré-teste e pós-teste...088

Tabela 4.1: Desempenho geral do GE e GC nos testes (pré e pós-testes)....113

Tabela 4.2: Distribuição do desempenho geral dos dois grupos – GE e GC – nos pré-testes...116

Tabela 4.3: Distribuição do desempenho geral dos dois grupos – GE e GC – nos pós-testes...116

(22)

LISTA DE ANEXOS

Anexo 1 – Pré – teste...187

Anexo 2 – Pós – teste...190

(23)

CAPÍTULO 1

APRESENTAÇÃO

1.1 INTRODUÇÃO

Nosso objetivo principal com o presente estudo é investigar a

possibilidade e eficiência de se introduzir o número inteiro negativo1 na 3a série

do Ensino Fundamental na Escola Pública.

A natureza desse número difere da idéia do número natural porque este

último está diretamente relacionado a quantidades palpáveis, tangíveis. Por

exemplo, ao nos referirmos ao número 5, podemos estar atribuindo a esse

número a quantidade de 5 lápis, que estão sobre a mesa, pois podemos

tocá-los, pegá-los e contar esses objetos. Mas para o número -5 não há como

relacioná-lo a uma quantidade de objetos concretos. Nesse sentido, podemos

dizer que os números negativos não correspondem às quantidades concretas,

tangíveis, não “existem fisicamente” na vida cotidiana. Para tanto, vamos

reaplicar parte do estudo desenvolvido por Passoni (2002).

Sendo assim é preciso investigar, no processo de aprendizagem escolar,

a passagem das grandezas (noções concretas) para os números (noções

abstratas).

A noção de número negativo pode ser introduzida desde cedo na escola

a partir de várias situações que estão de acordo com o mundo físico, conforme

ilustramos nas situações abaixo. Uma situação muito comum na qual os

números negativos aparecem são as representações de andares para as

1

(24)

garagens de um prédio, que geralmente ficam no subsolo, como ilustra a

figura 1.1 a seguir:

FIGURA 1.1: PROMAT, Grasseschi, Andretta, Silva, 2004, p.44.

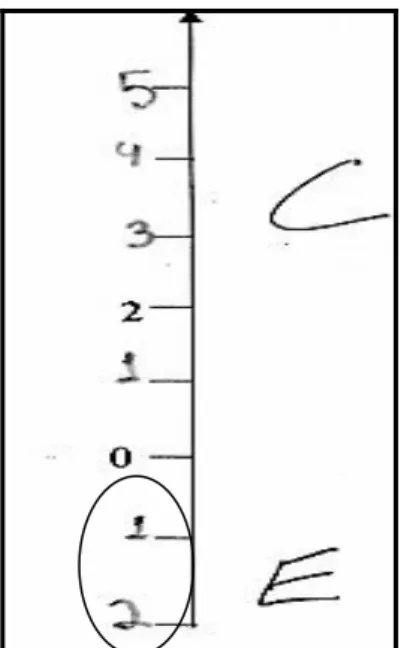
Os andares do prédio podem ser associados à reta numérica,

tomando-se o piso térreo como tomando-sendo o número zero, conforme detomando-senho acima, os

andares acima do térreo representam na reta numérica os números inteiros

positivos ou os números naturais, e as garagens, que estão abaixo do térreo

(zero), representam os números inteiros negativos que no exemplo acima são

(“-1” e “-2”).

Outra situação também comum que lida com os números inteiros

negativos são as situações presentes no painel do elevador. Por exemplo, num

elevador em um shopping, conforme ilustra a figura 1.2 abaixo, é

(25)

comum dizermos ao ascensorista que queremos ir para “garagem 2”, para

“G2”, ou ainda “para o menos 2”. Todas essas situações podem ser

representadas numericamente pelo número inteiro negativo “–2”, indicando que

queremos ir para 2 andares abaixo do térreo. Novamente adotamos o térreo

como zero, reforçando a idéia da reta numérica.

Mas os prédios ou elevadores não são as únicas situações em que

aparecem os números inteiros negativos. É comum dizermos frases do tipo:

“estou com 183 reais negativos no banco”.

Nesse caso, se tirarmos um extrato bancário irá aparecer um saldo

devedor de 183 reais, o qual costuma ser representado pelo número inteiro

negativo -183. Quando observamos um extrato bancário, notamos que os

números inteiros positivos representam os créditos da conta e os números

inteiros negativos os débitos, mostrando assim, o montante de dinheiro que

entrou e o que foi retirado de nossa conta bancária. Com isto podemos

estabelecer uma relação entre os valores do extrato bancário e a reta

numérica.

Continuando a exemplificar situações do dia-a-dia em que nos

deparamos com os números inteiros negativos, temos a do nível do mar

comumente considerada como marco zero. Neste, caso podemos ter uma

situação em que há um submarino que está a -125,2 metros do nível do mar

(ou abaixo do nível do mar 125,2 metros) e o avião está a 387,5 metros do

nível do mar (ou acima do nível do mar), como ilustra a figura 1.3 abaixo.

Novamente, a reta numérica pode ser desenhada fazendo-se

(26)

Ainda podemos ter situações relacionadas à temperatura, muito

utilizadas nos livros didáticos. Nesse caso podemos ter citações como:

Está noite fez muito frio no Rio Grande do Sul, pois tivemos -2 graus.

De fato, em situações de temperatura, costumamos usar terminologias

como: “2 graus negativos”, ou, ainda “menos 2 graus” para representar uma

temperatura abaixo de zero.

No caso dos números naturais podemos não só dizer que temos 100

reais no banco, como podemos ir até lá e retirá-lo, tocando assim no objeto a

que se refere essa quantidade (uma nota de 100 reais). Mas ao dizermos que

estamos 100 reais negativos, como nós podemos ir lá e retiramos -100 reais do

banco?

Todas essas situações apresentadas referem-se às situações em que os

números inteiros negativos estão associados às situações corriqueiras, isto é,

relacionando objetos (noção concreta) ou situações existentes aos números

(noção abstrata).

Dessa forma, o número, até então restrito a quantidades, ganha uma

dimensão mais ampla. Ele deixa de significar, simplesmente os objetos

quantificáveis, que podem ser efetivamente tocados, passando a ser uma idéia,

(27)

É notório que os números inteiros negativos fazem parte da vida das

crianças desde cedo, mas em contrapartida o seu ensino e sua implementação

na escola costumam ser difícieis e problemáticas.

Na minha experiência docente e em discussão com os colegas,

comenta-se freqüentemente sobre as dificuldades dos alunos em

compreenderem e se apropriarem de operações com números negativos.

A expressão “(

-a) – (- a) = 0

”, por exemplo, não é nada simples de ser

entendida, seja pelos alunos da 8a série, seja até por pessoas adultas que

tenham completado o Ensino Médio ou mesmo o Ensino Superior, pois temos

um mesmo símbolo (-) para:

Expressão “(

-a) – (- a) = 0

” símbolo operacional diático (2 elementos: -a e -a)

Expressão “(

-a) – (- a) = 0

” símbolo operacional monádico (1 elementos: -a)

A introdução do número negativo no ensino, normalmente no terceiro

ciclo (5ª ou 6ª série) do Ensino Fundamental, costuma ser vista como difícil e

um conteúdo “muito doloroso” para as crianças, e os professores queixam-se

bastante sobre a dificuldade de aprendizagem das crianças.

Refletindo a esse respeito, tendemos a acreditar que isso acontece

porque os alunos não vêem uma ligação entre o número inteiro negativo e o

mundo a sua volta, talvez por que esse número seja introduzido sem que haja

um aproveitamento dos contextos nos quais ele aparece no dia-a dia das

crianças.

Sob esse enfoque, a nossa preocupação é estudar então a possibilidade

de se introduzir número inteiro negativo, a partir de uma situação familiar, para

(28)

1.2 JUSTIFICATIVA

Quando observamos os sistemas de avaliação oficial, como o Sistema

de Avaliação e Rendimento Escolar do Estado de São Paulo (SARESP)

realizado em 1998, e o Sistema Nacional de Avaliação da Educação Básica

(SAEB) de 2001, notamos que praticamente não tivemos questões que

envolvessem os números inteiros negativos correspondentes à 4a ou na 8a

série do Ensino Fundamental. No último relatório do SARESP (1998) das 15

questões elaboradas para a 5ª série sobre números e operações, nenhuma

trazia um problema envolvendo números inteiros negativos; mas para o Ensino

Médio houve uma única questão, que consistia em localizar números na reta.

Quanto ao SAEB, havia um único problema, apresentado para os alunos

que estariam concluindo a 8a série, que envolveu números inteiros negativos

(ver figura 1.4 abaixo).

FIGURA 1.4: SAEB (2001), p.45

Notamos que se trata de um problema que não oferece um contexto

além do algoritmo, apresentando apenas uma expressão, resumindo-se ao já

tão conhecido “resolva”. O percentual de acerto nesta questão foi muito baixo

(29)

Fica claro que este exercício tem a finalidade de verificar, basicamente,

dois conhecimentos dos alunos: o primeiro diz respeito à operação entre sinais

dos números inteiros positivos e negativos; o segundo refere-se à ordem de

prioridade das operações, isto é multiplicações / divisões devem ser efetuadas

antes das adições / subtrações. Fica evidente, tendo em vista o resultado

inferior a 40% de acertos, que há uma necessidade premente de uma atenção

maior sobre esse tema e, ainda de se buscar maneiras para se trabalhar este

conteúdo de maneira mais satisfatória.

Em relação a outras pesquisas que apresentam problemas com

aprendizagem com os números inteiros podemos citar os índices encontrados

no estudo de Jahn (1994), que propõem a elaboração de uma pesquisa de

ensino para introdução do conceito e das operações aditivas dos números

inteiros, elaboradas em seqüências que proporcionam aos alunos uma tomada

de consciência da existência dos números inteiros negativos, a partir de

situações dentro do modelo ganho/perda.

Em Jahn (1994), observamos na página 97 que o maior índice de erros

foi na categoria 3, que inclui o item 9, subtração de um número inteiro negativo,

onde 9 alunos erraram dos 16 que responderam à questão. (43,7% de acertos)

(30)

O estudo de Damm (1992) visa a classificação dos problemas de adição

em conceituais, semânticos ou textuais com grupos de alunos de (6-9anos) e

(9-12 anos) da França e do Brasil.

Classificando em critérios conceituais como: Composição de 2

elementos de N; Operação de uma transformação; Relação estática entre 2

elementos; Composição e 2 transformações; Transformação entre duas

relações estáticas; Composição de relações. São aplicadas 8 questões no pré

e pós teste com o tipo de problema acumulativo (multiplicação e adição) e

comparação (multiplicação, adição e subtração).

A pesquisa de Alciony (2005) visa compreender como os erros de

números racionais são concebidos pelos professores e alunos no processo de

ensino e aprendizagem do Ensino Fundamental.

O estudo investiga no contexto do ensino aprendizagem da Matemática,

as práticas docentes utilizadas para o tratamento dos erros produzidos pelos

alunos numa escola pública do Município de Araucária/PR.

Os sujeitos da pesquisa são 2 professores que ministram aulas de

Matemática nas 5as, 6as e 7as séries e 17 alunos das referidas séries.

O estudo aponta a vigência de formas tradicionais de tratamento de

erros como a principal dificuldade dos docentes de ensinar os números

racionais de forma contextualizada, aliadas as dificuldades dos alunos no

processo de aprendizagem em relação a parte-todo, as dificuldades conceituais

e de operacionalização desse conjunto de números.

Alciony (2005) destaca alguns objetivos específicos neste trabalho

(31)

racionais e identificar as principais dificuldades dos alunos em relação aos

números racionais.

A pesquisa desenvolvida por Sbardellini (2005) visa demonstrar a

homogeneidade das estruturas ordenadas dos racionais.

A pesquisa desenvolvida por Nieto (1994) visa compreender antecipação

do ensino dos números inteiros negativos para a quarta série do primeiro grau:

um estudo das possibilidades.

O objetivo de Nieto (1994) é a princípio verificar se alunos de séries

anteriores à sexta série do 1º Grau, já se encontram capacitados para assimilar

os conceitos referentes dos números inteiros, uma vez que estes conceitos já

se apresentam com freqüência no cotidiano dos alunos, como por exemplo,

nas colunas esportivas. Portanto, tais conceitos, já bastante conhecidos pelos

alunos, ainda que de modo informal, que fortalecem a necessidade da presente

pesquisa.

Nieto (1994) buscou apoio na “Matemática informal”, aprendida pela

criança fora do processo educacional e estudada por Schliemann (1991), onde

separa seus testes em: Teste Formal e Teste Informal.

1.3 OBJETIVO E QUESTÕES DE PESQUISA

Por outro lado, Passoni (2002) propõe a introdução dos números

negativos, desde cedo, a partir de situações significativas para o aluno.

Passoni realizou uma intervenção de ensino com crianças de 3ª série de uma

escola particular da cidade de São Paulo com o intuito de introduzir os números

negativos, tendo como suporte teórico às idéias de Raymond Duval, no que

(32)

como característica os registros em atividades de tratamento e conversão.

Como dito anteriormente, o objetivo principal deste trabalho é o de avaliar a

possibilidade de uma intervenção de ensino, com alunos de 3ª série, para

introduzir o conceito de número inteiro negativo, com base na pesquisa de

Passoni.

Conforme veremos no Capítulo 2, página 23, o Aporte Teórico da

Representação do ponto de vista de Duval e no Capítulo 3, na página 81, os

Materiais utilizados na etapa de intervenção como a Metodologia

intervencionista da página 78 são os mesmos utilizados da pesquisa de

Passoni. As questões são as mesmas utilizadas na pesquisa de Passoni,

porém podemos trabalhar este conteúdo na forma interdisciplinar com os

conteúdos de Geografia e Português.

A partir desse objetivo, o presente estudo foi elaborado para responder

três questões de pesquisa, relacionadas entre si, a saber:

“Partindo de uma seqüência elaborada que utilize um contexto

familiar e significativo, qual a compreensão que crianças de 3ª série

passam a ter sobre os números negativos? Até onde tal seqüência pode

ajudar na introdução desse conceito? E, por último, em que consiste o

avanço?”.

Para responder a essas perguntas, vamos percorrer um caminho teórico e

metodológico, que descrevemos na próxima seção.

1.4 DESCRIÇÃO DOS CAPÍTULOS DA DISSERTAÇÃO

O Capítulo 1 trata da apresentação, justificativa, objetivo do estudo e,

(33)

O Capítulo 2 apresenta o nosso suporte teórico, no qual discutimos

principalmente as idéias Jean Piaget e Raymond Duval no que diz respeito à

idéia de representação. Para tanto, iniciamos o capítulo apresentando o

conceito de representação do ponto de vista da Língua Portuguesa, da

Filosofia, da Sociologia e da Semiótica. Esse capítulo apresenta as pesquisas

correlatas ao nosso estudo, como a de Passoni (2002), Damm (1992), Jahn

(1994), Nieto (1994), Alciony (2005) e Sbardellini (2005), todas abordando o

tema números inteiros negativos, na qual nos espelhamos de sobre maneira

para a construção de nosso trabalho.

E por último uma análise dos Livros Didáticos através dos Parâmetros

Curriculares Nacionais (PCN), em relação à introdução dos números inteiros

negativos.

O Capitulo 3 destina-se a descrição pormenorizada de nossa

Metodologia de Estudo, onde justificamos teoricamente o tipo de pesquisa

escolhida, apresentamos o estudo preliminar, a partir do qual pudemos refinar

o instrumento diagnóstico e, por fim, o estudo principal. Neste mesmo capítulo

descrevemos todo o desenho do experimento, isto é, os sujeitos envolvidos, o

material utilizado, a análise a priori das questões contidas no questionário (pré

e pós-testes), as atividades envolvidas na intervenção de ensino e, por fim, o

procedimento adotado no estudo.

No Capítulo 4 são apresentados e analisados os resultados, que serão

tratados do ponto de vista quantitativo e qualitativo. Por fim, apresentamos as

considerações finais de nosso estudo, tecendo comentários sobre os principais

resultados encontrados, retomando e respondendo às três questões de

(34)

CAPÍTULO 2

APORTE TEÓRICO

2.1 INTRODUÇÃO

O presente capítulo visa a atender quatro objetivos. O primeiro centra-se

na apresentação e reflexão das idéias teóricas, que usaremos como suporte

para compreender o processo de ensino-aprendizagem dos números

negativos. Pretendemos discutir em especial as idéias teóricas de Jean Piaget

e Raymond Duval. A escolha por essas Teorias baseia-se no fato de que

ambas discutem o papel da representação na formação (Piaget) e na

aprendizagem de conceitos (Duval).

O segundo objetivo é o de apresentar o estudo de Passoni (2002), no

qual nos baseamos para desenvolver nosso estudo empírico. Passoni

desenvolveu uma pesquisa intervencionista através de uma seqüência de

ensino voltada para introdução dos números negativos com crianças da

3ª.série do Ensino Fundamental.

O terceiro objetivo é o de procedermos uma revisão da literatura no que

concerne a estudos científicos que se relacionam com o nosso tema de

pesquisa. Discutiremos, particularmente, estudos realizados com números

negativos, como é o caso daqueles desenvolvidos por Regina Damm, Ana

Paula Jahn, Alciony Regina Herdérico Souza Silva, Luís Augusto Sbardellini e

(35)

O quarto e último objetivo deste capítulo é de correlacionar os PCN, os

livros didáticos e nosso estudo de pesquisa, para discussão de como os

números negativos são trabalhados em nosso dia-a-dia.

2.2 A

REPRESENTAÇÃO

Podemos iniciar a discussão sobre representação apresentando vários

pontos de vista, tais como o lingüístico, o filosófico, o psicológico, o semiótico e

o social.

Para Ferreira (1999), representação ganha os seguintes significados:

“1. Ato ou efeito de representar-se... 4.Reprodução daquilo que se pensa... 9.Filos. Conteúdo concreto aprendido pelos sentidos, pela imaginação, pela memória ou pelo pensamento.”(p.1747).

Notamos então que na Língua Portuguesa a representação tem relação

direta com a forma de pensar e com os sentidos. Nesse caso, representação

refere-se tanto ao pensamento, como à memória e à percepção.

Já na perspectiva filosófica (Ockham (Quodl, IV, q.3)), a representação é

tratada como:

(36)

Num enfoque filosófico podemos observar que a representação nos guia

a relação de três significados: o primeiro a representação como uma idéia no

sentido amplo e geral; no segundo nos remetendo a idéia de imagem e por

último trazendo-nos o próprio objeto.

Observemos agora a representação sob o aspecto, especificamente da

semiótica, apresentando a compreensão que Pierce (1999):

“[...] estar em lugar de isto é, estar numa relação com um outro que, para certos propósitos, é considerado por algumas mentes como se fosse o outro. Assim, um porta-voz, um deputado, um advogado, um agente, um vigário, um diagrama, um sintoma, uma descrição, um conceito, uma premissa, um testemunho, todos representam alguma outra coisa, de diferentes modos, para mentes que consideram sob esse aspecto. Veja-se o conceito de Signo. Quando se deseja distinguir entre aquilo que representa e o ato ou relação de representação, pode-se denominar o primeiro de representante e o último de representação”. (p.61).

Nesta ótica podemos verificar que o ato de representar pode ser

entendido como uma relação de uma incógnita qualquer, por exemplo x, com

algo que desejamos representar como medida, idade etc.

A representação do ponto de vista semiótico, segundo o psicólogo

francês contemporâneo Raymond Duval, nos diz que:

“[...] Descartes, até hoje, passando por Peirce e Piaget, muitas mudanças têm ocorrido na maneira de considerar as relações entre conhecimento e representação e, a natureza das representações parece tornar-se mais e mais complexa”. Duval (2000, p. 58).

“Muitos estudantes não discriminam o conteúdo da representação e o objeto representado: objetos mudam quando a representação muda!” (Ibid, p. 59).

Isso posto, notamos que não podemos falar de representação sem

(37)

Pois podemos ter exercícios com diferentes objetos com a mesma

representação.

Para a Psicologia, considerando a ótica de Piaget (1978) como um de

seus grandes representantes temos que:

“Diz representação, diz conseqüentemente reunião de um

significante que permite a evocação e de um significado

fornecido pelo pensamento”. (p.345).

Notamos que a capacidade de diferenciar significantes de significados é

condição básica para que ocorra a representação e, assim, ser capaz de

evocar e se referir a outro. Por exemplo, quando falamos de uma cadeira, a

palavra cadeira é o significante, enquanto a imagem da cadeira é o significado.

Para finalizar sob o enfoque social apresentamos uma definição clássica

segundo Jodelet (1985). Para representação social:

“São modalidades de conhecimento prático orientadas para a comunicação e para a compreensão do contexto social, material e ideativo em que vivemos. São, conseqüentemente, formas de conhecimento que se manifestam como elementos cognitivos — imagens, conceitos, categorias, teorias —, mas que não se reduzem jamais aos componentes cognitivos. Sendo socialmente elaboradas e compartilhadas, contribuem para a construção de uma realidade comum, que possibilita a comunicação” (p.469-494).

Sob este aspecto vemos que a representação é um campo que

possibilita questionar, de um lado, a natureza do conhecimento e, de outro, a

relação indivíduo-sociedade a partir do aspecto cognitivo.

O conceito de representação segundo Moscovici (1988):

(38)

vistas como a versão contemporânea do senso comum.” (p. 211).

Resumidamente, podemos falar em representação como uma forma de

conhecimento socialmente elaborada e partilhada, que tem um objetivo prático

e concorre para a construção de uma realidade comum a um conjunto social.

Pelo exposto vemos que a representação pode ser pensada e entendida

sob diversas perspectivas, dependendo da ciência ou do pensador que a

investigue. No item a seguir vamos nos restringir a duas óticas em especial, de

grande importância para o desenvolvimento de nosso estudo.

2.2.1 - A REPRESENTAÇÃO SOB DUAS ÓTICAS

Como dissemos na introdução deste capítulo, nosso objetivo é abordar o

papel da representação na formação e aprendizagem, que é o que faremos

nesta seção.

Para tanto, iniciamos com as idéias teóricas dos psicólogos Jean Piaget

e na seqüência as de Raymond Duval que tratam desse assunto.

2.2.2 - A REPRESENTAÇÃO DO PONTO DE VISTA DE PIAGET

Segundo Piaget (1995), é a partir da representação que surge o

conhecimento, ou seja, não há conhecimento sem representação.

“Há representação quando se imita um modelo ausente”. (p.12).

[...] é a capacidade de evocar por meio de um signo ou de uma imagem simbólica o objeto ausente ou a ação ainda não realizada. (PIAGET. 1975 p.231).

(39)

Essas afirmações de Jean Piaget nos permitem notar que, para ele,

representar é o ato de trazer a mente algo que está percentualmente ausente.

Assim, não é preciso estar diante de um coqueiro para poder representá-lo, ou

formar a sua imagem na mente. Neste sentido, representar significa o resultado

de uma ação que pode ser adquirida pela diferenciação ativa de significantes e

significados.

“A representação começa quando há, simultaneamente, diferenciação e coordenação entre significantes e significados ou significações”. (PIAGET 1978, p.11-12).

Então quando falamos de um coqueiro, a palavra coqueiro é o

significante, enquanto a imagem do coqueiro é o significado. Como já dissemos

anteriormente, segundo Piaget, a capacidade de diferenciar significantes de

significados é a condição básica para que ocorra a representação e, assim, ser

capaz de evocar um e referir-se ao outro, sem necessidade de estar perto do

objeto.

Agora partindo para uma análise mais profunda de representação temos

que Jean Piaget (1926, 1971) considera a existência de 2 tipos de

representação: Uma que está ligada a evocação do que já foi percebido

fisicamente. E a outra representação que não pode ser percebida como é o

caso do objeto matemático:

(40)

Essa capacidade representativa é denominada por Piaget função

simbólica. Para esse autor a evocação é o primeiro tipo de representação, já

que evocar é vista como a produção mental de um objeto em sua ausência

através de uma lembrança ou imagem do que já foi percebido em algum

momento. Nesse caso, a pessoa ao evocar um fato, acontecimento ou objeto

está, simplesmente, reproduzindo na mente o que já havia visto ou vivido

anteriormente.

Um segundo tipo de representação refere-se a trazer à mente algo que

não pode ser fisicamente percebido, como é o caso de um objeto matemático.

Tomemos como exemplo para este tipo de objeto, o número 1. Notamos que

muitos objetos concretos podem facilmente representar a quantidade referente

ao número 1, como um lápis, um giz, uma caneta ou até mesmo o dedo

indicador. Todos são fisicamente concretos e todos são diferentes do objeto

matemático número, que é abstrato.

Para ajudar a entender melhor a capacidade representativa da função

simbólica vamos olhar o que Piaget (1975), postula sobre o desenvolvimento

da criança. Ele pontua que esse desenvolvimento se dá por meio de quatro

estágios: o sensório-motor; o pré-operatório, o operatório-concreto e, por fim, o

operatório-formal, que seria o último estágio do desenvolvimento. Sendo que

os estágios acima não são regras padrões, inclusive não são os únicos fatores

que influenciam as crianças a aprender, por exemplo os números negativos.

“Eles (os estágios) não correspondem, por sua vez, as idades absolutas observando-se, pelo contrário, as acelerações ou retardamentos segundo os diversos meios sócios e a experiências adquiridas” (Piaget, 1982, p.45).

O estágio sensório-motor: É neste estágio que o bebê começa a

(41)

espaço, causalidade e tempo. Nesse período ele lança mão de seus reflexos

neurológicos básicos para começar assimilar mentalmente o meio, cujo contato

é direto e imediato, sem representações ou pensamentos.

O estágio pré-operatório, também denominado Inteligência simbólica, é

a fase em que surge, na criança, a capacidade de substituir um objeto ou

acontecimento por uma representação. Esta substituição é possível graças à

função simbólica.

No estágio subseqüente, chamado operatório concreto, ocorre o

desenvolvimento da reversibilidade, ou seja, a capacidade da representação de

uma ação no sentido inverso de uma anterior, anulando a transformação

observada.

Por fim, no estágio operatório formal as estruturas cognitivas da criança

alcançam seu nível mais elevado de desenvolvimento e tornam-se aptas a

aplicar o raciocínio lógico a todas as classes de problemas.

A representação agora permite à criança uma abstração total, não se

limitando mais à representação imediata e nem às relações previamente

existentes. Agora a criança é capaz de pensar logicamente, formular hipóteses

e buscar soluções, sem depender mais só da observação da realidade.

Após visualizarmos as fases de desenvolvimento da criança, na qual a

representação tem um papel fundamental, voltamos a tratar do aparecimento

da função simbólica que, para Jean Piaget, é um momento fundamental do

desenvolvimento cognitivo. É através da função simbólica que a inteligência

torna-se representativa; as ações e sua coordenação podem ser realizadas em

um novo nível, interno, sem ficarem subordinadas aos dados atuais e externos

(42)

A capacidade representativa é demonstrada pela função simbólica,

como vimos anteriormente e agora podemos representá-la em cinco padrões

de comportamentos que, segundo Piaget e Inhelder (1995), surgem

simultaneamente a partir do segundo ano de vida da criança. São eles: a

imitação, o jogo simbólico, o desenho, a imagem mental, a linguagem. Esses

comportamentos, apesar de começar por volta dos 2 anos, vão levar toda a

infância e parte da adolescência para se formarem completamente. Uma vez

adquiridos, serão sempre usados. São a partir desses comportamentos, que

nós adultos, formamos as imagens e são eles que, juntos, permitem criar a

representação. Para melhor entendermos esses 5 padrões de comportamento

utilizamos as idéias dePiagete Inhelder. (1995 p. 48).

“1) Há, primeiro que tudo,a imitação diferida, isto é aquela que principia na ausência do modelo. Numa conduta de imitação sensório-motora a criança começa imitando em presença do modelo (por exemplo, um movimento da mão), depois pode continuar a fazê-lo na ausência do modelo sem que isso implique em nenhuma representação em pensamento.

2) Há, em seguida, o jogo simbólico, ou jogo de ficção, desconhecido no nível sensório-motor. A mesma garotinha inventou o primeiro jogo simbólico ao fingir dormir, sentada e sorrindo largamente, mas de olhos fechados, cabeça inclinada, polegar na boca e segurando um canto de pano, que simula o canto do travesseiro, consoante o ritual costumeiro que observa ao adormecer; pouco depois, faz dormir o seu urso de pelúcia, enfia uma conchinha numa caixa dizendo “miau”(acaba de ver um gato num muro) etc.

3) O desenho ou imagem gráfica, nos seus primórdios, é intermediário entre o jogo e a imagem mental, embora quase não apareça antes dos 2 anos ou dos 2 ½ anos.

4) Vem, em seguida, mais cedo ou mais tarde, a imagem mental, da qual não se observa traço algum no nível sensório-motor (pois, do contrário, o descobrimento do objeto permanente seria grandemente facilitado) e que surge como imitação interiorizada.

(43)

Salientamos que Jean Piaget (Ibid) faz distinção entre dois tipos de

imagem mental: a estática, presa à memória e à percepção, e a dinâmica que

permite que atuemos sobre um determinado objeto, modificando-lhe o

tamanho, a posição, a coloração, a direção ou o sentido sem, contudo, deixar

de reconhecê-lo como sendo o mesmo objeto.

Para representar um objeto do mundo real, podemos fazê-lo lançando

mão de uma evocação. Para tanto, precisamos ter a capacidade de imitação,

do jogo simbólico, do desenho e até da imagem mental estática. Mas se nós

precisamos criar um objeto que não é palpável ou concreto, como é o caso de

objetos matemáticos, vamos precisar então da imagem mental dinâmica, da

memória de evocação e da linguagem. No caso da Matemática há conceitos

como, por exemplo, associado à idéia de simetria:

Se A = B então B =A

Que não é obvio que se tenha tal idéia internalizada, principalmente porque

não estamos nos referindo, necessariamente, a dois objetos concretos,

tangíveis. Da mesma forma, ao expressarmos a idéia de transitividade:

Se A >B >C então A > C,

Neste caso, estamos atuando sobre os objetos e sejam quais forem

eles, o primeiro (A) é maior que o segundo (B), que, por sua vez é maior que o

terceiro (C) e, portanto, podemos inferir que o primeiro é maior que o terceiro.

Assim podemos assumir que a partir dos primeiros conhecimentos a

criança é capaz de reproduzir alguma coisa. Por exemplo, pensemos em um

(44)

A criança pode representar essa figura geométrica porque ela reconhece

e desenha um quadrado, mas se ela estiver presa mais nos primeiros padrões

de representação, como imitação ou do desenho, ela pode representar esse

quadrado apenas no eixo ortogonal. Nesse caso, para Jean Piaget, a criança

estaria utilizando o que ele chamou de aspecto figurativo do conhecimento, que

acontece quando a criança lança mão apenas da percepção e da memória

para representar ou reconhecer um objeto. Porém, se ela trabalhar com a

imagem mental internalizada, ela será capaz de atuar sobre esse objeto e

então representá-lo ou reconhecê-lo mesmo que ele lhe seja mostrado em

posições não ortogonal ou não convencional.

Ela pode dizer que “continua sendo um quadrado” só que o quadrado

girou, pois continua com os lados de mesma medida e os ângulos retos. Nesse

caso, dizemos que ela está atuando sobre o objeto.

Com isso, podemos resumir que uma vez adquiridos estes padrões de

comportamento todo ser humano passa a usá-los sempre que for representar

algo.

Quando tratamos dos números negativos vamos precisar da imagem

mental dinâmica, da memória de evocação e da linguagem para podermos

representar esse objeto que não é palpável. Por exemplo, para uma dívida de

três reais, isto é, de –3 reais não há como relacioná-la com qualquer coisa

(45)

Assim, podemos dizer que a idéia de números inteiros negativos acaba

por destruir a idéia de número como sendo algo possível de ser quantificável

por meio de objetos concretos. Se no conjunto dos naturais um número podia

ser um objeto palpável a partir de sua correspondência com as coisas do

mundo tangível, agora ele passa, definitivamente, para o mundo das idéias. Se

antes considerávamos que um bom caminho para se introduzir o conceito de

número para a criança era relacioná-lo a objetos e coisas contáveis do mundo,

estabelecendo uma analogia entre o conceito de contagem com o da

quantificação de coisas ou de objetos, agora, em que tal situação, vemos que

isso não é mais possível.

Sendo assim há necessidade de se considerar dois tipos de objetos, os

concretos e os abstratos. Dentre os concretos ainda temos aqueles objetos

passíveis de serem vistos no mundo circundante – árvores, livros, cachorros

etc – e aquele que não enxergamos – micróbios, bactérias, átomos e outros.

Quanto aos objetos abstratos, nos referimos àqueles tais como amor, raiva, ar,

etc.

Isso posto, vemos que os estudos de Jean Piaget, de grande valia para

o entendimento sobre o surgimento e o desenvolvimento da representação,

ainda não são suficientes para explicar em suas diferentes nuanças e, por isso,

vamos recorrer às idéias de Raymond Duval sobre esse assunto.

2.2.3 A REPRESENTAÇÂO DO PONTO DE VISTA DE DUVAL

Segundo Raymond Duval (1999), a noção de registro de representação

semiótica traz como princípio a mobilização de vários registros como uma

maneira típica de se representar um objeto matemático, fazendo uma distinção

(46)

essa atividade. Isto é, mostrando o mesmo objeto matemático em vários

registros facilita o entendimento.

Duval mostra que há dois tipos de sistemas produtores da

representação: os dispositivos físicos (ligados aos neurônios e à percepção) e

os sistemas semióticos (relacionados à linguagem). Não faz sentido, portanto,

falar em representação sem levar em conta o seu sistema de produção.

“[...] Mas de Descartes, até hoje, passando por Peirce e Piaget, muitas mudanças têm ocorrido na maneira de considerar as relações entre conhecimento e representação e, a natureza das representações parece tornar-se mais e mais complexa”. Duval (2000 p. 58).

Essas afirmações nos permitem notar que, para Duval, a natureza das

representações necessita de uma análise estruturada do funcionamento dos

objetos matemáticos.

Numa análise mais específica para os registros de representação temos

que Duval (1999), classifica-os em quatro tipos: dois relativos à representação

discursiva: a língua natural e os sistemas de escritas e outros dois relativos à

representação não discursiva: registro figural e registro gráfico.

Este autor sustenta que para que um conhecimento, ou saber

matemático, possa ser colocado em funcionamento é necessário que se

apreenda não somente com um registro, mas com pelo menos dois registros de

representação e que se saiba também coordenar esses registros, buscando as

relações entre os objetos representados.

Por exemplo, podemos reconhecer um objeto matemático por meio de

(47)

Registro da língua natural

Registro do sistema escrito

Registro figural Registro gráfico

Considere a reta que passa pelos

pontos A e B AB A B

B

A

Tabela 2.1 – Registro da língua natural, registro do sistema escrito, registro figural, registro gráfico.

Para ajudar a entender melhor o registro de representação Duval (1999)

postula que não podemos falar de representação sem relacioná-la com seus

sistemas de produção. Mas se levamos em conta sistemas semióticos significa

focar as transformações de representações. Portanto precisamos distinguir

dois tipos de transformações, que são bem diferentes, a saber: “tratamento” e

“conversão”.

Os tratamentos são transformações de representações dentro de um

mesmo registro. Por exemplo, efetuar um cálculo ficando estritamente no

mesmo sistema de escrita ou de representações dos números.

Exemplo: 5 – 3 = 2 ou 5 + (-3) = 2

As conversões são transformações de representações que consistem

em mudar de registro conservando os mesmos objetos denotados. Por

exemplo, passar da escrita algébrica de uma equação a sua representação

gráfica.

TRANSFORMAÇÃO

(De uma dada representação semiótica para uma outra representação semiótica diferente)

Quadro 2.1: Duval, 2001, p.3. - sistema de tratamento ou conversão.

PERMANECENDO NO MESMO SISTEMA:

TRATAMENTO

MUDANDO O SISTEMA:

(48)

Salientamos que Duval (1999), postula a complexidade cognitiva da

conversão em que podemos observar duas situações importantes que são:

uma de congruência e outra de não congruência.

Em alguns casos a conversão é obvia e imediata. Como se a

representação de um registro de partida fosse transparente para a

representação do registro de chegada e, nesse caso, dizemos que a

conversão é congruente.

“As conversões congruentes são imediatas e espontâneas e para as não congruentes não há nada de imediato” (Passoni, 2002, p.11).

Exemplo de conversão congruente:

Conjunto de pontos cuja ordenada y é maior que a abscissa x, então: y > x

Isso posto, vemos que os estudos de Duval (1995) destaca que a

conversão congruente existe quando:

“Correspondência semântica entre as unidades significantes que as constituem, mesma ordem possível de apreensão dessas unidades nas duas representações e, para converter de uma unidade significante da representação de partida em uma só unidade significante na representação de chegada”. (pp. 5-6)

Salientamos que Duval (1999) destaca que a não congruência é o

fenômeno crucial para toda tarefa de conversão. As dificuldades e os

bloqueios mentais originam-se, freqüentemente, na inabilidade de se realizar a

conversão. Mas o mais surpreendente é o seu caráter unidimensional. Uma

(49)

Exemplo de conversãonão-congruente:

Conjunto de pontos cuja ordenada y e abscissa x tem o mesmo sinal:

x

.

y

>

0

Então quando falamos em conversão estamos nos referindo à

congruência ou não-congruência.

Buscamos agora uma explicação da direção da conversão para os que

obtiveram sucesso a conversão é congruente e fracasso, ou mesmo

bloqueios mentais, para a conversão não congruente, revelando uma falta de

coordenação entre os registros. E notamos que o entendimento conceitual só é

possível quando a coordenação é atingida. Por isso, que não podemos

confundir objetos matemáticos com o conteúdo de sua representação, que

podem ser vistos conforme quadro abaixo:

Compreensão Coordenação

Quadro 2.2: Representação e compreensão para o conhecimento matemático (Duval 2000, composição da figura 2, p.59 e da figura 6, p.65)

OBJETO

Denotação Denotação

Signos ou composição de signos Conteúdo A da representação Signos ou composição de signos Conteúdo B da representação

Produção de uma representação Por meio de limitações e possibilidades específicas de um sistema semiótico A.

(50)

Assim para qualquer objeto matemático podemos ter diferentes

representações produzidas por diferentes sistemas semióticos. Nesta

perspectiva Raymond Duval (2000) aprofunda:

“Sempre que um sistema semiótico muda, o conteúdo da representação muda, enquanto o objeto continua o mesmo. Mas, um objeto matemático não pode ser identificado por alguma de suas representações, muitos estudantes não discriminam o conteúdo da representação e o objeto representado: objetos mudam quando a representação muda!” (p. 59).

Para ajudar a entender melhor a capacidade representativa, que

consiste em desenvolver coordenações entre os vários tipos de registros, que

se classificam em quatro tipos segundo Raymond Duval (1995, 1996):

REPRESENTAÇÃO DISCURSIVA REPRESENTAÇÃO NÃO-DISCURSIVA REGISTROS MULTIFUNCIONAIS:

Os tratamentos não são algoritmizáveis.

Linguagem natural:

Associações verbais (conceituais).

Forma de raciocinar:

• Argumentação a

partir de

observações, de crenças...

• Dedução válida a partir de definição ou de teoremas.

Registro Figural:

Tabelas ou em perspectivas (configurações em dimensões 0,1,2 ou 3).

• Apreensão

operatória e não somente

perceptiva;

• Construção com

instrumentos. REGISTROS

MONOFUNCIONAIS: Os tratamentos são principalmente algoritmos

Sistema de Escrita:

• Numéricas

• Algébricas;

• Simbólicas

(línguas formais).

• Cálculo

Registro Gráfico:

• Mudanças de

sistema de coordenadas;

• Interpolação,

extrapolação. Quadro 2.3: (Duval, 2000, p.65)

(51)

predominância de registros monofuncionais discursivos parece crescer. Além disso, é com estes tipos de registros que a perda de significado é observada. Por quê? Acredita-se erradamente que a aplicação na vida diária ou em situações fora da Matemática podem ser as fontes de significado e de entendimento. Não! O principal problema é com os registros multifuncionais. Eles são necessários implicitamente ou explicitamente para a compreensão matemática, mas a maneira que eles trabalham nos processos de pensamento matemático é totalmente diferente da maneira com que eles trabalham em outros campos do conhecimento, e a fortiori, na vida cotidiana. Por essa razão, utilizar a língua natural como no discurso usual referindo-se à uma figura geométrica como se isso fosse tão óbvio como uma outra imagem visual não ajuda, mas aumenta a confusão na compreensão e aprendizagem. Aqui se abre um amplo campo de pesquisas. Se nós queremos entender o complexo mecanismo da aprendizagem matemática nós devemos analisar as maneiras específicas de trabalho dos registros multifuncionais, especialmente em demonstrações e visualizações na resolução de problemas geométricos. Nós já temos muitas variáveis cognitivas decisivas. (Duval, 2000, pp. 65-66).