Uma Introdução à Teoria Econômica dos Jogos

(1)

(2)

(3)

Publicações Matemáticas

Uma Introdução

à Teoria Econômica dos Jogos

Humberto Bortolossi

UFF

Gilmar Garbugio

UESB

Brígida Sartini

UFRRJ

impa

₂₆

o

(4)

22460-320 Rio de Janeiro, RJ Impresso no Brasil / Printed in Brazil Capa: Noni Geiger / Sérgio R. Vaz

26o Colóquio Brasileiro de Matemática

• Aspectos Ergódicos da Teoria dos Números - Alexander Arbieto, Carlos Matheus e Carlos Gustavo Moreira

• Componentes Irredutíveis dos Espaços de Folheações - Alcides Lins Neto

• Elliptic Regularity and Free Boundary Problems: an Introduction - Eduardo V. Teixeira

• Hiperbolicidade, Estabilidade e Caos em Dimensão Um - Flavio Abdenur e Luiz Felipe Nobili França

• Introduction to Generalized Complex Geometry - Gil R. Cavalcanti

• Introduction to Tropical Geometry - Grigory Mikhalkin

• Introdução aos Algoritmos Randomizados - Celina de Figueiredo, Guilherme da Fonseca, Manoel Lemos e Vinicius de Sá

• Mathematical Aspects of Quantum Field Theory - Edson de Faria and Welington de Melo

• Métodos Estatísticos Não-Paramétricos e suas Aplicações - Aluisio Pinheiro e Hildete P. Pinheiro

• Moduli Spaces of Curves - Enrico Arbarello

• Noções de Informação Quântica - Marcelo O. Terra Cunha

• Three Dimensional Flows - Vítor Araújo e Maria José Pacifico

• Tópicos de Corpos Finitos com Aplicações em Criptografia e Teoria de Códigos - Ariane Masuda e Daniel Panario

• Tópicos Introdutórios à Análise Complexa Aplicada - André Nachbin e Ailín Ruiz de Zárate

• Uma Introdução à Mecânica Celeste - Sérgio B. Volchan

• Uma Introdução à Teoria Econômica dos Jogos - Humberto Bortolossi, Gilmar Garbugio e Brígida Sartini

• Uma Introdução aos Sistemas Dinâmicos via Frações Contínuas - Lorenzo J. Díaz e Danielle de Rezende Jorge

ISBN: 978-85-244-0265-4 Distribuição: IMPA

(5)

H. J. B.

`

A minha m˜ae Rita e aos meus irm˜aos Humberto e Reginaldo.

B. A. S.

(6)

(7)

Sum´

ario

Pref´acio 3

1 Alguns marcos hist´oricos 5 2 Jogos na forma estrat´egica 10

2.1 O que ´e um jogo? . . . 10

2.2 Solu¸c˜oes de um jogo em estrat´egias puras . . . 13

2.2.1 Dominˆancia em estrat´egias puras . . . 14

2.2.2 Equil´ıbrio de Nash em estrat´egias puras . . . . 20

2.2.3 Rela¸cões entre dominância e equil´ıbrio de Nash 24 2.3 Estratégias mistas . . . 27

2.4 Solu¸c˜oes de um jogo em estrat´egias mistas . . . 31

2.4.1 Dominˆancia em estrat´egias mistas . . . 32

2.4.2 Equil´ıbrio de Nash em estrat´egias mistas . . . . 35

2.4.3 Rela¸cões entre dominância e equil´ıbrio de Nash 45 2.4.4 Como interpretar estratégias mistas? . . . 45

2.5 Jogos infinitos . . . 48

2.6 Exerc´ıcios . . . 50

3 O teorema de equil´ıbrio de Nash 60 3.1 Usando o teorema de Brouwer . . . 60

3.2 Usando o teorema de Kakutani . . . 65

3.3 Algumas propriedades dos equil´ıbrios de Nash . . . 69

(8)

4 Calculando equil´ıbrios de Nash 71

4.1 Equil´ıbrio de Nash via um problema de otimiza¸c˜ao . . 71

4.2 Equil´ıbrio de Nash via equa¸c˜oes polinomiais . . . 74

4.3 Jogos de soma zero . . . 82

4.3.1 Jogos de soma constante com dois jogadores . . 82

4.3.2 Equil´ıbrio de Nash em estrat´egias puras . . . . 86

4.3.3 Equil´ıbrio de Nash em estrat´egias mistas . . . . 91

4.3.4 O teorema minimax de von Neumann . . . 93

4.4 Equil´ıbrio de Nash via um problema de complementa-ridade . . . 101

4.4.1 Jogos bimatriciais . . . 101

4.4.2 O algoritmo de Lemke-Howson . . . 104

4.5 Gambit . . . 104

5 Jogos na forma extensa 108 5.1 Defini¸c˜ao . . . 108

5.2 Equil´ıbrio de Nash . . . 110

5.3 Indu¸c˜ao retroativa e equil´ıbrio perfeito em subjogos . . 114

5.4 O teorema de Kuhn-Zermelo . . . 118

6 Exemplos 120 6.1 O jogo Le Her simplificado . . . 120

6.2 O modelo de duop´olio de Cournot . . . 126

6.3 O modelo de duop´olio de Bertrand . . . 129

6.4 O modelo de duop´olio de Stackelberg . . . 131

6.5 A trag´edia dos comuns . . . 133

A Convexidade 137 B Programa¸c˜ao Linear 145 C Respostas dos exerc´ıcios 155 Bibliografia 173

(9)

Pref´

acio

Ateoria dos jogos´e uma teoria matem´atica criada para se modelar

fenˆomenos que podem ser observados quando dois ou mais “agentes de

decisão” interagem entre si. Ela fornece a linguagem para a descri¸cão de processos de decisão conscientes e objetivos envolvendo mais de um indiv´ıduo.

Suas aplica¸cões incluem elei¸cões, leilões, balan¸co de poder, evolu-¸cão genética, etc. Ela também é uma teoria matemática pura, que pode e tem sido estudada como tal, sem a necessidade de relacioná-la

com problemas comportamentais ou jogosper se.

Algumas pessoas acreditam que ateoria dos jogos formar´a, algum

dia, o alicerce de um conhecimento técnico estrito de como decisões são feitas e de como a economia funciona. A teoria ainda não atingiu este patamar e, hoje, é mais estudada em seus aspectos matemáticos puros e, em aplica¸cões, ela é usada como uma ferramenta ou alegoria que auxiliam no entendimento de sistemas mais complicados.

Neste texto trataremos da teoria matem´atica dos jogos n˜

ao-coope-rativos estáticos de informa¸cão completa e dos jogos dinâmicos de

informa¸c˜ao perfeita.

A Teoria Econˆomica dos Jogos n˜ao deve ser confundida com a

Teoria Combinatória dos Jogos, iniciada por Sprague e Grundy na década de 30. Enquanto que a primeira tem motiva¸cões predomi-nante econômicas e procura estabelecer métodos para se maximizar

o ganho (payoﬀ), a segunda se concentra nos aspectos combinat´orios

de jogos de mesa (por exemplo, a estrat´egia do jogo de nim) e n˜ao

permite “elementos imprevis´ıveis” como o lan¸camento de um dado ou o embaralhamento de cartas.

Acreditamos que o assunto seja estimulante para o estudante de matemática: ele terá a oportunidade de ver como conceitos de análise,

(10)

topologia, otimiza¸c˜ao e probabilidade se integram em uma teoria apli-cada.

Agradecimentos

Gostar´ıamos de agradecer a Hilmar Ilton Santana Ferreira, Polya-ne Alves Santos e Larissa Santana Barreto, que participaram ativa-mente dos semin´arios sobre teoria dos jogos realizados no per´ıodo

2003-2004, momento no qual uma vers˜ao preliminar deste texto foi

escrita. Também gostar´ıamos de agradecer a Rita de Cássia Silva Costa, Bernardo K. Pagnoncelli e, em especial, a Carlos Tomei, que leram o texto e fizeram várias sugestões. Finalmente, gostar´ıamos de

agradecer a Se¸cão de Referência (SRE) da Divisão de Bibliotecas e

Documenta¸cão da PUC-Rio pela agilidade e eficiência na aquisi¸cão de alguns artigos dif´ıceis de se encontrar.

Humberto Jos´e Bortolossi Br´ıgida Alexandre Sartini

Gilmar Garbugio

(11)

Alguns marcos

hist´

oricos

Neste cap´ıtulo apresentaremos alguns marcos históricos da teoria dos jogos relacionados principalmente com os tópicos que iremos ex-plorar no texto. Para uma cronologia mais completa, recomendamos as referências [46, 50, 65, 86, 95, 96].

O conceito de solu¸c˜ao de um jogo por estrat´egia mista1surgiu pela

primeira vez no estudo do jogoLe Her, realizado por James

Walde-grave e descrito por ele em uma carta a Pierre R´emond de Montmort, em 13 de novembro de 1713. Em seu estudo, ele procurou encontrar

uma estrat´egia que maximizasse a probabilidade de vit´oria do

joga-dor, independentemente da escolha de estratégia de seu oponente. Este jogo foi discutido por Montmort e por Nicholas Bernoulli em 1713 e os resultados foram publicados nesse ano por Montmort, que incluiu a solu¸cão de Waldegrave em um apêndice.

Em 1838, Augustin Cournot publicou sua obra Recherches sur

les Principes Mathematiques de la Theorie des Richesses, na qual analisou um caso especial de duop´olio. As empresas decidiam as quantidades a produzir e Cournot definiu o conceito de equil´ıbrio de

1_{Uma estrat´}_{egia pura ´}_{e uma das escolhas que o jogador pode fazer. Uma}

estratégia mista é uma distribui¸cão de probabilidades sobre o conjunto de es-tratégias puras. Defini¸cões formais serão apresentadas no próximo cap´ıtulo.

(12)

Figura 1.1: Antoine Augustin Cournot (1801–1877).

mercado como sendo a situa¸c˜ao em que ambas as empresas reagem

de forma ótima à decisão da empresa concorrente. Este conceito

de solu¸cão é uma versão do equil´ıbrio de Nash aplicado ao caso do duopólio.

No in´ıcio do s´eculo XX, apareceram v´arios artigos sobreteoria dos jogos. Ernst Zermelo, em 1913, publicou um teorema sobre o jogo

de xadrez no artigo Uber eine Anwendung der Mengenlehre auf die

Theorie des Schachspiels, afirmando que, em cada etapa do jogo, pelo menos um dos jogadores possui uma estratégia que o levará a vitória

ou ao empate. Contudo, Zermelo n˜ao demonstrou o teorema em seu

artigo. A primeira demonstra¸c˜ao foi dada por Laszlo Kalmar.

Apa-rentemente, foi Zermelo quem primeiro destacou o uso da semˆantica

de otimalidade em teoria dos jogos: “Whether one could calculate

with mathematical objectivity, or even give a participant some idea of, the value of a possible position in the game, as well as of the best move in this position: information without which the player would have to eliminate both subjective and psychological guesses and the opinions of ‘the perfect player’, etc.?” ([95]).

No per´ıodo de 1921 a 1927, ´Emile Borel publicou uma s´erie de

notas sobre jogos sim´etricos de soma zero com dois jogadores com

um n´umero finito n de estrat´egias puras para cada jogador. Borel

foi o primeiro a tentar formular matematicamente este jogo. Ele in-troduziu o conceito de “método de jogada” (o que hoje corresponde à estratégia pura) e procurou por uma solu¸cão em estratégias mis-tas (o que hoje é conhecido como solu¸cão minimax). Em 1921, ele

(13)

Figura 1.2: Ernst Friedrich Ferdinand Zermelo (1871–1953).

para n= 5 ([08]). Borel acreditava que o resultado de existˆencia

não seria válido para um n qualquer, mas como não encontrou um

contra-exemplo, deixou o problema em aberto.

Figura 1.3: F´elix Edouard Justin ´Emile Borel (1871-1956).

No artigo Zur Theorie der Gesellschaftsspiele de 1928, usando

topologia e cálculo funcional ([50]), John von Neumann demonstrou a existência de solu¸cão em estratégias mistas de um jogo finito de soma zero com dois jogadores e um número arbitrário de estratégias pura. Este artigo também introduziu a forma extensa de um jogo.

At´e a d´ecada de 40, os artigos publicados sobreteoria dos jogos

n˜ao tinham despertado muito o interesse dos cientistas sociais e de

outras ´areas que pesquisavam sobre conflitos de interesses. Talvez

isto se deva ao fato de que os artigos eram escritos por matem´aticos e publicados em revistas matem´aticas. Este panorama foi alterado

(14)

Behavior, escrito por John von Neumann e pelo economista Oskar

Morgenstern, um marco na teoria dos jogos.

Oskar Morgenstern John von Neumann

(1902-1977) (1903-1957)

Figura 1.4: Oskar Morgenstern e John von Neumann.

(15)

pesquisa-dores de diversas áreas. Na reedi¸cão de 1947, tomada como padrão, os autores estabeleceram os axiomas da teoria da utilidade. O livro foi republicado em 1953 e sua mais recente edi¸cão é de 1980.

Na Universidade de Princeton, John Forbes Nash Jr. escreveu sua

tese de doutorado em 1949, sob o t´ıtuloNon-Cooperative Games. Ele

definiu o conceito deponto de equil´ıbrio, atualmente conhecido como

equil´ıbrio de Nash de um jogo e provou sua existência para jogos não-cooperativos. Os resultados mais importantes de sua tese estão no

artigoEquilibrium Points in N-Person Games de 1950 ([66]) e, mais

detalhadamente, no artigo Non-Cooperative Games de 1951 ([69]).

Ainda em 1950, Nash escreveu sobre o problema da barganha em

The Bargaining Problem ([68]) e, no ano de 1953, sobre jogos

coo-perativos em Two Person Cooperative Games ([70]). Nestes, Nash

definiu o conceito de solu¸cão da barganha de Nash em um jogo coo-perativo com dois jogadores, estabeleceu um sistema de axiomas que esta solu¸cão deveria satisfazer e provou a existência e unicidade desta solu¸cão.

Em 1994, John Harsanyi, John Nash e Reinhard Selten receberam o Prêmio Nobel de Economia em reconhecimento ao trabalho pioneiro sobre análise de equil´ıbrio na teoria de jogos não-cooperativos.

(a) (b) (c)

(16)

Jogos na forma

estrat´

egica

2.1 O que ´

e um jogo?

A teoria dos jogos pode ser definida como a teoria dos modelos matemáticos que estuda a escolha de decisões ótimas sob condi¸cões

de conflito. O elemento b´asico em um jogo ´e o conjunto dejogadores

que dele participam. Cada jogador tem um conjunto deestrat´egias.

Quando cada jogador escolhe sua estrat´egia, temos ent˜ao uma

si-tua¸cão ou perfil no espa¸co de todas as situa¸cões (perfis) poss´ıveis. Cada jogador tem interesse ou preferências para cada situa¸cão no

jogo. Em termos matem´aticos, cada jogador tem uma fun¸c˜ao

uti-lidade que atribui um número real (o ganho ou payoff do jogador) a cada situa¸cão do jogo. Mais especificamente, um jogo tem os se-guintes elementos básicos: existe um conjunto finito de jogadores, representado por

G=_{g1, g2, . . . , gn_},

e cada jogadorgi∈Gpossui um conjunto finito

Si={si1, si2, . . . , simi}

(17)

de op¸c˜oes, denominadas estrat´egias puras do jogador gi (mi _≥ 2). Um vetor

s= (s1j1, s2j2, . . . , snjn),

onde siji é uma estratégia pura para o jogador gi ∈ G, é

denomi-nado umperfil de estrat´egias puras. O conjunto de todos os perfis de estrat´egias puras formam, portanto, o produto cartesiano

S=

n

i=1

Si=S1_×S2_{× · · · ×}Sn,

denominado espa¸co de estrat´egias puras do jogo. Para cada

joga-dorgi_∈G, existe umafun¸c˜ao utilidade

ui: S → R s _→ ui(s)

que associa o ganho (payoﬀ) ui(s) do jogador gi a cada perfil de

estratégias puras s _∈ S. Esta fun¸cão utilidade é uma forma de re-presentar a preferência do jogadorgicom rela¸cão aos vários perfis de estratégias do jogo ([13]).

Jogos descritos nesta forma s˜ao denominadosjogos estrat´egicos ou

jogos na forma normal. Neles, cada jogador deve fazer a sua escolha

de estrat´egiasem o conhecimento das escolhas dos demais jogadores.

Admite-se, contudo, que cada jogador conhece toda a estrutura do jogo. Por este motivo, jogos deste tipo tamb´em s˜ao denominados

jogos n˜ao-cooperativos de informa¸c˜ao completa.

Assume-se tamb´em que os jogadores sejamracionais, isto ´e, eles

sempre escolherão a¸cões que maximizem a sua fun¸cão utilidade. Além

de ser racional, cada jogador (1) sabe que seus advers´arios tamb´em

s˜ao racionais, (2) sabe que eles sabem que o jogador sabe que eles s˜ao racionais,ad infinitum.

Exemplo 2.1 (O dilema do prisioneiro)Possivelmente o exem-plo mais conhecido na teoria dos jogos ´e odilema do prisioneiro. Ele

foi formulado por Albert W. Tucker em 1950, em um semin´ario para

psic´ologos na Universidade de Stanford, para ilustrar a dificuldade de se analisar certos tipos de jogos.

(18)

poderem se comunicar entre si, o delegado de plantão faz a seguinte proposta: cada um pode escolher entre confessar ou negar o crime. Se nenhum deles confessar, ambos serão submetidos a uma pena de 1 ano. Se os dois confessarem, então ambos terão pena de 5 anos. Mas se um confessar e o outro negar, então o que confessou será libertado e o outro será condenado a 10 anos de prisão. Neste contexto, temos

G=_{Al,Bob_},

SAl ={confessar,negar}, SBob={confessar,negar}, S=SAl_×SBob=

{(confessar,confessar),(confessar,negar),

(negar,confessar),(negar,negar)_}.

As duas fun¸c˜oes utilidade

uAl:S _→R e uBob:S_→R s˜ao dadas por

uAl(confessar,confessar) =₋5, uAl(confessar,negar) = 0, uAl(negar,confessar) =₋10, uAl(negar,negar) =₋1,

(que representam os ganhos de Al) e

uBob(confessar,confessar) =₋5, uBob(confessar,negar) =₋10, uBob(negar,confessar) = 0, uBob(negar,negar) =−1

(que representam os ganhos de Bob). ´E uma pr´atica representar os

payoffs dos jogadores através de uma matriz, denominadamatriz de payoffs.

Bob

confessar negar

Al

confessar (₋5,₋5) (0,₋10)

negar (−10,0) (−1,−1)

Nesta matriz, os n´umeros de cada c´elula representam,

respectiva-mente, os payoﬀs de Al e Bob para as escolhas de Al e Bob

(19)

Exemplo 2.2 (A batalha dos sexos) Um homem e a sua mulher desejam sair para passear. O homem prefere assistir a um jogo de futebol enquanto que sua mulher prefere ir ao cinema. Se eles forem

juntos para o futebol, ent˜ao o homem tem satisfa¸c˜ao maior do que a

mulher. Por outro lado, se eles forem juntos ao cinema, ent˜ao a

mu-lher tem satisfa¸cão maior do que o homem. Finalmente, se eles sa´ırem sozinhos, então ambos ficam igualmente insatisfeitos. Esta situa¸cão também pode ser modelada como um jogo estratégico. Temos:

G={homem,mulher},

Shomem=_{futebol,cinema_}, Smulher=_{futebol,cinema_}, S=Shomem_×Smulher=

{(futebol,futebol),(futebol,cinema),

(cinema,futebol),(cinema,cinema)_}.

As duas fun¸c˜oes utilidade uhomem: S _→ R e umulher: S _→ R s˜ao

descritas pela seguinte matriz depayoﬀs:

Mulher

futebol cinema

Ho

m

em futebol (10,5) (0,0)

cinema (0,0) (5,10)

.

2.2 Solu¸

c˜

oes de um jogo em estrat´

egias

puras

Uma solu¸cão de um jogo é uma prescri¸cão ou previsão sobre o re-sultado do jogo. Existem vários conceitos diferentes de solu¸cão. Nesta

se¸c˜ao, investigaremos os dois conceitos mais comuns: dominˆancia e

equil´ıbrio de Nash.

(20)

se os dois prisioneiros querem minimizar1 _{o tempo de cadeia? Se}

analisarmos o jogo do ponto de vista de Al, ele pode raciocinar da seguinte maneira:

“Duas coisas podem acontecer: Bob pode confessar ou Bob pode negar. Se Bob confessar, ent˜ao ´e melhor para

mim confessar também. Se Bob não confessar, então eu

fico livre se eu confessar. Em qualquer um dos casos, ´e

melhor para mim confessar. Ent˜ao, eu confessarei.”

Se analisarmos agora o jogo do ponto de vista de Bob, podemos aplicar a mesma linha de racioc´ınio e concluir que Bob também irá confessar. Assim, ambos confessarão e ficarão presos por 5 anos.

Em termos da teoria dos jogos, dizemos que (1) os dois

joga-dores possuem uma estrat´egia dominante, isto ´e, todas menos uma

estratégia éestritamente dominada, (2) que o jogo é resolúvel por do-minância estrita iteradae (3) que o jogo termina em uma solu¸cão que é umequil´ıbrio de estratégia dominante, conceitos que definiremos a seguir.

2.2.1 Dominˆ

ancia em estrat´

egias puras

Freqüentemente, iremos discutir perfis de estratégia na qual ape-nas a estratégia de um único jogadorgi_∈Girá variar, enquanto que as estratégias de seus oponentes permanecerão fixas. Denote por

s−i= (s1j1, . . . , s(i−1)ji−1, s(i+1)ji+1, . . . , snjn)∈

S−i=S1× · · · ×Si−1×Si+1× · · · ×Sn

uma escolha de estrat´egia para todos os jogadores, menos o jogadorgi. Desta maneira, um perfil de estrat´egias pode ser convenientemente denotado por

s= (siji,s−i) = (s1j1, . . . , s(i−1)ji−1, siji, s(i+1)ji+1, . . . , snjn).

(21)

Defini¸cão 2.1 (Estratégia Pura Estritamente Domi-nada) Dizemos que uma estratégia pura sik _∈ Si do joga-dorgi_∈Géestritamente dominadapela estratégiasik′ ∈Sise,

independentemente das escolhas dos demais jogadores, o joga-dorgi ganhar mais escolhendosik′ do quesik, isto ´e, se

ui(sik′,s₋_i)> ui(sik,s₋_i),

para todos−i∈S−i.

Defini¸c˜ao 2.2 (em estrat´egias puras)

(a) (Dominância Estrita Iterada)Dominância estrita ite-radaé o processo no qual, seqüencialmente, se eliminam as estratégias que são estritamente dominadas.

(b) (Equil´ıbrio de Estrat´egia Estritamente

Dominan-te)Quando o processo de dominˆancia estrita iterada reduz

o jogo para um único perfil de estratégias purass∗, dizemos ques∗é umequil´ıbrio de estratégia estritamente dominante.

Exemplo 2.3 Considere o jogo determinado pela matriz depayoﬀs

abaixo.

g2

s21 s22 s23 s24

g1

s11 (5,2) (2,6) (1,4) (0,4)

s12 (0,0) (3,2) (2,1) (1,1)

s13 (7,0) (2,2) (1,1) (5,1)

(22)

Neste jogo, para o jogadorg2, a estrat´egias21 ´e estritamente

domi-nada pela estrat´egias24 e, assim, a primeira coluna da matriz pode

ser eliminada.

g2

s22 s23 s24

g1

s11 (2,6) (1,4) (0,4)

s12 (3,2) (2,1) (1,1)

s13 (2,2) (1,1) (5,1)

s14 (1,3) (0,2) (4,8)

Agora, nesta matriz reduzida, para o jogador g1, as estrat´egias s11

es14 são estritamente dominadas pelas estratégiass12 es13, respec-tivamente. Portanto, as linhas 1 e 4 podem ser eliminadas. Além disso, a estratégias23do jogadorg2é estritamente dominada pela

es-trat´egias22. Assim, a coluna 2 tamb´em pode ser eliminada. Obtemos

ent˜ao uma matriz reduzida 2_×2.

g2

s22 s24

g1 s12 (3,2) (1,1)

s13 (2,2) (5,1)

Finalmente, a estrat´egia s24 do jogadorg2 ´e estritamente dominada

pela estratégias22 e, na matriz 2_×1 resultante, a estratégias13 do jogadorg1é estritamente dominada pela estratégias12. Vemos então que (s12, s22) é o equil´ıbrio de estratégias estritamente dominantes do jogo: o jogadorg1escolhe a estratégias12(ganhando 3) e o jogadorg2

escolhe a estrat´egias22(ganhando 2).

(23)

mais simples, no sentido de que o conjunto de estratégias puras de um jogador (aquele que tem uma estratégia estritamente domi-nada) é substitu´ıdo por um subconjunto com menos elementos (ob-tido removense justamente as estratégias que são estritamente do-minadas). No exemplo acima, os conjuntos de estratégias puras ini-ciais dos dois jogadores são dados, respectivamente, por

S1=_{s11, s12, s13, s14_} e S2=_{s21, s22, s23, s24_}.

Como a estrat´egia puras21 ´e estritamente dominada pors24, o

con-juntoS2´e substitu´ıdo por_{s22, s23, s24_}=S2_−{s21_}. O conjuntoS1

permanece o mesmo. Sendo assim, podemos substituir o jogo original por um mais simples, onde os conjuntos de estrat´egias puras dos dois jogadores s˜ao dados por

S1(1)={s11, s12, s13, s14} e S (1)

2 ={s22, s23, s24}.

As fun¸cões utilidade do novo jogo são as restri¸cões das fun¸cões utili-dade do jogo original aos novos conjuntos de estratégias puras:

u1|S₁(1) e u2|S(1)₂ .

Para o novo jogo, vemos que as estrat´egiass11es14s˜ao estritamente

dominadas pelas estrat´egiass12 es13, respectivamente. Logo,

pode-mos simplificar o jogo mais uma vez, considerando os conjuntos de estrat´egias puras

S1(2)={s12, s13} e S (2)

2 ={s22, s23, s24}.

Seguindo com as outras elimina¸cões, terminamos com um jogo muito simples, onde cada conjunto de estratégias puras é unitário:

S₁(5)=_{s12_} e S₂(5)=_{s22_}.

Este processo de elimina¸c˜ao gerou, portanto, uma cadeia de espa¸cos de estrat´egias puras:

S=S1_×S2S(1)=S₁(1)_×S₂(1)S(2) =S₁(2)_×S₂(2)· · ·

(24)

Neste exemplo, a t´ecnica de dominˆancia estrita iterada forneceu um ´

unico perfil de estrat´egias como solu¸c˜ao do jogo, no caso, o perfil

(s12, s22)_∈S1(5)×S (5) 2 .

Contudo, pode acontecer da técnica fornecer vários perfis ou, até

mesmo, fornecer todo o espa¸co de estrat´egias, como ´e o caso da

bata-lha dos sexos, onde n˜ao existem estrat´egias estritamente dominadas.

Um outro conceito importante ´e o de estrat´egia pura fracamente dominada.

Defini¸cão 2.3 (Estratégia Pura Fracamente Domi-nada) Dizemos que uma estratégia pura sik _∈ Si do joga-dor gi _∈ G é fracamente dominada pela estratégia sik′ ∈ Si

se

ui(sik′,s₋_i)≥ui(sik,s₋_i),

para todos−i∈S−ie, pelo menos para algum s•−i∈S−i, ui(sik′,s•₋_i)> ui(sik,s•₋_i).

Em outras palavras, sik _∈ Si ´e fracamente dominada por

sik′ ∈Si se, independentemente das escolhas dos demais

joga-dores, o jogadorgi nada perde se trocar a estrat´egia sik _∈ Si

pela estrat´egiasik′ ∈ Si e, pelo menos para uma escolha dos

demais jogadores, esta troca d´a ao jogadorgi um ganho maior.

Defini¸c˜ao 2.4

(a) (Dominˆancia Fraca Iterada)Dominˆancia fraca iterada

é o processo no qual, seqüencialmente, se eliminam as es-tratégias que são fracamente dominadas.

(b) (Equil´ıbrio de Estrat´egia Fracamente Dominante)

(25)

Exemplo 2.4 Considere o jogo cuja matriz depayoﬀs´e dada por:

g2

s21 s22

g1 s11 (1,1) (1,0)

s12 (1,0) (0,1) .

A estrat´egia s12 do jogador g1 ´e fracamente dominada pela

estra-t´egias11. Eliminando-a, obtemos a matriz reduzida:

g2

s21 s22

g1 s11 (1,1) (1,0) .

Vemos agora que a estrat´egia s22 do jogador 2 ´e estritamente

do-minada pela estratégias21. Sendo assim, (s11, s21) é o equil´ıbrio de estratégias fracamente dominadas do jogo.

Uma pergunta natural é se o processo de elimina¸cão das estratégias

dominadas depende ou n˜ao da ordem em que s˜ao realizadas. Para

o caso de estrat´egias estritamente dominadas, pode-se mostrar que

esta ordem é irrelevante, isto é, independentemente da ordem em que as estratégias (estritamente dominadas) são eliminadas, obtém-se sempre a mesma matriz reduzida no final do processo. Por outro lado,

o processo de elimina¸c˜ao das estrat´egiasfracamente dominadas pode

conduzir a resultados diferentes, dependendo da ordem de elimina¸c˜ao. Considere, por exemplo, o jogo (conforme [32]):

g2

s21 s22 s23

g1 s11 (0,2) (0,0) (1,0)

(26)

Eliminando-se, em seqüência, as estratégias s23 (que é estritamente

dominada por s21), s11 (que ´e fracamente dominada por s12) e s22

(que ´e estritamente dominada por s21), obtemos (s12, s21) como

res-posta. Agora, eliminando-se, em seqüência, as estratégias s22 (que

´e estritamente dominada pors21), s12 (que ´e fracamente dominada

pors11) es23(que ´e estritamente dominada pors21), obtemos outra

resposta: (s11, s21). Para detalhes sobre este assunto, recomendamos

as referˆencias [01, 15, 26, 32, 47, 55].

Com rela¸cão à complexidade computacional, os resultados mos-tram que os problemas relacionados com estratégias estritamente do-minadas tendem a ser mais fáceis (no sentido que eles podem ser

resolvidos em tempo polinomial), enquanto que quest˜oes envolvendo

estratégias fracamente dominadas são mais dif´ıceis (no sentido que eles são NP-completos). Por exemplo, saber se uma dada submatriz

de uma matriz de payoﬀs pode ser obtida atrav´es do processo de

elimina¸cão de estratégias dominadas é um problema polinomial para o caso de estratégias estritamente dominadas e é um problema NP-Completo para o caso de estratégias fracamente dominadas. Detalhes sobre o assunto podem ser encontrados nas referências [18, 33].

2.2.2 Equil´ıbrio de Nash em estrat´

egias puras

Uma solu¸cão estratégicaou equil´ıbrio de Nashde um jogo é um

perfil de estrat´egias onde cada jogador n˜ao tem incentivo de mudar

sua estrat´egia se os demais jogadores n˜ao o fizerem.

Defini¸c˜ao 2.5 (Equil´ıbrio de Nash)Dizemos que um perfil de estrat´egias

s∗= (s∗

1, . . . , s∗(i−1), s∗i, s∗(i+1), . . . , s∗n)∈S

´e umequil´ıbrio de Nashse

ui(s∗

i,s∗−i)≥ui(siji,s ∗ −i)

(27)

Exemplo 2.5

(a) No dilema do prisioneiro (Exemplo 2.1), o perfil de estrat´egias (confessar, confessar) ´e um equil´ıbrio de Nash. De fato:

uAl(confessar,confessar) =₋5>₋10 =uAl(negar,confessar) e

uBob(confessar,confessar) =₋5>₋10 =uBob(confessar,negar).

Estas desigualdades mostram que, para o perfil de estrat´egias

(confessar, confessar), um prisioneiro n˜ao se sente motivado a

mudar a sua estratégia se o outro não o fizer (ele não vai ficar menos tempo na cadeia fazendo isto).

Já o perfil (negar, confessar) não é um equil´ıbrio de Nash do jogo pois, neste caso, dado que Bob decide confessar, Al fica menos tempo na cadeia se mudar a sua estratégia de negar para confessar. Em outras palavras, para o perfil (negar, confessar), Al se sente motivado a mudar a sua estratégia se Bob não o fizer. Os perfis (confessar, negar) e (negar, negar) também não são equil´ıbrios de Nash. Em (confessar, negar), Bob se sente moti-vado a mudar a sua estratégia se Al não o fizer e, em (negar, negar), cada um dos prisioneiros se sente motivado a mudar a sua estratégia se o outro não o fizer. Desta maneira, vemos que o único equil´ıbrio de Nash do jogo é (confessar, confessar).

(b) Na batalha dos sexos (Exemplo 2.2), os perfis de estratégia (fu-tebol, futebol) e (cinema, cinema) são os únicos equil´ıbrios de Nash do jogo.

(c) No Exemplo 2.3, o único equil´ıbrio de Nash do jogo é o perfil de estratégias (s12, s22).

Existem, contudo, jogos que n˜ao possuem equil´ıbrios de Nash em

estrat´egias puras. Este ´e o caso, por exemplo, do jogo de comparar

(28)

Exemplo 2.6 (Comparar moedas)Nesse jogo, dois jogadores exi-bem, ao mesmo tempo, a moeda que cada um esconde em sua m˜ao. Se ambas as moedas apresentam cara ou coroa, o segundo jogador

d´a sua moeda para o primeiro. Se uma das moedas apresenta cara,

enquanto a outra apresenta coroa, ´e a vez do primeiro jogador dar sua moeda para o segundo. Esse jogo se encontra representado por

sua matriz depayoﬀs dada abaixo.

g2

s21 s22

g1 s11 (+1,−1) (−1,+1) s12 (−1,+1) (+1,−1)

Observe que o perfil de estratégias (s11, s21) não é um equil´ıbrio de

Nash em estrat´egias puras, pois se o jogador g1 mantiver a sua

es-trat´egia s11, o jogador g2 ter´a um ganho maior se mudar sua

es-trat´egia des21 paras22, isto ´e, ele se sente motivado a mudar a sua

estrat´egia se o jogador g1 n˜ao mudar a sua escolha. O mesmo

com-portamento ocorre para o perfil de estratégias (s12, s22). Já, para os perfis (s11, s22) e (s12, s21), é o jogador g1 que se sente motivado a

mudar de estrat´egia para ganhar mais, se o jogadorg2mantiver a sua

estratégia. Isto mostra que o jogo de comparar moedas não possui equil´ıbrios de Nash em estratégias puras.

Existe uma maneira conveniente de se caracterizar equil´ıbrios de

Nash atrav´es das fun¸c˜oes de melhor resposta. De maneira informal,

a melhor resposta de um jogador para uma determinada escolha de estratégias dos demais jogadores é o conjunto de estratégias do jo-gador que maximizam o seu ganho quando os demais jojo-gadores não mudam as suas escolhas. Mais precisamente, temos a seguinte

Defini¸cão 2.6 (Funções de melhor resposta)A fun¸cão de melhor resposta do jogadorgié a aplica¸cão

(29)

definida por

MRi(s−i) = argmaxsi∈Siui(si,s−i)

= _{s∗

i ∈Si | ∀si∈Si, ui(s∗i,s−i)≥ui(si,s−i)},

coms−i∈S−i(aqui 2Sirepresenta o conjunto das partes deSi).

A fun¸cão de melhor resposta do jogo é a aplica¸cão

MR :S _→2S

definida por

MR(s) = (MR1(s−1),MR2(s−2), . . . ,MRn(s−n)),

com s _∈ S. Observa¸c˜ao: alguns autores usam as nota¸c˜oes

MRi:S−i⇒Si e MRi:S−i →→Si para representar a fun¸c˜ao

de melhor resposta MRi: S−i→2Si.

Exemplo 2.7

(a) No dilema do prisioneiro (Exemplo 2.1), temos

MRAl : SBob →→ SAl

confessar → {confessar}

negar → {confessar}

MRBob: SAl →→ SBob

confessar → {confessar}

negar → {confessar}.

(b) Na batalha dos sexos (Exemplo 2.2), temos

MRHomem: SMulher →→ SHomem

futebol → {futebol}

cinema → {cinema}

MRMulher: SHomem →→ SMulher

futebol → {futebol}

(30)

(c) No Exemplo 2.3, temos

MR1(s21) ={s14}, MR1(s22) ={s12},

MR1(s23) ={s12}, MR1(s24) ={s13},

MR2(s11) ={s22}, MR2(s12) ={s22},

MR2(s13) ={s22}, MR2(s14) ={s24}.

(d) No jogo de comparar moedas (Exemplo 2.6), temos

MR1(s21) ={s11}, MR1(s22) ={s12},

MR2(s11) ={s22}, MR2(s12) ={s21}.

A próxima proposi¸cão é uma conseqüência direta das defini¸cões de equil´ıbrio de Nash e fun¸cões de melhor resposta.

Proposi¸c˜ao 2.1 s∗ _{= (}_s∗

1, . . . , s∗i, . . . , s∗n)∈S ´e um equil´ıbrio

de Nash em estrat´egias puras se, e somente se,s∗

i ∈MRi(s∗−i)

para todoi= 1, . . . , n.

Observação. Como vimos, nem sempre um jogo possui um equi-l´ıbrio de Nash em estratégias puras. Contudo, é poss´ıvel garantir esta existência para certos tipos de jogos com estruturas especiais. O leitor interessado pode consultar os jogos descritos nos artigos [28, 61, 80, 94]. Para resultados quantitativos, veja [60].

2.2.3 Rela¸

c˜

oes entre dominˆ

ancia e equil´ıbrio de

Nash

Proposi¸cão 2.2 O processo de dominância estrita iterada não pode eliminar um equil´ıbrio de Nash ao simplificar um jogo.

(31)

com menos elementos, obtido removendo-se as estratégias do jogador que são estritamente dominadas. Cada elimina¸cão gera um espa¸co de estratégias puras com menos elementos o que, sucessivamente, sim-plifica o jogo original:

S=S1_{× · · · ×}Sn S(1)=S₁(1)_{× · · · ×}S_n(1)

· · ·S(k)=S(k)₁ _{× · · · ×}S_n(k).

Com esta nota¸cão, o enunciado da proposi¸cão pode ser colocado as-sim: ses∗_∈S é um equil´ıbrio de Nash, entãos∗_∈S(k)_.

A demonstra¸cão será feita por contradi¸cão: suponha, por absurdo, que exista s∗_{= (}_s∗

1, . . . , s∗n)∈S tal ques∗ ´e um equil´ıbrio de Nash,

mas s∗ _∈ _S(k)_{. Isto significa que existe} _i _{tal que} _s∗

i ∈ S (l) i mas s∗

i ∈S (l+1)

i para algum l= 0, . . . , k−1 (se l= 0, defina S (0) i =Si).

Sem perda de generalidade, vamos supor que esta propriedade ocorre pelaprimeira vez para o ´ındicei, isto ´e,s∗

i ´e a primeira estrat´egia do

perfil de estrat´egias

s∗= (s∗

1, . . . , s∗(i−1), s∗i, s∗(i+1), . . . , s∗n)

que ´e eliminada por uma estrat´egia estritamente dominante. Sendo assim, existes•

i ∈S (l)

i tal que

ui(s∗i,s−i)< ui(s•i,s−i)

para todos−i∈S−(l)i. Comos∗i ´e a primeira estrat´egia a ser eliminada,

isto significa ques∗₋_i _∈S₋(l)_i e, portanto,

ui(s∗

i,s∗−i)< ui(s•i,s∗−i).

Mas isto ´e um absurdo pois, por hip´otese, s∗ _{= (}_s∗

i,s∗−i) ´e um

equil´ıbrio de Nash.

Proposi¸cão 2.3 Se o processo de dominância estrita iterada deixa apenas um único perfil de estratégias purass∗, então s∗

(32)

Demonstra¸cão:Suponha que o processo de dominância estrita iterada gere uma cadeia de espa¸cos de estratégias puras

S=S1_{× · · · ×}SnS(1) =S₁(1)_{× · · · ×}S_n(1)

· · ·S(k)=S₁(k)_{× · · · ×}S_n(k),

onde o último conjunto da cadeia é unitário:

S(k)=S₁(k)_{× · · · ×}S(k)_n =_{s∗_}=_{(s∗

1, . . . , s∗i, . . . , s∗n)}.

Note que, em particular, s∗

1 ∈ S

(l)

1 , s∗2 ∈ S (l)

2 , . . . , s∗n ∈ S (l)

n , para

todo l = 0, . . . , k. Vamos mostrar que, nesta situa¸cão,s∗ é o único

equil´ıbrio de Nash do jogo. De fato, basta mostrar que s∗ ´e um

equil´ıbrio de Nash, pois a unicidade é uma conseqüência direta da

Proposi¸c˜ao 2.2. Suponha ent˜ao, por absurdo, que s∗ _n˜_{ao seja um}

equil´ıbrio de Nash. Neste caso, devem existir ´ındice i e estrat´egia

puras[1]

i ∈Si, coms

[1]

i =s∗i, tais que ui(s∗

i,s∗−i)< ui(s

[1]

i ,s∗−i).

Dado que (s[1]

i ,s∗−i)∈S(k)e dado ques∗ι ∈S (l)

ι para todoι= 1, . . . n

e para todo l= 0, . . . , k, segue-se que a estrat´egias[1]

i ´e estritamente

dominada por alguma outra estrat´egias[2]

i ∈Si. Segue-se ent˜ao que,

em particular, ui(s[1]

i ,s∗−i)< ui(s

[2]

i ,s∗−i) e, portanto,

ui(s∗

i,s∗−i)< ui(s

[1]

i ,s∗−i)< ui(s

[2]

i ,s∗−i).

Note que, por causa destas desigualdades, segue-se que s[2]

i =s

[1]

i e s[2]

i =s∗i. Como (s

[2]

i ,s∗−i) tamb´em n˜ao pertence aS(k), segue-se que a

estrat´egias[2]

i ´e estritamente dominada por uma outra estrat´egias

[3]

i ∈ Si. Sendo assim,ui(s[2]

i ,s∗−i)< ui(s

[3]

i ,s∗−i) e, portanto,

ui(s∗i,s∗−i)< ui(s

[1]

i ,s

∗

−i)< ui(s

[2]

i ,s

∗

−i)< ui(s

[3]

i ,s

∗ −i).

Como antes, destas desigualdades, segue-se ques[3]

i =s

[2]

i ,s

[3]

i =s

[1]

i e s[3]

i =s∗i. Prosseguindo desta maneira, construir´ıamos uma seq¨uˆencia

infinita (s[1]

i , s

[2]

i , s

[3]

i , . . . , s

[r]

i , . . .) de estrat´egias purasdistintas do

jo-gadorgi satisfazendo as desigualdades

ui(s∗i,s∗−i)< ui(s

[1]

i ,s∗−i)<· · ·< ui(s

[r]

(33)

Mas isto ´e um absurdo, poisSi ´e um conjunto finito.

A rec´ıproca da Proposi¸cão 2.3 é falsa, isto é, mesmo que o jogo tenha um único equil´ıbrio de Nash, ele não é necessariamente obtido a

partir do processo de dominˆancia estrita iterada. O jogo cuja matriz

depayoﬀs´e

g2

s21 s22 s23

g1

s11 (−1,+1) (+1,−1) (−1,+1)

s12 (+1,₋1) (₋1,+1) (+1,₋1)

s13 (−1,+1) (+1,−1) (+5,+5)

fornece um contra-exemplo: s∗ _{= (}_{s13, s23}_{) ´e o ´}_{unico equil´ıbrio de}

Nash do jogo, mas n˜ao existem estrat´egias estritamente dominadas.

A Proposi¸cão 2.2 é se trocarmos dominância estrita por

domi-nância fraca, isto é, o processo de dominância fraca iterada pode

eliminar um equil´ıbrio de Nash (veja o exerc´ıcio [10] na p´agina 58

para um contra-exemplo). Se o processo de dominˆancia fraca iterada

reduz o jogo para apenas um ´unico perfil de estrat´egias (como na

Proposi¸cão 2.3), então este perfil é obrigatoriamente um equil´ıbrio de Nash, contudo, ele não é necessariamente o único equil´ıbrio de Nash do jogo.

2.3 Estrat´

egias mistas

Como vimos no jogo de comparar moedas do Exemplo 2.6, existem jogos que não possuem equil´ıbrios de Nash em estratégias puras. Uma alternativa para estes casos é a de considerar o jogo do ponto de vista probabil´ıstico, isto é, ao invés de escolher um perfil de estratégias puras, o jogador deve escolher umadistribui¸cão de probabilidadesobre suas estratégias puras.

(34)

isto ´e,p_i ´e um elemento do conjunto

∆mi=

(x1, . . . , xmi)∈R

mi _|_x1_≥₀_{, . . . , xm}

i ≥0 e

mi

k=1 xk= 1

.

Assim, se p_i= (pi1, pi2, . . . , pimi), ent˜ao

pi1_≥0, pi2_≥0, . . . , pi_mi _≥0 e

mi

k=1

pik= 1.

Note que cada ∆mi ´e um conjunto compacto e convexo. Nas

Figuras 2.1 e 2.2 temos os desenhos de ∆2e ∆3, respectivamente. Os

pontos extremos (v´ertices) de ∆mi, isto ´e, os pontos da forma

e1= (1,0, . . . ,0,0), e2= (0,1, . . . ,0,0), . . . , emi = (0,0, . . . ,0,1)

dão, respectivamente, probabilidade 1 às estratégias puras si1, si2, . . . , simi. Desta maneira, podemos considerar a distribui¸cão de

pro-babilidade ek como a estrat´egia mista que representa a estrat´egia

purasik do jogadorgi.

O espa¸co de todos os perfis de estrat´egia mista ´e o produto car-tesiano

∆ = ∆m1×∆m2× · · · ×∆mn,

denominadoespa¸co de estrat´egias mistas. Como o produto cartesiano

de conjuntos compactos e convexos ´e compacto e convexo, vemos que ∆ ´e compacto e convexo.

Um vetor p∈ ∆ ´e denominado um perfil de estrat´egias mistas.

Como no caso de estrat´egias puras, usaremos a nota¸c˜ao p−i para

representar as estrat´egias mistas de todos os jogadores, excluindo-se

a do jogadorgi. Desta maneira, escreveremos

(p_i,p−i)

para representarp= (p₁, . . . ,p_i, . . . ,p_n). Como a estrat´egia purasik

pode ser identificada com a distribui¸c˜ao de probabilidades que d´a

peso 1 asik e peso 0 `as demais estrat´egias do jogadorgi, usaremos

(35)

1 0

1

x₁ x₂

Figura 2.1: ∆2=(x1, x2)∈R2 |x1≥0, x2≥0 ex1+x2= 1.

0

1

1 1

x₁

x₂ x₃

Figura 2.2: ∆3=

(x1, x2, x3)_∈R3

| x1_≥0,x2_≥0,x3_≥0 ex1+

(36)

como uma nota¸c˜ao alternativa para o perfil de estrat´egias mistas (ek,p−i). Do mesmo modo, usaremos

(p_i,s₋_i)

para indicar o perfil de estrat´egias mistas onde o jogadorgi escolhe

a distribui¸c˜ao de probabilidades p_i e os demais jogadores escolhem

distribui¸cões que dão peso 1 às estratégias puras ems−i.

Cada perfil de estratégias mistasp= (p₁, . . . ,p_n)_∈∆ determina umpayoffesperado (utilidade esperada), uma média dospayoffs pon-derada pelas distribui¸cões de probabilidadesp₁, . . . ,p_n. Mais preci-samente, se

p = (p₁,p₂, . . . ,p_n) = (p11, p12, . . . , p1m1

p₁

;p21, p22, . . . , p2m2

p₂

;. . .;pn1, pn2, . . . , pnmn

p_n

),

ent˜ao

ui(p) =

m1

j1=1

m2

j2=1

· · ·

mn

jn=1

p1j1·p2j2· · ·pnjn·ui(s1j1, s2j2, . . . , snjn).

(2.1)

Cuidado com o abuso de nota¸c˜ao: estamos usandouipara representar

a fun¸cão utilidade tanto em estratégias puras quanto em estratégias mistas.

Como exemplo, considere o jogo de comparar moedas na p´

agi-na 22. Se g1 escolhe a distribui¸cão de probabilidadep₁= (1/4,3/4) e g2 escolhe a distribui¸cão de probabilidade p₂ = (1/3,2/3), então os payoffs esperados associados ao perfil de estratégias mistas p = (p₁,p₂) = (1/4,3/4; 1/3,2/3) são dados por

u1(p) =

2

j1=1

2

j2=1

p1j1·p2j2·u1(s1j1, s2j2)

= p11_·p21_·u1(s11, s21) +p11_·p22_·u1(s11, s22) +

p12_·p21_·u1(s12, s21) +p12_·p22_·u1(s12, s22)

= 1

4 · 1

3·(+1) + 1 4·

2

3 ·(−1) + 3 4 ·

1

3 ·(−1) + 3 4 ·

2 3·(+1)

= +1

(37)

e, analogamente,

u2(p) =

2

j1=1

2

j2=1

p1j1·p2j2·u2(s1j1, s2j2)

= p11·p21·u2(s11, s21) +p11·p22·u2(s11, s22) +

p12_·p21_·u2(s12, s21) +p12_·p22_·u2(s12, s22)

= 1

4 · 1

3 ·(−1) + 1 4·

2

3·(+1) + 3 4 ·

1

3 ·(+1) + 3 4 ·

2 3 ·(−1) = −1₆.

Observac¸˜ao. Sep∗_{= (}_p∗

i,p∗−i)∈∆, ent˜ao a fun¸c˜aox→ui(x,p∗−i)

preserva combina¸c˜oes convexas. Mais precisamente, se x1, . . . ,xr ∈

∆mi eλ1, . . . , λrs˜ao escalares n˜ao-negativos com

r

k=1λk = 1, ent˜ao

ui

_r

k=1

λk_·xk,p∗−i

=

r

k=1

λk_·ui(xk,p∗−i). (2.2)

Em particular, se

p∗_i = (p∗

i1, . . . , p∗imi) = mi

k=1 p∗

ik·ek, (2.3)

comek o k-ésimo vetor da base canônica deRmi, então

ui(p∗_{) =}_ui₍_p∗

i,p∗−i) =ui

_m_i

k=1 p∗

ik·ek,p∗−i

= mi k=1 p∗

ik·ui(ek,p∗−i).

(2.4)

2.4 Solu¸

c˜

oes de um jogo em estrat´

egias

mistas

(38)

2.4.1 Dominˆ

ancia em estrat´

egias mistas

Defini¸cão 2.7 (Estratégia Mista Estritamente Domi-nada) Dizemos que uma estratégia mista p_i _∈ ∆mi do

joga-dorgi ∈G´e estritamente dominada pela estrat´egia p′_i _∈∆mi

se,independentemente das escolhas de distribui¸c˜oes de

proba-bilidade dos demais jogadores, o jogador gi ganha mais

esco-lhendop′

ido quepi, isto ´e, se

ui(p′_i,p₋_i)> ui(p_i,p₋_i),

para todop₋_i_∈∆−i= ∆m1×· · ·×∆mi−1×∆mi+1×· · ·×∆mn.

Como ospayoffs ui(p′_i,p₋_i) eui(p_i,p₋_i) são, respectivamente, combina¸cões convexas dos payoffs ui(p′_i,s−i) e ui(pi,s−i),

segue-se que a condi¸c˜ao acima ´e equivalente a

ui(p′_i,s−i)> ui(pi,s−i),

para todos perfis de estrat´egias purass−i∈S−i.

Exemplo 2.8 ([30], p´agina 21) Considere o jogo com a seguinte

matriz depayoﬀs:

g2

s21 s22

g1

s11 (5,3) (0,0)

s12 (0,0) (5,3)

s13 (2,1) (2,1) .

(39)

dominada pela estrat´egia mistap′₁= (1/2,1/2,0)_∈∆3, pois

u1(p′₁,p₂) =u1

1 2,

1

2,0;p21, p22

= 5

2 ·p21+ 5 2 ·p22=

5 2

>

u1(p₁,p₂) =u1

0,0,1;p21, p22

= 2 ·p21+ 2·p22= 2

para todo p₂ = (p21, p22) _∈ ∆2. Como p1 = (0,0,1) representa

a estrat´egia pura s13 do jogador g1, este exemplo tamb´em mostra

que uma estrat´egia pura pode n˜ao ser dominada por nenhuma outra

estrat´egia puras mas, ainda sim, ser dominada por uma estrat´egia mista.

Exemplo 2.9 ([31], página 7) Uma estratégia mista que atribui probabilidade positiva para uma estratégia pura estritamente domi-nada também é estritamente domidomi-nada (Exerc´ıcio [13]). Contudo, uma estratégia mista pode ser estritamente dominada mesmo que ela atribua probabilidades positivas apenas para as estratégias puras que

n˜ao s˜ao nem mesmo fracamente dominadas. Considere, por exemplo,

o jogo com a seguinte matriz de payoﬀs:

g2

s21 s22

g1

s11 (5,3) (2,0)

s12 (2,0) (5,3)

s13 (4,1) (4,1) .

As estratégias puras s11 e s12 não são fracamente dominadas, mas

a estratégia mista p₁ = (1/2,1/2,0) é estritamente dominada pela estratégia mistap′

(40)

pois

u1(p′₁,p₂) =u1

0,0,1;p21, p22

= 4 _·p21+ 4_·p22= 4

>

u1(p₁,p₂) =u1

1 2,

1

2,0;p21, p22

= 7

2 ·p21+ 7 2 ·p22=

7 2

para todo p₂= (p21, p22)∈∆2.

A defini¸cão de dominância estrita iterada para estratégias mistas que daremos aqui segue a linha proposta pelas referências [26, 31, 74]. Abordagens alternativas podem ser encontradas em [01, 15].

Defini¸cão 2.8 (Dominância Estrita Iterada em Estra-tégias Mistas)Sejam Si(0)=Si e ∆

(0)

mi = ∆mi. Defina,

recur-sivamente,

S_i(n)=_{s_∈S_i(n−1)_| ∄p_i_∈∆(nmi−1)tal que

∀s−i∈S (n−1)

−i , ui(pi, s−i)> ui(s, s−i)}

e

∆(n)_m_i =_{p_i= (pi1, . . . , pimi)∈∆mi |

∀k= 1, . . . , mi, pik >0 somente sesik _∈S_i(n)_}.

A interse¸c˜ao

Si∞=

∞

n=0 S(n)_i

(41)

∆∞

mi={pi∈∆mi |∄p ′

i ∈∆mi

tal que _∀s−i∈S−(∞i), ui(p′i, s−i)> ui(pi, si)}

´e o conjunto de todas as estrat´egias mistas do jogador gi que

sobreviveram a t´ecnica dedominˆancia estrita iterada.

Note queS(n)

i ´e o conjunto de estrat´egias puras emS

(n−1)

i que n˜ao s˜ao

estritamente dominadas pelas estrat´egias mistas em ∆(n−1)

mi e que ∆

(n)

mi

é o conjunto de estratégias mistas que dá probabilidades positivas apenas para as estratégias puras emS(n)

i .

Defini¸cão 2.9 (Equil´ıbrio de Estratégia Estritamente Dominante)Se, no processo de dominância estrita iterada, o

conjuntoS∞₌_S∞

1 × · · · ×S∞n é unitário, isto é, se S∞₌

{s∗_},

então dizemos ques∗é umequil´ıbrio de estratégia estritamente dominante.

Como no caso de estrat´egias puras, ´e poss´ıvel mostrar que os

con-juntos S∞₌_S∞

1 × · · · ×Sn∞ e ∆∞= ∆∞m1× · · · ×∆

∞

mn n˜ao

depen-dem da ordepen-dem em que as estratégias estritamente dominadas são removidas. Não apresentaremos a demonstra¸cão deste fato aqui. O leitor interessado poderá encontrá-la (bem como as defini¸cões e

resultados sobre estrat´egias mistas fracamente dominadas) nas

re-ferˆencias [01, 15, 26, 55].

2.4.2 Equil´ıbrio de Nash em estrat´

egias mistas

(42)

p∗_{= (}_p∗

1,p∗2, . . . ,p∗n)∈∆ = ∆m1×∆m2× · · · ×∆mn

´e umequil´ıbrio de Nashse

ui(p∗_i,p∗−i)≥ui(p,p∗−i)

para todo p _∈ ∆mi, isto ´e, nenhum jogador sente motiva¸c˜ao

de trocar a sua estrat´egia mista se os demais jogadores n˜ao o fizerem.

Exemplo 2.10

(a) No dilema do prisioneiro (Exemplo 2.1), o perfil de estrat´egias mistas

p∗_{= (}_p∗

1,p∗2) = (1,0; 1,0)

´e um equil´ıbrio de Nash, pois

u1(p₁,p∗₂) =u1(p11, p12; 1,0) = 5_·p11₋10_≤

−5 =u1(1,0; 1,0) =u1(p∗₁,p∗₂) para todop₁= (p11, p12)_∈∆2 e

u2(p∗₁,p₂) =u2(1,0;p21, p22) = 5·p21−10≤

−5 =u2(1,0; 1,0) =u2(p∗₁,p∗₂)

para todo p₂ = (p21, p22) _∈ ∆2. Observe que este equil´ıbrio

corresponde ao equil´ıbrio em estrat´egias puras

s∗= (confessar, confessar).

Mostraremos mais adiante que este é oúnicoequil´ıbrio de Nash em estratégias mistas do jogo.

(b) Na batalha dos sexos (Exemplo 2.2), os equil´ıbrios de Nash em estrat´egias mistas s˜ao

(43)

Os dois primeiros perfis de estratégias mistas correspondem às estratégias puras (futebol, futebol) e (cinema, cinema),

respec-tivamente. Mostraremos mais adiante que estes s˜ao os ´unicos

equil´ıbrios de Nash em estrat´egias mistas do jogo.

(c) No Exemplo 2.3, o ´unico equil´ıbrio de Nash em estrat´egia mista

´e o ponto

(0,1,0,0; 0,1,0,0)

que corresponde ao equil´ıbrio de Nash (s12, s22) em estrat´egias puras.

(d) No jogo de comparar moedas do Exemplo 2.6, o ´unico equil´ıbrio

de Nash em estrat´egias mistas ´e o ponto

(1/2,1/2; 1/2,1/2).

Como no caso de estratégias puras, podemos caracterizar equil´ı-brios de Nash em estratégias mistas através das fun¸cões de melhor resposta. Considere um jogo com espa¸co de estratégias mistas ∆ = ∆m1× · · ·×∆mi× · · ·×∆mn. No que se segue, usaremos as seguintes

nota¸c˜oes:

∆(Si) = ∆mi e ∆(S−i) = ∆m1× · · · ×∆mi−1×∆mi+1× · · ·∆mn.

Defini¸cão 2.11 (Funções de melhor resposta em estra-tégias mistas)A fun¸cão de melhor resposta do jogadorgié a aplica¸cão

MRi: ∆(S−i)→2∆(Si)

definida por MRi(p−i) = argmaxp_i∈∆(Si)ui(pi,p−i), isto ´e,

MRi(p−i)

=

{p∗_i _∈∆(Si)_{| ∀}p_i_∈∆(Si), ui(p∗_i,p−i)≥ui(pi,p−i)},

comp−i ∈ ∆(S−i). A fun¸c˜ao de melhor resposta do jogo ´e a

aplica¸c˜ao

(44)

definida por

MR(p) = (MR1(p−1),MR2(p−2), . . . ,MRn(p−n)),

comp∈∆.

Note que, como ∆(Si) ´e um conjunto compacto n˜ao-vazio e a

fun¸c˜aop_i_→ui(p_i,p−i) ´e cont´ınua, podemos usar o teorema de

Wei-erstrass para garantir que MRi(p−i) = argmaxp_i∈∆(Si)ui(pi,p−i) ´e

um conjunto n˜ao-vazio para todop₋_i_∈∆(S−i).

A próxima proposi¸cão é uma conseqüência direta das defini¸cões de equil´ıbrio de Nash e fun¸cões de melhor resposta em estratégias mistas.

Proposi¸c˜ao 2.4 p∗_{= (}_p∗

1, . . . ,p∗i, . . . ,p∗n)∈∆ ´e um equil´ıbrio

de Nash em estrat´egias mistas se, e somente se,p∗

i ∈MRi(p∗−i)

para todoi= 1, . . . , n, isto ´e,p∗_∈_MR(_p∗_).

Exemplo 2.11 Suponha que, na batalha dos sexos (Exemplo 2.2), a mulher escolha a estratégia mistap₂= (1/2,1/2). Qual é a melhor resposta do homem a esta estratégia da mulher? Para responder a esta pergunta, observe inicialmente que

uHomem(p₁,p₂) = uHomem(p11, p12;p21, p22)

= p11·p21·uHomem(futebol,futebol) +

p11_·p22_·uHomem(futebol,cinema) +

p12_·p21_·uHomem(cinema,futebol) +

p12_·p22_·uHomem(cinema,cinema) = 10_·p11_·p21+ 5_·p12_·p22

e, portanto, uHomem(p11, p12; 1/2,1/2) = 5_·p11+ (5/2)_·p12. Desta maneira,

(45)

Segue-se que a melhor resposta do homem à estratégia mista p₂ = (1/2,1/2) da mulher é obtida resolvendo-se o seguinte problema de otimiza¸cão:

maximizar 5_·p11+ (5/2)_·p12

sujeito a p11+p12= 1,

p11_≥0,

p12_≥0,

cuja solu¸c˜ao ´e (p∗

11, p∗12) = (1,0). Sendo assim, MRHomem(1/2,1/2) =

{(1,0)}.

No caso de jogos com apenas dois jogadores, cada um com apenas duas estratégias puras, é poss´ıvel escrever as estratégias mistas de uma maneira mais simplificada:

∆2={(p,1−p)∈R2 |0≤p≤1},

isto ´e, cada elemento de ∆2pode ser identificado com um n´umero real

no intervalo [0,1]. Com isto, as fun¸c˜oes de melhor resposta podem

ser reescritas de forma a depender de apenas de um n´umero real. Por

exemplo, se o homem escolhe uma estrat´egia mista (p,1−p)∈∆2,

qual é a melhor resposta da mulher a esta estratégia do homem? Escrevendo as estratégias mistas da mulher na forma (q,1₋q)_∈∆2,

vemos que

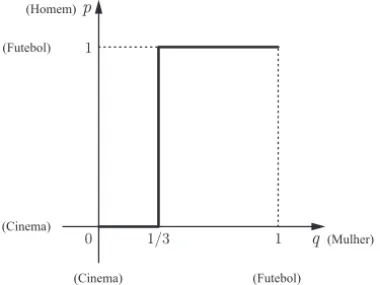
uMulher(p,1₋p;q,1₋q) = 15pq+ 10₋10q₋10p

= 5 (3p₋2)q+ 10 (1₋p).

Sendo assim,

MRMulher(p) = argmax(q,1−q)∈∆2(5 (3p−2)q+ 10 (1−p))

= argmaxq∈[0,1](5 (3p−2)q+ 10 (1−p)),

onde, por simplicidade, estamos escrevendo MRMulher(p) no lugar

de MRMulher(p,1−p). Assim, dada a escolha dep∈[0,1] do homem,

(46)

escolherq= 0. Sep= 2/3, ent˜ao 3p₋2 = 0 e, portanto, a utilidade

uMulher = 10 (1₋p) da mulher não dependerá deq. Neste caso, a mulher poderá escolher qualquer valor deqem [0,1]. Sep_∈(2/3,1], então 3p₋2>0 e, para maximizar a sua utilidade, a mulher deverá

escolherq= 1. Mostramos ent˜ao que

MRMulher(p) =

⎧ ⎨ ⎩

{0}, sep∈[0,2/3),

[0,1], sep= 2/3,

{1}, sep∈(2/3,1].

Esta fun¸c˜ao de melhor resposta pode ser representada graficamente, como mostra a Figura 2.3.

1 p(Homem) 0

1 q

2/3

(Cinema) (Cinema)

(Futebol) (Mulher)

(Futebol)

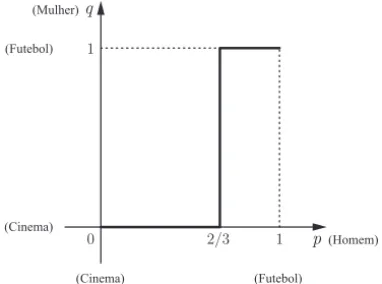
Figura 2.3: Representa¸cão gráfica da fun¸cão de melhor resposta da mulher no jogo da batalha dos sexos.

Do mesmo modo, se a mulher escolhe uma estrat´egia mista (q,1₋q)_∈ ∆2, ent˜ao

uHomem(p,1₋p;q,1₋q) = 15pq+ 5₋5q₋5p

= 5 (3q₋1)p+ 5 (1₋q),

de modo que

MRHomem(q) = argmax(p,1−p)∈∆2(5 (3q−1)p+ 5 (1−q))

(47)

Assim, dada a escolha de q _∈ [0,1] da mulher, o homem quer

en-contrar os valores de p_∈[0,1] que maximizam o valor de sua

utili-dadeuHomem= 5 (3q₋1)p+ 5 (1₋q). Seq _∈[0,1/3), ent˜ao 3q₋

1 < 0 e, para maximizar a sua utilidade, o homem dever´a

esco-lher p = 0. Se q = 1/3, ent˜ao 3q₋1 = 0 e, portanto, a utilidade

uHomem = 5 (1−q) do homem não dependerá de p. Neste caso, o homem poderá escolher qualquer valor depem [0,1]. Seq∈(1/3,1], então 3q−1>0 e, para maximizar a sua utilidade, o homem deverá

escolherp= 1. Mostramos ent˜ao que

MRHomem(q) =

⎧ ⎨ ⎩

{0_}, seq_∈[0,1/3),

[0,1], seq= 1/3,

{1_}, seq_∈(1/3,1].

Esta fun¸c˜ao de melhor resposta pode ser representada graficamente, como mostra a Figura 2.4.

1 q (Mulher) 0

1 p

1/3

(Cinema) (Cinema)

(Futebol) (Homem)

(Futebol)

Figura 2.4: Representa¸cão gráfica da fun¸cão de melhor resposta do homem no jogo da batalha dos sexos.

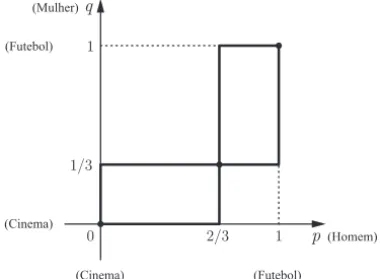
Agora, pela Proposi¸cão 2.4, segue-se que um perfil de estratégias mistas (p∗_,₁₋_p∗_;_q∗_,₁₋_q∗_{) é um equil´ıbrio de Nash se, e somente se,}

q∗_∈_MR

Mulher(p∗) e p∗ ∈MRHomem(q∗). Desta maneira, os valores

de p∗ _e _q∗ _{que geram equil´ıbrios de Nash correspondem aos pontos}

(48)

resposta da mulher e do homem, quando representadas em um mesmo sistema de eixos, como ilustra a Figura 2.5.

1 p(Homem) 0

1 q

2/3 1/3

(Cinema) (Cinema)

(Futebol) (Mulher)

(Futebol)

Figura 2.5: Calculando os equil´ıbrios de Nash usando as representa-¸cões gráficas das duas fun¸cões de melhor resposta.

Vemos, portanto, que a batalha dos sexos possui apenas 3 equil´ıbrios de Nash em estrat´egias mistas:

(0,1; 0,1), (2/3,1/3; 1/3,2/3) e (1,0; 1,0),

que correspondem, respectivamente, aos trˆes ´unicos pontos de

inter-se¸c˜ao (p∗_{, q}∗_{) = (0}_,_{0), (}_p∗_{, q}∗_{) = (2}_/₃_,₁_/_{3) e (}_p∗_{, q}∗_{) = (1}_,_{1) das}

duas representa¸c˜oes gr´aficas.

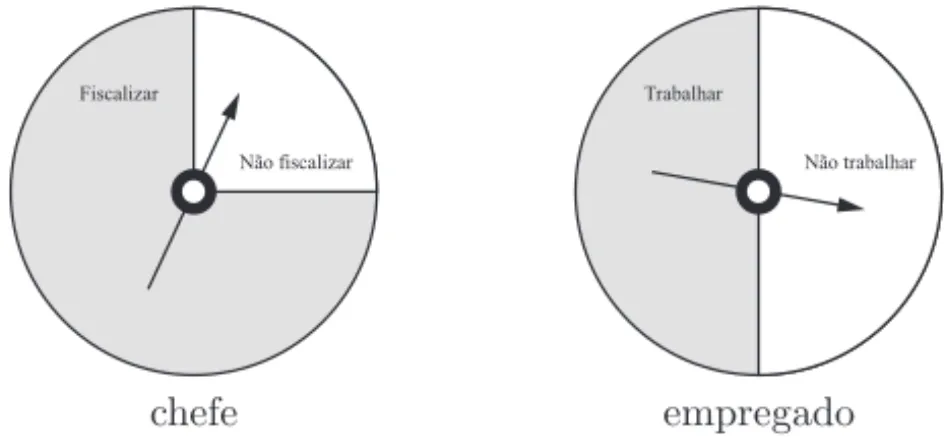
Exemplo 2.12 ([31], página 17) (O jogo da inspeção) O che-fe de uma empresa de computa¸cão desconfia que seu operador de computadores está usando o tempo de servi¸co para “bater papo”

na internet. Se o operador trabalha corretamente, ele gasta g em

esfor¸co e produz um lucro bruto de v unidades para a empresa. O

chefe, por sua vez, pode fiscalizar ou n˜ao o trabalho do operador.

Fiscalizar custahunidades para a empresa. Se o operador for pego

“batendo papo” na internet, ele perde o seu sal´ario de w unidades

(49)

que g > h > 0 e que w > g. Os dois jogadores escolhem suas estratégias simultaneamente (em particular, ao decidir se vai fiscalizar ou não, o chefe não sabe se o empregado decidiu trabalhar ou decidiu “bater papo” na internet). Neste contexto, o jogo da inspe¸cão tem a

matriz de payoﬀsindicada abaixo.

empregado

n˜ao trabalhar trabalhar

ch

ef

e fiscalizar (₋h,0) (v₋w₋h, w₋g)

n˜ao fiscalizar (−w, w) (v−w, w−g)

Observe que este jogo não possui equil´ıbrio de Nash em estratégias puras e, como ele deve se repetir em cada dia útil de trabalho, não é

sensato escolhersemprea mesma estrat´egia pura para todos os dias.

A solu¸cão, neste caso, é escolher entre as estratégias puras a cada dia seguindo uma distribui¸cão de probabilidades, isto é, através de es-tratégias mistas. Como as fun¸cões de melhor resposta do empregado e do chefe são dadas, respectivamente, por

MREmpregado(p) = argmaxq∈[0,1]((−wp+g)q+w−g)

= ⎧ ⎨ ⎩

{1_}, sep_∈[0, g/w),

[0,1], sep=g/w,

{0_}, sep_∈(g/w,1],

MRChefe (q) = argmaxp∈[0,1]((+wq−h)p+v(1−q)−w)

= ⎧ ⎨ ⎩

{0}, seq∈[0, h/w),

[0,1], seq=h/w,

{1}, seq∈(h/w,1],

segue-se que o (único) equil´ıbrio de Nash em estratégias mistas é

obtido tomando-se p∗ ₌ _g/w _e_q∗ ₌_h/w_{. Se, por exemplo,} _v _{= 5,}

w= 4,g= 3 eh= 2, ent˜ao

(p∗_,₁

−p∗_;_q∗_,₁

−q∗_{) = (3}_/₄_,₁_/_{4; 1}_/₂_,₁_/₂₎_.

Isto significa que o chefe deve escolher sua estrat´egia de acordo com

um gerador de números aleatórios com distribui¸cão de

(50)

com um gerador de números aleatórios com distribui¸cão de probabili-dade (1/2,1/2). Isto pode ser feito, por exemplo, com as duas “rodas da fortuna” da Figura 2.6.

Fiscalizar

Não fiscalizar

Trabalhar

Não trabalhar

chefe empregado

Figura 2.6: Distribui¸c˜oes de probabilidade que constituem um equil´ı-brio de Nash para o jogo do Exemplo 2.12.

A partir deste resultado, podemos calcular o valor ´otimo de contrato

do empregado, isto ´e, o valor de w que maximiza opayoﬀ esperado

do chefe:

uChefe(w) = (+wq∗−h)p∗+v(1−q∗)−w) =v

1−_wh

−w.

Se, por exemplo, √vh > g, então este valor ótimo é dado por w∗ ₌

√

vh(note queu′

Chefe(w∗) = 0 eu′′Chefe(w)≤0 paraw >0).

Jogos deste tipo tˆem sido usados para se estudar temas como controle de armas ([03, 10, 83]), preven¸c˜ao de crimes ([04]) e incentivos no trabalho ([53]).

(51)

que garante a existˆencia de equil´ıbrios em estrat´egias mistas para jogos finitos.

2.4.3 Rela¸

c˜

oes entre dominˆ

ancia e equil´ıbrio de

Nash

As Proposi¸cões 2.2 e 2.3 para estratégias puras continuam válidas para estratégias mistas: (1) o processo de dominância estrita ite-rada em estratégias mistas não pode eliminar um equil´ıbrio de Nash e (2) se o processo de dominância estrita iterada em estratégias mistas deixa apenas um único perfil de estratégias, então este perfil é um

equil´ıbrio de Nash do jogo. N˜ao apresentaremos as demonstra¸c˜oes

destes resultados aqui. O leitor interessado poderá encontrá-las nas referências [15, 26].

2.4.4 Como interpretar estrat´

egias mistas?

Existe muita controvérsia sobre as interpreta¸cões e usos de es-tratégias mistas ([02, 12, 17, 57, 74, 77, 81, 73, 92, 93]). Aumann, por exemplo, em [02], afirma que

“Mixed strategy equilibria have always been intuitively problematic because they are not ‘strict’: a player will not lose if he abandons the randomization and uses instead any arbitrary one of the pure strategy components of the randomization.”

(veja as Equa¸c˜oes 4.1 na p´agina 81) e, segundo Rardner e

Roshen-tal ([76]),

“One of the reasons why game-theoretic ideas have not found more widespread application is that randomization, which plays a major role in game theory, seems to have limited appeal in many practical situations.”

Ainda, segundo Rubinstein ([81]),

(52)

the game, goes against our intuition. We are reluctant to believe that our decisions are made at random. We prefer to be able to point to a reason for each action we take. Outside of Las Vegas we do not spin roulettes.”

De fato, testes experimentais recentes mostraram que jogadores não seguem a estratégia mista prevista pela teoria, mesmo quando o jogo possui um único equil´ıbrio de Nash em estratégias mistas ([57]).

Existem também certas análises feitas com estratégias mistas que

produzem resultados n˜ao-intuitivos. Considere, por exemplo, a

se-guinte situa¸cão. Um contribuinteCdeve decidir se vai ou não sonegar imposto, sabendo que existe um fiscalF que pode ou não fiscalizá-lo.

Na matriz de payoﬀs abaixo, vamos assumir que valem as seguintes

desigualdades

(1) c21> c11: o contribuinteC prefere n˜ao sonegar se souber que o fiscalF ir´a fiscalizar,

(2) c12> c22: o contribuinteC prefere sonegar se souber que o fis-calF n˜ao ir´a fiscalizar,

(3) f11> f12: o fiscalF prefere fiscalizar se souber que o contribuin-teC ir´a sonegar e

(4) f22> f21: o fiscalF prefere não fiscalizar se souber que o contri-buinteC não irá sonegar.

Você pode pensar que oscij são números negativos que representam

o quanto ser´a debitado deCpelo pagamento de imposto e que osfij

são números positivos que representam bônus salariais de F.