II
Agradecimentos
Finda a etapa final do meu percurso académico e concluído o maior projeto da minha vida, compete-me apresentar os mais sinceros agradecimentos a todos os que me rodeiam que me ajudaram e deram força para seguir sempre em frente.
À minha professora orientadora Maria Helena Martinho, pelo apoio e encorajamento constantes que foram seguramente necessários ao longo de todo este processo.
A todos os alunos das turmas com que estagiei, que ocuparão sempre um lugar no meu coração como os primeiros alunos com que trabalhei.
Às professoras cooperantes, pela sua disponibilidade para me receber a “invadir” as suas aulas e pelas aprendizagens que a observação do seu trabalho me proporcionaram.
Aos meus pais, por nunca terem deixado de acreditar em mim, apesar de todos os desvios que o meu caminho sofreu.
À sara, a pessoa que esteve sempre ao meu lado durante todo este percurso e me deu todo o apoio. Sem ela, isto nunca seria possível.
III
DECLARAÇÃO DE INTEGRIDADE
Declaro ter atuado com integridade na elaboração do presente trabalho académico e confirmo que não recorri à prática de plágio nem a qualquer forma de utilização indevida ou falsificação de informações ou resultados em nenhuma das etapas conducente à sua elaboração.
IV Explorando a relação entre o Hex e a Resolução de Problemas:
Uma experiência com alunos do 1.º e 2.º ciclos do Ensino Básico
Resumo
Este relatório de estágio foi realizado no âmbito de um projeto de intervenção pedagógica supervisionada, do Mestrado em Ensino do 1.º ciclo e de Matemática e Ciências no 2.º ciclo do Ensino Básico. Este projeto foi desenvolvido ao longo de um ano letivo com duas turmas, sendo que se trabalhou com uma turma no primeiro semestre e outra no segundo. A primeira turma observada em contexto de estágio foi uma turma do 2.º ano do 1.º ciclo e a segunda turma foi uma turma do 6.º ano do 2.º ciclo do ensino básico.
Ao longo do trabalho pretende-se compreender melhor de que forma o jogo matemático (neste caso, o Hex) se relaciona com a capacidade de resolução de problemas dos alunos e com as suas classificações escolares a Matemática. Para isso, estabeleceram-se as seguintes questões de investigação: Q1 - A capacidade de jogar jogos Matemáticos está relacionada com a capacidade de resolver problemas? Q2 - A capacidade de jogar jogos Matemáticos está relacionada com a classificações escolares a Matemática?
Para responder às questões de investigação propostas foi então planeada uma investigação quantitativa de carácter exploratório que pretende estudar as correlações entre as diferentes variáveis estudadas, tendo sido utilizados essencialmente como instrumentos de recolha de dados grelhas de registo, testes e a observação. O tratamento estatístico correlacional variou consoante as propriedades das variáveis estudadas, tendo sido utilizadas as fórmulas de Pearson e Spearman.
No geral, esta investigação permitiu compreender que existem relações entre o jogo matemático e a capacidade de resolução de problemas e entre o jogo matemático e as classificações escolares a Matemática, sendo essa relação caracterizada por uma correlação de força moderada. Para compreender melhor a natureza dessa relação seria necessária a realização de estudos adicionais sobre os temas abordados.
V Exploring the relationship between Hex and Problem Solving:
An experience with elementary and junior high school students
Abstract
This report was developed in the course unit Supervised pedagogical intervention project, of the Master in 1st cycle and Mathematics and Science in the 2nd cycle of Basic Education teaching. This project was developed over a school year with two classes, with one class being worked in the first semester and another in the second. The first class observed in the apprenticeship context was a 2nd grade of the 1st cycle and the second class was a 6th grade of the 2nd cycle of basic education.
Throughout the paper I intend to better understand how the mathematical game (in this case, the Hex) relates to the problem solving ability of students and their school classifications in mathematics. To this end, the following research questions were established: Q1 - Is the ability to play Mathematical games related to the ability to solve problems? Q2 - Is the ability to play math games related to math school grades?
In order to answer the proposed research questions, an exploratory quantitative research was then planned to study the correlations between the different variables studied, having been essentially used grids, tests and observation as data collection tools. The correlational statistical treatment varied according to the properties of the studied variables, using Pearson and Spearman formulas.
In general, this investigation allowed us to understand that there are relations between mathematical game and problem solving ability and between mathematical game and school classifications and mathematics, and this relationship is characterized by a moderate strength correlation. To better understand the nature of this relationship would require further studies on the topics addressed.
VI Índice
Capítulo 1 - Introdução ... 1
1.1 Contextualização e pertinência do tema ... 1
1.2 Objetivos e questões de investigação ... 3
1.3 Organização do relatório ... 4
Capítulo 2 – Fundamentação Teórica ... 5
2.1 Resolução de problemas ... 5
2.1.3 A importância do domínio da resolução de problemas no ensino da Matemática ... 5
2.1.1 O que é um problema? ... 6
2.1.2 Resolução de problemas ... 8
2.1.3 Tipologia de problemas ... 8
2.1.4 Modelos e estratégias de resolução de problemas ... 10
2.1.5 A resolução de problemas na sala de aula... 12
2.2 Os jogos ... 13
2.2.1 A definição de jogo ... 14
2.2.2 Tipologia de jogos ... 15
2.2.3 O papel do jogo na educação matemática ... 16
2.2.5 Os jogos matemáticos na sala de aula ... 19
2.2.6 Os jogos matemáticos e a resolução de problemas ... 19
2.2.7 HEX ... 20
Capítulo 3 – Opções Metodológicas ... 22
3.1 Participantes ... 22
3.1.1 Caracterização da turma do 2º ano de escolaridade ... 23
3.1.2 Caracterização da turma do 6º ano de escolaridade ... 23
3.2 Opções metodológicas ... 24
3.2.1 Correlação entre a capacidade de jogar Hex e a capacidade de resolução de problemas ... 24
VII
3.2.1 Análise dos valores e significância das correlações obtidas ... 25
3.3 Instrumentos de recolha de dados ... 26
3.3.1 Variável - Capacidade de resolução de problemas: ... 27
3.3.1 Variável - Capacidade de jogar Hex:... 29
3.3.2 Variável – Classificações de Matemática ... 29
Capítulo 4 – Plano geral e desenvolvimento das intervenções pedagógicas ... 30
1.º Ciclo – Turma do 2.º ano do 1.º ciclo ... 30
1.ª Intervenção ... 30
2.ª Intervenção ... 31
3.ª Intervenção ... 32
4.ª Intervenção ... 33
2.º Ciclo - Turma do 6.º ano do 2.º ciclo (Escola EB23 Dr. Francisco Sanches) ... 34
1.ª Intervenção ... 35
2.ª Intervenção ... 36
3.ª Intervenção ... 36
Capítulo 5 – Apresentação e discussão dos dados ... 39
5.1 Procedimentos para o tratamento dos dados ... 39
5.2 Descrição dos dados ... 41
5.2.1 Turma do 2.º ano do 1.º ciclo do ensino básico ... 41
5.2.1 Turma do 6.º ano do 2.º ciclo do ensino básico ... 46
5.3 Análise correlacional ... 50
5.3.1 Turma do 2.º ano do 1.º ciclo ... 50
5.3.2 Turma do 6.º ano do 2.º ciclo ... 53
Capítulo 6 - Conclusões ... 57
6.1 Correlação entre a capacidade de jogar Hex e a resolução de problemas ... 57
VIII
6.3 Discussão dos resultados e respetiva validade ... 58
6.2 Limitações da investigação ... 60
6.3 Considerações acerca da experiência de estágio ... 60
6.2 Visão pessoal do lugar do jogo na educação ... 61
Referências bibliográficas ... 63
Anexos ... 65
Anexo I: Ficha de problemas da atividade introdutória ao projeto na turma do 2.º ano ... 67
Anexo II: Exemplos de slides da apresentação criada para a atividade de construção do tabuleiro. . 68
Anexo III: Tabuleiros de Hex (para imprimir) utilizados nas atividades de jogo ... 69
Anexo IV: Enunciado do problema introdutório realizado com alunos do 6.º ano ... 70
Anexo V: Grelhas de registo para as recolhas de dados (exemplos) relativos à capacidade de resolução de problemas e capacidade de jogar Hex: ... 71
Índice de tabelas
Tabela 1 – Comparação de Palhares (2004) de dois modelos pedagógicos ... 17Tabela 2 – Planeamento das atividades do projeto de intervenção pedagógica com a turma do 2.º ano ... 30
Tabela 3 - Planeamento das atividades do projeto de intervenção pedagógica com a turma do 6.º ano ... 34
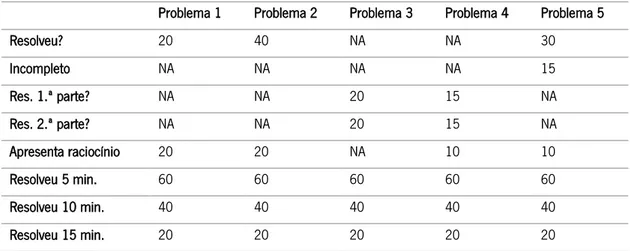
Tabela 4 - Grelha de pontuação dos problemas da turma do 2.º ano do 1.º ciclo ... 40
Tabela 5 - Grelha de pontuação dos problemas da turma do 6.º ano do 2.º ciclo ... 40
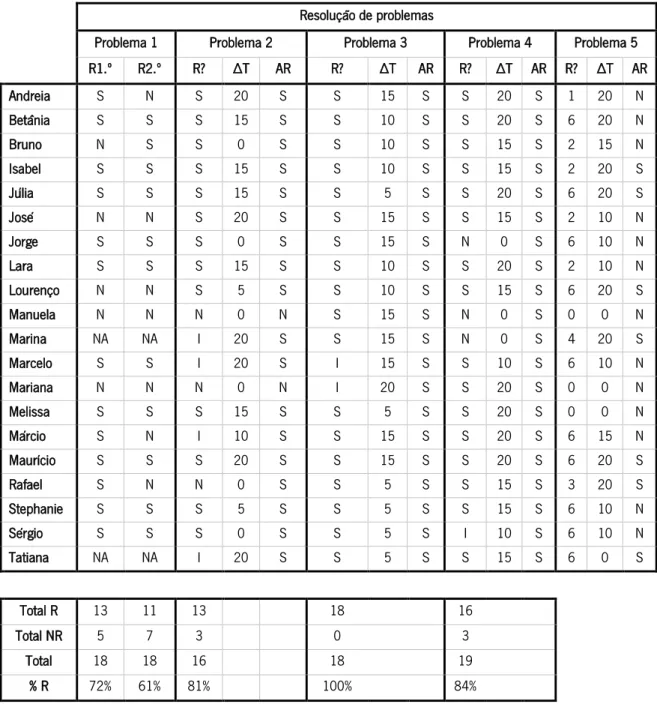
Tabela 6 – Registo das correções dos problemas da turma do 2.º ano ... 41
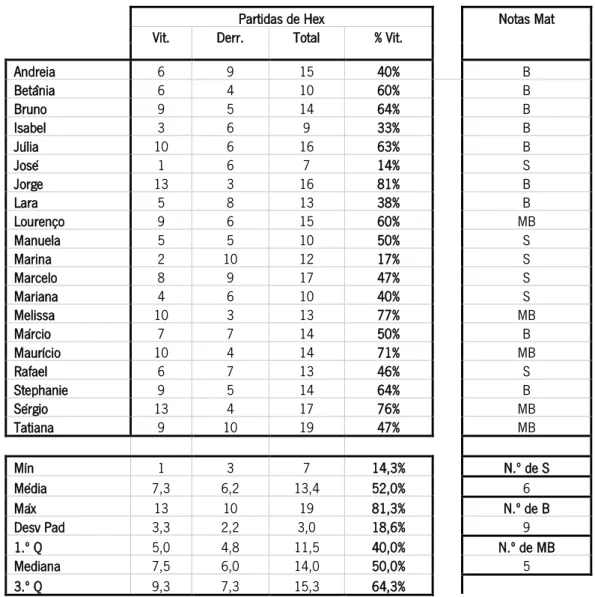
Tabela 7 – Registo das correções dos dados das partidas de Hex e classificações de Matemática da turma do 2.º ano ... 43
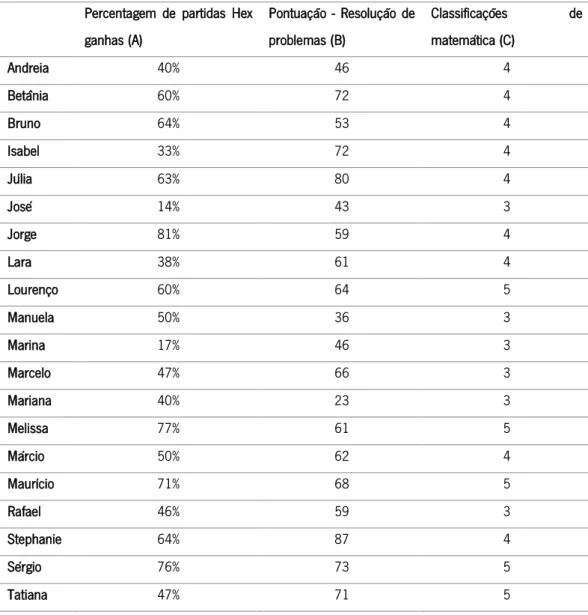
Tabela 8 – Tabela final com os dados para tratamento correlacional da turma do 2.º ano ... 44
Tabela 9 – Tratamento estatístico dos dados da resolução de problemas na turma do 2.º ano... 45
Tabela 10 – Registo das correções dos problemas da turma do 6.º ano ... 46
Tabela 11 – Registo das correções dos dados das partidas de Hex e classificações de Matemática da turma do 6.º ano ... 47
IX
Tabela 13 – Tratamento estatístico dos dados da resolução de problemas na turma do 2.º ano ... 49
Tabela 14 - Passos dados no cálculo da correlação de Pearson entre a Capacidade de jogar Hex e a Capacidade de resolver problemas (AxB) na turma do 2.º ano do primeiro ciclo. ... 51
Tabela 15 – Folha de cálculo para determinação do coeficiente de correlação de Spearman entre a capacidade de jogar e as classificações escolares a Matemática da turma do 2.º ano. ... 52
Tabela 16 - Passos dados no cálculo da correlação de Pearson entre a Capacidade de jogar Hex e a Capacidade de resolver problemas (AxB) na turma do 6.º ano. ... 54
Tabela 17 – Folha de cálculo para determinação do coeficiente de correlação de Spearman entre a capacidade de jogar e as classificações escolares a Matemática da turma do 6.º ano. ... 56
Índice de figuras
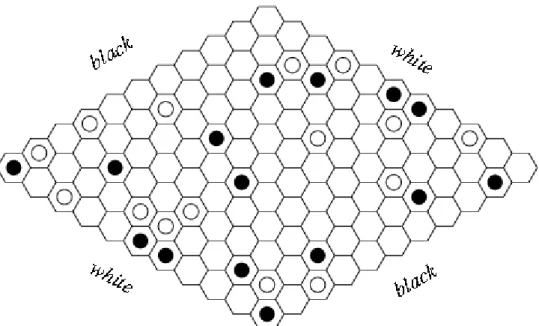
Figura 1 – Exemplo de tabuleiro de Hex (retirado de: http://mathworld.wolfram.com/GameofHex.html) ... 21Figura 2 – Enunciado de quadrado mágico ... 28
Figura 3 - Enunciado de 2.º problema (turma 2.º ciclo) ... 28
Figura 4 - Enunciado de 3.º problema (turma 2.º ciclo) ... 28
Figura 5 - Enunciado de 4.º problema (turma 2.º ciclo) ... 28
Figura 6 - Alunos do primeiro ciclo a construir e a decorar o seu tabuleiro ... 33
Figura 7 - Diagrama de dispersão das variáveis capacidade de jogar Hex e capacidade de resolução de problemas na turma do 1.º ciclo ... 50
Figura 8 - Diagrama de dispersão das variáveis capacidade de jogar Hex e classificações escolares a Matemática na turma do 1.º ciclo ... 52
Figura 9 - Diagrama de dispersão das variáveis capacidade de jogar Hex e capacidade de resolução de problemas na turma do 2.º ciclo ... 53
Figura 10 - Diagrama de dispersão das variáveis capacidade de jogar Hex e capacidade de resolução de problemas na turma do 2.º ciclo ... 55
1
Capítulo 1
Introdução
“A investigação em Pedagogia tem por objetivo promover a educação ajudando-a na realização do seu fim, que é o desenvolvimento holístico da pessoa” (Sousa, 2005, p. 29) O presente relatório de estágio, intitulado “Explorando a relação entre o Hex e a Resolução de Problemas: Uma experiência com alunos dos 1.º e 2.º ciclos do Ensino Básico” insere-se no âmbito da Unidade Curricular de Prática de Ensino Supervisionada do 2.º ano do Mestrado em Ensino do 1.º ciclo do ensino básico e de matemática e ciências naturais no 2.º ciclo do Ensino Básico, e consiste na documentação e interpretação do material recolhido no âmbito do projeto de investigação que realizei ao longo do estágio que decorreu no ano letivo de 2018/2019 com duas turmas do 1.º e 2.º ciclo do Ensino Básico. O objetivo desta investigação foi compreender de que forma a capacidade dos alunos no domínio matemático da resolução de problemas se relaciona com a sua capacidade de jogar jogos matemáticos. Nesta introdução começarei por contextualizar e justificar a pertinência do tema do projeto de intervenção, clarificando os motivos que levaram à sua escolha. De seguida serão enunciados os objetivos e questões de investigação que orientaram o decorrer do projeto. Este primeiro capítulo será terminado com a apresentação da estrutura do relatório.
1.1 Contextualização e pertinência do tema
O ensino da Matemática nos primeiros ciclos de aprendizagem é um processo que atualmente parece caracterizar-se por uma série de desafios relacionados com a motivação para aprender e o gosto pelo domínio da Matemática em si. Se refletirmos acerca do progresso que as crianças vivem até à entrada na escola, é fácil perceber que o processo de transição das dinâmicas dos jogos e brincadeiras típicos da idade pré-escolar para o ambiente de rigor e formalismo associado às tarefas escolares possa criar um clima de desinteresse. Podemos somar a este fator também o típico carácter abstrato da Matemática, tanto que o Programa de Matemática do Ensino Básico (DGE, 2013) recomenda que o ensino desta ciência deva ser feito de forma gradual, passando do concreto ao abstrato, “respeitando os tempos próprios dos alunos e promovendo assim o gosto por esta ciência e pelo rigor que lhe é característico” (p. 1). Para além disso, segundo Bianchini, Gerhardt e Dullius (2010) vivemos numa época em que os avanços da tecnologia e os recursos que esta proporciona à juventude são abundantes. Segundo as autoras, “grande parte da população convive constantemente em ambientes repletos de equipamentos sofisticados e com inúmeras funções, sendo estas muito estimuladoras” (p. 2).
2 É, portanto, natural que numa escola que priorize os recursos e as tarefas tradicionais em detrimento de outros recursos mais atrativos, o ambiente de ensino possa ser desmotivador e leve ao fracasso na aprendizagem da Matemática por parte de muitos alunos que possam apresentar até capacidades suficientes para tal. Devido aos atuais níveis pouco satisfatórios de literacia matemática refletidos pelos resultados das provas de aferição e exames nacionais, Mendes e Mamede (2012) alertam para a importância de se repensar o processo de ensino-aprendizagem da matemática, referindo que a “troca do lúdico como principal instrumento de trabalho por práticas transmissivas e demasiado restritivas facilmente resulta numa desmotivação por parte do aluno” (p. 107).
É como uma forma de contornar esta dificuldade no ensino da Matemática que surge como proposta de solução a atividade lúdica em sala de aula, mais especificamente o jogo matemático. De acordo com Silva e Santos (2011), os jogos revelam-se como uma das atividades mais cativantes para os jovens, sendo que “nenhuma outra atividade pode proporcionar o prazer de pensar de uma forma tão evidente, para além da Matemática” (p. 303).
A investigação reportada neste relatório foi realizada, conforme já referido, em contexto de estágio. Aquando do início do mesmo foi-me solicitado que definisse uma problemática de investigação a partir da minha experiência de observação inicial do primeiro grupo observado, sendo que seria importante que o processo de realização desta investigação trouxesse contributos positivos do ponto de vista pedagógico para a turma. Após algumas semanas de observação verifiquei que a prática de atividades lúdicas em tempo letivo era bastante pontual e que os alunos mostraram sempre bastante recetividade e envolvimento em situações que envolvessem o jogo, dentro e fora da sala de aula. A título de exemplo posso referir uma aula em que o jogo do “par-ou-ímpar?” foi usado como forma de explicar os números pares (e ímpares) e um intervalo de aula em que joguei UNO com um grupo de alunos no recreio. O entusiasmo que os alunos apresentaram foi claramente visível.
É também pertinente referir que Ferreira, Palhares e Silva (2013) sugerem que “quando se inicia um estudo, as razões a ele subjacentes podem ser de natureza diversificada, devendo o gosto pela temática a investigar ser uma das principais” (p. 75)
Desta forma, a escolha do jogo matemático como parte integrante da problemática desta investigação prendeu-se com os seguintes motivos:
• Necessidade de se alterar o paradigma escolar atual de forma a promover o interesse e envolvimento dos alunos nas atividades escolares, especialmente no domínio da matemática; • Frequência pontual de atividades lúdicas ou relacionadas com jogo na turma observada e forte
3 • Paixão pessoal pela temática dos jogos de estratégia;
Durante uma partida de um jogo de estratégia, estamos concentrados num processo que pode ser comparável à resolução de um problema, observando a cada instante as jogadas do nosso adversário e tentando compreender qual a melhor jogada para nos colocarmos em vantagem ou até vencer. É possível que a prática e a experiência de jogos diferentes com sistemas de regras diversificados tenha contributos no desenvolvimento de capacidades cognitivas utilizadas no processo de resolução de problemas. Através de investigações conduzidas já foi possível estabelecer relações entre a prática de jogos de estratégia em contexto escolar e certas capacidades cognitivas essenciais para a aprendizagem da matemática, como é o caso da identificação de padrões (Ferreira, Palhares & Silva, 2013).
Parece haver um consenso geral entre os investigadores acerca da existência de uma relação entre a prática de jogos e o desenvolvimento do raciocínio e da capacidade de resolução de problemas, facto que levou à escolha desta dimensão como um complemento à temática principal.
1.2 Objetivos e questões de investigação
Sousa (2005) refere que “o problema é o objetivo da investigação, a meta que se pretende atingir, a pergunta científica para a qual procuramos resposta” (p. 44). Este autor refere ainda que as hipóteses se estabelecem em função do problema (sendo este o ponto de partida da investigação), aconselhando modéstia, lucidez e prudência na sua definição.
Não pretendi com esta investigação averiguar de uma forma direta se a prática de jogos matemáticos desenvolve competências e capacidades cognitivas no domínio da resolução de problemas, mas sim compreender melhor de que forma o jogo matemático (ou de estratégia) e a capacidade de resolução de problemas se relacionam e se esta relação pode ter carácter preditivo. Assim, o principal objetivo desta investigação (a sua problemática) prende-se com a busca de uma relação entre a capacidade de jogar o jogo Hex e a capacidade de resolver problemas matemáticos em duas turmas do 1.º e 2.º ciclos do ensino básico do agrupamento escolar Francisco Sanches, tentando compreender se há existência de relação correlacional positiva entre a capacidade de resolver problemas nas turmas em que a ocorreu a intervenção pedagógica supervisionada. Aproveito também para estabelecer uma comparação o jogo e a Matemática em geral, estudando a relação entre a capacidade de jogar e as classificações obtidas a Matemática dos alunos das turmas observadas.
A partir dos objetivos delineados surgiram então as seguintes questões de investigação:
1. A capacidade de jogar jogos Matemáticos está relacionada com a capacidade de resolver problemas?
4 2. A capacidade de jogar jogos matemáticos está relacionada com as classificações escolares de
Matemática?
Para responder às questões apresentadas, foi planeada uma investigação quantitativa de carácter exploratório que visa apurar a existência das relações mencionadas.
1.3 Organização do relatório
A organização do relatório para esta investigação é inspirada no modelo proposto por Sousa (2005), estando organizado em x capítulos.
No primeiro capítulo foi feita a introdução do estudo, acompanhada de uma exposição dos motivos que levaram à escolha do tema e a sua pertinência. Este capítulo termina com a identificação dos objetivos e das questões que orientaram a investigação.
No capítulo 2 farei uma revisão da bibliografia em que será apresentada uma síntese das ideias dos autores consultados para a condução desta investigação e construção do relatório. Farei uma exposição dos conceitos associados ao jogo matemático e ao domínio da resolução de problemas e mencionarei pesquisas já realizadas com temas relacionados com os abordados nesta investigação.
No terceiro capítulo farei a apresentação das metodologias utilizadas na recolha e tratamento dos dados e dos fatores que justificaram a sua seleção. Farei também a caracterização da amostra de participantes na investigação.
No quarto capítulo apresentarei uma descrição das atividades que foram realizadas com as duas turmas do 1.º e 2.º ciclos do ensino básico em contexto de estágio e no âmbito do projeto de intervenção pedagógica supervisionada. Serão apresentados os objetivos das atividades e uma narrativa dos acontecimentos durante as atividades.
O quinto capítulo consiste na apresentação e tratamento dos dados e apresentação dos resultados da investigação. Os diferentes passos realizados no tratamento estatístico serão sucintamente descritos.
No sexto capítulo serão apresentadas as conclusões da investigação, acompanhadas de uma discussão dos resultados obtidos, da eficácia dos instrumentos de recolha escolhidos e das limitações da investigação. Será feita também uma reflexão final acerca dos contributos que a experiência de estágio me ofereceu. Terminarei com a apresentação da minha visão pessoal do papel do jogo na educação.
5
Capítulo 2
Enquadramento teórico
2.1 Resolução de problemas
Segundo Vale e Pimentel (2004) “resolver problemas faz parte da natureza humana” (p.8). De facto, se refletirmos acerca dos avanços da ciência e tecnologia que ocorreram ao longo da história de toda a humanidade, é certo que todo o conforto de que dispomos atualmente nas mais diversas áreas foi produto de um longo processo de contínua resolução de problemas nas mais diversas áreas de conhecimento.
A resolução de problemas teve, obviamente que se estender ao domínio da educação, com especial incidência na Matemática, como é natural. Vale e Pimentel (2004) sugerem que se iniciou uma chamada “era da resolução de problemas” (p. 8) no universo educativo em 1989 a partir de uma recomendação feita pela Organização de Professores de Matemática dos Estados Unidos da América (NCTM) que afirmava que “o foco do ensino da matemática escolar deve ser a resolução de problemas. De facto, Boavida (1993) refere que na atualidade o “desenvolvimento do raciocínio e do pensamento superior flexível (p. 14)” proporcionados pela resolução de problemas no ensino e na educação já não é uma prioridade exclusiva das escolas de elites, mas de todos. Assim, é possível afirmar que assistimos atualmente a um processo gradual de democratização do ensino.
2.1.3 A importância do domínio da resolução de problemas no ensino da Matemática
As rápidas transformações que a sociedade moderna enfrenta nesta era atual levam a constantes e sucessivas desatualizações de informação que fazem com que, para Boavida (1993), seja “difícil prever, com certeza, quais as habilitações necessárias à formação dos jovens no futuro” (p. 13). A criação de um currículo escolar apropriado às novas gerações da atualidade deve, portanto, contemplar, mais do que conhecimentos e conteúdos, competências e capacidades. Deve centrar-se na educação e formação de um indivíduo que “possua um pensamento crítico e desenvolva capacidades de aprender por si próprio, de comunicar com outros seres humanos e de resolver problemas individualmente ou em cooperação” (Húsen, 1989, citado por Boavida, 1993, p. 13). Assim, é atualmente um facto adquirido que é papel da escola proporcionar oportunidades aos alunos para o desenvolvimento da capacidade de resolver problemas de “forma flexível, crítica, criativa e eficaz”, sendo estas entendidas como “capacidades essenciais ao homem de hoje e do futuro” (ibidem, p. 92).
Porque resolver problemas é uma atividade que nos acompanha quase desde o nosso nascimento, sendo inerente à condição humana, Krulik e Rudnick (1993) defendem que é
6 responsabilidade do professor dos primeiros ciclos de ensino iniciar o ensino da capacidade de resolver problemas e que este domínio se deve manter prevalente ao longo de todo o percurso escolar, estabelecendo assim as bases que permitirão ao aluno lidar com eficácia e resolver com sucesso os problemas que lhe surgirão no futuro. Boavida (1993) salienta a importância de nas escolas os alunos se depararem com situações em que tenham a oportunidade de refletir e reorganizar as suas formas de pensar. Vale e Pimentel (2004) referem também que a importância da resolução de problemas não se resume à aquisição de estratégias de uso da Matemática no quotidiano, contribuindo também para o desenvolvimento de “processos e capacidades de pensamento” que são essenciais para a realização de tarefas de pensamento complexas, como “analisar, interpretar, criticar ou escolher” (p. 10).
2.1.1 O que é um problema?
Antes de discutir ou clarificar o conceito “resolução de problemas”, importa definir primeiro o que é um problema do ponto de vista da Matemática, uma vez que o conceito de problema pode ser bastante diversificado e varia consoante o contexto. Se numa conversa informal com um amigo ou um familiar este nos “desabafar” que está com um problema, é fácil deduzir que se refere a uma situação relacionada com a sua vida ou de alguém próximo e que lhe está a criar desconforto ou dificuldades. Se ouvirmos determinado indivíduo que se encontre na gerência ou direção de um estabelecimento ou empresa queixar-se de que tem um colaborador bastante problemático, intuitivamente perceberemos que provavelmente se trata de uma pessoa conflituosa ou pouco profissional com a qual é difícil trabalhar. Uma breve análise de senso comum leva-nos a crer que o conceito de problema está intimamente relacionado com o conceito de dificuldade. Esta noção estende-se também à noção de problema matemático, naturalmente.
O conceito de problema matemático foi definido de diferentes formas por uma série de autores e investigadores que se debruçaram sobre o tema: segundo Kantowski (1974, citado por Vale e Pimentel, 2004) “um indivíduo está perante um problema quando se confronta com uma questão a que não pode dar resposta ou uma situação que não sabe resolver, usando o conhecimento imediatamente disponível” (p. 13); Para Polya, (1980), “ter um problema significa procurar conscienciosamente alguma ação apropriada para atingir um objetivo claramente definido, mas não imediatamente atingível” (ibidem, p. 13). Mayer (1985) afirma que “um problema ocorre quando se é confrontado com uma situação inicial e se pretende chegar a outra situação final, sem se conhecer um caminho óbvio para a atingir” (ibidem, p. 13). Krulik e Rudnick (1993) já incluem na sua definição a possibilidade de resolução de um problema de forma coletiva, referindo que um problema é uma situação, quantitativa ou outra, que confronta um
7 indivíduo ou grupo de indivíduos, que requer resolução e para a qual não é conhecido nenhum caminho para chegar à sua resolução.
É evidente que quando se reflete acerca de um problema matemático do ponto de vista pedagógico, para que não sejam feitas confusões surge naturalmente a necessidade de fazer a distinção entre um problema e outros tipos de tarefas escolares, como exercícios. Kantowski (1980, citado por Lopes, 2001) distingue um problema de um exercício, afirmando que “o problema difere de um exercício pelo facto de o aluno não dispor de um procedimento ou algoritmo que conduzirá com certeza a uma solução” (p. 10). Vale e Pimentel (2004) corroboram esta ideia, dizendo que “só se tem um problema se não se sabe como chegar até à solução, pois, se uma questão não tem surpresas e pode ser resolvida confortavelmente utilizando procedimentos rotineiros e familiares, não interessando quão complicados sejam, é um exercício”. Krulik e Rudnick (1993) fazem esta mesma distinção, adicionando ainda uma terceira categoria. As três categorias, segundo estes autores, são: a questão, que pode ser respondida pelo aluno pelo simples apelo à sua memória; o exercício, que consiste na prática e reforço de algoritmos e processos já aprendidos pelo aluno; e o problema, que requer pensamento e síntese do conhecimento já aprendido para a sua resolução.
A discussão destas categorias é de alguma importância do ponto de vista pedagógico, pois na realidade docente parece nem sempre haver consenso no que diz respeito às distinções entre questão, exercício e problema. O resultado disto é a possibilidade de haver professores que trabalham com os seus alunos a prática de meros exercícios, convencidos que estão a trabalhar processos mentais de ordem superior que na realidade só a legítima resolução de problemas pode oferecer. Assim, em síntese, apesar das distintas definições apresentadas por diferentes autores, a chave para a definição do que é um problema reside desconhecimento do caminho necessário para chegar à resolução (Krulik & Rudnick, 1993).
É também pertinente mencionar os fatores interesse e motivação quando se fala em problemas, uma vez que estes poderão ser condicionantes do sucesso do aluno. Para Lester (1983, citado por Vale & Pimentel, 2004), por exemplo, uma “situação não pode ser considerada um problema se a realização da tarefa não for desejada pelo indivíduo” (p. 13). É, portanto, necessário que o problema seja aliciante e tenha o nível de dificuldade e desafio adequado ao aluno ou grupo a que é proposto, pois sendo demasiado fácil ou demasiado difícil, o interesse dos alunos pode perder-se com facilidade e a atividade não irá produzir os resultados positivos que se deseja, podendo até desmoralizar o aluno e ter um impacto negativo nas suas conceções acerca da Matemática.
8 Krulik e Rudnick (1993) apresentam uma síntese bastante interessante das condições necessárias para que uma tarefa possa ser considerada ou entendida como um problema: aceitação, bloqueio e exploração. A aceitação refere-se, obviamente, à capacidade que o aluno tem de aceitar iniciar o processo de resolução do problema, sendo que a mesma pode advir de motivação interna, motivação externa (no caso das pressões exercidas por colegas, pais e professores), ou até o simples desejo de experienciar o desafio inerente ao problema. O bloqueio consiste nas tentativas de resolução iniciais por parte do aluno, que normalmente não são bem sucedidas. A exploração: que envolve o envolvimento pessoal do aluno e o obriga a explorar novos métodos de ataque ao problema.
2.1.2 Resolução de problemas
O processo de resolução de um problema, segundo Lopes (2001), consiste na mobilização e aplicação de conhecimentos e conteúdos já adquiridos e abordados a uma situação nova, sendo que esses conhecimentos não são suficientes para a resolução do problema. Este processo implica a habilidade de pensar e refletir acerca do processo de pensamento. Krulik e Rudnick (1993, p. 6) têm uma visão bastante idêntica, sendo que para eles a resolução de problemas é um processo pelo qual um indivíduo usa conhecimentos, capacidades e competências de compreensão previamente adquiridos para satisfazer os requerimentos de uma situação desconhecida, sendo que este processo se inicia com uma confrontação inicial, continua com uma síntese das aprendizagens já realizadas e aplicação das mesmas à nova situação, e termina com a obtenção de uma resposta que cumpra as condições definidas inicialmente. “Resolver problemas é uma atividade complexa que envolve a coordenação de conhecimentos, experiências prévias, intuição, atitudes, convicções e várias habilidades” (Lopes, 2001).
Resolver problemas é uma atividade que exige, portanto, não apenas o recurso a conhecimentos prévios de conteúdos, como no caso de um exercício ou uma simples questão, mas a mobilização de uma série de capacidades e competências. Estas devem ser adquiridas e trabalhadas pelo aluno ao longo do seu percurso educativo, sendo responsabilidade do professor criar as condições necessárias para tal.
2.1.3 Tipologia de problemas
Diversos autores se têm debruçado sobre a temática da resolução de problemas, surgindo evidentemente a necessidade de os classificar a partir de determinados critérios:
Charles e Lester (citados por Vale e Pimentel, 2004, p. 18), criaram uma proposta de classificação de problemas própria para professores do ensino do 1.º ciclo que os distingue em cinco diferentes tipos: problemas de um passo, que requerem o uso de uma das quatro operações elementares
9 da aritmética; problemas de dois ou mais passos, que apenas diferem dos anteriores por exigirem a aplicação de mais do que uma das quatro operações da aritmética; problemas de processo, que não podem ser resolvidos da forma mecanizada própria dos problemas de um ou mais passos, exigindo o recurso a estratégias de resolução; problemas de aplicação, que por norma requerem recolhas de dados e o uso de operações e estratégias diversificadas; e os problemas tipo puzzle, que podem aparentar pouca relação com a Matemática e exigir um momento de inspiração repentino (ou “flash”), podendo estes últimos suscitar curiosidade e interesse pela matemática nos alunos.
Proudfit (1980, citado por Lopes, 2001) identifica nos currículos matemáticos dois tipos de problemas: os problemas standard do manual, que se centram na aplicação de conteúdos, fórmulas e algoritmos abordados segundo os programas curriculares de matemática e cuja função é reforçar e melhorar as habilidades dos alunos com as operações fundamentais; e os problemas de processo, que frequentemente têm mais do que uma solução e exigem partir de algo mais do que operações matemáticas para chegar à sua resolução, sendo necessário recorrer a estratégias diversas de resolução. Estes são os que mais se enquadram nos objetivos do que é a resolução de problemas, forçando os alunos a pensar mais além do que o simples aplicar de conteúdos.
O projeto do grupo de investigação em Resolução de Problemas (GIRP) apresenta uma tipologia de resolução de problemas com quatro tipos de problemas que admite a possibilidade de um problema não se enquadrar em apenas um tipo: Problemas de processo; problemas de conteúdo; Problemas de aplicação e problemas de aparato experimental. Problemas de processo não podem geralmente ser resolvidos diretamente com o uso de algoritmos, sendo necessário recorrer a estratégias de resolução de problemas diversas; problemas de conteúdo requerem o uso de conteúdos programáticos e conceitos matemáticos, podendo ser comparáveis aos problemas de um ou mais passos da classificação de Charles e Lester; problemas de aplicação exigem a recolha de dados na vida real, tomada de decisões, podem admitir múltiplas soluções e requerer o uso de uma ou mais estratégias de resolução; problemas de aparato experimental podem ser comparáveis a experiências científicas, na medida em que podem requerer o uso de métodos de investigação da área da estatística e das ciências experimentais (Vale, 2002, citada por Vale e Pimentel, 2004, p. 19-21).
Assim, as diversas tipologias de classificação de problemas baseiam-se no público a que se destinam, sendo que estes são classificados consoante diversos critérios por uma questão de necessidade devido ao facto de a abordagem da resolução de problemas ter que ser feita desde o início do percurso escolar e ao longo de todos os ciclos de ensino. Um professor do 1.º ciclo do ensino básico trabalha com os seus alunos a resolução de problemas com um carácter distinto dos problemas
10 trabalhados por um professor de matemática do 2.º ciclo, ou até um professor do ensino secundário. É natural, portanto, que diferentes tipos de professores observem este domínio e apelem a uma classificação baseada na ótica que mais se adeque aos seus alunos.
2.1.4 Modelos e estratégias de resolução de problemas
Polya (1990) apresenta em 1945 uma proposta de quatro fases para chegar à resolução de um problema que atualmente ainda é bastante utilizada. Estas quatro fases consistem em: 1. Compreender o problema; 2. Estabelecer um plano de resolução; 3. Execução do plano; 4. Verificar o resultado e refletir.
A primeira fase deste modelo, compreender o problema, implica perceber o que é pedido e qual a meta que se pretende atingir. É preciso tentar observar o problema de pontos de vista diversos e anotar os seus dados com a notação apropriada para obter pistas de eventuais possibilidades a partir das propriedades dos dados oferecidos. A segunda fase, estabelecimento de um plano, consiste em delinear uma proposta de uma sequência de operações ou cálculos (ou outras estratégias de resolução) que possam conduzir à resolução do problema. Esta proposta pode surgir subitamente ou exigir algum tempo de raciocínio. Uma boa maneira de criar um plano é pensar num problema parecido que já se tenha resolvido. A terceira fase, execução do plano, como o próprio nome indica, consiste na execução da proposta de sequência de passos de resolução que se planeou na fase anterior no sentido de chegar à resposta. É preciso não perder o plano de vista e deve-se corrigir devidamente cado passo para garantir que chegamos ao resultado final correto. A quarta e última fase, verificar o resultado e refletir, implica confirmar se o resultado satisfaz as exigências do problema proposto no enunciado e refletir acerca do caminho percorrido para resolver o problema. O autor afirma que esta é uma das fases mais importantes do processo de resolução, pois permite uma consolidação do conhecimento e um aperfeiçoamento da capacidade de resolução de problemas.
Também Guzmán (citado por Lopes, 2001) apresenta uma proposta de modelo de resolução bastante idêntica baseada em quatro fases, nas quais apenas os nomes das fases parecem mudar, parecendo que a criação desta proposta foi destinada especificamente aos alunos resolvedores de problemas. O modelo é o seguinte: 1. Antes de fazer, tenta entender; 2. À procura da estratégia; 3. Explora a estratégia; 4. Extrai o sumo do jogo e da tua experiência. (p. 17)
Lopes (2001) apresenta uma série de estratégias para resolver problemas que, obviamente, não implicam a sua utilização isolada, podendo ser conjugadas na resolução de um só problema. Estas são:
11 Construir um modelo; construir uma tabela; tentar, conferir, rever; simplificar; eliminar; e encontrar padrões.
Ao construir um modelo, uma criação abstrata, visa-se representar o mundo real. Um modelo pode ser uma equação, um algoritmo, uma fórmula, um esquema, um esboço, um desenho, um diagrama, etc. Nos níveis mais baixos de escolaridade e de abstração, os diagramas e desenhos são exemplos de modelos bastante úteis na resolução de problemas. Este método prevê a organização da informação de uma forma que mais facilmente permite a seleção de uma estratégia de resolução. Quando se constrói uma tabela, que pode também ser um gráfico ou quadro, mais facilmente se descobre relações e padrões entre os dados fornecidos, sendo que esta estratégia é frequentemente combinada com outras estratégias de resolução. Tentar, conferir e rever consiste na clássica estratégia “tentativa-erro”, não garantindo obviamente a chegada imediata à solução correta, mas permitindo uma melhor compreensão do problema. Quando se pretende fazer uso desta estratégia, três passos devem ser seguidos: 1. Supor uma resposta; 2. Conferir se a resposta satisfaz as condições do problema; 3. Usar a informação da alínea anterior para supor uma nova resposta; 4. Continuar este procedimento até obter uma resposta correta. Simplificar é essencialmente reduzir o problema a um problema mais simples, reformulando palavras, usando números menores ou resolvendo por etapas. Esta estratégia pode permitir uma melhor compreensão do problema ou até descobrir a estratégia que conduzirá à resolução. Eliminar é uma estratégia frequentemente usada no quotidiano a par com o raciocínio lógico e consiste em listar todas as possibilidades de resolução, eliminando as que não permitem progredir no
processo de resolução. Quando procuramos encontrar padrões analisamos o problema numa ótica de
busca de um padrão ou regularidade que possa ser estendido ou generalizado à totalidade do problema. Esta generalização deve ser desenvolvida com base nos dados do problema e estendida para confirmar a sua validade.
Vale e Pimentel (2004) oferecem também uma série de sugestões de estratégias úteis para a resolução de problemas, nas quais podemos encontrar paralelos com as propostas de Lopes (2001): descobrir um padrão ou regra/lei de formação, na qual se generaliza uma solução específica à totalidade do problema; fazer tentativas/conjeturas, em que se de certa forma se “adivinha” a solução e se confirma se cumpre as condições do problema; trabalhar do fim para o princípio, em que, como o próprio nome indica, se começa a resolver o problema partindo do fim; usar dedução lógica, encarando-se todas as hipóteses e eliminando as que não servem; reduzir a um problema mais simples, que como o próprio nome indica, se resume a simplificar um problema, por norma com o objetivo de encontrar um padrão; fazer uma simulação/experimentação/dramatização, em que se utiliza objetos ou dramatizações para
12 modelar o problema a resolver; fazer um desenho, diagrama, gráfico ou esquema; e fazer uma lista organizada, na qual se representam e organizam os dados do problema.
2.1.5 A resolução de problemas na sala de aula
Na aula de Matemática, a resolução de problemas é um domínio de relevo e cuja abordagem se revela essencial ao longo dos diversos anos de escolaridade do ensino básico, no sentido em que, juntamente com o progresso da compreensão matemática, contribui para a aquisição do “gosto pela matemática e pela redescoberta das relações e factos matemáticos” (Vale e Pimentel, 2008, p. ).
Apesar da reconhecida necessidade de trabalhar nas escolas a capacidade de resolução de problemas, há ainda muita dificuldade por parte dos professores em trabalhar este domínio com os alunos, sentindo-se os mesmos frequentemente “menos confiantes e mais desconfortáveis” (Boavida, 1993, p. 14) no que diz respeito à execução de atividades que envolvam resolver problemas. Vale e Pimentel (2004) afirmam que a abordagem deste domínio, mesmo que difícil, oferece aos alunos uma perceção única da relevância da Matemática no quotidiano, permitindo que os alunos a contextualizem e mais facilmente a usem para seu benefício no seu dia-a-dia.
É, portanto, necessário que se observe a resolução de problemas numa ótica alternativa à tradicional, na qual, segundo D’Ambrosio (1989, p. 16), a matemática é mostrada “como um corpo de conhecimentos acabado e polido. Ao aluno não é dado em nenhum momento a oportunidade ou gerada a necessidade de criar nada, nem mesmo uma solução mais interessante”. Para esta autora, estas práticas levam a que o aluno, ao observar a aprendizagem da Matemática como uma acumulação de fórmulas e algoritmos e a Matemática em si como “um corpo de conceitos verdadeiros e estáticos, do qual não se duvida ou questiona”, percam gradualmente o seu “bom-senso” matemático”, fazendo com que seja bastante comum os alunos perderem a motivação para a resolução de problemas com um certo grau de dificuldade (p. 16).
Krulik e Rudnick (199) referem a dicotomia aparente entre o sucesso dos alunos aquando da resolução de um problema e a persistência para continuar a ele inerentes, bem como o fracasso e consequente desmotivação e evasão a futuros problemas, alertando para a necessidade por parte do professor em criar uma sequência cuidadosamente selecionada de atividades de resolução de problemas adaptadas ao nível de desenvolvimento dos alunos, garantindo assim o seu interesse e envolvimento e a melhoria dos seus resultados e sua performance a nível escolar e académico.
Numa atividade dedicada à resolução de problemas, as estratégias de resolução devem ser sempre escolhidas pelo aluno, optando este pelas que lhe parecerem mais convenientes e devendo o professor incentivar o espírito criativo do aluno sem sugestões de exploração (Lopes, 2001). O aluno
13 deve ser estimulado a realizar o máximo de trabalho autónomo independente na resolução de um problema. Obviamente, que o professor deve ajudar sempre que necessário, visto que há a possibilidade de, sem qualquer apoio, o problema se revele demasiado difícil para que o aluno o consiga resolver, não havendo qualquer progresso. O desinteresse e a desmotivação são, naturalmente, o passo seguinte. Para evitar isto, o professor deve sempre tentar colocar-se no lugar do aluno e perceber qual é a sua dificuldade ou entrave na resolução do problema para conseguir oferecer apenas a ajuda necessária, tentando deixar sempre no aluno a perceção final de que foi ele que ultrapassou o desafio (Polya, 1990).
Polya (1986) publicou uma série de conselhos e sugestões destinados a professores de matemática (ou alunos interessados em aprofundar a arte de resolver problemas) de diversas formas de encarar e atacar um problema, que naturalmente podem ser conjugadas entre si, dos quais decidi aqui sintetizar alguns exemplos: questionar qual é a incógnita ou quais são as incógnitas. O professor deve sempre focar a atenção dos alunos na meta a atingir, para que não a percam de vista, pois só se estiverem concentrados no resultado a que desejam chegar é que conseguirão deduzir meios de o alcançar. Para guiar os alunos neste sentido e para garantir que compreenderam claramente o problema o professor pode apresentar questões como: Do que precisamos? O que queremos? O que devemos procurar?; tentar lembrar-se de um problema correlato. partindo do princípio de que não é frequente depararmo-nos com um problema totalmente distinto, deve sempre surgir no processo de resolução de um problema a questão de se não haverá nenhum problema que já se tenha resolvido que tivesse alguma relação com o presente. Ao considerar um problema já resolvido podemos deste retirar elementos auxiliares adequados à resolução do nosso problema atual (ibidem, p. 36 e 69). A utilização de um problema auxiliar consiste simplesmente em sugerir aos alunos que tentem conceber uma versão simplificada do problema (que será o problema auxiliar) como um meio de resolver o problema original (ibidem, p. 119 e 120).
É pertinente concluir este capítulo referindo a opinião de Vale e Pimentel (2004, p. 25), que acreditam que “se pode aprender a resolver problemas (…) se se for disciplinado na forma de pensar e de estruturar os seus pensamentos”, cabendo ao professor de matemática garantir que os alunos adquirem e compreendem um modelo de resolução e um espólio de estratégias diversificadas que lhes permitam encarar um problema de forma confiante e sem se sentirem intimidados pela sua dificuldade.
2.2 Os jogos
Segundo Ferreira (2008), a história não conseguiu ainda determinar as origens do primeiro jogo. No entanto, já foram encontrados diversos vestígios da prática de jogos em civilizações antigas, como o antigo Egito. Jogos como as Damas, o Xadrez e o Go são antiquíssimos e têm sido transmitidos ao longo
14 de imensas gerações, sendo ainda hoje em dia bastante populares e a sua prática apreciada por um vasto público. Neto e Silva (2004) referem que o ato de jogar acompanha a civilização desde o início da sua existência, dando como exemplo o jogo Ur, o jogo mais antigo cujas regras se conhece, e que era jogado na antiga Mesopotâmia. Costa (2004) afirma que certos tipos de jogos, entre eles os jogos de azar e de estratégia são tão antigos como a civilização humana e o seu estudo permitiu até o desenvolvimento de novos campos da Matemática durante o período da idade média da parte de Matemáticos como Pascal e Fermat.
Para Rino (2004) o “jogo é uma atividade tão antiga como o homem” (p. 9), sugerindo uma necessidade biológica do lúdico inerente ao ser humano como via do seu desenvolvimento e da aquisição de uma maior complexidade para o trabalho e para a sobrevivência.
Parece haver um consenso relativamente às capacidades que o jogo tem no desenvolvimento do ser humano, nomeadamente na aquisição de regras, conhecimento das coisas e das suas relações e desenvolvimento de competências de socialização, mas diferentes autores divergem na importância que lhe atribuem e na pertinência de os usar na sala de aula ou em contexto escolar (Ibidem, p. 10)
Na realidade atual do nosso país, a atividade que constitui o jogo parece ser constantemente acompanhada de um estigma social que a observa como uma mera brincadeira, diversão ou passatempo sem utilidade. Consultando o significado de “jogo” no dicionário online Infopedia, a primeira definição que nos surge é: “atividade lúdica executada por divertimento, recreio, distração”. Muita gente associa o conceito de jogo ao “jogo a dinheiro”, espoletando de imediato sentimentos negativos acerca da sua prática. Segundo Palhares (2004), “os jogos são por parte da sociedade portuguesa ligados a situações de aposta, havendo até em muitos municípios portugueses posturas proibindo os jogos em cafés” (p. 132). Havendo esta resistência manifesta por parte da comunidade em geral em aceitar esta atividade em contextos de lazer públicos, é natural que a sua aplicação num contexto educativo se apresente para a opinião pública como igualmente indesejável. “Os próprios professores têm muita resistência ao uso de jogos, atendendo a este caráter de inutilidade, até mesmo de vício, que lhes é dado pela sociedade” (ibidem, p. 132).
2.2.1 A definição de jogo
Segundo Ferrero (1991), em geral considera-se o jogo como um “ejercicio recreativo sometido a reglas” (p. 11). Para este autor, o termo jogo define uma ampla variedade de atividades humanas de carácter lúdico, que vão desde a atividade física, no caso dos jogos desportivos de competição, à atividade intelectual, no caso dos jogos matemáticos e de estratégia, passando também pela atividade recreativa, no caso dos jogos de cartas e azar.
15 Huizinga (2003) apresenta uma definição bastante completa do conceito de jogo. Para este autor “o jogo é uma atividade ou ocupação voluntária, exercida dentro de certos e determinados limites de tempo e de espaço, segundo regras livremente consentidas, mas absolutamente obrigatórias, dotado de um fim em si mesmo, acompanhado de um sentimento de tensão e de alegria e de uma consciência de ser diferente da vida quotidiana” (p. 23)
Assim, quando falamos de jogo é necessário ter em conta que se trata de um conceito muito abrangente, estendendo-se num longo espectro que pode ir desde atividades desportivas de competição a jogos de azar em casinos. No caso desta investigação, importam-me os jogos de regras ou de estratégia, também conhecidos como jogos matemáticos.
Para Costa (2004), “jogos matemáticos são jogos cujas regras, estratégias e resultados são explicados pela Matemática”, não havendo, portanto, a presença do fator sorte nem informação escondida, como é o caso dos jogos de cartas ou dominós, onde a distribuição das cartas deve ser feita de forma aleatória e cada jogador só tem informação das suas cartas ou peças.
Rino (2004) atribuí três características fundamentais aos jogos de regras: “Começam a ser jogados a partir de uma determinada altura (quando a criança atinge a maturidade suficiente para compreender e aceitar as regras) e prolongam-se pela vida adulta; exigem regras, ou seja, uma estrutura cognitiva; e estabelecem relações interpessoais” (p. 26).
Silva e Santos (2001, p. 24) referem que a grande maioria dos jogos tradicionais possuem variantes, que correspondem a variações das regras oficiais do jogo (se é que as há), e que podem ser antigas e de origem regional, como é o caso das damas e do dominó, sendo que em diferentes países se joga diferentes versões desses dois jogos.
2.2.2 Tipologia de jogos
Os jogos podem ser classificados e agrupados segundo uma diversa série de critérios, definidos consoante os contextos em que são utilizados ou jogados. Neste caso, importam as classificações
Bishop (2004, p. 23) sugere uma tipologia de jogos que parece bastante própria aos ciclos iniciais da educação, como o pré-escolar e o primeiro ciclo. Distingue os jogos em: imaginativos, se apresentam fantasia ou humor; realistas, se é feito recurso a materiais concretos, sendo o caso das brincadeiras com barros ou plasticina; imitativos, se implicarem a mímica de aspetos da natureza ou do comportamento dos adultos; discriminativos, como é o caso do esconde-esconde ou as adivinhas; competitivos, como as lutas ou combates; propulsivos, que geralmente consistem no lançamento de objetos; e por fim, os jogos de prazer, como as canções e danças, por exemplo.
16 Ferrero (1991, p. 15) distingue os jogos nas seguintes classes: Jogos de competição inteligente, jogos solitários, jogos de lápis e papel e jogos com números e truques numéricos. Jogos de competição inteligente são jogos dinâmicos que consistem em colocar ou retirar fichas e que exigem que cada jogador intua ou preveja a jogada do adversário e caracterizam-se por terem dois participantes que têm que agir racionalmente de forma a delinear e adaptar as suas estratégias. Solitários, como o nome indica, são jogos de um só jogador, no qual este deve, tal como nos competitivos, agir racionalmente, priorizando algumas ações em detrimento de outras e seguindo uma estratégia de resolução. Jogos de lápis e papel são bastante convenientes, pois implicam poucos recursos, e desenvolvem as capacidades de compreensão do espaço. Jogos com números e truques numéricos: são jogos que não são centrados apenas no desenvolvimento do cálculo mental, permitindo também a aquisição de conceitos, a descoberta de regularidades e o desenvolvimento de estratégias.
Neto e Silva (2004, p. 11) afirmam que do ponto de vista do ensino da Matemática, os jogos que normalmente mais devem interessar ao professor são os jogos de informação perfeita ou abstratos: jogos de estratégia que não possuem o fator sorte e em que a cada momento cada jogador possui a mesma informação que o seu adversário. Estes autores apresentam uma tipologia de classificação dedicada especificamente a este tipo de jogos baseada no tipo de objetivo para chegar à vitória: jogos de território, jogos de bloqueio, jogos de captura, jogos de posição, jogos de padrões e jogos de conexão. Nos Jogos de território o objetivo é conquistar a maior área possível no tabuleiro e temos como exemplo o célebre Go. Nos jogos de bloqueio, o vencedor é aquele que conseguir impedir o adversário de jogar. Os Jogos de captura ganham-se capturando um conjunto de peças adversárias. Um dos exemplos mais conhecidos
é as damas; os jogos de posição terminam quando um jogador desloca uma ou mais peças para uma
zona específica do tabuleiro. Nos jogos de padrões, quem obtiver um padrão, geralmente uma linha de peças, ganha. O jogo Semáforo ou o Quatro-em-linha são exemplos populares. Nos jogos de conexão, dos quais o Hex é o exemplo mais célebre, o objetivo é criar um grupo de peças que satisfaça um determinado critério, que normalmente consiste em estabelecer uma ligação entre duas pontas do tabuleiro.
2.2.3 O papel do jogo na educação matemática
Uma série de autores parecem concordar que a prática de jogos tem contributos positivos no desenvolvimento integral das crianças e jovens. A questão que surge é se a prática de jogos tem lugar na escola.
Palhares (2004) apresenta uma comparação entre duas visões particulares e opostas do ensino que importam mencionar: a visão instrumental, em que a criança é encarada como um recipiente vazio
17 e recetor passivo do conhecimento e o professor como o seu transmissor; e a visão construtivista, em que o aluno é o construtor ativo do seu conhecimento. Estes dois modelos colidem em diversos aspetos no processo de ensino e aprendizagem da matemática, incluindo os aspetos relativos à prática de atividades lúdicas em contexto educativo:
Tabela 1 – Comparação de Palhares (2004) de dois modelos pedagógicos
Visão Instrumental Visão Construtivista
Preenchimento das aulas
Resolução de exercícios - tarefas com pensamento matemático de baixo nível.
Resolução de problemas – tarefas com pensamento matemático de alto nível.
Interesse na
atividade matemática
Produtos obtidos corretos e conseguidos rapidamente.
Processos desencadeados aquando da atividade matemática, pouco importando o produto final.
Preocupação dos professores
Manter a ordem e o controlo. Garantir que os alunos estejam em
genuína atividade matemática. Conhecimentos
informais do
aluno
Não têm lugar na escola e não se reconhece necessidade em usá-los
para recontextualizar os
conhecimentos formais da escola
Devem ser tidos em conta e usados juntamente com materiais para facilitar a passagem do concreto ao abstrato.
Atividades recreativas
Não há lugar a atividades recreativas na seriedade da Matemática.
Bem aceites pela promoção da motivação e de uma atitude mais positiva nos alunos.
Visão da
Matemática
Divisão da matemática em blocos distintos e isolamento de outras ciências e áreas de conhecimento.
Existem conexões entre os diversos domínios da matemática e entre a matemática e todas as áreas do saber.
Evidentemente, o movimento educativo atual tende a beneficiar as práticas do modelo construtivista, onde o jogo e as atividades lúdicas em geral são entendidos como ferramentas pedagógicas úteis e a sua prática é bem-vinda na escola, bem como a aprendizagem da resolução de problemas (em detrimento do exercício).
Bishop (2004), refere que os educadores de Matemática têm vindo gradualmente a acrescentar o uso de jogos matemáticos nas suas atividades com finalidades diversas, tais como aprender conceitos,
18 aprender a trabalhar em grupo ou competir, por exemplo. Este autor afirma que a investigação neste campo tem cada vez mais vindo a apoiar o uso do jogo como uma ferramenta de ensino.
Sendo o jogo uma atividade que todos fazemos naturalmente e por prazer, Ferreira (2008) sugere aos professores que aproveitem esta apetência (que se manifesta com mais evidência nas crianças) e a emotividade a ela associada para promover as aprendizagens dos seus alunos. Bianchini, Gerhardt, e Dullius (2010) afirmam que a prática de jogos na aula de Matemática pode ajudar alunos com dificuldades neste domínio a ultrapassar os seus receios e ganharem mais confiança para a aprendizagem.
Para além das aprendizagens, a prática de jogos a pares e em grupo permite ao aluno desenvolver “capacidades afetivas, como a autoconfiança, a autonomia, o espírito de equipa e de cooperação, a capacidade de argumentar e tomar decisões (ibidem, p. 21). A partir de uma investigação que conduziu, Rino (2004, p. 55) observou que alunos que jogaram jogos de na escola a pares manifestaram uma intensificação das suas relações interpessoais e se tornaram mais pacientes na aceitação de regras, concluindo que “o jogo não didático, de regras e intelectual, a pares, influi positivamente nas interações sociais das crianças/alunos e nas representações que têm da matemática”. Silva e Santos (2011, p. 303) comentam que o desempenho dos estudantes de matemática parece beneficiar-se com a prática de jogos de tabuleiro e de estratégia, afirmando que “este tipo de jogos estimula os jovens a pensar”. As regras e interações próprias do jogo podem ser bastante úteis em contexto escolar na aquisição de capacidades cognitivas e sociais, e essenciais para a formação de um cidadão responsável e autónomo (Rino, 2004, p. 21).
Rino (2004) afirma que o jogo traz grandes contributos ao desenvolvimento de interações sociais, desenvolvimento afetivo-social e desenvolvimento cognitivo
Palhares (2004, p. 142) refere que a escola deve proporcionar momentos dedicados ao “ensino de jogos de estratégia que comportam no seu decorrer situações de resolução de problemas”, alegando que no seu decorrer se experiencia um “ambiente de resolução de problemas que não sendo estritamente matemático tem relações óbvias e contributos importantes para a criação da apetência pela resolução de problemas e para o desenvolvimento da capacidade de resolução de problemas.” Mendes e Mamede (2012, p. 115) afirmam que “é papel do professor tirar partido de cada uma das possíveis vertentes do jogo e permitir a sua vivência por parte das crianças”.
19 2.2.5 Os jogos matemáticos na sala de aula
Parece haver alguma discordância por parte de alguns autores relativamente à forma como os jogos podem ou devem ser utilizados em contexto pedagógico, havendo quem afirme que estes não devem ser utilizados em sala de aula e para transmissão de conteúdos, e quem afirme o contrário.
Ferreira (2008) afirma que o “jogo é mais uma ferramenta de trabalho a que o professor pode e deve recorrer para desenvolver nos seus alunos capacidades que poderão permitir um melhor desempenho na área da matemática” (p. 24). Esta autora sugere ainda a prática de jogos, como o geomutante e o tangrix, como forma de trabalhar conteúdos na área da geometria.
Há autores que afirmam que o jogo tem benefícios, mas que a sua prática em sala de aula deve reservar-se apenas a momentos em que o tempo o permita. Segundo Silva e Santos (2011), apesar do valor inerente à prática de jogos e ao estímulo mental que estes proporcionam, os mesmos não devem ser utilizados como uma forma de transmissão de conteúdos curriculares, ficando a sua utilização num contexto educativo reservada a uma prática de carácter complementar. Apesar disso, os autores referem que dentro de um prazo alargado, o uso de jogos como atividade extracurricular constituí “uma prática intelectualmente sofisticada cujas vantagens se poderão fazer sentir” (p.303).
Bianchini, Gerhardt, e Dullius (2010) defendem que o jogo pode e deve ser utilizado em contexto de sala de aula e que as vantagens da sua utilização compensam largamente as desvantagens, como o uso de tempo letivo para atividades não escolares e até eventuais comportamentos de indisciplina dos alunos. Estes autores afirmam que enquanto joga, a criança aprende sem o compromisso de aprender pensando em estratégias e hipóteses, em contraste com os trabalhos teóricos escolares.
2.2.6 Os jogos matemáticos e a resolução de problemas
Conforme já referido, uma série de autores parece ter apresentado bastante interesse no potencial pedagógico de jogos de estratégia e jogos matemáticos, por vezes especificamente pela sua relação com determinadas competências matemáticas, como a capacidade de identificar padrões ou resolver problemas, por exemplo. Evidentemente, estes estudos normalmente têm por objetivo a compreensão do potencial pedagógico dos jogos como ferramentas de promoção de capacidades cognitivas.
Ferreira, Palhares e Silva (2013), através de uma investigação correlacional realizada com alunos do 1.º ciclo do ensino básico, verificaram a existência de uma relação positiva entre a capacidade de jogar Semáforo (um conhecido jogo de estratégia no mundo do ensino da matemática) e a capacidade de identificar padrões, bem como as classificações obtidas nas provas de aferição. Foi também possível evidenciar uma relação entre a força de jogo em xadrez e a capacidade de identificar padrões numéricos
20 e geométricos (com especial incidência em padrões numéricos) em alunos do 1.º e 2.º ciclos (Ferreira & Palhares, 2007, p. 20). Curiosamente, não foi encontrada uma relação significativa entre a capacidade de jogar Hex, Pontos e quadrados e Ouri e a capacidade de resolver problemas com padrões (Ferreira, Palhares & Silva, 2008).
Os processos mentais convocados para uma partida de um jogo de estratégia com um nível de complexidade adequado ao desenvolvimento do jogador podem facilmente ser comparados com o processo de resolução de um problema. Krulik e Rudnick (1993, citados por Ferreira, 2008, p. 23) apresentam uma comparação bastante interessante entre estes dois domínios (jogo e resolução de problemas) baseado nas quatro fases de resolução de problemas de Polya:
1. Ler as regras, compreender como se joga e analisar o jogo - Compreender o problema; 2. Escolher as linhas de jogo que possam conduzir a uma vitória - Estabelecer um plano; 3. Pôr em prática a estratégia de jogo escolhida - Executar o plano;
4. Refletir sobre o jogo, verificar se a estratégia se aplica a outros jogos e procurar jogadas alternativas - Reflexão e avaliação;
Segundo Silva e Santos (2011), “os aspetos mais técnicos dos jogos, como o registo de partidas, a construção de estratégias, a memória de experiências passadas (…), a partilha de experiências, são instâncias que têm paralelos naturais na resolução de problemas matemáticos” (p. 303). Smole, Diniz e Cândido (2007, citados por Ferreira, Palhares e Silva, 2013) “referem que a utilização de jogos permite o desenvolvimento da observação, da reflexão, da argumentação, do raciocínio lógico e da resolução de problemas” (p. 76). Ferreira e Palhares (2007) mencionam a existência de estudos que evidenciaram a capacidade do xadrez em: promover a capacidade de resolução de problemas e identificar padrões, melhorar o pensamento lógico, a memória, a concentração e o QI.
Verifico que existe um consenso geral na opinião de diversos autores e investigadores relativamente à relação entre os jogos e a resolução de problemas e até à possibilidade de a prática sistemática de jogos promover o desenvolvimento de certas capacidades cognitivas, como a capacidade de resolução de problemas e a identificação de padrões (por exemplo).
2.2.7 HEX
O jogo Hex, curiosamente, foi inventado por dois diferentes autores. Em 1942 foi inventado pelo matemático e poeta dinamarquês Piet Hein e em 1948 pelo matemático americano John Nash. Nessa altura, o aparecimento deste jogo deu uma nova visibilidade à família dos jogos de conexão (Neto & Silva, 2004). Este jogo chamou-se inicialmente Nash ou John, como homenagem ao autor. Só em 1952, com a comercialização de uma versão do jogo pela Parker Brothers, surgiu o nome Hex, naturalmente pelo
21 facto de se jogar num tabuleiro com casas hexagonais ("Game of Hex -- de Wolfram MathWorld", 2019). Existem atualmente imensos jogos de conexão e variações inspirados no Hex, como o Nex, o Havana e o projex, por exemplo (Neto & Silva, 2004).
Na obra que compila uma série de jogos de estratégia de Ferrero (1994), o Hex encontra-se na lista dos jogos de lápis e papel, sendo que se tivermos o tabuleiro impresso, este jogo é pouco exigente a nível de recursos. Este autor refere ainda que este jogo pode ser jogado com tabuleiros de dimensões variadas, consoante o nível de dificuldade e de duração de partida que se pretender.
O Hex joga-se num tabuleiro em forma de losango cujas casas são hexágonos e o objetivo de cada jogador é ligar as com as suas peças os seus dois lados do tabuleiro. As regras são: decide-se à sorte quem começa o jogo; Cada jogador, no seu turno, coloca uma peça sua ou marca o seu símbolo numa casa vazia do tabuleiro; considera-se que as quatro casas que formam os vértices do tabuleiro pertencem aos limites dos lados dos dois jogadores (Ferrero, 1994). Quem conseguir ligar os dois lados do tabuleiro primeiro, ganha. Neto e Silva (2004) mencionam a regra do equilíbrio, que dita que o segundo jogador, na sua primeira jogada, pode aproveitar a jogada do adversário, trocando de cor com este.