Aula 12 – Introdu¸
c˜
ao ao conceito de ´
area
Objetivos
• Introduzir o conceito de ´area de uma figura plana
• Apresentar as f´ormulas para o c´alculo da ´area de algumas figuras planas
Introdu¸
c˜
ao
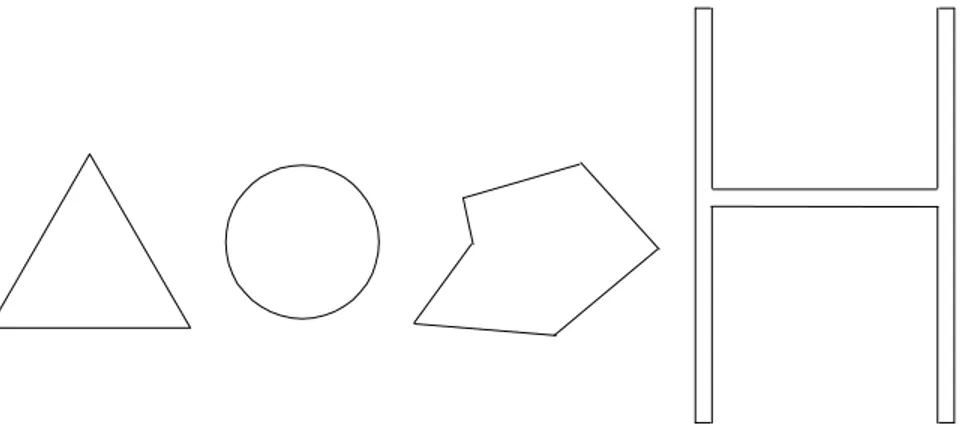
Dentre as figuras abaixo, qual vocˆe diria que ´e a maior?
Fig. 228: Figuras planas.
Note que os formatos das figuras s˜ao diferentes. Quando se trata de figuras semelhantes, ´e natural saber qual ´e a maior, mas para comparar o tamanho de figuras de formatos diferentes ´e preciso um cuidado especial. Nesta aula vamos iniciar o estudo de ´areas de figuras planas. Vamos ver que o conceito de ´area nos permitir´a decidir qual o “tamanho” do espa¸co que uma figura ocupa no plano. Vamos primeiro ver alguns exemplos.
Devemos concordar que:
• Dada qualquer parede, utiliza-se uma quantidade bem determinada de tinta para pint´a-la (com uma camada de tinta da espessura referida).
• Se duas paredes tˆem o mesmo tamanho e a mesma forma (ou seja, s˜ao congruentes), utiliza-se a mesma quantidade de tinta para pintar cada uma delas.
• Se uma parede ´e a uni˜ao de dois peda¸cos de parede, de forma que esses dois peda¸cos se juntam apenas em beiradas, ent˜ao a quantidade de tinta necess´aria para pintar tal parede ´e a soma das quantidades de tinta necess´arias para pintar cada peda¸co.
Vejamos um outro exemplo. Suponha que um agricultor utilize uma por¸c˜ao de sementes para semear um terreno que tem a forma de um qua-drado. Dado qualquer outro terreno de qualquer tamanho e forma, ´e claro que existe uma quantidade bem determinada de sementes necess´aria para seme´a-lo (com a mesma concentra¸c˜ao de sementes do primeiro). Essa quan-tidade de sementes, comparada com a quanquan-tidade de sementes para semear o terreno quadrado, d´a uma medida de qu˜ao maior (ou menor) esse terreno ´e em rela¸c˜ao ao primeiro. Devemos concordar que:
• Dado qualquer terreno, existe uma quantidade bem determinada de sementes necess´aria para seme´a-lo.
• Para semear dois terrenos congruentes (mesmo tamanho e forma), utiliza-se a mesma quantidade de utiliza-sementes em cada um deles.
• Se um terreno ´e dividido em dois peda¸cos, a quantidade de sementes necess´aria para semear o terreno ´e a soma das quantidades de sementes necess´arias para semear cada peda¸co.
Da mesma forma, se um agricultor utiliza 1 por¸c˜ao de semente para semear um terreno quadrado e utiliza 5,8 por¸c˜oes de sementes para semear um determinado terreno, pode-se dizer que tal terreno ´e 5,8 vezes maior que o terreno quadrado inicial, ou que esse terreno ocupa 5,8 vezes mais espa¸co que aquele. Dizemos que a ´area do terreno ´e 5,8. Assim, para determinar a ´area de um terreno, bastaria seme´a-lo e verificar a quantidade de sementes utilizada.
Na pr´atica, por´em, deseja-se muitas vezes fazer o caminho contr´ario: o pintor gostaria de saber o quanto de tinta seria necess´ario comprar para pin-tar uma parede, e o agricultor gospin-taria de saber quantas por¸c˜oes de sementes v˜ao ser necess´arias para semear um dado terreno. Devemos, ent˜ao, ser ca-pazes de determinar a ´area de paredes e terrenos sem que seja necess´ario recorrer a m´etodos pr´aticos, como pintar ou semear. Para isso, fixamos uma unidade de comprimento, e escolhemos um quadrado de lado 1 comounidade de medida de ´area. Dizemos que esse quadrado tem ´area igual a 1: se o lado do quadrado mede 1cm, por exemplo, sua ´area ´e 1cm2 (lˆe-se ”um cent´ımetro
quadrado”), se o lado do quadrado mede 1m, sua ´area ´e 1m2 (”um metro
quadrado”), e assim por diante. A determina¸c˜ao da ´area das figuras planas ser´a feita com base nas trˆes propriedades a seguir:
P1 : “ Toda figura” plana limitada tem uma ´area. A medida da ´area ´e expressa por um n´umero real positivo.
P2 : Figuras planas congruentes tˆem a mesma ´area (por exemplo, dois triˆangulos congruentes ou dois c´ırculos de mesmo raio).
P3 : Se uma figura planaF ´e a uni˜ao de duas figuras planasF1 eF2, ondeF1 eF2 se intersectam somente em linhas, ent˜ao a ´area de
F ´e a soma das ´areas de F1 eF2.
Fig. 229: Figura para o c´alculo da ´area de um quadrado.
Como todas as nove partes s˜ao congruentes, pelas propriedades anteri-ores, cada uma delas tem ´area igual a um nono da ´area do quadrado inicial. Como consideramos a ´area do quadrado inicial igual a 1, cada uma das partes obtida ter´a ´area igual a 1
9.
Em geral, dividindo-se os lados do quadrado inicial em n partes iguais, e tra¸cando-se paralelas aos lados, como no exemplo, obt´em-se n2 quadrados
de mesma ´area. Cada um dos quadrados obtidos ter´a ´area igual a 1
n2. Com
isso provamos que a ´area de um quadrado cujo lado mede 1/n´e igual a 1
n2.
Observe que...
Na figura 230, quandoleh
s˜ao n´umeros naturais, o retˆangulo cont´em exatamentel×hquadrados
de lado 1.
Determinaremos agora a ´area de um retˆanguloABCD cujos lados me-dem l e h (veja a figura 230). Indicaremos tal ´area porAABCD.
A B
D C
l h
Fig. 230: Figura para c´alculo da ´area de um retˆangulo.
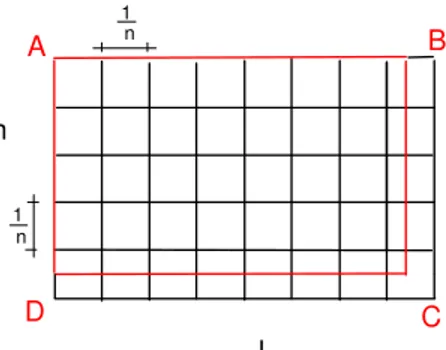
Para fazer o c´alculo da ´area, vamos escolher um n´umero natural n e verificar quantos segmentos de comprimento 1
n cabem nos segmentos AB
e AD. Pelas extremidades desses segmentos, tra¸camos retas paralelas aos lados do retˆangulo ABCD. Seja p o n´umero de segmentos de comprimento 1/n que cabem em AB e q o n´umero desses segmentos que cabem em AD
B 1
n
1 n A
C D
h
l
Fig. 231: C´alculo da ´area do retˆangulo.
Ent˜ao, de modo geral, num retˆangulo gen´erico, teremos as seguintes desigualdades envolvendoseus lados:
p1
n ≤l <(p+ 1)
1
n
e
q1
n ≤h <(q+ 1)
1
n .
Usando as desigualdades acima conclu´ımos que
pq 1
n2 ≤lh <(p+ 1)(q+ 1)
1
n2 . (2)
Por outro lado, considerando o retˆangulo globalmente, existem pq qua-drados de lado 1/ninteiramente contidos no retˆangulo ABCD(marcados na figura 231). Como cada um desses quadrados tem ´area 1/n2, conclu´ımos que
a ´area do retˆangulo ABCD satisfaz
AABCD ≥pq 1
n2 . (3)
Al´em disso, o retˆangulo ABCDest´a inteiramente contido no retˆangulo formado pela uni˜ao dos (p+ 1)(q+ 1) quadradinhos (veja de novo a figura 231), e, portanto
AABCD <(p+ 1)(q+ 1) 1
n2. (4)
Juntando as inequa¸c˜oes (3) e (4), obtemos
pq 1
n2 ≤AABCD <(p+ 1)(q+ 1)
1
n2 . (5)
Das inequa¸c˜oes (2) e (5), vemos que os dois n´umeros AABCD e lh est˜ao
compreendidos entrepq 1
n2 e (p+ 1)(q+ 1)
1
n2. Disso conclu´ımos que
|AABCD−lh|<(p+ 1)(q+ 1) 1
n2 −pq
1
n2 = (p+q+ 1)
1
Como p
n ≤l, q
n ≤h e
1
n ≤1, conclu´ımos que
|AABCD−lh|<(l+h+ 1) 1
n .
A ´ultima desigualdade vale qualquer que tenha sido a escolha inicial de
n. Bom, se o n for escolhido muito grande, o lado direito da inequa¸c˜ao ser´a muito pequeno, e a ´unica possibilidade para que a inequa¸c˜ao seja verdadeira para qualquer escolha de n ´e se |AABCD −lh| = 0 (lembre-se de que um m´odulo nunca ´e negativo). Da´ı, tem-seAABCD =lh.
Provamos assim a seguinte proposi¸c˜ao:
Proposi¸c˜ao 27
A ´area de um retˆangulo ´e o produto da medida da base pela medida da altura.
´
Area de um triˆangulo
Vocˆe conhece como calcular a ´area de um retˆangulo. Vamos partir para outras figuras geom´etricas?
a) Triˆangulos Retˆangulos
Considere um triˆangulo retˆangulo ABC, com ˆangulo reto no v´ertice A
e portanto com catetosb =AC e c=AB. Ent˜ao
´
AreaABC = b·c 2 .
A prova desta f´ormula segue-se facilmente da observa¸c˜ao que um triˆangulo retˆangulo “´e a metade de um retˆangulo” cujos lados s˜ao os catetos do triˆangulo.
Na figura 232, a seguir, est´a representado o triˆangulo retˆangulo ABC
como parte de um retˆangulo. Ent˜ao,
.
A B
C D
c b
Fig. 232:
´
AreaABC = 1
b) ´Area de um Triˆangulo Qualquer
A ´area de um triˆangulo arbitr´ario pode ser calculado como metade do produto de um lado (referido como base) pela altura do v´ertice oposto a este lado.
Na figura 233 abaixo, temos dois triˆangulos que cobrem os dois casos poss´ıveis para os triˆangulos. Em rela¸c˜ao `a baseBC do triˆangulo ABC, com altura h em rela¸c˜ao `a base, temos situa¸c˜oes onde o p´e da altura pertence a base do triˆangulo ou est´a fora do segmento que representa a base.
. .
A A
B
B C D C
h h
Fig. 233:
No primeiro caso,
´
AreaABC = ´AreaBDA+ ´AreaADC
= BD·h
2 +
DC·h
2 =
BC·h
2 .
No segundo caso,
´
AreaABC = ´AreaADC −AreaADB´
= DC·h
2 −
DB·h
2 =
BC·h
2 .
Ent˜ao em qualquer caso, a ´area do triˆangulo ´e igual `a metade do produto da base pela altura.
Acabamos de provar uma proposi¸c˜ao.
Proposi¸c˜ao 28
´
Area de um Paralelogramo
Antes de encontrarmos uma f´ormula para calcular a ´area de um para-lelogramo, vamos a algumas id´eias de base.
A distˆancia entre duas retas paralelas r e s ´e o comprimento AB do segmento obtido pela interse¸c˜ao das paralelas com uma reta perpendiculart. Veja a figura abaixo.
.
.
A
B
t
s
r
Fig. 234:
Note que qualquer que fosse a reta perpendicular o resultado da distˆancia entre as paralelas n˜ao muda.
Estamos em condi¸c˜oes de provar a pr´oxima proposi¸c˜ao.
Proposi¸c˜ao 29
Dado um paralelogramo ABCD, a ´area pode ser calculada pelo produto de um lado, pela distˆancia deste lado ao lado oposto.
Nota: A distˆancia referida acima ´e tamb´em denominada altura do
paralelo-gramo.
Prova:
Observe a figura 235 abaixo, onde est´a representado um paralelogramo
ABCD, a diagonal BD e a distˆancia (altura) entre os lados opostos AB e
DC.
.
A B
C D
h
Ent˜ao,
´
AreaABCD = ´AreaABD+ ´AreaBCD.
Mas,
´
AreaABD = 1
2 AB×h , AreaBCD´ = 1
2 DC×h.
Note que h representa, ao mesmo tempo, a altura do triˆangulo ABD
relativa ao lado AB e a altura do triˆangulo BCD relativa ao lado DC.
Como DC =AB, ent˜ao
´
AreaABCD =AB×h.
Para concluir esta aula, vamos calcular a ´area de um tipo especial de quadril´atero: o trap´ezio. O trap´ezio, como vimos na aula 7, ´e um quadril´atero que possui dois lados paralelos. Esses dois lados s˜ao chamados bases do trap´ezio. A altura do trap´ezio´e sempre tomada com rela¸c˜ao `as bases.
Proposi¸c˜ao 30
A ´area de um trap´ezio ´e o produto da sua altura pela m´edia aritm´etica das medidas de suas bases.
Prova:
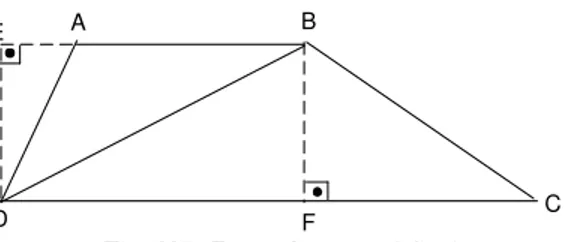
Seja ABCD um trap´ezio cujos lados paralelos s˜ao AB e DC. Pelo ponto B, tracemos a perpendicular `a reta ←→DC, obtendo o ponto F, e pelo pontoD, tracemos a perpendicular `a reta ←→AB, obtendo o pontoE, como na figura 236.
Curiosidade
A f´ormula que os babilˆonicos usavam para calcular a ´area de um quadril´atero convexo
ABCDqualquer era
m(AB) +m(CD)
2 .
m(BC) +m(AD)
2 .
Pode-se provar que essa f´ormula s´o ´e correta no caso em que o quadril´atero ´e um retˆangulo.
A B
C D
E
F
Fig. 236: Prova da proposi¸c˜ao 4.
O quadril´ateroEBF D´e um retˆangulo, e da´ı se conclui que os segmen-tosBF eDE s˜ao congruentes. Sua medida ´e a altura do trap´ezio.
Queremos provar que
AABCD =m(BF)
m(AB) +m(DC)
Para isso, tracemos a diagonal DB, dividindo o trap´ezio ABCD nos triˆangulos ABD e DCB (veja a figura 237).
A B
C D
E
F
Fig. 237: Prova da proposi¸c˜ao 4.
Usando a f´ormula da ´area do triˆangulo, que j´a deduzimos, e a proprie-dade P3 de ´areas, obtemos
AABCD =AABD+ADCB = 1
2m(AB)m(DE) + 1
2m(DC)m(BF).
Lembrando que os segmentos DE e BF s˜ao congruentes, conclu´ımos que
AABCD =m(BF)
m(AB) +m(DC)
2 .
Q.E.D.
Resumo
Nesta aula vocˆe aprendeu...
• O conceito de ´area.
Exerc´ıcios
1. Se dois triˆangulos ABC e DEF s˜ao semelhantes com raz˜ao de
seme-lhan¸ca igual a k, mostre que AABC
ADEF =k2.
2. Na figura 238, ABCD ´e um retˆangulo, EG//BC e HF//AB.
A B
C D
E
F
G H
P
Fig. 238: Exerc´ıcio 2.
(a) Mostre que os retˆangulos EBF P e HP GD tˆem a mesma ´area, qualquer que seja P ∈AC.
(b) Determine P para queEBF P tenha ´area m´axima.
3. Na figura 239, AF//EB eAEDCF = 20cm2.
A
B
C D
E
F
Fig. 239: Exerc´ıcio 3.
Determine AABCDE.
4. Na figura 240,ABCDeEF GHs˜ao quadrados,AM F N R = 1 eAQRP H = 4.
A B
C D
I
L
J
K
E F
G H
M
N
P
Q R
Fig. 240: Exerc´ıcio 4.
5. Determine a ´area de um losango, sabendo que o lado mede 5cme uma das diagonais mede 8cm.
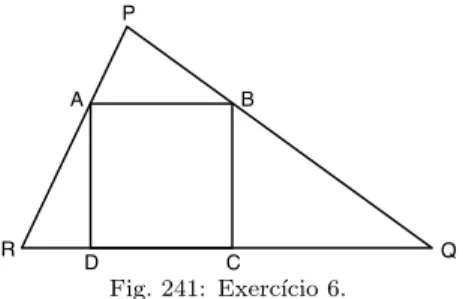
6. Na figura 241, ABCD ´e um quadrado, QC ≡ BC, m(RD) = 3cm,
AP QR = 75cm2 e a altura deP AB relativa ao ladoAB ´e igual a 4cm.
A B
C D
P
Q R
Fig. 241: Exerc´ıcio 6.
Determine a medida do lado do quadrado.
7. Na figura 242, ABC ´e um triˆangulo equil´atero de lado medindo 4cm, eDEGF ´e um quadrado.
A
B C
D E
F G
Fig. 242: Exerc´ıcio 7.
Determine a ´area deDEGF.
8. Prove que as medianas de um triˆangulo determinam nele seis triˆangulos de ´areas iguais.
9. Na figura 243, m(BD) = 1
4m(BC), m(AE) = 1
3m(AC), m(F C) = 1
6m(AC) e AABC = 20cm
2.
A
B D C E
F
10. Na figura 244, ABCD´e um paralelogramo de ´area igual a 10cm2 e M
´e o ponto m´edio deDC.
A B
C D
E
M
Fig. 244: Exerc´ıcio 10.
Determine AEM C.
11. ´E poss´ıvel determinar a ´area dos seguintes triˆangulos? Em caso afir-mativo, determine-as.
A
B
C 4
30o 45o
(a)
30o
5
6 (b) D
E F
Fig. 245: Exerc´ıcio 11.
12. (CESGRANRIO-1977) Cinco quadrados de lado ℓ formam a cruz da figura 246.
D
A
B
C
Fig. 246: Exerc´ıcio 12.
A ´area do quadril´atero ABCD´e:
13. (CESGRANRIO-1980) A base de um retˆangulo de ´areaS ´e aumentada de 20% e sua altura ´e diminu´ıda de 20%. A ´area do novo retˆangulo formado ´e:
(a) 1,04S (b) 1,02S (c) S (d) 0,98S (e) 0,96S
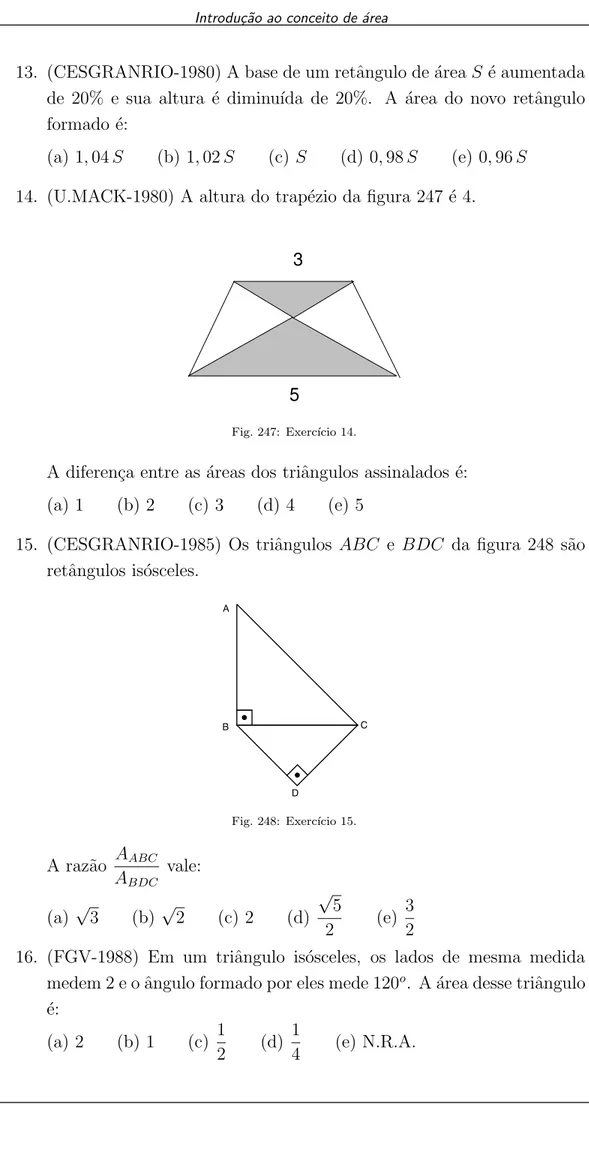
14. (U.MACK-1980) A altura do trap´ezio da figura 247 ´e 4.
3
5
Fig. 247: Exerc´ıcio 14.
A diferen¸ca entre as ´areas dos triˆangulos assinalados ´e:
(a) 1 (b) 2 (c) 3 (d) 4 (e) 5
15. (CESGRANRIO-1985) Os triˆangulos ABC e BDC da figura 248 s˜ao retˆangulos is´osceles.
A
B C
D
Fig. 248: Exerc´ıcio 15.
A raz˜ao AABC
ABDC vale:
(a) √3 (b) √2 (c) 2 (d) √
5
2 (e) 3 2
16. (FGV-1988) Em um triˆangulo is´osceles, os lados de mesma medida medem 2 e o ˆangulo formado por eles mede 120o. A ´area desse triˆangulo ´e:
(a) 2 (b) 1 (c) 1
2 (d) 1
17. (UFRJ, 2001) O retˆangulo ABCD est´a inscrito no retˆangulo W XY Z, como mostra a figura 249.
A B
C D
X
Y
Z W
θ
Fig. 249: Exerc´ıcio 17.
Sabendo quem(AB) = 2 em(AD) = 1, determine o ˆanguloθ para que a ´area de W XY Z seja a maior poss´ıvel.
18. (UFF, 1996) A figura 250 representa dois retˆangulosXY ZW eP QZX, de ´areas S1 eS2, respectivamente.
X Y
Z W
P
Q
Fig. 250: Exerc´ıcio 18.
Pode-se afirmar que S1
S2 ´e igual a:
(a) 0,6 (b) 0,7 (c) 0,8 (d) 0,9 (e) 1,0
19. (UFF, 1999) Na reprodu¸c˜ao de uma figura, a primeira c´opia obtida reduziu em 30% a ´area dessa figura. A seguir, essa c´opia foi reproduzida com amplia¸c˜ao de 40%. A ´area da figura obtida na segunda c´opia, comparada com a ´area da figura original, ´e:
(a) 98 % menor (b) 90 % maior (c) exatamente igual
20. (F´ormula de Her˜ao.) O objetivo deste exerc´ıcio ´e provar a f´ormula de Her˜ao, segundo a qual a ´area A de um triˆangulo de lados medidno
a, b e c´e dada por
A=pp(p−a)(p−b)(p−c)
onde p = (a+b+c)/2. Para isso, considere um triˆangulo ABC com
m(AB) = c,m(AC) = bem(BC) = a. Podemos supor quea´e o maior dos trˆes n´umeros a, b e c. Seja AD a altura de ABC relativa a BC e sejam n=m(BD),m=m(DC) eh =m(AD) (veja a figura 251).
C B A b c h m n D
Fig. 251: Exerc´ıcio 20.
Her˜ao de Alexandria.
10 d.C. - 75 d.C.
Her˜ao de Alexandria foi um importante pesquisador de Geometria e Mecˆanica. Um grande n´umero de trabalhos de Her˜ao tem sobrevivido at´e hoje, embora a autoria de alguns deles seja disputada. Os trabalhos est˜ao relacionados com v´arias categorias: trabalhos t´ecnicos, trabalhos sobre Mecˆanica e sobre Matem´atica. Dentre seus trabalhos podemos destacar o chamadoM´etrica, dividido
em trˆes volumes. No volume I, Her˜ao calcula a ´area do triˆangulo usando as medidas dos lados e do
semi-per´ımetro. Consulte:
http://www-groups.dcs. st-and.ac.uk/~history/ Mathematicians/Heron.html
Use o Teorema de Pit´agoras nos triˆangulos retˆangulos ABD e ACD
para provar que
m = b
2
−c2+a2
2a
Use novamente o Teorema de Pit´agoras para obter
h2 = [(a+b) 2
−c2][c2
−(a−b)2]
4a2
segue que
A2 = 1 4a
2
h2 = [(a+b)
2−c2][c2−(a−b)2]
16
= a+b+c
2 .
a+b−c
2 .
a−b+c
2 .
−a+b+c
2
21. Determine as alturas de um triˆangulo de lados medindo 3cm, 5cm e 7cm.
22. Prove que o raio do c´ırculo inscrito em um triˆangulo de lados medidno
a,b ec´e dado por
r= s
(p−a)(p−b)(p−c)
p onde p=
a+b+c
2 .
Sugest˜ao: Use o incentro do triˆangulo para divid´ı-lo em trˆes triˆangulos menores. Cada um desses triˆangulos tem altura r. Use a f´ormula de Her˜ao.
23. Prove que o raio do c´ırculo circunscrito a um triˆangulo de lados medindo
a,b ec´e dado por
R = abc
4pp(p−a)(p−b)(p−c)
Sugest˜ao: Seja ABC um triˆangulo com m(BC) = a, m(AB) = c e
m(AC) =b. Seja AD a altura relativa ao lado BC e seja Γ o c´ırculo circunscrito a ABC. Considere o triˆangulo ABE, onde AE ´e diˆametro de Γ (veja figura 252).
C
B A
E D
Fig. 252: Exerc´ıcio 23.
Use a semelhan¸ca entre os triˆangulos ADC e ABE para obter
R = bc